Nucleation of shear bands in amorphous alloys

Significance

A shear band is a region of highly localized plastic flow that develops during loading in both crystalline and amorphous materials. Shear bands directly determine the ductility of an amorphous phase, but relatively little is known about their nucleation. We use nanoindentation to probe shear band nucleation by measuring the first pop-in event during loading which is associated with shear band formation. We analyze a large number of independent measurements on four different metallic glasses and reveal a bimodal distribution of nucleation events that operate at different stress levels. The discovery of multiple shear band nucleation sites challenges the current view of a single type of site and offers opportunities for controlling the ductility of amorphous alloys.

Abstract

The initiation and propagation of shear bands is an important mode of localized inhomogeneous deformation that occurs in a wide range of materials. In metallic glasses, shear band development is considered to center on a structural heterogeneity, a shear transformation zone that evolves into a rapidly propagating shear band under a shear stress above a threshold. Deformation by shear bands is a nucleation-controlled process, but the initiation process is unclear. Here we use nanoindentation to probe shear band nucleation during loading by measuring the first pop-in event in the load–depth curve which is demonstrated to be associated with shear band formation. We analyze a large number of independent measurements on four different bulk metallic glasses (BMGs) alloys and reveal the operation of a bimodal distribution of the first pop-in loads that are associated with different shear band nucleation sites that operate at different stress levels below the glass transition temperature, T_g. The nucleation kinetics, the nucleation barriers, and the density for each site type have been determined. The discovery of multiple shear band nucleation sites challenges the current view of nucleation at a single type of site and offers opportunities for controlling the ductility of BMG alloys.

Deformation by shear bands occurs in both crystalline and amorphous phases over a wide range of size scales. In geological materials with a granular nature such as sand (1, 2) or within rocks, shear bands are of macroscopic size (3); in polymers and crystalline metals, shear bands are several micrometers in size; in metallic glasses (MGs), shear bands are of the order of 10–20 nm in thickness (4). The onset of shear bands in metallic glasses represents initial plastic yielding and induces a highly localized plastic flow that limits ductility and is responsible for strain softening (4, 5). Because shear bands directly determine the capability of an amorphous phase to sustain plastic flow and exhibit ductile behavior, there have been numerous studies on the propagation of shear bands to promote shear band branching and additional nucleation to achieve useful ductility (6–9). On a microscopic scale, the initiation of shear bands in MGs is considered to be controlled by the activation of a shear transformation zone (STZ) (10, 11) that represents a localized atomic arrangement. The STZs are activated by a two-stage process starting with a flow-induced dilatation that broadens homogeneously in the initial stage, but subsequently narrows into a shear band autocatalytically at the expense of shear flow in the surrounding material (10, 12). The localization of plastic flow would become predominant at low temperatures because the diffusive atomic rearrangements are too slow to disperse the dilatation effect quickly enough. Clearly, the nucleation of shear bands is of critical importance in the deformation behavior, but the detailed examination of the nucleation kinetics behavior has received only limited study (5, 13, 14).

At the same time, there have been numerous simulation studies and modeling analyses on the atomic arrangements in metallic glasses that have identified specific cluster motifs in an amorphous phase that can affect deformation (15, 16). The earliest comprehensive study by Argon was based upon detailed observations of the deformation of an amorphous bubble raft model binary system (i.e., two bubble sizes) (10, 17). During dynamic deformation of the system, two distinct, independent shear transformation configurations were identified as concentrated and diffuse with different activation barriers. More recent work on colloidal glass systems with one particle size also revealed the details of the deformation dynamics, but only one type of transformation site was observed to be active (18). Besides the analog simulations, there have been a number of computational approaches to simulate glass structure and deformation response (19, 20). Whereas those studies have offered insight into the details of the atom rearrangement under an imposed shear stress for specific interatomic potentials, the system sizes are small and the strain rates are exceedingly high so that the direct application of the findings to actual experimental conditions is somewhat unclear. Moreover, recent experimental studies have revealed the presence of nanoscale spatial heterogeneities in amorphous alloys that have not been considered in the simulations, but may affect deformation (21–26).

Results

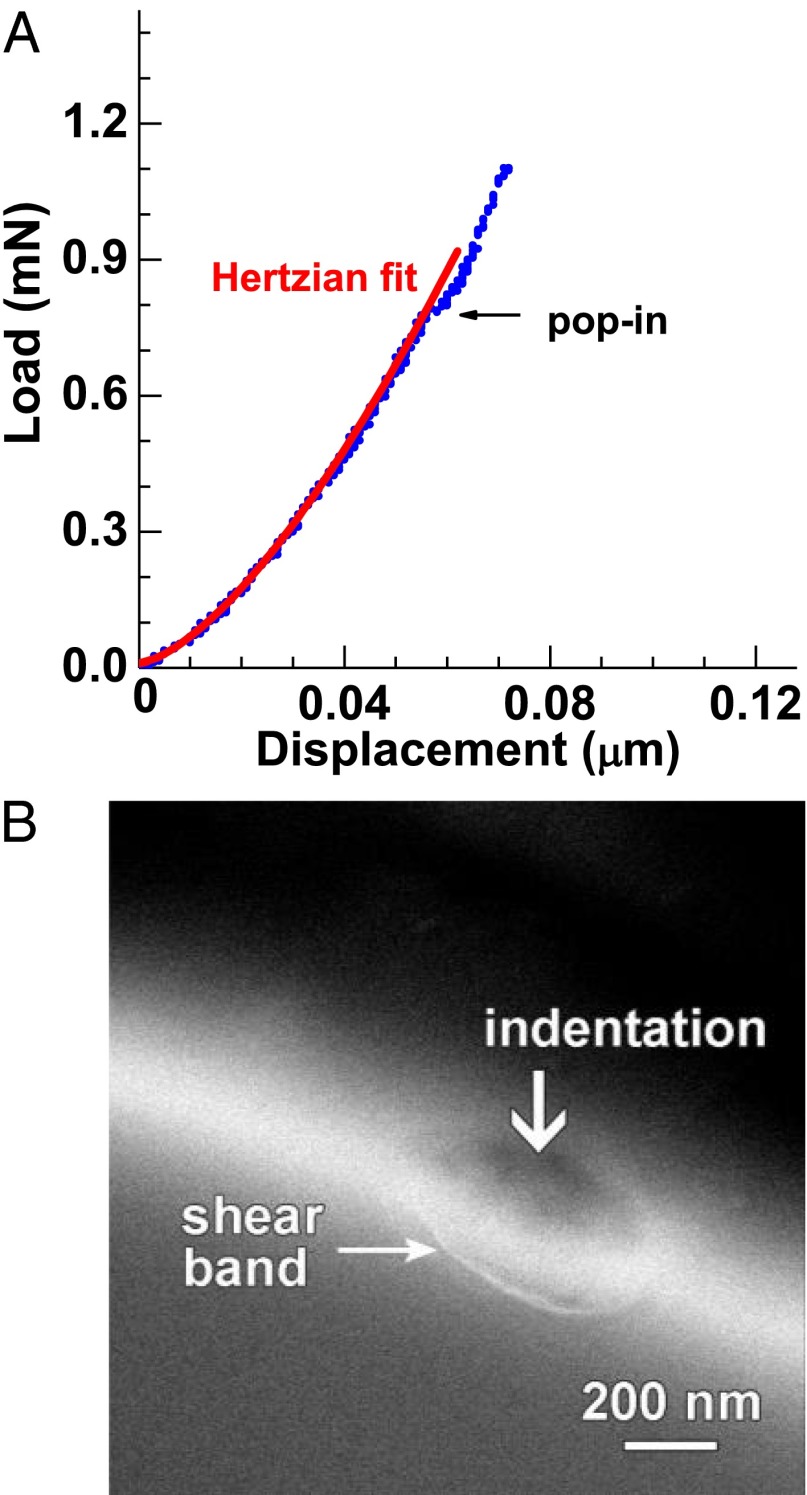
Because nucleation is a stochastic process, a proper study of shear band nucleation requires a statistically significant number of observations for analysis. During the mechanical testing of macroscopic bulk metallic glass (BMG) samples by conventional compression or tension methods, yielding below T_g occurs by shear band initiation and propagation that can be strongly influenced by loading conditions (such as sample alignment and machine stiffness) and material flaws (such as pores and inclusions) that mask the intrinsic sample behavior. Instead, an effective strategy to approach shear band nucleation is based upon instrumented nanoindentation measurements. Due to the small volume probed during a nanoindentation measurement, the method offers the important attribute to avoid the spurious influence of sample synthesis defects and uncertain loading conditions. During nanoindentation, the material response is initially elastic following a Hertzian response in a load versus displacement test (3) (SI Text). The termination of the elastic response is marked by a pop-in event as shown in Fig. 1A where there is a rapid increase in displacement depth h at a constant load P. To establish the relation between the first pop-in and shear band nucleation, a rectangular slab was machined in a Zr₆₀Cu₂₀Fe₁₀Al₁₀ (at. %) BMG and subjected to nanoindentation. As noted in Fig. 1 A and B, there is a correspondence between the first pop-in event and the initiation of a shear band. Thus, the first pop-in event is associated with the threshold load (or stress) for shear band nucleation in the stressed volume under the indenter. Due to the rapid propagation of a shear band (27, 28), the pop-in event is a nucleation-controlled process. Moreover, in a given amorphous alloy and for identical loading conditions, the initial pop-in P and h values will not be identical in multiple independent (i.e., well-separated) indentations in undeformed glass, but will exhibit a distribution or scatter that represents the nucleation statistics.

Fig. 1.

Representative nanoindentation curve with single pop-in and corresponding sample image with a single shear band for a Zr₆₀Cu₂₀Fe₁₀Al₁₀ BMG. (A) Nanoindentation trace with one pop-in, in the form of a load versus depth plot. The blue dots are the experimental data with a loading rate of 0.07 mN/s (spherical indenter with 2.5-μm radius), and the red curve is the fitting result according to Hertzian elastic contact theory. (B) SEM image of the indentation. A single shear band can be seen clearly beneath the indentation.

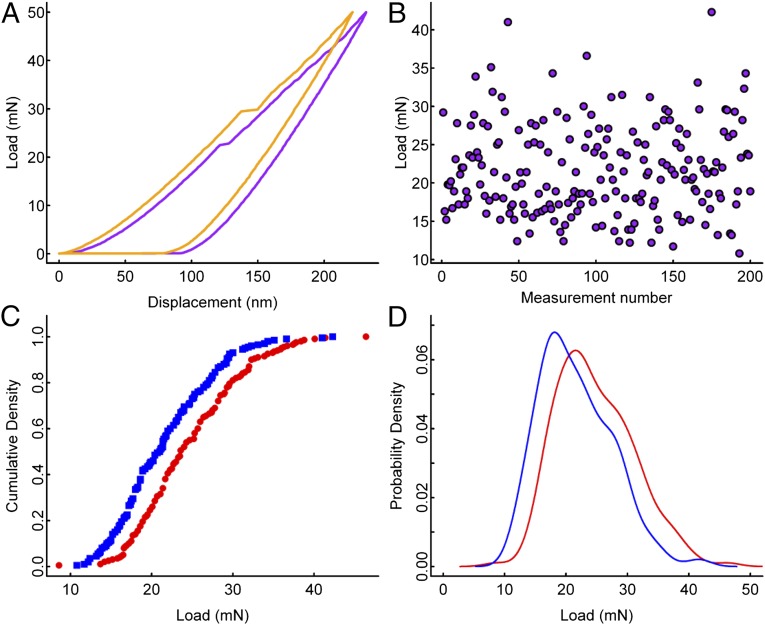
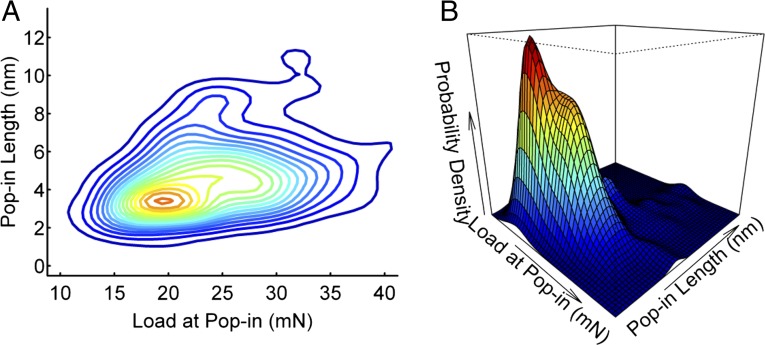
Examination of first pop-in data from four different BMG alloys (Tables S1 and S2 and Figs. S1–S3) based upon 100–200 individual nanoindentation measurements in each sample demonstrates a multimodal distribution character. Fig. 2 presents the load versus pop-in data as a cumulative distribution and a probability distribution for an Fe-based BMG alloy in the as-cast and annealed condition (Fig. S4) where a distinct shoulder is present on the high load side of the distribution and the entire distribution shifts to higher loads after relaxation annealing. The smooth translation of the distribution after annealing which involved repolishing the sample as well as a finite-element analysis of stresses generated during nanoindentation of a roughened surface indicate that the shear bands were not initiated at the surface (SI Text and Fig. S5). The nanoindentation results for the Zr-, Cu-, and Au-based BMG alloys show a similar character (SI Text). Analysis of the data, in the order they were taken, shows no indication of systematic drift over the course of the indentations (i.e., the data are uncorrelated; Fig. 2B). Whereas there is certainly a threshold load of elastic deformation that must be crossed for shear band formation and propagation, the variability in the threshold load indicates that the process is in fact a stochastic one. In addition we have plotted, in Fig. 3 A and B, 2D and 3D density plots of the load at pop-in against the length of the pop-in. The probability density reveals the development of two maxima that further supports the operation of a bimodal distribution of initiation sites (Fig. S6).

Fig. 2.

Statistical analysis of the first pop-ins. (A) Two load-displacement traces from nanoindentation tests demonstrating the range of pop-in values under the same conditions (displacement of the solid curve has been offset by 10 nm for ease of viewing). (B) The observed data show no systematic drift over the course of experimentation. (C) Cumulative density and (D) probability density for as-cast (blue) and relaxed (red) Fe-BMG samples.

Fig. 3.

Bimodal distribution of the first pop-ins. Bivariate probability density plots shown as (A) 2D contours and (B) 3D wiremesh as a function of load at pop-in and pop-in length. There is a distinct peak as a shoulder on the high load side of the data. In A the main peak can be observed at ∼19 mN and 3 nm. A secondary peak can also be observed at ∼27 mN and 4 nm. From these figures it is seen that the natural trend for the length of pop-in to increase with the load means that when projected onto the load axis, part of the bimodal nature that is more obvious in the 2D plot is obscured.

Discussion

To extract the nucleation rate from the observed first pop-in distributions, we evaluate a kernel density for the probability density function f(t) in terms of time t where the time is related to load at a constant loading rate. The smoothed f(t) is then integrated to obtain the cumulative distribution function, F(t). The hazard rate λ(t) represents the probability that a sample which had survived up until time t will have an event during the next Δt amount of time (29) and is defined as λ(t) = f/(1−F). The hazard function is related to the nucleation rate J by J = λ/V_e, where V_e is the amount of volume at a given load which satisfies the minimum criteria for a pop-in event that is evaluated as 0.01V_d, the volume deformed by the indenter (SI Text). Following the standard practice (6, 10, 11, 17), J is related to an activation barrier by

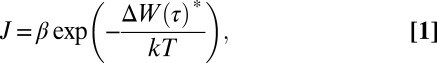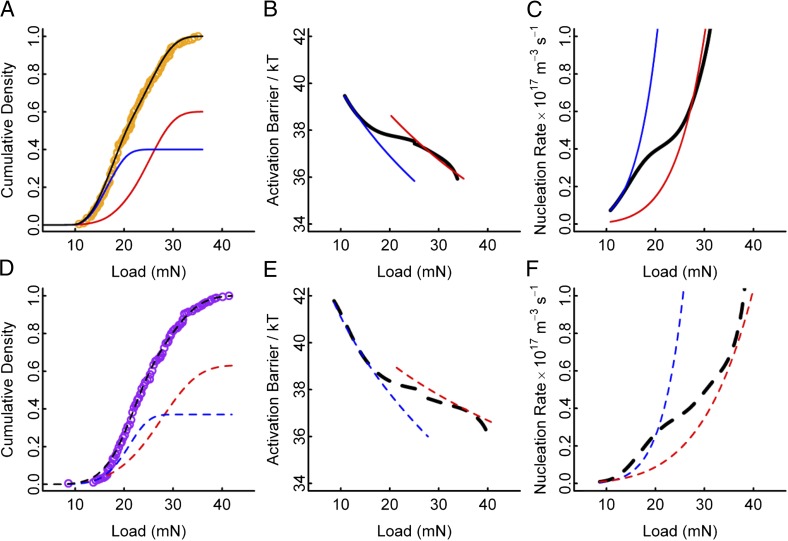
where ΔW(τ)* is the activation barrier for shear band nucleation that is a function of the operating shear stress τ, and β is the frequency per unit volume which is the product of an attempt frequency taken as 10¹³ s⁻¹ and the number density of sites. Based upon the character of the bimodal distribution of pop-in events we can derive an independent evaluation of the nucleation site density, m (SI Text). For example, for the as-cast Fe-based BMG shown in Fig. 2 and considering a Poisson distribution of nucleation sites within the volume, we obtain m_L = 1 × 10²⁰ m⁻³ for the low load peak and m_H = 9 × 10¹⁹ m⁻³ for the high load peak. From the site density evaluation we determine the activation barriers and nucleation rates as a function of load as shown in Fig. 4 and Table S2. From these results it is apparent that to identify shear band nucleation characteristics such as the bimodal distribution, it is necessary to obtain a significant dataset and analyze the full range of measurement. It is noteworthy that the site density of about 10²⁰ m⁻³ derived from our nanoindentation experiments is consistent with the transition volume from shear band deformation to homogeneous flow in pillar compression tests reported by Volkert et al. (30) and discussed by others (31–33). As the volume decreases, the chance of having a shear band nucleation site decreases so that below the transition volume the specimen is free of nucleation sites and homogeneous flow is the only available option for deformation.

Fig. 4.

Activation energy barrier and nucleation rates of the first pop-ins in the Fe-BMG samples. (A–C) For the as-cast sample. (D–F) For the annealed sample. (A and D) The experimental cumulative density function is displayed together with the separate calculated contributions from each of the two nucleation sites. There is a close agreement between the fitted cumulative distribution and the measurements over the entire range including the endpoints. (B and E) The trend of activation barrier and the resultant nucleation rates as a function of load are separated and indicate the existence of two nucleation sites with an overlapping load range of operation. In the low load range where the nucleation barrier ranges from 42kT to 36kT, the nucleation rate (C and F) reaches 0.4 × 10¹⁷ m⁻³⋅s⁻¹ when a transition occurs to operation of the high load site.

In the analysis of shear band development, the models proposed by Argon (10) and Johnson and Samwer (34) relate the activation barrier for heterogeneous flow to the applied shear stress, τ. Often, in the analysis of the onset of plasticity and the deformation trajectory the path of maximum τ is considered to be controlling (35). However, Packard and Schuh (36) have demonstrated that for amorphous alloys the appropriate path is one in which τ is sufficient for both the initiation and propagation of shear bands. The operative τ along this path is related to the mean contact pressure P_m by τ ∼ 0.07P_m, which is determined from Hertzian mechanics (SI Text). This allows for the scaling τ = CP^1/3 with C a constant.

The Johnson and Samwer model considers the cooperative shear motion STZs. Yielding occurs when the applied τ causes a critical density of minimum barrier STZs to become unstable. The model expresses W(τ)*/kT as

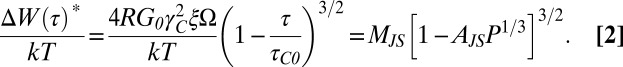This model has similarities to the concentrated shear mechanism of Argon (10). In the Argon model, the concentrated shear mechanism is expected to operate at low temperature, whereas at high temperature (≥0.67T_g) the diffuse shear mechanism should control homogeneous flow. For the diffuse shear transformation mechanism, the activation barrier is higher than that for the concentrated shear mechanism and is given by

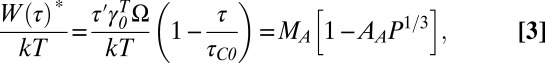where the parameters in Eqs. 2 and 3 are defined in refs. 34 and 10, respectively. To compare the trends in Fig. 4 to the model predictions, the stress-independent terms M_A, M_JS, A_A, and A_JS are treated as constant. The Johnson and Samwer model-predicted trends of ΔW(τ)*/kT with load are indicated in Fig. 4 B and E and provide a good agreement with the observed behavior in the low load range. The analysis results for the four BMG alloys (SI Text) reveal a similar agreement for the room temperature measurements that represent a range below the glass transition temperature T_g from 0.37 to 0.74T_g. The experimental data in the high load range do not extend over a wide enough range to determine clearly the stress dependence; however, the trend is consistent with the Argon diffuse shear model. Moreover, the values of ΔW(τ)* that were determined at 300 K are comparable to the reported energy density results (37–39) and the activation energy ranges (12, 38, 40–42) for shear band activity reported in different amorphous alloys and reveal the important role of the applied stress in lowering the barrier magnitude.

Conclusion

The current work demonstrates clearly that the onset of heterogeneous deformation by shear band formation is itself a heterogeneous nucleation process initiating on defect sites with a bimodal distribution that act to catalyze shear band nucleation at different load levels. This basic behavior has not been revealed in the computational simulations of amorphous alloy deformation where spatial heterogeneities were not included in the analysis (19, 20, 43). The specific defects have not been identified here, but it seems likely that they are local nanoscale heterogeneities that promote STZ activity. Indeed, some estimates of the relative STZ size and equivalent number of atoms have been calculated, but the range of values is broad enough from 10 to hundreds of atoms (8, 44, 45) that it could represent more than one type; a recent report indicates that a fine structure exists within this range (45). Further evaluation of the models is necessary, but the key finding of a bimodal distribution of nucleation sites may provide guidance to promote nucleation to enhance shear band activity and ductile behavior.

Materials and Methods

Fabrication of BMGs.

The ingots of the alloys were prepared by arc-melting elemental mixtures (purity >99.9 wt. %) in nominal compositions under a Ti-gettered argon atmosphere. The alloys were remelted four times to ensure homogeneity. The ingots were then remelted in a quartz tube by induction under an argon protective atmosphere and subsequently injected into a copper mold to obtain BMG rods with diameters of 3∼8 mm.

Characterization of BMGs.

The amorphous nature of the alloys was characterized by a differential scanning calorimeter (Perkin-Elmer DSC 8) and by X-ray diffraction (Bruker D8 Advance, Cu Kα).

Sample Preparation for Nanoindentation.

The samples were progressively polished with diamond abrasive films (South Bay Technology, Inc.) of 30, 15, 6, 3, 1, 0.5, and 0.3 μm to a mirror finish. Continuous water flow was applied during polishing to prevent any temperature rise due to friction.

Nanoindentation Measurement.

Nanoindentation experiments were conducted with a UMIS 2000 Ultra Micro-Indentation System (Commonwealth Scientific and Industrial Research Organisation) nanoindenter equipped with a spherical tip. The effective radius of the tip (about 5 μm) was calibrated by measuring the elastic modulus of fused silica. After allowing some minutes for the instrument to reach a stable temperature, the head was lowered and locked tightly. The tests were conducted in a load-control mode at a constant loading rate of 20 μN/s. The measurements were programmed by selecting the indenting parameters: maximum force (50 mN), number of increments (200), dwell time (0), number of indents (100), linear spacing between indents (40 μm), and direction of the indents. With the iron-based sample, after the first set of nanoindentations was completed, the sample was heated up to 540 °C, which is just above T_g, and cooled for structural relaxation but no crystallization. The differential scanning calorimeter trace in Fig. S4 reveals that after this annealing treatment the T_g value did decrease, indicating some relaxation of the sample. The sample was then repolished for further examination of the annealed sample. To avoid influence of the previous indents, a thick layer of material was removed from the surface with diamond abrasive film of 30 μm. The surface was then polished to mirror finish again.

Finite-Element Stress Analysis.

To assess the influence of surface roughness, ANSYS, a commercial finite-element analysis software, was used to model the 3D nanoindentation. The specimen, assumed to be a cylinder with diameter of 20 μm and height of 10 μm, was modeled as an elastic solid for a smooth surface and as an elastoplastic solid with isotropic plastic hardening for a rough surface with 100-nm periodic undulations roughness, which is on the scale of the diamond particles used for sample polishing. For a virtual specimen material, the elastic modulus and Poisson’s ratio are assumed to be 100 GPa and 0.33, respectively.

Evaluation of Nucleation Rates and Site Density.

The nucleation sites were assumed to follow Poisson distribution. The Hazard function (29) in statistical analysis and a classical nucleation model were applied in analyzing the nucleation rate and site density.