In vivo X-ray cine-tomography for tracking morphological dynamics

Significance

X-ray microtomography is a well-established tool to study the three-dimensional morphology of static biological samples. To capture motion in living specimen in real time, movies of X-ray projections are frequently used. However, the resulting loss of information about the third spatial dimension has limited the applicability of such acquisition protocols. Now, by combining ultrafast X-ray microtomography and sophisticated motion analysis, we developed X-ray cine-tomography as a tool to visualize the internal dynamics of nontranslucent millimeter-sized samples in three-dimensional space. We demonstrate the technique by analyzing the fast-moving screw-and-nut–type hip joint inside a living weevil. The method may be applied to a wide range of samples and processes across materials and life sciences.

Abstract

Scientific cinematography using ultrafast optical imaging is a common tool to study motion. In opaque organisms or structures, X-ray radiography captures sequences of 2D projections to visualize morphological dynamics, but for many applications full four-dimensional (4D) spatiotemporal information is highly desirable. We introduce in vivo X-ray cine-tomography as a 4D imaging technique developed to study real-time dynamics in small living organisms with micrometer spatial resolution and subsecond time resolution. The method enables insights into the physiology of small animals by tracking the 4D morphological dynamics of minute anatomical features as demonstrated in this work by the analysis of fast-moving screw-and-nut–type weevil hip joints. The presented method can be applied to a broad range of biological specimens and biotechnological processes.

The best method to study morphological changes of anatomic features and physiological processes is to observe their dynamics in 4D, that is, in real time and in 3D space. To achieve this we have developed in vivo X-ray cine-tomography to gain access to morphological dynamics with unrivaled 4D spatiotemporal resolution. This opens the way to a wide range of hitherto inaccessible, systematic investigations of small animals and biological internal processes such as breathing, circulation, digestion (1), reproduction, and locomotion (2).

At the micrometer resolution range, state-of-the-art optical imaging techniques can achieve high magnifications to visualize tissues and even individual cells for 4D studies. These methods however are confined to transparent or fluorescent objects, or are limited either by low penetration depth <1 mm or poor time resolution (3). For optically opaque living organisms X-ray imaging methods are highly appropriate due to the penetrating ability of the radiation. Modern synchrotron radiation facilities provide brilliant and partially coherent radiation suitable for high-resolution volume imaging methods such as X-ray computed microtomography (SR-µCT). For static specimens SR-µCT has proven to be a powerful tool to study small animal morphology in 3D (4–6). The benefits of various physical contrast mechanisms, high spatial resolution, and short measuring times, as well as enormous sample throughput compared with laboratory X-ray setups, have led to its widespread use in life sciences.

Real-time in vivo X-ray imaging with micrometer spatial resolution was realized so far by recording time sequences of 2D projection radiographs of different organisms (1, 6, 7), providing time information about functional dynamics but losing any information about the third spatial dimension.

Recently, 4D in vivo X-ray experiments have been performed to study cell migration in frog embryos (8, 9) using tomographic sequences of a few seconds exposure time per tomogram interrupted by longer nonexposure time slots. In this way the authors followed relatively slow dynamics and morphological changes during embryonic development with 2-µm resolution over total time intervals of several hours. The fastest 4D time series yet reported were realized with a temporal resolution of 0.5 s and spatial resolution of 25 µm (10), applied to a living caterpillar used as test specimen for imaging, but without any analysis of dynamics.

In this paper, we demonstrate the quantitative 4D investigation of morphological dynamics by in vivo X-ray 4D cine-tomography, introduced here as the combination of ultrafast SR-µCT and motion analysis procedures. Using this approach allows us to investigate previously inaccessible 3D morphological dynamics in small animals, presently with feature sizes in the micrometer range and with temporal resolution down to a few tens of milliseconds. In the past, ultrafast in vivo imaging was hardly possible for such applications, due to the strongly competing requirements for simultaneous high contrast, high signal-to-noise ratio (SNR), and concurrent low radiation dose, as well as the need for simultaneous high spatial resolution and maximum temporal resolution.

In the following we describe how in vivo X-ray 4D cine-tomography meets the above challenges by optimizing image contrast, SNR, and spatial and temporal resolution in the ultrafast SR-µCT system and by establishing a dedicated data analysis pipeline, all within a unified framework (Fig. S1). We demonstrate the potential of the technique by investigating morphological dynamics in fast-moving weevils, focusing here on the exoskeletal joints.

Results and Discussion

The huge data flow generated by ultrafast SR-µCT together with the tracking of 3D structures requires automated data processing and analysis, image reconstruction, and motion analysis procedures. Because 4D cine-tomography focuses on the study of morphological dynamics, the most critical elements of the SR-µCT system and the data analysis pipeline need to be customizable to the actual biological application. This feature enables experimental conditions to match both the requirements for motion analysis and acceptable X-ray dose (Fig. S1). In our ultrafast SR-µCT system we optimize for shortest exposure times by band-pass filtering a white beam while keeping low noise for all radiographs (Fig. 1C). In this way we exploit a large fraction of the hard X-ray photon spectrum of the synchrotron radiation beam emitted by the bending magnet of the 2.5-GeV synchrotron storage ring ANKA to achieve a high flux, while simultaneously reducing the radiation dose from the especially dose-intensive lower energy part of the spectrum.

Fig. 1.

In vivo X-ray 4D cine-tomography experiment. (A) Photograph of S. granarius, dorsal view. (B) Experimental setup for ultrafast X-ray microtomography showing bending magnet (1), rotation stage (2), fixed specimen (3), and detector system (4). (C) Radiographic projection. (D) Three-dimensional rendering of the reconstructed volume with thorax cut open and revealing hip joints (arrows). (E) In vivo cine-tomographic sequence of moving weevil, overview scan.

SNR is increased by integrating newly developed scintillators with improved quantum efficiency [due to their high stopping power and fluorescence yield (11)] into the setup, resulting in an ultrafast, high-resolution, and X-ray–efficient detector configuration. X-ray images are converted into latent optical images, these being subsequently magnified by a highly light-transmissive optical lens system and finally read out by a high-speed active pixel sensor camera detecting up to 100,000 frames per s. Scintillator screens of various thicknesses are well adapted (Materials and Methods) to the respective pixel sizes, and their energy-dependent photon detection efficiency counteracts beam hardening effects. Further, the X-ray camera system has been designed to withstand the intense white synchrotron beam without degradation of image quality even during extended observation times (Materials and Methods). Simultaneous image acquisition and continuous rotation provides dead-time–free measurements.

In addition to attenuation due to absorption, we exploit the partial spatial coherence properties of the X-ray wave field to improve the intrinsic physical contrast by in-line propagation-based phase contrast (10). This allows the projection images to sample regions of nonzero Laplacian (second derivatives) of the real part of the refractive index (which for X-rays is related to the specimen electron density distribution and is especially sensitive to soft biological tissues).

In our data analysis pipeline, we combine noise reduction filtering and 3D reconstruction using overlapping projection data, subsequent motion estimation, 3D tracking, and motion analysis. We capture displacements of morphological structures by a robust 3D optical flow method based on variational techniques (Materials and Methods). For this method, it is crucial that the structural information represented by well-resolved spatial gradients of image brightness is maximized. These gradients can be effectively amplified by in-line phase contrast measured at short propagation distances, which highlights sharp interfaces due to so-called “edge enhancement” (12). At larger distances, edge enhancement might even increase but also, depending on the actual coherence conditions, be accompanied by formation of blurred Fresnel diffraction patterns. In principle, and depending on the quality of data (SNR, blurring of the Fresnel diffraction patterns, etc.) and on the particular constraints of the respective phase contrast algorithms, even phase retrieval might be applicable (13–15).

For 3D tomographic imaging of static samples, quantitative phase retrieval is usually highly valuable. However, when tracking morphological structures over time, it may not provide optimal data in every case, especially if SNR becomes critical. In the latter case the enhanced interface contrast between moving internal features within the raw images, and its preservation over the entire data-processing chain facilitates reliable and accurate motion estimation. The enhanced contrast is conserved via the application of edge-preserving noise reduction algorithms and filtered back-projection with appropriate filtering (Fig. S2). After the computation of the displacement field we automatically distribute landmarks, which are subsequently tracked by using the computed flow field. Here, only reliable tracks are selected based on a forward–backward cross-check (Materials and Methods). The tracking results allow analysis of the complex kinematics of individual morphological structures.

The optimization of the critical imaging components and the introduction of automated optical flow algorithms into this framework (Fig. S1) permit significantly higher spatiotemporal resolution (50 ms per tomogram at 6.6-µm voxel size and 130 ms at 1.2-µm voxel size, respectively) compared with the literature (6, 10, 11), while at the same time assuring 3D image sequences of suitable quality for quantitative 4D motion studies within adequate observation times.

We demonstrate the potential of X-ray 4D cine-tomography with the example of real-time investigation inside small, living arthropods. These organisms constitute more than 80% of all animal species (16) and include insects, crustaceans, and arachnids. Presently there is remarkably little known about their functional morphology, and biologists have a major interest in elucidating their morphological diversity and related physiology. Our technique now enables in vivo 4D motion studies to understand their functionality.

In a recent paper, 3D X-ray microtomography was applied to dried Trigonopterus weevils, thereby discovering a biological screw-and-nut system (17), which serves as a hip joint. This peculiar type of joint may constitute a basic characteristic of the weevil family. We have recorded 4D time lapses of the complete small animal (Fig. 1E and Movie S1). In the following we will restrict our evaluation to the exoskeletal joints, which are also of considerable interest in biomimetic research (18). In particular, we report the example of a hip joint of the wheat weevil Sitophilus granarius (Fig. 1A and Movie S2), which is an important pest to grains (19).

Tracking the movement of the left hind leg hip joint (Fig. 2 A–C), we extract 4D spatiotemporal information about its complex kinematics allowing us to visualize its functionality (Fig. 2 G–I and Movies S3 and S4). We can further improve the morphological data by correlating the images with data taken from the same specimen postmortem (with increased exposure time) (Fig. 2D).

Fig. 2.

Morphological dynamics and kinematics analysis of the moving screw joint, based on high-resolution scan. (A–C) Time-lapse sequence of tomographic slices, corresponding to 0, 400, and 800 ms. (D) Tomographic slice of postmortem scan with increased exposure time. (E) Manual labeling of coxa (green) and trochanter (yellow). (F) Three-dimensional model of the screw joint based on manual labeling. (G) Three-dimensional motion field computed from 0 and 130 ms. (H) In vivo morphological dynamics of the screw joint based on the 3D model (F) and automated motion estimation (G). (I) Kinematics analysis: global displacement of the whole screw-and-nut system with respect to the main body (green plot); sudden translation of the trochanter inside the coxa (blue plot); linear rotational movement of the trochanter (yellow plot).

Weevil legs possess three major articulations: the coxa-trochanteral (hip joint), the trochantero-femoral, and the femoro-tibial (“knee”) joint, the latter two being hinge joints. The combined movement of these three joints, in conjunction with the articulation between thorax and coxa, facilitates walking and climbing. The hip joints are composed of two parts: coxa (hip) and trochanter. Whereas the circular apical openings of the coxae mark the start of well-defined inner threads, the trochanters possess conspicuous external spiral threads fitting into the coxae. Because of the great dorso-ventral mobility facilitated by the screw joints, weevil legs are particularly well-suited for climbing. The movements of the specimen during the overview scan (Materials and Methods) closely corresponded to its natural motion observed with a stereo microscope before the tomographic scan.

We manually label coxa and trochanter (Fig. 2 E and F) and reconstruct the actual morphological dynamics of the system (Fig. 2H). We evaluate the global displacement of the whole screw-and-nut system with respect to the main body by tracking the geometrical center of the coxa (Fig. 2I).

Furthermore, we separate the angular velocities, in this case of the trochanter, from its translational motion deep inside the coxa. In the scan shown, the trochanter rotated within 0.8 s around 92.9° clockwise (from the viewpoint of an outside observer). The rotation was combined with an inward translation along the axis of rotation of 94.4 µm (Fig. 2I). The relation of rotary and translatory movements is found to be nonlinear, which is possible due to the comparatively wide opening observed between the trochanteral and coxal thread (Fig. 2 G–I and Movie S4). This type of motion would be impossible for the narrow hip joints described for Trigonopterus oblongus (17), as the defensive strategy of the genus (20) relies on more narrow type of screw joints. Thus, our findings also provide evidence for the functional variability of the constriction of leg joints in weevils, which may be closely related to their ecology.

Conclusions

By using an ultrafast SR-µCT system and a data analysis pipeline optimized to particular constraints of motion analysis, the fastest reported computed tomography sequences for sub-10-µm spatial resolution have been realized. By reconstructing the complete 4D spatiotemporal kinematics of a joint of a wheat weevil, X-ray 4D cine-tomography has been proven to be a promising tool to study morphological dynamics in millimeter-sized animals. The presented method can be easily applied to many kinds of biological specimens and processes, and may also be used to investigate structure evolution in biomaterials (21) and biotechnological processes (see Movie S5 for the example of a biological combustion process).

Materials and Methods

In the following we outline the cine-tomographic experiment optimized for our particular application––a fast-moving weevil (section 1). Fig. S1 illustrates a general decision diagram and our workflow to implement 4D X-ray cine-tomography. Depending on the required spatiotemporal dynamics in the sample we condition the X-ray beam and the detector characteristics to provide sufficient contrast and SNR (section 2). In contrast with static 3D imaging, for cine-tomography, the 2D input (section 3) for 3D reconstruction (section 4) needs to be optimized based on the requirements of the 4D motion estimation (section 5) and further analyses (sections 6–9).

1. Sample Preparation.

We used a laboratory strain of the wheat weevil S. granarius. The living weevils were glued on their backs onto paper stubs, which were fixed on goniometer heads. Before starting the tomographic scan, the hip joint movements were inspected with a stereo microscope. The metacoxal joint was aligned to coincide with the axis of rotation.

2. Experimental Setup and Data Acquisition Protocol.

Data acquisition was performed at the TOPO-TOMO beamline of the ANKA synchrotron radiation facility at Karlsruhe Institute of Technology (22). A white X-ray beam emitted by a 1.5-T bending magnet source of the 2.5-GeV storage ring was filtered by 0.2-mm aluminum, resulting in a photon energy window of 9.6–24 keV with the maximum flux density located at 14.5 keV.

For high-speed tomography an air-bearing rotary stage (ABRT-150;Aerotech) was used. A Micos UPL160 linear stage was used to move the sample into the beam shortly after reference radiographs were acquired. The total motion error at the position of the sample was less than 300 nm.

For high spatial resolution, the indirectly converting X-ray area detector system was optimized to achieve an effective pixel size of 1.2 µm, with a field of view of 2.464 mm. This combines a 12-µm-thick terbium-doped lutetium orthosilicate scintillator deposited on 170-µm ytterbium orthosilicate substrate, an infinity-corrected Mitutoyo LWD 10× objective with a numerical aperture of 0.28, a tube lens with a focal length of 180 mm, and a pco.dimax camera with 2,016 × 2,016 pixels, allowing us to acquire data from the moving joint region with a high frame rate.

Overview radiographs (Fig. 1C) and tomograms (Fig. 1D) were acquired using a detector system consisting of a free-standing cerium-doped yttrium aluminium garnet scintillator of 200-µm thickness optically coupled via a custom 0.26 N.A. and 3× magnification microscope to a Photron SA1.1. In this case, the resulting pixel size was 6.6 µm, with a field of view of 6.6 mm.

Both configurations used a light path folding mirror to remove the sensitive optical components from the direction of the primary X-ray beam, avoiding darkening of the lens system due to exposure to high-energy radiation. The chosen scintillator materials and thicknesses made it possible to achieve an acceptable compromise between spatial and temporal resolution for our application. The high absorption and high light yield of the scintillators sufficiently overcome the read-out noise of the camera also for short exposure times.

In the radon domain, the transfer function which is attributed to the data acquisition process can be expressed as

where 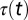is the temporal deexcitation function of the scintillator, and represents the averaging process due to simultaneous image integration and continuous rotation. Because the angular rotation velocity is constant throughout the tomographic data acquisition process, the temporal variable is linearly related to the angular position, i.e., . The detector response function depends on the material properties of the scintillator, the numerical aperture of the optical system, and the energy spectrum incident on the detector. It is given by

where is the depth-dependent absorbed X-ray intensity inside the scintillator and its visible light output (23, 24). The frequency response of an optical system with circular aperture is

with denoting the frequency variable, and , where is the emission wavelength of the scintillator (25). The focal shift from the Gaussian reference sphere is given by , where the refractive index of the scintillator is denoted by , the numerical aperture of the optical system by N.A., and the defect of focus by . Thus, the optimum scintillator materials and thicknesses, and corresponding transfer functions, can be concluded. The optimization steps lead to a reduction of the effective dose by a factor of 8 compared with the scan protocol described in ref. 11. Due to the highly parallel synchrotron radiation beam, it is sufficient to acquire radiographs for an angular range of 180 degrees to obtain the complete information required for reconstructing a tomographic volume. To acquire overview tomograms of the motion of the whole weevil (Fig. 1E), the specimen was imaged with a temporal resolution of 20 tomograms per s, realizing continuous rotation with 10 revolutions per s and an imaging rate of 5,000 frames per s, or equivalently 250 projections per tomogram. The sample-to-detector propagation distance of the wave field was 50 cm.

To image the moving hip joint region (Fig. 2 A–C) we recorded high-resolution radiographs while the specimen was continuously rotating with 3.25 revolutions per s. An imaging rate of 1,500 frames per s was used. Recording 200 projections for a full tomogram, the resulting temporal resolution was therefore 7.5 volumes per second. The sample-to-detector propagation distance of the wave field was 20 cm.

For both detector configurations, the survival time of the samples in the X-ray beam was ∼10 s. After the in vivo scans, the same specimen was scanned postmortem to obtain high-quality static volumes of the joint region. In this case 1,000 projections were collected with a frame rate of 100 frames per s. All other scan parameters were left unchanged.

3. Noise Removal.

As a result of the short exposure time during the acquisition process, a high noise level in individual images is unavoidable. Before volume reconstruction we use a noise removal procedure to restore the true image from its noisy representation , where represents noise and is a linear pixel index which encodes its position.

A popular choice for image denoising is the Gaussian low-pass filter, because the SNR tends to decrease for high spatial frequencies due to the signal recording process. This filter restores the pixel value by averaging its spatial neighborhood. Thus, this filter does not discriminate between image features and high spatial frequencies introduced by noise, resulting in a loss of signal details.

Several classes of filtering algorithms have been proposed to reduce the detrimental influence of averaging dissimilar neighboring pixels, such as adaptive smoothing (26), which respect image feature directions. Neighborhood filters (27) average pixels that are spatially close to the target pixel, but only under the condition that their gray level is close enough to the pixel to be restored. The nonlocal-means (NLM) denoising algorithm (28) can be regarded as an extension which avoids their characteristic shock and staircase artifacts (27).

It was shown that the NLM algorithm minimizes the mean-square error between the noisy and the true image for signal-independent additive white noise, and is superior to Gaussian, anisotropic, Yaroslavski, and total variation filters (29).

The NLM filtered image is given by

with weights dependent on the similarity of image patches centered at pixel positions and . The weights are given by

A square gray level neighborhood of fixed size centered at position is denoted by . satisfies the conditions and . As a result of its construction, pixels with similar gray value neighborhoods have larger weights in the averaging step. The parameter h controls the decay of the exponential function and therefore the relative weight contribution to the averaging as a function of the Euclidean distance of the image patches. Additionally, it depends linearly on the SD of the noise distribution, and is suggested to be set to 10 (27).

In our case, the noise is the realization of a Poisson distribution, and thus not independent of the image intensity. Therefore, we apply a noise variance equalizing transformation (29) before filtering. We take the absolute value of the signal amplitude by applying a pixelwise square root transformation to the normalized intensity values. After this step, the square root transformation is inverted before passing the data to the volume reconstruction procedure.

In effect, important image details are preserved whereas high-frequency noise is significantly reduced. This permits the use of high-frequency preserving filters in the later reconstruction step. For this example, preservation of interface enhancement by phase contrast is more important than quantitative phase retrieval (Fig. S2).

4. Three-Dimensional Reconstruction.

Before reconstruction the radiographs were normalized to the incident irradiation by flat-field corrections without the specimen in the field of view. Volumes were reconstructed using a parallel implementation of the filtered back-projection (FBP) method on graphics processing units in conjunction with a ramp filter (30, 31). Usually, a windowed filter function such as the Shepp–Logan (32) or the Hamming (33) filter is used for the FBP, which suppresses noise by attenuating high spatial frequencies. In our case, however, the separate noise removal step was performed before the volume reconstruction, permitting us to use a nonwindowed filter function. This preserves feature details required for robust motion estimation, while still maintaining adequate noise levels in the reconstruction. The FBP reconstruction technique was selected because it is parameter-free and noniterative.

5. Optical Flow.

A 3D variational optical flow method was designed to be robust against image artifacts and yet be sensitive to low-contrast image details. The unknown 3D displacement vector for each voxel position between two successive 3D volumes and is determined as a solution of a global optimization problem in a general form , where , are data and smoothness terms, respectively, is a motion smoothness regularization parameter, and represents 3D image domain.

For the data term we assumed a constancy of image brightness to track corresponding pixels. Assuming that displacement components are small, one may approximate this nonlinear equation using Taylor expansion (34) to obtain a so-called linearized optical flow constraint, given by , where denote spatial image gradients and denotes gradient in temporal direction. Instead of using a popular total variation approach to model the data term, we employ quadratic penalization to augment the contribution of large image gradients (representing boundaries between structures), which were deliberately preserved throughout the entire image processing and reconstruction pipeline.

To discard image artifacts we selectively modeled data constancy. A first run of optical flow computation was performed to localize data outliers. This confidence map was then applied during the second computation to reduce the influence of problematic image regions and thus to refine the motion field (35). We further improved robustness against noise using a combined local–global approach (36), which takes information from a local region into account. This can be implemented by convolution of optical flow constraints with a Gaussian function , where the size of Gaussian kernel controls the integration scale, and such step could be regarded as motion regularization in the image domain.

The optical flow cannot be uniquely computed within homogeneous image regions. For this purpose we regularize the motion field via the image and flow-driven smoothness method (37). Such an approach imposes more strict smoothness constraints inside homogeneous image regions and preserves motion boundaries near separate structures.

To capture the whole range of movements including a fast rotation of the trochanter, we used a multilevel computation procedure based on image warping (34). A crucial step of median filtering of the intermediate flow field between computation levels was done to suppress data outliers already at early stages (38).

The final variational model of our robust 3D optical flow is given by

where is an image and flow-driven smoothness term and is a penalty function with a small positive constant . This variational functional is then minimized with an iterative solver (34). The overall optical flow computation procedure is given as a pseudocode (SI Text).

6. Automated Tracking.

The fully automated tracking of individual joint parts was performed using the results of optical flow computation on reconstructed volumes. Within the first time frame of the in vivo scan we distributed 70 and 130 landmarks for coxa and trochanter, respectively. For each landmark at a time frame , the target landmark on the time frame is provided by the corresponding displacement vector .

To ensure high tracking accuracy we applied filtering of reliable trajectories by means of a forward–backward cross-check, which assures consistency of tracking results computed in both directions. Evaluating the difference between the location of initial landmark and its new position tracked in the opposite direction a possible outlier could be identified. We discriminated data points with the discrepancy of forward–backward check of (i) more than 3 pixels and (ii) more than 5% of total traveled distance. To further improve the selection of reliable tracking points we performed a rigidity check by analyzing the relative spatial arrangement of landmarks; 30% of landmarks showing the most deviations from the rigidity constraint were filtered out. The remaining high-confidence landmarks were fed to the global transformation estimation procedure.

7. Kinematics Analysis.

For the estimation of global transformation between two sets of landmarks and extraction of motion components we used the Python module “transformations.py” (www.lfd.uci.edu/∼gohlke/). A rigid transformation matrix M_t, which transforms landmark positions between successive time frames, was calculated using Kabsch’s algorithm (39). The resulting matrix was then decomposed to obtain translational components and rotation angles (Fig. 2I). For the trochanter, both quantities were evaluated with respect to its approximate axis on the initial time frame. We compared the performance of automated tracking and motion analysis with the manual procedure. We achieved an average error of coxa displacement of 0.7 pixels with the average/maximum actual displacement of 3.7/5.2 pixels; an average error of trochanter displacement of 3.7 pixels with the average/maximum actual displacement of 10.7/18.0 pixels; an average error of trochanter rotation of 2.5 degrees with the average/maximum actual rotation of 55.4/94.8 degrees.

8. Labeling.

The 3D volumes of the static tomogram and the first frame of the high-resolution in vivo 4D scans were imported into the software Amira 5.4. Coxa and trochanter were labeled manually using the Brush and Lasso tools of the software's segmentation editor. For the static scan, parts of thorax, abdomen, and femur were labeled in addition to coxa and trochanter parts (Movie S1). To examine morphological dynamics in best resolution, coxa and trochanter from the static tomogram were aligned manually to match the first frame of the in vivo scan. The high-quality labeled data were then transformed according to its actual motion calculated during kinematics analysis. This was done in the ImageJ 3D Viewer software using Transformation->Set Transform and providing a transformation matrix M_t.

9. Visualization.

Time-lapsed labels were loaded back to Amira, where “materials” of coxa and trochanter were isolated to create polygon meshes. This was performed with the SurfaceGen module at default settings. With the Simplification Editor the numbers of polygons of the original meshes (SURF files) were reduced to 10% of their original values to reduce the file sizes. The files were subsequently saved in the Wavefront format (OBJ). The polygon meshes of the tomograms were imported into the software CINEMA 4D R14 and smoothed to reduce labeling artifacts. The obtained positions served as key frames, whereas the frames in between were interpolated by the software to provide a smooth animation (Movie S4).