Abstract
Förster resonance energy transfer (FRET) describes a physical phenomenon widely applied in biomedical research to estimate separations between biological molecules. Routinely, genetic engineering is used to incorporate spectral variants of the green fluorescent protein (GFPs), into cellular expressed proteins. The transfer efficiency or rate of energy transfer between donor and acceptor FPs is then assayed. As appreciable FRET occurs only when donors and acceptors are in close proximity (1–10 nm), the presence of FRET may indicate that the engineered proteins associate as interacting species. For a homogeneous population of FRET pairs the separations between FRET donors and acceptors can be estimated from a measured FRET efficiency if it is assumed that donors and acceptors are randomly oriented and rotate extensively during their excited state (dynamic regime). Unlike typical organic fluorophores, the rotational correlation-times of FPs are typically much longer than their fluorescence lifetime; accordingly FPs are virtually static during their excited state. Thus, estimating separations between FP FRET pairs is problematic. To overcome this obstacle, we present here a simple method for estimating separations between FPs using the experimentally measured average FRET efficiency. This approach assumes that donor and acceptor fluorophores are randomly oriented, but do not rotate during their excited state (static regime). This approach utilizes a Monte-Carlo simulation generated look-up table that allows one to estimate the separation, normalized to the Förster distance, from the average FRET efficiency. Assuming a dynamic regime overestimates the separation significantly (by 10% near 0.5 and 30% near 0.75 efficiencies) compared to assuming a static regime, which is more appropriate for estimates of separations between FPs.
Keywords: GFP, Kappa squared
1. Introduction
The discovery and optimization of genetically encoded fluorophores [1,2], such as green fluorescent protein (GFP) and its derivatives (FPs), has stimulated interest in using microscopy to identify and measure protein–protein interactions within living cells [3,4]. Förster resonance energy transfer (FRET) describes a physical phenomenon in which energy is transferred from a donor fluorophore in its excited state to a near-by acceptor fluorophore in its ground state [3–8]. FRET can only occur between a pair of molecules that utilize approximately the same amount of energy to transition between their ground and excited states. Specifically, the energy liberated when an excited donor transitions to its ground state must be equivalent to the energy required to excite an acceptor. The suitability for two fluorescent molecules to transfer energy using FRET is proportional to the overlap of the donor emission and acceptor absorption spectra or overlap integral, J. For a pair of fluorophores with non-zero J, the FRET transfer rate constant, kT, has an inverse sixth power dependence on the distance between donor and acceptor fluorophores (RDA).
| (1) |
where τ0D is the fluorescence lifetime of the donor, and R0 is the Förster distance, the separation at which 50% of the donor excitation events result in energy transfer to the acceptor for a particular donor-acceptor pair. The value of R0 is given by:
| (2) |
where N′ is Avogadro's number per mmole, 6.022 × 1020, n the refractive index of the nearby medium [9], κ2 the orientation factor for dipole–dipole coupling, which equals 2/3 in the dynamic isotropic limit, R̄0 is R0 when kappa-squared is 2/3, QD the fluorescence quantum yield of the donor in the absence of the acceptor, and the numerical factor 0.02108 applying when J is defined in units of nm4 cm2/mmole.
Energy transfer efficiency, E, is defined by the ratio of the transfer rate constant to the total donor deactivation rate:
| (3) |
Substitution from Eq. (1) for kT reveals that E does not depend on the donor lifetime, only on R0 and RDA:
| (4) |
Using Eq. (4), the FRET efficiency can be used to estimate the distance separating fluorescently labeled sites (RDA) within and between biomolecules [10,11]. In most FRET experiments the average FRET efficiency, 〈E〉, is measured for a population of potential donors and acceptors, not the FRET efficiency, E, for an individual pair. Accordingly, to estimate distances from an experimentally measured average FRET efficiency it is either assumed that all donors in the population are paired with acceptors that have approximately the same FRET efficiency, or corrections are required to account for those donors that are not paired with an acceptor or have significantly different FRET efficiencies [11,12].
In addition to separation, the FRET transfer rate is also dependent on the angular position of the acceptor relative to the donor's emission dipole vector (θ), and on the orientation of the acceptors absorption dipole vector relative to the electric field of the donor at the acceptors location (ω) [13–15]. These two angles define κ2, the orientation factor for the required dipole–dipole coupling.
| (5) |
Because cos2θ and cos2ω can have values ranging from 0 to 1, κ2 can have values ranging from 0 to 4. The physical basis of κ2 is depicted in Fig. 1A. Based on Eqs. (1), (2), and (4) it is clear that if κ2 is zero, FRET cannot occur, while if κ2 is 4, the maximal rate and FRET efficiency can be achieved for any specific separation. In biological FRET experiments the actual values for θ, ω, and therefore κ2 are not known. For free donors and acceptors in solution, and often for fluorophores coupled to biological molecules via a flexible linker, it is assumed that θ and ω have random orientations (isotropic). With this ‘isotropic’ assumption, the probability distribution of κ2 values will range from 0 to 4, with a mode value of 0 and an average value of 2/3 (Fig. 1B). In most FRET experiments, and when calculating the Förster distance (R0) for a specific donor-acceptor pair, κ2 is assumed to have a value of 2/3 [15–18]. The use of 2/3, the average value for κ2 in an isotropic distribution, in FRET calculations is predicated on the assumptions that (1) θ and ω have random orientations (from an isotropic distribution of orientations), and (2) that during the donors excited state lifetime the values of θ and ω change rapidly and independently as a result of rapid molecular rotation [18]. For non-tethered, or loosely tethered small organic fluorophores that can rotate rapidly relative to their fluorescence lifetimes it is reasonable to assume that θ and ω will assume many different random orientations during the excited state lifetime of the donor, thus the average value of the κ2 probability distribution, 2/3, can be used in calculations. With these assumed conditions, formally called dynamic isotropic, donor-acceptor separation can be calculated from a measured average FRET efficiency and the Förster distance for the specific donor-acceptor pair.
Fig. 1.

Isotropic κ2 distribution. (A) Cartoon illustrating how the dipole orientation factor κ2 is determined by 2 angles, θ and ω (see Eq. (5)). Blue arrow depicts the position and orientation of the donor emission dipole. Yellow arrows depict the position and orientation of four possible acceptor absorption dipoles, each the same distance from the donor. Red lines depict the local orientation of the electric field created by the excited state of the donor emission dipole. (B) Monte Carlo simulation of the κ2 probability distribution assuming that θ and ω are randomly distributed (isotropic). Note that the mode of this distribution is 0 and the average is 2/3.
| (6) |
Eq. (6) can be rewritten as:
| (7) |
where Φ is:
| (8) |
Φ is the separation normalized to the Förster distance and can be thought of as the fractional dependence of RDA on 〈E〉. Unfortunately, Eqs. (6 and 8) cannot be used for large fluorophores, such as GFP, because the κ2 value of 2/3, inherent in the R̄0 value of Eqs. (6) and (8), is not appropriate for a random isotropic population of FRET donors and acceptors that rotate slowly relative to the excited state lifetime of the donor [14,15,18,19]. In fact, under these conditions, formally called the static random isotropic orientational regime, there is no single value for κ2 that is appropriate for all separations [15,16]. Nonetheless, Eq. (7) does describe the correspondence between 〈E〉 and RDA in the static random isotropic orientational regime, but there is no simple equation, such as Eq. (8), for calculating the value Φ as a function of 〈E〉. Here we use Monte Carlo simulations to generate a look-up table applicable to FPs, that can be used in conjunction with Eq. (7) to estimate distances between FP donors and acceptors based on experimentally determined average FRET efficiencies.
2. Methods
2.1. Monte Carlo simulations
Monte Carlo simulations were performed in Igor Pro (ver6.22) to generate populations of FRET efficiencies in the static random isotropic orientational regime. Each simulation was based on generating 1,000,000 random replicate E values for a given Φ value. Two hundred and fifty Φ values were generated between a starting value of 0.01 and a final value of 2.5 in 0.01 increments. For each replicate the following equation was used to calculate a single FRET efficiency:
| (9) |
where κ2 was stochastically generated for each replicate to simulate FRET in the isotropic static regime. A distribution of 1,000,000 κ2 values was generated from random values for the angles θ and ω, generated as previously described [18]. In brief, a uniform distribution of numbers ranging from 0 to 1 was generated using the Igor Pro enoise command. Next, the inverse cosine of these values was calculated to generate a population of angles expected for an isotropic distribution. These values of θ and ω were used in Eq. (5) to generate the population of κ2 values, and these in turn were used in Eq. (9) to calculate FRET efficiencies in the static regime.
The average FRET efficiency, 〈E〉, standard deviation, SD, skewness, and kurtosis of Monte Carlo simulation generated FRET efficiency populations were calculated using the Igor Pro wavestats command, using the following equations:
| (10) |
| (11) |
| (12) |
| (13) |
3. Results
Monte Carlo simulations were used to model the distribution of FRET efficiencies in 250 populations each having progressively larger separations. The Förster distance was set to 1 in these simulations and the separations varied, in Förster distance units, from 0.01 to 2.5 in 0.01 increments for each population. When the Förster distance is normalized to a value 1, the distance, RDA, is equivalent to Φ, the Förster distance normalized dependence of RDA on 〈E〉. Each individual simulation population consisted of 1 million FRET pairs each with the same separation but with random isotropic values for θ and ω. Probability density histograms, p(E), of three of these populations are plotted in Fig. 2. These correspond to static isotropic populations with Φ values of 0.66 (panel A), 0.89 (B), and 1.14 (C), and average FRET efficiencies 〈E〉, of 0.75, 0.50, and 0.25, respectively. These FRET efficiency probability distributions are broad, and strikingly non-Gaussian. In each case the mean of the distribution is dramatically different from the population mode and median. This can be quantified by examining the skewness (symmetry around the mean) and kurtosis (peakedness) of these distributions; a Gaussian distribution has zero skewness and kurtosis.
Fig. 2.
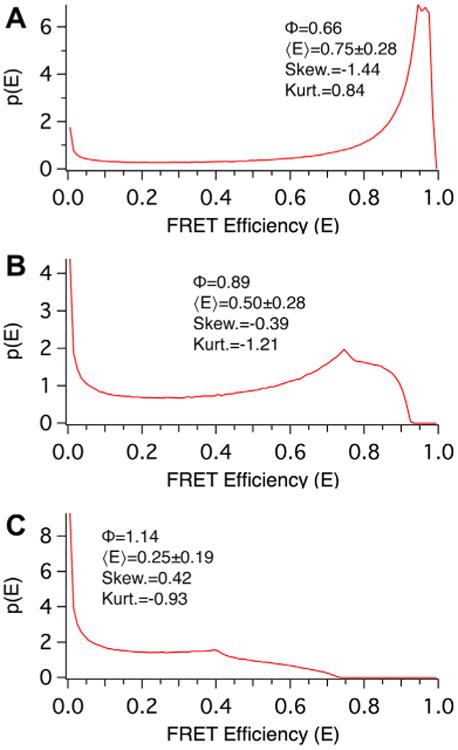
Monte Carlo simulations used to determine the relationship between average FRET efficiency and Separation under static isotropic conditions. The probability distribution of FRET efficiencies derived from Monte Carlo simulations where separation, normalized to the Förster distance (Φ), was set to values of 0.66 (A), 0.89 (B), and 1.14 (C), corresponding to average population FRET efficiencies, 〈E〉, of approximately 75%, 50%, and 25%, respectively. Note the irregular shapes of all three populations.
We have previously described an analytical solution for the probability density p(E) of FRET efficiencies in static isotropic regime populations [18]. These distributions have 3 phases, the first describes the probability of having a FRET efficiency, E, falling between zero and F/(1 + F), is defined by Eq. (14):
| (14) |
where F, is defined as:
| (15) |
Note, for this first phase the most probable FRET efficiency is zero. The second phase, describes the probability of having FRET efficiencies between F/(1 + F) and 4F/(1 + 4F) and is described by Eq. (16):
| (16) |
This second phase has a peak at F/(1 + F) and decreases to its lowest probability at 4F/(1 + 4F). The third phase has a value of zero for all FRET efficiencies greater than 4F/(1 + 4F).
For each of the 250 simulated populations the mean FRET efficiency, the standard deviation of the mean FRET efficiency, the population skewness, and kurtosis was calculated and is plotted in Fig. 3. In panel 3A the dependence of 〈E〉 on Φ is plotted for the static isotropic regime (RED curve) and for comparison the dependence of E on Φ using Eq. (4) with a R0 value of 1 is plotted for the dynamic isotropic regime (dashed BLUE curve). Note that in the dynamic isotropic regime the FRET efficiency is 50% when Φ equals 1. This is not true in the static isotropic regime, where a FRET efficiency of 50% is observed when Φ equals ∼0.89 (see Fig. 2B). The dynamic and static isotropic curves are nearly identical when Φ has a value greater than 1.4. Fig. 3B depict how the standard deviations of the FRET efficiency distributions in the static isotropic regime change as a function of Φ. When Φ equals 0.51 the standard deviation of the population is greater than 25% of the average FRET efficiency. As Φ increases, the fractional deviation observed in these populations asymptotical approaches the mean FRET efficiency. It is clear that most of these distributions are quite broad. Fig. 3C and D depict the skewness and kurtosis of these FRET efficiency distributions. These values are generally different from zero, the value expected for a Gaussian distribution.
Fig. 3.
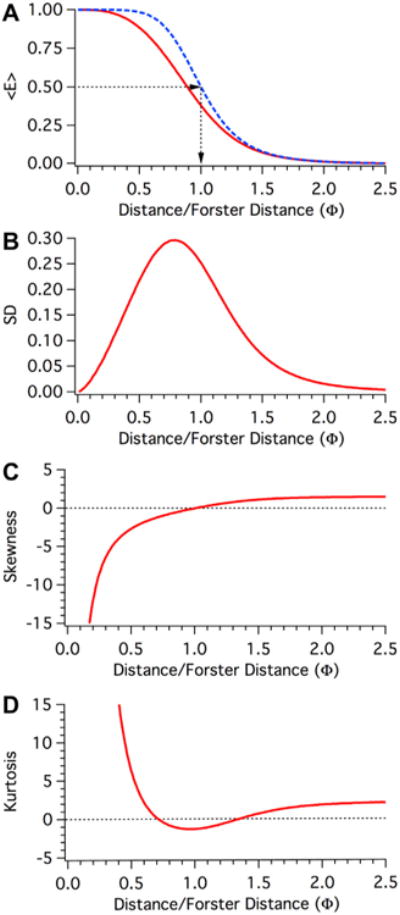
Moment Analysis of the dependence of FRET efficiency on Separation under static isotropic conditions. A. The dependence of 〈E〉 (the first moment of these populations) on Φ under isotropic dynamic (dashed Blue) or static (Red) conditions. (B) The dependence of variance (the second moment) on Φ under isotropic static conditions (Red). Plotted is the standard deviation of the distribution, which is the positive square root of the variance. (C) The dependence of skewness (the third moment) on Φ under isotropic static conditions (Red). The skewness represents symmetry within the distribution; a positive value indicates a heavier tail to the right, while a negative value indicates a left skewed distribution. (D). The dependence of kurtosis (the fourth moment) on Φ under isotropic static conditions (Red). The kurtosis represents the distribution peakedness relative to a normal distribution. A positive value indicates an acute peak in the distribution, while a negative value indicates a broad flat distribution.
The objective of this study is to devise a simple method to estimate the distance between a FRET pair in the static isotropic regime, based on experimentally determined average FRET efficiency values. Because of the complex and non-Gaussian shapes of the probability density histograms for FRET pairs in the static isotropic regime, solving for a simple analytical equation that accurately describes how RDA changes as a function of 〈E〉 in the static isotropic regime is challenging. Accordingly, we decided upon a simpler (albeit less elegant) strategy based on generating a lookup table of sufficient precision, that equates experimentally-measured average FRET efficiency values to specific and unique values of Φ. Multiplying Φ value derived from this table by the Förster distance (R0) of the specific FRET pair used in an experiment will then yield an estimated separation (see Eq. (7)). Sets of 250 Monte Carlo simulations, as described above for Fig. 3, were repeated in triplicate. The mean 〈E〉 value of the three replicates for each of the 250 different Φ values is presented in Table 1 with the unique Φ values used to generate these values in the Monte Carlo simulations. The average FRET efficiencies ranged from 0.999 to 0.004, with FRET efficiency increments of ∼0.012 or lower. An alternative to Monte Carlo simulation is a mixed analytical-numerical approach based on simplifying the E*p(E) integral from E = 0 to E = 4F/(1 + 4F) over the two non-zero phases of p(E) given in Eqs. (14) and (16), resulting in the following expression:
Table 1.
The dependence of separation (Φ) on the average FRET efficiency (<E>) in the static isotropic regime.
| <E> | Φ | <E> | Φ | <E> | Φ | <E> | Φ |
|---|---|---|---|---|---|---|---|
| 0.999 | 0.01 | 0.771 | 0.64 | 0.163 | 1.27 | 0.020 | 1.90 |
| 0.999 | 0.02 | 0.762 | 0.65 | 0.158 | 1.28 | 0.019 | 1.91 |
| 0.999 | 0.03 | 0.752 | 0.66 | 0.153 | 1.29 | 0.019 | 1.92 |
| 0.999 | 0.04 | 0.742 | 0.67 | 0.147 | 1.30 | 0.018 | 1.93 |
| 0.999 | 0.05 | 0.732 | 0.68 | 0.142 | 1.31 | 0.018 | 1.94 |
| 0.999 | 0.06 | 0.722 | 0.69 | 0.138 | 1.32 | 0.017 | 1.95 |
| 0.999 | 0.07 | 0.712 | 0.7 | 0.133 | 1.33 | 0.017 | 1.96 |
| 0.999 | 0.08 | 0.701 | 0.71 | 0.129 | 1.34 | 0.016 | 1.97 |
| 0.999 | 0.09 | 0.691 | 0.72 | 0.124 | 1.35 | 0.016 | 1.98 |
| 0.999 | 0.10 | 0.680 | 0.73 | 0.120 | 1.36 | 0.015 | 1.99 |
| 0.998 | 0.11 | 0.669 | 0.74 | 0.116 | 1.37 | 0.015 | 2.00 |
| 0.998 | 0.12 | 0.658 | 0.75 | 0.112 | 1.38 | 0.014 | 2.01 |
| 0.997 | 0.13 | 0.647 | 0.76 | 0.108 | 1.39 | 0.014 | 2.02 |
| 0.997 | 0.14 | 0.636 | 0.77 | 0.104 | 1.40 | 0.013 | 2.03 |
| 0.996 | 0.15 | 0.624 | 0.78 | 0.101 | 1.41 | 0.013 | 2.04 |
| 0.996 | 0.16 | 0.613 | 0.79 | 0.098 | 1.42 | 0.013 | 2.05 |
| 0.995 | 0.17 | 0.602 | 0.80 | 0.094 | 1.43 | 0.012 | 2.06 |
| 0.994 | 0.18 | 0.590 | 0.81 | 0.091 | 1.44 | 0.012 | 2.07 |
| 0.993 | 0.19 | 0.579 | 0.82 | 0.088 | 1.45 | 0.012 | 2.08 |
| 0.992 | 0.20 | 0.567 | 0.83 | 0.085 | 1.46 | 0.011 | 2.09 |
| 0.991 | 0.21 | 0.556 | 0.84 | 0.082 | 1.47 | 0.011 | 2.10 |
| 0.989 | 0.22 | 0.545 | 0.85 | 0.079 | 1.48 | 0.011 | 2.11 |
| 0.988 | 0.23 | 0.533 | 0.86 | 0.077 | 1.49 | 0.010 | 2.12 |
| 0.986 | 0.24 | 0.522 | 0.87 | 0.074 | 1.50 | 0.010 | 2.13 |
| 0.984 | 0.25 | 0.510 | 0.88 | 0.071 | 1.51 | 0.010 | 2.14 |
| 0.982 | 0.26 | 0.499 | 0.89 | 0.069 | 1.52 | 0.009 | 2.15 |
| 0.980 | 0.27 | 0.487 | 0.90 | 0.067 | 1.53 | 0.009 | 2.16 |
| 0.978 | 0.28 | 0.476 | 0.91 | 0.064 | 1.54 | 0.009 | 2.17 |
| 0.976 | 0.29 | 0.465 | 0.92 | 0.062 | 1.55 | 0.009 | 2.18 |
| 0.973 | 0.30 | 0.454 | 0.93 | 0.060 | 1.56 | 0.008 | 2.19 |
| 0.971 | 0.31 | 0.443 | 0.94 | 0.058 | 1.57 | 0.008 | 2.20 |
| 0.968 | 0.32 | 0.432 | 0.95 | 0.056 | 1.58 | 0.008 | 2.21 |
| 0.965 | 0.33 | 0.421 | 0.96 | 0.054 | 1.59 | 0.008 | 2.22 |
| 0.962 | 0.34 | 0.410 | 0.97 | 0.053 | 1.60 | 0.007 | 2.23 |
| 0.958 | 0.35 | 0.400 | 0.98 | 0.051 | 1.61 | 0.007 | 2.24 |
| 0.955 | 0.36 | 0.389 | 0.99 | 0.049 | 1.62 | 0.007 | 2.25 |
| 0.951 | 0.37 | 0.378 | 1.00 | 0.047 | 1.63 | 0.007 | 2.26 |
| 0.947 | 0.38 | 0.368 | 1.01 | 0.046 | 1.64 | 0.007 | 2.27 |
| 0.943 | 0.39 | 0.358 | 1.02 | 0.044 | 1.65 | 0.007 | 2.28 |
| 0.939 | 0.40 | 0.348 | 1.03 | 0.043 | 1.66 | 0.006 | 2.29 |
| 0.934 | 0.41 | 0.338 | 1.04 | 0.042 | 1.67 | 0.006 | 2.30 |
| 0.929 | 0.42 | 0.329 | 1.05 | 0.040 | 1.68 | 0.006 | 2.31 |
| 0.925 | 0.43 | 0.319 | 1.06 | 0.039 | 1.69 | 0.006 | 2.32 |
| 0.919 | 0.44 | 0.310 | 1.07 | 0.038 | 1.70 | 0.006 | 2.33 |
| 0.914 | 0.45 | 0.301 | 1.08 | 0.036 | 1.71 | 0.006 | 2.34 |
| 0.908 | 0.46 | 0.292 | 1.09 | 0.035 | 1.72 | 0.005 | 2.35 |
| 0.903 | 0.47 | 0.283 | 1.10 | 0.034 | 1.73 | 0.005 | 2.36 |
| 0.897 | 0.48 | 0.275 | 1.11 | 0.033 | 1.74 | 0.005 | 2.37 |
| 0.890 | 0.49 | 0.266 | 1.12 | 0.032 | 1.75 | 0.005 | 2.38 |
| 0.884 | 0.50 | 0.258 | 1.13 | 0.031 | 1.76 | 0.005 | 2.39 |
| 0.877 | 0.51 | 0.250 | 1.14 | 0.030 | 1.77 | 0.005 | 2.40 |
| 0.870 | 0.52 | 0.242 | 1.15 | 0.029 | 1.78 | 0.005 | 2.41 |
| 0.863 | 0.53 | 0.235 | 1.16 | 0.028 | 1.79 | 0.004 | 2.42 |
| 0.856 | 0.54 | 0.228 | 1.17 | 0.027 | 1.80 | 0.004 | 2.43 |
| 0.848 | 0.55 | 0.220 | 1.18 | 0.026 | 1.81 | 0.004 | 2.44 |
| 0.841 | 0.56 | 0.213 | 1.19 | 0.026 | 1.82 | 0.004 | 2.45 |
| 0.833 | 0.57 | 0.206 | 1.20 | 0.025 | 1.83 | 0.004 | 2.46 |
| 0.825 | 0.58 | 0.200 | 1.21 | 0.024 | 1.84 | 0.004 | 2.47 |
| 0.816 | 0.59 | 0.193 | 1.22 | 0.023 | 1.85 | 0.004 | 2.48 |
| 0.808 | 0.60 | 0.187 | 1.23 | 0.022 | 1.86 | 0.004 | 2.49 |
| 0.799 | 0.61 | 0.181 | 1.24 | 0.022 | 1.87 | 0.004 | 2.50 |
| 0.790 | 0.62 | 0.175 | 1.25 | 0.021 | 1.88 | ||
| 0.781 | 0.63 | 0.169 | 1.26 | 0.020 | 1.89 | ||
| (17) |
where . For Φ≫1, 〈E〉Φ≫1 = Φ−6, and for Φ≪1, . Outside of these limiting regions, the integral in Eq. (17) must be done numerically. For Φ values of 0.3, 1.0, and 2.0, numerical integration was used to validate the Monte Carlo algorithm and confirm the values in Table 1 (data not shown). For our purposes, the simplicity of the Monte Carlo algorithm was preferable to numerical integration of Eq. (17).
The data from Table 1 is plotted in Fig. 4 to illustrate the dependence of normalized separation (Φ) on the average FRET efficiency, 〈E〉, under isotropic static conditions. The dependence of Φ on 〈E〉 is quasi-linear between average FRET efficiency values 0.17 and 0.90, but is highly non-linear at extreme values of 〈E〉 (RED tinted regions of Fig. 4 and Table 1). The RED tinted regions of Table 1 should not be used for estimating separation from experimental FRET efficiencies because in these regions small errors in 〈E〉 result in large errors in Φ. A table listing Förster distances (R0) for 19 popular fluorescent protein FRET pairs is presented Table 2.
Fig. 4.
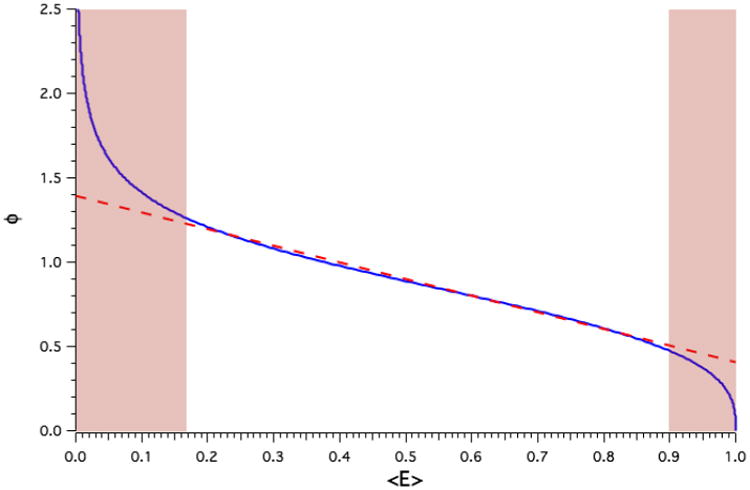
The dependence of Separation on average FRET efficiency under static isotropic conditions. The dependence of Φ on 〈E〉 under isotropic static (Blue) conditions. Dashed RED line depicts a linear fit to the central portion of the curve, while the RED tinted regions highlights average FRET efficiencies that correspond to the non-linear portions of the curve.
Table 2.
Förster distances (R0) for common fluorescent protein FRET pairs.
| FP FRET-Pair | R0 | Refs. |
|---|---|---|
| ECFP-EYFP | 4.7 | a |
| ECFP-Citrine | 4.8 | b |
| mCerulean–mCherry | 4.8 | a |
| ECFP-Venus | 5.0 | b |
| mCerulean-EYFP | 5.0 | a |
| Cerulean–Venus | 5.2 | b |
| mCerulean–mVenus | 5.3 | a |
| SECFP-SEYFP | 5.4 | b |
| EGFP-mCherry | 5.4 | b |
| TagGFP-TagRFP | 5.7 | b |
| mTFP1-Citrine | 5.7 | b |
| mTFP1-mOrange | 5.7 | b |
| Citrine-mKate2 | 5.8 | b |
| Clover-mCherry | 5.8 | b |
| mVenus-mCherry | 5.8 | a |
| mVenus-mOrange | 5.8 | a |
| mTurquoise1-SEYFP | 5.8 | b |
| mTurquoise2-SEYFP | 5.9 | b |
| Clover-mRuby2 | 6.3 | b |
To illustrate how Tables 1 and 2 can be used to estimate distances from experimentally determined average FRET efficiencies between fluorescent protein donors and acceptors we applied this strategy to estimate the distance between mCerulean and mVenus in five commonly used FRET reference standards: C5V, C17V, C32V, C40V, and C50V [20,21]. Each of these constructs has a Cerulean donor fluorophore and a Venus acceptor fluorophore connected by a variable length amino acid linkers consisting of 5, 17, 32, 40, and 50, amino acids respectively. As expected, the average FRET efficiency, 〈E〉, measured for these constructs decreases as the amino acid linker length increases (see Table 3). To estimate separation in the isotropic static regime average FRET efficiency values were first transformed into Φ values using Table 1. Next these corresponding Φ values were multiplied by 5.3, the Förster distance (R0) for the mCerulean–mVenus FRET pair (from Table 2) in nanometers. This calculation yields the estimated separations (RDA Static, Table 3, RED font) between Cerulean and Venus in these constructs under the assumption that the static isotropic condition is applicable. Note that for the C50V construct the measured average FRET efficiency was 0.13, a value that falls in the non-linear portion of Table 1. Thus, the predicted separation between mCerulean and mVenus of 7.1 nm for this construct might be imprecise. For comparison, Eq. (6) was used to calculate the estimated separation distance (RDA Dynamic, Table 3, ORANGE font) for these constructs with the assumption of dynamic isotropic conditions, i.e. κ2 = 2/3. Furthermore, errors in the published values of R0 will influence the accuracy of separation determinations.
Table 3.
Estimating separation for fluorescent protein FRET standards.
The approach outlined above for estimating separation under static isotropic conditions should be applied to multiple replicates of average FRET efficiency measurements, rather than to the average of such measurements, so that errors in 〈E〉 measurements or in extrapolation using Table 1 can be accounted for in terms of the error in estimated separation.
4. Discussion
Monte Carlo simulations were used to generate a look-up table equating the average measured FRET efficiency, 〈E〉, to the Förster distance normalized separation, Φ, for resonance energy transfer occurring in the static random isotropic orientational regime (Table 1). FRET efficiency derived Φ values can be multiplied by the Förster distance for the specific FRET pair used (see Table 2) to estimate the distance between a donor transferring energy to an acceptor. We have used a set of FRET constructs with 5 different amino-acid linker lengths connecting mCerulean to mVenus to demonstrate how distances can be estimated from FRET measurements and compared this approach with the widely used approach for estimating distance by assuming that κ2 has a value of ⅔ (applicable only to the dynamic random isotropic orientational regime). For all five constructs the estimated distances using the approach outlined here was shorter than estimates assuming an isotropic dynamic regime (see Table 3). Differences between the estimated distances calculated using these two methods were more pronounced for samples with higher FRET efficiencies.
The validity of this method for estimating distances relies on certain assumptions: (1) Energy transfer occurs between a single donor excited state and a single ground-state acceptor, (2) There is a discrete separation between the donor and the acceptor, (3). This distance represents a homogeneous population of separations, (4) The orientation of the donor's emission dipole and the acceptor's absorption dipole is random (isotropic), (5) The separation and relative orientation of the donor and acceptor dipoles do not change during the excited state of the donor (static), (6) Donor and acceptor chromophores do not participate in blinking, bleaching, or any other photo-physical process that may modulate their ability to act as a FRET donor or acceptor. The more standard method of estimating distances by using Eq. (6) and assuming that κ2 = ⅔ relies on all of the same assumptions listed above except for assumption 5. To use Eq. (6) it must be assumed that during the donors excited state the distance between the donor and acceptor does not change, but the donor and acceptor orientations relative to each other change rapidly (dynamic) and randomly (isotropic relationship is maintained). Because fluorescent proteins rotate much slower relative to their excited state lifetimes, it is clear that the static assumption listed above better represents the conditions under which FRET between fluorescent proteins occurs than does the dynamic orientational assumption. Each of the other assumptions outlined here must be thoughtfully considered before applying this approach to a specific biological FRET measurement. For example, an enzyme often exists in two different states, inactive and active. When such a protein is engineered with a FRET donor and acceptor, two distinct donor and acceptor separations might be observed, corresponding to the active and inactive states. In a cell there can be multiple copies of this engineered enzyme and therefore an ensemble FRET measurement from a cell, or even a sub-cellular compartment, might represent a heterogeneous population (see assumption 3 above) comprised, in this example, of a mixture of two discrete separations. To accurately estimate the separation of each state, and the relative abundance of these states, some strategy must be developed (such as the use of mutants that are always active or always inactive) in which the average FRET efficiency of each state can be measured from a homogenous population. The method described here can then be used to estimate the separation from 〈E〉 for each of these two states. Furthermore, once these average FRET efficiencies have been determined, linear algebra can be used to approximate the relative abundance of these two states in a heterogeneous population.
The dimensions of fluorescent proteins, roughly cylindrical with a diameter of ∼2 nm and a length of ∼4 nm [22,23], should be considered when estimating separation from FRET data. It is unlikely that donors and acceptors of this size and shape can assume a truly random population of dipole orientations, the isotropic assumption, if these molecules are on average closer than 4 nm from each other. At these close distances steric hindrance between individual fluorescent protein surfaces are likely to limit the possible orientations of the two dipoles involved in FRET. For example, using the mCerulean-mVenus FRET pair, with a R0 value of 5.3 nm (Table 2), experimentally determined average FRET efficiencies higher than 0.65 would at first glance indicate a separation of less than 4 nm assuming static isotropic conditions. But as just mentioned, at these distances isotropic distributions are unlikely, so the validity of this estimation must be questioned. Such high average FRET efficiency values could also indicate the presence of multiple FRET acceptors [4,24], or non-random dipole orientations; the assumptions required for estimating distance under static isotropic conditions outlined here would not be warranted.
In biological experiments, less than ideal experimental conditions and reagents might undermine the application of this approach. For example, some fluorescent proteins are thought to have multiple excited states [25–27], as well as flickering or blinking activity [28–30]. Extended imaging might also result in partial bleaching of donors and acceptors at different rates. Differential rates of fluorescent protein biosynthesis and chromophore maturation might yield similar aberrant results [31]. Furthermore, with free donors and acceptors (intermolecular FRET) it is unlikely that every donor in the population will be paired with one and only one acceptor. Even when donors are coupled to an acceptor at a 1:1 ratio in a single construct, as is often the case for biosensors, the linkers used might result in a heterogeneous distribution of separations [18], as well as correlated donor and acceptor dipole orientations [32]. Corrections for many of the departures from the assumptions used in our method have been published [11,12], and potentially can be adapted for use with Table 1 to yield more accurate estimates of FRET distances in the static regime. We emphasize that the approach described yields only an estimate of the distance between static donors and acceptors. However, our approach yields more accurate estimates of separation for FRET between fluorescent proteins from an isotropic population than calculations based on dynamic conditions.
5. Note added in proof
It has recently come to our attention that R.E. Dale has described an approximation for estimating the value of <κ2> in the isotropic static regime (Acta Physica Polonica Vol. A54, pg 743-56,1978.). Using the ‘Dale approximation’, , an alternative method for estimating separation in the static isotropic regime as a function of <E> can be readily formulated. Using this approach we derive, . This equation yields distance values in excellent agreement with the values presented in Table I with deviation typically ≤ 1%.
Acknowledgments
This work was funded by intramural programs of the National Institutes of Health, National Institute on Alcohol Abuse and Alcoholism, and the Eunice Kennedy Shriver National Institute of Child Health and Human Development Bethesda, MD 20892, USA.
References
- 1.Chalfie M, Tu Y, Euskirchen G, Ward WW, Prasher DC. Science. 1994;263:802–805. doi: 10.1126/science.8303295. [DOI] [PubMed] [Google Scholar]
- 2.Heim R, Prasher DC, Tsien RY. Proc Natl Acad Sci USA. 1994;91:12501–12504. doi: 10.1073/pnas.91.26.12501. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Clegg RM. In: FRET and FLIM Techniques. Gadella TWJ, editor. Elsevier; Amsterdam: 2009. pp. 1–57. [Google Scholar]
- 4.Vogel SS, Thaler C, Koushik SV. Sci STKE. 2006;2006:re2. doi: 10.1126/stke.3312006re2. [DOI] [PubMed] [Google Scholar]
- 5.Jares-Erijman EA, Jovin TM. Curr Opin Chem Biol. 2006;10:409–416. doi: 10.1016/j.cbpa.2006.08.021. [DOI] [PubMed] [Google Scholar]
- 6.Sekar RB, Periasamy A. J Cell Biol. 2003;160:629–633. doi: 10.1083/jcb.200210140. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Piston DW, Kremers GJ. Trends Biochem Sci. 2007;32:407–414. doi: 10.1016/j.tibs.2007.08.003. [DOI] [PubMed] [Google Scholar]
- 8.Förster T. Fluoreszenz Organischer Verbindungen. Vandenhoeck & Ruprecht; Göttingen: 1951. [Google Scholar]
- 9.Knox RS, van Amerongen H. J Phys Chem B. 2002;106:5289–5293. [Google Scholar]
- 10.Stryer L, Haugland RP. Proc Natl Acad Sci USA. 1967;58:719–726. doi: 10.1073/pnas.58.2.719. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Hoppe A, Christensen K, Swanson JA. Biophys J. 2002;83:3652–3664. doi: 10.1016/S0006-3495(02)75365-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Wlodarczyk J, Woehler A, Kobe F, Ponimaskin E, Zeug A, Neher E. Biophys J. 2008;94:986–1000. doi: 10.1529/biophysj.107.111773. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Dale RE, Eisinger J. Proc Natl Acad Sci USA. 1976;73:271–273. doi: 10.1073/pnas.73.2.271. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Dale RE, Eisinger J, Blumberg WE. Biophys J. 1979;26:161–193. doi: 10.1016/S0006-3495(79)85243-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.van der Meer BW. J Biotechnol. 2002;82:181–196. doi: 10.1016/s1389-0352(01)00037-x. [DOI] [PubMed] [Google Scholar]
- 16.Steinberg IZ, Haas E, Katchalski-Katzir E. In: Time-Resolved Fluorescence Spectroscopy in Biochemistry and Biology. Cundall RB, Dale RE, editors. Plenum Press; New York: 1983. pp. 411–450. [Google Scholar]
- 17.Lakowicz JR. Principles of Fluorescence Spectroscopy. third. Springer; New York: 2006. [Google Scholar]
- 18.Vogel SS, Nguyen TA, van der Meer BW, Blank PS. PLoS One. 2012;7:e49593. doi: 10.1371/journal.pone.0049593. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Hunt J, Keeble AH, Dale RE, Corbett MK, Beavil RL, Levitt J, Swann MJ, Suhling K, Ameer-Beg S, Sutton BJ, Beavil AJ. J Biol Chem. 2012 doi: 10.1074/jbc.M111.331967. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Chen H, Puhl HL, 3rd, Koushik SV, Vogel SS, Ikeda SR. Biophys J. 2006;91:L39–41. doi: 10.1529/biophysj.106.088773. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Koushik SV, Chen H, Thaler C, Puhl HL, 3rd, Vogel SS. Biophys J. 2006;91:L99–L101. doi: 10.1529/biophysj.106.096206. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Rekas A, Alattia JR, Nagai T, Miyawaki A, Ikura M. J Biol Chem. 2002;277:50573–50578. doi: 10.1074/jbc.M209524200. [DOI] [PubMed] [Google Scholar]
- 23.Malo GD, Pouwels LJ, Wang M, Weichsel A, Montfort WR, Rizzo MA, Piston DW, Wachter RM. Biochemistry. 2007;46:9865–9873. doi: 10.1021/bi602664c. [DOI] [PubMed] [Google Scholar]
- 24.Koushik SV, Blank PS, Vogel SS. PLoS One. 2009;4:e8031. doi: 10.1371/journal.pone.0008031. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Heikal AA, Hess ST, Baird GS, Tsien RY, Webb WW. Proc Natl Acad Sci USA. 2000;97:11996–12001. doi: 10.1073/pnas.97.22.11996. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Heikal A, Hess ST, Webb WW. Chem Phys. 2001;274:37–55. [Google Scholar]
- 27.Liu Y, Kim HR, Heikal AA. J Phys Chem B. 2006;110:24138–24146. doi: 10.1021/jp062164t. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Schwille P, Kummer S, Heikal AA, Moerner WE, Webb WW. Proc Natl Acad Sci USA. 2000;97:151–156. doi: 10.1073/pnas.97.1.151. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Malvezzi-Campeggi F, Jahnz M, Heinze KG, Dittrich P, Schwille P. Biophys J. 2001;81:1776–1785. doi: 10.1016/S0006-3495(01)75828-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Dickson RM, Cubitt AB, Tsien RY, Moerner WE. Nature. 1997;388:355–358. doi: 10.1038/41048. [DOI] [PubMed] [Google Scholar]
- 31.Nagai T, Ibata K, Park ES, Kubota M, Mikoshiba K, Miyawaki A. Nat Biotechnol. 2002;20:87–90. doi: 10.1038/nbt0102-87. [DOI] [PubMed] [Google Scholar]
- 32.VanBeek DB, Zwier MC, Shorb JM, Krueger BP. Biophys J. 2007;92:4168–4178. doi: 10.1529/biophysj.106.092650. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Kremers GJ, Goedhart J. In: FRET and FLIM Techniques. Gadela TWJ, editor. Vol. 334. Elsevier; 2009. pp. 171–223. [Google Scholar]
- 34.Lam AJ. Nat Methods. 2012;9:1005–1012. doi: 10.1038/nmeth.2171. http://dx.doi.org/10.1038/nmeth.2171. [DOI] [PMC free article] [PubMed] [Google Scholar]


