A Power-Efficient Wireless Capacitor Charging System Through an Inductive Link

Abstract

A power-efficient wireless capacitor charging system for inductively powered applications has been presented. A bank of capacitors can be directly charged from an ac source by generating a current through a series charge injection capacitor and a capacitor charger circuit. The fixed charging current reduces energy loss in switches, while maximizing the charging efficiency. An adaptive capacitor tuner compensates for the resonant capacitance variations during charging to keep the amplitude of the ac input voltage at its peak. We have fabricated the capacitor charging system prototype in a 0.35-μm 4-metal 2-poly standard CMOS process in 2.1 mm² of chip area. It can charge four pairs of capacitors sequentially. While receiving 2.7-V peak ac input through a 2-MHz inductive link, the capacitor charging system can charge each pair of 1 μF capacitors up to ±2 V in 420 μs, achieving a high measured charging efficiency of 82%.

I. Introduction

Inductive power transmission across the skin is currently the only viable solution to deliver sufficient power to implantable medical devices (IMDs) without imposing size and capacity constraints of rechargeable batteries [1]. In these IMDs, large capacitors have been utilized as temporary energy sources, which supply the low-power IMDs or augment the inductive power when it is interrupted or insufficient [2], [3]. Capacitors are also used in neural stimulation by storing charge and transferring it to the tissue periodically at high efficiency [4], [5]. Therefore, it is important to rapidly charge implanted capacitors efficiently not from batteries but directly through inductive transcutaneous links, while reducing the IMD size and the risk of tissue damage from overheating.

Charging capacitors from a voltage source through a switch achieves maximum 50% efficiency, wasting half of input energy in the switch. On the other hand, charging capacitors with a current source can minimize the switching loss as the fixed charging current becomes smaller [6]. Fig. 1 shows the conventional Li-ion battery charging techniques in inductively powered devices. AC–DC converters, e.g., a rectifier or a voltage doubler, convert an ac input voltage from an inductive link to a dc supply voltage V_DD, resulting in ac–dc power loss [7]. In Fig. 1(a), the current source (CS) charges the capacitor directly without switches by controlling its gate voltage [8]. However, the current source still wastes energy because of the difference between supply and capacitor voltages V_DD – V_C. Generating an adaptive supply voltage AV_DD in Fig. 1(b)−keeps the dropout voltage of the current source small AV_DD – V_C, while suffering from the additional dc–dc power loss [9]. The charging system in Fig. 1(c) utilizes a back telemetry link to control the inductive power, adjusting V_DD depending on the V_C level to reduce the voltage drop across the current source [10]. However, it requires additional sensing and control circuits as well as an external feedback loop through an optical link.

Fig. 1.

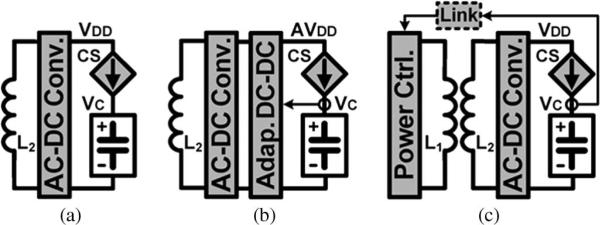
Conventional inductive Li-ion battery charging techniques in CS mode from (a) a fixed supply voltage [8], (b) an adaptive supply voltage [9], and (c) a supply voltage adjusted by an external control loop [10].

In this brief, we propose a novel capacitor charging system, which charges a bank of capacitors efficiently with a fixed charging current, directly from an ac input voltage through an inductive link. A series charge injection capacitor following the secondary L₂C₂ tank generates a predefined charging current, like a current source, while the voltage drop across this capacitor does not dissipate power. Consequently, the fixed charging current reduces the energy loss in the charger switches, boosting the capacitor charger efficiency. The proposed system can be utilized for a power-efficient neural stimulator which efficiently charges capacitor banks and injects charge into the neural tissue periodically [5]. In the rest of this brief, Section II describes the concept and implementation of the proposed wireless capacitor charging system. Section III presents circuit details and design considerations, including an active switch driver, an adaptive capacitive tuner, and a dual-output V_TH-compensated rectifier. Measurement results are in Section IV, followed by conclusions in Section V.

II. System Architecture

A. Capacitor Charging Concept

The concept of the proposed capacitor charging system starts from utilizing a series charge injection capacitor as a current source, which generates a fixed amount of predefined charging current. Fig. 2 shows the simplified circuit diagram of the inductive capacitor charging system, which charges a pair of positive and negative capacitors C_P and C_N, respectively. The secondary coil L₂ and its parallel resonant capacitor C₂, which generate a coil voltage V_COIL, are followed by a series charge injection capacitor C_S, which provides an input voltage V_IN to C_P and C_N through switches SW_P and SW_N, respectively. SW_P turns on when V_IN > V_CP form positive C_P charging, and SW_N turns on when V_IN < V_CN for negative C_N charging with respect to the ground GND. When V_CN < V_IN < V_CP, both switches turn off, and V_IN follows V_COIL. Then, when either SW_P or SW_N turns on, the switch connects V_IN to a positive or negative capacitor voltage V_CP or V_CN, holding V_IN relatively constant and generating a fixed charging current I_CH through C_S. For example, when V_IN > V_CP, SW_P connects V_IN to V_CP to hold V_IN around V_CP, while V_COIL keeps increasing. Thus, the voltage variation across C_S, V_COIL – V_IN, generates the positive I_CH until V_COIL reaches its positive peak.When V_COIL starts decreasing from its peak, V_IN also decreases below V_CP, and SW_P turns off. The charging current I_CH can be expressed as

$$I_{\mathrm{CH}}=C_S\times d(V_{\mathrm{COIL}}-V_{\mathrm{IN}})∕dt.$$ (1)

Fig. 2.

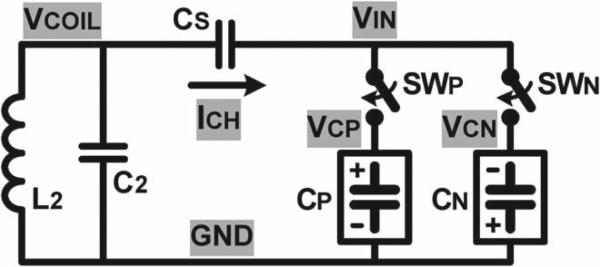
Simplified circuit diagram of the inductive capacitor charging system.

The I_CH value can be adjusted by choosing proper C_S, which will be discussed in Section II-B. Fixed I_CH minimizes the switch loss, while unlike a real current source, the voltage drop across C_S does not dissipate power, improving the charging efficiency from L₂ to the capacitor pair.

B. Charging Time and Efficiency Analysis

The smaller the charging current, the higher the capacitor charging efficiency and the smaller the power loss in switches, leading to longer charging time. Hence, the charging current I_CH should be optimized to charge the capacitors efficiently within a desired period. We modeled the charging time and efficiency depending on I_CH with simplified voltage and current waveforms of the capacitor charging system in Fig. 3. In this analysis, f_c is the carrier frequency that is received via V_COIL, n is the number of charging cycle, and t[n] is the transition time of V_IN when V_CN < V_IN < V_CP. In this simplified model, we assume the following: 1) V_COIL is sinusoidal with a constant peak voltage V_Peak; 2) switches turn on and off at ideal times, and V_IN becomes equal to V_CP or V_CN with negligible voltage drop across closed switches when connected to capacitors; 3) during each charging cycle, V_CP and V_CN are constant, and small voltage increments ΔV_CP and ΔV_CN are added to V_CP and V_CN at the end of each cycle, respectively; and 4) C_P and C_N are equal and charged by the same amount of I_CH, i.e., V_CP = –V_CN.

Fig. 3.

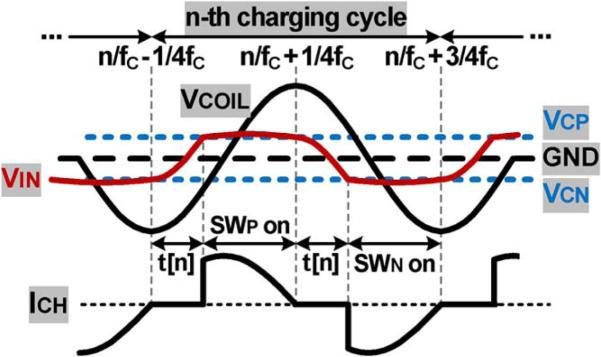
Simplified voltage and current waveforms of the capacitor charging system for modeling and theoretical analysis.

When V_IN is connected to V_CP or V_CN for charging, V_COIL and I_CH can be expressed as

$$V_{\mathrm{COIL}}\left(t\right)=V_{\mathrm{Peak}}\sin \left(2\pi f_{c}t\right)$$ (2)

$$I_{\mathrm{CH}}\left(t\right)=2\pi f_c{C}_S{V}_{\mathrm{Peak}}\cos \left(2\pi f_{c}t\right).$$ (3)

V_CP at the nth charging cycle V_CP[n] can be obtained from

$$V_{\mathrm{CP}}\left[n\right]=\sum _{i=1}^n\Delta V_{\mathrm{CP}}\left[i\right]$$ (4)

where ΔV_CP[n] is the V_CP increment at the nth charging cycle, from the initial condition of V_CP[0] = V_CN[0] = 0 V.

At the nth charging cycle, t[n] is equal to the transition time, in which V_IN increases from V_CN[n–1] to V_CP[n–1]. Therefore,

$$\begin{array}{cc}\hfill V_{\mathrm{CP}}[n-1]-V_{\mathrm{CN}}[n-1]=& 2V_{\mathrm{CP}}[n-1]\hfill \\ \hfill =& {\left[V_{\mathrm{COIL}}\left(t\right)\right]}_{\frac{n}{f_c}-\frac{1}{4f_c}+t\left[n\right]}^{\frac{n}{f_c}+\frac{1}{4f_c}}\hfill \\ \hfill =& V_{\mathrm{Peak}}{\left[\sin \left(2\pi f_{c}t\right)\right]}_{\frac{n}{f_c}-\frac{1}{4f_c}+t\left[n\right]}^{\frac{n}{f_c}+\frac{1}{4f_c}}.\hfill \end{array}$$ (5)

In (5), t[n] can be written as

$$t\left[n\right]=\frac{{\sin }^{-1}\left(-1+\frac{2V_{\mathrm{CP}}[n-1]}{V_{\mathrm{Peak}}}\right)}{2\pi f_c}+\frac{1}{4f_c}.$$ (6)

With t[n] in (6), ΔV_CP[n] can be derived as

$$\begin{array}{cc}\hfill \Delta V_{\mathrm{CP}}\left[n\right]=& \frac{1}{C_P}{\int }_{\frac{n}{f_c}-\frac{1}{4f_c}+t\left[n\right]}^{\frac{n}{f_c}+\frac{1}{4f_c}}{I}_{\mathrm{CH}}\left(t\right)dt\hfill \\ \hfill =& \frac{C_S}{C_P}{V}_{\mathrm{Peak}}{\left[\sin \left(2\pi f_{c}t\right)\right]}_{\frac{n}{f_c}-\frac{1}{4f_c}+t\left[n\right]}^{\frac{n}{f_c}+\frac{1}{4f_c}}\hfill \\ \hfill =& 2\frac{C_S}{C_P}{V}_{\mathrm{Peak}}\left(1-\frac{V_{\mathrm{CP}}[n-1]}{V_{\mathrm{Peak}}}\right).\hfill \end{array}$$ (7)

Therefore, the charging period T_CH during which C_P and C_N are charged to a target charging voltage ±V_TG at the n_CHth charging cycle, can be obtained from

$$T_{\mathrm{CH}}=\frac{n_{\mathrm{CH}}}{f_c},\text{where}{V}_{\mathrm{CP}}\left[n_{\mathrm{CH}}\right]=\sum _{i=1}^{n_{\mathrm{CH}}}\Delta V_{\mathrm{CP}}\left[i\right]=V_{\mathrm{TG}}.$$ (8)

The total energy loss in SW_P and SW_N during n_CH charging cycles E_SW[n_CH] can be calculated as a sum of switching energy losses in each cycle ΔE_SW[n]

$$\Delta E_{\mathrm{SW}}\left[n\right]=2{\int }_{\frac{n}{f_c}-\frac{1}{4f_c}+t\left[n\right]}^{\frac{n}{f_c}+\frac{1}{4f_c}}{I}_{\mathrm{CH}}^2\left(t\right)\times R_{\mathrm{SW}}dt$$ (9)

$$E_{\mathrm{SW}}\left[n_{\mathrm{CH}}\right]=\sum _{i=1}^{n_{\mathrm{CH}}}\Delta E_{\mathrm{SW}}\left[i\right]$$ (10)

where R_SW is the switch resistance.

The capacitor charging efficiency η_CAP from L₂ to the C_P and C_N pair of capacitors can be expressed as

$${\eta }_{\mathrm{CAP}}=\frac{E_{\mathrm{CP}}+E_{\mathrm{CN}}}{E_{\mathrm{CP}}+E_{\mathrm{CN}}+E_{\mathrm{SW}}\left[n_{\mathrm{CH}}\right]+E_{\mathrm{SYS}}}$$ (11)

where E_CP and E_CN are the stored energies in C_P and C_N, respectively, which are $E_{\mathrm{CP}}=C_P{V}_{\mathrm{TG}}^2∕2$ and $E_{\mathrm{CN}}=C_N{V}_{\mathrm{TG}}^2∕2$, respectively, and E_SYS is the energy consumed by the rest of the system during n_CH charging cycles.

Smaller I_CH increases T_CH in (4)–(8), while smaller I_CH and R_SW increase η_CAP in (9)–(11). Therefore, when the maximum tolerable T_CH is known, I_CH can be selected to be as small as it takes T_CH to charge C_P and C_N for C_S and V_Peak values in (3)–(8). C_S should be smaller than C_R, and V_Peak > V_TG.

C. Implementation of the Capacitor Charging System

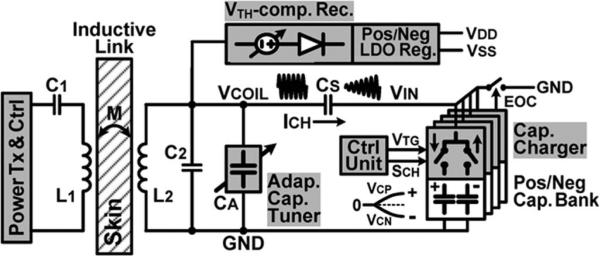
The overall architecture of the proposed capacitor charging system is shown in Fig. 4. A power transmitter drives the primary coil L₁ at the designated carrier frequency f_c, which induces V_COIL across L₂. The capacitor charger consists of switches driven by high-speed active drivers to charge a bank of four pairs of capacitors C_P and C_N. A control unit sets a user-defined target charging voltage V_TG and generates a sequence signal S_CH to operate the four-channel capacitor charger sequentially, which can be utilized in a programmable multielectrode neural stimulation [5]. When charging, the capacitor charger connects V_IN to positive and negative capacitors alternately to hold V_IN at V_CP or V_CN, while generating the fixed charging current I_CH through C_S. In other words, C_S operates like a current source that does not dissipate power, while reducing the switching loss in the capacitor charger and significantly improving the charging efficiency from L₂ to the capacitor bank.

Fig. 4.

Overall architecture of the proposed power-efficient capacitor charging system through an inductive link.

In this capacitor charging system, the secondary resonance capacitance C_R, connected across L₂, can be expressed as

$$C_R=C_2+C_A+\frac{C_S{C}_{\mathrm{Eff}}}{C_S+C_{\mathrm{Eff}}}$$ (12)

where C₂ is the parallel resonant capacitor, C_A is the adaptive tuning capacitor, and C_Eff is the effective capacitance of the capacitor bank, which varies as the capacitor bank voltage and switching duty cycle change. An adaptive capacitor tuner compensates for C_Eff variations by automatically adjusting C_A to keep C_R constant. Therefore, the secondary L₂C₂ tank is maintained at resonance during charging, while maximizing V_COIL. After the charging cycle, an end-of-charge (EOC) signal connects V_IN to GND, and the adaptive capacitor tuner is deactivated, setting C_R = C₂ + C_S. A dual-output V_TH-compensated rectifier followed by low-dropout regulators generates the supply voltages V_DD and V_SS from V_COIL, which has little effect on the charging operation as long as the V_COIL amplitude is kept constant by the adaptive capacitor tuner.

III. Circuit Details and Design Considerations

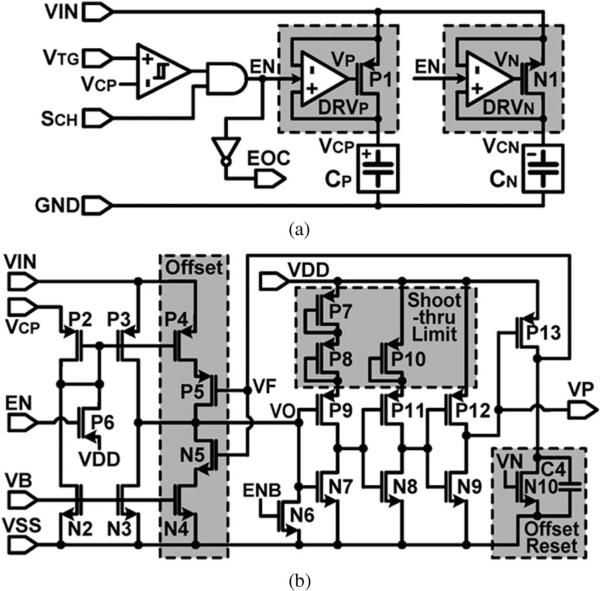
Fig. 5 shows the schematics of the capacitor charger and one of its active switch drivers. In Fig. 5(a), if V_TG > V_CP and S_CH = high, the capacitor charger starts charging the capacitor bank C_P and C_N, with EN = high. When V_IN > V_CP, the active switch driver DRV_P turns on the switch P₁ with V_P = low to provide the positive charging current +I_CH to C_P with a small switch loss. Fig. 5(b) shows the active switch driver (DRV_P ) in which P₂, P₃, N₂, and N₃ form a common-gate comparator, whose inputs are connected to V_CP and V_IN. Since the current drawn from V_IN is much smaller than the charging current, it has little effect on the charging operation. An offset block, which consists of current sources P₄ and N₄ and control switches P₅ and N₅, injects additional positive or negative offset current, depending on a feedback voltage V_F, to expedite V_O transition for fast P₁ switching, maximize the forward current delivered to the capacitor, and minimize the back current to improve the charging efficiency [11]. Since the V_O level depends on V_IN amplitude, which varies during charging, shoot-through limited inverters level-shift V_O to supply levels to drive P₁ with proper V_P levels. An offset reset switch N₁₀, which is driven by V_N, resets the offset by pulling V_F = low after P₁ turns off and V_IN < V_CN for the next C_P charging cycle. Here, the timing of the reset signal depends on V_IN, which, unlike the process-dependent inverter delay in [11], is independent of process variations. DRV_N has a symmetrical structure with respect to DRV_P.

Fig. 5.

Schematic diagrams of (a) the capacitor charger and (b) one of its active switch drivers DRV_P.

Fig. 6 shows the schematic diagram of the adaptive capacitor tuner. A dynamic bias and envelope detector sense the positive V_COIL amplitude and compare it to a threshold window around V_REF =1.2 V. If V_COIL is outside a designated window (2.7–2.8 V_P), UP or DN signals from comparators CMP₁ or CMP₂ trigger a 7-bit up/down counter to progressively adjust a 7-bit binary-scaled set of tuning capacitors C_A =0~127×(8 pF), between V_COIL and GND, to bring V_COIL amplitude back within this window. C_A can accommodate the capacitance variations in (12), which result from C_S (=1 nF in this system) in series with C_Eff as it varies with V_CP,_CN. The switches for tuning capacitors P₁₇ to P₂₃ are driven by V_DDH, which is the higher voltage between V_DD and V_COIL, to ensure proper turnoff.

Fig. 6.

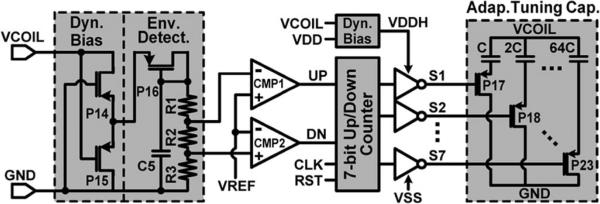
Schematic diagram of the adaptive capacitor tuner.

Fig. 7 shows the schematic diagram of the dual-output V_TH-compensated rectifier. V_COIL is converted to two half waves V_INP and V_INN to prevent overvoltage across the following transistors that constitute a positive and negative rectifier pair, generating V_RECP and V_RECN, respectively. In the positive rectifier, V_TH(P28) of the diode-connected transistor P₂₈ compensates for V_TH(P27) of the rectifying switch P₂₇, resulting in a small voltage drop of V_GS(P27) – V_GS(P28) and high ac–dc power conversion efficiency. R₄ reduces the gate voltage of P₂₇ by discharging C₆ in case V_RECP decreases.

Fig. 7.

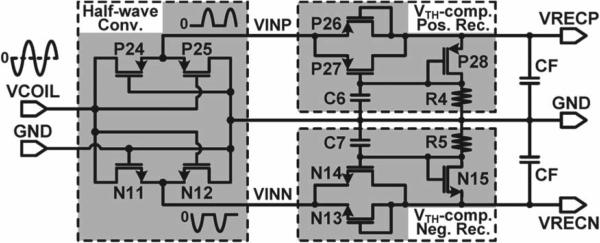
Schematic diagram of the dual-output V_TH-compensated rectifier.

IV. Measurement Results

A. Chip Micrograph and Measured Waveforms

The four-channel capacitor charging system was fabricated in the TSMC 0.35-μm 4M2P n-well standard CMOS process, occupying 2.1 mm². Fig. 8 shows the chip micrograph and floor plan of the charging system along with the inductive powering setup. A class-E power amplifier on the transmitter side drives the primary coil (L₁ = 6.8 μH and ${\varnothing }_1=4\mathrm{cm}$) at 2 MHz and delivers power across a 15-mm gap to the secondary coil (L₂ = 1.2 μH and ${\varnothing }_2=1\mathrm{cm}$).

Fig. 8.

(a) Chip micrograph and (b) testing setup through an inductive link.

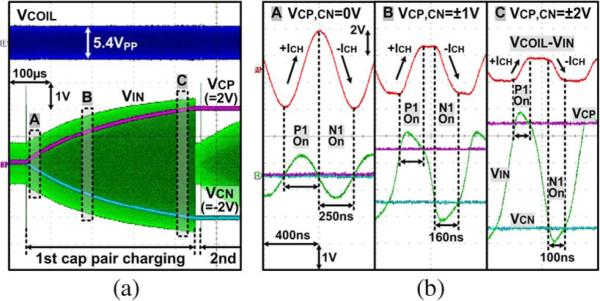
The waveforms in Fig. 9 show how the capacitor bank is being efficiently charged from V_COIL. In Fig. 9(a), the peaks of V_IN follow V_CP and V_CN traces during charging because the fixed charging current I_CH results in a small constant voltage drop across the capacitor charger switches P₁ and N₁. With C_P = C_N = 1 μF, each capacitor pair was charged to V_CP = 2 V and V_CN = –2 V in 420 μs when V_COIL = 2.7 V_P. Fig. 9(b) shows the active switching waveforms when V_CP,_CN = 0, ±1, and ±2 V. When V_IN > V_CP, P₁ turns on, holding V_IN to V_CP plus voltage drop across SW_P, and the voltage across C_S, V_COIL – V_IN, starts to increase, flowing +I_CH into C_P. As V_CP increases, the switching duty cycle decreases while the slope of V_COIL – V_IN remains almost the same, generating a fixed charging current.

Fig. 9.

Measured waveforms of (a) the capacitor charger and (b) its zoomed-in switching as V_CP,CN of 1-μF capacitor pairs reach ±2 V in 420 μs.

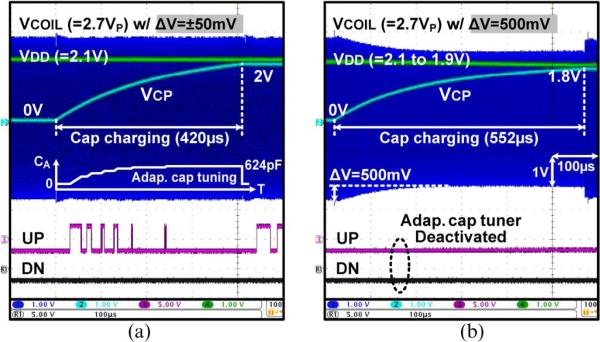
Fig. 10 shows how the adaptive capacitor tuner compensates for the C_Eff variations and maintains V_COIL amplitude constant during charging. In Fig. 10(a), the UP signal triggers the up/down counter, automatically increasing the adaptive tuning capacitor C_A to 624 pF as V_CP increases. Therefore, C_A compensates for the C_Eff variations, and the secondary resonance capacitance C_R in (12) stays at C₂ + C_S during charging, generating a relatively constant V_COIL with small ΔV_COIL = ±50 mV variations. In Fig. 10(b), where the adaptive capacitor tuner is deactivated, the V_COIL amplitude has dropped by 500 mV because of the resonance capacitor detuning, resulting in V_DD reduction and limitation of V_CP to only 1.8 V, instead of the 2-V target. Therefore, the adaptive capacitor tuner ensures proper charging operation with sufficient V_COIL amplitude against C_R detuning.

Fig. 10.

Measured waveforms of V_COIL and V_CP,CN variations during capacitor charging (a) with and (b) without the adaptive capacitor tuning mechanism.

B. Capacitor Charging Time and Efficiency

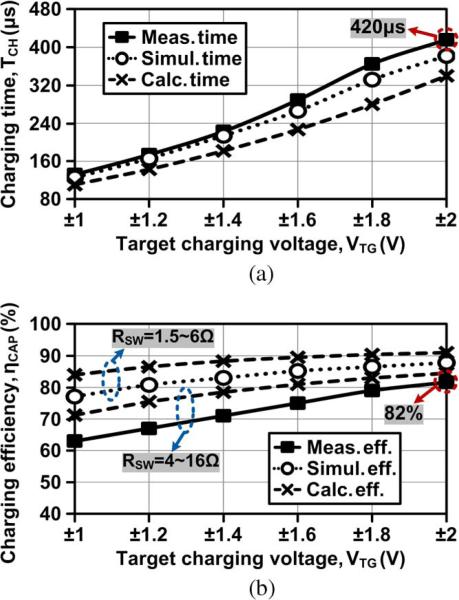
Fig. 11 shows the measured, simulated, and calculated values of the capacitor charging time and efficiency, while sweeping the target charging voltage V_TG from ±1 to ±2 V, to verify the accuracy of our measurement as well as provide insight for further improvements. The calculated charging time and efficiency have been derived from (4)–(8) and (9)–(11) in Section II-B, respectively, with f_c = 2 MHz, C_S = 1 nF, C_P = C_N = 1 μF, and V_Peak = 2.7 V. We assumed that R_SW = 1.5–6 Ω depending on V_CP,CN and the system supply power P_SYS = 400 μW from simulations. In Fig. 11(a), the 1-μF capacitor pair was charged up to ±2 V in 420 μs. The amount of charging current at each charging cycle gradually decreases as capacitors are charged up because V_IN needs longer transition time t[n] in (6) before charging. Therefore, as the capacitor voltages increase, capacitors require longer charging time for the same amount of voltage increment. Shorter charging time in calculations is the result of the ideal switching of SW_P and SW_N, regardless of V_CP,CN levels, which also indicates the maximum possible capacitor charging efficiency.

Fig. 11.

Measured, simulated, and calculated (a) capacitor charging time and (b) charging efficiency versus target charging voltage at f_c = 2 MHz, C_S = 1 nF, C_P = C_N = 1 μF, and V_Peak = 2.7 V.

In Fig. 11(b), the charging efficiency was defined as the stored dc energy in the capacitor bank over the total input ac energy of the capacitor charging system. The highest efficiency of 82% was measured when 1-μF capacitors were charged up to V_TG = ±2 V. Lower |V_CP,CN increases R_SW of P₁ and N₁ switches, leading to larger switching loss and lower charging efficiency as V_TG decreases. Discrepancies between measured and simulated efficiencies mainly result from larger R_SW of the chip, which was estimated about 4–16 Ω by observing voltage drops across switches, compared–to the simulated R_SW = 1.5–6 Ω. The calculated charging efficiency with R_SW = 4–16 Ω shows closer results to the measured efficiency. While R_SW can be further reduced by optimizing the switch sizes, the proposed capacitor charging system achieves a high measured charging efficiency of 63%–82% with C_P = C_N = 1 μF charged up to ±1 ~ ±2 V in 132–420 μs. Table I summarized the specifications of the current inductive capacitor charging system prototype. Table II compares the estimated capacitor charging efficiencies η_CAP when the conventional Li-ion battery charging methods in Fig. 1 are applied to charge capacitors from 0 to 4.2 V in current source mode.

TABLE I.

Capacitor Charging System Specifications

Overall System		Capacitor Charger
Process	0.35 μm CMOS	# of channel	4
L2/C2/CS	1.2μH / 4nF / 1nF	Target voltage	±1 ~ ±2 V
Carrier freq.	2 MHz	Charging off.	63 ~ 82%
Coil distance	1.5 cm	Charging time	132 ~ 420 μs
Vcoil peak	2.7 V	CP/CN	1 μF / 1 μF
Area	2.1 mm2	PSupply(Charging)	240 μW
Rectifier / Regulator		Adaptive Capacitor Tuner
VRECP / VRECN	2.25 V / -2.25 V	Tuning bit	7-bit
VDD / VSS	2.1 V / -2.1 V	Adaptive cap.	0 ~ 1024 pF
Rec. PCE	72% w/50 kΩ	PStatic	20 μW*

^*Simulation

TABLE II.

Benchmarking Capacitor Charging Efficiency

Ref.	VC(V)	VDD(V)	ICS(mA)	ηACDC(%)*	ηDCDC(%)	ηCHG(%)**	ηCAP(%)***
[8]	0~4.2	4.3	3	80	-	48.8	39
[9]	0~4.2	VC+0.2	800	80	90	91.3	65.7
[10]	0~4.2	VC+0.3	698	80	-	87.5	70
This work	0~±2	2.7VPeakAC (Vcoil)	34 (max)	Not needed	-	82	82

^*Power efficiency of the active rectifier in [7]

^**Charger efficiency, η_CHG = avg (V_C / V_DD)

^***η_CAP = η_ACDC × η_DCDC × η_CHG.

V. Conclusion

We have demonstrated a power-efficient wireless capacitor charging system for inductively powered applications. A fixed charging current generated by applying part of the coil voltage across a series charge injection capacitor charges a capacitor bank with small energy loss, improving the charging efficiency. During charging, an adaptive capacitor tuner maintains the inductive link at resonance, providing a constant coil voltage within a designated window. The charging time and efficiency of the system have also been analyzed to provide designers with better insight toward maximizing the charging efficiency for given charging time and capacitor bank values. This system is expected to improve the overall power efficiency in IMDs that utilize capacitor banks for energy storage and stimulation [5].