A Reexamination of Connectivity Trends via Exponential Random Graph Modeling in Two IDU Risk Networks

Abstract

Patterns of risk in injecting drug user (IDU) networks have been a key focus of network approaches to HIV transmission histories. New network modeling techniques allow for a reexamination of these patterns with greater statistical accuracy and the comparative weighting of model elements. This paper describes the results of a reexamination of network data from the SFHR and P90 data sets using Exponential Random Graph Modeling. The results show that “transitive closure” is an important feature of IDU network topologies, and provides relative importance measures for race/ethnicity, age, gender, and number of risk partners in predicting risk relationships.

INTRODUCTION

Patterns of social and risk bearing connectivity in injecting drug user (IDU) risk networks have been a consistent concern as researchers attempt to understand disease transmission among people who inject drugs (PWID) and between their networks and surrounding communities. Until recently, however, statistical modeling of network connectivity has posed considerable difficulty. The reasons for this are straightforward: ordinary statistical modeling techniques involve linear regression and other forms of tests-against-randomness to determine the relative importance of model factors as they influence the likelihood of particular data samples. Such tests against randomness, however, are not feasible when considering patterns of connectivity in networks, even with recent gains in computational power.¹

For this reason, past analyses of IDU and other social network data has had to be content with insights derived from the cross-tabulation of connection data (how many men, for example, connect to other men, versus how many men connect to women). While insightful and capable of answering questions of the dependence and independence of network variables, such statistics do not provide measures of certainty or error, nor relative weights of model elements vis-à-vis one another; nor can they tell us how likely the observed patterns are to be the product of random assortment (rather than the result of actual connection preferences among network members). Exponential Random Graph Modeling provides an alternative to these techniques. Described in more detail below, ERGM techniques can provide likelihood-based estimates of how factors such as gender, age, or race/ethnicity, injection history or network position influence overall network connection tendencies where ordinary statistical methods cannot.

A discussion of the results of a reanalysis of the two well-known IDU network data sets follows. The strategy employed here was (step 1) to use ERGM techniques to consider each of several potential network-influencing variables in isolation, and then (step 2) to isolate the effects of attribute homophily (the tendency of people with “like” attributes to form connections with one another) from disproportionate interconnectedness that may be due to differences in the network size of subcategories of each variable (i.e. “degree homophily,” as when, for example, men to have larger risk networks than women and thus wind up with more connections to men, not through choice but due to the sheer size of their networks). In the 3-nal stage of the analysis, several multivariate models composed of elements shown to be significant in steps 1 and 2 are tested. These results allow us to see the relative importance of a number of model variables to the patterns of connectivity demonstrated by two well-known IDU risk networks, thereby extending and clarifying many of the findings by the initial study authors, and allowing us to reflect on current trends in disease prevention advocated for PWID.²

Exponential Random Graph Modeling

ERGM is a statistical technique aimed at determining the extent to which the likelihood of network linkages appears to be biased towards (or against) the creation of specified network substructures, above and beyond what is expected by chance occurrence. Such substructures can be as simple as the tendency of “like” nodes to be connected (at a greater rate than expected by a random distribution of connections), or as complex as specific substructures of connection between several individuals (Bearman, Moody, & Stovel, 2004). ERGM is a relatively new technique, and at present is the only technique available capable of producing results akin to those expected for the statistical analysis of nonnetwork social data. The theoretical basis for ERGM analysis was laid down by Holland and Leinhardt (1981) and Frank and Straus (1986), but estimation questions were only finally settled recently (Snijders et al., 2006).

Like ordinary statistical regression analysis, ERGM modeling aims to determine the probability, as a linear function, of one or more predictors for the distribution of a set of observations (in this case, the observed set connections in the network under consideration). In this paper, we follow the analytical lead of Goodreau, Kitts and Morris (2009) in using ERGM to ascertain the importance of both specific network substructures (triads) and node-based homophily (the tendency of association between “like” nodes). The same analysis is carried out over two separate and well-known IDU/Sexual Risk networks.

According to Kolaczyk (2010, p. 180–181), an exponential family random graph takes the following form: given a random graph G = (V, E) with binary random variable Y = [Y_ij] that expresses the presence or absence of an network connection e ε E from i to j, then the probability of a set of ties Y can be given as

$$P_{\theta }(Y=y)=\frac{1}{k}exp\left\{\sum _H{\theta }_H{g}_H(y)\right\},$$ (1)

where H is a possible set of edges in G. Here, g_H(y) is taken to be 1 if H actually occurs in y, or 0 if it does not, and a non-zero value for θ_H is said to exist where Y_ij are dependent for all pairs {i,j} in H. The normalizing constant κ = κ(θ) is defined as

$$\kappa (\theta )=\sum _{y}exp\left\{\sum _H{\theta }_H{g}_H(y)\right\}.$$ (2)

As with ordinary statistical regression analysis, here g_H(y) can stand for a series of model covariates that may be deemed important to network formation and which may be calculated on y: g₁ g₂ g₃ … g_h. The coefficients of g_h, (θ₁, θ₂, θ₃ … θ_h) determine the weight of the respective covariates which are to be estimated by the ERGM process.

Following Goodreau et al. (2009, p. 109), Equation (1) can be reexpressed as the conditional log odds of individual ties (in logit form):

$$\mathit{logit}(P(Y_{ij}=1\mid n\text{actors},Y_{ij}^c))={\sum }_{h=1}^H{\theta }_h\delta z_h(y),$$ (3)

where $Y_{ij}^c$ is all dyads other than Y_ij and δz_h(y) is the amount by which the covariate g_h(y) changes when Y_ij is changed from 0 → 1, or from 1 → 0. Here, $Y_{ij}^c$ ensures the mutual dependence of ties in the conditional, and obviously a single tie may affect multiple covariates.

The interpretation of θ in the expression above is that, where the addition of a tie i → j increases z_h by 1, then the log odds of that tie forming increases by θ_h. According to Goodreau et al. (2009, p. 109), this interpretation requires three assumptions. The first is that the ties in the network are homogenous, such that the change measured in the z statistic (say, when counting the number of such connections in the network between “like nodes,” or the number of ties which complete a triad) with the toggling of i → j would treat all other examples of such ties present in the network as equally probable. Second, when modeling the effect of node-based attributes (such as gender or age) on the presence or absence of ties between nodes, the model assumes that the importance of a given attribute on a dyad pair will be determined based only on the presence or absence of that attribute, and not on the value of other ties in the network. That is, where a node attribute is considered for its importance in tie formation, the effects of this attribute are assumed to function independent of the effects of other attributes.³

And finally, as Goodreau et al. (2009, p. 109–110) point out, the determination of θ which provides the maximum likelihood of the known graph is problematic, given that the normalizing constant κ(θ) is incalculable for all but the smallest networks (see note 7, above). However, the estimation of κ(θ) can be undertaken using Markov Chain Monte Carlo methods, as shown by Snijders (2002; Snijders et al., 2006) and others (Hunter, Handcock, Butts, Goodreau, & Morris, 2008; Morris et al., 2008; Robins, Pattison, Kalish & Lusher, 2007). As Goodreau et al., (2009, p. 110–111) discuss, such procedures can be used to simulate network dynamics (Goodreau, 2007) and to test for model degeneracy as well. Such a system can also make use of any number of ordinary network measures (such as “centrality measures” or “constraint”), the number of ties incident to a specific attribute class, or network-structure-based characteristics like the tendency to “transitive closure.” In such a case, each of these is treated as a distinct model variable, and each assigned a separate coefficient.

In the following analysis, special attention is paid to homophily and transitive closure. Homophily is the tendency of “like” nodes to connect with one another—in this case as a variable that measures the extent to which, respectively, racial/ethnic affiliation, age, or gender “sameness” affects the likelihood of there being a connection among two randomly chosen nodes (individuals) in the network above a level expected by simple random mixing. In addition, we also investigate the extent to which network importance—in this case as indicated by self-estimated total number of injection partners—displays homophilous tendencies as well.⁴

Beyond homophily in gender, age, race/ethnicity, and number of injection partners, another significant variable traced here is transitive closure, also known as network transitivity (Goodreau, Kitts, & Morris, 2009). Transitive closure in this sense is the tendency of two nodes (or people) to share a connection with one another given their simultaneous mutual connection to a third node, independent of other considerations (such as homophily of degree or some other attribute). Thus in Figure 1, transitive closure is defined as the tendency for A to form a connection with C, given their mutual connection with B (over and above the likelihood of that connection existing via random mixing).

FIGURE 1.

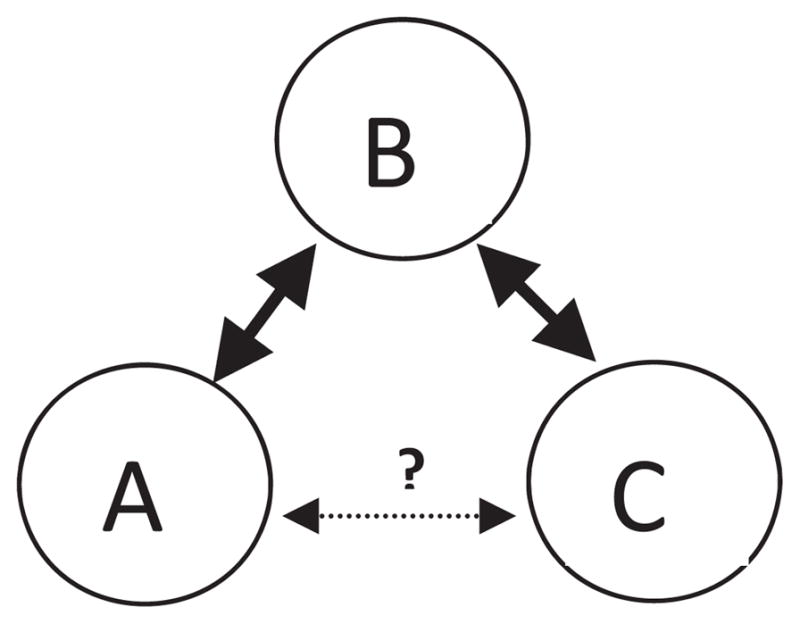
An example of transitive closure.

As above, the strategy of the ERGM analysis that follows contains three steps. In the first step, we isolate each potential variable and test its influence on the formation of network connections (given the total size and density of the network; see Table 1a and b). In this case, we draw on the conclusions of the studies’ original authors. Specifically, the variables we tested were homophily with regard to race/ethnicity, disease status of HIV and syphilis, gender, marital status, income, age, education level, work as prostitute, number of injection partners, transitive closure, and cycle lengths of 4 and 5. This produces a table for each of the two studies in which each individual variable found to be significant, and each of its possible categorical values, is assigned an exponent, together with an error score and significance level. These tables provide the extent to which each variable, taken in isolation, appears to influence the pattern of connectivity in each network. Of the variables we tested, we found that ethnicity, gender, age, number of injection partners, and transitive closure were the most influential (and statistically significant) in predicting observed network topologies in the SFHR and P90 data.

TABLE 1a.

Individual variable results for SFHR)^#.

Variable name	Edges value	Θ	Error	p
Edges	−6.343		0.044	***
Transitive closure	−6.257	3.422	0.076	***
Gender homophily (all)	−6.520	0.286	0.092	**
Gender (male)	–	0.257	0.096	**
Gender (female)	–	0.439	0.111	**
Race/ethnic homophily (all)	−7.044	1.394	0.094	***
R/E (Black)	–	1.043	0.120	***
R/E (Hispanic)	–	1.801	0.122	***
R/E (White)	–	1.513	0.121	***
R/E (Other)	–	–Inf	NA	NA
Age homophily (all)	−6.43338	0.382	0.099	***
Age (15–19)	–	3.794	1.036	***
Age (20–24)	–	0.229	1.002	0.819
Age (25–29)	–	0.306	0.199	0.125
Age (30–34)	–	0.478	0.170	**
Age (35–39)	–	0.341	0.160	*
Age (40–44)	–	0.329	0.196	0.093
Age (45–49)	–	0.904	1.003	0.368
Age (50–54)	–	1.934	1.007	0.055
Age (55–59)	–	–Inf	NA	NA
Age (60+)	–	–Inf	NA	NA
# Injection partners last 30 days homophily (all)	−6.457	0.418	0.094	***
0 partners	–	1.348	0.504	**
1 partners	–	0.276	0.106	**
2 partners	–	0.731	0.204	***
3 partners	–	1.155	0.321	***
4+ partners	–	2.418	0.508	***

^#In Table 1a, and all subsequent tables, the exponent value –Inf indicates a situation where too few nodes of the respective variable value (Age 55–59, for example) were present to allow for estimation. As a result, no exponent is estimated and the resulting error and significance levels are labeled Not Applicable (NA).

^***(p < .001);

^**(p < .01);

^*(p < .05).

TABLE 1b.

Individual variable results for P90

Variable name	Edges	Θ	Error	p
Edges	−4.668		0.037	***
Transitive closure	−5.000	1.673	0.036	***
Gender homophily (all)	−4.701	0.082	0.075	0.274
Gender (male)	–	−0.877	0.140	***
Gender (female)	–	0.54091	0.080	***
Race/ethnic homophily (all)	−4.99091	0.750	0.074	***
R/E (Black/AA)	–	0.585	0.080	***
R/E (Hispanic)	–	1.509	0.122	***
R/E (White)	–	0.909	0.221	***
R/E (Other)	–	1.612	0.590	**
Age homophily (all)	−4.77483	0.582	0.088	***
Age (15–19)	–	1.278	0.509	*
Age (20–24)	–	0.767	0.173	***
Age (25–29)	–	0.671	0.139	***
Age (30–34)	v	0.343	0.156	*
Age (35–39)	–	0.337	0.241	0.161
Age (40–44)	–	1.137	0.340	***
Age (45–49)	–	–Inf	NA	NA
Age (50–54)	–	–Inf	NA	NA
Age (55–59)	–	–Inf	NA	NA
Age (60+)	–	–Inf	NA	NA
Injection partners last 5 years homophily (all)	−5.066	1.053	0.074	***
0 partners	–	1.070	0.076	***
1 partner	–	0.574	0.322	0.075
2–3 partners	–	0.792	0.284	**
4–6 partners	–	1.162	0.455	*
6 or more partners	–	1.314	0.251	***

^***(p < .001);

^**(p < .01);

^*(p < .05).

The second step in the analysis involved examining the effects of different average personal network size on the results of step 1, to eliminate the possibility that homophiles discovered in step 1 may be due to differences in the average level of connectedness of any one of the subgroups within each attribute class (Table 2a & b). In the third and final step, a series of composite models are tested to determine the relative importance of each attribute versus transitive closure, and a full model of the variables from Table 1a and b is produced to indicate the relative importance of all variables relative to one another. All three steps are carried out for each data set: both SFHR and P90. As discussed below, while the distributions of race/gender/age/injection pairings within both of these networks has been well documented, the likelihood of the pattern of connections appearing as discovered (given the size and density of each network) has not been previously analyzed, largely because such methods were not possible until long after these studies were concluded.⁵ The purposes of the analysis here is to do just that.

TABLE 2a.

Degree-based homophily comparison results for SFHR

Variable subcategory	θ	Error	p
Gender (male)	−3.160	0.030	***
Gender (female)	−3.198	0.054	***
Age (15–19)	−3.469	0.408	***
Age (20–24)	−3.323	0.163	***
Age (25–29)	−3.213	0.067	***
Age (30–34)	−3.039	0.058	***
Age (35–39)	−3.093	0.055	***
Age (40–44)	−3.312	0.070	***
Age (45–49)	−3.308	0.191	***
Age (50–54)	−3.335	0.249	***
Age (55–59)	−3.757	0.577	***
Age (60+)	−3.467	1.001	***
R/E (Black/AA)	−2.848	0.277	***
R/E (Hispanic)	−3.049	0.052	***
R/E (White)	−3.144	0.050	***
R/E (Other)	−3.295	0.047	***

^***(p < .001).

TABLE 2b.

Degree-based homophily comparison results for P90

Variable subcategory	θ	Error	p
Gender (male)	−3.084	0.043	***
Gender (female)	−2.521	0.031	***
Race/ethnicity (Black/AA)	−2.780	0.032	***
Race/ethnicity (Hispanic)	−2.536	0.051	***
Race/ethnicity (White)	−3.047	0.080	***
Race/ethnicity (Other)	−2.916	0.146	***
Age (15–19)	−2.756	0.123	***
Age (20–24)	−2.768	0.063	***
Age (25–29)	−2.591	0.049	***
Age (30–34)	−2.810	0.054	***
Age (35–39)	−2.746	0.066	***
Age (40–44)	−3.029	0.111	***
Age (45–49)	−3.470	0.291	***
Age (50–54)	−2.723	0.177	***
Age (55–59)	−3.883	0.503	***
Age (60+)	−2.971	0.282	***

^***(p < .001).

The SFHR and P90 Data

Existing publications from the SFHR and Project 90 studies focus on the unique topology of their respective “risk” networks, with a view to explaining disparate rates of sex/injection transmitted infections, including HIV transmission and prevalence within geographically-differentiated high-risk populations; in retrospect, the Bushwick and Colorado Springs networks appear as complementary examples, helping to clarify trends that might seem idiosyncratic to one or the other, while ultimately revealing mutually supporting findings between network location and HIV risk.

The SFHR study produced a wealth of landmark data on network substructures, and their relationship to HIV/infection transmission (Friedman et al., 2010). Conducted between 1990 and 1993, SFHR was a cross-sectional, mixed methods project that asked 767 out-of-treatment IDUs about their risk networks and HIV risk behaviors in the prior 30 days. Interested in both individuals’ network composition (namely, the presence of high-risk partners) and sociometric risk position, the SFHR study produced several major findings relevant to risk populations with high HIV prevalence and low secondary incidence (Friedman, Furst, et al., 1998; Friedman, Mateu-Gelabert et al., 2007; Goldstein et al., 1995; Des Jarlais et al., 1998; Jose et al., 1993; Kottiri et al., 2002; Neaigus et al., 1994, 1995). SFHR documented 92 connected components among 767 subjects, including a 105-member 2-core within a large connected component of 230 individuals. With subjects located within the 2-core more likely to be infected with HIV (Friedman et al., 1997), the study emphasized the importance of HIV prevention within densely-connected network. Yet the unique microstructures of the SFHR network also explained surprisingly low rates of ongoing HIV transmission among IDUs and their contacts, particularly in the absence of network saturation with HIV. Where the relatively small sizes of subnetworks consisting wholly of HIV-negative individuals limited the likelihood of large-scale outbreaks, the authors posited the importance of network “firewalls,” i.e., long-term HIV-positive individuals, whose infectivity had diminished over time (Friedman et al., 2000). Investigation of the causes of several of the phenomena noted by SFHR study remains ongoing and of particular importance to HIV prevention and control.

Among the most central findings, SFHR characterized the salience of personal network composition with regards to race/ethnicity. While membership in the 2-core was roughly the same across ethnic groups, SFHR documented significantly higher rates of HIV infection among African-American and Hispanic subjects. Study authors ultimately tied elevated HIV prevalence in these groups to homophily in edge formation along ethnic/racial lines (Friedman et al., 1997). Writing that HIV spread more rapidly among African American and Hispanic individuals in the earliest stages of the epidemic, SFHR reasoned that the tendency among study subjects to form ethnically homogeneous networks accelerated HIV infection within existing high prevalence groups (Kottiri et al., 2002).

Conducted between 1988 and 1992 in Colorado Springs, Project 90 was a prospective study of heterosexual subjects who were defined as being at “high-risk” for STI/HIV infection (Klovdahl et al. 1994; Potterat et al., 2002). Eligible subjects reported at least one of the following behaviors in the past 12 months: exchanging sex for money or drugs, sex (paying or nonpaying) with a prostitute, injection of illicit drugs, or sex with an injection drug user. Unlike the cross-sectional SFHR, the Project 90 study followed its subjects for up to 5 years, with no requirement for year-to-year continuity; new subjects were additionally recruited each year. Five hundred ninety-five enrolled individuals produced 1091 interviews, which named 8164 network contacts overall. The multitude of papers arising from the Project 90 study linked the low prevalence and incidence of HIV in Colorado Springs to the relative dearth of HIV positive individuals in the densely connected network core (Klovdahl et al., 1994; Potterat, Rothenberg, & Muth, 1999; Potterat et al., 1993; Potterat et al., 2002; Rothenberg, Potterat, & Woodhouse, 1996; Woodhouse et al., 1994). While 36 subjects in the cumulative study population (including reported contacts) were HIV positive, only 16 were located within the large connected component of the network linking 7151 individuals, and they occupied peripheral positions therein; no HIV-positive individuals were found within the 3-core of the largest connected component—the “heart of the risk network” (Potterat et al., 2002, p. 103). Although Project 90 revealed a densely-connected network of individuals involved in high-risk behaviors, it simultaneously spoke to the importance of network centrality for infected individuals in predicting the epidemic spread of HIV.

Description of Data Manipulation

Original data from the Project 90 and SFHR studies was procured with the full consent of all original authors. While each study collected overlapping network information on IDU subjects, their respective research goals and study designs varied widely, requiring limited manipulation of existing data for reanalysis. The design of the Project 90, a multiwave prospective study, also posed a unique analytic challenge.

The SFHR study collected baseline information on the demographic traits, risk behaviors, and risk network of 767 subjects, additionally documenting 662 edges within the network. All SFHR subjects and their mutual connections were included in this reanalysis, and the original coding of subject attributes was retained for use as partition data in the ERGM analysis. While Project 90 collected similar demographic data on all subjects, all variables were recoded for concordance with SFHR. In addition, not all subjects in the Project 90 data set were included in this analysis. Subjects eligible for inclusion in this analysis included only those who (1) received an HIV test during the original study, (2) completed at least one survey during the study period, and (3) were linked to at least one other study subject who also met criteria 1 and 2. In the end, this reanalysis included 401 vertices and 921 edges from the original Project 90 data set.⁶

Results: Step 1

In the tables below, a number of models are presented. In the first set of analyses (Table 1a & b), ERGM analysis was used to obtain an initial “edges” measure (row 1). The value of the “edges” measure represents the log odds that a randomly chose pair of nodes in the network will have a connection between them based only on the total number of connections in the network. Such a statistic is given because it provides a “baseline” measure against which the influence of the other “tested” variables can be determined. Thus, in each subsequent model, the edges measure is tested in bivariate mode with another single variable (transitive closure, age, gender, race/ethnicity, and number of partners) to determine the extent to which homophily in the second variable (i.e., age, race/ethnicity, gender, and number of injection partners) and network considerations (i.e., transitive closure) influence edge formation over and above that expected when only the density of the graph (shown as edges) is considered. This adjusted θ_edges value is given in the “edges” column in each table for easy comparison with the θ_variable value for each covariate. In these bivariate cases, the edges coefficient is expected to diminish in those cases where the additional variable exerts significant positive influence on the pattern of connectivity. Thus, for the interpretation of each model (i.e., row), one first examines the edges value and compares the subsequent variable value θ to determine the relative influence of the identified variable against the value expected given a random distribution seen in edges.⁷

Several observations can be made from the above data.

• Both Table 1a and b show transitive closure to be the most significant factor, when taken in isolation, in determining the given patterns of edge formation. Put another way, in comparison with the other variables (considered individually), structural features trump attribute features in determining the patterns of connection seen in both the SFHR and P90 networks by a considerable margin.

• For P90, homophily across self-identified number of injection partners proved more important than other forms of homophily. That is, the tendency of people to partner with others who share roughly the same number of partners was a more important consideration than age, race/ethnicity, or gender in predicting the pattern of connections seen in the network documented by researchers in Colorado Springs.

• Homophily among self-estimated number of injection partners was also significant among network members in the SFHR network, although it was of less importance there than race/ethnicity.

• In both networks, the highest level of homophily among number of injection partners was seen among particular variable values, i.e., those with higher numbers of partners—three or more partners in the SFHR network; four or more partners in the P90 network. Homophily levels among those with lower numbers of self-identified partners were much lower. Thus, in both networks, those with the greatest number of partners tended to be connected to one another, validating the findings of a tightly connected core in both the P90 and SFHR studies.

• Gender homophily was not significant in the P90 data, though the overall nature of the measure in the aggregate may have masked an important feature of the network. In the Colorado Springs data, men and women showed robust but opposite trends. Men showed significant (p < .001) negative homophily (sometimes called heterophily) in their risk relationships—indicating that, as per the original design of the study, heterosexual sex was a primary risk relationship governing connectivity trends. Women in the same data set, on the other hand, showed a lower but equally robust trend to homophily (also p < .001).⁸

• The same was not true of gender in the SFHR network, where both men and women showed positive trends toward homophily, though here too women showed a stronger trend to mutual association in their risk relationships than men.

• Age homophily was significant in both networks, though in both cases it applied only narrowly across age variable values. The overall effect, although, was a significant if somewhat less important source of connectivity dynamics than either race or structural considerations.

Results: Step 2

To determine whether the homophily results shown in Tables 1a and b were the result of attribute homophily rather than degree homophily, a further set of analyses were done (Tables 2a and b). Such tests are necessary where potential differences in average degree across attribute values can mistakenly appear as tendencies to mutual affiliation. For example, in a network where the average number of network connections of women is twice that of men, a random distribution of edges that follows the degree patterns would result in many more connections between women than between men, even where the number of men and women were the same, and even where no actual preference for same-gender affiliation was present. The latter would be an example of degree-based confounding of attribute homophily.

For purposes of determining whether differences in average degree by attribute value figured importantly in the distribution of connections, ERGM analysis was used to determine the probability of an edge appearing between two randomly selected nodes where either one of the nodes was a member of the subcategory in question. Such a test isolates degree-based values from any homophily considerations by considering the attribute in only one half of the dyad pair. Thus Table 2a, line 1 shows that the likelihood of a randomly chosen connection in the SFHR network will have a single node identified as male as one of its end points. In this case the value of e^−3.16 in line 1 can be compared with the value for women, e^−3.20 in line 2, to see that gender value has little effect on the likelihood of being incident to a connection. In such a case, the gender homophily for the SFHR network (in the corresponding Table 1a) can be seen as largely the result of gender assortment preferences, and not the result of markedly different levels of connection between men and women.

Put more generally, similar values for exponents across the list of values for a particular attribute indicate that differences in average degree across those same categories do not play a significant role in explaining the homophily scores identified in Tables 1a and b. When we turn to Table 2a and b, then, the result of degree-based tests for all attribute values (with the exception of self-estimated number of injection partners, which is already associated with network degree in both networks) shows that the results are robust with respect to degree in all cases except gender in the P90 network.

According to the results shown in Table 2a and b, the following observations can be made:

• The results of these analyses indicate that for the SFHR network (Table 2a), degree considerations do not play a major role in any of the attribute homophily trends seen in Table 1a. Large differences in the θ value for attribute values in Table 2a are rare, appearing mainly at the lowest and highest age brackets, and accompanied there by relatively large error scores.

• In the P90 network, noticeable differences appear between genders (θ = −3.08 for men; = −2.52 for women). Such a score indicates that women are e^{−2.52−(−3.08)} = e^.56 = 1.75 times more likely to be part of a dyad because of differences in average degree than are men. Given that this difference is roughly equivalent to the homophily exponent for women in the P90 network (θ_{women (attribute homophily)} = 0.541 in Table 1b; θ_{women (degree homophily difference)} = 0.563 from Table 2b), it is likely that the majority of the homophily between women in the P90 network seen in Table 1b may be due to differences in average degree rather than tendencies for women to engage in risk relationships with one another (at a higher rate than predicted by random assortment, and at a higher rate than their male network counterparts).

• Similar differences exist among a small number of age categories in the P90 data as well. Such differences are difficult to quantify across a large number of subcategories, but a comparison of these subcategories with their exponents given in Table 1b indicates that all of the divergent values (age 45–49, age 55–59) appear in subcategories whose internal connectedness was too low to compute meaningful homophily scores (as indicated in Table 1b by the –inf value of θ).

Results: Step 3

Given these results, several larger multivariate models were tested to determine the effect of various model parameters on one another, and to get a better understanding of the relative importance of network-based (i.e., transitive closure) versus node attribute-based (i.e., homophily across personal attributes) factors in both networks. These results are available in Table 3a and b. In both cases, four models were tested. In the first three, transitive closure was tested against the influence of age-based, gender-based, and race/ethnicity-based homophily. In the final model (4), a composite of transitive closure, self-estimated number of injection partners, and the three attributes from models 1–3 was tested.

TABLE 3a.

Multivariate models for SFHR

Model	Variables	Edges	θ	Error	p
1	Transitive closure	−6.976	4.902	0.076	***
	Age homophily	–	0.821	0.103	***
2	Transitive closure	−6.917	4.306	0.076	***
	Gender homophily	–	0.277	0.096	**
3	Transitive closure	−7.390	3.715	0.000	***
	Race/ethnicity homophily	–	0.843	0.006	***
4	Transitive closure	−7.583	3.592	0.020	***
	Age homophily	–	0.367	0.115	**
	Gender homophily	–	0.058	0.102	0.566
	Race/ethnicity homophily	–	1.205	0.098	***
	Injection partner homophily	–	0.460	0.104	***

^***(p < .001);

^**(p < .01);

^*(p < .05).

TABLE 3b.

Multivariate models for P90

Model	Variables	Edges	θ	Error	p
1	Transitive closure	−5.517	2.501	0.036	***
	Age homophily	–	−0.101	0.095	0.290
2	Transitive closure	−4.845	1.740	0.037	***
	Gender homophily	–	−0.145	0.083	0.081
3	Transitive closure	−5.170	1.710	0.037	***
	Race/ethnicity homophily	–	0.659	0.319	***
4	Transitive closure	−5.438	1.375	0.000	***
	Age homophily	–	0.458	0.001	***
	Gender homophily	–	−0.360	0.000	***
	Race/ethnicity homophily	–	0.614	0.001	***
	Injection partner homophily	–	0.574	0.000	***

^***(p < .001);

^**(p < .01);

^*(p < .05).

• As in Tables 1a and b, transitive closure continues to show far greater exponent values than any other variable. This is true for both the SFHR and P90 data sets, with the greater differences seen in the SFHR network. Given that the values given in Tables 3a and b represent log odds, they can be interpreted to indicate that (see model 4 in Table 3a) transitive closure is:

  • e^{3.592–0.367} = e^3.225 = ~25 times more important than age,

  • e^{3.592–1.205} = e^2.387 = ~11 times more important than race/ethnicity,

  • and e^{3.592–0.460} = e^3.132 = ~23 times more important than the number of recent injection partners, in determining the likelihood of individual connection choices.

• Similar, although smaller differences can be seen in Table 3b, model 4. There, structural features (i.e., transitive closure) are:

  • e^{1.375–0.458} = e^0.917 = ~2.5 times more important than age,

  • e^{1.375–0.360} = e^2.387 = ~2.8 times more important than gender,

  • e^{1.375–0.614} = e^0.761 = ~2.1 times more important than race/ethnicity

  • and e^{1.375–0.574} = e^0.801 = ~2.2 times more important than the number of recent injection partners, in determining the likelihood of individual connection choices.

• In the SFHR network, race/ethnicity remained the second most important factor in determining node connection patterns, as discussed by the original research (Friedman et al., 1997; Friedman et al., 2010). This was true for the P90 network as well, though here the differences with other attributes were less.

• Interestingly, gender dropped out of significance in the SFHR network (Table 3a, model 4), indicating that its significance in Table 1a likely masked a more significant covariation relationship with one of the other attributes. The opposite was true for the P90 network. Here, gender was not statistically significant in Table 1b, but is (at the p < .001 level) in Table 3b. As discussed above, this is perhaps due to the greater number of men in the network than women, and possible to the fact that the positive homophily shown for women in Table 1b was a mask for degree considerations (as indicated in Table 2b)—a confounding relationship (with injection partners) that was uncovered in the multivariate analysis.

DISCUSSION

The most noteworthy observation from the analysis above is the extent to which structural features of the network play a role in determining the potential paths of risk among drug injectors. Individuals in the SFHR network choose partners of current partners far more frequently than any other category, by a factor approaching 10–20 times more likely. Similar if less dramatic results obtained for the P90 network as well. Together, these findings lend weight and credibility to those approaches to risk that emphasize specific network topological features over individual behavior in understanding disease risk management and community dynamics.

The findings presented here also extend a central analytical emphasis in the SFHR analysis. Prior analysis emphasized the presence of a core group of drug users with markedly different behavioral, HIV, and risk profiles (Curtis et al., 1995; Friedman et al., 1997; Friedman et al., 2000). The discovery of transitive closure as a paramount consideration in understanding patterns of risk underscores these findings. Coupled with the finding that individuals with high numbers of risk partners tend to associate with one another at levels higher than any consideration including race/ethnicity (except transitive closure), we find a ready explanation for how the core of Bushwick network was formed and maintained. Indeed, among those with the highest number of injection partners, similarity of degree (i.e. number of partners) outweighed all factors except transitivity in explaining connection preferences (with an exponent value of θ_4+partners = 4.418, compared to θ_race = 1.394). Repeated emphasis on such close clustering can be easily seen to lead to the sort of network core described by SFHR authors (Curtis et al., 1995; Friedman et al., 1997), and provides further evidence for a network-based approach to IDU risk (Dombrowski et al., 2012; Friedman, Neaigus et al., 1998).

In considering the causes of such a pattern, several phenomena noted for the Bushwick network suggest themselves. Foremost among these is the central role that shooting galleries played as venues for drug use (Curtis et al., 1995; Friedman et al., 2010). These and other forms of enforced propinquity were encouraged by significant changes in drug enforcement regimes in New York at the time. During the 1991–1993 time frame, New York City as a whole (Curtis, 1998; Curtis & Wendel, 2000), and Bushwick in particular was undergoing a change in drug interdiction regimes aimed at closing down “open air” drug markets and injection locations (Curtis, 1996; Dombrowski et al., 2013). This strategy involved broad “sweeps” in which outdoor users were routinely arrested for small amounts of drug possession. As places serving as outdoor drug use locations were increasingly systematically pursued by law enforcement, outdoor drug use became increasingly precarious, and indoor, more discreet drug use locations (shooting galleries) grew in importance as a result (Curtis & Sviridoff, 1994). Local estimates place them at 5 or 6 in Bushwick at any given time over the course of the 2 year study, and fluidity among locations was constant as interdiction turned toward these locations as well. All of these factors could be seen as contributing to a situation where drug use partners of a single respective third party were likely to see much more of one another, and where frequent users were much more likely to find themselves in close proximity of those whose use patterns were similar to their own.

Transitive closure played a smaller but still important role in the P90 network, on a par with the most important of attribute-based determinants. This is interesting because the P90 network was initially aimed at heterosexual risk vectors, for which partners of partners would, one suspects, play a lesser role (Potterat et al., 2002). Certainly, the negative value of gender homophily in the composite model (Table 3b, model 4: θ = −0.360) supports the idea that heterosexual risk vectors were prominent and important. However, the fact that θ_{transitive closure} = 1.375 in this same model points to the fact that other vectors of risk uncovered in the study play an even more important role. Whether these risks are sexual or injection based is not clear (although we suspect the latter, especially given that one of our criteria for inclusion when recoding the P90 data was IDU use). Indeed, one can speculate that in the process of researching heterosexual risk, researchers in the P90 project uncovered an IDU network whose dynamics play a significant part in determining the pattern of risk connections in the Colorado Springs network as a whole. The relatively lower value of the transitive closure exponent, however, lends much support and provides some explanation for the relatively small size of the risk core, as discussed by P90 researchers (Klovdahl et al., 1994; Rothenberg, Potterat, & Woodhouse, 1996).

These results also confirm many prior conclusions from the original analyses of the two data sets—SFHR and P90. Among those conclusions is the central role of race/ethnic homophily in the SFHR network, which is found here to play an important role in structuring network connections. From Table 1a, one notes that homophily levels differed for various variable values, with Hispanics showing the highest levels of in-group preference for risk partners, and whites showing the second highest level. The same ordering of homophily levels held true in the P90 data as well, with Hispanics showing the higher levels, followed by whites and African Americans. Here, however, the Other category showed the highest levels, slightly higher than Hispanics.

Of interest in both networks is the high levels of homophily shown by younger network members (Table 1a and b: θ_{SFHR Age15–19} = 1.394 and θ_{P90 Age15–19} = 1.278). Here we find that younger members of both networks tend show a much higher preference for in-group affiliation than do those older than them. Likewise, those at the highest age levels (over 40) show a similar pattern, though these results are difficult to interpret given the high errors and lack of statistical certainty associated with exponent values. Minimally, we can see that age factors quite differently in the connectivity trends depending on the age category involved.

The implications of these findings for current HIV and related disease prevention and harm reduction programs are significant. Currently, the bulk of intervention strategies stem from the Centers for Disease Control funded (and frequently mandated) Diffusion of Evidence Based Interventions (DEBIs). The majority of these programs are aimed at behavioral change, with little or no recognition of network elements of risk, whether for PWID or those engaged in high risk sexual activity. Programs such as Holistic Health Recovery Program⁹, and Modelo de Intervencion Psycomedica¹⁰, which target PWID, continue to stress behavioral modifications which target individuals and ignore network contexts entirely. Programs such as the Safety First¹¹, Popular Opinion Leader¹², and Community PROMISE¹³ advocate attention to social networks, but assume few network dynamics other than popularity or “leadership.” The findings discussed above could potentially improve programs which use peer-educators to diffuse information such as SHIELD (Self-Help in Eliminating Life-threatening Diseases)¹⁴, by pointing out ways in which the influence of peers will be shaped by specific social factors (race or specific age group homophily, for example) which may not act consistently or uniformly across age categories or ethnic/racial groups (Costenbader, Astone, & Latkin, 2006; Tobin et al., 2007). Where age based homophily is different for young, middle age, and older participants, the social reach of peer transfers of information can be expected to vary considerably, even given the similar training and personal effectiveness of those involved. As importantly, the differences in the two networks considered here show that assumptions about risk relationships in one area (the importance of gender homophily in determining patterns of risk, for example, or the level of transitive closure relative to attribute-based considerations) may not hold true in other networks. In such cases, the demonstrated effectiveness of an intervention may be contingent on network factors largely unaccounted for in the planning of the intervention. Indeed, knowledge of the network topological structure in and through which the intervention takes place appears in none of the institutional readiness guidelines associated with the DEBI program.

In more general terms, the importance of network transitivity to IDU networks indicates that strategies that target the partners of currently high risk individuals may be stopping short of reaching the next most likely to be at risk, the current partners of those partners. As above, cousers one step removed from one’s current partners represent the next most likely risk partners, regardless of race, gender, age, or general couse level. Yet continued stigmatization of HIV infection and risk of infection has discouraged link tracing in prevention strategies. Such issues have even been underwritten by laws that discourage a network approach to prevention; current state-level reporting requirements have no network component. To wit, many harm reduction/syringe exchange programs have recognized the importance of “secondary exchange” as a regular part of program effectiveness (Bryant & Hopwood, 2009; Irwin et al., 2006; Des Jarlais et al., 2009; Latkin, Davey, & Hua, 2006). Yet few have embraced this as a crucial topic for analysis (Des Jarlais et al., 2009). The fact that risk relationships seem to occupy a similar niche should encourage more intensive and focused investigation of this phenomenon, including especially its current network structure.

More broadly, research on the causes of injection and sexual network patterns, and of changes in these patterns, has been pointed to as a major priority for AIDS-related social research (Friedman, Bolyard et al., 2007; Friedman et al., 2006). Such research was recommended in part because of its direct prevention implications, as discussed above. We would add here that in the context of widespread discussion of structural interventions, understanding how these interventions might affect risk networks is essential (Auerbach, Parkhurst, & Cáceres, 2011; Friedman et al., 2006; Ogden et al., 2011; Wendel et al., 2011). It was also recommended as basic research that is essential to understand HIV, hepatitis C and other infectious disease epidemiology (Friedman, Bolyard et al., 2007; Friedman et al., 2006). Finally, it was recommended as important policy research. As discussed in this paper, network patterns shape the HIV vulnerability of communities, so anything that can help us understand how to reduce that vulnerability is important. In policy terms, “big events” like wars, transitions, revolutions, and perhaps economic crises can lead to major changes in both social and risk networks, and these may unleash new epidemics (Friedman, Bolyard et al., 2007; Friedman et al., 2006; Friedman & Rossi, 2011; Friedman, Rossi, & Braine, 2009). It is important to know everything we can about what changes networks so policies and programs can be put in place to counteract network changes that may increase community vulnerability.

GLOSSARY

Dyad

Dyad is a pair of network nodes, in the context used here, two potential risk network partners in the same risk network

ERGM

Exponential random graph modeling, a technique to determine the statistical likelihood of a risk connection existing between two network members given the presence of absence of particular actor or nearby network traits

Homophily

As used here, it is the tendency of an actor to engage in risk behavior with a network alter that shares some attribute, such as gender, ethnic affiliation, or degree of network importance

Network degree

The number of risk partners an individual risk network member has in the network

Patterns of connectivity

Recurring formal structures of interconnection within a risk network, which could include the tendency of individuals to engage in risk behaviors with the alters of their network connections, or which might include a tendency to homophily in the risk network

Risk network

A set of behavioral interactions between distinct individuals whereby harmful pathogens such as HIV may be transmitted among them

Transitive closure

The tendency for two previously unconnected network alters of a common risk partner to themselves become risk partners

Biographies

Kirk Dombrowski is trained as an anthropologist, with a dissertation centered on the impact of native land claims on public health, food security, and household violence. He began working on social network techniques in 2004 after realizing that he needed new ways to think about rural inequality. Since 2006 he has worked closely with Khan, Curtis, and Wendel on techniques that can bridge the gap between on-the-ground fieldwork and network theory/modeling. In September 2013, he joined the Sociology Department at the University of Nebraska-Lincoln to help develop a special doctoral training focused on network analysis and health disparities.

Bilal Khan has been involved in the development of large scale network simulation development for over 15 years, including developmental work CASiNO, SEAN, PRouST, TRON, CHIME, and OPTIPRISM. He is presently Professor of Mathematics and Computer Science at John Jay College. His research areas span networks, algorithms, and graph theory. In recent years, he has developed simulations of networks in the context of fundamental research in wireless communications. He also recently coauthored a book on network simulation, Network Modeling and Simulation: A Practical Perspective.

Ric Curtis is a professor of anthropology at John Jay College of Criminal Justice and has conducted research in New York City since 1978. He was the lead ethnographer on the SFHR project discussed here. He worked with Friedman at NDRI from 1988–1998 where he conducted research on drug injectors for this and a number of studies. He continues to work with drug injectors as a Board of Directors member at 3 New York City harm reduction programs.

Katherine McLean is a PhD student in sociology at the CUNY Graduate Center. Her dissertation, currently in progress, focuses on the production of risk and subjectivity in needle exchange. She graduated with a BA in biology from Columbia and an MS in International Health from Harvard. She has taught courses ranging from Drugs and Society to Culture and Crime at Hunter College, Queens College, and John Jay College. She has been working with SNRG since 2009.

Evan Misshula is a research fellow of the Social Network Research Group at CUNY John Jay and a PhD candidate in Criminal Justice at the CUNY Graduate Center. His interests include simulation, optimal stochastic control, and data mining. His prior work has applied these techniques to political violence, victimization reporting, HIV transmission, and prisoner reentry.

Travis Wendel, JD, PhD, is a Research Associate and Scholar-In-Residence in the Department of Anthropology, John Jay College of Criminal Justice, City University of New York. He has been an ethnographer working with New York City drug users and distributors since 1996. His current activities include serving as Principal Investigator of the New York City National HIV Behavioral Surveillance study, and a study of the repeal of the Rockefeller drug laws in New York State. His research interests center around the social organization of the distribution and consumption of illegal commodities, and the role of social networks in those processes.

Samuel R. Friedman is Director of HIV/AIDS Research at National Development and Research Institutes, Inc. and the Director of the Interdisciplinary Theoretical Synthesis Core in the Center for Drug Use and HIV Research, New York City. He also is associated with the Department of Epidemiology, Johns Hopkins University, and with the Dalla Lana School of Public Health, University of Toronto. Dr. Friedman is an author of about 400 publications on HIV, hepatitis C, hepatitis C, STI, and drug use epidemiology and prevention. Honors include the International Rolleston Award of the International Harm Reduction Association (2009), the first Sociology AIDS Network Award for Career Contributions to the Sociology of HIV/AIDS (2007), and a Lifetime Contribution Award, Association of Black Sociologists (2005). He has published many poems in a variety of publications and a book of poetry (Seeking to make the world anew: Poems of the Living Dialectic. 2008. Lanham, Maryland: Hamilton Books).