Perspectives in Magnetic Resonance: NMR in the Post-FFT Era

Abstract

Multi-dimensional NMR spectra have traditionally been processed with the fast Fourier transformation (FFT). The availability of high field instruments, the complexity of spectra of large proteins, the narrow signal dispersion of some unstructured proteins, and the time needed to record the necessary increments in the indirect dimensions to exploit the resolution of the highfield instruments make this traditional approach unsatisfactory. New procedures need to be developed beyond uniform sampling of the indirect dimensions and reconstruction methods other than the straight FFT are necessary. Here we discuss approaches of non-unifom sampling (NUS) and suitable reconstruction methods. We expect that such methods will become standard for multi-dimensional NMR data acquisition with complex biological macromolecules and will dramatically enhance the power of modern biological NMR.

1. Introduction

Conventional linear sampling of the indirect dimensions in multi-dimensional NMR experiments together with the fast Fourier transformation (FFT) have dominated data acquisition since the introduction of 2D NMR (1–3). However, the development of spectrometers working at very high field, and research targeting larger and more complex biological macromolecules rendered this process inadequate. Thus, advanced methods beyond linear sampling and FFT processing are emerging and are increasingly adopted by the NMR community.

Clearly, the most important innovation in NMR spectroscopy since its initial invention was the introduction of pulsed excitation and data processing with the Fourier transformation (4). This has been used ever since as the prime method for processing one-dimensional and multi-dimensional NMR experiments. The processing method requires acquisition of arrays of spectra at linear increments of dwell times so that the Fast Fourier Transformation (FFT) can be applied. This has been extremely successful and was key for instating NMR spectroscopy as one of the methods for structure determination in solution at an atomic resolution. However, when targeting increasingly larger proteins and nucleic acids, spectra are more crowded as more resonances fall into the same standard spectral widths. Even when dispersing signals in three and four dimensions, unambiguous peak assignments can remain a challenge. This is particularly difficult for membrane proteins where the transmembrane regions are full of methyl groups but often have only a few aromatic residues and exhibit only a narrow disperion of cross peaks. Thus, it is very important to record spectra at the highest resolution, with precise, accurate and reproducible chemical shift definition across multiple experiments. However, high-precision measurements that are theoretically possible with current state-of-the-art high-field NMR spectromters are not pratically reachable with standard routines of recording and processing 3D and 4D NMR spectra. When sampling linearly all indirect dimensions of the Nyquist grid of 3D and 4D experiments spectra can only be recorded at very low resolution within a reasonable overall measuring time. As a consequence, essentially all uniformly sampled 3D and 4D NMR experiments are obtained far below the resolution that would be achievable with modern high field NMR hardware.

Besides obtaining high resolution, NUS also permits faster acquisition of standard resolution spectra if the signal-to-noise ratio is sufficiently high. In addition, if optimal sampling schedules are used the sensitivity of detecting weak signals can be increased. However, there are also numerous obstacles to overcome, and it may take some time to make this approach generally available for routine data acquisition. There is a large body of literature covering NUS and reconstruction methods. Here we focus primarily on our own work; however, we also try to reference other approaches, which must be incomplete within the format of a perspectives article.

2. Advantages of NUS

2.1 High resolution obtainable with non-uniform sampling

The advent of high field spectrometers promises higher resolution. An unfortunate consequence of this is that high field magnets have shorter dwell times for a given spectral width (in ppm). Thus one needs longer time to reach the same resolution in the indirect dimension on a high field magnet when compared to a low field magnet and substantially longer time if one were to exploit the resolution the high-field magnet is capable of, in particular when recording 3D and 4D spectra.

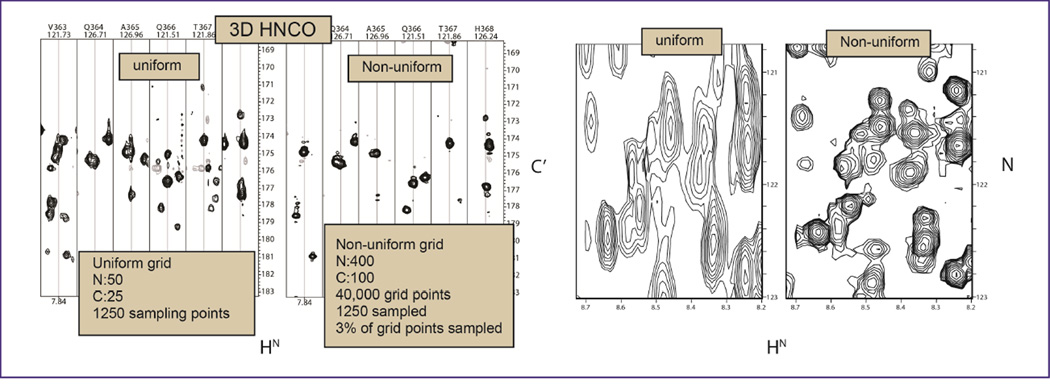
High resolution in the indirect dimensions can only be obtained in a reasonably short time with non-uniform sampling (NUS) in the indirect dimensions. An early example is shown in Fig. 1, adapted from Hyberts et al. (5). A total of 1250 indirect points were sampled either linearly with 50 and 25 increments in the nitrogen and carbon dimensions or non-linearly covering 400 and 100 grid points in the two indirect dimensions, respectively. Typical H^N-C’ strips are shown on the left, and H^N-N projections are on the right. Both spectra were recorded for the same total measuring time of six hours. The projections (right) clearly demonstrate the superior resolutions obtainable with NUS, the strips reveal that the higher resolution achievable with NUS eliminates the “bleading through” between adjacent strips, and peaks are narrower in the C’ direction.

Figure 1.

Comparison of linearly and non-linearly recorded 3D HNCO spectra for the 50 kDa C-domain of the enterobactin synthase EntF. Both spectra were recorded within six hours and processed with the FM reconstruction method as described previously (5).

2.2 The size of space to be sampled with respect to resolution

This question relates to how many points should be sampled per line width. Following the discussion in (6), the Number of Points per Linewidth, NPL, can be expresses as:

$$NPL=\frac{L}{SW/N}=L•N•\mathrm{\Delta }t$$ (1)

where L is the line width, N is the number of sampling points and Δt is the dwell time. For simplicity we assume that there is no zero filling and the number of points in the frequency domain is the same as that in the time domain. We are interested in how many points N should we sample to get a desired NPL. From equation (1) we get for the number of points to be sampled in the Nyquist grid N is:

$$N=\frac{NPL}{L}SW$$ (2)

For example, if we want to separate two frequency data points, NPL=2, for a line width of 1 Hz and a spectral width of 5,000 Hz we would have to sample 1000 points.

We can express this in terms of relaxation rates assuming

$$L=\frac{R_2}{\pi }$$ (3)

we get

$$N=\frac{NPL}{R_2}SW•\pi$$ (4)

These obvious relations tell us the trivial fact that we have to sample more data points, the larger the SW and the sharper the lines. However, the number of frequency points per line width L can be increased by zero filling and/or linear prediction. Nevertheless, the relations tell us that it is impractical to sample that many points in 2D, 3D and 4D spectra with traditional sampling.

2.3 The size of space to be sampled with respect to sensitivity

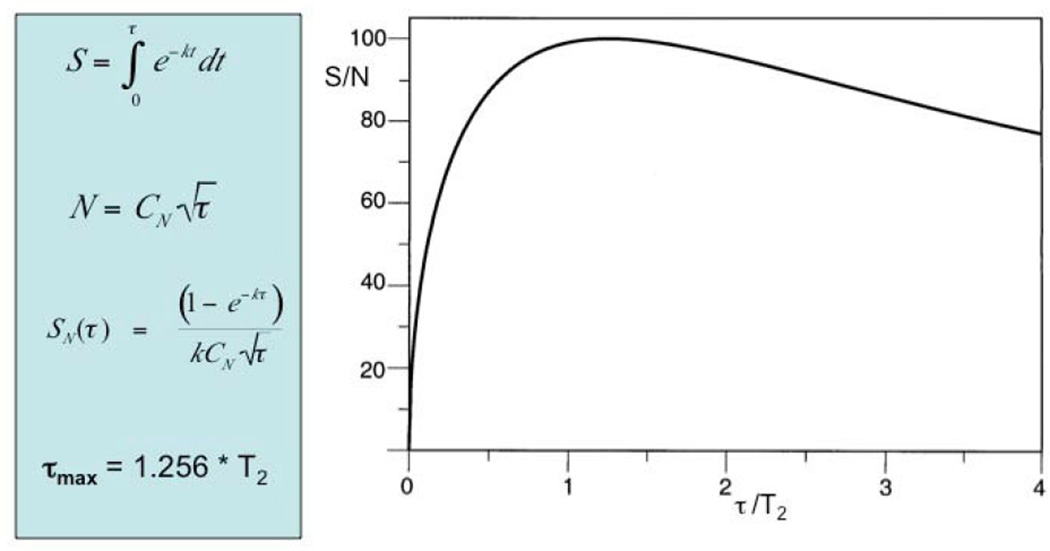
This question has been treated in detail by Rovnyak et al. (6). It was pointed out that the best sensitivity is obtained for

$$t_{\text{max}}=\frac{\pi }{2R_2}=N•\mathrm{\Delta }t=\frac{N}{SW}$$ (5)

After this value for t_max each additional increment adds more noise than signal (Fig. 2), and it seems advantageous to sample points with evolution times out at t_max and no further to avoid diminishing returns on time. However, sampling beyond t_max can be considered if sensitivity is not a problem as samples that extend to π/R₂ will, for example, increase resolution.

Figure 2.

Dependence of the signal-to-noise ratio on the maximum evolution time and the relaxation rate. The signal height is obtained from the integral over the envelope of the FID while the noise is proportional to the square root of the number of sampling points. Up to ~ 1.26 T₂ each scan adds more signal than noise, beyond that point each increment adds more noise than signal (adapted from Rovnyak et al. (6)).

When sampling to this t_max we have for the number of points N to be sampled

$$N=\frac{\pi }{2R_2}SW=\frac{1}{2L}SW$$ (6)

This can be compared with equations 2 and 4 above and tells us that we obtain optimal sensitivity when sampling only 0.5 points per line width. A table of the desired number of increments has been given in (6). However, the number of time-domain data points to be sampled for optimal sensitivity is impractical for recording multi-dimensional NMR spectra with conventional linear sampling in solution NMR. This is easily accomplished in solid state NMR due to the fast relaxation, and it has indeed been suggested (7, 8).

2.4 How sparse can we sample?

Although the advantage of sparse sampling is now increasingly accepted it is not yet clear what is the lower limit of sparsity. This may depend on the many conditions of the spectra to be recorded, such as spectral width, number of signals in the spectrum and/or line width. However, when concerned with typical protein spectra, it appears that the vast majority of spectra obtained can be sampled reliably at 20% sparsity for each indirect dimension. Practically this means that we can sample a NUS-HSQC at 20%, a NUS 3D triple resonance spectrum, such as HNCA at 4%, and a 4D NUS acquired methyl-methyl TROSY NOESY at 0.8% (see examples in (9)).

Obviously this is a rule of thumb only, and a definite answer to this question is still missing although several suggestions regarding sparsiness have been made. Already prior to the proposal by Jeener for recording two-dimensional spectra, a general theory for non-uniform sampling was proposed by Landau (10) who stated: “The average sampling rate (uniform or otherwise) must be twice the occupied bandwidth of the signal, assuming it is a priori known what portion of the spectrum was occupied”.

This means that the amount of sampling is not dependent on the product of sweepwidth and resolution, as the Nyquist theorem proposes, but rather a function of the number of signals in the spectrum. Further research in the field of signal theory finds that given various types of reconstruction algorithms, and pre-exsisting models, the exact number of sampling points varies somewhat. That is, with no noise and assuming pure Lorenzian lineshape, exaclty S number of sampling points in the time domain are required for correct representation of S signals in the frequency domain (11). However, not all signals have Lorenzian lineshape, and most spectra of interest are far from noise free.

Non-Uniform Sampling is closely related to Compressed Sensing (CS), a term introduced for imaging applications. While images are not sparse in contrast to NMR spectra many aspects of data acquisition are related. Thus, the term CS is now frequently used also for NUS of high-resolution NMR spectra. In particular, the problem of sparseness in CS was treated generally by Candés and Wakin (12) who discussed the parameters that influence the possible sparseness of sampling. This general theory would have to be adapted to the NMR situation and be calibrated. However, there are a number of different approaches for reconstructing NUS or CS spectra, including minimization of target functions, using Lagrangian multipliers. Thus, while CS covers essentially all NUS applications it is also used for a multitude of reconstruction methods that vary largely in the strategy and speed of reconstruction.

2.5 Speeding up data acquisition

The most important use of NUS appears to be enabling acquisition of high-resolution multidimensional spectra; however, it also can significantly enhance speed of data acquisition for experiments of less complexity. This includes recording suites of triple resonance experiments for small proteins (13), measuring relaxation parameters, residual dipolar couplings, hydrogen exchange rates, pH titrations in 2D correlated spectra, or characterizing metabolite mixtures. For such experiments it is important to obtain accurate peak positions, or reliable signal intensities. The former can obviously be achieved but the latter deserves more consideration.

Relaxation measurements typically use sets of ¹H-¹³C or ¹H-¹⁵N HSQC spectra recorded with different waiting delays and fitting the time dependence of peak intensities or heights. Recording the spectra can be accelerated dramatically with NUS. The relative values of relaxation rates are essentially identical to those obtained with traditional US methods. However, it appears that the absolute values of the rates obtained by fitting time courses of decaying signals may be up to 5% faster than those meassured with US. However, this bias is usually well within the precission of the measurements; moreover, the bias can readily be compensated for (to be published).

Applying NUS to 2D spectra of metabolite samples is straight forward, such as speeding up ¹H-¹³C HSQC or ¹H-¹³C HMBC experiments. The transverse relaxation of ¹³C in metabolites is typically very slow relative to the sweep width, and collecting in the order of 8k complex data points in the indirect dimension is not unreasonable to approach 1.26 T₂ (see equation (6)). To cover this, only a small fraction needs to be acquired in a non-uniform manner. This can speed up acquiring spectra of metabolite mixtures at natural abundance ¹³C; however, it can be a game changer when recording spectra obtained with ¹³C enriched precursors.

2.6 Enhancing Signal to Noise Ratio (SNR) and Detection Sensitivity

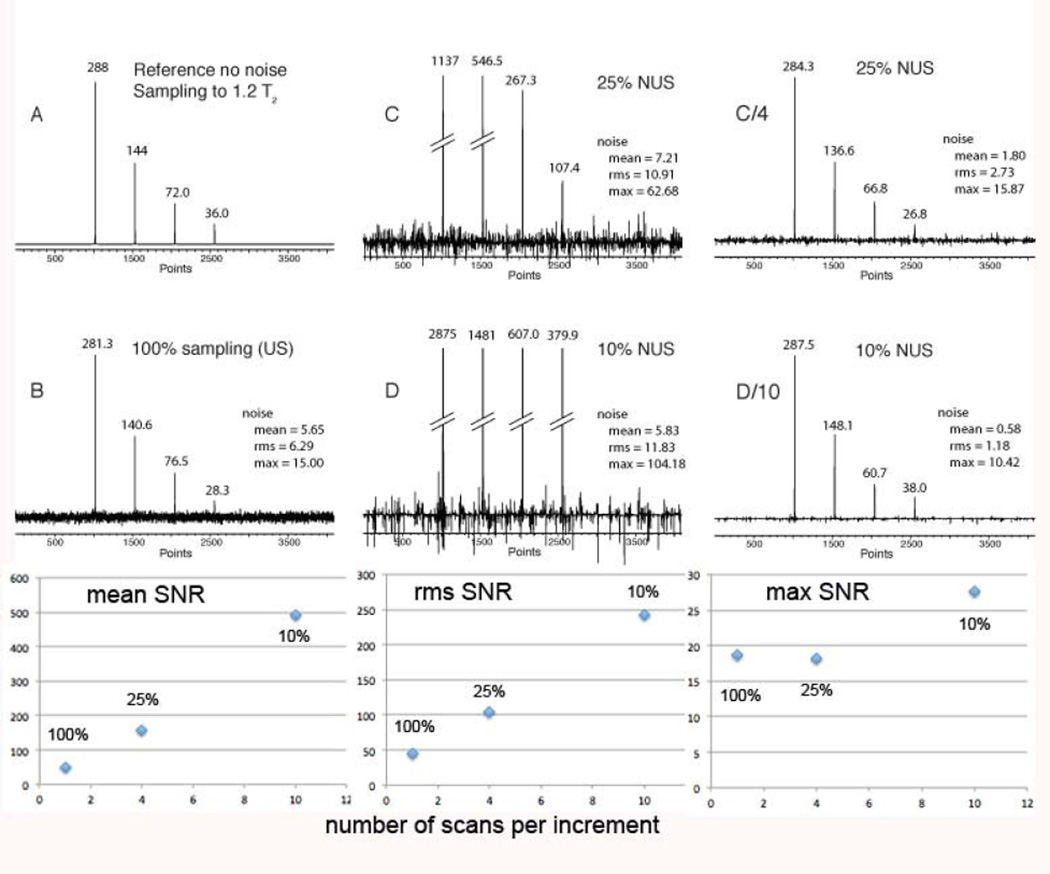
When analyzing SNR and detection sensitivity we compare time-equivalent spectra. For a 1/n sparse NUS experiment n-fold more scans are recorded than the equivalent US experiment, resulting in the same total measuring time. As we have shown recently, the peak heights in the NUS are n-fold higher than in the time-equivalent US spectra while the noise increases by less than a factor of n, resulting in a de-facto enhancement of the SNR. However, quantifying the SNR enhancement depends on how the noise is measured. For example, median, mean or maximum noise measurements can be used. As can be seen in the simulation displayed in Figure 3, the mean noise does not increase from US to 25% NUS or 10% NUS. This results in a dramatic increase of the signal-to-mean noise, essentially by the factor n. Similarly, the mean noise increases by approximately the square root of n. On the other hand, the maximum noise (peak noise) increases equally with the hight of the signal. Thus, time equivalent NUS increases the SNR when using mean or rms noise as the noise metric. However, SNR doesn’t increase signifiantly when using the peak noise metric.

Figure 3.

Simulation of the effect of NUS on the signal to noise ratio (SNR) in time-equivalent spectra (adapted from (14)). A. Spectrum simulated with an array of four Lorentzian signals of different height without simulated noise. The time-domain signal is sampled to 1.2 T₂. The FID contains 2k complex points. B. The same as A, but noise was added and time domain data were transformed with FFT. C. NUS (25% density, SSW=2, 4 × NS) D. NUS (10% density, SSW=2, 10 × NS). The NUS time domains were reconstructed with hmsIST. In all cases the final time domain signals were zero filled and Fourier transformed without apodization. The generated peak heights are marked in the figure. In addition three measures of the noise are annotated, mean, rms and max noise. Bottom: The three measures of the SNR are plotted for the strongest peak vs the number of scans per increment.

It may be possible that false positives (peak noise) can be recognized based on the line shape since it appears as sharp spikes. However, this needs further examination.

3. NUS sampling schedules

3.1 Overview of sampling schedules

As is discussed in the Compressed Sensing literature (12), the “goodness” of the sampling schedule comes into question when determening how sparse we can sample. If the “goodness” of the sampling schedule did not matter we could, without penalty, sample (a) everything in the beginning (this is the case of Linear Prediction) and predict the remainder of the time domain data, or (b) we should be able to sample, say, every other point without the penalty of folding. This obviously doesn’t work.

Thus, CS recommends complete random sampling. This is an intuitive solution, and works well for CS when applied to its original problem of imaging. Random sampling was also pursued in the early publication on NUS in NMR by Barna et al (15) with the modification of an additional exponential weighting to take in account NMR signal relaxation.

“Random” is, however, a poorly defined term and a mathematically challenging concept, although there is an intuitive understanding of the concept. The traditional random schedule implementation is to create a vector or matrix, and to pick points by essentially ‘throwing darts’, modelled by a random number generator, or more correctly, a “pseudo-random generator”. An example pseudo-random generator is the C “drand48” function that produces non-negative double-precision floating-point values uniformly distributed between [0.0, 1.0). The generated values are then weighted to span the length of the vector or matrix. Presently, there are many suggestions in the literature for Computational Science of “blue-noise” weighting by Poisson-disks. The implementation with Poisson-disks in NMR spectroscopy has also been suggested by Kazimierczuk et al (16).

3.2 Poisson-Gap sampling

As shown previously (17), we found that the fidelity of the reconstruction varies dramatically when using different seed values to initiate the ‘dart throwing’ algorithm, especially for sparse sampling of relatively short time domain data sets, such as picking 256 of 1024 data points. Studying this by eye, we made three observations: (1) large gaps in the sampling schedule are generally unfavorable, (2) gaps at the beginning or end of the sampling are worse than those in the middle and (3) the sampling requires sufficiently random variation to minimize folding-like artifacts that would be severe when selecting, for example, every 5th point.

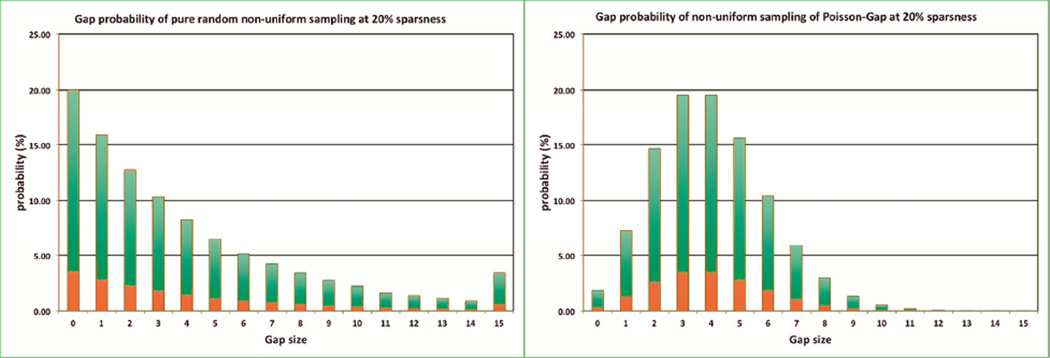
When investigating the distribution of the gap lengths generated by the non-weighted “dart throwing” algorithm, one finds that this creates an exponential distribution of the gaps. By creating a very long array (>100,000) and allowing for 20% hits, one creates the distribution shown in Figure 4 (left). Note, the value of 15 is a cumulative value of 15 and above. This number is just less than 3.5% but is not negligible. On the other hand, by postulating a Poisson distribution, one finds a much tighter distribution around the average value of 4. The value of 15 and above here is around 0.0020 %. In other words, the probability of generating a relative large gap is low when using a schedule generated according to the Poisson distribution. Additionally, the distribution is sufficiently “random” to fulfill the third criterion above.

Figure 4.

Distribution of gap lengths when using non-weighted dart-throwing algorithms (left) and Poisson-gap sampling (right). The bar at 15 represents the sum of gaps that are 15 or more. Obviously, the Poisson-Gap sampling avoids large gaps very efficiently.

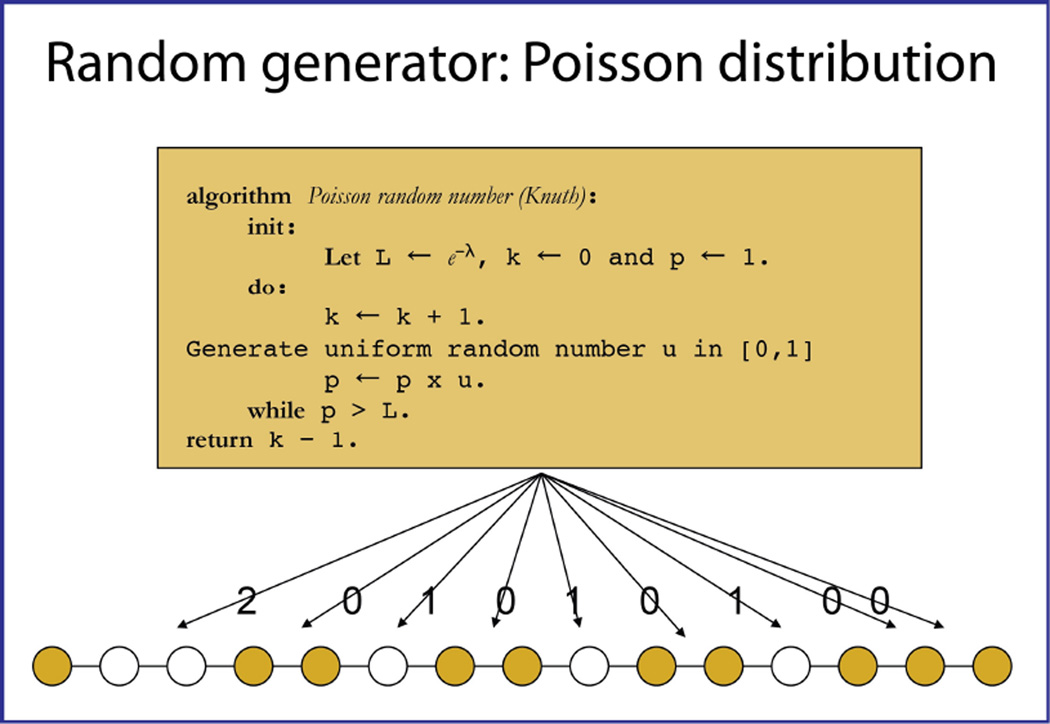
In order to create a Poisson distribution (18) for the gap lengths, an algorithm is created by a method illustrated in Figure 5.

Figure 5.

Illustration of the procedure for creating a Poisson-Gap schedule (19).

A data point that it going to be observed is generated. We call this point “the anchor”. As it is good practice to always sample the first data point, this is the filled circle at the left bottom of Figure 5. A well-known algorithm for generating a Poisson distributed random number is then used (19). Here, λ is the average gap length the user provides as input, which defines a value of e^−λ in the interval [0,1] as a termination point. The value of p=1 is multiplied with a random number u in [0,1]. If p × u is larger than e^−λ the process is repeated until p × u is smaller than this value, and the number of rounds the loop is repeated, k-1, yields the number of skipped time domains points.

In our example of Figure 5, a “2” is generated. This means that the next two points are not acquired however the fourth data point in this sequence is acquired. Marking this, we return to the algorithm, and in this case a “0” is generated. This means that the next point is being acquired, the fifth one, and there is no gap. The procedure is repeated until the vector is complete. Note there is no guarantee that the last point is being acquired. Also, there is no guarantee that the requested number of data points to be acquired is created correctly. Hence the procedure is repeated until the requested number of points is created correctly, all with different seed values for the pseudo-random number generator. The only parameter that is used for this procedure is the value of lambda (λ). This parameter is defined in the equation for the Poisson distribution:

$$f(k;\lambda )=\frac{{\lambda }^k{e}^{-\lambda }}{k!}$$

λ describes the average of the function. It is equal to 1.0/(sparseness) – 1.0. The values of k are the integer values representing a particular gap size, i.e. the values of “2” and “0” above. The functional value is the probability, and is represented in Figure 5.

With regards to the second observation (that gaps at the beginning and end of the vector are bad), we simply vary the value of the average gap length lambda (λ) along the vector, and we do this in a sinusoidal form. In a first option, which we call sinusoidal weight 1, or ssw=1, we make the average gap sizes λ small both at the beginning and the end of the time domain according to λ = (λ)₀ sin(x), and letting the value of × be 0 in the beginning of the vector and π in the end. In addition, to be able to ensure the proper number of data points to be acquired and achieve the desired sparsity, (λ)₀ is iteratively varied between trials. Here, the initial value of (λ)₀ is equal to 1.0/(sparseness) – 1.0.

The second type of refining is to vary the values of × in the formula λ = (λ)₀ sin(x) between × in the beginning of the vector and π/2 at the end. We call this: sinusoidal weight 2 or ssw=2. The rationale of this is that the acquisition is often done on relaxing signals so that emphasis should be in the beginning. This is very much similar to the situation with exponentially weighted random sampling. Also, data are typically apodized before Fourier transform. This is especially important when acquiring data with constant time evolution. Should the data not being apodized, the very sharp, truncated signals generate so-called sinc-wiggle artifacts. On the other hand, if data are acquired with t_max ≥ T₂, and no apodization is applied, either ssw=1 or ssw=2 could be used depending on the aim of the measurement. ssw=2 will of course yield an intrinsically better response regarding the signal but ssw=1 may yield a better shape of the signal. However, acquiring a signal with t_max » T₂ may only be practical for highly concentrated samples. For completeness, if we do no sinusoidal weighing, we call this sinusoidal weight 0, or ssw=0.

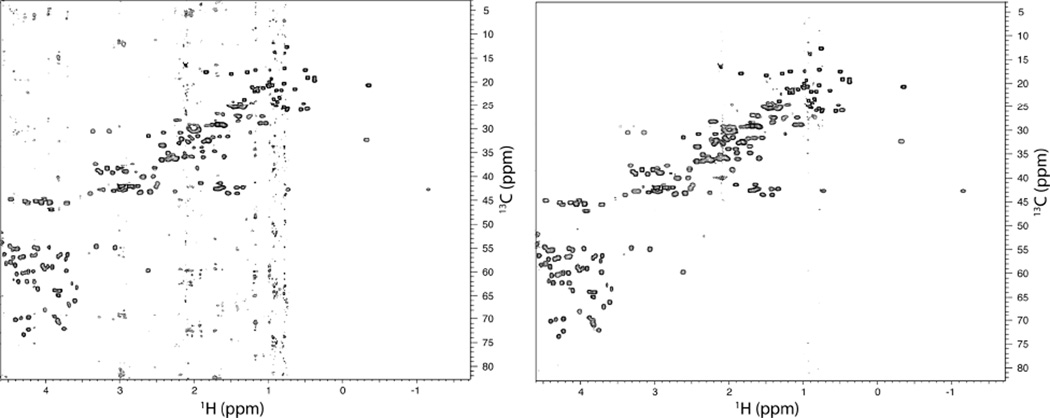
Is Poisson-Gap sampling superior to pure random sampling? This is certainly supported by extensive simulations (20) but also experiments. As an example we recorded a ¹H-¹³C HSQC spectrum of the protein GB1 with a sampling schedule created with a standard random number generator and with Poisson-Gap sampling (Figure 6). As can be seen the spectrum at the left contains folding and T₁ noise-like artifacts, which seem to be due to the existence of large gaps. These artifacts are entirely absent in the spectrum recorded with the Poisson-Gap sampling procedure.

Figure 6.

Comparison of regular random sampling (left) and Poisson-Gap random sampling (right) of the aliphatic region of a ¹H-¹³C HSQC of the B1 domain of protein G (GB1). Both spectra were collected on the same sample with the same conditions and for equal time (field: 600 MHz, GB1 concentration: 0.5 mM, number of scans: 40, sampling density: ~20% or 52 out of 256 points). Reconstruction was performed using hmsIST with identical parameters (apart from the schedule) and spectra plotted to the same contour level. Significant T₁ noise artifacts are present on the regular random sampling spectrum compared to Poisson-Gap random sampling.

Extending the Poisson-Gap procedure from one to multiple NUS dimensions is non-trivial as the algorithm intrinsically works in an ordered way along a single vector or dimension. The concept of ‘order’ is something that is mathematically lost when going from one to multiple dimensions. That is, the natural numbers have order; coordinates do not. Instead, to construct sampling schedules of higher dimensionality than one, different “strands” of Poisson-Gap sampling vectors are woven into sections of larger dimensional order. This is to say; first one vector is constructed and placed on one of the axis. Next, a second vector is constructed orthogonal to the first one, using the already set value of the first vector as an anchor. To eliminate as much preference between the dimensions, the third vector is constructed parallel to the second but moved one step along the first dimension. This is then followed by a forth and a fifth vector in the first dimension, parallel to the first vector. This is continued until all points in the matrix are marked as either to be sampled or not to be sampled.

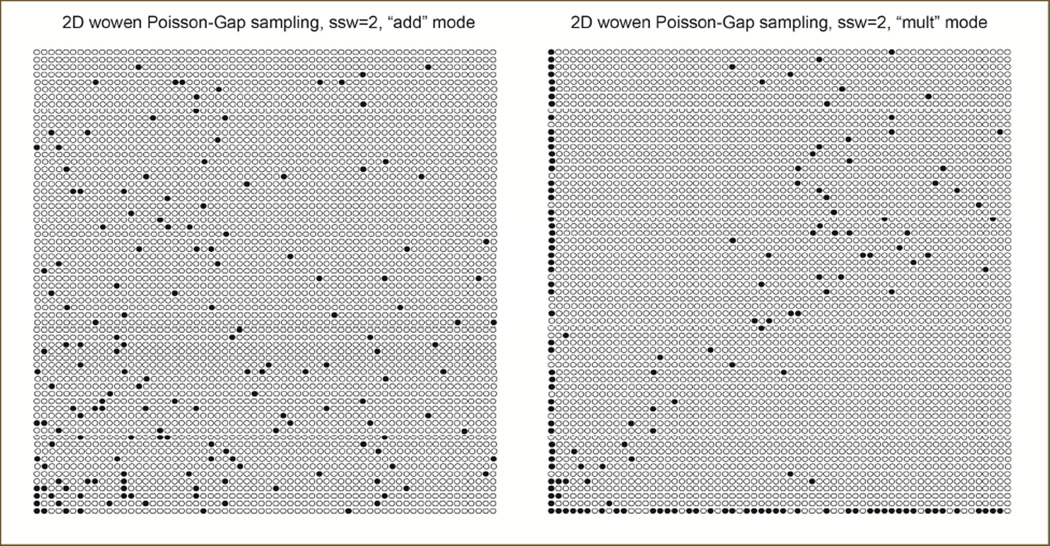
There are a couple of caveats to be considered. First, just about all 2D matrixes, from an NMR vantage, are rectangular and hardly ever square. The number of vectors can be adjusted such that for every vector created in one dimension, the number in the other is adjusted so that a rectangular shape is produced. Second, when looking for an anchor point, which is required to be set for the Poisson-Gap sampling, one needs to create a parallel vector to the axis on the negative side that shadows the vectors already in place. This is important because not all points are being sampled. From the perspective of the Poisson-Gap vector, the first data point in its direction, which already has been managed, will be the anchor point. If there is none set, the “shadow” vector is used. Third and most importantly, one has to decide with what value the weighting has to be done. Is it (i) a multiplication of individual weighting functions in the two dimensions, or (ii) an addition of the coordinates? Both approaches have their merit. Multiplication could be considered, as relaxation may be different in the two dimensions. On the other hand, addition may be more appropriate as the relaxation is occurring as the sum of the coordinates. The former approach is implemented as “mult”, the second as “add”. “mult” results in predominate sampling along the axis; “add” yields a more triangular distribution. This issue of course applies to other types of sample generators, and is not limited to that of multi-dimensional Poisson-Gap sampling.

Examples of 2D Poisson-Gap sampling produced with the “add” and “mult” strategy and ssw=2 are presented in Figure 7:

Figure 7.

Example of a 4% 2D Poisson sampling schedule produced with the “add” (left) and the “mult” approach (right). We use the “add” approach as default.

When extending the algorithm to three NUS sampled dimensions first a “sheet” is created in two dimensions as described above. Subsequently, another “sheet” is created orthogonally. As it sits on the first sheet it starts at the Nyquist index 2 in the second dimension and is one row too long. Thus, the last row of the second sheet has to be deleted. This is followed by the third “sheet” orthogonal to the two priors, which starts at the Nyquist indices 2 of the first and second dimension and the final vectors not touching the first two sheets have to be eliminated to maintain the dimensions. The order of placing the following “sheets” is oscillating back and forth between the orientations in order not to create preferences. The time it takes doing this is not negligible, which means that it may take uncomfortably long to create a cube with the desired number of selected points for acquisition. This process has to be repeated several times in order to obtain the desired sparsity (λ)₀. To reduce the time of creating a schedule with a defined sparsity, the request of sampled data points is relaxed to a given range. After a sampling schedule with three indirect dimensions is created there are options in which order to actually record the data. We prefer to visit the sampling points in a randomized order but the sampling point without increments is always acquired first. The random order of visiting sampling points has the advantage that the complete Nyquist cube is represented in case the experiment has to be terminated due to time constraints or environmental problems, such as power failure or incorrect estimate of total measuring time. An example of a 3D Poisson-Gap sampling schedule with 2% sparsity is presented in Figure 8:

Figure 8.

NUS Poisson-Gap schedule (2% sparsity) for the three indirect dimensions of a 4D ¹³C dispersed methyl-methyl TROSY NOESY.

4. Reconstruction methods

4.1. Brief background

Processing of NUS and US data is closely related. In principle, processing of NUS with straight DFT is the simplest “reconstruction”. Whereas this leaves a large amount of sampling artifacts, it is the fastest method to get a quick insight into the performance of a running experiment. However, better reconstruction methods are needed to fully exploit the information content of NUS data.

Initial reconstruction methods mostly used various forms of a Maximum Entropy procedures (15) which were most successfully implemented as MaxEnt and used extensively (21, 22). Additionally, the traditional CLEAN method, which predatates the use of Maximum Entropy methods for image reconstruction within astrophysics (23), has been implemented for reconstruction of NMR spectra in various forms (24, 25). Applications of reduced dimensionality acquisition and transformation with methods other than FT have also been investigated (26, 27).

Drawbacks with the above methods except recent implementations of CLEAN, are either residual artifacts due to the sparse sampling, unfavorable dynamic range response of the signals and/or issues with the linearity of the reconstructed signal heights. In an effort to reduce or eliminate these drabacks, we approached the problem of MaxEnt in a different way, resulting in “Forward Maximum Entropy” reconstruction (5). This approach eliminated the drawbacks mentioned above. As it is also a minimization procedure, however, the computational power required makes this algorithm slow. A fast version of FM exists however, FFM (28), that promises sufficient speed for reconstruction of NMR spectra.

It occurred to us that the target function in our minimizer could be altered from maximizing the entropy, to allow for alternative implementations of entropy such as that proposed by Skilling (15, 29, 30) as well as that of Hoch and Stern (31, 32). In addition we implemented an iterative process closely related to iterative soft thresholding that we called the ‘Destill’ process (5). However, we found that FM reconstruction was not able to process 3D and 4D data sufficiently fast even though we made use of high end workstations equipped with GPU processors.

In parallel and somewhat predating FM reconstruction, Orekhov and co-workes developed the multi-dimensional decomposition (MDD) approach (33, 34). MDD assumes that a multidimensional spectrum can be written as a sum of components written as a direct product of 1D line shapes. MDD then approximates the spectrum as a sum of components of not yet known line shapes. It defines a target function written as the square of the difference between the spectrum S and a sum of components but only evaluated at the sampled points. The target function is then minimized using principle component analysis which needs line shapes and amplitudes of the multidimensional peaks. This approach has been further developed since.

Alternatively, the Filter Diagonalization Method (FDM) has been developed, which fits time domain data to sums of decaying sinusoidals and has been used for reconstruction of 1D and 2D data (35, 36). FDM has been further developed and can handle phase sensitive spectra robustly (37).

Finally, one may circumvent the reconstruction completely, and simply depend on the fact the the Fourier Transform is using an orthogonal set of test fuctions. One is at liberty to reduce this set either in the time domain (38) or in the frequency domain (39) for very fast conversion of the time domain to the frequency domain. As long as the spectra in question have little or no dynamic variation of the expected signals, this use is straight forward. It may even be applied to 4D NUS C,C-NOESY spectra under specific circumstances (40). The former use (the time domain) can alternatively be implementd by setting zeros in the place of non-acquired data points when using FFT. In its more recent application (the frequency domain) it enables the use of high dimensional spectra interpretation without reconstructing the whole spectrum. Also, the groups of Kazimerczuk and Kozminski have written several reviews on NUS and reconstruction methods, such as in (41).

4.2. Algorithms related to Compressed Sensing

In the field of Compressed Sensing, the minimization of choice is that of ‘norm’. In principle, this choice is arbritary. The use of minimum ℓ ₁-norm existed prior to the the field of CS, however, this type of minimization is closely associated with CS. Minimization of other norms are being actively explored, especially that of ℓ_→0 -norm in the form of Iteratively Re-weighted Least Squares minimization (42). MaxEnt is also effectively a minimization of norm, although MaxEnt is not commonly connected with CS.

As one may see from the above, minimization of the ℓ₁-norm can be done explicilty. However, Stern et al. have shown that the Iterative Soft Threshold (IST) algorithm is equivalent to minimization of the ℓ₁-norm (21). This is very important, as IST can be implemented in n· log(n) time, which is faster than an n² algorithm.

4.3 Implementation of a fast version of IST (hmsIST, (9))

While there were several methods for reconstructing NUS available they contained several shortcomings which motivated us to search for better reconstruction procedures.

The main reason for developing hmsIST was enhanced reconstruction speed. None of the previous reconstruction methods available to us could reconstruct high-resolution NUS 3D and 4D spectra in a reasonable amount of time. The slow reconstruction speed of earlier methods is probably a major reason why NUS hadn’t been widely accepted in the NMR community even in our own research environment. After becoming aware of the IST principle (43) this approach seemed to offer the potential of faster reconstruction. Indeed, our implementation of this approach (hmsIST) results in an acceptable reconstruction time for high-resolution 3D and 4D spectra (9).

Another reason for developing hmsIST was to have software that has only a limited or no need for setting parameters. Here one only has to select the threshold and the number of iterations before termination. Benefits are the high fidelity of reconstruction and the virtual absence of artifacts (9).

Our implementation of IST (hmsIST) starts with FFT of the sparse time domain data set. This yields a spectrum with a large amount of artifacts, which are proportional to the largest signals. To reduce these artifacts and initiate reconstruction, a top percentage of the frequency-domain signals is cut off and stored at a different location of the computer memory. The truncated spectrum is converted back to the time domain by inverse Fourier transformation, and the skipped time domain data points are again set to zero. This sparse time domain signal is again transformed with the FFT algorithm. Since the strongest signals are reduced the artifacts are slightly smaller. This proces is iterated until the time domain signal is completely depleted, or until temination criteri are reached. While we could terminate the process before the noise level is hit and obtain noiseless reconstructions we generally prefer to also reconstruct the noise. A detailed description is found in (9).

The variables of the IST algorithm are i) the choice of the level of thresholding and ii) the number of iterations. Too aggressive thresholding typically leads to the loss of reconstructed signals; too few iterations in assocation with the particular setting of the thresholding leads to incomplete reconstruction whereas too many iterations may lead to numerical problems. It is possible to provide stop critera to the algorithm, although we so far consider this not necessary and the implementation of termination criteria is still pending. Visualization of the reconstructed spectrum and reconstruction with different settings is a fast process and does not rely on a particular algorthimg for terminaton.

In short, we find following combinations of thresholding and iterations useful:

1. 12 iterations of 0.50 threshold.

2. 25 iterations of 0.70 threshold.

3. 80 iterations of 0.90 threshold.

4. 400 iterations of 0.98 threshold.

5. 2000 iterations of 0.995 threshold.

The time for reconstruction is proportional by the number of iterations, wheareas the resultant dynamic range is specified by (threshold)^{(number of iterations)}. In other words, the above setting provides a dynamic range approximately of 1 to 3,000 at increasing time consumption but also accuracy. If greater dynamic range is required, additional iterations are necessary. We have set point #4 as our default. This means that it is probably possible to do the reconstruction faster than this default; we however recommend that this is done with a degree of scepticism and especially recommend point #1 only as a general check or diagnostics about the progress of data acquisition at the spectrometer. Point #5 has been used mainly for control purposes during simulations. Anyone may of course find different levels that suit their purpose for appropriate reconstruction.

4.4. Considerations associated with IST reconstruction

The choice of a reconstruction method is of course a subjective one. A user may have specific requirements regarding time, accuracy and even computational restraints. Using a threshold of 0.98 and 400 iterations, and running the algorithm on a workstation or laptop with a modern hyperthreading CPU, we find that reconstruction of a 2D NUS-HSQC takes seconds (a significant amount of time is taken simply writing data back to disk). A typical 3D triple resonance NUS acquired spectrum takes less than 30 minutes (usually around 10 minutes) to process. Memory requirements are low as reconstruction involves only a single 2D plane at any particular time, i.e. the entire 3D spectrum is never held in memory at one time. We have successfully used and typically use MacBook Pros with quad core Intel i7 CPUs at 2.3 GHz and 8 or more Gbyte of RAM, but any equivalent hardware running linux or Mac OSX will give similar results. We also exploit the ability to run 8 parallel threads by using a perl script called “parallel”.

Reconstruction of highly resolved 4D NUS acquired spectra require a somewhat more advanced computational environment in order to finish in hours or a few days. A higher end workstaion or a cluster with multiple nodes and a queuing system is essentially required. Frustratingly, we have found that computational power on a cluster is not the limiting factor. Instead, access time of the cluster file system is a larger technical challenge. For this we are investigating non-NFS setups as well as faster solid state drives.

Recently, a pulication by Orekhov et al. investigates the speed and requirement of several reconstruction methods (44). All in all, we find our implementation of hmsIST to be “fast-enough” as well as “good-enough” for routine reconstruction of NUS spectra up to four dimensions. In fact, we find the routine suprisingly robust. Table 1 provides an overview of reconstruction times with typical computers and lists measured reconstruction times for well defined computing environments.

Table 1.

Execution time, etc, for specified situations using hmsIST for reconstruction

4D (i)	Size of cube	Sampling density	Allocation of memory (RAM) (ii)	Runtime (wall) (iii)	Sample (iv)
1 cube / 1 thread	60 × 150 × 150	0.8%	2.6 Gbyte	57 m 5.39 s	(a)
176 cubes / threads (v)	60 × 150 × 150	0.8%	20.8 Gbyte (vi)	23 h 10 m 12.15 s	(a)
176 cubes / 16 threads (vii)	60 × 150 × 150	0.8%	41.6 Gbyte (vi)	19 h 11 m 36.16 s	(a)
1 cube / 1 thread	48 × 80 × 80	5.0 %	605 Mbyte	13 m 5.15 s	(b)
410 cubes / 16 threads (vii)	48 × 80 × 80	5.0%	9.7 Gbyte	10 h 42 m 36.97 s	(b)
1 cube / 1 thread	28 × 44 × 96	22.8%	234 Mbyte	4 m 55.72 s	(c)
200 cubes / 16 threads (vii)	28 × 44 × 96	22.8%	3.8 Gbyte	2 h 17 m 24.16 s	(c)
3D (viii)	Size of plane	Sampling density	Allocation of memory (RAM) (ix)	Runtime (wall) (x)	Sample (iv)
512 planes / 8 threads (v)	256 × 128	4 %	132.8 Mbyte	26 m 17.84 s	(d)
512 planes / 8 threads (v)	128 × 50	32 %	29.6 Mbyte	4 m 29.71 s	(e)
512 planes / 8 threads (v)	36 × 74	22 %	15.1 Mbyte	2 m 53.66 s	(f)
2D (viii)	Size in indirect dimension	Sampling density	Allocation of memory (RAM) (ix)	Runtime (wall) (x)	Sample (iv)
512 lines / 1 thread	400	10 %	Not meassured / rel. insignificant	17.87 s	(g)
512 lines / 1 thread	256	20 %	Not meassured / rel. insignificant	9.49 s	(h)

⁽ⁱ⁾Entries indicate number of cubes used for run and how many threads were used for processing. Runs, unless otherwise specified, were made on a 3 year old AMAX ServMax Linux computer, 2×Quad-Core Intel Xeon X5550 (2.66 GHz), threaded to 16 threads, 6×2GB DDR3 1333MHz ECC Reg. w/parity RAM, running Red Hat Enterprise Linux Server release 5.8 (Tikanga). The computer is additionally equipped with 4 C2050 NVIDIA GPU cards, of which none was used. Unpublished efforts indicate that the overhead using these outweigh the benefits when running hmsIST (400 iterations). All runs were done off a locally mounted 3 Tbyte HDD drive. The hmsIST program is written in c and was compiled statically using icc (Intel C++ Compiler).

⁽ⁱⁱ⁾One cube allocation of RAM is approximately 2048*X*Y*Z bytes.

⁽ⁱⁱⁱ⁾Time for calculating 1 cube on 1 core on specified system with 400 iterations is approximately equal to 1.2*10⁻⁴*X*Y*Z*(log₂X+log₂Y+log₂Z) seconds.

^(iv)Sample:

^a4D HC-NOESY-CH experiment recorded with a 0.9 mM sample of the B1 domain of protein G (GB1) (45) figure 6a

^b4D HC-NOESY-CH (4D HMQC-NOESY-HMQC) experiment recorded with ceSKA1 MTDB sample at a concentration of ~ 700uM (46)

^c4D HC-NOESY-CH (4D HMQC-NOESY-HMQC) experiment recorded with murine cytomegalovirus (MCMV) pM50 protein at a concentration of 286uM. (unpublished)

^d3D HNCA with a 0.9 mM sample of the B1 domain of protein G (GB1) (unpublished)

^e3D ¹⁵N Edited NOESY on a yeast Gal11 KIX domain sample at a concentration of 1mM.

^f3D HNCO (purposely small reconstruction for illustration) with a 0.9 mM sample of the B1 domain of protein G (GB1) (unpublished)

^g15N HSQC with a 0.9 mM sample of the B1 domain of protein G (GB1) (unpublished)

^h13C HSQC with a 0.9 mM sample of the B1 domain of protein G (GB1) (see figure 6)

^(v)Full spectral reconstruction run on 8 simultaneous threads using the perl-script “parallel”. (Tange, Ole (2013-09-21). “GNU Parallel 20130922 (‘Manning’)”; https://lists.gnu.org/archive/html/parallel/2013-09/msg00002.html)

^(vi)Using 9×8GB DDR3 1333MHz ECC Reg. w/parity RAM.

^(vii)As (v), but using all 16 threads. Note that the speed is proportional the lesser of the number of threads used and the maximum number of cores available. The requirement of memory is proportional to the number of threads started. Occasionally, it is advantageous of using all threads available, especially on a shared system.

^(viii)CPU: 2.4 GHz Intel Core i7 (4 Cores, 8 Threads) in MacBook Pro laptop configuration. OS: Mac OSX 10.9. Number of simultaneous threads used is indicated.

^(ix)Using 16 GB of RAM.

^(x)Calculated as the average of three runs. System was allowed to temperature equilibrate between runs for > 20 minutes. Note: The time of reconstruction is found to vary drastically depending on CPU temperature.

5. Experiments that benefit most from NUS

NUS has been sucessfully implemented by a number of labs for collection and processing of traditional backbone triple resonance experiments. As mentioned above, one should use NUS to sample far out into the indirect dimensions to fully harness the resolution and sensitivity that the high field spectrometers can provide, however, there are pratical limitations. In typical backbone triple resonance experiments the Nitrogen dimension is constant-time which limits the number of points that could be aquired. This problem could be overcome by replacing the constant-time evolution with a semi-constant time evolution. In a typical experiment that encodes CA (HNCA/HNCOCA) the number of points that can be aquired in the indirect carbon dimension is limited by the CA-CB coupling (~35Hz). One could alleviate this problem by using band selective CB decoupling (47) to refocuse the CB coupling. Alternatively one could appy virtual decoupling during processing to remove this coupling (48). In experiments with CO evolution homonuclear coupling should not be a problem, whereas CSA relaxation could be the limiting factor especially at higher field. Experiments involving CB evolution are a bit more complex due to CG couplings and labeling strategies where only the CA and CB carbon are labeled should be explored. It should be noted that NUS can be easily combined with fast techniques like BEST- or SOFAST methods (49, 50) to additionally speed up acquisition times.

In addition to backbone triple resonance experiments NUS has been used in standard side chain experiments such as HCCH-TOCSY, HCCONH, CCONH and HCCH-COSY. These experiments have low sensitivity but are in high demand for large proteins. Since they are often performed on partially or fully deuterated proteins the heteronuclei relax more slowly, and experiments can greatly benefit from NUS by collecting fewer points and more scans per increment.

NUS methods provide a real boon when looking for resolution in NOESY type experiments. NUS has been sucessfully employed in a variety of 3D and 4D NOESY expeiments such as 3D-¹⁵N, ¹³C, ¹⁵N-¹³C time-shared NOESY, 4D-¹³C-HMQC-NOESY-HMQC and 4D-¹⁵N-¹³C time-shared HMQC-NOESY-HMQC. An important consideration in a NOESY type experiement is the fidelity of peak intensity in the reconstructed spectrum as these intensities will be used to derive distance restrains. We have previously shown that IST resconstruction is able to faithfully reconstruct the spectrum without any intensity bias (17).

NUS methods become a necessity with ILV labeled samples of large proteins. One can utilize the favorable relaxation properties of the methyl groups along with the sharp TROSY lines of the amide Nitrogen in a deuterated background to collect high resolution 4D spectra. With the ability to stereoselectively label only one of the methyl groups in Leucine and Valine residues these resonances relax even slower yielding a large time domain space to sample for achieving high resolution (51, 52).

Measuring relaxation and RDCs will strongly benefit from NUS methods. Traditional relaxation experiments (T₁, T₂ and heteronuclear NOE) are usually recorded as 2D HSQC spectra. However, for large proteins and intrinsically unstructured proteins which have substantial overlap in their ¹⁵N HSQC spectra, the accurate quantitation of peak intensities is difficult. In the same time it takes to record a 2D spectrum uniformly one can record a series of 3D CO dispersed relaxation experiments using NUS. This will allow for accurate quantitation of cross peaks that would be overlapped in 2D (Robson et al, in prepration). A similar approach can be applied for measuring RDCs where the CO dimension is used to resolve the NH resonanes. Similarly, metabolic flux studies, which require rapid acquisition of data at successive time points would benefit largely from NUS (53).

6. Practical aspects of NUS and Remaining Challenges

Non-uniform sampling, coupled with good reconstruction methods, has been established as a theorectically valid method of data acquisition. However, the practicalities of bringing this technology into the hands of the typical NMR spectroscopist has proven difficult. These difficulties have primarily resulted from the improvised way in which NUS experiments were intially acquired on spectrometers, a problem that in a few respects continues today. It should be noted that commerical providers of spectrometer hardware and software have made the acquisition of NUS experiments significantly easier with modern software implementations that contain simple ‘turn on’ buttons for NUS. However there is much legacy hardware still in use today that can not be run with the modern software, so specially written pulse sequences and schedule ‘tricks’ are still in use. Even with the modern implementation of NUS, the deviation from the normal protocol of data collection is enough to confuse many who are new to NUS. Below is a discussion of some of the practical issues that arise when collecting data in a non-uniform manner and some advice and guidance is offered.

6.1 Practical problems with the correct implementation of schedules

The Nyquist theorem gurantees that all frequencies within a given bandwidth can be measured so long as a certain number of points are collected with a consistent dwell time between each point. NUS violates this criterion by sampling a subset of these points. Practically, this means that data collection skips some of these points. This is accomplished by using a schedule file that describes either the evolution delay times and the associated phases for each point desired or more commonly a list of integer points where the integers represent at how many dwell times should be used for frequency labeling. Making a pulse program understand a schedule file was traditionally done in a number of improvised way by different labs. However this aspect in now automatic and hidden from the user with new versions of the software. Nonetheless, a schedule file is still required for executing the experiment and it is also needed for reconstruction purposes after data acquisition.

6.1.1 What is a schedule file?

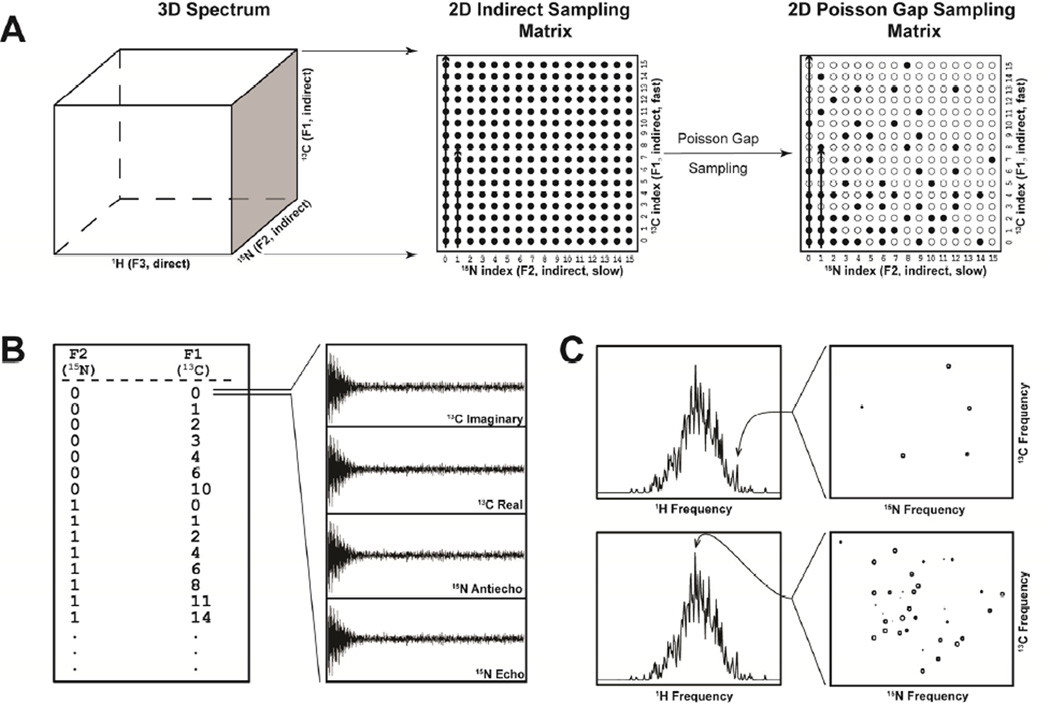
Apart from instances where evolution delay times are explicitly listed, a schedule file consists of a list of integer values that describe which complex or hypercomplex points should be recorded. For instance, in the case of a 2D spectrum one dimension is indirectly and nonuniformly acquired. The schedule file consists of a single column and is simply a series of lines where each line is a single integer between (usually) 0 and N – 1, where N is the final point. Because NUS allows skipping of points, not all numbers between 0 and N-1 are needed. Each line will result in 2 FIDs being recorded (the real and imaginery signals, or echo and antiecho signals, for that point). When collecting a 3D spectrum, two indirectly acquired dimensions are acquired non-uniformly (Figure 9 panel A). The schedule file consists of two columns of integers separated by white spaces (the nature of the white space is usually ignored and only used to separate columns). While there is no convention established, usually the first column refers to the F2 dimension and the second column to the F1 dimension. Each line refers to a hypercomplex point within the 2D matrix of the indirectly acquired dimensions. Thus, each hypercomplex point results in 4 FIDs being recorded (Figure 9 panel B). By extension, a 4D spectrum with 3 indirectly acquired dimensions consists of points composed of 3 integers per line. In this case, 8 FIDs are recorded per hypercomplex point.

Figure 9.

A) Schematic of the production of a Poisson-Gap sampling matrix. To the left, a 3D spectrum is represented. The indirect dimensions constitute a 2D plane (shaded). In the case of uniform sampling (center), a full Nyquist grid 2D sampling matrix is created and every point on this grid is acquired (filled circles). Either dimension can be acquired faster than the other, in this case, the F1 dimension is acquired fast (see arrow). Poisson-Gap sampling samples a subset of the full matrix (right). B) The Poisson-Gap sampling matrix is converted into a list of points. Each line contains an integer for each dimension in the sampling matrix (in this case 2 integers). The order of the columns is arbitary, however we show the F1 (fast) dimension as the last column. Each row of the list will result in 2ⁿ FIDs being collected (where n is the dimensionality of the sampling matrix). Here, each line results in 4 FIDs. For a typical triple resonance spectrum, these 4 FIDs will represent the ¹⁵N Echo, ¹⁵N Antiecho, ¹³C Real and ¹³C Imaginary components of the hypercomplex point. C) Illustration of sparse and dense planes during reconstruction. Indirect planes are reconstructed individually from as many data points as there are sampled points in the schedule. At top, a sparse plane results from a less dense ¹H frequency (usually in a dispersed area or from a sample with a low number of signals). At bottom is a plane from a dense ¹H frequency. Such a plane might result from an unfolded protein or a sample with many signals. The number of points sampled should take into consideration the possibility of densely populated planes like these.

6.1.2 Order of points and offset values

In principle there is no reason the points in the schedule file need to be in any particular order. In practice, most schedulers (including the Poisson Gap scheduler) internally create schedules for 2 or more indirect dimensions ‘in order’ with the right-most column (F1) being the fastest acquired dimension. When implemented in this manner, reconstruction of a plane consisting of the F1 dimension and the direct dimension can be done very early on during an experiment. This can be used to verify that a pulse sequence is working, much like checking a US spectrum by collecting 2D planes. On the other hand, a randomized schedule, in which the points are shuffled, allows for complete reconstruction of the entire spectrum, at the final resolution, at virtually any stage of data collection. It should be noted that the earlier reconstruction takes place, more artifacts may populate the spectrum as large gaps will be present in the schedule.

Collection of the “traditional first point”, (where there is zero evolution in all indirect dimensions) as the first point in the NUS schedule is recommended as viewing the data in this point helps establish whether the experiment is running correctly or not. The first FID is used to determine the phase correction for the direct dimension before reconstruction. The FIDs of this first point also have an expected pattern, based on the acquisition method (Complex/States/States-TPPI/Echo-AntiEcho) of the indirect dimensions. More details on checking the progress of experiments is given in Section 6.2.

Should the first point in a 2D schedule be labeled “0 0” or “1 1”? This depends on the system and pulse program being used. Our schedule generating programs use the “0” offset internally when generating a schedule. It is trivial to add a “1” to all points to create a schedule offset of “1” for use in pulse sequences that require a “1” offset.

6.1.3 Selecting the sparsity of a schedule

The number of points required for successful reconstruction is covered in section 2.3. In practice, these guidelines work well. However, spectra that are crowded or poorly dispersed can benefit from a more conservative approach, at least in the case of hmsIST reconstructions. For a standard triple resonance experiment reconstruction of a ¹³C/¹⁵N plane takes place for every direct point along the ¹H amide dimension. Consider a 200 amino acid unfolded protein compared to a 200 amino acid structured protein. The number of expected peaks in the ¹³C/¹⁵N plane at a ¹H amide point at 7.5 ppm is much higher for the unfolded protein than for a folded, well dispersed protein. Even for a typical well folded protein, the middle of the amide region is usually the densest (see Figure 9 panel C). Significant peak density in these ¹³C/¹⁵N planes may warrant the use of higher sampling densities above and beyond the 20% per axis suggestion. This recommendation for higher sampling densities should also be considered in the case of dense NOE data where many signals are expected.

6.1.4 Generating schedule files

The initial methods of acquiring NUS data required generating a schedule outside the acquisition software. Modern acquisition software usually provides an automatic way to generate schedules, however no commerical software for NMR data acquisition creates Poisson Gap sampling schedules by default. Given the superior performance of this procedure (see section 3.2) we expect the the Poisson-Gap schedule will be part of commerical NMR software soon. Fortunately, it is possible to introduce Poisson Gap sampling schedules into the modern versions of acquisition software as well as legacy pulse sequences. There are a few ways in which a Poisson Gap sampling schedule can be generated. 1) A java applet with instructions can be download from http://gwagner.med.harvard.edu/intranet/hmsIST/gensched_old.html. This java applet can be run locally by a user. 2) A web based schedule generator is available at http://gwagner.med.harvard.edu/intranet/hmsIST/gensched_new.html. The page allows for schedules to be generated anywhere with access to a modern web browser. There is a ‘simple’ option where the number of points required in each dimension and sparseness is all that is required for a schedule to be generated. An advanced option is under development where the relaxation of evolving nuclei are taken into consideration to maximize signal-to-noise and/or resolution. In addition, constant time evolution can be checked to see if the number of points in a dimension exceeds the permissible amount. 3) A Bruker Topspin macro that will generate a Poisson Gap schedule for the currently opened experiment at the console is also available from us. This requires the NUS capabilities of Topspin 3.0+.

6.1.5. Implementing sampling schedules on commercial instruments

The latest versions of both Agilent and Bruker softwares readily support NUS sampling. In Agilent instruments using software VNMRJ 4.0 and above, with the latest patch, setting up and NUS experiments involves the following steps.

1. Using automatically generated schedule.

   • Step 1: Setup Parameters including spectral width, pulselength etc as one do for a linear expriment.
   • Step 2: Choose the option for NUS/Sparse sampling and specify the sampling density preferred.
   • Step 3: The experiment is ready to be excecuted with NUS.
2. Using user provided schedule

   • Step 1: Setup Parameters including spectral width, pulselength etc as one do for a linear expriment.
   • Step 2: Copy a sampling schedule into current experiment directory (curexp/sampling.sch)
   • Step 3: Choose or type sampling='sparse' and CStype='i'
   • Step 4: The experiment is ready to be excecuted with NUS.

The experiment is ready for NUS sampling as dictated by the sampling schedule sampling.sch

In Bruker instruments using Topspin version 3.0 and above, setting up and NUS experiments involves the following steps.

1. Using auomatically generated schedule.

   • Step 1: Setup Parameters including spectral width, pulselength etc as one do for a linear expriment.
   • Step 2: Choose “non-uniform_sampling” option for FnTYPE in eda
   • Step 3: Click on the NUS tab on the left frame and fill in the details about sampling density, J modulation, esitmated T₂ etc.
   • Step 4: The experiment is ready to be excecuted with NUS.

2. Using user provided schedule

In the above setting replace the schedule which is located in the vc directory with the namenuslist_”expno” with the user provided schedule. NUS can also be easily carried out on olderversions of both Agilent and Bruker softwares but the implementation is more involved and might require recoding pulse sequences in older Bruker software. Both Agilent and Bruker also provide softwares to process spectra that were acquired in NUS manner.

6.2 Checking the progress of experiments

New users are often skeptical of conducting NUS experiments because it is not possible to do conventional processing of data at early stages, meaning a few days can be spent collecting data non-uniformly, only to later find out an error was made during setup of the experiment. There are two ways in which NUS data can be checked before completion of the experiment. Firstly, the initial complex or hypercomplex point should be looked at to see if correct signals are present. Secondly, the entire spectrum can be processed before completion of data collection if acquired in random order.

6.2.1 Understanding the first complex/hypercomplex point

As stressed above, schedule files should always begin with the zero point. This means the first point acquired will be equivalent to the first point collected during conventional acquisition. Because this point has no frequency evolution a 1D transform of the FIDs for this point should result in spectra with signals without any frequency evolution in the indirect dimensions. For a complex point, the real FID should, in most cases, contain a high signal level while the imaginery part may contain zero signal (no phase correction). For an echoantiecho point, both FIDs will contain data. When two indirect dimensions are used, the first 4 FIDs will represent the first point. It should be noted that for dimensions in which frequency evolution is sine modulated (instead of cosine modulated), no signal will be present for the first point.

6.2.2 ‘In progress’ reconstructions

Experiments that are partially acquired can be processed, while still being acquired, to gauge the relative success or failure of an experiment. This is a natural consequence of collecting data non-uniformly as processing can be done using a truncated schedule file that encompasses the data that has been collected to that point. A schedule file that is randomly ordered will quickly span the resolution range of the final spectrum however the large gaps that result will initially lead to many artifacts. On the other hand, an in-order schedule file will slowly acquire one of the dimensions leading to reconstructions that poorly resolve that dimension. However, early data collection with either random or in-order schedules can be reconstructed and spectrum details can be seen very early on.

6.3 Remaining challenges

The application of non-uniform sampling is less widespread in the NMR community compared to traditional linear acquisition. The change over to non-uniform sampling still requires overcoming some difficulties and challenges.

6.3.1 More extensive use of semi-constant time

Constant time based aquisition methods is not sufficient to fully exploit NUS protocols. For example, at a ¹H frequency of 800 MHz and a sweep width of 36 ppm in a ¹⁵N dimension, only about 64 complex points can be acquired within the constant time period. With a deuterated protein and exploiting TROSY transfers, sensitivity is still increasing when 64 complex points in the ¹⁵N dimension have been acquired. To fully exploit NUS, semi-constant and/or constant time/real time experiments should be more widely available.

6.3.2 Full exploitation of signal to noise maximum at 1.26*T2 may not be feasible

The power of non-uniform sampling is the ability to sample out to very long evolution times within a tractable amount of collection time. This is particularly useful in dimensions where T₂ relaxation is low, for example exploiting TROSY transfers for backbone ¹⁵N and the ¹³Cα evolution of deuterated proteins. It has been established that maximal signal-to-noise is achieved when 1.26 times the T₂ decay time has been acquired (6). Calculations of expected T₂ relaxation times for a 30 kDa deuterated protein at 800 MHz with sweep widths of 36 ppm for ¹⁵N and 40 ppm for ¹³Cα shows that maximal signal would be acquired at 384 ¹⁵N points and 1233 ¹³Cα points in an HNCA experiment. Assuming a schedule that acquired 4% of these points, the number of scans set to 8 and a recycle delay time of 1.5 seconds, this experiment would take approximately 10.5 days to complete. Clearly this defeats the purpose of rapid data collection. Therefore, compromises may need to be made when attempting to collect signal maximally. In practice the selection of the number of points in each dimension will depend on sample conditions, the isotope labelling scheme employed and availability of pulse programs that can fully exploit long frequency evolution times. The best practice is to balance how much resolution (points) a user wants in each dimension while making sure that collection time does not become too long. For example, during 3D or 4D NOESY acquisition, a user will probably want to balance collecting many points in an indirect ¹H dimension while shortening any indirect heteronuclear dimensions to fit the available time to collect data.

6.3.3 The limits of spectrum file size

NUS permits collection of a large number of points per dimension. This leads to very large file sizes for spectra when the entire spectrum is composed into a single file. A 3D spectrum with 512 × 512 × 512 points can exceed the 2 GB file size limit present on some 32 bit operating systems and some spectrum analysis software. Also, software that attempts to hold all 2+ GB of spectrum data in RAM may run slow as system memory runs low. This problem is compounded for 4D spectra. Future implements of analysis software may need to consider addressing the problem of dealing with very large spectra that can result from ultra high resolution that is possible with non-uniform sampling.

7. Conclusions

After the initial proposal to use non-linear sampling acquisition of 2D NMR data (15) this approach has been used and further developed by only a small minority of NMR spectroscopists. However, recent developments of optimal sampling schedules and efficient reconstruction methods have created more awareness of the potential of this approach. Thus, commercial spectrometer providers have started to implement early versions in their spectrometer and processing software. Correctly acquired NUS data can now be reconstructed essentially free of artifacts and very fast so that 3D and 4D spectra can be obtained at unprecedented resolution and high precision of peak positions. This will facilitate correct assignment of peaks in 3D and 4D NOESY spectra and speed up structural studies. Besides providing higher resolution, carefully applied NUS can also significantly enhance the ability to detect weak peaks, which indeed will enable detection of more NOE peaks for structural studies. Obviously, the speed-up obtainable with NUS can readily be combined with other methods of fast acquisition. Thus, we expect that NUS and advanced reconstruction methods will become mainstream and enhance the impact of NMR in structural biology and molecular biology in general.

Highlights.

NUS is needed to exploit the power on modern instruments in 3D and 4D protein NMR

Random sampling schedules with Poisson-distributed gap lengths minimize artifacts

Enhanced reconstruction speed of hmsIST makes NUS suitable for routine protein NMR