Abstract
The analysis of very large DNA molecules intrinsically supports long-range, phased sequence information, but requires new approaches for their effective presentation as part of any genome analysis platform. Using a multi-pronged approach that marshaled molecular confinement, ionic environment, and DNA elastic properties–but tressed by molecular simulations–we have developed an efficient and scalable approach for presentation of large DNA molecules within nanoscale slits. Our approach relies on the formation of DNA dumbbells, where large segments of the molecules remain outside the nanoslits used to confine them. The low ionic environment, synergizing other features of our approach, enables DNA molecules to adopt a fully stretched conformation, comparable to the contour length, thereby facilitating analysis by optical microscopy. Accordingly, a molecular model is proposed to describe the conformation and dynamics of the DNA molecules within the nanoslits; a Langevin description of the polymer dynamics is adopted in which hydrodynamic effects are included through a Green’s function formalism. Our simulations reveal that a delicate balance between electrostatic and hydrodynamic interactions is responsible for the observed molecular conformations. We demonstrate and further confirm that the “Odijk regime” does indeed start when the confinement dimensions size are of the same order of magnitude as the persistence length of the molecule. We also summarize current theories concerning dumbbell dynamics.
Introduction
Much of the human genome is comprised of DNA sequences that are present in multiple copies. Although such elements play an important role in biological regulation and evolution their presence troubles current DNA sequencing approaches. Accordingly, serious issues arise when trying to complete the sequencing of human, or cancer genomes because short analyte molecules, currently used by major sequencing platforms, often present redundant sequence data. Like trying to assemble a jigsaw puzzle with pieces bearing no uniquely discernable features, such sequence data make it difficult to assemble the sequence of an entire genome. Furthermore, our ability to assess genomic alterations within populations as mutations, or polymorphisms is also limited. To meet this challenge, genome-wide analysis1–3 systems are now featuring modalities that present large, genomic DNA analytes3,4 for revealing genomic alterations through bioinformatic pipelines. Achieving utility for genome analysis using nanoconfinement approaches requires integration of system components that are synergistically poised for dealing with large data sets. Such components include sample preparation, molecular labeling, presentation of confined DNA molecules, and detection, complemented by algorithms incorporating statistical considerations of experimental error processes for data analysis.5–8 Here, electrokinetic loading of large DNAs into nanoslits offers new routes to stretching of random coils and presentation as analyte arrays. Nanoslits, or channels with aspect ratios > 1, realize genomically scalable nanoconfinement conditions that facilitate acquisition of large datasets. Nanoslits also allow inexpensive fabrication through large-scale replication of disposable devices from electron-beam fabricated masters. Moreover, low-ionic strength conditions increase a DNA molecule’s persistence length, thereby leading to nanoconfinement of DNA in devices that are compatible with the inherent geometric limitations of silastic materials.5,9 In a first generation of "Nanocoding," the mapping of confined DNA molecules was carried out with sequence-specific labels.5 The value of such mapping data for genomic analysis was shown to depend on marker density6 and molecular stretch S/L (where S is the apparent length of a molecule and L is its contour length).
While a number of approaches to confine DNA molecules have been examined and implemented in the past few years,5,10–15 few elongate DNA molecules close to their contour length. Kim et al.,9 for example, elongated λ –DNA within Poly(dimethylsiloxane) (PDMS) replicated nanochannels (250 nm × 400 nm) and achieved a stretch of 0.88 using ultra-low ionic strength conditions (0.06 mM). To our knowledge, it was the longest stretch reported for DNA molecules within nanochannels, using low ionic strength buffers. In different work, Reisner et al.11 used 50 nm fused silica nanochannels with higher ionic strength conditions (~5 mM) to elongate DNA molecules up to 0.83. Although the stretch with these two approaches was higher than 0.8, both techniques exhibit limitations. The approach of Reisner et al. is demanding in that it requires fabrication of extreme nanoconfinement devices, smaller than the molecular persistence length,16 to elongate DNA molecules close to the molecular contour length, thereby increasing the complexity of the molecular loading process.
Through a concerted experimental and theoretical approach outlined in previous work,5 we reasoned that engaging DNA "dumbbell" conformations within our nanoslits would greatly enhance DNA stretching through entropic, elastic, and hydrodynamic forces. In this paper, we define a DNA dumbbell as comprising two relaxed coils (lobes) within a microchannel flanking intervening polymer segments residing within a nanoslit (Fig. 1). Our experiments indeed show that molecular dumbbells increase DNA stretch within nanoslits up to the full molecule contour length using the same ionic strength and "spacious" confinement conditions (slit dimensions: 100 nm × 1,000 nm) as in previous experiments.5 More importantly, DNA dumbbells overcome limitations of current approaches, including ionic strengths below 0.06 mM, or severe confinement (below 50 nm). A combination of the lobes’ entropic recoil, hydrodynamic interactions, and electrostatic interactions, mediated by low-ionic strength conditions, produces tension across the DNA molecule backbone within the nanoslit, further elongating the molecule. For the first time, a dumb-bell conformation allows the elongation of DNA molecules within nanoslits demonstrating stretch up to 1.06 ± 0.19. Our results indicate that the "Odijk regime" is achieved once the persistence length is equal to the effective confinement (including electrostatic considerations), in apparent contradiction to other theories that suggested that the effective DNA diameter is the relevant parameter for the de Gennes-Odijk transition.11 In addition, we find that once the contour length of the molecule is longer than twice the nanoslit length, the dumbbell’s relaxation time is on the order of minutes, and increases with lobe size. The stretch remains independent of the molecular weight. Such molecular presentation greatly enhances the entrapment of stretched molecules (i.e., out-of equilibrium metastable states), thereby making this approach a practical component for genome analysis systems.
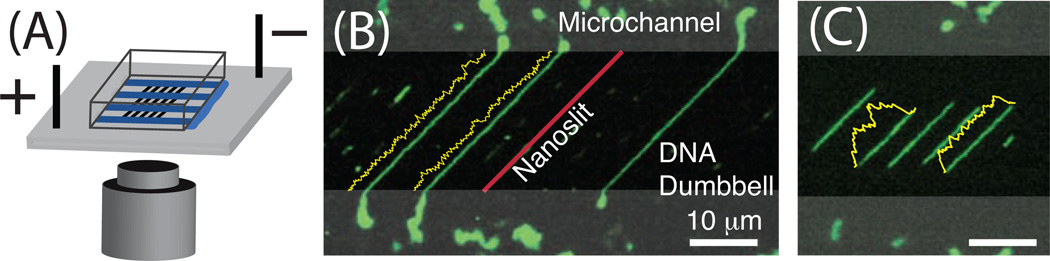
Figure 1.
Microchannel-nanoslit device supporting formation of molecular dumbbells (see movie supplement S1). (A) PDMS device adhered to cleaned glass coverslip, immersed in buffer (not shown), for electrokinetic loading of DNA molecules. (B) Dumbbells form when loaded T4 DNA molecules (166 kb; 74.5 µm, dye adjusted contour length) exceed the nanoslit length (28 µm); molecule ends flanking nanoslits become relaxed coils within the microchannels (lobes), thereby enhancing the stretch of intervening segments within the nanoslits to (0.85 ± 0.16, I = 0.51 mM); yellow traces show fluorescence intensity variations along molecular backbones. (C) λ –DNA molecules (48.5 kb, 21.8 µm) are too short to form dumbbells and are thus completely confined within the nanoslits; a lower stretch (S/L = 0.62 ± 0.08, I = 0.48 mM) is further evidenced by uneven fluorescence intensity profiles.
Recently, Yeh et al.17 also performed experiments on confined DNA molecules in combined micro- and nano-scale devices similar to those employed by Kim et al.9 They observed that under some circumstances long DNA was able to form dumbbells. They explained their observations in terms of quasi-static arguments, highlighting an entropy-driven single molecule tug-of-war (TOW) scheme that enables study of the statics and the dynamics of entropic recoil under strong confinement. In this work we show that this quasi-static regime, corresponding to symmetric lobes within the micro-scale confinement, has a vanishing probability of appearance. The confined molecules are under non-equilibrium conditions and the uneven size of the lobes controls molecular recoil. By taking account of non-equilibrium conditions, we show that several mechanisms can control molecule dynamics and dumbbell lifetimes.
Materials and Experimental Methodology
Device fabrication and setup
Microchannel-nanoslit device masters were fabricated by electron beam lithography using the JEOL JBX-5DII system (CNTech, UW-Madison). Nanoslits (1 µm wide × 100 nm high × 28 µm long) were etched into a silicon wafer by CF4 reactive ion etching and modified SU8 microchannels (20 µm wide × 1.66 µm high × 10 mm long) were overlaid (see Figure 1). PDMS replicas were created by soft lithography, made hydrophilic by O2 plasma treatment and stored in distilled water for 24 hours then the devices are utilized for a couple of months. Nanoslit devices were mounted on acid cleaned negatively charged glass surfaces.1 Platinum electrodes (wire, 0.013” diameter) were placed in a diagonal orientation, nearly parallel to the nanoslits, in the buffer chamber, a glass surface affixed to the bottom of a Plexiglas holder, and attached to Kepco (model BOP 100-1M) bipolar operational power supply. DNA solutions were loaded into the microchannels using capillary action, and devices were immersed in buffer [TE with final concentrations of: 2-mercaptoethanol (0.006%) and POP6 (0.00015%; Applied Biosystems) for 20 minutes allowing buffer equilibration before measurements. After the device is immersed, DNA molecules were electrokinetically driven into the nanoslits, timed before they completely exited, so that they were trapped as dumbbells.
DNA samples and stretching
DNA samples, stained with YOYO-1 (1, 1-[1, 3-propanediylbis [(dimethyliminio)-3, 1-propanediyl]] bis [4-[(3-methyl- 2(3H) benzoxazolylidene) methyl]-Quino-linium iodide, Molecular Probes)5 (Molecular Probes), included [(unstained/stained contour length), L; assuming an intercalation rate of 1 dye/4 bp): λ –bacteriophage (New England Biolabs) 48.5 kb (L = 16.5 µm/21.8 µm), T4 bacteriophage (Wako Chemicals) 166 kb (L = 56.3 µm/74.5 µm), λ –concatemers (New England Biolabs, λ concatemer ladder, size range = 137.4 – 582.0 kb), M. florum (ApaI digest: 252 kb, L = 85.7 µm/113.2 µm; 541 kb, L = 184.2 µm/243.2 µm. DNA solutions also contained 4% (v/v) 2-mercaptoethanol, 0.1% (w/v) POP6 (Applied Biosystems) and TE buffer (1X: 10 mM Tris-HCl and 1 mM EDTA pH 7.9) ranging from 0.01X to 0.1X; ionic strength was determined by conductivity using a NaCl standard.9
Image capture and analysis
YOYO-1 stained molecules were imaged (Manual Collect software5) using a Hamamatsu CCD camera (Orca-ER), coupled to a Zeiss 135M epifluorescence microscope (63× Zeiss Plan-Neofluar oil immersion objective), illuminated by an argon ion laser (488 nm; 8 µW to 200 µW measured at nosepiece) for stretch and relaxation time experiments. A more sensitive camera (Andor iXon–888 EMCCD) was used to image the relaxation kinetics of T4 dumbbell molecules. Images were analyzed using ImageJ18 to subtract background using the “rolling ball” algorithm,19 segment by thresholding the molecule from the background and measure molecular fluorescence intensities and length.
Mesoplasma florum preparation
M. florum20 was grown in ATCC 1161 at 30°C then pelleted. Cells were washed with a solution of 10 mM Tris-HCl, pH 7.6, and 1 M NaCl then pelleted and resuspended. Warmed cells, 37°C, were mixed with 1:1 (v/v) with 1% low melting temperature agarose and dispensed in an insert tray. Inserts21,22 were pooled in a 50 ml conical tube and incubated in 6 mM Tris-HCl pH 7.6, 1 M NaCl, 100 mM EDTA, 1% N-lauroylsarcosine, and 20 µg/ml RNase, overnight at 37°C. Inserts were then transferred to 0.50 M EDTA pH 8.0, 1% N-lauroylsarcosine, with 1 mg/ml Proteinase K) and incubated overnight at 50°C followed by 0.1 mM phenylmethylsulfonyl fluoride then dialyzed ten times with 0.50 M EDTA, pH 9.5. Inserts were twice dialyzed against 1X TE, then dialyzed in 0.1X TE for electroelution.
Determination of surface charge density
Surface charge density was estimated using electroosmotic flow measurement in the nanoslit device with two ports. Electroosmotic flow was measured in a setup similar to that described by Huang et al.23 Ports were cut into an oxygen plasma treated nanoslit device with a standard razor blade. Platinum electrodes, spaced 20 mm apart, were placed in the ports and connected to an EC-105 power supply (EC Apparatus Corporation) with a 195 Ω resistor, between second reservoir and the ground. A multimeter was connected directly across the resistor to measure the potential drop as an external electrical potential was applied. 20 mM phosphate buffer, pH 7.0, was added to load and flush the system then 10 mM phosphate buffer pH 7.0 is added, followed by application of ~ 100 V (3 minutes); the voltage polarity was then reversed for an additional 3 minutes. A linear fit identified the intercept (time, t) between the forward and reverse bias for each set of experiments. The electroosmotic mobility (μEOF) was calculated by
| (1) |
where LC is the microchannel length, E is the electric field and t is time. From the electroosmotic mobility, the charge density on a surface (σe) is
| (2) |
where ζ is zeta potential, κ−1 is Debye length, rw is the normal distance from the surface, ε the relative permittivity, and ε0 is the permittivity of a vacuum. Accordingly, the surface density of the device interior was found to be 1.1 to 1.3 e/nm2.
Bead diffusion under nanoconfinement
YG carboxyl terminated beads (24 nm; Molecular Probes) in 0.20 mM and 10 mM NaCl, κ−1 = 22 and 3 nm, respectively) within nanoslits were imaged using Total Internal Reflection Fluorescence Microscopy (TIRF) microscopy using a Zeiss TIRF 100X 1.46 NA objective and 135TV inverted microscope. The optical train comprised: 488 nm illumination (argon-ion laser, Coherent); quarter wave plate; Galilean telescope (40 mm and 200 mm focal length lenses (Edmund Industrial Optics)); broadband filter 485/20 (Semrock); and 525/50 excitation filter (Chroma); beam was then mapped by a 125 mm field length convex lens onto the objective. TIRF excitation produced a penetration depth of ~ 70 nm (less than nanoslit depth; 100 nm); images passed through a 525/50 emission filter (Chroma) onto an Andor iXon-888 camera, running Andor SOLIS software, which were then background subtracted with a "rolling ball" algorithm for shading correction;19 a Kalman stack algorithm was implemented to decrease image noise. The periodicity of bead fluorescence intensity fluctuations was analyzed using a Fast Fourier Transform (FFT) for discerning maxima peaks.
DNA Model and Simulation Approach
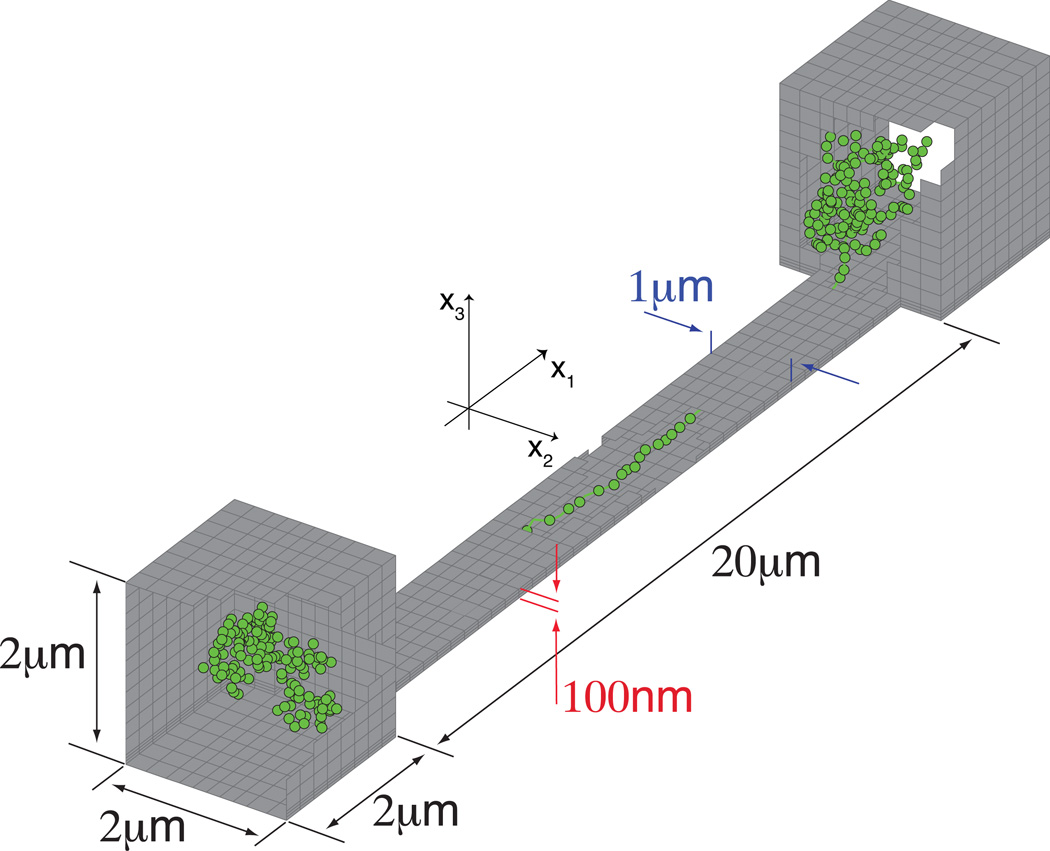
Brownian dynamics (BD) simulations were performed to simulate the DNA dumbbell conformation within the nanoslits. Long range hydrodynamic interactions were included through a Green’s function formalism and calculated with the O(N) General Geometry Ewald-like Method (GGEM).24–31 There is a combination of confinement effects for the dumbbell conformation. A molecule in a slit experiences a de Gennes’ regime (confinement size ~ Rg)32 in the microchannel and within the nanoslit width, an Odjik regime (confinement size ~ lp)16,33,34 in the nanoslit height. This combination of regimes places a number of restrictions on the model to be used to describe the slits considered in this work (see Figure 2).
Figure 2.
Simulated nanoslit geometry. An snapshot of a T4-DNA molecule (166kb, L = 74.5µm) forming a dumbbell is shown. Simulated slit lengths were 10, 20 and 30 µm, the results were equivalent due to the fact that the molecule stretch is independent of molecular weight. The results presented here were calculated using a 20 µm long nanoslit.
Available descriptions of DNA range from detailed atomistic models,35 to mesoscale models that use multiple sites to define a nucleotide,36–39 to coarse grained models that describe multiple nucleotides in terms of individual beads (and springs).40–42 Notable examples include the Kratky-Porod model with a continuous worm-like chain (WLC) model, bead-spring models that use Marko and Siggia interpolation,43–47 and non-linear elastic spring (FENE) based models.26,27,48 The appropriate model must resolve the length scales of the nano-confinement without a finite discretization of the persistence length, because characteristic times for segmental diffusion are several orders of magnitude smaller than characteristic chain-diffusion times. Kratky-Porod or higher resolution models are computationally demanding (there is a time scale separation of 8 orders of magnitude between the bead and chain diffusion times). At the other end of the spectrum, a continuous WLC model describing 10–20 persistence lengths in terms of a single spring does not have the resolution required to describe nanoslit confinement.
Yeh et al.17 performed simulations of bead-spring chains connected by springs to described their experiments on DNA dumbbells. Starting from a WLC representation of the springs, however, they modified the law until agreement was observed between the model and experiments. It is unclear, however, whether such an approach would be able to describe large DNA molecules over a wide range of conditions and whether it would be truly predictive. A good compromise, and one that we adopt in this work, is provided by the Underhill-Doyle (UD) model.49–51 The UD model was originally developed for a θ –solvent; in this work we include excluded volume forces and hydrodynamic interactions to describe good-solvent conditions and to generate Zimm scaling. The polymer molecule, dissolved in a viscous solvent, is represented by a bead-spring chain consisting of Nb beads connected through Ns = Nb −1 springs. The conditions of our confined systems are such that the Reynolds number is zero, and inertia is neglected. The force balance on each bead requires
| (3) |
for bead ı, is the hydrodynamic force, is the bead-to-bead excluded volume force, is the bead-wall excluded volume force, is the Brownian force and is the UD spring force. This model, developed using a constant stretch mechanical ensemble, is used for the connectivity between adjacent molecule beads. This model is defined as follows49–51
| (4) |
where r̂ = r/q0, q0 is the maximum spring extension and r = |x|, x = (x, y, z). The coefficients of this polynomial expansion are defined by
| (5) |
| (6) |
| (7) |
| (8) |
where and Np,s is the number of persistence lengths per spring. In the development of the model, Underhill and Doyle49 did an error estimation of the spring law as a function of Np,s, and found that it reproduces DNA behavior with a maximum error of 1% for Np,s ≥ 4. We selected the maximum length resolution of the UD model given by Np,s = 4.
For the non-bonded bead-bead interactions, we use a Gaussian excluded volume potential. Neutron scattering data for dilute solutions of linear polymers in good solvent conditions indicate ideal chain behavior at small distances along the chain and good solvent behavior at long distances.52–57 We consider the increase in energy due to the overlap of two submolecules (or molecular blobs). Each submolecule is considered to have a Gaussian probability distribution with second moment , where Np,s is the number of persistence lengths per spring. Considering the energy penalty due to overlap of two Gaussian coils, one arrives at the following expression for the excluded volume potential between two beads of the chain:53,55
| (9) |
where fν = −∇Φν, ων is the excluded volume parameter related to the DNA effective diameter,54,55 kB is the Boltzmann constant and T is the temperature. A repulsive Lennard-Jones potential58,59 is used to describe bead-wall excluded volume interactions, where the Euclidean distance is replaced by the wall normal direction.
The dynamics of the bead-spring DNA molecules are described by evolving the configurational distribution function. The diffusion equation for that function has the form of a Fokker-Planck equation; the force balance described above corresponds to the following system of stochastic differential equations of motion for the bead’s positions:55,60,61
| (10) |
where R is a vector containing the 3Nb coordinates of the beads that constitute the polymer chain, with xı denoting the Cartesian coordinates of bead ı. The vector U0 of length 3Nb represents the unperturbed velocity field, i.e. the velocity field in the absence of any polymer molecule. The vector F has length 3Nb, with fı denoting the total non-Brownian, non-hydrodynamic force acting on bead ı. Finally, the 3Nb independent components of dW are obtained from a real-valued Gaussian distribution with zero mean and variance dt. The motion of a bead of the chain perturbs the entire flow field, which in turns influences the motion of other beads. These hydrodynamic interactions (HI) enter the polymer chain dynamics through the 3 × 3 block components (Dıμ) of the 3Nb × 3Nb diffusion tensor, D = kBTM (M is the mobility tensor), which may be separated into the bead Stokes drag and the hydrodynamic interaction tensor, Ωıμ;
| (11) |
Here δ is a 3 × 3 identity matrix, δıμ is the Kronecker delta and ξ is the bead friction coefficient. The Brownian perturbation is coupled to the hydrodynamic interactions through the fluctuation-dissipation theorem: D = B · BT. The characteristic length, time, and force scales describing the system are set by the bead hydrodynamic radius a, the bead diffusion time ξa2/kBT, and kBT/a, respectively. The bead friction coefficient ξ is related to the solvent viscosity η and a through Stokes’ law, i.e., ξ = 6πηa.
In conventional Green’s function-based methods, M is computed explicitly; the resulting matrix-vector operation to determine the fluid velocity requires O(N2) operations. Additionally, for non-periodic domains, appropriate boundary conditions must be included in order to correctly calculate the velocity; for example, u(x) = 0 for no-slip boundaries. Jendrejack et al.2,57,62–64 enforced the boundary conditions with solutions using finite element methods (FEMs), where the quadratic scaling limits analysis to small systems. Hernández-Ortiz et al.65 generalized a method developed by Mucha et al.66 that scales as O(N1.66 logN), but is restricted to slit geometries. There are other approaches that allow the calculation of M · F by O(NlogN) calculations in periodic domains. For instance, there are Ewald sum and particle-mesh Ewald (PME) methods that are based on the Hasi-moto67 solution for Stokes flow driven by a periodic array of point forces. In this work, the fluid velocity (M · F) is calculated using the O(N) General Geometry Ewald-like Method (GGEM) introduced by Hernández-Ortiz et al.25–31,68 GGEM yields M · F without explicit construction of M and, when combined with Fixman’s69,70 mid-point integration algorithm and Fixman’s71 Cheby-shev polynomial approximation for B · dW, it allows us to evolve the chains in time through an efficient O(N) matrix-free formulation.26–29 Details of this method and its implementation are described in the Appendix.
The ionic strength influences DNA conformations through electrostatic interactions between the charges on the DNA phosphate backbone and interactions with nanoslit walls. These interactions are screened over the Debye length (κ−1), defined by: κ2 = 2NAe2I/ε0εkBT (where NA is Avogadro’s number, e the electronic charge, I is the ionic strength, ε0 is the permittivity of free space and ε is the dielectric constant of water). As the Debye length increases (from 10 to 30 nm) due to the decrease in ionic strength (1.0 to 0.11 mM), the persistence length of the molecule increases due to backbone like-charge repulsions, and due to the decrease in the effective height of the channel (which is in turn due to surface-DNA charge repulsions). Odijk34 and Skolnick and Fixman72 (OSF) have estimated theoretically how the persistence length (lp) of a worm-like poly-electrolyte coil is affected by a short-ranged electrostatic potential. Baumann et al. confirmed their theoretical predictions through experiments on large DNA molecules,73 achieving a quantitative prediction with an expression of the form
| (12) |
where lp,0 is the intrinsic persistence length corresponding to fully screened electrostatic contributions (lp,0 = 50 nm). In our experiments, the persistence length of the dumbbell molecules ranges from 82.4 to 358 nm. Although predictions of the OSF theory have raised concerns,74 OSF is known to give the correct scaling for the persistence length with respect to the ionic strength.73,75 As alluded to earlier, the ionic environment also plays a major role in the confinement because the surface of the device has a charge density of 1.1 to 1.3 e/nm2, with its own Debye length. Our BD simulations do not include electrostatic interactions with the walls directly; instead, the model was parameterized to account for the change in persistence length, and the wall-excluded volume was modified according to the Debye length. Note that we are currently implementing a full HI-electrostatic DNA model to account for these effects more accurately and results will be presented in the future. The model parameterization was performed using experimental data for λ –DNA in the bulk; we use L = 21 µm, Rg = 0.7 µm, < S > = 1.5 µm, lp = 53 nm at I = 10.798 mM, and a Zimm diffusion coefficient (HI chains) of DZ = 0.0115 µm2/s in a 43.3 cP solvent at 23°C47 (Note that the actual viscosity (ηs) is much lower).
Scaling arguments were then used to find the model parameters at different ionic strengths:
| (13) |
where ω ~ κ−1 + κ−1 log (νeffκ−1) is the effective diameter of DNA76,77 and νeff is an effective DNA line charge78,79). The UD model was subsequently parameterized to produce the necessary scaling dictated by the ionic strength and persistence length; thus, the range of the bead-bead excluded volume was modified to to follow the scaling given in Eqn. (13),54 while the bead-wall excluded volume range was increased in order to account for the wall Debye length.
Theoretical Considerations on nanoconfined DNA dumbbells
An analytical theory is used to provide interpretation for the dynamical behavior of the nanoconfined DNA molecules.
Free energy of a lobe
If we momentarily neglect the opening of the nanoslit, we may view the DNA chain within one lobe of the dumbbell as a long flexible coil of contour length s restricted by a hard smooth wall. The partition function of a coil with two ends fixed is known to be given by a Gaussian function in free space minus its mirrored version induced by an image charge80–82 (if the chain is ideal). This is because its value must reduce to zero at the wall. Integrating over the configuration of one end point, one derives the partition function G(z;s), where z is the distance of the other end of the lobe to the wall and the lobe consists of s/A Kuhn segments of length A = 2lp. G is actually a function of z/s1/2A1/2 only which for z ≪ s1/2A1/2 reduces to81
| (14) |
The area of the opening of the nanoslit is D × h (h ≪ D). Eqn. (14) is strictly valid if z > h. Here, h = O(lp) so the DNA within the nanoslit (with zero or few back folds) is joined to the lobe with z >~ h by a short intervening section of DNA whose description is challenging. The free energy of the latter maybe neglected, however, so the free energy of the lobe is expressed as
| (15) |
If the DNA of total contour length L translocates through a nanopore instead of a nanoslit, Eqn. (15) then leads to a total free energy
| (16) |
as argued by Sung and Park.83 If the lobes are asymmetric, there is a force
| (17) |
on the DNA driving it out of the nanopore. A similar force should play a dominant role when the DNA translates through a nanoslit in the deflection regime, provided there are two lobes. The effect of excluded volume is rather weak; it merely changes the numerical coefficient in Eqn. (15).81
Symmetrical dumbbell
It is of interest to study the equilibrium of the symmetrical dumbbell. If we suppose the nanoslit is long and we neglect electrostatics, we may write the total free energy of the DNA
| (18) |
from Eqn. (15). We have added an ideal chain term for the stretched DNA spanning the nanoslit of length ls . A long chain slithers back and forth along the channel and has a global persistence length g ≪ ls. Therefore, the force on the DNA
| (19) |
is nearly equal to zero; an exactly symmetrical dumbbell conformation cannot exist in equilibrium. The two lobes must retract into the nanoslit. The counterintuitive nature of the free energy of a single lobe has been emphasized before by Farkas et al.84 An isolated chain experiences a deflection force away from a wall (s is constant but z becomes larger in Eqn. (14)). But for a lobe attached to a section of DNA within the nanoslit, z = h is held fixed and s is variable. We note that the entropic force arising from the lobes in Eqn. (19) is generally quite weak.
Excluded-volume effect and non-draining limit
How well do the physical properties of the DNA samples used in Figure 6 conform to asymptotic regimes? The excluded volume parameter zel is a measure of the excluded-volume effect between two Kuhn segments85
| (20) |
where the DNA effective diameter is ω = 74.9 nm at I = 0.51 mM. The total persistence length equals 113.5 nm from Eqn. (12). Hence, zel ranges from 2.5 to 5.0 for the DNA samples in Figure 6 (molecule sizes ranging from 146 to 582 kb). The excluded volume effect may regarded as close to asymptotic (zel ≫ 1).
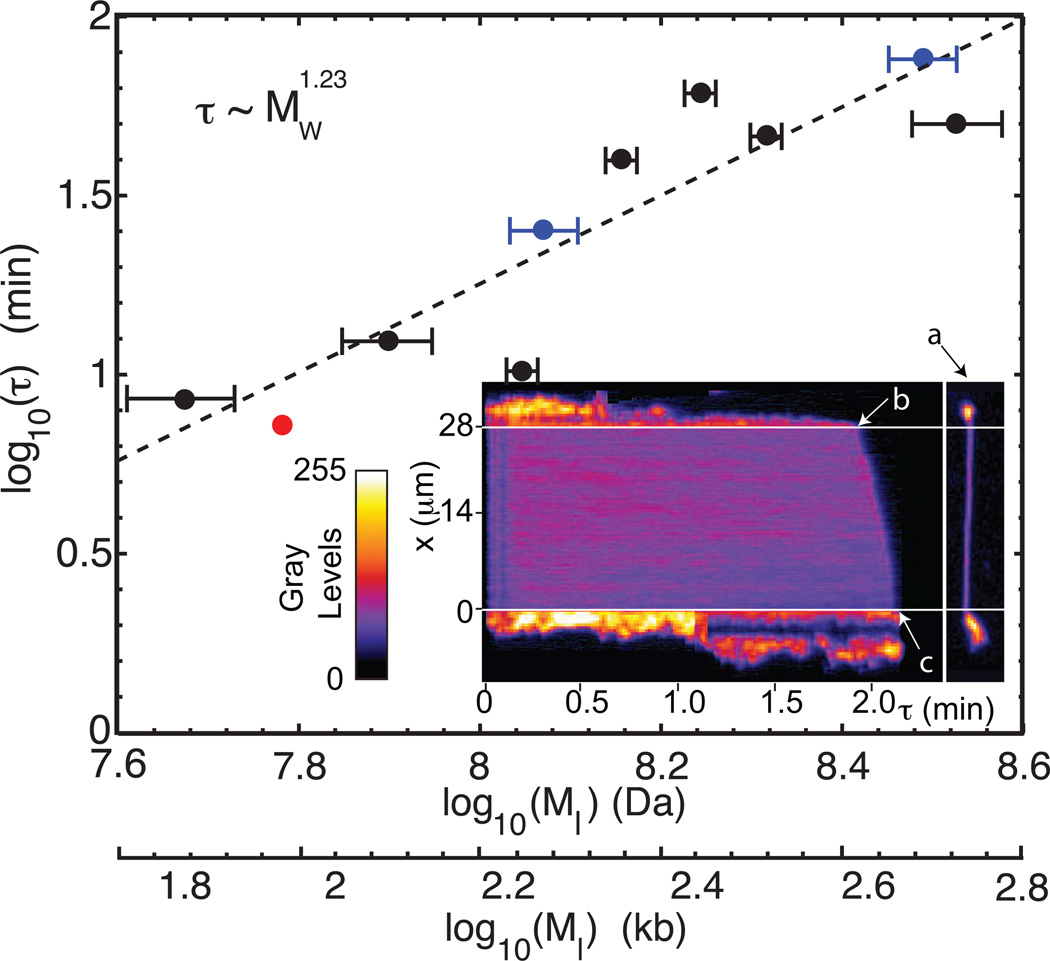
Figure 6.
Dumbbell relaxation times as a function of molecule size for T4 (red bullets (•), N = 105 molecules), λ –DNA concatemers (black bullets (•), N = 4 – 21 molecules), and M. florum DNA (blue bullets ( ), N = 11 – 59 molecules) digested with the restriction enzyme ApaI. Each circle represents a mean relaxation time (Rt) for a given molecule size (146 kb − 582 kb; x–axis error bars show 95% confidence intervals). Linear regression fit to the log-log plot shows an exponent of 1.23 ± 0.09 (R2 = 0.82). The exponent error is determined with a consistency test that includes each point’s mean and x–axis error. (Inset) Dumbbell dynamics for a T4 DNA molecule imaged as a movie (Supplemental Movie S1) shown here as compiled time slices (arrow a shows one slice; 0.440 s per slice).
), N = 11 – 59 molecules) digested with the restriction enzyme ApaI. Each circle represents a mean relaxation time (Rt) for a given molecule size (146 kb − 582 kb; x–axis error bars show 95% confidence intervals). Linear regression fit to the log-log plot shows an exponent of 1.23 ± 0.09 (R2 = 0.82). The exponent error is determined with a consistency test that includes each point’s mean and x–axis error. (Inset) Dumbbell dynamics for a T4 DNA molecule imaged as a movie (Supplemental Movie S1) shown here as compiled time slices (arrow a shows one slice; 0.440 s per slice).
If a DNA molecule is regarded as a wormlike chain with a hydrodynamic diameter d ≈ 2 nm, the draining properties depend on the parameters L/2lp and d/2lp ≈ 0.01. Yamakawa and Fujii have developed a theory for the translational friction coefficient in their classic work.86 Here, the DNA coils turn out to be long enough so that their hydrodynamics is, effectively, in the non-draining limit.
Nanoconfinement-mediated ejection
In the case where there is only a single lobe, the DNA is ejected from the nanoslit because there is a substantial free energy difference between the nanoconfined DNA and its equivalent in the remaining lobe.87–89 Burkhardt computed the coefficient C1 in the expression for the free energy of a DNA chain in a nanoslit numerically.90
| (21) |
where C1 = 1.1036 and x = L − s. This clearly often overwhelms the contribution from the lobe (Eqn. (15)) and the force fs = −∂FcL/∂x on the chain is constant.
The DNA is forced out of the nanoslit; the force f must overcome the hydrodynamic friction on the DNA, which may be viewed effectively as a straight rod under the ionic conditions imposed here. The coefficient of friction in the longitudinal dimension may be written as53
| (22) |
This is independent of D because the upper cut-off in the hydrodynamics is the smaller scale h, which itself is much larger than d. Therefore to a first approximation, the equation of motion of the sliding DNA maybe expressed as
| (23) |
The lobe increases in size as the DNA is ejected, but the frictional force on it may be neglected in Eqn. (23). From the previous section, we know its size R(s) scales as s3/5 so that we have dR/dt = −3/5(R(t)/s(t))dx(t)/dt. Moreover, in the non-draining limit, the coefficient of friction on the expanding lobe is ηR(t) so the lobe friction is a higher order term. Another issue is how well bulk hydrodynamics applies within the slit. There is evidence for a possible breakdown of this assumption for very tight silica nanoslits (h equal to about 20 nm).91,92 In our case, the PDMS nanoslits, which are less tight, are also expected to be smoother although we feel a thorough investigation of the magnitude of the friction is warranted in the future.
Eqn. (23) is readily solved and leads to a parabolic equation as has been presented before87–89
| (24) |
| (25) |
It has been assumed that the DNA fills the entire nanoslit at t = 0. If we set h= 0.1 µm, D = 1 µm, lp = 0.1135 µm, L = 28 µm, ηs = 1 cP, and d = 2 nm, we compute a force |fs| = 13kbT/µm and an ejection time τs = 12 s. The latter agrees well with the time the T4 DNA molecule is ejected from the nanoslit in the Supplement Movie S1. A tentative conclusion is that bulk hydrodynamics indeed applies within the nanoslit. By contrast, the experimental friction on the DNA in the square silica nanochannels of Mannion et al.89 was found to be five times higher than predicted by an expression analogous to Eqn. (22). This discrepancy is unexplained.
Lobe translocation
Numerous computational and analytical studies have been devoted to the translocation of a flexible polymer chain through a nanopore, as has been reviewed recently.93 In our experiments, the DNA stretch is very high within the nanoslit, so we think it is plausible that the translocation dynamics of the DNA lobe should be quite similar to that in a nanopore device. A full analysis of all chain fluctuations will be needed to bear this out in the future.
Often the time τl a chain needs to translocate through a nanopore scales as a power law in terms of the number of segments N, i.e.
| (26) |
A main objective has been to complete β precisely but this has engendered considerable controversy.93 This is beyond the scope of this work; though we have summarized several representative predictions for β in Table 1.
Table 1.
Exponent β of the lobe translocation time τl ~ Nβ as a function of the number of segments N. In forced translocation, the time is inversely proportional to the force. The excluded-volume exponent ν is chosen here to be equal to 3/5.
In the case of unbiased translocation Chuang et al.94 argued that the polymer chain cannot be viewed as a single particle diffusing across an entropic barrier given by Eqn. (15). The diffusion through the nanopore is collective and Rouse-like across a distance R ~ sν, the size of the lobe. The translocation time τl should then scale as NR2(N) ~ N1+2ν (see entry in Table 1). With hydrodynamic interactions, the frictional factor proportional to N reduces to Nν ~ R.
Recently, it has been proposed that this simple scenario should be amended.95 The presence of the nanopore (or nanoslit) implies the dynamics of translocation is strongly inhomogeneous. The diffusion of segments across the pore causes an imbalance in tension between the two lobes. The translocation time affected by these memory effects becomes effectively longer (see Table 1).
When the extending force f on a lobe is large enough (fR(s) > kBT), the translocation becomes forced and τl is inversely proportional to f. We have corroborated the entry in Table 1 for the case without memory effects because it disagrees with an earlier estimate.96 Our argument is based on the rate of dissipation dF/dt. On the one hand, this equals the velocity of the chain Vı at the opening of the nanopore times the force f reeling the lobe in. In view of the fact that the radius of the lobe R ~ sν, we know that Vı = −ds/dt = −(s/νR)dR/dt. On the other hand, the rate of dissipation in the Rouse limit within the contracting lobe is given by N f0(dR/dt) where f0 = ζ0(dR/dt) is the typical force on a segment with a friction coefficient of ζ0. The typical velocity of a segment is dR/dt. The two rates must be identical, thus leading to the entry in Table 1. Memory effects give rise to non-trivial exponents97 also presented in Table 1.
Results and Discussion
Dumbbell formation completely stretches DNA molecules and requires hydrodynamic considerations
Using experimental and simulation approaches we explored the idea that elastic and hydrodynamic contributions to DNA stretch, originating from the coil itself (a dumbbell lobe), in addition to contributions from just nanoconfinement, would greatly enhance DNA elongation. We created DNA dumbbells within our nanoslit device, shown in Figure 1, by strategically threading DNA molecules through nanoslits, using carefully timed electrical pulses. Conditions were adjusted allowing DNA ends to occupy the two microchannels bounding nanoslit entrances creating dumbbell lobes comprising random coils. DNA stretch within nanoslit portions of the device is estimated by fluorescence intensity measurements comparing nanoslit vs. microchannel portions of the same molecule: S/L = lsfm/Smfs; where fm is the integrated fluorescence intensity of the entire molecule, fs and ls are the fluorescence intensity and length of the molecular portion within a slit, and Sm is the known length of the molecule (µm; dye corrected).
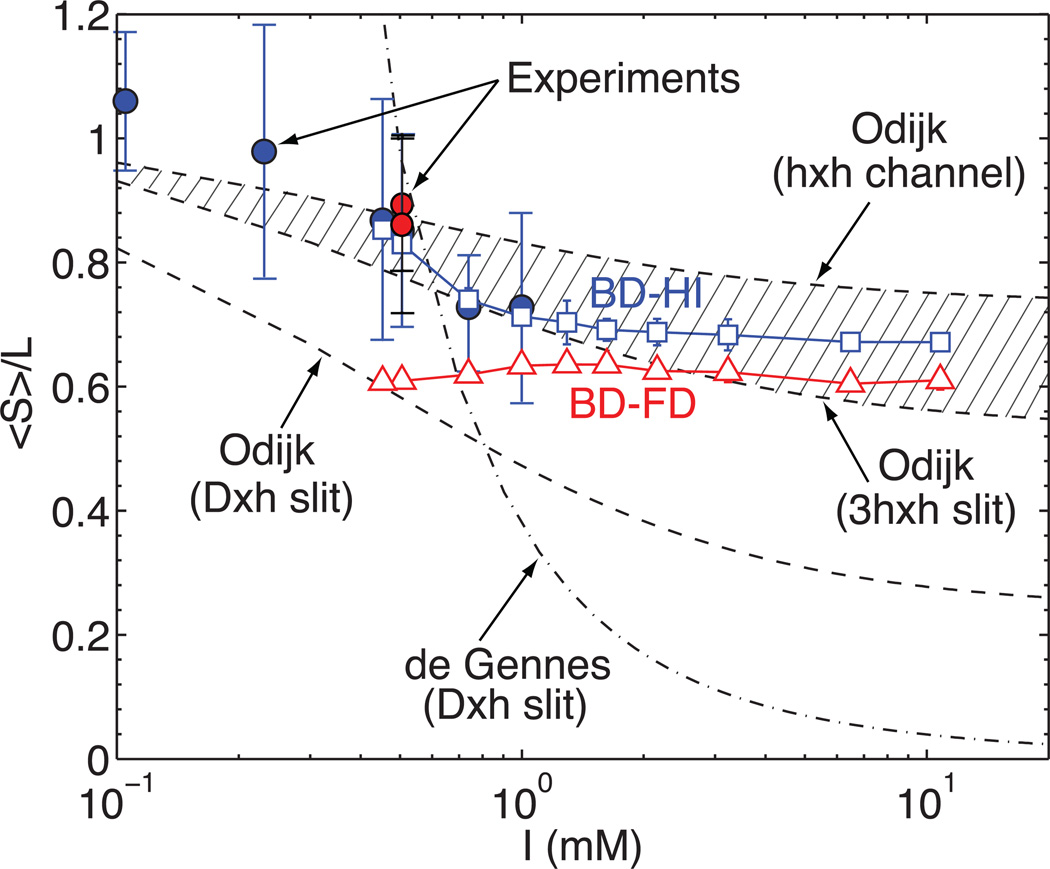
We expect ionic strength affecting DNA stretch by the electrostatic contributions to persistence length, or polymer stiffness, and the electrostatic environment presented by the device.5 Accordingly, we evaluated these collective effects on DNA stretch by varying the buffer ionic strength enveloping both sample and device. Figure 3 shows DNA stretch, using T4 and λ –bacteriophage DNA, as a function of ionic strength, I ∈ [0.11, 1.0] mM from experiments and from BD simulations (I ∈ [0.5, 10] mM; see Materials and Experimental Methodology). As the ionic strength decreases, DNA stretch within a nanoslit increases, as previously reported Jo et al.5 Here, however, the additional coupling of dumbbell elastic forces greatly enhance DNA stretch by a substantial 23% (S/L = 0.85 ± 0.16; I = 0.51 mM) over molecular nanoconfinement without dumbbells (S/L = 0.62 ± 0.08; I = 0.47 mM). Further reduction of ionic strength enables presentation of fully stretched (S/L = 1.06 ± 0.19; I = 0.11 mM) DNA molecules. We further validate these stretch estimations using λ –DNA as an internal fluorescence standard of known size, within slits, for normalizing integrated fluorescence intensities of λ –concatamer DNA dumbbells (confined portions): (0.87 ± 0.14, N = 231; I = 0.48 mM), which is similar to the previous value found for T4 DNA (0.85 ± 0.16; I = 0.51 mM). The stretch values found for T4 and λ experiments agreed (Fig. 3), indicating consistency and reproducibility of the stretch measurement approaches.
Figure 3.
Stretch as a function of ionic strength for T4 DNA (blue bullets ( ); error bars show SD on means, N = 51 – 101 molecules) dumbbells showing good concordance between experiments, simulation, and Odijk theory. Red bullets (•) show: λ concatemer data from Figure 5, and measurements using an internal standard (see text). Successive dilutions of 1X TE buffer varied ionic strength: 1.0, 0.74, 0.51, 0.45, 0.23, and 0.11 mM. Triangles (△) show results from BD simulations without considering hydrodynamic interactions (FD). Boxes (□) show results from BD simulations with fluctuating hydrodynamics interactions (HI). Dotted lines correspond to de Gennes and Odijk scaling predictions. The shaded region encompasses the Odijk scaling between an effective h × h channel and a 3h × h slit.
); error bars show SD on means, N = 51 – 101 molecules) dumbbells showing good concordance between experiments, simulation, and Odijk theory. Red bullets (•) show: λ concatemer data from Figure 5, and measurements using an internal standard (see text). Successive dilutions of 1X TE buffer varied ionic strength: 1.0, 0.74, 0.51, 0.45, 0.23, and 0.11 mM. Triangles (△) show results from BD simulations without considering hydrodynamic interactions (FD). Boxes (□) show results from BD simulations with fluctuating hydrodynamics interactions (HI). Dotted lines correspond to de Gennes and Odijk scaling predictions. The shaded region encompasses the Odijk scaling between an effective h × h channel and a 3h × h slit.
Figure 3 also shows the results of our theoretical predictions by BD simulations, as compared to experiments. For completeness, results are shown for calculations that include fluctuating hydrodynamic interactions (HI), and calculations when such interactions are neglected (free-draining model, FD). Note that part of the chain is in the nanoslit, and here, HI are expected to be screened and play a minor role. However, as the results in Figure 3 indicate, HI significantly contributes to the dumbbell dynamics and greatly influences molecular stretch. This can be explained by the fact that Zimm dynamics of the lobes in the microchannel (outside the slit) influence the dynamics of chain segments within the intervening nanoslit. Two trends are discernible in the simulation results: for I > 1.0 mM the stretch is nearly constant, and for I ≤ 0.74 mM a sudden increase is observed. Within this latter range, the persistence length of the chain reaches values comparable to the nanoslit height (~ 100 nm), thereby placing the level of confinement in the Odijk regime. Note that the confinement size, at this ionic strength conditions, is smaller than 100 nm because the walls have their own ion cloud. At this point, the underlying physics becomes complicated due to interactions between the ion clouds associated with the chain and walls. However, one major effect is the reduction of the effective confinement size, i.e. the chain persistence length increases and the "free" available space between the walls decreases. Our simulations of stretch follow the experimentally observed trends, but slightly under-predict (≤ 5%) the experimental data. We attribute the discrepancy to the fact that full electrostatic interactions are not included in our model. Also note that it is not possible to use the current model for the two lowest ionic strength conditions considered in experiments because the persistence length is higher than the confinement (lp > 100 nm). These points aside, the simulations reveal the underlying physical phenomena behind dumbbell-mediated stretch, and most importantly, the critical interplay between HI acting at the lobes and the electrostatic interactions helping to confine and elongate DNA molecules.
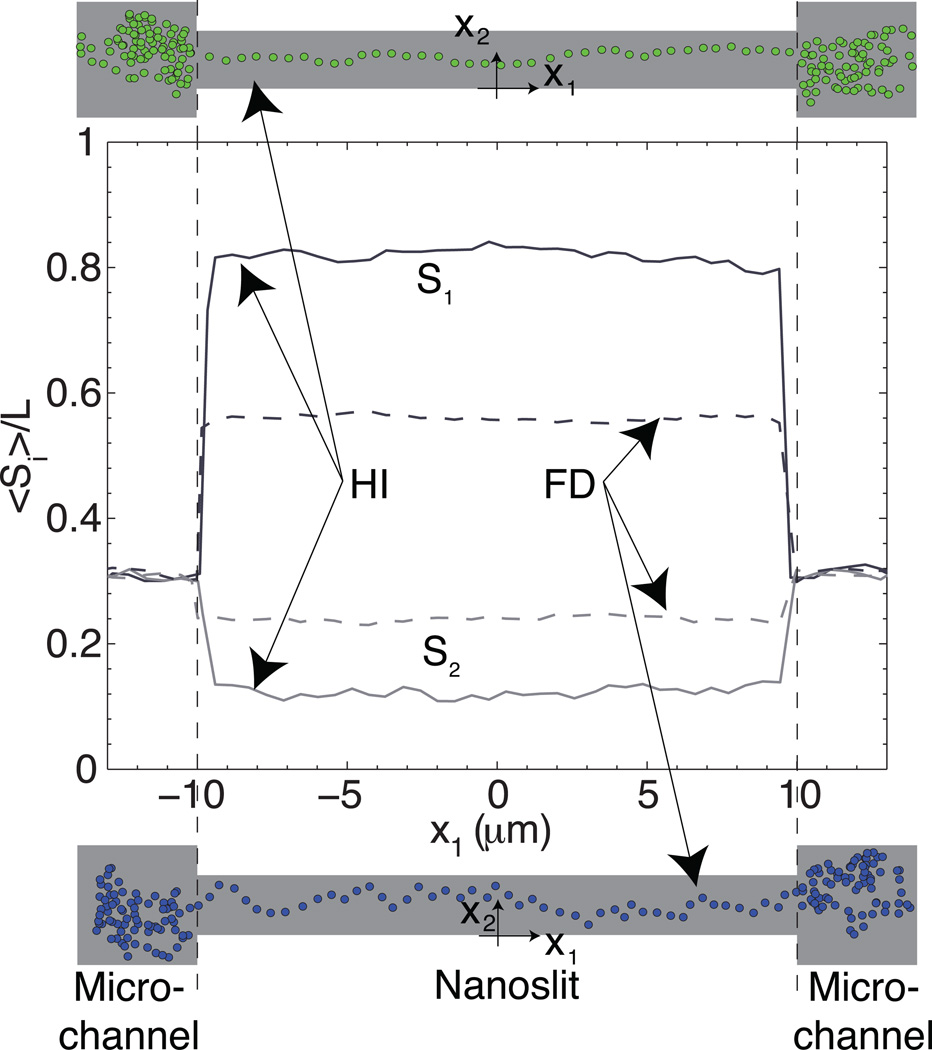
Figure 4 provides a comparison of molecular stretch in different directions, both in the presence and absence of HI. Outside the nanoslits, the stretch in all directions, S1 (axial), S2 (perpendicular) and S3 (confinement) is in the range 30–32% (where Si = |max(xi) − min(xi)|ı, for the ith–direction of the chain ı). Thus, Si is the distance between the two segments of the chain having the longest separation in each direction. In contrast, the segment inside the nanoslits exhibits distinct differences in the three directions when HI are included. First, the stretch in the axial direction, S1, is always higher with HI than without (FD chains). The HI S1 stretch is always around 5–7% below the total stretch, indicating that it is the major contributor to the total stretch. The FD S1 stretch, on the other hand, remains constant with ionic strength in the range 55–60%. The S2 stretch in the nanoslits, in the perpendicular direction, is in the range 20–25% without HI (FD chains); similar to that observed outside the nanoslit. The HI S2 stretch inside the nanoslits is 10–15%. This change in the perpendicular stretch indicates a clear difference between the HI and FD molecular conformations within the nanoslits. The FD chains do not "feel" the dumbbell lobes, thereby allowing the chain to perform a pseudo-random walk in the nanoslit width direction (blue chain in Figure 4); in contrast, HI dumbbells exhibit a "collective" behavior that increases the stretch in the axial direction and impedes the chain from moving freely in the nanoslit width direction; the net result is the creation of a "rigid" dumbbell (green chain in Figure 4). To summarize, the dumbbell conformation leads to elongation of DNA molecules within a pseudo-nanochannel. Electrostatic interactions, enhanced by our low ionic strength conditions, accentuate the confinement of DNA molecules. Note that Debye lengths range from 3 nm at 11 mM to 30 nm at 0.11 mM. Importantly, at low ionic strength, the Debye length is comparable to the nanoslit height, an effect that cannot be overlooked.98 This electrostatic effect, combined synergistically with collective HI and nano-confinement, greatly enhances DNA stretch.
Figure 4.
Stretch along the nanoslit axial and width directions as a function of nanoslit axial position for T4 DNA dumbbells at I = 0.51 mM. The predicted stretches are shown for HI (continuous lines) and FD (dotted lines) chains. Snapshots of an HI chain (green) and an FD chain (blue) are included (Supplementary Movies S2).
Debye length considerations
Given these simulation results, which highlight electrostatic contributions by the device walls to DNA stretch, we experimentally investigated how the Debye length affects nanoconfinement99 by studying the diffusion kinetics of negatively charged latex beads (24 nm) within nanoslits using TIRF microscopy (see Materials and Experimental Methodology). The idea is that bead diffusivity would be measurably perturbed, as a function of ionic strength, due to the accrued Debye lengths of the device (22 nm, I = 0.20 mM; 3 nm, I = 10 mM) and the beads (24 nm). The average periodicity was measurably different for 0.1997 mM and 9.987 mM NaCl, namely 8 ± 3 s and 12 ± 4 s, respectively (N = 16 beads), thereby implying that the Debye length effectively limits the height of the nanoslit (i.e., bead diffusion is more confined at lower ionic strengths). These observations confirm the sudden decrease of chain motilities in the confined direction, once the ionic strength is decreased. Simulated DNA motility (diffusion) in the confined direction was ~ 90 nm at the higher ionic strength conditions, which shifted to a very small 1 – 5 nm at lower ionic strength conditions.
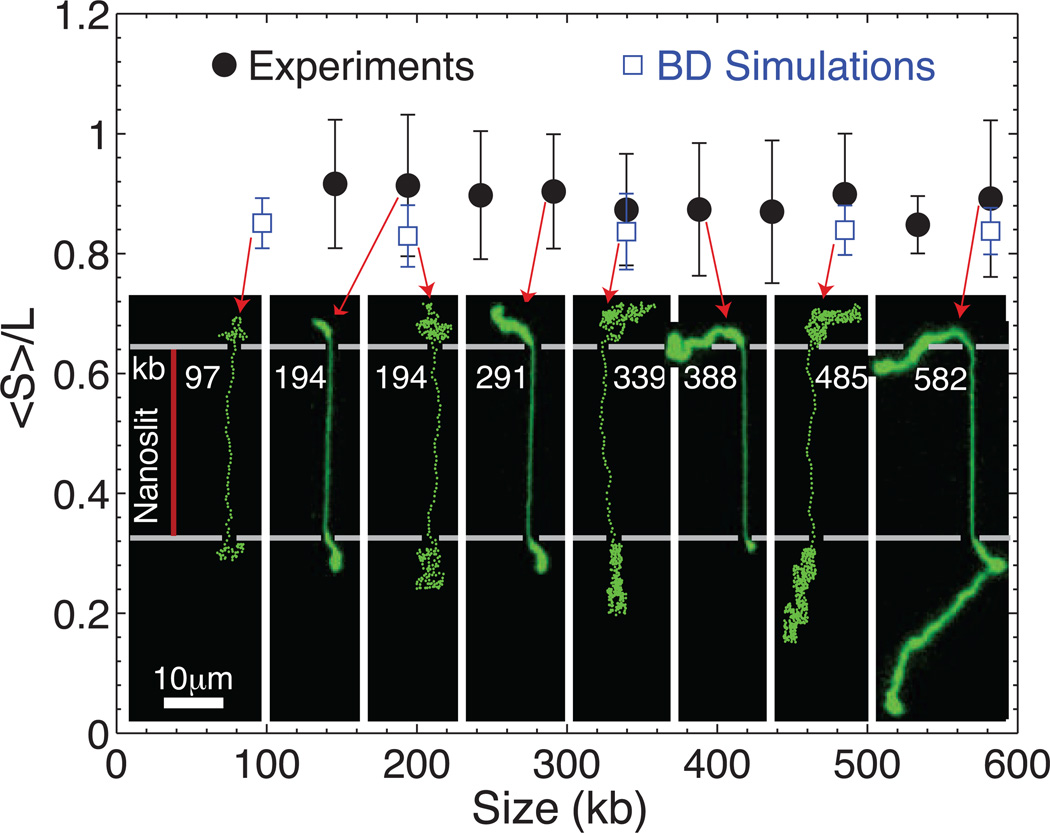
How DNA size affects dumbbell stretching and relaxation time
Figure 5 shows DNA stretch as a function of molecular size (97 kb–582 kb; I = 0.51 mM), using a series of λ con-catemers. Note that the same device can be used for uniform presentation of molecules of any size, once the molecule contour length exceeds twice the nanoslit length for ensuring confident dumbbell formation. In the figure, experimental and simulated results are included. For a dumbbell conformation, we calculate the mean squared variation of the axial position of chain segments within the nanoslit. Importantly, this mobility indicates how reliable an optical measurement of labeled DNA features is inside the nanoslit; the simulation results show a mobility of 150 ± 20 bp for I = 11 mM, and 100 ± 20 bp for I = 0.51 mM. We note that ultimately the two lobes of the dumbbell do not stabilize the conformation, even when the dumbbell is symmetric (see the Theoretical Considerations section).
Figure 5.
Stretch of λ –DNA concatemer dumbbells as a function of size: experiment compared to BD simulation. Red arrows link experimental and simulation results to graphical outputs and a montage of micrographs; error bars show SD on the means (black dots) for N = 9 – 93 molecules. Cartoon shows a red line delineating a nanoslit; horizontal white lines indicate nanoslit boundaries. Dumbbell lobes enlarge with increasing molecular size for a given slit/microchannel geometry and show a compelling similarity to simulation.
The effective relaxation time of dumbbell molecules was analyzed by loading the molecules in the same manner as in the stretching experiments. In the dynamical experiments, however, some molecules had to be imaged over a 7 hr time course using attenuated illumination to prevent photo-cleavage which would destroy dumbbells. Bright dumbbell lobes are thresholded in the image data for their analysis, leaving invisible the connecting DNA backbones within the nanoslits. The last time point at which a molecule was observed determined the relaxation time of a dumbbell within a slit; we then averaged all relaxation times for a given molecular size, irrespective of relative lobe size. Molecules remaining after completion of measurements were checked for spurious surface-attachment by applying an electrical field; adhered molecules are not included in our datasets. Also, molecules ≤ 100 kb were excluded because they formed small lobes that rapidly relaxed. The relaxation time is the translocation time of a single DNA lobe plus the ejection time of the DNA chain out of the nanoslit. The latter time turns out to be quite short, typically about 10 s (see Supplemental Movie S1). This agrees well with our theoretical estimate of 12 s based on entropic ejection; the viscosity of the aqueous solvent inside the nanoslit would appear to be close to that of the bulk. The ejection time is a simple, minor correction, which we have subtracted from the relaxation time. The resulting translocation times are plotted in Figure 6 for the λ concatemers (black), T4 (red), and M. florum (blue) DNA molecules. The dependent variable is not the actual molecular mass of the DNA molecules, but the molecular mass of the two lobes of the dumbbell (Ml) because we have subtracted the DNA mass within the nanoslit from this. This correction is significant for the lower masses. In Figure 6, we have fitted the lobe translocation time with a power law τ ~ MI1.23 (If we had plotted the original relaxation times, the exponent would have been 1.71). The dumbbell lobe fluorescence intensities fluctuate over time until one lobe slips into the nanoslit (arrow b), then the molecule transits the nanoslit into the bottom microchannel and exits into the microchannel (arrow c).
Our exponent 1.23 rules out unbiased translocation (See Table 1; where we also show that the DNA chains are effectively non-draining and the excluded-volume effect is quite fully exerted). It is comparable with the exponent 1.13 predicted for forced translocation with hydrodynamic interactions in the nanopore case.97 At present, it is, however, difficult to rule out a theory of translocation without memory effects. In the bulk, the frictional properties of a long DNA chain may be non-draining. But the polymer conformations are strongly inhomogeneous for a lobe attached to a nanoslit or nanopore. It may be argued that a portion of the chain conforms to Rouse dynamics, so the predicted exponent would be somewhere between 0.8 and 1.2 (Table 1). Our exponent 1.23 also appears to agree with the value 1.27 measured by Storm et al.100–102 for DNA translocating through a silicon-oxide nanopore. But their ionic strength was high (I = 1 M), so the excluded volume was weak and their chains were close to ideal (ν = 1/2 in Table 1). Our own (unpublished) analysis shows that the top lobe in Figure 6 is indeed being translocated into the nanoslit under an external force, which appears to be constant. The origin of this force is obscure at present; it cannot be of entropic origin as discussed in the Theoretical Considerations, for this force is much too weak. This mild forces leads to lengthy translocation and relaxation times.
Discussion
There is some debate or confusion in the literature11,103–105 regarding the transition between de Gennes and Odijk confinement regimes. The set of experiments presented here help clarify one issue in that debate, because they have been performed at very low salt concentrations. The decrease of ionic strength has two major consequences: an increase of the chain persistence length, and an enhanced, effective confinement induced by the Debye length of the device’s surface. Our experimental observations show that once the effective confinement is equal to the chain persistence length the Odijk regime is achieved. This feature apparently contradicts other conclusions,11 which suggested that the effective DNA diameter, ω, has a major effect on the de Gennes-Odijk transition. However, the contradiction is apparent because the ionic strength in ref.11 is much higher than used here. Wang et al.106 have attempted to show how the results of ref.11 fit in with the intermediate regimes. Figure 3 includes the stretch predictions of de Gennes theory (S/L ~ (ωlp)1/3(Dh)−1/3) and Odijk theory (S/L ~ 1 − [(D/lp)2/3+(h/lp)2/3]), for D = 1 µm × h = 100 nm nanoslit. Initially, one may infer from the figure that the experiments do not follow any scaling regime; however, we must recall that the dumbbell conformation emulates nano-channel confinement. In other words, the DNA dumbbells "feel" an effective, lower channel width. Once this effect is included, the experiments follow the Odijk predictions that the shadow region encompasses (Figure 3); namely, an Odijk prediction for a 3h × h nanoslit and for a h × h channel. As pointed out by T. Odijk,16,33,34 his theory does not include severe electrostatic interactions; accordingly, his method will slightly under-predict stretch at the lower ionic strength conditions considered here. We are currently developing an improved molecular model to account for full electrostatic interactions.25 Once the dumbbells are formed and the molecule is presented in a fully stretched manner, a natural question is to examine the mobility of the chains within the nanoslit and the dumbbell’s relaxation time. However, the dumbbell dynamics reported here show relaxation times that will support genomic analysis schemes using imaging, which require consistently stretched DNA molecules. The addition of sucrose to the low ionic strength solutions and the decreased of temperature (i.e., shifted after loading) would increase solution viscosity and extend the relaxation time of dumbbell molecules.
Conclusion
Modern genome analysis demands long-range sequence information that is uniquely presented by large DNA molecules. As such, the findings presented here, using tightly coupled experimental and simulation approaches, have provided an experimental and theoretical infrastructure for the design and implementation of the newer genome analysis systems. These advances may provide the means for fully leveraging the informational advantages intrinsically offered by very long DNA molecules in ways that will greatly enhance our understanding of genome structures.
Supplementary Material
Shown is the relaxation of a T4 dumbbell in a nanoslit (Figure 6 inset). A T4 DNA molecule (166 kb, 74.5 µm dye adjusted contour length) already in a dumbbell conformation is seen to relax and finally exit a nanoslit into an abutting microchannel. Because lobes are not equally sized, the larger lobe dominates, directing DNA segments towards it, culminating in complete ejection from the nanoslit into adjoining microchannel. T4 DNA molecule stretch is 0.85 ± 0.02 (I = 0.51 mM). Original movie duration is 127 s, but is compressed here to run 14 × faster; movie field is 17.1 × 18.3 µm.
Shown is the dumbbell dynamics of a hydrodynamically interacting T4 dumbbell (green molecule) and a free-draining (FD) T4 dumbbell (blue molecule) in a nanoslit at I = 0.54 mM. The HI molecule’s lobes move collectively, the chain feels the walls sterically and hydrodynamically, thus generating a "rigid" dumbbell. The FD chain dynamics only includes steric effects of the walls and the chain segments move independently. Inside the nanoslit the chain conformation changes dramatically between the HI and FD chains.
Acknowledgement
We thank Artak Isoyan, Anphong Ho, Quinn Leonard (Synchrotron Radiation Center, University of Wisconsin-Madison), Konstantinos Potamousis, Shiguo Zhou, and Tim Schramm; Thomas Knight for providing M. florum; funding: NIH National Human Genome Research Institute grant HG000225 (D.C.S), The NSF Nanoscale Science and Engineering Center on Driven Assembly, grant DMR0425880 (J.J.dP), and a Morgridge fellowship (K.L.K.S.).
Abbreviations
- BD
Brownian Dynamics
- GGEM
General Geometry Ewald-like Method
- HI
hydrodynamic interactions
- TE
Tris EDTA
- TIRF
Total Internal Reflection Fluorescence Microscopy
Appendix
General Geometry Ewald-like Method and O(N) algorithm25–31
The fluid velocity M · F is calculated using the O(N) General Geometry Ewald-like Method (GGEM) introduced by Hernández-Ortiz et al.28 A brief description of the GGEM starts with considering the stokes system of equations for a flow driven by a distribution of Nb point forces,
| (27) |
where η is the fluid viscosity and the force density is
| (28) |
where fı is the force exerted on the fluid at point xı. The solution of (27) can be written in terms of a Stokeslet28,107 and combined into the M · F product. If computed explicitly, this product is a matrix-vector operation requiring O(N2) calculations. GGEM determines the product implicitly for any geometry (with appropriate boundary conditions) without performing the matrix-vector manipulations. It starts with the restatement of the force-density expression in (27), ρ(x) = ρl(x) + ρg(x) using a smoothing function g(x), similar to conventional particle-mesh Ewald methods.108–110 This screening function satisfies
| (29) |
By linearity of the Stokes equation, the fluid velocity is written as a sum of two parts, with separate solutions for each force-density. The “local density”
| (30) |
drives a local velocity, ul(x), which is calculated assuming an unbounded domain:
| (31) |
where Gl(x) is composed of a free-space Green’s function, or Stokeslet, minus a smoothed Stokeslet obtained from the solution of Stokes equations with the forcing term modified by the smoothing function g(x). For the Stokes equations we found that a modified Gaussian smoothing function defined by
| (32) |
yields a simple expression for Gl(x):
| (33) |
Because Gl(x) decays exponentially on the length scale α−1, in practice the local velocity can be computed, as in conventional Ewald methods, by only considering near-neighbors to each particle ı.58,111
For the present work, the point-particle approximation is not desired; in particular, as the chain size increases, the probability that particles will overlap, having un-physical velocities, increases. To avoid this problem, the bead hydrodynamic radius, a, can be used to define a new smoothed-force density that gives a non-singular velocity. This is achieved by replacing the Stokeslet by a regularized Stokeslet, using the same modified Gaussian with α replaced by ξ, with ξ ~ a−1, yielding
| (34) |
where the superscript R stands for regularized force density. For , the maximum fluid velocity is equal to that of a particle with radius a and the pair mobility remains positive-definite.28,112
The global velocity, ug(x), is due to the force distribution ρg(x), which is given by
| (35) |
For a general domain, we find the solution to Stokes’ equation numerically, requiring that ul(x) + ug(x) satisfy appropriate boundary conditions. At a no-slip boundary we would require ug(x) = −ul(x). For problems with periodic boundary conditions, Fourier techniques can be used to guarantee the periodicity of the global velocity ug(x). The periodicity on the local velocity, ul(x), is obtained using the minimum image convention.
In the present case, the global contribution is solved with a Finite Element Method (FEM) formulation, where 8-noded brick elements27,113 are used for the velocity and constant elements are used for the corresponding global pressure. The solution of the linear system is done through a fast LU decomposition solver for sparse matrices, SUPER-LU.114,115 The LU decomposition of the matrix is only done at the beginning of the simulation; during the time advancement, the only necessary computation is the back-substitution, making the GGEM algorithm highly efficient (~ O(N), given the sparse characteristic of the matrix). Given the fact that the GGEM solution is independent of α, the appropriate selection of this parameter is based on the optimization of the computational time. In the global calculation, to reach an accurate solution, the mesh size must be smaller than the scale of the smoothing function, which is α−1. Therefore, the mesh resolution scales as M ~ α3; the cost of each back-substitution scales as M2, leading to a total global cost that scales as α6. In the local calculation, the contribution of all pairs that lie within a neighbor list determined by the decay of the local Green’s function must be calculated. The local Green’s function decays over a distance α−1, so the number of neighbors for each particle scales as Nα−3. The calculation must be performed over all pairs, which is the number of particles times the number of neighbors per particle, resulting in a local calculation cost that scales as N2α−3. Minimizing the total (local and global) computational cost with respect to α gives an optimal α that scales as αopt ~ N2/9 and a total cost that scales as O(N4/3). If we had chosen a different, linear, method for the solution (GMRES, Bi-conjugate methods116), the global cost would have scaled as α3, leading to an optimal value of αopt ~ N1/3 and a total computational cost that would scale as O(N).
Because GGEM yields M · F without explicit construction of M, it is desirable to time-integrate Eq. (10) without requiring this product i.e., a “matrix-free” formulation. Fixman69,70 proposed a method to time-integrate this system without needing to evaluate ∂ / ∂R · D:
| (36) |
The only remaining step is to evaluate B−1 · dW in a matrix-free way. As also noted by Fixman,71 this can be done by a Chebyshev polynomial approximation method that requires only matrix-vector products, not the matrix itself. This approach has already been implemented in unbounded or periodic domains;26–28,30,62,64,117,118 with GGEM it can be directly generalized to arbitrary domains.
Footnotes
This material is available free of charge via the Internet at http://pubs.acs.org/.
References
- 1.Dimalanta E, Lim A, Runnheim R, Lamers C, Churas C, Forrest D, de Pablo J, Graham M, Coppersmith S, Goldstein S, Schwartz D. Analytical chemistry. 2004;76:5293–5301. doi: 10.1021/ac0496401. [DOI] [PubMed] [Google Scholar]
- 2.Jendrejack RM, Dimalanta ET, Schwartz DC, Graham MD, de Pablo JJ. Phys. Rev. Lett. 2003;91:038102. doi: 10.1103/PhysRevLett.91.038102. [DOI] [PubMed] [Google Scholar]
- 3.Teague B, et al. PNAS. 2010;107:10848. doi: 10.1073/pnas.0914638107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Antonacci F, Kidd JM, Marques-Bonet T, Teague B, Ventura M, Girirajan S, Alkan C, Campbell CD, Vives L, Malig M. Nature Genetics. 2010;42:745–750. doi: 10.1038/ng.643. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Jo K, Dhingra D, Odijk T, de Pablo J, Graham M, Runnheim R, Forrest D, Schwartz D. PNAS. 2007;104:2673. doi: 10.1073/pnas.0611151104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Valouev A, Li L, Liu TC, Schwartz DC, Yang Y, Zhang Y, Waterman MS. J. Comp. Chem. 2006;13:442–462. doi: 10.1089/cmb.2006.13.442. [DOI] [PubMed] [Google Scholar]
- 7.Valouev A, Schwartz DC, Zhou S, Waterman MS. PNAS. 2006;103:15770. doi: 10.1073/pnas.0604040103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Valouev A, Zhang Y, Waterman MS, Waterman MS. Bioinformatics. 2006;22:1217–1224. doi: 10.1093/bioinformatics/btl063. [DOI] [PubMed] [Google Scholar]
- 9.Kim Y, Kim KS, Kounovsky KL, Chang R, Jung GY, dePablo JJ, Jo K, Schwartz DC. Lab Chip. 2011;11:1721. doi: 10.1039/c0lc00680g. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Das SK, Austin MD, Akana MC, Deshpande P, Cao H, Xiao M. Nucleic Acids Research. 2010;38:e177–e177. doi: 10.1093/nar/gkq673. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Reisner W, Beech JP, Larsen NB, Flyvbjerg H, Kristensen A, Tegenfeldt JO. Phys. Rev. Lett. 2007;99:058302. doi: 10.1103/PhysRevLett.99.058302. [DOI] [PubMed] [Google Scholar]
- 12.Reisner W, Morton K, Riehn R, Wang Y, Yu Z, Rosen M, Sturn J, Chou S, Frey E, Austin R. Phys. Rev. Lett. 2005;94:196101. doi: 10.1103/PhysRevLett.94.196101. [DOI] [PubMed] [Google Scholar]
- 13.Reccius C, Mannion J, Cross J, Craighead H. Phys. Rev. Lett. 2005;95:268101. doi: 10.1103/PhysRevLett.95.268101. [DOI] [PubMed] [Google Scholar]
- 14.Reccius C, Stavis S, Mannion J, Walker L, Craighead H. Biophys J. 2008;95:273. doi: 10.1529/biophysj.107.121020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Mannion J, Reccius C, Cross J, Craighead H. Biophys J. 2006;90:4538. doi: 10.1529/biophysj.105.074732. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Odijk T. Macromol. 1983;16:1340. [Google Scholar]
- 17.Yeh J, Taloni A, Chen Y. Nano Letters. 2012 [Google Scholar]
- 18.Abramoff M, Magelhaes P, Ram SJ. Biophotonics Intern. 2004;11:36. [Google Scholar]
- 19.Sternberg S. Computer. 1983;16:22. [Google Scholar]
- 20.Institute B. Mesoplasma florum Sequencing Project. Broad Institute; http://www.broad.mit.edu. [Google Scholar]
- 21.Herschleb J, Ananiev G, Schwartz DC. Nature Protocols. 2007;2:677. doi: 10.1038/nprot.2007.94. [DOI] [PubMed] [Google Scholar]
- 22.Schwartz DC, Cantor CR. Cell. 1984;37:67. doi: 10.1016/0092-8674(84)90301-5. [DOI] [PubMed] [Google Scholar]
- 23.Huang X, Gordon MJ, Zare RN. Analytical Chemistry. 1988;60:1837–1838. [Google Scholar]
- 24.Geier S, Hernandez-Ortiz JP, de Pablo JJ. Chemie Ingenieur Technik. 2011;83:900–906. [Google Scholar]
- 25.Hernández-Ortiz JP. DYNA-Colombia. 2012;79:105. [Google Scholar]
- 26.Hernández-Ortiz JP, Chopra M, Geier S, de Pablo J. J. Chem. Phys. 2009;131:044904. doi: 10.1063/1.3184798. [DOI] [PubMed] [Google Scholar]
- 27.Hernández-Ortiz JP, Ma H, Pablo JJD, Graham MD. Korea-Aust Rheol J. 2008;20:143–152. [Google Scholar]
- 28.Hernández-Ortiz JP, de Pablo J, Graham MD. Phys. Rev. Lett. 2007;98:140602. doi: 10.1103/PhysRevLett.98.140602. [DOI] [PubMed] [Google Scholar]
- 29.Hernández-Ortiz JP, Underhill PT, Graham MD. J. Phys. Condensed Matter. 2009;21:204107. doi: 10.1088/0953-8984/21/20/204107. [DOI] [PubMed] [Google Scholar]
- 30.Miller C, Hernández-Ortiz JP, Abbott NL, Gelman SH, de Pablo JJ. Journal of Chemical Physics. 2008;129:015102. doi: 10.1063/1.2928700. [DOI] [PubMed] [Google Scholar]
- 31.Pranay P, Anekal SG, Hernandez-Ortiz JP, Graham MD. Phys. Fluids. 2010;22:123103. [Google Scholar]
- 32.Brochard F, de Gennes PG. J. Chem. Phys. 1977;67:52–56. [Google Scholar]
- 33.Odijk T. Phys. Rev. E. 2008;77:060901. doi: 10.1103/PhysRevE.77.060901. [DOI] [PubMed] [Google Scholar]
- 34.Odijk T. J. Polym. Sci. B - Polym. Phys. 1997;15:477. [Google Scholar]
- 35.Mergell B, Ejtehadi M, Everaers R. Phys. Rev. E. 2003;68:021911. doi: 10.1103/PhysRevE.68.021911. [DOI] [PubMed] [Google Scholar]
- 36.Knotts TA, Rathore N, Schwartz DC, de Pablo JJ. J. Chem. Phys. 2007;126:084901. doi: 10.1063/1.2431804. [DOI] [PubMed] [Google Scholar]
- 37.Sambriski EJ, Ortiz V, Pablo JJD. J Phys-Condens Mat. 2009;21:034105. doi: 10.1088/0953-8984/21/3/034105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Sambriski EJ, Schwartz DC, de Pablo JJ. Biophys. J. 2009;96:1675. doi: 10.1016/j.bpj.2008.09.061. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Sambriski EJ, Schwartz DC, de Pablo JJ. PNAS. 2009;106:18125. doi: 10.1073/pnas.0904721106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Locker CR, Fuller SD, Harvey SC. Biophys. J. 2007;93:2861. doi: 10.1529/biophysj.106.094771. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Locker CR, Harvey SC. Multiscale Model. Simul. 2006;5:1264. [Google Scholar]
- 42.Petrov AS, Lim-Hing K, Harvey SC. Structure. 2007;15:807. doi: 10.1016/j.str.2007.05.005. [DOI] [PubMed] [Google Scholar]
- 43.Bustamante C, Marko JF, Siggia ED, Smith S. Science. 1994;265:1599. doi: 10.1126/science.8079175. [DOI] [PubMed] [Google Scholar]
- 44.Marko JF, Siggia ED. Macromol. 1995;28:8759. [Google Scholar]
- 45.Marko JF, Siggia ED. Macromol. 1994;27:981. [Google Scholar]
- 46.Chen Y-L, Graham MD, de Pablo JJ, Randall GC, Gupta M, Doyle PS. Phys. Rev. E. 2004;70:060901(R). doi: 10.1103/PhysRevE.70.060901. [DOI] [PubMed] [Google Scholar]
- 47.Chen Y-L, Graham MD, de Pablo JJ, Jo K, Schwartz DC. Macromolecules. 2005;38:6680. doi: 10.1021/ma050238d. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Hernández-Ortiz JP, Ma H, de Pablo JJ, Graham MD. Phys. Fluids. 2006;18:123101. [Google Scholar]
- 49.Underhill PT, Doyle PS. J. Rheology. 2006;50:513. [Google Scholar]
- 50.Underhill PT, Doyle PS. J. Rheol. 2005;49:963. [Google Scholar]
- 51.Underhill PT, Doyle PS. J. non-Newt. Fluid Mech. 2004;122:3. [Google Scholar]
- 52.Farnoux B, Bou F, Cotton JP, Daoud M, Jannink G, Nierlich M, de Gennes PG. J. Phys. (Paris) 1978;39:77. [Google Scholar]
- 53.Doi M, Edwards S. The Theory of Polymer Dynamics. Oxford: Oxford University Press; 1986. [Google Scholar]
- 54.Rubinstein M, Colby R. Polymer Physics. Oxford University Press; 2003. [Google Scholar]
- 55.Öttinger H-C. Stochastic Processes in Polymeric Fluids. Berlin: Springer; 1996. [Google Scholar]
- 56.Strobl GR. The Physics of Polymers. Berlin: Springer-Verlag; 1997. [Google Scholar]
- 57.Jendrejack RM, de Pablo JJ, Graham MD. J. Chem. Phys. 2002;116:7752–7759. [Google Scholar]
- 58.Allen M, Tildesley D. Computer Simulation of Liquids. Oxford: Oxford Science Publications; 1987. [Google Scholar]
- 59.Frenkel D, Smith B. Understanding Molecular Simulations-From Algorithms to Applications. San Diego: Academic Press; 1996. [Google Scholar]
- 60.Risken H. The Fokker-Planck Equation. 2nd ed. Berlin: Springer; 1989. [Google Scholar]
- 61.Gardiner C. Handbook of Stochastic Methods. Berlin: Springer; 1985. [Google Scholar]
- 62.Jendrejack RM, Schwartz DC, de Pablo JJ, Graham MD. J. Chem. Phys. 2004;120:2513–2529. doi: 10.1063/1.1637331. [DOI] [PubMed] [Google Scholar]
- 63.Jendrejack RM, Schwartz DC, Graham MD, de Pablo JJ. J. Chem. Phys. 2003;119:1165–1173. doi: 10.1063/1.1637331. [DOI] [PubMed] [Google Scholar]
- 64.Jendrejack RM, Graham MD, de Pablo JJ. J. Chem. Phys. 2000;113:2894. doi: 10.1063/1.1637331. [DOI] [PubMed] [Google Scholar]
- 65.Hernández-Ortiz JP, de Pablo JJ, Graham MD. J. Chem. Phys. 2006;125:164906. doi: 10.1063/1.2358344. [DOI] [PubMed] [Google Scholar]
- 66.Mucha PJ, Tee S-Y, Weitz DA, Shraiman BI, Brenner MP. J. Fluid Mech. 2004;501:71–104. [Google Scholar]
- 67.Hasimoto H. J. Fluid Mech. 1959;5:317–328. [Google Scholar]
- 68.Hernández-Ortiz JP, Stoltz CG, Graham MD. Phys. Rev. Lett. 2005;95:204501. doi: 10.1103/PhysRevLett.95.204501. [DOI] [PubMed] [Google Scholar]
- 69.Fixman M. J. Chem. Phys. 1978;69:1527. [Google Scholar]
- 70.Grassia P, Hinch E, Nitsche L. J. Fluid. Mech. 1995;282:373. [Google Scholar]
- 71.Fixman M. Macromolecules. 1986;19:1204. [Google Scholar]
- 72.Skolnick J, Fixman M. Macromol. 1977;10:944. [Google Scholar]
- 73.Baumann C, Smith S, Bloomfield V, Bustamante C. PNAS. 1997;94:6185. doi: 10.1073/pnas.94.12.6185. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 74.Hsieh C-C, Doyle PS. Korea-Aust Rheol J. 2008;20:127–142. [Google Scholar]
- 75.Ullner M. J Phys Chem B. 2003;107:8097–8110. [Google Scholar]
- 76.Stigter D. Biopolymers. 1977;16:1435–1448. doi: 10.1002/bip.1977.360160705. [DOI] [PubMed] [Google Scholar]
- 77.Stigter D. J Colloid Interf Sci. 1975;53:296. [Google Scholar]
- 78.Vologodskii A, Cozzarelli N. Biopolymers. 1995;35:289. doi: 10.1002/bip.360350304. [DOI] [PubMed] [Google Scholar]
- 79.Hsieh C-C, Balducci A, Doyle PS. Nano Lett. 2008;8:1683–1688. doi: 10.1021/nl080605+. [DOI] [PubMed] [Google Scholar]
- 80.Chandrasekhar S. Rev. Mod. Phys. 1943;15:1. [Google Scholar]
- 81.Eisenriegler E, Kremer K, Binder K. The Journal of Chemical Physics. 1982;77:6296. [Google Scholar]
- 82.DiMarzio EA, McCrackin FL. The Journal of Chemical Physics. 1965;43:539. [Google Scholar]
- 83.Sung W, Park PJ. Physical Review Letters. 1996;77:783–786. doi: 10.1103/PhysRevLett.77.783. [DOI] [PubMed] [Google Scholar]
- 84.Farkas Z, Derényi I, Vicsek T. Journal Of Physics-Condensed Matter. 2003;15:S1767. [Google Scholar]
- 85.Odijk T. Biopolymers. 1979;18:3111–3113. doi: 10.1002/bip.1979.360181215. [DOI] [PubMed] [Google Scholar]
- 86.Yamakawa H, Fujii M. Macromolecules. 1973;6:407–415. [Google Scholar]
- 87.Turner S, Cabodi M, Craighead HG. Physical Review Letters. 2002;88:128103. doi: 10.1103/PhysRevLett.88.128103. [DOI] [PubMed] [Google Scholar]
- 88.Milchev A, Klushin L, Skvortsov A, Binder K. Macromolecules. 2010;43:6877–6885. [Google Scholar]
- 89.Mannion J, Reccius C, Cross J, Craighead HG. Biophysical Journal. 2006;90:4538–4545. doi: 10.1529/biophysj.105.074732. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 90.Burkhardt TW. Journal of Physics A: Mathematical, Nuclear and General. 1997;30:167–172. [Google Scholar]
- 91.Cross JD, Strychalski EA, Craighead HG. Journal Of Applied Physics. 2007;102:024701. [Google Scholar]
- 92.Salieb-Beugelaar GB, Teapal J, Nieuwkasteele J, Wijnperle D, Tegenfeldt JO, Lisdat F, Van Den Berg A, Eijkel JCT. Nano Letters. 2008;8:1785–1790. doi: 10.1021/nl080300v. [DOI] [PubMed] [Google Scholar]
- 93.Milchev A. Journal Of Physics-Condensed Matter. 2011;23:103101. doi: 10.1088/0953-8984/23/10/103101. [DOI] [PubMed] [Google Scholar]
- 94.Chuang J, Kantor Y, Kardar M. Phys. Rev. E. 2001;65:011802. doi: 10.1103/PhysRevE.65.011802. [DOI] [PubMed] [Google Scholar]
- 95.Panja D, Barkema GT, Ball RC. J. Phys.: Condens. Matter. 2007;19:432202. doi: 10.1088/0953-8984/21/9/098002. [DOI] [PubMed] [Google Scholar]
- 96.Kantor Y, Kardar M. Phys. Rev. E. 2004;69:021806. doi: 10.1103/PhysRevE.69.021806. [DOI] [PubMed] [Google Scholar]
- 97.Vocks H, Panja D, Barkema GT, Ball RC. Journal Of Physics-Condensed Matter. 2008;20:095224. [Google Scholar]
- 98.Stein D, Deurvorst Z, van der Heyden FHJ, Koopmans WJA, Gabel A, Dekker C. Nano Lett. 2010;10:765–772. doi: 10.1021/nl902228p. [DOI] [PubMed] [Google Scholar]
- 99.Popov KI, Nap RJ, Szleifer I, de la Cruz MO. Journal Of Polymer Science Part B-Polymer Physics. 2012 [Google Scholar]
- 100.Storm AJ, Chen JH, Zandbergen HW, Dekker C. Phys. Rev. E. 2005;71:051903. doi: 10.1103/PhysRevE.71.051903. [DOI] [PubMed] [Google Scholar]
- 101.Storm AJ, Chen JH, Ling XS, Zandbergen HW, Dekker C. Journal Of Applied Physics. 2005;98 014307–014307–8. [Google Scholar]
- 102.Storm A, Storm C, Chen J, Zandbergen H, Joanny J, Dekker C. Nano Letters. 2005;5:1193–1197. doi: 10.1021/nl048030d. [DOI] [PubMed] [Google Scholar]
- 103.Tegenfeldt J, Prinz C, Cao H, Chou S, Reisner W, Riehn R, Wang Y, Cox E, Sturm J, Silberzan P, Austin R. Proc. Natl. Academy Sci. 2004;101:10979. doi: 10.1073/pnas.0403849101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 104.Micheletti C, Orlandini E. Soft Matter. 2012;8:10959–10968. [Google Scholar]
- 105.Orlandini E, Micheletti C. Journal of biological physics. 2013;39:267. doi: 10.1007/s10867-013-9305-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 106.Wang Y, Tree DR, Dorfman KD. Macromolecules. 2011;44:6594–6604. doi: 10.1021/ma201277e. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 107.Pozrikidis C. Boundary Integral and Singularity Methods for Linearized Viscous Flow. Cambridge: Cambridge University Press; 1992. [Google Scholar]
- 108.Deserno M, Holm C. J. Chem. Phys. 1998;109:7678. [Google Scholar]
- 109.Deserno M, Holm C. J. Chem. Phys. 1998;109:7694. [Google Scholar]
- 110.Essmann U, Perera L, Berkowitz M. J. Chem. Phys. 1995;103:8577. [Google Scholar]
- 111.Hockney RW, Eastwood JW. Computer Simulation using Particles. Taylor & Francis; 1988. [Google Scholar]
- 112.Power H, Wrobel LC. Boundary Integral Methods in Fluid Mechanics. Southampton: Computational Mechanics Publications; 1995. [Google Scholar]
- 113.Osswald TA, Hernández-Ortiz JP. Polymer Processing: Modeling and Simulation. Munich: Carl Hanser-Verlag; 2006. [Google Scholar]
- 114.Demmel JW, Eisenstat SC, Gilbert JR, Li XS, Liu JWH. SIAM J. Matrix Analysis and Applications. 1999;20:720–755. [Google Scholar]
- 115.Demmel JW, Gilbert JR, Li XS. SIAM J. Matrix Analysis and Applications. 1999;20:915–952. [Google Scholar]
- 116.Press WH, Teukolsky SA, Vetterling WT, Flannery BP. Numerical Recipes in Fortran 77. 2nd ed. Cambridge: Cambridge University Press; 1992. [Google Scholar]
- 117.Banchio AJ, Brady JF. J. Chem. Phys. 2003;118:10323–10332. [Google Scholar]
- 118.Stoltz C, de Pablo JJ, Graham MD. J. Rheol. 2006;50:137. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Shown is the relaxation of a T4 dumbbell in a nanoslit (Figure 6 inset). A T4 DNA molecule (166 kb, 74.5 µm dye adjusted contour length) already in a dumbbell conformation is seen to relax and finally exit a nanoslit into an abutting microchannel. Because lobes are not equally sized, the larger lobe dominates, directing DNA segments towards it, culminating in complete ejection from the nanoslit into adjoining microchannel. T4 DNA molecule stretch is 0.85 ± 0.02 (I = 0.51 mM). Original movie duration is 127 s, but is compressed here to run 14 × faster; movie field is 17.1 × 18.3 µm.
Shown is the dumbbell dynamics of a hydrodynamically interacting T4 dumbbell (green molecule) and a free-draining (FD) T4 dumbbell (blue molecule) in a nanoslit at I = 0.54 mM. The HI molecule’s lobes move collectively, the chain feels the walls sterically and hydrodynamically, thus generating a "rigid" dumbbell. The FD chain dynamics only includes steric effects of the walls and the chain segments move independently. Inside the nanoslit the chain conformation changes dramatically between the HI and FD chains.