Exponential-family random graph models for valued networks

Abstract

Exponential-family random graph models (ERGMs) provide a principled and flexible way to model and simulate features common in social networks, such as propensities for homophily, mutuality, and friend-of-a-friend triad closure, through choice of model terms (sufficient statistics). However, those ERGMs modeling the more complex features have, to date, been limited to binary data: presence or absence of ties. Thus, analysis of valued networks, such as those where counts, measurements, or ranks are observed, has necessitated dichotomizing them, losing information and introducing biases.

In this work, we generalize ERGMs to valued networks. Focusing on modeling counts, we formulate an ERGM for networks whose ties are counts and discuss issues that arise when moving beyond the binary case. We introduce model terms that generalize and model common social network features for such data and apply these methods to a network dataset whose values are counts of interactions.

1. Introduction

Networks are used to represent and analyze phenomena ranging from sexual partnerships (Morris and Kretzschmar, 1997), to advice giving in an office (Lazega and Pattison, 1999), to friendship relations (Goodreau, Kitts and Morris, 2008; Newcomb, 1961), to international relations (Ward and Hoff, 2007), to scientific collaboration, and many other domains (Goldenberg et al., 2009). More often than not, the relations of interest are not strictly dichotomous in the sense that all present relations are effectively equal to each other. For example, in sexual partnership networks, some ties are short-term while others are long-term or marital; friendships and acquaintance have degrees of strength, as do international relations; and while a particular individual seeking advice might seek it from some coworkers but not others, he or she will likely do it in some specific order and weight advice of some more than others.

Network data with valued relations come in many forms. Observing messages (Freeman and Freeman, 1980; Diesner and Carley, 2005), instances of personal interaction (Bernard, Killworth and Sailer, 1979–1980), or counting co-occurrences or common features of social actors (Zachary, 1977; Batagelj and Mrvar, 2006) produce relations in the form of counts. Measurements, such as duration of interaction (Wyatt, Choudhury and Bilmes, 2009) or volume of trade (Westveld and Hoff, 2011) produce relations in the form of (effectively) continuous values. Observations of states of alliance and war (Read, 1954) produce signed relationships. Sociometric surveys often produce ranks in addition to binary measures of affection (Sampson, 1968; Newcomb, 1961; Bernard, Killworth and Sailer, 1979–1980; Harris et al., 2003).

Exponential-family random graph models (ERGMs) are generative models for networks which postulate an exponential family over the space of networks of interest (Holland and Leinhardt, 1981; Frank and Strauss, 1986), specified by their sufficient statistics (Morris, Handcock and Hunter, 2008), or, as with Frank and Strauss (1986), by their conditional independence structure leading to sufficient statistics (Besag, 1974). These sufficient statistics typically embody the features of the network of interest that are believed to be significant to the social process which had produced it, such as degree distribution (e.g., propensity towards monogamy in sexual partnership networks), homophily (i.e., “birds of a feather flock together”), and triad-closure bias (i.e., “a friend of a friend is a friend”). (Morris, Handcock and Hunter, 2008)

A major limitation of ERGMs to date has been that they have been applied almost exclusively to binary relations: a relationship between a given actor i and a given actor j is either present or absent. This is a serious limitation: valued network data have to be dichotomized for ERGM analysis, an approach which loses information and may introduce biases. (Thomas and Blitzstein, 2011)

Some extensions of ERGMs to specific forms of valued ties have been formulated: to networks with polytomous tie values, represented as a constrained three-way binary array by Robins, Pattison and Wasserman (1999) and more directly by Wyatt, Choudhury and Bilmes (2009; 2010); to multiple binary networks by Pattison and Wasserman (1999); and the authors are also aware of some preliminary work by Handcock (2006) on ERGMs for signed network data. Rinaldo, Fienberg and Zhou (2009) discussed binary ERGMs as a special case and a motivating application of their developments in geometry of discrete exponential families.

A broad exception to this limitation has been a subfamily of ERGMs that have the property that the ties and their values are stochastically independent given the model parameters. Unlike the dependent case, the likelihoods for these models can often be expressed as generalized linear or nonlinear models, and they tend to have tractable normalizing constants, which allows them to more easily be embedded in a hierarchical framework. Thus, to represent common properties of social networks, such as actor heterogeneity, triad-closure bias, and clustering, latent class and position models have been used and extended to valued networks. (Hoff, 2005; Krivitsky et al., 2009; Mariadassou, Robin and Vacher, 2010)

In this work, we generalize the ERGM framework to directly model valued networks, particularly networks with count dyad values, while retaining much of the flexibility and interpretability of binary ERGMs, including the above-described property in the case when tie values are independent under the model. In Section 2, we review conventional ERGMs and describe their traits that valued ERGMs should inherit. In Section 3, we describe the framework that extends the model class to networks with counts as dyad values and discuss additional considerations that emerge when each dyad’s sample space is no longer binary. In Section 4, we give some details and caveats of our implementation of these models and briefly address the issue of ERGM degeneracy as it pertains to count data. Applying ERGMs requires one to specify and interpret sufficient statistics that embody network features of interest, all the while avoiding undesirable phenomena such as ERGM degeneracy. Thus, in Section 5, we introduce and discuss statistics to represent a variety of features commonly found in social networks, as well as features specific to networks of counts. In Section 6 we use these statistics to model social forces that affect the structure of a network of counts of conversations among members of a fraternity. Finally, in Section 7, we discuss generalizing ERGMs to other types of valued data.

2. ERGMs for binary data

In this section, we define notation, review the (potentially curved) exponential-family random graph model and identify those of its properties that we wish to retain when generalizing.

2.1. Notation and binary ERGM definition

Let N be the set of actors in the network of interest, assumed known and fixed for the purposes of this paper, and let n ≡ |N| be its cardinality, or the number of actors in the network. For the purposes of this paper, let a dyad be defined as a (usually distinct) pair of actors, ordered if the network of interest is directed, unordered if not, between whom a relation of interest may exist, and let 𝕐 be the set of all dyads. More concretely, if the network of interest is directed, 𝕐 ⊆ N × N, and if it is not, 𝕐 ⊆ {{i, j} : (i, j) ∈ N × N}. In many problems, a relation of interest cannot exist between an actor and itself (e.g., a friendship network), or actors are partitioned into classes with relations only existing between classes (e.g., bipartite networks of actors attending events), in which case 𝕐 is a proper subset of N × N, excluding those pairs (i, j) between which there can be no relation of interest.

Further, let the set of possible networks of interest (the sample space of the model) 𝒴 ⊆ 2^𝕐, the power set of the dyads in the network. Then a network y ∈ 𝒴, can be considered a set of ties (i, j). Again, in some problems, there may be additional constraints on 𝒴. A common example of such constraints are degree constraints induced by the survey format (Harris et al., 2003; Goodreau, Kitts and Morris, 2008).

Using notation similar to that of Hunter and Handcock (2006) and Krivitsky, Handcock and Morris (2011), an exponential-family random graph model has the form

$${\text{Pr}}_{\mathit{\theta };\mathit{\eta },\mathit{g}}(\mathit{Y}=\mathit{y}|\mathit{x})=\frac{\text{exp}(\mathit{\eta }(\mathit{\theta })·\mathit{g}(\mathit{y};\mathit{x}))}{{\kappa }_{\mathit{\eta },\mathit{g}}(\mathit{\theta };\mathit{x})},\mathit{y}\in 𝒴,$$ (1)

for random network variable Y and its realization y; model parameter vector θ ∈ Θ (for parameter space Θ ⊆ ℝ^q) and its mapping to canonical parameters η : Θ → ℝ^p; a vector of sufficient statistics g : 𝒴 → ℝ^p, which may also depend on data x, assumed fixed and known; and a normalizing constant (in y) κ_η,g : ℝ^q → ℝ which ensures that (1) sum to 1 and thus has the value

$${\kappa }_{\mathit{\eta },\mathit{g}}(\mathit{\theta };\mathit{x})=\sum _{\mathit{y}\prime \in 𝒴}\text{exp}(\mathit{\eta }(\mathit{\theta })·\mathit{g}(\mathit{y}\prime ;\mathit{x})).$$

Here, we have given the most general case defined by Hunter and Handcock (2006). Usually, q = p and η(θ) ≡ θ, so the exponential family is linear. For notational simplicity, we will omit×for the remainder of this paper, as g incorporates it implicitly.

2.2. Properties of binary ERGM

2.2.1. Conditional distributions and change statistics

Snijders et al. (2006), Hunter et al. (2008), Krivitsky, Handcock and Morris (2011), and others define change statistics or change scores, which emerge when considering the probability of a single dyad having a tie given the rest of the network and provide a convenient local interpretation of ERGMs. To summarize, define the p-vector of change statistics

$${\mathbf{\Delta }}_{i,j}\mathit{g}(\mathit{y})\equiv \mathit{g}(\mathit{y}+(i,j))-\mathit{g}(\mathit{y}-(i,j)),$$

where y + (i, j) is the network y with edge or arc (i, j) added if absent (and unchanged if present) and y − (i, j) is the network y with edge or arc (i, j) removed if present (and unchanged if absent). Then, through cancellations,

$${\text{Pr}}_{\mathit{\theta };\mathit{\eta },\mathit{g}}({\mathit{Y}}_{i,j}=1|\mathit{Y}-(i,j)=\mathit{y}-(i,j))={\text{logit}}^{-1}(\mathit{\eta }(\mathit{\theta })·{\mathbf{\Delta }}_{i,j}\mathit{g}(\mathit{y})).$$

It is often the case that the form of Δ_i,jg(y) is simpler than that of g(y) both algebraically and computationally. For example, the change statistic for edge count |y| is simply 1, indicating that a unit increase in η_|y|(θ) will increase the conditional log-odds of a tie by 1, while the change statistic for the number of triangles in a network is |y_i ∩ y_j|, the number of neighbors i and j have in common, suggesting that a positive coefficient on this statistic will increase the odds of a tie between i and j exponentially in the number of common neighbors. Hunter et al. (2008) and Krivitsky, Handcock and Morris (2011) offer a further discussion of change statistics and their uses, and Snijders et al. (2006) and Schweinberger (2011) use them to diagnose degeneracy in ERGMs. It would be desirable for a generalization of ERGM to valued networks to facilitate similar local interpretations.

Furthermore, the conditional distribution serves as the basis for maximum pseudo-likelihood estimation (MPLE) for these models. (Strauss and Ikeda, 1990)

2.2.2. Relationship to logistic regression

If the model has the property of dyadic independence discussed in the Introduction, or, equivalently, the change statistic Δ_i,jg(y) is constant in y (but may vary for different (i, j)), the model trivially reduces to logistic regression. In that case, the MLE and the MPLE are equivalent. (Strauss and Ikeda, 1990) Similarly, it may be a desirable trait for valued generalizations of ERGMs to also reduce to GLM for dyad-independent choices of sufficient statistics.

3. ERGM for counts

We now define ERGMs for count data and discuss the issues that arise in the transition.

3.1. Model definition

Define N, n, and 𝕐 as above. Let ℕ₀ be the set of natural numbers and 0. Here, we focus on counts with no a priori upper bound — or counts best modeled thus. Instead of defining the sample space 𝒴 as a subset of a power set, define it as $𝒴\subseteq {\mathbb{N}}_0^{𝕐}$, a set of mappings that assign to each dyad (i, j) ∈ 𝕐 a count. Let y_i,j = y(i, j) ∈ ℕ₀ be the value associated with dyad (i, j).

A (potentially curved) ERGM for a random network of counts Y ∈ 𝒴 then has the pmf

$${\text{Pr}}_{\mathit{\theta };h,\mathit{\eta },\mathit{g}}(\mathit{Y}=\mathit{y})=\frac{h(\mathit{y})\text{exp}(\mathit{\eta }(\mathit{\theta })·\mathit{g}(\mathit{y}))}{{\kappa }_{h,\mathit{\eta },\mathit{g}}(\mathit{\theta })},$$ (2)

where the normalizing constant

$${\kappa }_{h,\mathit{\eta },\mathit{g}}(\mathit{\theta })=\sum _{\mathit{y}\in 𝒴}h(\mathit{y})\text{exp}(\mathit{\eta }(\mathit{\theta })·\mathit{g}(\mathit{y})),$$

with η, g, and θ defined as above, and

$$\mathbf{\Theta }\subseteq {\mathbf{\Theta }}_{\mathrm{N}}=\{\mathit{\theta }\prime \in {ℝ}^q:{\kappa }_{h,\mathit{\eta },\mathit{g}}(\mathit{\theta }\prime )<\infty \}$$ (3)

(Barndorff-Nielsen, 1978, pp. 115–116; Brown, 1986, pp. 1–2), with Θ_N being the natural parameter space if the ERGM is linear. Notably, while (3) is trivial for binary networks because their sample space is finite, for counts it can be a fairly complex constraint.

For the remainder of this paper, we will focus on linear ERGMs, so unless otherwise noted, p = q and η(θ) ≡ θ.

3.2. Reference measure

In addition to the specification of the sufficient statistics g and, for curved families, mapping η of model parameters to canonical parameters, an ERGM for counts depends on the specification of the function h : 𝒴 → [0, ∞). Formally, along with the sample space, it specifies the reference measure: the distribution relative to which the exponential form is specified. For binary ERGMs, h is usually not specified explicitly, though in some ERGM applications, such as models with offsets (Krivitsky, Handcock and Morris, 2011, for example) and profile likelihood calculations of Hunter et al. (2008), the terms with fixed parameters are implicitly absorbed into h.

For valued network data in general, and for count data in particular, specification of h gains a great deal of importance, setting the baseline shape of the dyad distribution and constraining the parameter space. Consider a very simple p = 1 model with g(y) = (∑ _(i,j)∈𝕐 y_i,j), the sum of all dyad values. If h(y) = 1 (i.e., discrete uniform), the resulting family has the pmf

$${\text{Pr}}_{\mathit{\theta };h,\mathit{\eta },\mathit{g}}(\mathit{Y}=\mathit{y})=\frac{\text{exp}(\mathit{\theta }{\sum }_{(i,j)\in 𝕐}{\mathit{y}}_{i,j})}{{\kappa }_{h,\mathit{\eta },\mathit{g}}(\mathit{\theta })}=\prod _{(i,j)\in 𝕐}\frac{\text{exp}(\mathit{\theta }{\mathit{y}}_{i,j})}{1-\text{exp}(\mathit{\theta })},$$

giving the dyadwise distribution ${\mathit{Y}}_{i,j}\stackrel{\mathrm{i}.\mathrm{i}.\mathrm{d}.}{~}\text{Geometric}(p=1-\text{exp}(\mathit{\theta }))$, with θ < 0 by (3). On the other hand, suppose that, instead, h(y) = ∏_(i,j)∈𝕐(y_i,j!)⁻¹. Then,

$${\text{Pr}}_{\mathit{\theta };h,\mathit{\eta },\mathit{g}}(\mathit{Y}=\mathit{y})=\frac{\text{exp}(\mathit{\theta }{\sum }_{(i,j)\in 𝕐}{\mathit{y}}_{i,j})}{{\kappa }_{h,\mathit{\eta },\mathit{g}}(\mathit{\theta }){\prod }_{(i,j)\in 𝕐}{\mathit{y}}_{i,j}!}=\prod _{(i,j)\in 𝕐}\frac{\text{exp}(\mathit{\theta }{\mathit{y}}_{i,j})}{{\mathit{y}}_{i,j}!\text{exp}(\mathit{\theta })},$$

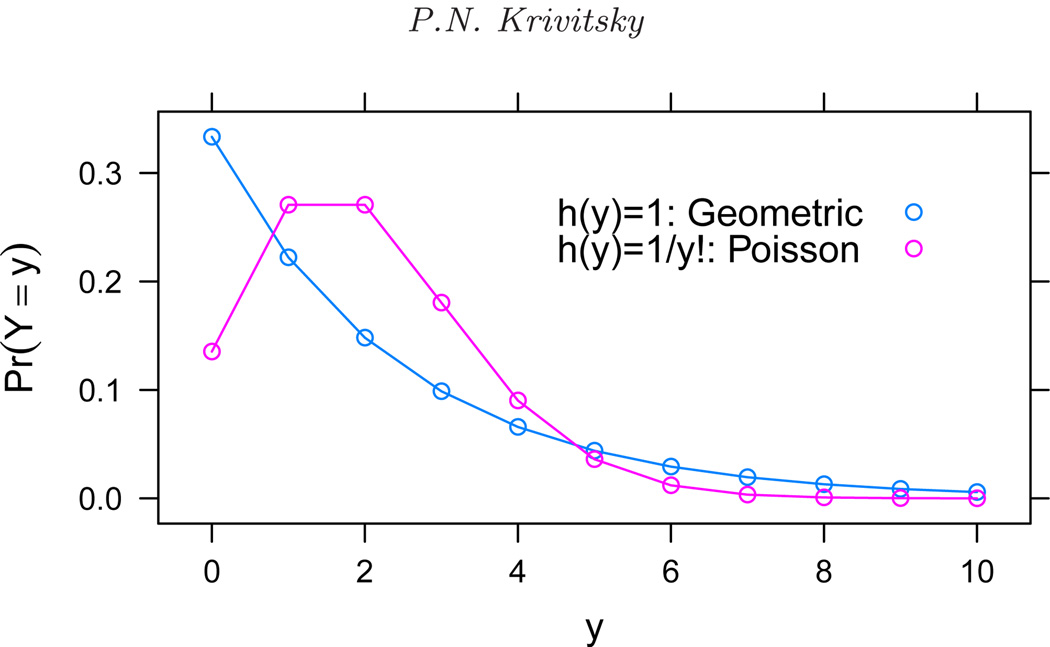
giving ${\mathit{Y}}_{i,j}\stackrel{\mathrm{i}.\mathrm{i}.\mathrm{d}.}{~}\text{Poisson}(\mu =\text{exp}(\mathit{\theta }))$, with Θ_N = ℝ. The shape of the resulting distributions for a fixed mean is given in Figure 1.

Fig 1.

Effect of h on the shape of the distribution. (The mean is fixed at 2.)

The reference measure h thus determines the support and the basic shape of the ERGM distribution. For this reason, we define a geometric-reference ERGM to have the form (2) with h(y) = 1 and a Poisson-reference ERGM to have h(y) = ∏_(i,j)∈𝕐(y_i,j!)⁻¹.

Note that this does not mean that any Poisson-reference ERGM will, even under dyadic independence, be dyadwise Poisson. We discuss the sufficient conditions for this in Section 5.2.1.

4. Inference and implementation

As exponential families, valued ERGMs, and ERGMs for counts in particular, inherit the inferential properties of discrete exponential families in general and binary ERGMs in particular, including calculation of standard errors and analysis of deviance. They also inherit the caveats. For example, the Wald test results based on standard errors depend on asymptotics which are questionable for ERGMs with complex dependence structure (Hunter and Handcock, 2006), so, in Section 6 we confirm the most important of the results using a simple Monte Carlo test: we fit a nested model without the statistic of interest and simulate its distribution under such a model. The quantile of the observed value of the statistic of interest can then be used as a more robust P-value.

At the same time, generalizing ERGMs to counts raises additional inferential issues. In particular, the infinite sample space of counts means that the constraint (3) is not always trivially satisfied, which results in some valued ERGM specifications not fulfilling regularity conditions. We give an example of this in Section 5.2.3 and Appendix B. Additional computational issues also arise.

4.1. Computational issues

The greatest practical difficulty associated with likelihood inference on these models is usually that the normalizing constant κ_h,η,g(θ) is intractable, its exact evaluation requiring integration over the sample space 𝒴. However, the exponential-family nature of model also means that, provided a method exists to simulate realizations of networks from the model of interest given a particular θ, the methods of Geyer and Thompson (1992) for fitting exponential families with intractable normalizing constants and, more specifically, their application to ERGMs by Hunter and Handcock (2006), may be used. These methods rely on network sufficient statistics rather than networks themselves and can thus be used with little modification. More concretely, the ratio of two normalizing constants evaluated at θ′ and θ can be expressed as

$$\frac{{\kappa }_{h,\mathit{\eta },\mathit{g}}(\mathit{\theta }\prime )}{{\kappa }_{h,\mathit{\eta },\mathit{g}}(\mathit{\theta })}=\frac{{\sum }_{\mathit{y}\in 𝒴}h(\mathit{y})\text{exp}(\mathit{\eta }(\mathit{\theta }\prime )·\mathit{g}(\mathit{y}))}{{\kappa }_{h,\mathit{\eta },\mathit{g}}(\mathit{\theta })}=\frac{{\sum }_{\mathit{y}\in 𝒴}h(\mathit{y})\text{exp}((\mathit{\eta }(\mathit{\theta }\prime )-\mathit{\eta }(\mathit{\theta }))·\mathit{g}(\mathit{y}))\text{exp}(\mathit{\eta }(\mathit{\theta })·\mathit{g}(\mathit{y}))}{{\kappa }_{h,\mathit{\eta },\mathit{g}}(\mathit{\theta })}=\sum _{\mathit{y}\in 𝒴}\text{exp}((\mathit{\eta }(\mathit{\theta }\prime )-\mathit{\eta }(\mathit{\theta }))·\mathit{g}(\mathit{y}))\frac{h(\mathit{y})\text{exp}(\mathit{\eta }(\mathit{\theta })·\mathit{g}(\mathit{y}))}{{\kappa }_{h,\mathit{\eta },\mathit{g}}(\mathit{\theta })}={\mathrm{E}}_{\mathit{\theta };h,\mathit{\eta },\mathit{g}}(\text{exp}((\mathit{\eta }(\mathit{\theta }\prime )-\mathit{\eta }(\mathit{\theta }))·\mathit{g}(\mathit{Y}))),$$

so given a sample Y⁽¹⁾,…, Y^(S) from an initial guess θ, it can be estimated

$$\frac{{\kappa }_{h,\mathit{\eta },\mathit{g}}(\mathit{\theta }\prime )}{{\kappa }_{h,\mathit{\eta },\mathit{g}}(\mathit{\theta })}\approx \sum _{s=1}^S\text{exp}((\mathit{\eta }(\mathit{\theta }\prime )-\mathit{\eta }(\mathit{\theta }))·\mathit{g}({\mathit{Y}}^{(s)})).$$

Another method for fitting ERGMs, taking advantage of the equivalence of the method of moments to the maximum likelihood estimator for linear exponential families, was implemented by Snijders (2002), using the algorithm by Robbins and Monro (1951) for simulated statistics to fit the model. This approach also trivially extends to valued ERGMs.

Furthermore, because the normalizing constant (if it is finite) is thus accommodated by the fitting algorithm, we may focus on the unnormalized density for the purposes of model specification and interpretation. Therefore, for the remainder of this paper, we specify our models up to proportionality, as Geyer (1999) suggests.

That (3) is not trivially satisfied for all θ ∈ ℝ^q presents an additional computational challenge: even for relatively simple network models, the natural parameter space Θ_N may have a nontrivial shape. For example, even a simple geometric-reference ERGM

$${\text{Pr}}_{\mathit{\theta };h,\mathit{\eta },\mathit{g}}(\mathit{Y}=\mathit{y})\propto \prod _{(i,j)\in 𝕐}\text{exp}(\mathit{\theta }·({\mathit{x}}_{i,j}{\mathit{y}}_{i,j})),$$

a geometric GLM with a covariate p-vector x_i,j, has

$${\mathbf{\Theta }}_{\mathrm{N}}=\{\mathit{\theta }\prime \in {ℝ}^p:{\forall }_{(i,j)\in 𝕐}\mathit{\theta }·{\mathit{x}}_{i,j}<0\},$$

an intersection of up to |𝕐| half-spaces (linear constraints). Models with complex dependence structure may have less predictable parameter spaces, and, due to the nature of the algorithm of Hunter and Handcock (2006), the only general way to detect whether a guess for θ had strayed outside of Θ_N may be by diagnostics on the simulation. Bayesian inference with improper priors faces a similar problem, and addressing it in the context of ERGMs is a subject for future work. For this paper, we focus on models in which parameter spaces are provably unconstrained or have very simple constraints.

We base our implementation on the 𝖱 package ergm for fitting binary ERGMs. (Handcock et al., 2012) The design of that package separates the specification of model sufficient statistics from the specification of the sample space of networks (Hunter et al., 2008), so we implement our models by substituting in a Metropolis-Hastings sampler that implements our 𝒴 and h of interest. (A simple sampling algorithm for realizations from a Poisson-reference ERGM, optimized for zero-inflated data, is described in Appendix A.) This implementation will be incorporated into a future public release of ergm.

4.2. Model degeneracy

Application of ERGMs has long been associated with a complex of problems collectively referred to as “degeneracy”. (Handcock, 2003; Rinaldo, Fienberg and Zhou, 2009; Schweinberger, 2011) Rinaldo, Fienberg and Zhou, in particular, list three specific, interrelated, phenomena: 1) when a parameter configuration — even the MLE — induces a distribution for which only a small number of possible networks have non-negligible probabilities, and these networks are often very different from each other (e.g., a sparser-than-observed graph and a complete graph) for an effectively bimodal distribution; 2) when the MLE is hard to find by the available MCMC methods; and 3) when the probability of the observed network under the MLE is relatively low — the observed network is, effectively, between the modes. This bimodality and concentration is often a consequence of the model inducing overly strong positive dependence among dyad values. For example, Snijders et al. (2006) use change statistics to show that under models with positive coefficients on triangle and k-star (k ≥ 2) counts — the classic “degenerate” ERGM terms — every tie added to the network increases the conditional odds of several other ties and does not decrease the odds of any, creating what Snijders et al. call an “avalanche” toward the complete graph, which emerges as by far the highest-probability realization. (More concretely, under a model with a triangle count with coefficient θ_Δ, adding a tie (i, j) increases the conditional odds of as many ties as i and j have neighbors by exp (θ_Δ).) Adjusting other parameters, such as density, down to obtain the expected level of sparsity close to that of the observed graph merely induces the bimodal distribution of Phenomenon 1.

An infinite sample space makes Phenomenon 1, as such, unlikely, because the “avalanche” does not have a maximal graph in which to concentrate. However, it does not preclude excessive dependence inducing a bimodal distribution at the MLE, even if neither mode is remotely degenerate in the probabilistic sense. The observed network being between these modes, this may lead to Phenomenon 3, and, due to the nature of the estimation algorithms, such a situation may, indeed, lead to failing estimation — Phenomenon 2.

In this work, we seek to avoid this problem by constructing statistics that prevent the “avalanche” by limiting dependence or employing counterweights to reduce it. (An example of the former approach is the modeling of transitivity in Section 5.2.6, and an example of the latter is the centering in the within-actor covariance statistic developed in Section 5.2.5.) Formal diagnostics developed to date, such as those of Schweinberger (2011) do not appear to be directly applicable to models with infinite sample spaces, so we rely on MCMC diagnostics (Goodreau et al., 2008) instead.

5. Statistics and interpretation for count data

In this section, we develop sufficient statistics for count data to represent network features that may be of interest and discuss their interpretation. In particular, unless otherwise noted, we focus on the Poisson-reference ERGM without complex constraints: $𝒴={\mathbb{N}}_0^{𝕐}$ and h(y) = ∏_(i,j)∈𝕐(y_i,j !)⁻¹.

5.1. Interpretation of model parameters

The sufficient statistics of the binary ERGMs and valued ERGMs alike embody the structural properties of the network that are of interest. The tools available for interpreting them are similar as well.

5.1.1. Expectations of sufficient statistics

In a linear ERGM, if Θ_N is an open set, then, for every k ∈ 1..p, and holding θ_k′, k′ ≠ k, fixed, it is a general exponential family property that the expectation E_θ;h,η,g(g_k(Y)) is strictly increasing in θ_k. (Barndorff-Nielsen, 1978, pp. 120–121) Thus, if the statistic g_k is a measurement of some feature of interest of the network (e.g., magnitude of counts, interactions between or within a group, isolates, triadic structures), a greater value of θ_k results in a distribution of networks with more of the feature measured by g_k present.

5.1.2. Discrete change statistic and conditional distribution

Binary ERGM statistics have a “local” interpretation in the form of change statistics summarized in Section 2.2.1, and we describe similar tools for “local” interpretation of ERGMs for counts here.

Define the set of networks

$${𝒴}_{i,j}(\mathit{y})\equiv \{\mathit{y}\prime \in 𝒴:{\forall }_{(i\prime ,j\prime )\in 𝕐\backslash \{(i,j)\}}{\mathit{y}}_{i\prime ,j\prime }^{\prime }={\mathit{y}}_{i\prime ,j\prime }\}.$$

That is, 𝒴_i,j(y) is the set of networks such that all dyads but the focus dyad (i, j) are fixed to their values in y while (i, j) itself may vary over its possible values; and define ${\mathit{y}}_{(i,j)=k}\equiv (\mathit{y}\prime \in {𝒴}_{i,j}(\mathit{y}):{\mathit{y}}_{i,j}^{\prime }=k)$ to be the network with non-focus dyads fixed and focus dyad set to k. Then, let the discrete change statistic

$${\mathbf{\Delta }}_{i,j}^{k_1\to k_2}\mathit{g}(\mathit{y})\equiv \mathit{g}({\mathit{y}}_{(i,j)=k_2})-\mathit{g}({\mathit{y}}_{(i,j)=k_1}).$$

This statistic emerges when taking the ratio of probabilities of two networks that are identical except for a single dyad value:

$$\frac{{\text{Pr}}_{\mathit{\theta };h,\mathit{\eta },\mathit{g}}({\mathit{Y}}_{i,j}={\mathit{y}}_{(i,j)=k_2}|\mathit{Y}\in {𝒴}_{i,j}(\mathit{y}))}{{\text{Pr}}_{\mathit{\theta };h,\mathit{\eta },\mathit{g}}({\mathit{Y}}_{i,j}={\mathit{y}}_{(i,j)=k_1}|\mathit{Y}\in {𝒴}_{i,j}(\mathit{y}))}=\frac{h_{i,j}(k_2)}{h_{i,j}(k_1)}\text{exp}(\mathit{\theta }·{\mathbf{\Delta }}_{i,j}^{k_1\to k_2}(\mathit{y})),$$

where h_i,j : ℕ₀ → ℝ is the component of h associated with dyad (i, j), such that h(y) ≡ ∏_(i,j)∈𝕐 h_i,j(y_i,j), if it can be thus factored. For a Poisson-reference ERGM, h_i,j(k) = (k!)⁻¹. This may be used to assess the effect of a particular ERGM term on the decay rate of the ratios of probabilities of successive values of dyads (Shmueli et al., 2005) and on the shape of the dyadwise conditional distribution: the conditional distribution of a dyad (i, j) ∈ 𝕐, given all other dyads (i′, j′) ∈ 𝕐\{(i, j)},

$${\text{Pr}}_{\mathit{\theta };h,\mathit{\eta },\mathit{g}}({\mathit{Y}}_{i,j}={\mathit{y}}_{i,j}|\mathit{Y}\in {𝒴}_{i,j}(\mathit{y}))=\frac{h_{i,j}({\mathit{y}}_{i,j})\text{exp}(\mathit{\theta }·\mathit{g}(\mathit{y}))}{{\sum }_{\mathit{y}\prime \in {𝒴}_{i,j}(\mathit{y})}h{({\mathit{y}}_{i,j}^{\prime })}_{i,j}\text{exp}(\mathit{\theta }·\mathit{g}(\mathit{y}\prime ))}=\frac{h_{i,j}({\mathit{y}}_{i,j})\text{exp}(\mathit{\theta }·{\mathbf{\Delta }}_{i,j}^{k_0\to {\mathit{y}}_{i,j}}\mathit{g}(\mathit{y}))}{{\sum }_{k\in {\mathbb{N}}_0}{h}_{i,j}(k)\text{exp}(\mathit{\theta }·{\mathbf{\Delta }}_{i,j}^{k_0\to k}\mathit{g}(\mathit{y}))},$$

for an arbitrary baseline k₀.

5.2. Model specification statistics

We now propose some specific model statistics to represent common network structural properties and distributions of counts.

5.2.1. Poisson modeling

We begin with statistics that produce Poisson-distributed dyads and model network phenomena that can be represented in a dyad-independent manner. As a binary ERGM reduces to a logistic regression model under dyadic independence, a Poisson-reference ERGM may reduce to a Poisson regression model.

In a Poisson-reference ERGM, the normalizing constant has a simple closed form if g(y′) is linear in ${\mathit{y}}_{i,j}^{\prime }$ and does not depend on any other dyads ${\mathit{y}}_{i\prime ,j\prime }^{\prime },(i\prime ,j\prime )\ne (i,j)$:

$${\forall }_{\mathit{y}\in 𝒴}{\forall }_{{\mathit{y}}_{i,j}^{\prime }\in {\mathbb{N}}_0}{\mathbf{\Delta }}_{i,j}^{0\to {\mathit{y}}_{i,j}^{\prime }}\mathit{g}(\mathit{y})={\mathit{y}}_{i,j}^{\prime }{\mathit{x}}_{i,j}.$$ (4)

for ${\mathit{x}}_{i,j}\equiv {\mathbf{\Delta }}_{i,j}^{k\to k+1}\mathit{g}(\mathit{y})$ for any k ∈ ℕ₀. Then,

$${\mathit{Y}}_{i,j}\stackrel{\mathrm{i}\mathrm{n}\mathrm{d}.}{~}\text{Poisson}(\mu =\text{exp}(\mathit{\theta }·{\mathbf{\Delta }}_{i,j}^{0\to 1}\mathit{g}(\mathit{y}))),$$

giving a Poisson log-linear model, and ${\mathbf{\Delta }}_{i,j}^{0\to 1}\mathit{g}$ effectively becomes the covariate vector for Y_i,j. (If g(y′) is linear in ${\mathit{y}}_{i,j}^{\prime }$ but does depend on other dyads — x_i,j in (4) depends on ${\mathit{y}}_{i\prime ,j\prime }^{\prime }$ but not on ${\mathit{y}}_{i,j}^{\prime }$ itself — the dyad distribution is conditionally Poisson but not marginally so. An example of this arises in Section 5.2.4.)

Morris, Handcock and Hunter (2008) describe many dyad-independent sufficient statistics for binary ERGMs. All of them have the general form

$${\mathit{g}}_k(\mathit{y})\equiv \sum _{(i,j)\in 𝕐}{\mathit{y}}_{i,j}{\mathit{x}}_{i,j,k},$$

where x_i,j,k ≡ Δ_i,jg_k and x_i,j,k may be viewed as exogenous (to the model) covariates in a logistic regression for each tie. They could then be used to model a variety of patterns for degree heterogeneity and mixing among actors over (assumed) exogenous attributes. For example, for a uniform homophily model, x_i,j,k may be an indicator of whether i and j belong to the same group. If y_i,j are counts, these statistics induce a Poisson regression type model (for a Poisson-reference ERGM), where the effect of a unit increase in some θ_k on dyad (i, j) is to increase its expectation by a factor of exp (xi,j,k). Krivitsky et al. (2009) use this type of model to model Slovenian periodical “co-readerships” (Batagelj and Mrvar, 2006) — numbers of readers who report reading each pair of periodicals of interest — using as exogenous covariates the class of periodical (daily, weekly, regional, etc.) and the overall readership levels of each periodical.

Curved (i.e., η(θ) ≠ θ, p > q, and η not a linear mapping) ERGMs, in which the g satisfy (4) and dyadic independence, may induce nonlinear Poisson regression. An example of this is the likelihood component of some latent space network models, with latent space positions being treated as free parameters: the likelihoods of the hierarchical models of Hoff (2005) and Krivitsky et al. (2009) are special cases of such an ERGM, with η(θ) = (η_i,j(θ))_(i,j)∈𝕐 and g(y) = (y_i,j)_(i,j)∈𝕐 (i.e., the sufficient statistic is the network), and η_i,j(θ) mapping latent space positions and other parameters contained in θ to the logarithms of dyad means (i.e., the dyadwise canonical parameters).

5.2.2. Zero modification

We now turn to model terms that may reshape the distribution of the counts away from Poisson. Social networks tend to be sparse, and larger networks of similar nature tend to be more sparse (Krivitsky, Handcock and Morris, 2011). If the interactions among the actors are counted, it is often the case that if two actors interact at all, they interact multiple times. This leads to dyadwise distributions that are zero-inflated relative to Poisson.

These features of sparsity can be modeled using statistics developed for binary ERGMs, applied to a network produced by thresholding the counts (at 1, for zero-modification). For example, a Poisson-reference ERGM with p = 2 and

$$\mathit{g}(\mathit{y})={(\sum _{(i,j)\in 𝕐}{\mathit{y}}_{i,j},\sum _{(i,j)\in 𝕐}{1}_{{\mathit{y}}_{i,j}>0})}^{\top }$$

has dyadwise distribution

$${\text{Pr}}_{\mathit{\theta };h,\mathit{\eta },\mathit{g}}(\mathit{Y}=\mathit{y})\propto \prod _{(i,j)\in 𝕐}\text{exp}({\mathit{\theta }}_1{\mathit{y}}_{i,j}+{\mathit{\theta }}_2{1}_{{\mathit{y}}_{i,j}>0})/{\mathit{y}}_{i,j}!.$$

This is a parametrization of a zero-modified Poisson distribution (Lambert, 1992), though not a commonly used one, with the probability of 0 being (1 + exp (θ₂) (exp (exp (θ₁)) − 1))⁻¹ and nonzero values being distributed (conditionally on not being 0) Poisson(μ = exp (θ₁)), both reducing to Poisson’s when θ₂ = 0. Notably, the probability of 0 decreases as θ₁ increases, rather than being solely controlled by θ₂.

5.2.3. Dispersion modeling

Consider the social network of face-to-face conversations among people living in a region. A typical individual will likely not interact at all with vast majority of others, have one-time or infrequent interaction with a large number of others (e.g., with clerks or tellers), and a lot of interaction with a relatively small number of others (e.g., family, coworkers). Some of this may be accounted for by information about social roles and preexisting relationships, but if such information is not available, this leads to a highly overdispersed distribution relative to Poisson, or even zero-inflated Poisson. Overdispersed counts are often modeled using the negative binomial distribution. (McCullagh and Nelder, 1989, p. 199) However, the negative binomial distribution with an unknown dispersion parameter is not an exponential family, making it difficult to fit using our inference techniques. We thus discuss two purely exponential-family approaches for dealing with non-Poisson-dispersed interaction counts in general and overdispersed counts in particular.

Conway–Maxwell–Poisson Distribution

Conway–Maxwell–Poisson (CMP) distribution (Shmueli et al., 2005) is an exponential family for counts, able to represent both under- and overdispersion: adding a sufficient statistic of the form

$${\mathit{g}}_{\mathrm{C}\mathrm{M}\mathrm{P}}(\mathit{y})=\sum _{(i,j)\in 𝕐}\text{log}({\mathit{y}}_{i,j}!),$$ (5)

to a Poisson-reference ERGM otherwise fulfilling conditions for Poisson regression described in Section 5.2.1 turns a Poisson regression model for dyads into a CMP regression model.

Its coefficient, θ_CMP, constrained by (3) to θ_CMP ≤ 1, controls the degree of dispersion: θ_CMP = 0 retains the Poisson distribution; θ_CMP < 0 induces underdispersion relative to Poisson, approaching the Bernoulli distribution as θ_CMP → −∞; and θ_CMP > 0 induces overdispersion, attaining the geometric distribution at θ_CMP = 1, its most overdispersed point.

Normally, the greatest hurdle associated with using CMP is that its normalizing constant does not, in general, have a known closed form. In our case, because intractable normalizing constants are already accommodated by the methods of Section 4, using CMP requires no additional effort.

At the same time, CMP is neither regular nor steep (per Appendix B), so the properties of its estimators are not guaranteed, particularly for highly overdispersed data. We have found experimentally that counts as dispersed as geometric distribution or more so often cause the fitting methods of Section 4 to fail.

Variance-like parameters

Some control over the variance can be attained by adding a statistic of the form ${\mathit{g}}_{{·}^a}(\mathit{y})={\sum }_{(i,j)\in 𝕐}{\mathit{y}}_{i,j}^a$, a ≠ 1. Statistics with a > 1, such as ${\mathit{g}}_{{·}^2}(\mathit{y})={\sum }_{(i,j)\in 𝕐}{\mathit{y}}_{i,j}^2$, suffer the same problem as a Strauss point process (Kelly and Ripley, 1976): for any θ, ε > 0, lim_y→∞ exp(θy^1+ε)/y! = ∞, leading to (3) constraining θ ≤ 0, able to represent only underdispersion.

Thus, we propose to model dispersion by adding a statistic of the form

$${\mathit{g}}_{\sqrt{·}}(\mathit{y})=\sum _{(i,j)\in 𝕐}{\mathit{y}}_{i,j}^{1/2}=\sum _{(i,j)\in 𝕐}\sqrt{{\mathit{y}}_{i,j}}.$$ (6)

To the extent that the counts are Poisson-like, the square root is a variance-stabilizing transformation (McCullagh and Nelder, 1989, p. 196). Then, a model with p = 2 and dyadwise sufficient statistic

$$\mathit{g}(\mathit{y})={(\sum _{(i,j)\in 𝕐}\sqrt{{\mathit{y}}_{i,j}},\sum _{(i,j)\in 𝕐}{\mathit{y}}_{i,j})}^{\top }$$ (7)

may be viewed as a modeling the first and second moments of $\sqrt{{\mathit{y}}_{i,j}}$. That the highest-order term is still on the order of y_i,j guarantees that Θ_N = ℝ^p — a practical advantage over CMP.

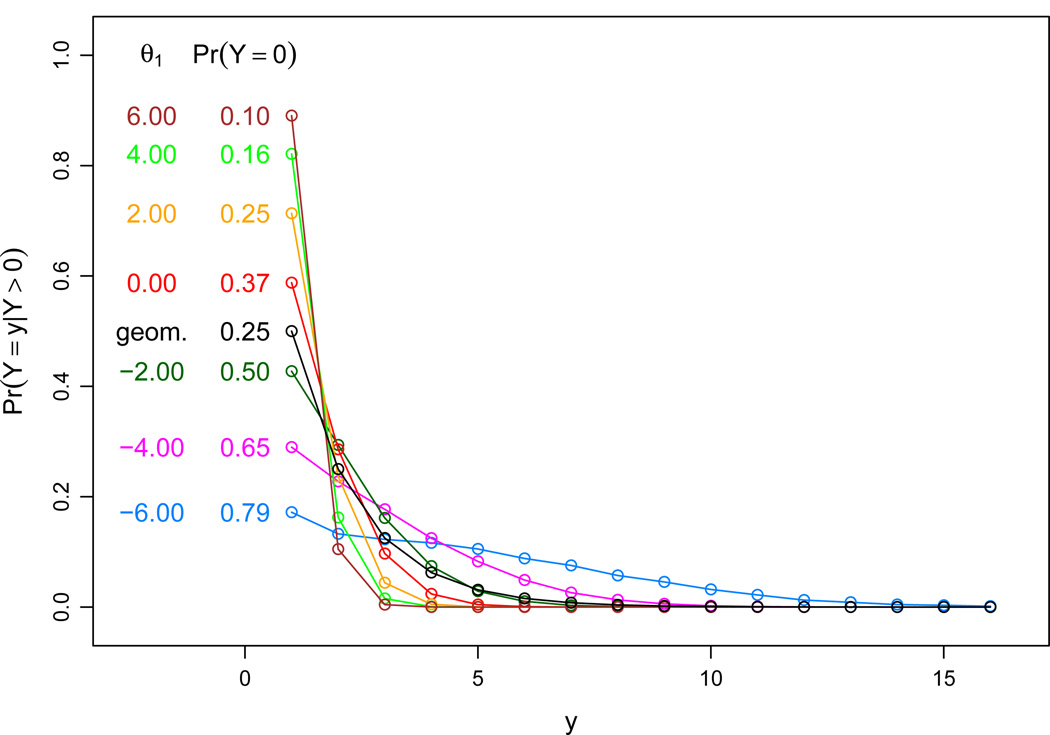
As with CMP, the normalizing constant is intractable. To explore the shape of this distribution, we fixed θ₁ at each of a range of values and found θ₂s such that the induced distribution had the expected value of 1. We then simulated from the fit. The estimated pmf for each configuration and the comparison with the geometric distribution with the same expectation is given in Figure 2. Smaller coefficients on (6) (θ₁) correspond to greater dispersion, with coefficients on dyad sum (θ₂) increasing to compensate, and vice versa, with θ₁ = 0 corresponding to a Poisson distribution. As the dispersion increases, the mean is preserved in part by increasing Pr(Y_i,j = 0) and, for sufficiently high values of y_i,j, the geometric distribution still dominates. Thus, there is a trade-off between the convenience of a model without complex constraints on the parameter space and the ability to model greater dispersion. In practice, if the substantive reasons for overdispersion are due to unaccounted-for heterogeneity, the latter might not be a serious disadvantage, and excess zeros can be compensated for by a term from Section 5.2.2.

Fig 2.

Dyadwise distributions attainable by the model (7). Because Pr(Y = 0) varies greatly for different θ₁ yet can be adjusted separately by an appropriate model term, we plot the probabilities conditional on Y > 0.

5.2.4. Mutuality

Many directed networks, such as friendship nominations, exhibit mutuality — that, other things being equal, if a tie (i, j) exists, a tie (j, i) is more likely to exist as well — and binary ERGMs can model this phenomenon using a sufficient statistic g_↔(y) = ∑ _{(i,j)∈𝕐,i<j} y_i,jy_j,i = ∑ _{(i,j)∈𝕐,i<j} min(y_i,j, y_j,i), counting the number of reciprocated ties. (Holland and Leinhardt, 1981) Other sufficient statistics that can model it include g_↔(y) = ∑_{(i,j)∈𝕐,i<j} 1_{yi,j ≠yj,i} and g_↔(y) = ∑_{(i,j)∈𝕐,i<j} 1_yi,j=yj,i, the counts of asymmetric and symmetric dyads, respectively. (Morris, Handcock and Hunter, 2008)

In the presence of an edge count term, these three are simply different parametrizations of the same distribution family:

$${\mathit{y}}_{i,j}{\mathit{y}}_{j,i}=\frac{({\mathit{y}}_{i,j}+{\mathit{y}}_{j,i})-1_{{\mathit{y}}_{i,j}\ne {\mathit{y}}_{j,i}}}{2}=\frac{({\mathit{y}}_{i,j}+{\mathit{y}}_{j,i})-1+1_{{\mathit{y}}_{i,j}={\mathit{y}}_{j,i}}}{2}.$$

Nevertheless, these three different statistics suggest two major ways to generalize the terms to count data: by evaluating a product or a minimum of the values, or by evaluating their similarity or difference. We discuss them in turn.

Product

It is tempting to model mutuality for count data in the same manner as for binary data, with y_i,j and y_j,i being values rather than indicators. For example, a simple model with overall dyad mean and reciprocity terms, with p = 2 and

$$\mathit{g}(\mathit{y})={(\sum _{(i,j)\in 𝕐}{\mathit{y}}_{i,j},\sum _{(i,j)\in 𝕐,i<j}{\mathit{y}}_{i,j}{\mathit{y}}_{j,i})}^{\top }$$

would have a conditional Poisson distribution:

$${\mathit{Y}}_{i,j}={\mathit{y}}_{i,j}|\mathit{Y}\in {𝒴}_{i,j}(\mathit{y})~\text{Poisson}(\mu =\text{exp}({\mathit{\theta }}_1+{\mathit{\theta }}_2{\mathit{y}}_{j,i})),$$

a desirable property. However, because for any c > 0, lim_y→∞ exp(cy²)/(y!)² = ∞, for θ₂ > 0, representing positive mutuality, (3) is not fulfilled. (Note that the expected value of Y_i,j is exponential in the value of Y_j,i and vice versa. Again, a Strauss point process exhibits a similar problem. (Kelly and Ripley, 1976))

Geometric mean

As with dispersion, the problem can be alleviated by using the geometric mean of y_i,j and y_j,i instead of their product. As in Section 5.2.3, this choice may be justified as an analog of covariance on variance-stabilized counts. This changes the shape of the distribution in ways that are difficult to interpret: if

$$\mathit{g}(\mathit{y})={(\sum _{(i,j)\in 𝕐}{\mathit{y}}_{i,j},\sum _{(i,j)\in 𝕐,i<j}\sqrt{{\mathit{y}}_{i,j}{\mathit{y}}_{j,i}})}^{\top },$$

then

$${\text{Pr}}_{\mathit{\theta };h,\mathit{\eta },\mathit{g}}({\mathit{Y}}_{i,j}={\mathit{y}}_{i,j}|\mathit{Y}\in {𝒴}_{i,j}(\mathit{y}))\propto \text{exp}({\mathit{\theta }}_1{\mathit{y}}_{i,j}+({\mathit{\theta }}_2\sqrt{{\mathit{y}}_{j,i}})\sqrt{{\mathit{y}}_{i,j}})/{\mathit{y}}_{i,j}!,$$

and, with nonzero y_j,i, the probabilities of greater values of Y_i,j are inflated by more. The analogy to covariance further suggests centering the statistic:

$${\mathit{g}}_{\leftrightarrow }(\mathit{y})=\sum _{(i,j)\in 𝕐,i<j}(\sqrt{{\mathit{y}}_{i,j}}-\overline{\sqrt{\mathit{y}}})(\sqrt{{\mathit{y}}_{j,i}}-\overline{\sqrt{\mathit{y}}}),$$

for

$$\overline{\sqrt{\mathit{y}}}\equiv \frac{1}{|𝕐|}\sum _{(i\prime ,j\prime )\in 𝕐}\sqrt{{\mathit{y}}_{i\prime ,j\prime }}.$$ (8)

Minimum

An alternative generalization is to take the minimum of the two values. For example, if

$$\mathit{g}(\mathit{y})={(\sum _{(i,j)\in 𝕐}{\mathit{y}}_{i,j},\sum _{(i,j)\in 𝕐,i<j}\text{min}({\mathit{y}}_{i,j},{\mathit{y}}_{j,i}))}^{\top },$$

then

$${\text{Pr}}_{\mathit{\theta };h,\mathit{\eta },\mathit{g}}({\mathit{Y}}_{i,j}={\mathit{y}}_{i,j}|\mathit{Y}\in {𝒴}_{i,j}(\mathit{y}))\propto \text{exp}({\mathit{\theta }}_1{\mathit{y}}_{i,j}+{\mathit{\theta }}_2\text{min}({\mathit{y}}_{i,j}-{\mathit{y}}_{j,i},0))/{\mathit{y}}_{i,j}!.$$ (9)

Thus, a possible interpretation for this term is that the conditional probability for a particular value of Y_i,j, y_i,j is deflated by exp (θ₂) for every unit by which y_i,j is less than y_j,i. In a sense, y_j,i “pulls up” y_i,j to its level and vice versa.

Negative difference

Generalizing the concept of similarity between y_i,j and y_j,i leads to a statistic of difference between their values. We negate it so that a positive coefficient value leads to greater mutuality. Then,

$$\mathit{g}(\mathit{y})={(\sum _{(i,j)\in 𝕐}{\mathit{y}}_{i,j},\sum _{(i,j)\in 𝕐,i<j}-|{\mathit{y}}_{i,j}-{\mathit{y}}_{j,i}|)}^{\top },$$ (10)

and

$${\text{Pr}}_{\mathit{\theta };h,\mathit{\eta },\mathit{g}}({\mathit{Y}}_{i,j}={\mathit{y}}_{i,j}|\mathit{Y}\in {𝒴}_{i,j}(\mathit{y}))\propto \text{exp}({\mathit{\theta }}_1{\mathit{y}}_{i,j}-{\mathit{\theta }}_2|{\mathit{y}}_{i,j}-{\mathit{y}}_{j,i}|)/{\mathit{y}}_{i,j}!,$$

so the conditional probability of a particular y_i,j is deflated by exp (θ₂) for every unit difference from y_j,i, in either direction. Thus, y_j,i “pulls in” y_i,j and vice versa. Of course, other differences (e.g., squared difference) are also possible.

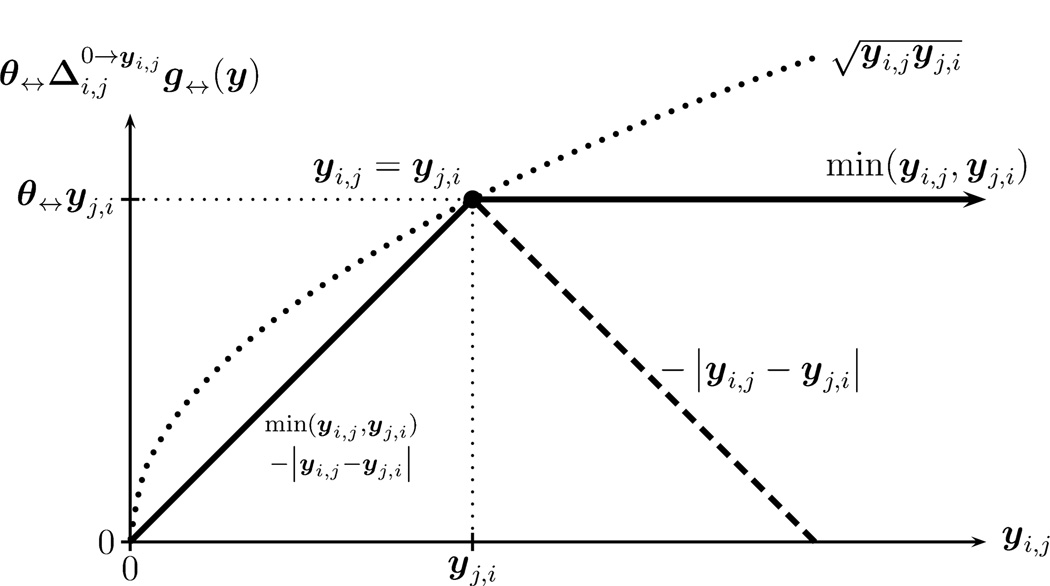
We use the discrete change statistic to visualize the differences among these variants in Figure 3, plotting the ${\mathit{\theta }}_{\leftrightarrow }{\mathbf{\Delta }}_{i,j}^{0\to {\mathit{y}}_{i,j}}{\mathit{g}}_{\leftrightarrow }(\mathit{y})$ summand of

$$\text{log}\frac{{\text{Pr}}_{\mathit{\theta };h,\mathit{\eta },\mathit{g}}({\mathit{Y}}_{i,j}={\mathit{y}}_{i,j}|\mathit{Y}\in {𝒴}_{i,j}(\mathit{y}))}{{\text{Pr}}_{\mathit{\theta };h,\mathit{\eta },\mathit{g}}({\mathit{Y}}_{i,j}=0|\mathit{Y}\in {𝒴}_{i,j}(\mathit{y}))}=\mathit{\theta }·{\mathbf{\Delta }}_{i,j}^{0\to {\mathit{y}}_{i,j}}\mathit{g}(\mathit{y})$$

for each variant. Lastly, while the conditional distributions, and hence the parameter interpretations for the minimum and the negative difference statistic, are different, models induced by (9) and (10) are also reparametrizations of each other: $\text{min}({\mathit{y}}_{i,j},{\mathit{y}}_{j,i})=\frac{1}{2}(({\mathit{y}}_{i,j}+{\mathit{y}}_{j,i})-|{\mathit{y}}_{i,j}-{\mathit{y}}_{j,i}|)$.

Fig 3.

Effect of proposed mutuality statistics (g_↔) with parameter θ_↔ > 0 on the distribution of Y_i,j, given that Y_j,i = y_j,i. Whereas the min(y_i,j, y_j,i) statistic deflates the probabilities of those values of y_i,j that are less than y_j,i, thus inflating all of those of y_i,j above or equal to it, thus “pulling Y_i,j up”, the −|y_i,j − y_j,i| statistic deflates the probabilities in both directions away from y_j,i, thus inflating those that are the closest, “pulling Y_i,j in”. $\sqrt{{\mathit{y}}_{i,j}{\mathit{y}}_{j,i}}$ inflates greater values of y_i,j in general, inflating by more for greater $\sqrt{{\mathit{y}}_{j,i}}$.

5.2.5. Actor heterogeneity

It is often the case that different actors in a network have different overall propensities to have ties: they are heterogeneous in their gregariousness, popularity, and/or (undirected) sociality. Some of this heterogeneity may be accounted for by exogenous covariates. For the unaccounted-for heterogeneity, two major approaches have been used: conditional, in which actor-specific parameters are added to the model to absorb its effects, and marginal, in which statistics are added that represent the effects of heterogeneity on the overall network features. Examples of the conditional approach include the very first exponential-family model for networks, the p₁, which used a fixed effect for every actor (Holland and Leinhardt, 1981); and the p₂ model and latent space models, which used random effects instead (van Duijn, Snijders and Zijlstra, 2004; Hoff, 2005; Krivitsky et al., 2009; Mariadassou, Robin and Vacher, 2010). The marginal approach includes the count of k-stars for k ≥ 2 (Frank and Strauss, 1986), which, for a fixed network density, become more prevalent as heterogeneity increases, at the cost of often inducing ERGM degeneracy; alternating k-stars and geometrically weighted degree statistics (Snijders et al., 2006; Hunter and Handcock, 2006), which attempt to remedy the degeneracy of k-stars; and statistics such as the square root degree activity/popularity, which sum each actor’s degree taken to 3/2 power, which also increases with greater heterogeneity, but not as rapidly as 2-stars do (Snijders, van de Bunt and Steglich, 2010), avoiding degeneracy. In the conditional approach, using fixed effects lacks parsimony and using random effects creates a problem with a doubly-intractable normalizing constant, beyond the scope of this paper, so we develop a marginal approach here.

Actor heterogeneity may be viewed marginally as positive within-actor correlation among the dyad values. Following the discussion in the previous sections, we propose a form of pooled within-actor covariance of variance-stabilized dyad values, scaled to the same magnitude as the dyad sum:

$${\mathit{g}}_{\text{out cov}.}(\mathit{y})=\sum _{i\in N}\frac{1}{n-2}\sum _{j,k\in {𝕐}_{i\to }\wedge j<k}(\sqrt{{\mathit{y}}_{i,j}}-\overline{\sqrt{\mathit{y}}})(\sqrt{{\mathit{y}}_{i,k}}-\overline{\sqrt{\mathit{y}}}),$$ (11)

for 𝕐_i→ being the set of actors to who whom i may have ties (≡ {j′ : (i, j′) ∈ 𝒴}) and $\overline{\sqrt{\mathit{y}}}$ defined in (8). This statistic would increase with greater out-tie heterogeneity, an analogous statistic can be specified for in-tie heterogeneity, and dropping the directionality produces an undirected version of this statistic.

We have considered other variants, including the uncentered version, in which each summand in (11) is simply $\sqrt{{\mathit{y}}_{i,j}{\mathit{y}}_{i,k}}$. We found that in undirected networks in particular, such a model term can induce a degeneracy-like bimodal distribution of networks. (This is likely because in undirected networks, the positive dependence is not contained within each actor, so subtracting $\overline{\sqrt{\mathit{y}}}$ serves as a counterweight to avert the “avalanche”.)

5.2.6. Triad-closure bias

We now turn to the question of how to represent triad-closure bias — friend-of-a-friend effects — in count data. As with mutuality, merely multiplying values of the dyads in a triad leads to a model that cannot have positive triad closure bias. In addition, ERGM sufficient statistics that take counts over triads often exhibit degeneracy. (Schweinberger, 2011) For these reasons, we describe a family of statistics that sum over dyads instead. Wyatt, Choudhury and Blimes (2010) use a generalization of the curved geometrically-weighted edgewise shared partners (GWESP) statistic (Hunter and Handcock, 2006), though it is not clear whether it is suitable for data with an infinite sample space. We thus describe a more conservative family of statistics.

One term used to model triad closure in binary dynamic networks by Snijders, van de Bunt and Steglich (2010) is the transitive ties effect, the most conservative special case of the GWESP (Hunter and Handcock, 2006) statistic. This statistic counts the number of ties (i, j) such that there exists at least one path of length 2 (two-path) between them — a third actor k such that y_i,k = y_k,j = 1. (Unlike the triangle count, each tie may contribute at most +1 to the statistic, no matter how many such ks exist.)

One generalization of this statistic to counts is

$${\mathit{g}}_{\text{trans}.\text{ties}}(\mathit{y})=\sum _{(i,j)\in 𝕐}\text{min}({\mathit{y}}_{i,j},\underset{k\in N}{\text{max}}(\text{min}({\mathit{y}}_{i,k},{\mathit{y}}_{k,j}))).$$ (12)

Intuitively, define the strength of a two-path from i to j to be the minimum of the values along the path. The statistic is then the sum over the dyads (i, j) of the minimum of the value of (i, j) and the value of the strongest two-path between them. The interpretation is thus somewhat analogous to that of the minimum mutuality statistic, with y_j,i replaced by max_k∈N(min(y_i,k, y_k,j)). The motivation for using minimum, as opposed to negative absolute difference, to combine the two-path value with the focus dyad value is that the intuitive notion of friend-of-a-friend effect that this statistic embodies suggests that while the presence of a mutual friend may increase the probability or expected value of a particular friendship (i.e., “pull it up”), it should not limit it (i.e., “pull it in”) as an absolute difference would. These interpretations are somewhat oversimplified: it is just as true that a positive coefficient on this statistic results in y_i,j “pulling up” the potential two-paths between i and j.

In a directed network, (12) would model transitive (hierarchical) triads, while

$${\mathit{g}}_{\text{cycl}.\text{ties}}(\mathit{y})=\sum _{(i,j)\in 𝕐}\text{min}({\mathit{y}}_{i,j},\underset{k\in N}{\text{max}}(\text{min}({\mathit{y}}_{j,k},{\mathit{y}}_{k,i})))$$

would model cyclical (antihierarchical) triads.

The statistic (12) is a fairly conservative one, less likely to induce excessive dependence and bimodality, at the cost of sensitivity. More generally, one may specify a triadic statistic using three functions: first, ${\upsilon }_{2-\text{path}}:{\mathbb{N}}_0^2\to ℝ$, how the “value” of a two-path i → j → k is computed from its constituent segments; second, υ_combine : ℝ^{n − 2} → ℝ, how the values of the possible two-paths from i to j are combined with each other to compute the strength of the pressure on i and j to close the triad or increase their interaction; and third, υ_affect : ℕ₀ × ℝ → ℝ how this pressure affects Y_i,j. Given these,

$${\mathit{g}}_{\upsilon }(\mathit{y})=\sum _{(i,j)\in 𝕐}{\upsilon }_{\text{affect}}({\mathit{y}}_{i,j},{\upsilon }_{\text{combine}}({\upsilon }_{2-\text{path}}{({\mathit{y}}_{i,k},{\mathit{y}}_{k,j})}_{k\in N\backslash \{i,j\}})).$$ (13)

Thus, for example, one could set υ_combine to sum its arguments rather than take their maximum, or one can replace taking the minimum with taking a geometric mean. We illustrate the difference it makes in Section 6.

6. Application to interactions within a fraternity

In a series of studies in the 1970s, Bernard, Killworth and Sailer (1979–1980) assessed accuracy of retrospective sociometric surveys in a number of settings, including a college fraternity whose 58 occupants had all lived there for at least three months. To record the true amounts of interaction, for several days, unobtrusive observers were sent to periodically walk through the fraternity to note students engaged in conversation. Obtaining these network data from Batagelj and Mrvar (2006), we model these observed pairwise interaction counts.

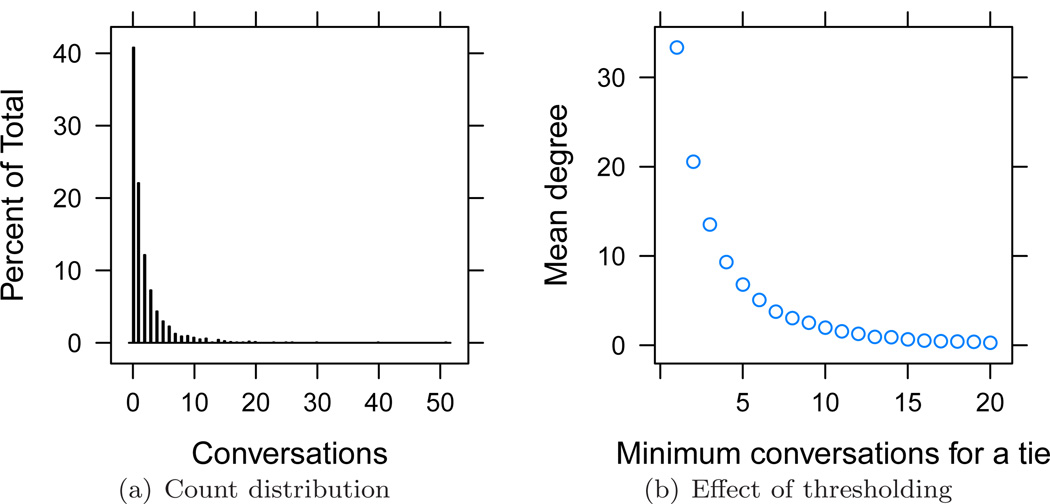
The raw distribution of counts, given in Figure 4(a), appears to be strongly overdispersed relative to Poisson, and, indeed, relative to the geometric distribution: the mean of counts is 1.9, while their standard deviation (not variance) is 3.4. At least some of this is due to actor heterogeneity: the square root of the within-actor variance of the counts is 3.1. Excluding extreme observations (all values over 20) does not make a qualitative difference. (The statistics become 1.8, 2.8, and 2.5, respectively.) Nor does there appear to be a natural place to threshold the counts to produce a binary network. (See Figure 4(b).) We thus model the baseline shape of the distribution of counts using the following terms: baseline propensity to have ties: number of dyads with nonzero value; baseline intensity of interactions: sum of dyad values; and underdispersion: the statistic (6).

Fig 4.

Conversation count summaries for Bernard, Killworth and Sailer fraternity network

(We have also attempted to use CMP (via (5)) but found the process to be unstable due to the greater-than-geometric level of dispersion.)

Little was recorded about the social roles of the fraternity members, so we consider the effects of endogenous social forces: actor heterogeneity: the undirected version of (11); transitivity of intensities: the statistic (12).

Faust (2007), in particular, found that in many empirical networks, much of the apparent triadic effects are accounted for by variations in degree distribution and other lower-order effects. Thus, we consider four models: baseline shape only (B), baseline with heterogeneity (BH), baseline with transitivity (BT), and all terms (BHT), to explore this concept in a valued setting.

We report the model fits in Table 1. MCMC diagnostics, described by Goodreau et al. (2008), show adequate mixing and unimodal distributions of sufficient statistics, and networks simulated from these fits have, on average, statistics equal to the observed sufficient statistics. The baseline dyadwise distribution terms are difficult to interpret, but the highly negative coefficient on under-dispersion suggests a a strong degree of overdispersion, as expected. Some of this overdispersion appears to be absorbed by modeling actor heterogeneity, however. There are indications of a high degree of heterogeneity in individuals’ propensity to interact, over and above that expected for even the overdispersed baseline distribution. (Monte Carlo P-val. < 0.001 based on 10,000 draws.)

Table 1.

Results from fitting the models to Bernard, Killworth and Sailer fraternity network

		Estimates (Std. Errors)
Term	B	BH	BT	BHT
Ties	5.60 (0.21)	4.96 (0.17)	6.24 (0.21)	4.98 (0.17)
Intensity	3.65 (0.05)	3.13 (0.06)	3.40 (0.07)	3.12 (0.06)
Underdispersion	−9.71 (0.22)	−8.23 (0.20)	−10.52 (0.22)	−8.26 (0.19)
Heterogeneity		1.48 (0.06)		1.46 (0.07)
Transitivity			0.46 (0.05)	0.03 (0.04)

Coefficients statistically significant at α = 0.05 are bolded.

Standard errors incorporate the uncertainty introduced by approximating the likelihood using MCMC (Hunter and Handcock, 2006).

Without accounting for actor heterogeneity (i.e., Model BT), there appears to be a strong transitivity effect — a friend of a friend is a friend — and the Monte Carlo test confirms this with a similar P-value. However, if actor heterogeneity is accounted for, the transitivity effects vanish (simulated one-sided P-val. = 0.43), suggesting that the underlying social process is better explained by a relatively small number of highly social individuals whose ties to each other and to (less social) third parties create excess transitive ties for the overall amount of interaction observed. At the same time, if, instead of using (12) as the test statistic, we use a less conservative statistic of the form (13) with ${\upsilon }_{2-\text{path}}(x_1,x_2)=\sqrt{x_1{x}_2}(\text{geometric mean}),{\upsilon }_{\text{combine}}(x_1,\dots ,x_{n-2})={\sum }_{k=1}^{n-2}{x}_k$, and ${\upsilon }_{\text{affect}}(x_1,x_2)=\sqrt{x_1{x}_2}$, the effect’s significance seems to increase (one-sided P-val. = 0.07). However, when we attempted to fit the model with this effect, the process exhibited the degeneracy-like bimodality. This suggests that there is a trade-off between stability and power to detect subtle effects.

7. Discussion

We have generalized the exponential-family random graph models to networks whose relationships are unbounded counts, explored the issues that arise when generalizing, and proposed ways to model several common network features for count data. We demonstrated our development by a study of the interaction of individual heterogeneity and friend-of-a-friend effects in a network with a hard-to-model dyadwise count distribution.

This paper focused on modeling counts. More generally, one can define a valued ERGM by replacing the set of possible dyad values ℕ₀ by a more general set 𝕊 and replacing h(y) with a more general σ-finite measure space (𝒴, 𝖸, P_h) with reference measure P_h, then postulating a probability measure P_θ;Ph,η,g with Radon-Nikodym derivative of P_θ;Ph,η,g with respect to P_h,

$$\frac{d{P}_{\mathit{\theta };P_h,\mathit{\eta },\mathit{g}}}{d{P}_h}(\mathit{y})=\frac{\text{exp}(\mathit{\eta }(\mathit{\theta })·\mathit{g}(\mathit{y}))}{{\kappa }_{P_h,\mathit{\eta },\mathit{g}}(\mathit{\theta })},$$

(Barndorff-Nielsen, 1978, pp. 115–116; Brown, 1986, pp. 1–2) with the normalizing constant

$${\kappa }_{P_h,\mathit{\eta },\mathit{g}}(\mathit{\theta })={\int }_{𝒴}\text{exp}(\mathit{\eta }(\mathit{\theta })·\mathit{g}(\mathit{y}))d{P}_h(\mathit{y}).$$

For binary and count data, and discrete data in general, P_h could be specified as a function relative to the counting measure, while for continuous data, it could be defined with respect to the Lebesgue measure. Still, as with count data, the shape of this function would need to be specified.

Other scenarios might call for more complex specifications of the reference measure. Some network data, such as measurements of duration of conversation (Wyatt, Choudhury and Blimes, 2010) and international trade volumes (Westveld and Hoff, 2011) are continuous measurements except for having a positive probability of two actors not conversing at all or two countries having no measured trade. Westveld and Hoff use a normal distribution to model the log-transformed trade volume, imputing 0 = log(1) for 0 observed trade volumes (all nonzero trade volumes being greater than 1 unit), and they note this issue and address it by pointing out that in their (latent-variable) model, an impact of such an outlier would be contained. Valued ERGMs may provide a more principled approach by specifying a semicontinuous P_h, such as one that puts a mass of 1/2 on 0 and 1/2 on Lebesgue measure on (0, ∞).

We have also focused on data that do not impose any constraints on the sample space: 𝒴 ≡ 𝕊^𝕐. But, some types of network data, such as those where each actor (ego) ranks the others (alters) (Newcomb, 1961, for example) can be viewed in this framework as having a constrained sample space: setting 𝕊 = {1..n − 1} and constraining 𝒴 to ensure that each ego assigns a unique rank to each alter gives a sample space of permutations that could, with a counting measure, serve as the reference measure for an ERGM on rank data. These, and other applications are a subject for ongoing and future work.

This paper focuses on models for cross-sectional networks, where a single snapshot of relationship states or relationships aggregated over a time period are observed. For longitudinal data, comprising multiple snapshots of networks over the same actors over time, binary ERGMs have been used as a basis for discrete-time models for network tie evolution by Robins and Pattison (2001), Wyatt, Choudhury and Bilmes (2009; 2010), Hanneke, Fu and Xing (2010), Krivitsky and Handcock (2010), and others. Valued ERGMs can be directly applied to the temporal ERGMs of Hanneke, Fu and Xing (2010) although their adaptation to the work of Krivitsky and Handcock (2010) may be less straight-forward, especially if the benefits to interpretability of the separable models are to be retained.

In practice, networks are not always observed completely. Handcock and Gile (2010) develop an approach to ERGM inference for partially observed or sampled binary networks. It would be natural to extend this approach to valued networks and valued ERGMs.

Some methods for assessing a network model’s fit, particularly MCMC diagnostics (Goodreau et al., 2008) can be used with little or no modification. Others, like the goodness-of-fit methods of Hunter, Goodreau and Handcock (2008) may require development of characteristics meaningful for valued networks. It may also be possible to extend the stability criteria of Schweinberger (2011) to models with infinite sample spaces.

Appendix A: A sampling algorithm for a Poisson-reference ERGM

We use a Metropolis-Hastings sampling algorithm (Algorithm 1) to sample from a Poisson-reference ERGM, using a Poisson kernel with its mode at the present value of a dyad and, occasionally (with a specified probability π₀), proposing a jump directly to 0. Because, as we discuss in Section 5.2.2, counts of interactions are often zero-inflated relative to Poisson, setting π₀ > 0 can be used to speed-up mixing. For highly overdispersed distributions, a Poisson kernel may be trivially replaced by a geometric or even negative-binomial kernel.

This algorithm selects the dyad on which the jump is to be proposed at random. A possible improvement to this algorithm would be to adapt to it the tie-no-tie (TNT) proposal (Morris, Handcock and Hunter, 2008), which optimizes sampling in sparse (zero-inflated) networks by focusing on dyads which have nonzero values.

Algorithm 1.

Sampling from a Poisson-reference ERGM with no constraints, optimized for zero-inflated distributions

Let:
	RandomChoose(A) return a random element of a set A
	Uniform(a, b) return a random draw from the Uniform(a, b) distribution
	Poisson≠y(λ) return a random draw from the Poisson(λ) distribution, conditional on not drawing y
	$p(y^{*};y)=\frac{\text{exp}(-(y+\frac{1}{2})){(y+\frac{1}{2})}^{y^{*}}/y^{*}!}{1-\text{exp}(-(y+\frac{1}{2})){(y+\frac{1}{2})}^y/y!}$, the pmf of a ${\text{Poisson}}_{\ne y}(y+\frac{1}{2})$ draw
Input: y(0) ∈ 𝒴, T sufficiently large, 𝕐, g, η, π0 ∈ [0, 1)
Output: a draw from the specified Poisson-reference ERGM
1:	for t ← 1‥T do
2:	(i, j) ← RandomChoose(𝕐) {Select a dyad at random.}
3:	if yi,j ≠ 0 ∧ Uniform(0, 1) < π0 then
4:	y* ← 0 {Propose a jump to 0 with probability π0.}
5:	else
6:	$y^{*}\leftarrow {\text{Poisson}}_{\ne {\mathit{y}}_{i,j}^{(t-1)}}\left({\mathit{y}}_{i,j}^{(t-1)}\right)$ {Propose a jump to a new value.}
7:	$q\leftarrow \{\begin{array}{cc}\frac{{\pi }_0+(1-{\pi }_0)p(0;y^{*})}{p(y^{*};0)}\hfill & {\mathit{y}}_{i,j}^{(t-1)}=0\hfill \\ \frac{p({\mathit{y}}_{i,j}^{(t-1)};0)}{{\pi }_0+(1-{\pi }_0)p(0;{\mathit{y}}_{i,j}^{(t-1)})}\hfill & {\mathit{y}}_{i,j}^{(t-1)}\ne 0\wedge y^{*}=0\hfill \\ \frac{(1-{\pi }_0)p({\mathit{y}}_{i,j}^{(t-1)};y^{*})}{(1-{\pi }_0)p(y^{*};{\mathit{y}}_{i,j}^{(t-1)})}\hfill & \text{otherwise}\hfill \end{array}$
8:	$r\leftarrow q\times \frac{{\mathit{y}}_{i,j}^{(t-1)}!}{y^{*!}}\times \text{exp}(\mathit{\eta }(\mathit{\theta })·{\mathbf{\Delta }}_{i,j}^{{\mathit{y}}_{i,j}^{(t-1)}\to y^{*}}({\mathit{y}}^{(t-1)}))$
9:	if Uniform(0, 1) < r then
10:	${\mathit{y}}^{(t)}\leftarrow {\mathit{y}}_{(i,j)=y^{*}}^{(t-1)}$ {Accept the proposal.}
11:	else
12:	y(t)←y(t−1) {Reject the proposal.}
13: return y(T)

Appendix B: Non-steepness of the Conway–Maxwell–Poisson family

Expressed in its exponential-family canonical form, a random variable X with the Conway–Maxwell–Poisson distribution has the pmf

$${\text{Pr}}_{\mathit{\theta };\mathit{\eta },\mathit{g}}(X=x)=\frac{\text{exp}({\mathit{\theta }}_{1}x+{\mathit{\theta }}_2\text{log}(x!))}{{\kappa }_{\mathit{\eta },\mathit{g}}(\mathit{\theta })},x\in {\mathbb{N}}_0$$

with the normalizing constant

$${\kappa }_{\mathit{\eta },\mathit{g}}(\mathit{\theta })=\sum _{x\prime =0}^{\infty }\frac{\text{exp}({\mathit{\theta }}_{1}x\prime +{\mathit{\theta }}_2\text{log}(x\prime !))}{{\kappa }_{\mathit{\eta },\mathit{g}}(\mathit{\theta })}.$$

Theorem B.1. The Conway–Maxwell–Poisson family is not regular.

Proof. The natural parameter space of CMP is

$${\mathbf{\Theta }}_{\mathrm{N}}=\{\mathit{\theta }\prime \in {ℝ}^2:{\mathit{\theta }}_2<0\vee ({\mathit{\theta }}_2=0\wedge {\mathit{\theta }}_1<0)\}$$

(Shmueli et al., 2005). Due to the boundary at θ₂ = 0, Θ_N is not an open set, and hence the family is not regular (Brown, 1986, p. 2).

Theorem B.2. The Conway–Maxwell–Poisson family is not steep.

Proof. A necessary and sufficient condition for a non-regular exponential family to be steep is that

$${\forall }_{\mathit{\theta }\in {\mathbf{\Theta }}_{\mathrm{N}}\backslash {\mathbf{\Theta }}_{\mathrm{N}}^{\mathrm{o}}}{\mathrm{E}}_{\mathit{\theta };\mathit{\eta },\mathit{g}}(\Vert \mathit{g}(X)\Vert )=\infty ,$$

where ${\mathbf{\Theta }}_{\mathrm{N}}^{\mathrm{o}}$ is the open interior of Θ_N, and their set difference is thus the non-open boundary of the natural parameter space that is contained within it. (Brown, 1986, Proposition 3.3, p. 72) For CMP, this boundary

$${\mathbf{\Theta }}_{\mathrm{N}}\backslash {\mathbf{\Theta }}_{\mathrm{N}}^{\mathrm{o}}=\{\mathit{\theta }\prime \in {ℝ}^2:{\mathit{\theta }}_2=0\wedge {\mathit{\theta }}_1<0\}.$$

There, X ~ Geometric(p = 1−exp (θ₁)). Noting that X ≥ 0 a.s., log(X!) ≥ 0 a.s., and $\text{log}(x!)\le (x+1)\text{log}(\frac{x+1}{e})+1$,

$${\mathrm{E}}_{\mathit{\theta };\mathit{\eta },\mathit{g}}(\Vert \mathit{g}(X)\Vert )={\mathrm{E}}_{\text{Geometric}(p=1-\text{exp}({\mathit{\theta }}_1))}(\Vert {[X,\text{log}(X!)]}^{\top }\Vert )\le {\mathrm{E}}_{\text{Geometric}(p=1-\text{exp}({\mathit{\theta }}_1))}(X+\text{log}(X!))\le {\mathrm{E}}_{\text{Geometric}(p=1-\text{exp}({\mathit{\theta }}_1))}(X+(X+1)\text{log}(\frac{X+1}{e})+1)\le {\mathrm{E}}_{\text{Geometric}(p=1-\text{exp}({\mathit{\theta }}_1))}(X+{(X+1)}^2+1)<\infty ,$$

since the first and second moments of the geometric distribution are finite. Therefore, CMP is not steep.

Because the non-steep boundary corresponds to the most dispersed distribution that CMP can represent, maximum likelihood estimator properties for data which are highly overdispersed are not guaranteed.