Abstract
While radiation absorbed dose (Gy) to the skin or other organs is sometimes estimated for patients from diagnostic radiologic examinations or therapeutic procedures, rarely is occupationally-received radiation absorbed dose to individual organs/tissues estimated for medical personnel, e.g., radiologic technologists or radiologists. Generally, for medical personnel, equivalent or effective radiation doses are estimated for compliance purposes. In the very few cases when organ doses to medical personnel are reconstructed, the data is usually for the purpose of epidemiologic studies, e.g., a study of historical doses and risks to a cohort of about 110,000 radiologic technologists presently underway at the U.S. National Cancer Institute. While ICRP and ICRU have published organ-specific external dose conversion coefficients (DCCs), i.e., absorbed dose to organs and tissues per unit air kerma and dose equivalent per unit air kerma, those factors have been primarily published for mono-energetic photons at selected energies. This presents two related problems for historical dose reconstruction, both of which are addressed here. It is necessary to derive conversion factors values for (i) continuous distributions of energy typical of diagnostic medical x rays (bremsstrahlung radiation), and (ii) for energies of particular radioisotopes used in medical procedures, neither of which are presented in published tables. For derivation of DCCs for bremsstrahlung radiation, combinations of x-ray tube potentials and filtrations were derived for different time periods based on a review of relevant literature. Three peak tube potentials (70 kV, 80 kV, and 90 kV) with four different amounts of beam filtration were determined to be applicable for historic dose reconstruction. The probability of these machine settings were assigned to each of the four time periods (earlier than 1949, 1949-1954, 1955-1968, and after 1968). Continuous functions were fit to each set of discrete values of the ICRP/ICRU mono-energetic DCCs and the functions integrated over the air-kerma weighted photon fluence of the 12 defined x-ray spectra. The air kerma-weighted DCCs in this work were developed specifically for an irradiation geometry of anterior to posterior (AP) and for the following tissues: thyroid, breast, ovary, lens of eye, lung, colon, testes, heart, skin (anterior side only), red bone marrow (RBM), heart, and brain. In addition, a series of functional relationships to predict DT per Ka values for RBM dependent on body mass index [BMI (kg m−2) ≡ weight per height2] and average photon energy were derived from a published analysis. Factors to account for attenuation of radiation by protective lead aprons were also developed. Because lead protective aprons often worn by radiology personnel not only reduce the intensity of x-ray exposure but also appreciably harden the transmitted fluence of bremsstrahlung x rays, DCCs were separately calculated for organs possibly protected by lead aprons by considering three cases: no apron, 0.25 mm Pb apron, and 0.5 mm Pb apron. For estimation of organ doses from conducting procedures with radioisotopes, continuous functions of the reported mono-energetic values were developed and DCCs were derived by estimation of the function at relevant energies. By considering the temporal changes in primary exposure-related parameters, e.g., energy distribution, the derived DCCs and transmission factors presented here allow for more realistic historical dose reconstructions for medical personnel when monitoring badge readings are the primary data on which estimation of an individual's organ doses are based.
INTRODUCTION
Dose reconstruction for medical radiologic personnel presents unique challenges for a variety of reasons, including: (1) radiation doses to medical staff cannot be estimated with the same dose coefficients as for patients who typically undergo specific diagnostic radiologic examinations according to established imaging protocols and with small well-defined fields, (2) personnel monitoring badge data has to be carefully interpreted to give credible organ doses that properly account for photon energy distribution and irradiation geometry, and (3) organ doses to medical staff will typically be highly uncertain since there are numerous assumptions about exposure conditions that usually must be made to estimate organ doses.
Historical doses for patients can be reconstructed using published dosimetric factors, e.g., from the work of Rosenstein (1988), though knowledge or assumptions about beam filtration and field size are required. For purposes of estimating organ doses from occupational radiation where there is no defined field size and the half-value layer may not be known, DCCs are needed that consider whole-body exposure and that use data for the relevant x-ray technique factors, i.e., tube potential and total filtration.
The dosimetric factors described here are being used in a dose reconstruction at the National Cancer Institute (NCI) (Sigurdson et al. 2003, Simon et al. 2006) for approximately 110,000 medical x-ray technologists who were occupationally exposed throughout the 20th century beginning in 1916. These factors may, more generally, have application to dose reconstruction for occupational cohorts who were exposed to medical radiation in their jobs. This analysis is concerned with exposure received from conducting radiography and fluoroscopy and to exposures received from the use of radioisotopes in nuclear medicine, but does not address dose reconstruction for personnel who conducted mammography, computed tomography, or other specialized imaging technologies that had different energy distributions.
METHODS
Reconstruction of organ doses to medical personnel from occupational exposure depends on the availability of individual monitoring data. While radiation doses may sometimes be estimated based on published measurement data, such data are often mean values relevant to a particular group and can only be assigned to an individual with great uncertainty. This analysis presumes that individual monitoring data (e.g., readings from film badges) or monitoring data from the individual's work environment (e.g., exposure measurements) are available.
Today, personnel monitoring doses are reported in the U.S. for regulatory and compliance purposes as personal dose equivalent (ICRU 1992, 1993), in units of mrem in the U.S. or in mSv in countries using SI units. In this paper, however, the term badge dose is used in lieu of personal dose equivalent, because this analysis covers periods of time (i.e., before 1960s) when film badge measurements represented a measure of air ionization (Roentgens) as well as at later times when the quantities of deep dose, dose equivalent, and personal dose equivalent were used.
Theory
In order to convert badge dose measurements to organ doses such that temporal changes in x-ray machine settings (primarily tube potential and filtration) during the 20th century are accounted for, 12 different combinations of technical parameters (x-ray machine settings) were derived from the literature, three in each of four time periods (Table 1). To estimate DCCs for each time period, realistic x-ray fluence spectra (IPEM 1997) were combined with results from mono-energetic radiation transport calculations (ICRP 1997).
Table 1.
Assumptions about x-ray beam quality derived from literature for purposes of reconstructing organ doses to medical radiologic personnel.
| <1949 | 1949 to 1954 | 1955 to 1968 | >1968 | |
|---|---|---|---|---|
| Peak tube potential (kV)a,b (average photon energy, keV) | 70 (32.1) | 70 (36.0) | 70 (38.5) | 70 (40.0) |
| 80 (35.5) | 80 (39.3) | 80 (42.1) | 80 (43.6) | |
| 90 (38.8) | 90 (42.6) | 90 (45.5) | 90 (47.1) | |
| Filtrationc (mm Al) | 0.5 | 1.5 | 2.5 | 3.0 |
| Ripple (%) | 15 | 15 | 10 | 5 |
Values of kV within each time-period are considered as equally probable.
kV (peak) based on USPSH (1964), average x-ray energy based on IPEM (1997).
Based on Shockley and Kathren (2004) and Shockley et al. (2008).
In an earlier report of the dosimetry of the NCI study of radiation technologists (Simon et al, 2006), 35 keV was assumed as the average photon energy used in radiography and fluoroscopy prior to 1985 and that average photon energy was used to estimate DCCs. That assumed average x-ray machine potential agreed well with the assumptions of Chinese dose reconstruction studies of technologists where 34 keV was reported as the average photon energy (Zhang et al. 1998). In this analysis, a range of peak potentials (kV) have been derived from literature review to account for the uncertainty of the average tube potential used by individual U.S. technologists when averaged over a working year. In a survey of literature on radiologic technique over the 20th century conducted for the purposes of this work (but not considering mammography, CT, and other digital techniques), tube potentials (peak) were found to routinely be in the range from 50 to 120 kV. Those values are in good agreement with values of tube potential reported in a comprehensive U.S. Public Health Service study in 1964 study (USPHS 1964) on trends in x-ray exposure where it was reported that 75% of diagnostic medical x rays were conducted at tube potentials between 55 and 94 kV. Because the extreme values of kV were reported with considerably less frequency in the many literature references surveyed, it is assumed here that the kV in a given year averaged over all the procedures performed by a single technician, was likely to have been between 70 and 90 kV with roughly equal probability. For that reason, DCCs are presented here for 70, 80, and 90 kV with filtrations specified by time-period as derived from findings by Shockley and Kathren (2004) and Shockley et al. (2008). The average photon energy of the 12 spectra presented in Table 1, determined from published x-ray spectra (IPEM 1997), range from 32 to 47 keV, depending on the tube potential and the filtrations assumed, giving mean photon energies values that are only modestly different from the previously assumed value of 35 keV (Simon et al. 2006).
Depending on the time-period, organ absorbed doses can be reconstructed based on measurements from badges that were calibrated in terms of: (1) exposure, X, reported in Roentgens, or (2) personal dose equivalent Hp(d), reported in mrem. While the usage of exposure (roentgens, R) as a measurement quantity was common prior to 1960, film badges provided by the largest supplier of personnel monitoring devices continued to be calibrated in terms of roentgens with back-scatter through 19842. The strategy for calculating organ doses, based either on a badge calibrated in terms of personal dose equivalent or in units of exposure is described below.
Organ or tissue dose (denoted as DT) can be derived for mono-energetic radiation via eqns. 1 and 2 from data provided by ICRP Report 74 (1997). In the following equations, ratios in rounded brackets are values provided by Report 74 (ICRP 1997) at specific photon energies.
| (1) |
where,
DT = tissue or organ dose (Gy or rad)
Hp(d) = badge dose measurement when calibrated as personal dose equivalent (Sv or rem)
Ka = air kerma (Gy or rad)
For those years when exposures were reported in roentgens (R), Hp(d) can be estimated as shown in eqn (2) and substituted into eqn (1) for the purpose of organ dose computation.
| (2) |
where,
X = measurement of exposure (R)
For those cases when it is of interest to estimate the absorbed dose to an organ or tissue protected by a protective lead apron, one has to consider two possible cases: (i) when the badge was worn on the outside of the apron (eq. 3) and, (ii) when the badge was worn under the apron (eq. 4).
| (3) |
| (4) |
The estimation of absorbed dose to red bone marrow (RBM) is a special case since the entirety of the RBM is not shielded by a lead apron. For all organs other than skin and RBM, the organ is either completely shielded or not shielded at all by the apron. The dose to RBM when a protective lead apron is used can be estimated as:
| (5) |
where,
TF is an energy spectrum-specific transmission factor,
fRBM-s and fRBM-ns are the fractions of the total-body RBM that are shielded by the lead apron and the fraction not-shielded, respectively.
In eqns. (3 and 5), TF is an energy spectrum-specific transmission factor defined here as the ratio of air kerma beneath a lead apron to the air kerma outside the apron:
| (6) |
where,
UA and OA refer to “under apron and “outside apron”, respectively.
Finally, there may have been occasions when a badge was worn under the apron, but an estimate of the personal dose equivalent outside of the apron is desired. In that case, it can be estimated:
| (7) |
There is no single well-defined measure of the protective effectiveness of lead aprons. Consequently, the degree of protection afforded by aprons is often expressed in simple approximate terms, e.g., the reduction in exposure or dose rate to air, though, often, the photon energy or kV is not specified. In this work, the transmission factor is defined as the ratio of air kerma under an apron to that outside the apron (eqn. 6) for a single exposure and for each of the 12 combinations of tube potential (kV) and filtration presented in Table 1. For each combination of kV and filtration, the TFs were estimated by calculating the reduction of total air kerma for the x-ray spectrum after passing through aprons of both 0.25 and 0.5 mm thick Pb apron. For these calculations, the spectrum was defined by the fluence of photons in 0.5 keV increments (normalized to 1 mA.s), from about 10 keV (the minimum energy needed to penetrate the inherent filtration of the x-ray tube) to the maximum potential specified. Neither the air kerma under or over the apron in eqn. 6 includes backscatter, but is expressed as free-in-air, since backscatter is already included in the definition of Hp(d).
In eqns. (1) through (4) and (7), Hp(d) refers to a measured value, and [Ka X−1], the ratio of air kerma to exposure is a constant (ICRU 1992, 1998). The other factors needed for dose calculations (Hp Ka−1 and DT Ka−1) must be derived from radiation transport calculations, e.g., the quantities reported in ICRP Report 74 (1997). Given an understanding, or a set of assumptions, about the energy distribution and the irradiation geometry, the dose coefficients presented in ICRP 74 (1997) can be integrated, as shown in eqns. 8 and 9, over the energy distributions specified in Table 1 to derive the DCCs (mGy mGy−1 for eqn. 8, mGy mSv−1 for eqn. 9) useful for dose reconstruction to medical radiologic personnel:
| (8) |
| (9) |
where,
is the tissue (organ) dose (mGy) per unit air kerma (mGy) and is a function of photon energy, E (keV),
ϕ(E) is the photon fluence (# photons per cm2) and is a function of photon energy, E (keV),
S(E) is the energy distribution (# photons per mA.s.mm2) per keV) and is a function of photon energy, E (keV),
is the air kerma (mGy) per unit fluence and is a function of photon energy, E (keV),
and
is the personal dose equivalent (mSv) per unit air kerma (mGy) and is a function of photon energy, E (keV).
Input data
Here, the various input data required for eqns. 1 through 9 are discussed in the context of (i) conducting radiographic and fluoroscopic procedures, and (ii) conducting procedures involving radioisotopes.
X-ray energy distributions
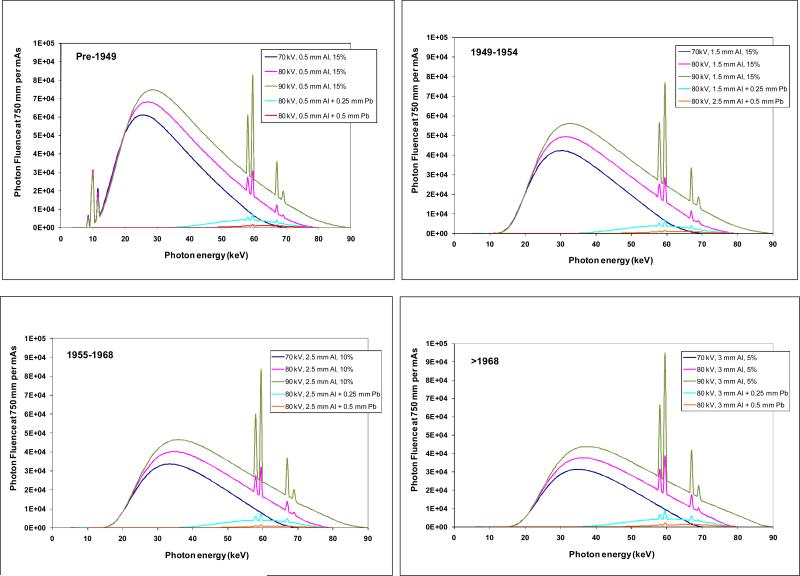
X-ray energy fluence spectra for the assumptions of Table 1 are shown in Fig. 1. The data used in these figures provide S(E) in eqns. (8) and (9). Those data, derived from IPEM (1997), clearly show the changes resulting from increased filtration in later years. Because the component of low energy photons are increasingly diminished by additional filtration, the average energy increased over time for the same tube potential (Table 1).
Fig. 1.
X-ray energy fluence spectra assumed for estimating organ doses from conducting radiography and fluoroscopy examinations in four time-periods: pre-1949 (top left), 1949-1954 (top right), 1955-1968 (bottom left), after 1968 (bottom right). The fluence spectra transmitted through a filter equal to the thickness of protective aprons is also shown (turquoise line is 0.25 mm Pb, red line is 0.5 mm Pb). Spectral data are from IPEM (1997).
Input radiation transport data
In this work, the energy-dependent functions to be integrated in eqns. (3) and (4) were derived by fitting values derived from radiation transport calculations for a variety of tissues and organs as reported in ICRP Report 74 (1997). Both the sources of the data, the type of functions fit, and the fitted parameter values, determined by regression, are presented in the Appendix. All regressions had coefficient of determination (R2) values greater than 0.995. It is worthwhile to note here that the values reported in ICRP Report 74 were derived primarily from radiation transport calculations using the Adam and Eva mathematical anthropometric phantoms (see Table 4 of ICRP Report 74). While many newer phantoms have been developed since the publication of ICRP Report 74, the use of the ICRP 74 data provide a single consistent set of energy-dependent DCCs that are accurate enough for most historic dose reconstructions which almost always have many sources of possible errors and uncertainty. The single exception here to using only ICRP Report 74 data is for the estimation of the dose to red bone marrow which is discussed in a later section.
Table 4.
Derived values of Hp(10) per Ka and Hp(0.07) per Ka with badge under 0.25 mm Pb apron.
| Tube potential (kV)a | Multiplier |
|||
|---|---|---|---|---|
| <1949 | 1949-1954 | 1955-1968 | >1968 | |
| All organs but skin: Hp(10) per Ka | ||||
| 70 | 1.75 | 1.75 | 1.77 | 1.78 |
| 80 | 1.81 | 1.82 | 1.83 | 1.84 |
| 90 | 1.85 | 1.85 | 1.86 | 1.86 |
|
Skin: Hp(0.07) per Ka | ||||
| 70 | 1.62 | 1.63 | 1.63 | 1.64 |
| 80 | 1.66 | 1.67 | 1.67 | 1.68 |
| 90 | 1.68 | 1.69 | 1.69 | 1.69 |
values within single time-periods are considered as equally probable
DCCs for skin
The DT per Ka value for skin exposed in AP geometry was assumed to equal twice the value calculated directly from ICRP 74 data since the ICRP factors are derived by averaging the absorbed energy over the entire skin surface, regardless of the actual irradiation geometry. As noted earlier, exposure of technologists is assumed to occur almost exclusively from the anterior side of the body. Based on simulations of the ADAM and EVA phantoms used for the ICRP Report 74 calculations, increasing the DCC for AP exposure by two-fold may slightly overestimate the correct value, e.g., 18% at 40 keV (the approximate average energy assumed in Table 1)3. However, the DCCs for skin derived here are much closer to the true values for that fraction of skin actually exposed than would be estimated using the ICRP 74 values directly.
In this context, the dose to the anterior portion of the skin is estimated since exposure of skin of medical personnel generally takes place when they are facing the source of x radiation. Some skin dose on the side of the body facing away from the source of radiation would result from radiation transmitted through the body, though it is almost always extremely small compared to the anterior skin dose. Very small doses to the posterior skin might also be received from radiation scattered in the examination room.
Methods for DCCs for red bone marrow
In this paper, nominal values of the DCC for RBM are presented. Those values pertain to the same ADAM and EVA phantoms used for radiation transport calculations in ICRP Report 74. As might be expected, however, radiation transport calculations for phantoms with significantly different anthropometric characteristics would yield different DCCs, particularly for RBM. Here, a strategy is described to individualize values of the DCC for RBM, i.e., to modify the DT Ka −1 values for red bone marrow, based on an individual's body mass index (BMI), where BMI (kg m−2) is defined as the quotient of weight (kg) to height2 (m2).
The strategy described here to adjust the RBM DT Ka−1 values for variations of BMI is based on an analysis presented in NCRP Report 158 (2007) where an empirical relationship for the DT Ka−1 coefficients for RBM was derived for 60 kV x rays and from calculations on 12 phantoms, each with their own unique BMI value. Results of a linear regression of the RBM DT Ka−1 values (at 60 kV) as a function of BMI was of the form (NCRP 2007):
| (10) |
where,
y = estimated DT Ka−1 with units of (mGy to RBM) (mGy to air)−1
m is the slope with units of (mGy to RBM) (mGy to air)−1 per unit of BMI,
x is an empirical value of BMI (kg m−2), and
b is the y-intercept with the same units as for DT Ka−1
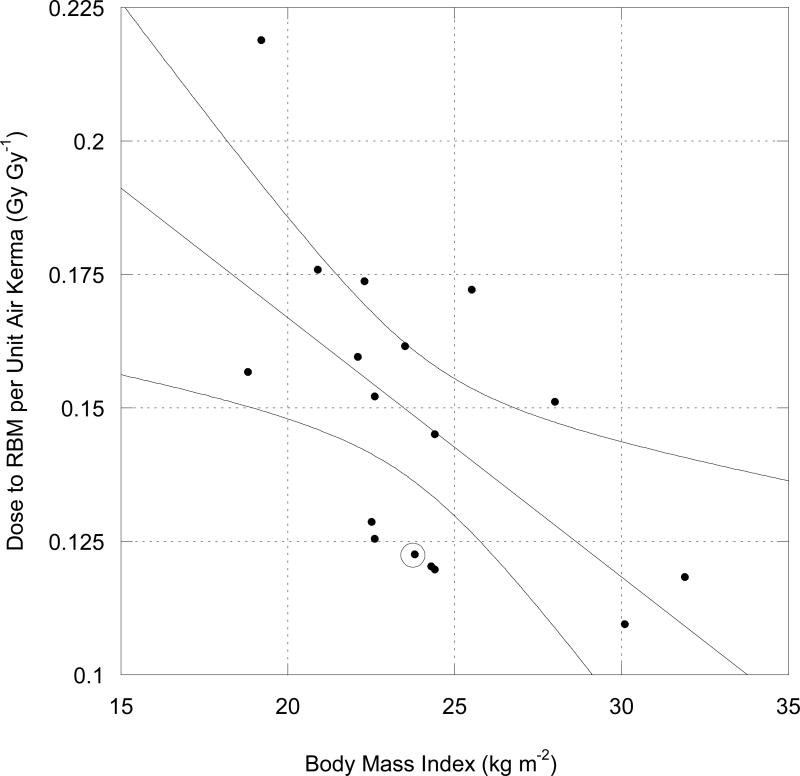
For a 60 kV well-filtered spectrum (average photon energy of about 37 keV), the NCRP (2007) found a rate of change (slope of linear relationship) of about −5 mGy to RBM per mGy to air per unit of BMI (Fig. 2). Additional analysis by the NCRP (unpublished results) at 90 kV (with average photon energy of about 47 keV) and 120 kV (average photon energy of 56 keV) gave slopes of −7.4 and −9.0, respectively. Moreover, there was a highly significant linear relation between the slope of the DT Ka−1 relationship with BMI and average incident photon energy. While tube potentials of interest in this study were limited to 70, 80, and 90 kV, average photon energies of the x-ray spectra varied from 32 to 47 keV (Table 1) depending on filtration. A set of linear functions between the RBM DT Ka−1 values and BMI were derived for each average photon energy given in Table 1 by linearly interpolating the results of the analysis of the 60, 90, and 120 kV data sets. One qualification is worth noting: the linear form of eqn. 10 was selected for purposes of simplicity only, and has no obvious theoretical basis; a decreasing exponential relationship fit equally well.
Fig. 2.
DT per Ka for RBM at 60 kV (tube potential) as a function of BMI with AP irradiation geometry. Circled data point represents value derived from ICRP (1997). Curved lines represent 95% confidence interval on regression line. Figure used with permission of National Council on Radiation Protection and Measurements.
DCCs for medical isotope procedures
The derivation of DCCs for estimating doses from conducting isotope procedures, like the situation for radiography, requires some assumptions or knowledge about exposure conditions. The most important variables are, as usual, irradiation geometry and energy. Here again, it is assumed that the most common exposure geometry for medical personnel is anterior to posterior and the DCCs derived in this work are exclusively for that geometry. As important is an understanding of the isotopes used in different decades, their relative frequency of use, and their emission energies. In this work, DCCs are presented for some commonly used isotopes that have photon emissions over a range of energies from about 0.1 MeV to over 0.7 Mev. These include 201Tl (0.1 MeV), 99mTc (0.14 MeV), 131I (0.36 MeV), PET isotopes (0.511 MeV) and 226Ra (effective energy of 0.74 MeV), an isotope used in nuclear medicine therapy in decades before the 1960s. This set of isotopes covers the range of energies typical of most isotopes used in nuclear medicine.
RESULTS AND DISCUSSION
Radiography and fluoroscopy
The bremsstrahlung x-ray energy distributions described in Table 1 were assumed to represent the energy distributions commonly used in radiography and fluoroscopy over the decades noted. Values of the derived multiplier to convert from exposure (R) to Hp(10) or to Hp(0.07) (rem) for those energy distributions are presented in Table 2. As can be noted, for many x-ray energy distributions, the conversion is near to unity and illustrates the basis for the rule-of-thumb used for many years that a “roentgen equals a rad.” However, for x-ray distributions with little filtration, i.e., that have a considerable low-energy component, the conversion is considerably less than unity such that one rem (dose equivalent) is less than one roentgen free-in air. For moderately well filtered x rays, the conversion is close to unity.
Table 2.
Multiplier to convert exposure (roentgen, R) to personal dose equivalent [Hp(10) or Hp(0.07), rem].
| Tube potential (kV)a | Multiplier |
|||
|---|---|---|---|---|
| <1949 | 1949-1954 | 1955-1968 | >1968-1984b | |
| All organs but skin | ||||
| 70 | 0.646 | 0.918 | 1.04 | 1.09 |
| 80 | 0.716 | 0.983 | 1.10 | 1.15 |
| 90 | 0.783 | 1.04 | 1.16 | 1.21 |
|
Skin | ||||
| 70 | 0.986 | 1.08 | 1.13 | 1.16 |
| 80 | 1.02 | 1.11 | 1.17 | 1.19 |
| 90 | 1.04 | 1.14 | 1.20 | 1.22 |
Values within single time-periods are considered as equally probable
Table entries would apply, in theory, for times beyond 1984. In this work, however, it is assumed that exposure (R) was not used for personnel monitoring after 1984.
Derived values of Hp(10) per Ka and Hp(0.07) per Ka, for the case when no protective apron is worn, are presented in Table 3 separately for all organs except skin, and for skin separately. These calculations illustrate that a significant portion of the difference in Hp(10) or Hp(0.07) compared to Ka is the inclusion of back-scatter. Backscatter factors for x rays with the range discussed here are typically 1.3 to 1.5 (Petoussi-Hens et al. 1998, ICRU 2005). As is evident from entries in the table, for most moderately filtered x-ray distributions, the value of Hp(10) is 30% to 40% greater than the air kerma.
Table 3.
Derived values of Hp(10) per Ka and Hp(0.07) per Ka when no protective apron is used.
| Tube potential (kV)a | Multiplier |
|||
|---|---|---|---|---|
| <1949 | 1949-1954 | 1955-1968 | >1968 | |
| Hp(10) per Ka (all organs but skin) | ||||
| 70 | 0.744 | 1.06 | 1.19 | 1.25 |
| 80 | 0.824 | 1.13 | 1.27 | 1.33 |
| 90 | 0.901 | 1.20 | 1.33 | 1.39 |
|
Skin: Hp(0.07) per Ka (skin) | ||||
| 70 | 1.14 | 1.24 | 1.30 | 1.33 |
| 80 | 1.17 | 1.28 | 1.34 | 1.37 |
| 90 | 1.20 | 1.32 | 1.38 | 1.41 |
values within single time-periods are considered as equally probable
In a parallel fashion to Table 3, Tables 4 and 5 present derived values of Hp(10) per Ka and Hp(0.07) per Ka for use with eqn. 4. These values pertain to the air kerma that would be present beneath either a 0.25 mm Pb protective apron or a 0.5 mm Pb apron. Those values can be computed from the TF factor derived via eqn. 6 and the measured Ka value outside the apron. There is little difference in the Hp(10) per Ka values under the two different apron thicknesses because the low-energy component is filtered out nearly completely by the thinner apron.
Table 5.
Values of Hp(10) per Ka and Hp(0.07) per Ka with badge under 0.5 mm Pb apron.
| Tube potential (kV)a | Multiplier |
|||
|---|---|---|---|---|
| <1949 | 1949-1954 | 1955-1968 | >1968 | |
| All organs but skin: Hp(10) per Ka | ||||
| 70 | 1.84 | 1.84 | 1.85 | 1.86 |
| 80 | 1.89 | 1.89 | 1.89 | 1.90 |
| 90 | 1.90 | 1.90 | 1.90 | 1.91 |
|
Skin: Hp(0.07) per Ka | ||||
| 70 | 1.68 | 1.68 | 1.69 | 1.69 |
| 80 | 1.71 | 1.71 | 1.71 | 1.71 |
| 90 | 1.72 | 1.72 | 1.72 | 1.72 |
values within single time-periods are considered as equally probable
Apron transmission factors, as defined by eqn. 6, were computed and are presented in Table 6. For comparison, some literature states that the x-ray intensity and exposure rate beneath protective aprons are decreased by about 80%, that is, they assume a 20% transmission of x-ray intensity or exposure rate (see McGuire et al. 1983). Other literature gives more realistic values of apron transmission and they agree well with the estimates made here. For example, attenuation by aprons based on reported reductions in exposure rate for a tube potential of 70 kV (Christodoulou et al. 2003, Murphy et al. 1993, Servomaa and Karppinen 2001, Yaffe and Mawdsly 1991) are in good agreement with the estimates reported here. For example, those references suggest that the transmission through a 0.25 and 0.5 mm Pb apron is about 7% and 1%, respectively. The values for the transmission factor calculated here are in excellent agreement with values from the literature that presumably assume moderately heavy filtration as is commonplace today, though such comparisons can only be approximate since the spectral energy distributions used in the literature are not usually reported. Estimated TFs in this work range between 3% and 5.3% for 0.25 mm Pb and between 0.5% and 1.2% for 0.5 mm Pb (Table 6). Transmission factors, tailored to specific x-ray energy distributions are rarely if ever reported and may be unique to this work. For the purposes of dose reconstruction for epidemiologic studies, these values potentially add realism to the calculations if it can be reliably determined that the incident spectra are appropriate to the actual conditions.
Table 6.
Transmission Factors for protective lead aprons in percent (%) transmitted air kerma based on x-ray energy distributions specified by time period in Table 1. Average photon energies (keV) for incident spectra are shown in parentheses of the left-most column while the average photon energies after passing through a lead apron are shown in parentheses in columns 2 through 5.
| Tube potentiala in kV (mean photon energy, keV) | <1949 | 1949-1954 | 1955-1968 | >1968 |
|---|---|---|---|---|
| 0.25 mm Pb | ||||
| 70 (32.1) | 0.70 (52.2) | 1.5 (52.4) | 2.3 (53.1) | 2.9 (53.9) |
| 80 (35.5) | 1.4 (57.2) | 2.8 (57.4) | 4.1 (58.2) | 5.1 (59.1) |
| 90 (38.8) | 2.4 (61.5) | 4.5 (61.7) | 6.4 (62.5) | 7.6 (63.4) |
|
0.5 mm Pb |
||||
| 70 (32.1) | 0.090 (56.5) | 0.20 (56.5) | 0.33 (57.0) | 0.44 (57.8) |
| 80 (35.5) | 0.27 (62.0) | 0.55 (62.1) | 0.87 (62.7) | 1.1 (63.5) |
| 90 (38.8) | 0.62 (66.7) | 1.2 (66.8) | 1.7 (67.6) | 2.2 (68.5) |
values within single time-periods are considered as equally probable
Table 7 presents the results of calculations of DT Ka−1 factors for the tissues and organs considered. Values are presented for three cases: no protective apron, use of a 0.25 mm thick apron, and use of a 0.5 mm thick Pb apron. It is of interest to note, that while aprons are highly efficient at reducing the transmitted air kerma, the Dt per Ka factors increase with the increased thickness, i.e., the factors increase with the added filtration provided by the aprons. This finding is expected on theoretical grounds since the distributions of photon energies are “hardened” or weighted towards a higher mean energy after passing through the lead apron. Average energies of the transmitted x rays are 35% to 75% greater than for the incident x-ray distributions as indicated in Table 6.
Table 7.
Calculated Dose Conversion Coefficients (DT per Ka)a for 11 organs at three potentials (kV peak) in four time periods (see Table 1 for defining parameters) without protective lead aprons and for two thicknesses of lead aprons.
| Organ or tissue | kV peak | No Apron |
0.25 mm Pb Apron |
0.5 mm Pb Apron |
|||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| <1949 | 1949-1954 | 1955-1968 | >1968 | <1949 | 1949-1954 | 1955-1968 | >1968 | <1949 | 1949-1954 | 1955-1968 | >1968 | ||
| RBMb | 70 | 0.062 | 0.109 | 0.145 | 0.165 | 0.418 | 0.421 | 0.435 | 0.450 | 0.503 | 0.505 | 0.514 | 0.526 |
| 80 | 0.085 | 0.141 | 0.184 | 0.208 | 0.498 | 0.502 | 0.516 | 0.530 | 0.585 | 0.586 | 0.596 | 0.606 | |
| 90 | 0.110 | 0.174 | 0.222 | 0.247 | 0.550 | 0.554 | 0.565 | 0.574 | 0.630 | 0.631 | 0.638 | 0.644 | |
| Skin (front only) | 70 | 1.06 | 1.29 | 1.40 | 1.45 | 1.90 | 1.91 | 1.92 | 1.94 | 2.00 | 2.00 | 2.01 | 2.02 |
| 80 | 1.13 | 1.36 | 1.47 | 1.52 | 1.99 | 1.99 | 2.01 | 2.02 | 2.08 | 2.08 | 2.09 | 2.10 | |
| 90 | 1.19 | 1.42 | 1.53 | 1.58 | 2.04 | 2.04 | 2.05 | 2.06 | 2.12 | 2.12 | 2.12 | 2.13 | |
| Thyroid | 70 | 0.562 | 0.860 | 1.01 | 1.08 | 1.66 | 1.67 | 1.68 | 1.70 | 1.77 | 1.77 | 1.78 | 1.79 |
| 80 | 0.645 | 0.947 | 1.10 | 1.17 | 1.75 | 1.75 | 1.77 | 1.78 | 1.84 | 1.84 | 1.85 | 1.86 | |
| 90 | 0.728 | 1.03 | 1.18 | 1.25 | 1.79 | 1.80 | 1.81 | 1.82 | 1.87 | 1.87 | 1.88 | 1.88 | |
| Breast | 70 | 0.614 | 0.891 | 1.02 | 1.07 | 1.51 | 1.52 | 1.53 | 1.54 | 1.59 | 1.59 | 1.60 | 1.60 |
| 80 | 0.686 | 0.959 | 1.09 | 1.14 | 1.57 | 1.57 | 1.58 | 1.59 | 1.63 | 1.63 | 1.64 | 1.64 | |
| 90 | 0.756 | 1.02 | 1.15 | 1.20 | 1.60 | 1.60 | 1.61 | 1.61 | 1.65 | 1.65 | 1.65 | 1.65 | |
| Ovary | 70 | 0.123 | 0.227 | 0.308 | 0.352 | 0.850 | 0.856 | 0.876 | 0.896 | 0.976 | 0.978 | 0.990 | 1.01 |
| 80 | 0.168 | 0.290 | 0.382 | 0.431 | 0.957 | 0.962 | 0.981 | 0.999 | 1.07 | 1.08 | 1.09 | 1.10 | |
| 90 | 0.216 | 0.351 | 0.450 | 0.499 | 1.02 | 1.03 | 1.04 | 1.05 | 1.12 | 1.13 | 1.13 | 1.14 | |
| Lens of eye | 70 | 0.935 | 1.13 | 1.20 | 1.23 | - | - | - | - | - | - | - | - |
| 80 | 0.979 | 1.17 | 1.23 | 1.26 | - | - | - | - | - | - | - | - | |
| 90 | 1.02 | 1.20 | 1.26 | 1.29 | - | - | - | - | - | - | - | - | |
| Lung | 70 | 0.192 | 0.338 | 0.439 | 0.490 | 1.02 | 1.03 | 1.04 | 1.06 | 1.14 | 1.14 | 1.15 | 1.16 |
| 80 | 0.246 | 0.407 | 0.517 | 0.572 | 1.11 | 1.12 | 1.13 | 1.15 | 1.21 | 1.21 | 1.22 | 1.23 | |
| 90 | 0.302 | 0.473 | 0.587 | 0.641 | 1.17 | 1.17 | 1.18 | 1.19 | 1.25 | 1.25 | 1.26 | 1.26 | |
| Brain | 70 | 0.074 | 0.137 | 0.185 | 0.212 | - | - | - | - | - | - | - | - |
| 80 | 0.102 | 0.176 | 0.232 | 0.262 | - | - | - | - | - | - | - | - | |
| 90 | 0.132 | 0.214 | 0.275 | 0.306 | - | - | - | - | - | - | - | - | |
| Colon | 70 | 0.176 | 0.319 | 0.419 | 0.470 | 1.04 | 1.05 | 1.07 | 1.10 | 1.19 | 1.19 | 1.20 | 1.22 |
| 80 | 0.232 | 0.392 | 0.503 | 0.560 | 1.16 | 1.17 | 1.19 | 1.21 | 1.29 | 1.29 | 1.30 | 1.31 | |
| 90 | 0.291 | 0.464 | 0.580 | 0.637 | 1.23 | 1.23 | 1.25 | 1.26 | 1.34 | 1.34 | 1.35 | 1.35 | |
| Testes | 70 | 0.694 | 1.016 | 1.167 | 1.232 | 1.76 | 1.76 | 1.78 | 1.79 | 1.85 | 1.85 | 1.86 | 1.87 |
| 80 | 0.778 | 1.097 | 1.248 | 1.313 | 1.83 | 1.83 | 1.84 | 1.85 | 1.90 | 1.90 | 1.91 | 1.91 | |
| 90 | 0.860 | 1.171 | 1.318 | 1.380 | 1.86 | 1.87 | 1.87 | 1.88 | 1.92 | 1.92 | 1.93 | 1.93 | |
| Heart | 70 | 0.214 | 0.378 | 0.493 | 0.552 | 1.31 | 1.32 | 1.32 | 1.33 | 1.44 | 1.44 | 1.44 | 1.44 |
| 80 | 0.276 | 0.459 | 0.585 | 0.648 | 1.39 | 1.39 | 1.40 | 1.40 | 1.48 | 1.48 | 1.48 | 1.48 | |
| 90 | 0.341 | 0.536 | 0.668 | 0.731 | 1.42 | 1.43 | 1.43 | 1.43 | 1.48 | 1.48 | 1.48 | 1.48 | |
Ka refers to air kerma directly above personnel monitoring device in the absence of a protective apron, but underneath the apron when the protective device is worn. Ka under a protective apron is estimated from Ka outside the apron and the TF (eq. 5 and Table 6).
Nominal values for a phantom of BMI equal to 23.6 kg m−2 based directly on mono-energetic dose coefficients from ICRP (1977) and air kerma weighting methods as described in the text.
Included in Table 7 are the estimated DCCs for RBM as derived from air kerma weighting the mono-energetic values of ICRP Report 74 (1997). As described earlier, however, an analysis of RBM DCCs from phantoms with varying BMI (Table 8) provided a means for adjusting RBM DT Ka−1 values to individual subjects whose morphological characteristics deviate significantly from the Adam and Eva phantoms. Table 9 presents the parameters of eqn. 10 for estimating DT Ka−1 for RBM for all the spectral conditions described in Table 1, while Table 10 presents data on the fraction of the total body red bone marrow shielded by lead aprons and the fraction that is not shielded.
Table 8.
Phantoms considered in RBM analysis of the RBM DCC (see Fig. 2), BMI of each, and literature references.
| Phantom Name | BMI of phantom (kg m−2) | References |
|---|---|---|
| IRENE | 19.2 | Petoussi-Henss et al. (2003); Zankl et al. (2002); Fill et al. (2004) |
| VOXELMAN | 22.1 | Zubal et al. (1994) |
| GOLEM | 22.3 | Zankl et al. (2001, 2002) |
| FAX | 22.5 | Kramer et al. (2004) |
| EVA | 23.1 | Kramer et al. (1982) |
| ICRP | 23.6 | ICRP (1996) |
| MAX | 24.3 | Kramer et al. (2003) |
| ADAM | 24.4 | Kramer et al. (1982) |
| DONNA | 25.5 | Petoussi-Henss et al. (2003); Zankl et al. (2002); Fill et al. (2004) |
| HELGA | 28.0 | Petoussi-Henss et al. (2003); Zankl et al. (2002); Fill et al. (2004) |
| VIP-MAN | 30.1 | Xu et al. (2000) |
| VISIBLE HUMAN | 31.9 | Zankl et al. (2002) |
Table 9.
Estimates of slope and y-intercept for predictive equations of DT Ka−1 for RBM as a function of BMI (eq. 10).
| Tube potential (kV) | Apron | Parameter estimated | Time Period |
|||
|---|---|---|---|---|---|---|
| <1949 | 1949-1954 | 1955-1968 | >1968 | |||
| 70 | none | Slopea | −0.00398 | −0.00480 | −0.00533 | −0.00565 |
| y-interceptb | 0.1674 | 0.2426 | 0.2978 | 0.3290 | ||
| 80 | none | Slope | −0.00470 | −0.00550 | −0.00609 | −0.00640 |
| y-intercept | 0.2116 | 0.2970 | 0.3620 | 0.3980 | ||
| 90 | none | Slope | −0.00539 | −0.00619 | −0.00680 | −0.00714 |
| y-intercept | 0.2576 | 0.3526 | 0.4240 | 0.4617 | ||
| 70 | 0.25 mm Pb | Slope | −0.00821 | −0.00825 | −0.00840 | −0.00857 |
| y-intercept | 0.6904 | 0.6950 | 0.7151 | 0.7369 | ||
| 80 | 0.25 mm Pb | Slope | −0.00926 | −0.00931 | −0.00947 | −0.00966 |
| y-intercept | 0.8103 | 0.8161 | 0.8367 | 0.8578 | ||
| 90 | 0.25 mm Pb | Slope | −0.01017 | −0.01021 | −0.01038 | −0.01057 |
| y-intercept | 0.8935 | 0.8992 | 0.9163 | 0.9314 | ||
| 70 | 0.5 mm Pb | Slope | −0.00912 | −0.00912 | −0.00922 | −0.00939 |
| y-intercept | 0.8128 | 0.8152 | 0.8284 | 0.8466 | ||
| 80 | 0.5 mm Pb | Slope | −0.01027 | −0.01029 | −0.01042 | −0.01059 |
| y-intercept | 0.9376 | 0.9393 | 0.9541 | 0.9700 | ||
| 90 | 0.5 mm Pb | Slope | −0.01126 | −0.01128 | −0.01145 | −0.01164 |
| y-intercept | 1.0144 | 1.0161 | 1.0283 | 1.0399 | ||
units of (mGy to RBM) (mGy to air)−1 per unit of BMI
units of (mGy to RBM) (mGy to air)−1
Table 10.
Estimates of proportion of red bone marrow (RBM) unshielded by protective lead aprons designed prior to 1960 and after 1960.
| Portion of skeleton | RBM, % of total (Cristy 1981): average of data for 20 and 40 y ages | RBM (%) unshielded assuming pre-1960 apron designs | RBM (%) unshielded assuming post-1960 apron designs |
|---|---|---|---|
| Cranium | 7.65 | 7.7 | 7.7 |
| Mandible | 0.8 | 0.8 | 0.8 |
| Cervical vertebrae | 3.8 | 3.7 | 3.7 |
| Scapulae | 2.85 | 0 | 0 |
| Clavicles | 0.8 | ~0.4 | ~0 |
| Sternum | 3 | 0 | 0 |
| Ribs | 15.6 | 0 | 0 |
| Thoracic vertebrae | 15.7 | ~5.2 (4 of 12 vertebrae unshielded) | ~3.9 (3 of 12 vertebrae unshielded) |
| Lumbar vertebrae | 12 | 0 | 0 |
| Humeri, upper-half | 2.4 | 2.4 | ~1.2 |
| SUM | ~20 | ~17 | |
Based on the distribution of red bone marrow in the adult human (Cristy 1981) and the design of lead aprons in the U.S., the fraction of the total body red bone marrow not shielded by an apron appears to be 15% to 20%. The principle parts of the skeleton with unshielded RBM would be the cranium and mandible (about 8.5% of the total RBM), the cervical vertebrae (about 4%), the top 4 or 5 thoracic vertebrae (about 4 to 5% of the total RBM) and part of the upper half of the humeri (2.4% or less). Through on an extensive review of advertisements of lead aprons in an historical collection of factory sales catalogs housed at the National Library of Medicine and of advertisements over many decades in published journals (e.g., Am J Roentgenol, The X-Ray Technician, Radiologic Technology), the design of lead aprons through the 1950s appear to have been characterized by a protective frontal shield held below the fourth thoracic vertebrae by non-protective thin straps hung over the shoulders. After about 1960, lead aprons appear to have been designed to give greater protection to the upper thoracic vertebrae, the clavicle, and the humeri head (Fig. 3). This change in design, suggests a modest change in the proportion of the total body RBM that is unshielded, from about 20% prior to 1960 to about 17% post-1960 (Table 10). These fractions are applicable to eqn. (5).
Fig. 3.
Comparison of protective apron designs. Left panel: pre-1960 design (photo from catalog, X-Ray Supplies and Accessories, Picker X-Ray Corp., New York City, NY, circa 1940). Right panel: present day design, characteristic of post-1960 styles (photo courtesy of Techno-Aide, Inc., Nashville, TN).
While adjustments of the DCCs for other deep-seated organs could also be made on the basis of variation in BMI, the correction would be less than for RBM because other tissues are at shallower depths when considering AP irradiation geometry. For that reason, no other adjustments to DCCs have been made at this time.
There are several assumptions implicit in using the factors presented here for retrospective dose reconstruction. These include: (1) radiation was received by medical personnel almost exclusively on the anterior surface of the body (i.e., AP irradiation geometry), (2) the scattered (incident) x-ray energy distributions were not significantly different from the generated x-ray energy distributions, and (3) the scattered radiation field was relatively uniform from, at least, the lower boundary of the pelvis to the top of the head. While there may be departures from these assumptions in some cases, these appear reasonable for a variety of reasons discussed below.
The assumption that most exposure is received on the anterior body surface follows from the simple requirement that the medical practitioner usually must be able to see the patient during the examination and, hence, likely faced the patient and the source of radiation. The assumption that the scattered x-ray energy distributions are not significantly different from the emitted x-ray energy distributions follows from numerous investigations on scattering of medical x rays (Trout and Kelley 1972; Marshall et al. 1996; Balter 2001; McVey and Weatherburn 2004). The assumption about the uniformity of the scattered radiation field is clearly a simplification because radiographic examination rooms can have widely varying geometry, orientation, and scattering surfaces. This assumption is probably the most difficult to generalize, however, assuming that the field is relatively uniform from, at least, the height of the pelvis, to the head is supported by some measurements (McVey and Weatherburn 2004). While there may be departures from these assumptions in practice, assumptions are always required for retrospective dose reconstruction because of limitations or lack of completeness of necessary data (Simon et al. 2006, 2010).
Radioisotope procedures
The factors needed for estimating doses from conducting radioisotope procedures (8ns. 1 through 8), while simple to derive from published data (ICRP 1997), may, in practice, require special considerations for use in historical dose reconstruction. In particular, in decades past, before the present-day specialization of medical technologists, many practitioners who were involved in the use of radiation in medicine may have received occupational exposure from conducting a range of different types of procedures involving varying (but unknown) combinations of radiography, fluoroscopy, and nuclear medicine. In such cases, the reading from a single monitoring badge would not be informative about the proportion of exposure received from lower energy radiations (typical of radiography) compared to the proportion of exposure received from higher energy radiations (typical of isotopes). Uncertainty about the energy of the radiation would result in considerable uncertainty about which DCC to use to estimate organ doses. Hence, the conversion factors presented here for isotope procedures (Table 11) are most useful for estimating organ doses when it can be reliably assumed that the reading of the personnel monitoring device applied exclusively (or nearly so) to conducting isotope procedures.
Table 11.
Factors needed for reconstruction of occupational doses from conducting medical procedures with some historically- and presently-used radioisotopes. Values derived from ICRP (1997).
| 201Tl (0.104 MeV) | 99mTc (0.14 MeV) | 131I (0.364 MeV) | Uncertain combination of 210Tl, 99mTc, 131I: central value (range) | PET Isotopes (0.511 MeV) | 226Ra (0.74 MeVa) | |
|---|---|---|---|---|---|---|
| Hp(10) per Ka | 1.79 | 1.64 | 1.32 | 1.58 (1.32 – 1.79) | 1.25 | 1.20 |
| Hp(0.07) per Ka | 1.66 | 1.54 | 1.29 | 1.50 (1.29 – 1.66) | 1.24 | 1.20 |
| Dt/Ka | ||||||
| RBM | 0.822 | 0.807 | 0.751 | 0.793 (0.751 - 0.822) | 0.757 | 0.766 |
| Skin (anterior only) | 2.18 | 2.12 | 1.94 | 2.11 (1.93 - 2.22) | 1.94 | 1.94 |
| Thyroid | 1.85 | 1.71 | 1.32 | 1.69 (1.29 – 1.94) | 1.32 | 1.29 |
| Breast | 1.58 | 1.48 | 1.18 | 1.47 (1.15 - 1.67) | 1.18 | 1.15 |
| Ovary | 1.27 | 1.20 | 0.943 | 1.17 (0.929 - 1.26) | 0.946 | 0.929 |
| Lens of eye | 1.52 | 1.45 | 1.20 | 1.43 (1.16 - 1.55) | 1.20 | 1.16 |
| Lung | 1.28 | 1.19 | 1.01 | 1.19 (1.00 - 1.33) | 1.01 | 1.00 |
| Brain | 0.826 | 0.811 | 0.793 | 0.808 (0.793 - 0.826) | 0.801 | 0.817 |
| Colon | 1.40 | 1.31 | 1.04 | 1.29 (1.03 - 1.45) | 1.05 | 1.03 |
| Testes | 1.83 | 1.68 | 1.26 | 1.66 (1.23 - 1.95) | 1.26 | 1.23 |
| Heart | 1.50 | 1.37 | 1.12 | 1.37 (1.02 - 1.57) | 1.07 | 1.02 |
| TF (0.25 mm Pb) | 0.39 | 0.57 | 0.90 | 0.62 (0.39 - 0.90) | 0.94 | 0.97 |
| TF (0.5 mm Pb) | 0.15 | 0.32 | 0.80 | 0.43 (0.15 - 0.80) | 0.89 | 0.94 |
effective energy for 226Ra in equilibrium with progeny
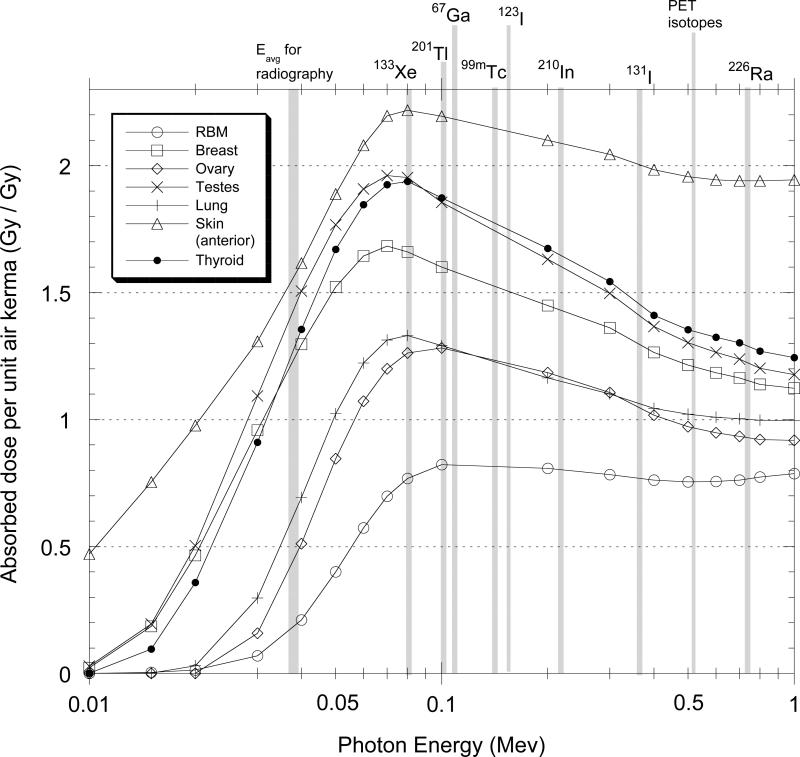
An additional difficulty likely to be encountered in reconstructing doses from the use of medical radioisotopes is uncertainty on which isotopes were used and their relative frequency of use. Given reliable frequency of use data, it would be possible to weight the appropriate DCCs for those isotopes. This source of uncertainty, however, is not as great as might be presumed because the relative change of the DCCs with energy is modest at energies from 0.1 to 2 MeV. Here it is shown (Fig. 3) that uncertainty about the isotopes used has little relevance to estimating dose to red bone marrow or other deep-seat organs because the change with energy is inconsequentially small. For shallower organs, the uncertainty in the isotopes used might translate to a relative error in dose of ± 25% or less.
An additional important assumption is that the most common irradiation geometry was anterior to posterior and that the phantoms used in the radiation transport calculations (ICRP 1997) were realistic to a sufficient degree for the intended purposes, keeping in mind that there are numerous sources of uncertainty in retrospective dose estimation.
Noteworthy in these data are the very high TFs for energies typical of medical radioisotopes. The transmitted air kerma varies from about 39% at 0.1 Mev with a 0.25 mm Pb apron to 90% or more for PET isotopes, regardless of the apron thickness. The high TFs emphasize the need for protection of medical personnel by the use of lead containers and partial- or whole-body shields.
Uncertainty
The issue uncertainty of ICRP dose coefficients is usually neglected in the context of dose calculations for radiation protection and regulatory compliance since it has been clearly stated that the ICRP coefficients are published as “reference values” with no associated uncertainty (Harrison and Streffer 2007). The issue of uncertainty of dose estimation is important, however, for applications in epidemiology and radiation risk estimation (Simon et al. 2006; Gilbert and Schafer et al. 2006, Harrison and Streffer 2007). The uncertainty of DCCs for external dose estimation was considered in depth in NCRP Report 158 (2007) and, here, the findings of that analysis is used as a basis for estimation of uncertainty. One over-arching finding of NCRP Report 158 was that the uncertainty associated with radiation transport calculations will not capture the entire uncertainty if the true incident spectrum or exposure geometry is not well known.
Assuming that the incident energy distribution and exposure geometry is well characterized, the uncertainty of the conversion from dose equivalent (e.g., Hp(10)) to air kerma may only be a few tens of percent or less (NCRP 2007) while the uncertainty of DT Ka−1 values is almost always greater and reflects differences among phantoms and with the person whose dose is to be estimated. Based on the variation of DT Ka−1 values derived from literature-reported calculations on 12 different phantoms, NCRP Report 158 (2007) reported an uncertainty of DT Ka−1 for 60 and 90 kV tube potential in AP geometry to be a geometric standard deviation (GSD) of 1.11 – 1.21 depending on the organ. For purposes of epidemiologic applications, a GSD of 1.2 would be reasonable for all organs.
The uncertainty of the DT Ka−1 values for RBM needs to be modified, however, when the value is estimated from a functional relationship with BMI as in eqn. 10. As shown in NCRP 158 (2007), the standard error of a predicted value of the DT Ka−1 for RBM for 60 kV x rays is approximately ± 30% (see Table 4.25, NCRP Report 158, 2007). The uncertainty of predicted values can be derived from the appropriate t-value and the SE, and in this context, the SE (expressed on a percentage basis) for the 60 kV relationship can be extended, as an approximation, to all the BMI relationships presented in Table 10.
According to the analysis presented in NCRP Report 158 (2007), the uncertainty of the DCCs for irradiation by radioisotope sources does not vary greatly from the uncertainty of DCCs estimated for medical x rays. Specifically, Table 4.10 of NCRP 158 (2007) suggests the uncertainty of the DT Ka−1 values for AP irradiation geometry is characterized by a GSD of 1.18 at 140 keV (e.g., for 99mTc) and about 1.12 at 0.511 keV (e.g., for positron emitting radioisotopes).
CONCLUDING REMARKS
As discussed here, historical organ absorbed doses for medical radiologic personnel can be estimated in a dose reconstruction study or in a retrospective epidemiologic investigation by making necessary assumptions about the sources of medical exposure such that the irradiation conditions (primarily geometry and energy distribution) as well as the temporal changes of those conditions can be properly accounted for. While the use of the DCCs presented here require certain assumptions, these coefficients will potentially reduce misclassification of radiation dose and reduce uncertainty compared to estimates of organ doses based on generalized assumptions.
Broadly speaking, to reconstruct reliable and unbiased organ doses from diagnostic medical radiation, the DCCs must reflect the true irradiation geometry as well as possible and account for temporal changes in energy distribution (for radiography) or account for the use of radioisotopes. Given an understanding of those factors, DCCs may be derived. In theory, DCCs for bremsstrahlung radiation can be computed directly from radiation transport calculations by using the complete x-ray energy distribution as input. However, because of the number of possible combinations of geometry, tube potential, and filtration used over the decades, few such calculations have been completed and there is no single compendium of DCCs for the range of irradiation conditions. The method presented here, uses published mono-energetic DCCs and the concept of air-kerma weighting to develop DCCs for specific irradiation conditions which, in theory, can be easily modified by changing the weighting according to the fluence spectrum of interest.
Several other useful methodologic strategies are presented here for use in historical dose reconstruction for medical personnel. These include: protective apron transmission factors, each tailored to specified x-ray energy distributions characteristic of time-periods in the 20th century, a more realistic means of estimating bone marrow dose based on the DCC for an individual's BMI, and finally, a means for characterizing uncertainty in estimated doses by multiple estimates of DCCs, based on the assumed likelihood in each time period. Randomized choice of the DCCs, each based on their own probability, is a practical means to characterize uncertainty of doses due to unknowns about the irradiation conditions. The estimation of organ doses from use of medical radioisotopes presents some additional challenges, in particular, when the occupational exposure resulted from a combination of exposures from radiography / fluoroscopy and nuclear medicine. As noted here, however, lack of knowledge about the isotopes used contributes less uncertainty than is often contributed by poor historical monitoring data or other types of poorly assessed, recorded, or missing information.
Fig. 3.
Continuous functions representing reported values (ICRP 1997) of absorbed dose per unit air kerma for seven organs and tissues and energies typical of radiography/fluoroscopy and selected radioisotopes commonly used in medical procedures now and in past decades. Factors shown for skin are twice reported values, specific for exposure on one side of the body, as discussed in text.
Table A1.
Parameter values for fitted equations A1 through A4.
| Parameter | Ka per ϕ | Hp(10) per Ka | Hp(0.07) per Ka |
|---|---|---|---|
| a | −1.018 × 100 | −1.21 × 101 | 2.207 × 10−1 |
| b | 7.088 × 100 | 3.35 × 102 | 2.228 × 102 |
| c | −3.408 × 10−1 | 2.63 × 10−1 | 2.970 × 102 |
| d | −1.913 × 10−2 | −3.44 × 103 | −8.051 × 103 |
| e | 8.720 × 10−4 | −2.95 × 10−3 | −1.037 × 104 |
| f | - | 1.25 × 104 | 1.093 × 105 |
| g | - | 1.23 × 10−5 | 1.611 × 105 |
Table A2.
Parameter values for fitted equations A5 through A14 (regression parameter values shown to four significant digits).
| DT/ Ka | ||||||
|---|---|---|---|---|---|---|
| Parameter | RBM | Skin | Thyroid | Breast | Ovary | Lens of eye |
| a | −2.700 × 10−4 | 1.189 × 104 | −2.614 × 100 | −6.788 × 10−1 | −1.719 × 100 | 1.682 × 100 |
| b | −8.407 × 101 | −1.282 × 104 | 1.464 × 102 | 9.034 × 101 | 1.096 × 102 | 4.524 × 100 |
| c | −4.860 × 100 | −3.146 × 103 | 1.246 × 10−2 | −9.890 × 10−3 | −1.592 × 103 | −4.085 × 101 |
| d | 1.110 × 105 | −5.227 × 101 | −1.606 × 103 | −1.056 × 103 | 1.038 × 104 | −1.971 × 10−2 |
| e | 9.718 × 104 | −1.190 × 104 | 6.000 × 10−6 | 8.880 × 10−5 | −2.568 × 104 | 5.500 × 10−5 |
| f | 5.050 × 105 | - | 5.783 × 103 | 3.900 × 103 | −1.719 × 100 | 1.682 × 100 |
| Parameter | Lung | Brain | Colon | Testes | Heart |
|---|---|---|---|---|---|
| a | −7.545 × 10−1 | −1.162 × 100 | −2.865 × 10−2 | −8.840 × 10−1 | −4.952 × 10−1 |
| b | 3.836 × 10−1 | −5.608 × 10−1 | −2.064 × 101 | 1.082 × 102 | 3.700 × 10−1 |
| c | 4.445 × 10−2 | −2.926 × 10−3 | −2.234 × 101 | −1.169 × 10−2 | 4.447 × 10−2 |
| d | - | - | 2.292 × 105 | −1.258 × 103 | - |
| e | - | - | 4.269 × 105 | 1.122 × 10−4 | - |
| f | - | - | 6.296 × 106 | 4.604 × 103 | - |
ACKNOWLEDGEMENTS
The author appreciates the assistance of Stephen M. Seltzer of the National Institute of Standards and Technology (NIST) for review and correction of the method for the air kerma weighting and of Robert Weinstock for discussions on mathematical issues. This research was supported by the Intramural Research Program of the National Cancer Institute, National Institutes of Health.
APPENDIX
The strategy for making the calculations of eqns. 8 and 9 from the spectral data found in IPEM (1997) and the mono-energetic coefficients provided in ICRP 74 (1997) was as follows. The values in the rounded brackets of eqns. 8 and 9 were derived at 0.5 keV intervals by fitting continuous functions to the discrete values in the tables of ICRP Report 74 listed below. The forms of the equations fitted to the ICRP data are presented in eqns. A1 through A9. The integrals of eqns. 8 and 9 were evaluated numerically.
: Table A.1 (ICRP, 1997).
: Table A.24 (ICRP, 1997).
: Table A.25 (ICRP, 1997).
for RBM: Table A.3 (ICRP, 1997),
for skin: Table A.14 (ICRP, 1997),
for thyroid: Table A.16 (ICRP, 1997).
for breast: Table A.5 (ICRP, 1997),
for ovary: Table A.7 (ICRP, 1997),
for lens of eye: Table A.18 (ICRP, 1997),
for lung: Table A.11 (ICRP, 1997),
for brain: derived from same phantoms as used in ICRP (1997), data provided by personal communication.‡
for colon: Table A.6 (ICRP, 1997),
for testes: Table A.8 (ICRP, 1997),
for heart: derived from same phantoms as used in ICRP (1997), data provided by personal communication.‡
The following equations were fit to the discrete energy data in the tables list above, from 0.010 to 0.1 MeV (where E in the following equations has units of MeV):
| (A1) |
| (A2) |
| (A3) |
| (A4) |
| (A5) |
| (A6) |
| (A7) |
| (A8) |
| (A9) |
| (A10) |
| (A11) |
| (A12) |
| (A13) |
| (A14) |
Footnotes
Personal communication from R.C. Yoder, Launder, Inc. 2006.
Personal communication, M. Zankl to S. Simon, December, 2005.
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
REFERENCES
- Balter S. Stray radiation in the cardiac catheterisation laboratory. Radiat. Prot. Dosim. 2001;94:183–188l. doi: 10.1093/oxfordjournals.rpd.a006468. [DOI] [PubMed] [Google Scholar]
- Christodoulou EG, Goodsitt MM, Larson SC, Darner KL, Satti J, Chan HP. Evaluation of the transmitted exposure through lead equivalent aprons used in a radiology department, including the contribution from backscatter. Med Phys. 2003;30(6):1033–1038. doi: 10.1118/1.1573207. [DOI] [PubMed] [Google Scholar]
- Cristy M. Active bone marrow distribution as a function of age in humans. Phys. Med. Biol. 1981;26(3):389–400. doi: 10.1088/0031-9155/26/3/003. [DOI] [PubMed] [Google Scholar]
- Fill UA, Zankl M, Petoussi-Henss N, Siebert M, Regulla D. Adult female voxel models of different stature and photon conversion coefficients for radiation protection. Health Phys. 2004;86(3):253–272. doi: 10.1097/00004032-200403000-00003. [DOI] [PubMed] [Google Scholar]
- Harrison JD, Streffer C. The ICRP protection quantities, equivalent and effective dose: their basis and application. Radiation Protection Dosimetry. 2007;127:12–18. doi: 10.1093/rpd/ncm248. [DOI] [PubMed] [Google Scholar]
- HHS. Rosenstein M. Report 89-8031. Health and Human Services Publication (FDA); 1988. Handbook of selected tissue doses for projections common in diagnostic radiology. [Google Scholar]
- ICRP . Annals of the ICRP 26/3. ICRP Publication 74; 1997. Conversion Coefficients for Use in Radiological Protection Against External Radiation, International Commission on Radiological Protection. [Google Scholar]
- ICRU . ICRU Report No. 57. Oxford University Press; Cary, North Carolina: 1998. Conversion Coefficients for Use in Radiological Protection Against External Radiation, International Commission on Radiation Units and Measurements. [Google Scholar]
- ICRU . ICRU Report No. 47. Oxford University Press; Cary, North Carolina: 1992. Measurement of Dose Equivalents from External Photon and Electron Radiations, International Commission on Radiation Units and Measurements. [Google Scholar]
- ICRU . ICRU Report No. 74. Oxford University Press; Cary, North Carolina: 2005. Patient Dosimetry for X Rays Used in Medical Imaging. International Commission on Radiation Units and Measurements. [Google Scholar]
- ICRU . ICRU Report 51. Oxford University Press; Cary, North Carolina: 1993. Quantities and Units in Radiation Protection Dosimetry. International Commission on Radiation Units and Measurements. [Google Scholar]
- IPEM. Institute of Physics and Engineering in Medicine . Report 78: Catalogue of Diagnostic X Ray Spectra and Other Data (CD-ROM version only) IPEM Publications; York, UK: 1997. [Google Scholar]
- Kramer R, Vieira JW, Khoury HJ, Lima FRA, Fuelle D. All about MAX: a Male Adult voxel phantom for Monte Carlo calculations in radiation protection dosimetry. Phys. Med. Biol. 2003;48:1239–1262. doi: 10.1088/0031-9155/48/10/301. [DOI] [PubMed] [Google Scholar]
- Kramer R, Zankl M, Williams G, Drexler G. GSF-Bericht S-885, Gesellschaft für Strahlen- und Umweltforschung mbH. Munich, Germany: 1982. The calculation of dose from external photon exposure using reference human phantoms and Monte Carlo methods. Part I: the male (ADAM) and female (EVA) adult mathematical phantoms. [Google Scholar]
- Kramer R, Khoury HJ, Vieira JW, Loureiro ECM, Lima VJM, Lima FRA, Hoff G. All about FAX: a Female Adult voxel phantom for Monte Carlo calculations in radiation protection dosimetry. Phys. Med. Biol. 2004;49:5203–5216. doi: 10.1088/0031-9155/49/23/001. [DOI] [PubMed] [Google Scholar]
- Marshall NW, Faulkner K, Warren H. Measured scattered x-ray energy spectra for simulated irradiation geometries in diagnostic radiology. Medical Physics. 1996;23(7):1271–1276. doi: 10.1118/1.597690. [DOI] [PubMed] [Google Scholar]
- McGuire EL, Baker ML, Vandergrift JF. Evaluation of radiation exposures to personnel in fluoroscopic x-ray facilities. Health Physics. 1983;45(5):975–980. doi: 10.1097/00004032-198311000-00003. [DOI] [PubMed] [Google Scholar]
- McVey G, Weatherburn H. A study of scatter in diagnostic X-ray rooms. Br J Radiol. 2004;77:28–38. doi: 10.1259/bjr/93969091. [DOI] [PubMed] [Google Scholar]
- Murphy PH, WU Y, Glaze SA. Attenuation properties of lead composite aprons. Radiology. 1993;186(1):269–272. doi: 10.1148/radiology.186.1.8416577. [DOI] [PubMed] [Google Scholar]
- NCRP. National Council on Radiation Protection and Measurements . NCRP Report No. 158, Uncertainties in the Measurement and Dosimetry of External Radiation. NCRP; Bethesda, MD: 2007. [Google Scholar]
- Petoussi-Henss N, Zankl M, Drexler G, Panzer W, Regulla D. Calculation of backscatter factors for diagnostic radiology using Monte Carlo methods. Phys.Med. Biol. 1998;43:2237–2250. doi: 10.1088/0031-9155/43/8/017. [DOI] [PubMed] [Google Scholar]
- Petoussi-Henss N, Zankl M, Fill U, Regulla D. The GSF family of voxel phantoms. 2003;47:89–106. doi: 10.1088/0031-9155/47/1/307. [DOI] [PubMed] [Google Scholar]
- Rosenstein M. Handbook of Selected Tissue Doses for Projections Common in Diagnostic Radiology. Health and Human Services Publ. FDA 89-8031. 1988 Dec; [Google Scholar]
- Schafer DW, Gilbert ES. Some statistical implications of dose uncertainty in radiation dose-response analysis. Radiation Research. 2006;(1, Part 2):303–312. doi: 10.1667/RR3358.1. [DOI] [PubMed] [Google Scholar]
- Servomaa A, Karppinen J. The dose-area product and assessment of the occupational dose in interventional radiology. Radiat Prot Dosimetry. 2001;96(1-3):235–6. doi: 10.1093/oxfordjournals.rpd.a006590. [DOI] [PubMed] [Google Scholar]
- Shockley V, Kathren R. Occupational Medical Dose. ORAU Team-NIOSH Dose Reconstruction Project. 2004 Document No. ORAU-TKBS-0008-3. [Google Scholar]
- Shockley V, Kathren R, Thomas EM. Reconstruction of doses for occupationally related medical x-ray examinations. Health Physics. 2008;95(1):107–11. doi: 10.1097/01.HP.0000290611.81586.75. [DOI] [PubMed] [Google Scholar]
- Sigurdson AJ, Doody MM, Rao RS, Freedman DM, Alexander BH, Hauptmann M, Mohan AK, Yoshinaga S, Hill DA, Tarone R, Mabuchi K, Ron E, Linet MS. Cancer incidence in the US radiologic technologists health study, 1983-1998. Cancer. 2003;97(12):3080–3089. doi: 10.1002/cncr.11444. [DOI] [PubMed] [Google Scholar]
- Bouville Simon, SL A., Kleinerman R, Ron E. Dosimetry For Epidemiologic Studies: Learning From The Past, Looking To The Future. Radiation Research. 2006;(1, Part 2):313–318. doi: 10.1667/RR3536.1. [DOI] [PubMed] [Google Scholar]
- Simon SL, Weinstock RM, Doody MM, Neton J, Wenzel T, Stewart P, Mohan AK, Yoder RC, Freedman M, Hauptmann M, Bouville A, Cardarelli J, Feng HA, Linet M. Estimating historical radiation doses to a cohort of U.S. radiologic technologists. Radiat Res. 2006;166:174–192. doi: 10.1667/RR3433.1. [DOI] [PubMed] [Google Scholar]
- Trout ED, Kelley JP. Scattered radiation from a tissue-equivalent phantom for x rays from 50 to 200 kVp. Radiology. 1972;104:161–169. doi: 10.1148/104.1.161. [DOI] [PubMed] [Google Scholar]
- USPHS, U.S. Public Health Service. Population Exposure to X-Rays . A report of the Public Health Service. U.S. Government Printing Office; 1964. Pub. No. 1519 1964. [Google Scholar]
- Xu XG, Chao TC, Bozkurt A. VIP-Man: an image-based whole-body adult male model constructed from color photographs of the Visible Human Project for multi-particle Monte Carlo calculations. Health Phys. 2000;78:476–486. doi: 10.1097/00004032-200005000-00003. [DOI] [PubMed] [Google Scholar]
- Yaffe MJ, Mawdsley GE. Composite materials for x-ray protection. Health Physics. 1991;60(5):661–664. doi: 10.1097/00004032-199105000-00004. [DOI] [PubMed] [Google Scholar]
- Zankl M, Wittman A. The adult male voxel model “Golem” segmented from whole-body CT patient data. Radiat. Environ. Biophys. 2001;40:153–162. doi: 10.1007/s004110100094. [DOI] [PubMed] [Google Scholar]
- Zankl M, Petoussi-Henss N, Fill U, Regulla D. Part IV: Organ doses for adults due to idealized external photon exposures,GSF-Report 13/02. GSF National Research Center for Environment and Health; Neuherberg, Germany: 2002. Tomographic anthropomorphic models. [Google Scholar]
- Zubal IG, Harrell CR, Smith EO, Rattner Z. Gindi, G, Hoffer PB. Computerized three-dimensional segmented human anatomy. Med. Phys. 1994;21:299–302. doi: 10.1118/1.597290. [DOI] [PubMed] [Google Scholar]
- Zhang L, Jia D, Chang H, Zhang W, Dai G, Ku M, Zhao Y, Zhang C, Aoyama T, Noriuma T, Sugahara T. A retrospective dosimetry method for occupational dose for Chinese medical diagnostic X-ray workers. Radiat. Prot. Dosim. 1998;77:69–72. [Google Scholar]