Massively parallel nonparametric regression, with an application to developmental brain mapping

Abstract

We propose a penalized spline approach to performing large numbers of parallel non-parametric analyses of either of two types: restricted likelihood ratio tests of a parametric regression model versus a general smooth alternative, and nonparametric regression. Compared with naïvely performing each analysis in turn, our techniques reduce computation time dramatically. Viewing the large collection of scatterplot smooths produced by our methods as functional data, we develop a clustering approach to summarize and visualize these results. Our approach is applicable to ultra-high-dimensional data, particularly data acquired by neuroimaging; we illustrate it with an analysis of developmental trajectories of functional connectivity at each of approximately 70000 brain locations. Supplementary materials, including an appendix and an R package, are available online.

1 Introduction

This paper is concerned with performing large numbers of nonparametric analyses in parallel. More specifically, we are interested in (i) testing a parametric null regression model against a nonparametric alternative and (ii) fitting a nonparametric regression model, for each of tens of thousands of sets of responses, but with a common design matrix.

Our methodology has potential applications in genomics and other disciplines concerned with very high-dimensional data, but the motivation for our work comes from neuroimaging-based studies of brain development. Modern imaging technologies can measure a quantity y of biomedical interest at each of tens of thousands of locations in the human brain; most often these locations are “voxels,” or volume units. When such images are acquired for a sample of individuals of different ages, it is possible to examine how y varies with age at each voxel. It is common practice for neuroscientists to consider polynomial models.

Consider, for example, the application that motivated our work. The data were derived from 193 individuals, age 7–50, who were scanned (cross-sectionally, i.e. one visit per subject) with resting-state functional magnetic resonance imaging (fMRI) in a study reported by Zuo et al. (2010). FMRI records a time series representing brain activity at each voxel; “resting-state” means that the participants are scanned while attending to no stimulus in particular, as opposed to the common use of fMRI to study brain activity in individuals exposed to some stimulus or performing a task. Resting-state functional connectivity studies have recently emerged as a powerful tool for elucidating the brain’s intrinsic functional networks (e.g., Biswal et al., 1995; Fox et al., 2005; Shehzad et al., 2009). For each individual, Zuo et al. (2010) computed “homotopic functional connectivity,” the correlation between the time series for each of 71287 pairs of voxels at corresponding locations in the left and right hemispheres. (To make voxel locations comparable across subjects, all locations are with respect to a standardized space devised at the Montreal Neurological Institute [MNI].) This data set enables us to examine how connectivity for each homotopic pair of voxels varies with age, and the results may contribute to our understanding of brain development.

More precisely, the ith individual’s fMRI scan yields time series ${\mathit{s}}_{i\ell }^L=(s_{i\ell 1}^L,\dots ,s_{i\ell T}^L)$ for the ℓth left-hemisphere voxel, and ${\mathit{s}}_{i\ell }^R=(s_{i\ell 1}^R,\dots ,s_{i\ell T}^R)$ for the symmetrically opposite right-hemisphere voxel (ℓ = 1, …, 71287). The measure of interest for subject i at voxel ℓ (as in (3.1) below) is

$$y_{i\ell }=\frac{1}{2\sqrt{T-c-3}}\log \frac{1+r_{\ell }}{1-r_{\ell }},$$ (1.1)

where r_ℓ is the partial correlation of ${\mathit{s}}_{i\ell }^L$ and ${\mathit{s}}_{i\ell }^R$, adjusting for c nuisance covariates regressed out during fMRI preprocessing. This is the well-known Fisher (1921) transformation of the sample correlation to a random variable that is approximately normal with unit variance. Henceforth, we shall refer to (1.1) as the “connectivity,” and for brevity, we shall speak of “voxels” when referring to homotopic pairs of voxels.

A standard analysis in developmental neuroimaging would fit constant, linear, quadratic and cubic models for each voxel’s mean connectivity as a function of age, as in Fig. 1(b). Using a model selection criterion such as the corrected Akaike information criterion (Sugiura, 1978), one can determine, for each voxel, which of these models best describes how connectivity develops with age. The results can then be mapped as in Fig. 1(a).

Figure 1.

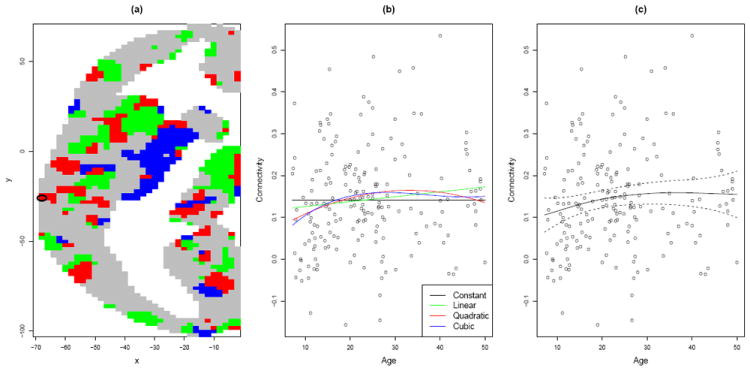
(a) Voxels in an axial slice of the brain—the z = 24 plane in MNI coordinates—are colored grey, green, red, or blue, depending on whether the dependence of homotopic functional connectivity on age is best described by a constant, linear, quadratic or cubic function. (White space represents areas outside the grey matter portion of the brain.) The horizontal and vertical axis labels refer to x- and y-coordinates in MNI space. (b) Fitted polynomial functions for the voxel circled in (a). (c) A penalized spline fit with approximate 95% Bayesian confidence interval.

From a neuroscientific standpoint, at least two major objections can be raised against these polynomial models for age effects. First, Fjell et al. (2010) showed that key features of an estimated trajectory, such as where it attains its peak, can be highly sensitive to the range of ages considered when a polynomial model is used. Second, quantities of interest often exhibit developmental trajectories that may not be well described by polynomial dependence on age, such as marked early change followed a plateau that is essentially maintained for the remainder of the lifespan. A case in point is the voxel that is circled in Fig. 1(a), the data for which are displayed in Fig. 1(b). There is some suggestion of an age-related increase in homotopic connectivity; but it is not obvious which of the polynomial models best captures this trajectory, and accordingly, classification of the voxel according to one of these models may be unreliable and uninformative.

Penalized spline models (e.g., O’Sullivan, 1986; Wood, 2006) can overcome both of these limitations of polynomial models: Fjell et al. (2010) showed them to be very insensitive to the age range of the data, and they have the flexibility to adapt to non-polynomial trajectories (as in Fig. 1(c)). These application-specific considerations, as well as the general statistical benefits of penalized splines (see Green and Silverman, 1994, in particular p. 49), led us to pursue a penalized spline approach to problems (i) and (ii) introduced at the outset of the paper.

The key barrier here is computational. The penalized spline procedures for both testing and regression depend upon finding an optimal smoothing parameter, and whereas fast automatic methods exist for performing this step a single time, repeating it tens of thousands of times would impose a major computational burden.

The principal contribution of this paper is methodology that virtually eliminates this burden. By cutting computation times from hours to minutes for typical data sets, our algorithms make it possible to perform not only a single massively parallel nonparametric analysis, but repeated analyses such as would be required for comparing alternative models, resampling, or simulation studies. Consequently, our methods represent a significant advance in the applicability of nonparametric techniques to ultra-high-dimensional data sets of a type arising in neuroimaging as well as in other biomedical fields.

Our main development begins in Section 2 with a review of the mixed model formulation of penalized smoothing, a crucial prerequisite for the rest of the paper. Sections 3 and 4 describe our methodology for massively parallel testing and smoothing, respectively, which we have implemented in R (R Development Core Team, 2012). Section 5 takes up the question of how voxelwise spline smooths can be summarized in maps analogous to Fig. 1(a), and proposes a solution based on clustering of functional data. We apply our methods to the homotopic connectivity data in Section 6, and conclude with some discussion in Section 7.

2 Penalized smoothing and mixed models

Suppose our data consist of predictors x₁, …, x_n ∈ S ⊂ R and responses y₁, …, y_n ∈ R arising from the model

$$y_i=g(x_i)+{\epsilon }_i(i=1,\dots ,n),$$ (2.2)

with an unknown smooth function g : S → R, and independent errors ε_i ~ N (0, σ²) for some σ² > 0. We assume that, with negligible approximation error, this function has the form g(x) = θ^T b(x), where b(·) = [b₁(·), …, b_K(·)]^T for some basis functions b₁, …, b_K : S → R such as cubic B-splines. The coefficient vector θ ∈ R^K is estimated by minimizing the penalized sum of squared errors

$${\Vert \mathit{y}-\mathit{B\theta }\Vert }^2+\mathrm{\lambda }{\mathit{\theta }}^T\mathit{P\theta },$$ (2.3)

where y = (y₁, …, y_n)^T, B = [b_j(x_i)]_{1≤i≤n,1≤j≤K}, λ ≥ 0 is a tuning parameter, and P is a symmetric nonnegative definite K × K matrix such that θ^T Pθ is an index of the roughness of the function g(·) = θ^T b(·); a popular choice is

$$\mathit{P}={\left[{\mathit{\int }}_S{b}_i^{″}(x)b_j^{″}(x)\mathit{dx}\right]}_{1\le i,j\le K},$$ (2.4)

implying θ^T Pθ = ∫_S g″ (x)² dx. The roughness penalty prevents overfitting by shrinking the estimate of g toward the space

$$\left\{{\mathit{\theta }}^T\mathit{b}(·):{\mathit{\theta }}^T\mathit{P\theta }=0\right\}=\left\{{\mathit{\theta }}^T\mathit{b}(·):\mathit{\theta }\in \mathrm{null}\mathit{P}\right\},$$ (2.5)

with the extent of this shrinkage controlled by the smoothing parameter λ.

Choosing λ is crucial, and it has become popular to do so by representing the minimizer of (2.3) as the best linear unbiased predictor (BLUP) arising from a linear mixed model, in which “smooth” (unpenalized) and “wiggly” (penalized) components correspond to fixed and random effects, respectively (e.g., Speed, 1991; Ruppert et al., 2003). An explicit mixed model representation can be derived using the singular value decomposition P = U DU^T where U is a K × K matrix with orthonormal columns and D is diagonal. If P has rank r then we can write $\mathit{D}=\left[\begin{array}{cc}{\mathit{D}}_1& \mathbf{0}\\ \mathbf{0}& \mathbf{0}\end{array}\right]$ where D₁ is an r × r nonsingular matrix. Writing U = (U₁ U₂) where U₁ is K × r, one can easily show that (2.3) equals

$${\Vert \mathit{y}-\mathit{X\beta }-\mathit{Zu}\Vert }^2+\mathrm{\lambda }{\mathit{u}}^T\mathit{u}$$ (2.6)

where X = BU₂, $\mathit{\beta }={\mathit{U}}_2^T\mathit{\theta }$, $\mathit{Z}=\mathit{B}{\mathit{U}}_1{\mathit{D}}_1^{-1/2}$, and $\mathit{u}={\mathit{D}}_1^{1/2}{\mathit{U}}_1^T\mathit{\theta }$. Expression (2.6) equals −2σ² times the joint log-likelihood of (y, u) in the linear mixed model

$$\mathit{y}=\mathit{X\beta }+\mathit{Zu}+\epsilon$$ (2.7)

with $\left[\begin{array}{c}\mathit{u}\\ \epsilon \end{array}\right]~N\left(0,\left[\begin{array}{cc}({\sigma }^2/\mathrm{\lambda }){\mathit{I}}_r& \mathbf{0}\\ \mathbf{0}& {\sigma }^2{\mathit{I}}_n\end{array}\right]\right)$, in which λ can be interpreted as the ratio of the error variance to the random effects variance. Accordingly, one can choose λ by restricted maximum likelihood (REML) estimation (Patterson and Thompson, 1971) of the mixed model parameters. REML-based smoothing parameter selection has been justified on a variety of theoretical and practical grounds (e.g., Wahba, 1985; Ruppert et al., 2003; Krivobokova and Kauermann, 2007; Reiss and Ogden, 2009; Wood, 2011).

For hypothesis testing, it will be more convenient to write

$$\left[\begin{array}{c}\mathit{u}\\ \epsilon \end{array}\right]~N\left(\mathbf{0},\left[\begin{array}{cc}\gamma {\sigma }^2{\mathit{I}}_r& \mathbf{0}\\ \mathbf{0}& {\sigma }^2{\mathit{I}}_n\end{array}\right]\right)$$ (2.8)

where γ = 1/λ. An ostensibly more general formulation (e.g., Crainiceanu and Ruppert, 2004; note that their λ is the same as our γ) takes Var(u) = γσ²Σ for some known symmetric positive definite r×r matrix Σ; the model then corresponds to the penalized sum of squared errors criterion ∥y − X β − Zu∥² + λu^T Σ⁻¹ u. But the “canonical” reparametrization of the previous paragraph simplifies the model by setting Σ = I_r (Wand and Ormerod, 2008).

The log restricted likelihood of model (2.7), (2.8) is a function of β, σ², and γ, but since our interest centers on γ (or its inverse, λ) we may maximize with respect to β and σ² as in Crainiceanu and Ruppert (2004) to obtain the profile log restricted likelihood given (up to a constant) by

$$\begin{array}{lll}2{\ell }_R(\gamma )& =& 2{\ell }_R(\gamma ;\mathit{y},\mathit{X},\mathit{Z})\\ & =& -(n-p)\log [{\mathit{y}}^T\{{\mathit{V}}_{\gamma }^{-1}-{\mathit{V}}_{\gamma }^{-1}\mathit{X}{({\mathit{X}}^T{\mathit{V}}_{\gamma }^{-1}\mathit{X})}^{-1}{\mathit{X}}^T{\mathit{V}}_{\gamma }^{-1}\}\mathit{y}]-\log |{\mathit{V}}_{\gamma }|-\log |{\mathit{X}}^T{\mathit{V}}_{\gamma }^{-1}\mathit{X}|,\end{array}$$ (2.9)

where V_γ = Cov(y)/σ² = I_n + γZZ^T and p is the number of columns of X (here this is just K − r, but the notation p allows for more general models such as those considered in Section 7). Expression (2.9) plays a central role in solving both of the problems with which this paper began:

1. Testing a parametric null hypothesis against a smooth alternative. Under formulation (2.7), (2.8) of model (2.2), a zero random effects variance, or γ = 0, implies that g belongs to the space (2.5). What this space is depends on the basis and penalty, but most often it corresponds to a parametric model: for example, for cubic B-splines with either a second derivative penalty as above or a second-order difference penalty (Eilers and Marx, 1996), it is the space of linear functions. Thus, testing a parametric null hypothesis against the general smooth alternative (2.2) reduces to testing H₀ : γ = 0 vs. H_A : γ > 0, for which Crainiceanu and Ruppert (2004) propose the restricted likelihood ratio test statistic r(y, X, Z) = sup_γ≥0 2ℓ_R(γ) − 2ℓ_R(0). As these authors show, the null distribution of this statistic is nonstandard but can be easily simulated.

2. Optimal smoothing. For given λ, our estimate for model (2.2) is ĝ(x) = θ̂^T b(x) where θ̂ = (B^T B + λP)⁻¹ B^T y is the minimizer of (2.3). The REML approach to smoothing chooses λ such that γ = 1/λ maximizes (2.9).

As the next two sections will demonstrate, the form of expression (2.9) enables us to solve both of these problems a large number of times in parallel.

3 Parallel restricted likelihood ratio tests

3.1 Naïve algorithm

In the massively parallel (henceforth, MP) version of problem (i), we are given an n × L outcome matrix

$$\mathit{Y}={(y_{i\ell })}_{1\le i\le n,1\le \ell \le L}=({\mathit{y}}_1\dots {\mathit{y}}_L)$$ (3.1)

and wish to perform L simultaneous RLRTs with outcome vectors y₁, …, y_L but with common design matrices X, Z. Naïvely, this requires one to repeat the following steps for ℓ = 1, …, L:

1. Simulate the null distribution of r(y_ℓ) (we suppress the dependence on X, Z) as given by Crainiceanu and Ruppert (2004).

2. Choose a grid of candidate values 0 = γ₍₁₎ < … < γ_(G), and for g = 1, …, G, compute ℓ_R(γ_(g); y_ℓ).

3. Assuming a sufficiently fine grid, r(y_ℓ) is well approximated by

   $$\underset{g\in \{1,\dots ,G\}}{\sup }2{\ell }_R({\gamma }_{(g)};{\mathit{y}}_{\ell })-2{\ell }_R(0;{\mathit{y}}_{\ell }),$$

   which is referred to the simulated null distribution.

3.2 Efficient algorithm

Since the null distribution of r(y_ℓ) depends only on X and Z, but not y_ℓ, step 1 need not be repeated L times. The main computational task, then, is step 2: forming the matrix [ℓ_R(γ_(g); y_ℓ)]_{g=1,…,G,ℓ=1,…,L}.

Further substantial computational savings can be attained by observing that, by (2.9),

$$2{\ell }_R(\gamma ;{\mathit{y}}_{\ell })=-(n-p)\log ({\mathit{y}}_{\ell }^T{\mathit{M}}_{\gamma }{\mathit{y}}_{\ell })+h_{\gamma },$$ (3.2)

where ${\mathit{M}}_{\gamma }={\mathit{V}}_{\gamma }^{-1}-{\mathit{V}}_{\gamma }^{-1}\mathit{X}{({\mathit{X}}^T{\mathit{V}}_{\gamma }^{-1}\mathit{X})}^{-1}{\mathit{X}}^T{\mathit{V}}_{\gamma }^{-1}$ and $h_{\gamma }=-\log |{\mathit{V}}_{\gamma }|-\log |{\mathit{X}}^T{\mathit{V}}_{\gamma }^{-1}\mathit{X}|$; note that these two quantities need to be computed only once for a given γ. The main task thus reduces to computing

$$\{{\mathit{y}}_{\ell }^T{\mathit{M}}_{{\gamma }_{(g)}}{\mathit{y}}_{\ell }:g=1,\dots ,G,\ell =1,\dots ,L\}.$$ (3.3)

But it is easily shown that

$$1^T[\mathit{Y}☉({\mathit{M}}_{\gamma }\mathit{Y})]={({\mathit{y}}_1^T{\mathit{M}}_{\gamma }{\mathit{y}}_1,\dots ,{\mathit{y}}_L^T{\mathit{M}}_{\gamma }{\mathit{y}}_L)}^T,$$ (3.4)

where ☉ denotes the Hadamard product of two matrices of equal dimension, i.e., the matrix of the same dimension obtained by componentwise multiplication. Thus (3.3) can be obtained by computing (for γ = γ₍₁₎, …, γ_(G)) the left side of (3.4). Although either side of (3.4) entails O(n² L) operations, for large L the matrix operations on the left side are much faster than individually computing the quadratic forms ${\mathit{y}}_{\ell }^T{\mathit{M}}_{\gamma }{\mathit{y}}_{\ell }(\ell =1,\dots ,L)$ on the right side (see Chambers, 2008, p. 214). This is an instance of the principle that vector and matrix operations are often more efficient than computing the same quantities by looping.

Computational efficiency can be further improved by a diagonalization method described in Section 1 of the supplementary appendix.

4 Parallel smoothing

We now consider MP problem (ii): fitting a model of the form (2.2) to each column of (3.1), i.e., y_iℓ = g_ℓ (x_i) + ε_iℓ with independent errors ${\epsilon }_{i\ell }~N(0,{\sigma }_{\ell }^2)$ for ℓ = 1, …, L.

To smooth the L response vectors we must, for ℓ = 1, …, L, (a) choose λ_ℓ such that γ_ℓ = 1/λ_ℓ maximizes (2.9) with y = y_ℓ, and then (b) compute the basis coefficient estimate θ̂_ℓ = (B^T B + λ_ℓP)⁻¹ B^Ty_ℓ. The problem of rapidly performing (a) L times was in effect solved above. Finding the maximizer λ_ℓ of (2.9) for each ℓ entails essentially the same computations as finding the maximum, as is done for the parallel RLRT; once again the key is to form [ℓ_R(γ_(g); y_ℓ)]_{g=1,…,G,ℓ=1,…,L} by computing the left side of (3.4) for each candidate value of γ = 1/λ.

For (b), Demmler-Reinsch orthogonalization (e.g., Ruppert et al., 2003, Appendix B.1) enables us to compute the entire K × L matrix Θ̂ ≡ (θ̂₁ … θ̂_L) without repeated inversions of K × K matrices of the form B^T B + λ_ℓ P. First find a K × K matrix R such that R^T R = B^T B, say by Cholesky decomposition. In practice we replace B^T B here by B^T B + δ P for, say, δ = 10⁻¹⁰, as recommended by Ruppert et al. (2003). This has no appreciable effect on the result, but ensures that we can obtain an invertible R, allowing us to define UDiag(τ)U^T, where τ = (τ₁, …, τ_K)^T, as the singular value decomposition of R^−T PR⁻¹. We then have

$${\widehat{\mathit{\theta }}}_{\ell }={\mathbf{R}}^{-1}\mathit{U}\mathrm{Diag}\left(\frac{1}{1+{\mathrm{\lambda }}_{\ell }\mathit{\tau }}\right){\mathit{U}}^T{\mathit{R}}^{-T}{\mathit{B}}^T{\mathit{y}}_{\ell }$$ (4.1)

for ℓ = 1, …, L. By the identity υ ☉ w = Diag(υ)w, (4.1) equals the ℓth column of the K × L matrix R⁻¹ U[M ☉ (U^T R^−T B^T Y)], where M is the K × L matrix ${\left(\frac{1}{1+{\mathrm{\lambda }}_{\ell }{\tau }_i}\right)}_{1\le i\le K,1\le \ell \le L}$. Thus the L vector equations (4.1) can be collected into the single matrix equation

$$\widehat{\mathbf{\Theta }}={\mathit{R}}^{-1}\mathit{U}[\mathit{M}☉({\mathit{U}}^T{\mathit{R}}^{-T}{\mathit{B}}^T\mathit{Y})].$$

The ℓth column of the matrix on the right side of this equation gives the K basis coefficients determining our estimate for g_ℓ. Pointwise Bayesian confidence intervals for g₁, …, g_L can also be obtained very rapidly, as detailed in Section 2 of the supplementary appendix.

5 Visualization by functional-data clustering

We argued in the Introduction that voxelwise spline smoothing is more flexible and informative than the popular polynomial models for estimating developmental trajectories. But precisely because of their flexibility, it is not immediately obvious how spline fits for each voxel can be summarized in the form of a brain map, as they must be if the approach of Section 4 is to be useful to neuroscientists. To address this challenge, we consider optimal partitioning (Tarpey et al., 2010) of large collections of curves. The goal, for our motivating application, is to form, and visualize, clusters of voxels with similar developmental trajectories.

Our approach is to view each of the voxelwise developmental trajectory estimates as a functional datum (Ramsay and Silverman, 2005); we can then apply a variant of k-means clustering (MacQueen, 1967; Hartigan and Wong, 1979) suitable for functional data. Whereas clustering is sometimes conceptualized as identifying distinct subpopulations from which a sample arises, k-means aims at an optimal partitioning, which is meaningful whether or not distinct subpopulations exist. For multivariate data, Flury (1993) showed that the k-means clustering algorithm provides consistent estimators of k principal points that optimally represent the distribution, in the sense that mean squared distance from a given point to the closest of the k points is minimized. Tarpey and Kinateder (2003) extended results on principal points from the multivariate to the functional data setting, in which the k principal points estimated by the cluster means can be interpreted as prototype curves.

A straightforward strategy for k-means clustering of the voxelwise trajectories is to expand these functions with respect to the functional principal component (FPC) basis (Silverman, 1996; see Tarpey and Kinateder, 2003, for a theoretical rationale for this particular choice of basis), thereby reducing the functional data to multivariate data—namely, the FPC scores—to which ordinary k-means clustering can be applied.

In developmental applications, the shape of a trajectory may be more important than its mean, and hence it is advisable to cluster derivatives of the curves (which are readily available for spline basis functions) rather than the raw curves (Tarpey and Kinateder, 2003). Our approach consists of functional principal component analysis on the voxelwise first derivative curves, followed by k-means clustering on the leading FPC scores. The procedure is extremely fast and appears to give rise to reasonable clusters (see Fig. 5 below; for computational details, see Section 3 of the supplementary appendix).

Figure 5.

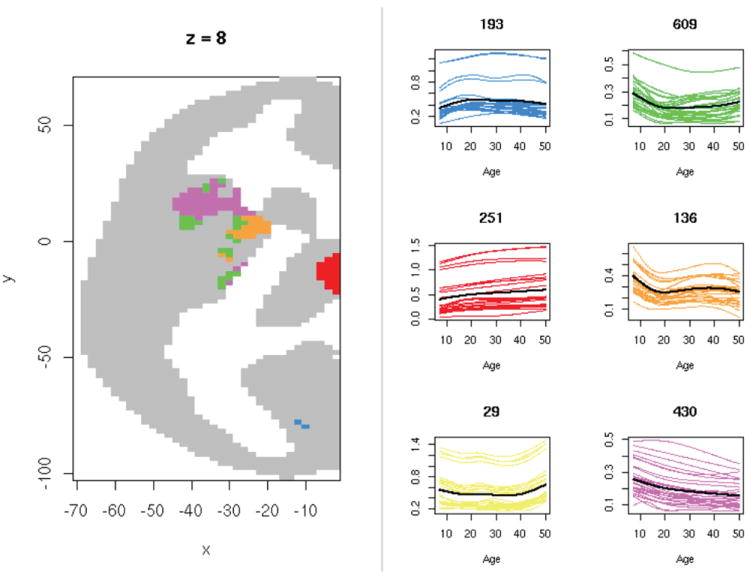
Six-means clustering solution for the voxelwise mean developmental trajectories of homotopic connectivity, restricted to the 1648 voxels for which the RLRT yielded FDR < 0.1. Left: An axial slice (the z = 8 plane in MNI coordinates), color-coded by the identified clusters (one of the six clusters contains no voxels in this slice). Grey indicates voxels not meeting the FDR < 0.1 threshold. Right: Estimated trajectories for 30 randomly selected voxels in each cluster, with colors corresponding to those at left. In each case, the black curve is the cluster mean, and the number of voxels assigned to the cluster is shown above the plot.

6 Homotopic connectivity data

6.1 Voxelwise RLRT

The first question of interest for the homotopic connectivity data is: For which voxels is there evidence for an effect of age on connectivity? The null hypothesis for the ℓth voxel is thus H_0ℓ : g_ℓ = constant. To test H₀₁, …, H_0L by the MP RLRT of Section 3, we must choose a penalty matrix P such that, assuming g_ℓ lies in the span of B-spline functions b₁, …, b_K, H_0ℓ holds if and only if g_ℓ belongs to the space (2.5). Thus an appropriate choice for the given null hypothesis is $\mathit{P}={\left[{\mathit{\int }}_S{b}_i^{\prime }(x)b_j^{\prime }(x)\mathit{dx}\right]}_{1\le i,j,\le K}$, which implies ${\mathit{\theta }}^T\mathit{P\theta }={\mathit{\int }}_S{g}^{\prime }{(x)}^2\mathit{dx}$.

6.2 Timing

For our analyses of the homotopic connectivity data, we used K = 15 B-spline basis functions, with equally spaced knots spanning the range of the ages. As explained above in Sections 3 and 4, the main step in either of our MP algorithms is to compute (3.2) for each of a grid of values of γ = 1/λ (for RLRT) or of λ (for smoothing). Accordingly, as shown by the roughly parallel best-fit lines in Fig. 2, the running time for either algorithm is dominated by an amount directly proportional to the number of grid points. Whereas our methods can perform either RLRT or smoothing for the entire brain, with up to 100 grid points, in under 6 minutes, a naïve approach based on looping through all 71287 voxels (see Section 4 of the supplementary appendix) would require a total of approximately 119 minutes for RLRT and 110 minutes for smoothing.

Figure 2.

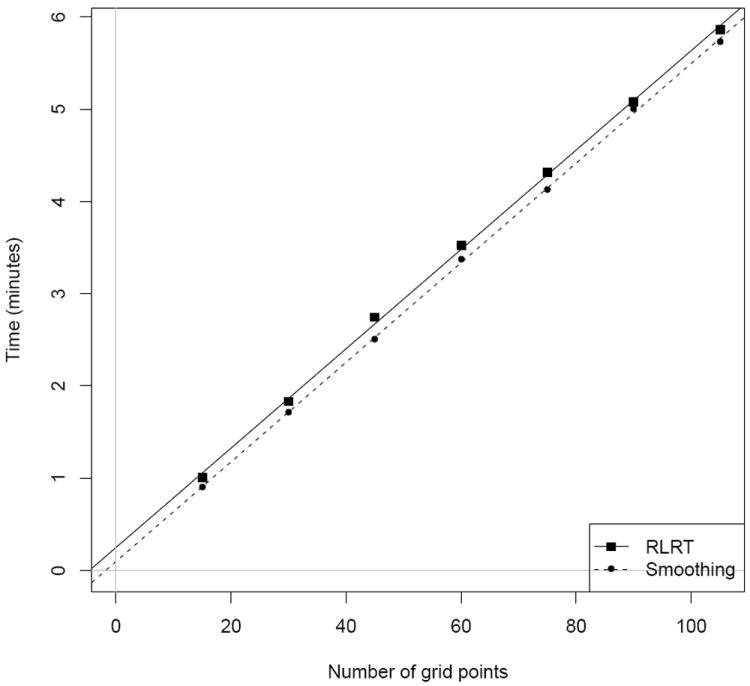
Time required to compute voxel-by-voxel RLRT and scatterplot smoothing, as a function of the number of grid points used for the (inverse) smoothing parameter. All times are based on 64-bit R, version 2.12.1, running on a MacBook Pro with a 2.66 GHz Intel Core i7 processor.

6.2.1 Comparison with polynomial-based testing

We applied the massively parallel RLRT of Section 3, using a grid of 100 equally-spaced values of log(γ) from -22 to 0. For comparison, we also applied to each voxel a polynomial-based testing procedure as in Shaw et al. (2007), an influential paper in developmental neuroimaging. We fitted a cubic model; if the cubic term was not significant at p < .05, we removed it and tested the quadratic term; and so on. This sequential testing procedure leads to a classification of each voxel’s trajectory as constant, linear, quadratic, or cubic, which is cross-tabulated with the RLRT outcome in Table 1. Since the polynomial procedure entailed up to three tests at the .05 level, it is not surprising that it yielded a higher total number of voxels for which the trajectory differs “significantly” from a constant. There are, however, 430 voxels for which the cubic, quadratic and linear terms were all found non-significant, but the RLRT rejected the null. Inspection of fitted curves suggests that for many of these voxels, the mean trajectory increases during adolescence, then attains a plateau.

Table 1.

Cross-tabulation of voxelwise developmental trajectory types, classified by backward elimination of polynomial terms vs. by the RLRT.

Sequential test result	RLRT p-value		Total
	≥ .05	< .05
Constant	52039	430	52469
Linear	1929	3611	5540
Quadratic	4999	3612	8611
Cubic	3019	1648	4667
Total	61986	9301	71287

6.2.2 False discovery rate

The above results are based on raw p-values. But in most applications of voxelwise hypothesis testing, it is appropriate to correct for multiple testing. The simplest of the methods commonly applied for this purpose is the false discovery rate (FDR) of Benjamini and Hochberg (1995) (see Genovese et al., 2002). We used a standard formula (Benjamini et al., 2006, p. 493; implemented by the R function p.adjust) to convert the raw RLRT p-values to “FDR-adjusted” p-values, and found that 1648 of the 71287 voxels attained an FDR below 0.1. (One of the cell counts in Table 1 is also 1648, but these two sets of voxels do not coincide.) Fig. 3 displays the FDR values within 11 axial slices. Most of the voxels for which FDR< 0.1 occur in regions of the thalamus, hippocampus and frontal operculum. In particular the significant cluster in the frontal operculum (see the z = 8 slice in Fig. 3) corresponds to regions found by Zuo et al. (2010) to show a significant quadratic or cubic effect.

Figure 3.

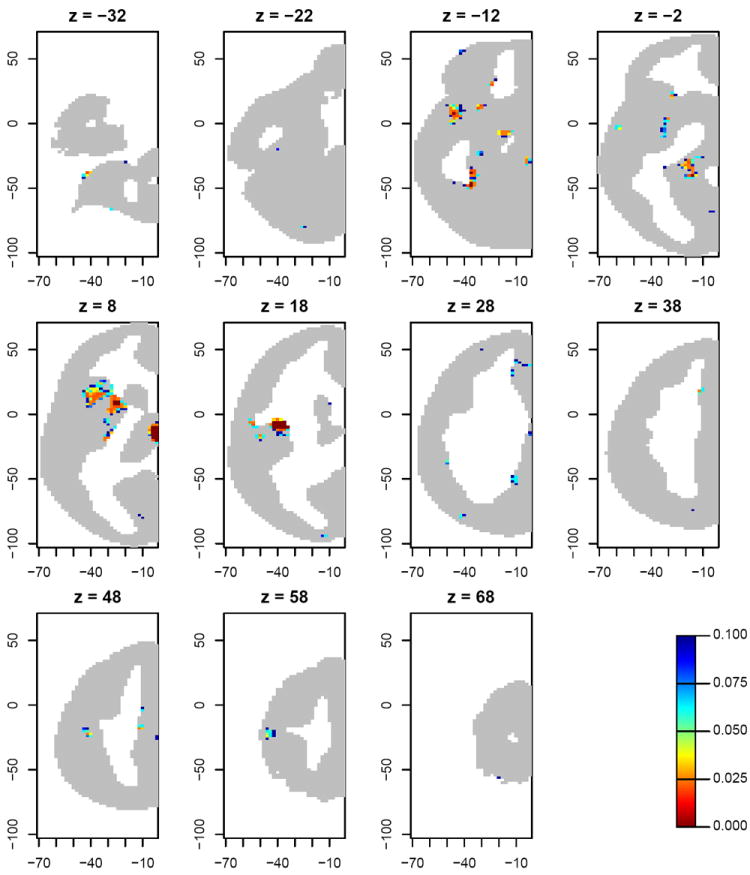
FDR estimates, thresholded at 0.1, for the RLRT testing for an effect of age on homotopic connectivity at each voxel. The titles give MNI z-coordinates of the displayed axial slices; the horizontal and vertical axis labels refer to x- and y-coordinates in MNI space.

6.3 Voxelwise smoothing

For scatterplot smoothing, we used penalty (2.4), so that the roughness penalty shrinks the function estimate toward the best-fit line. To rule out overfitting, we fixed a maximum effective degrees of freedom (df) of 6. The df for the spline fit minimizing (2.3) is conventionally defined as the trace of the “hat matrix” H = B(B^T B + λP)⁻¹ B^T, so named because the fitted values ŷ = Bθ̂ satisfy ŷ = Hy. We considered a grid of 100 equally spaced values of log λ from 5.73 (implying 6 df) to 22 (which is effectively infinite, i.e., a linear fit).

Fig. 4 compares the MP results with REML smooths obtained by the gam function in the R package mgcv (Wood, 2006, 2011), for 200 randomly selected voxels. Panels (a) and (b) display the log smoothing parameter and the effective degrees of freedom, respectively, for the two methods. Note that higher values along each axis in (a) correspond to lower values in (b), and vice versa.

Figure 4.

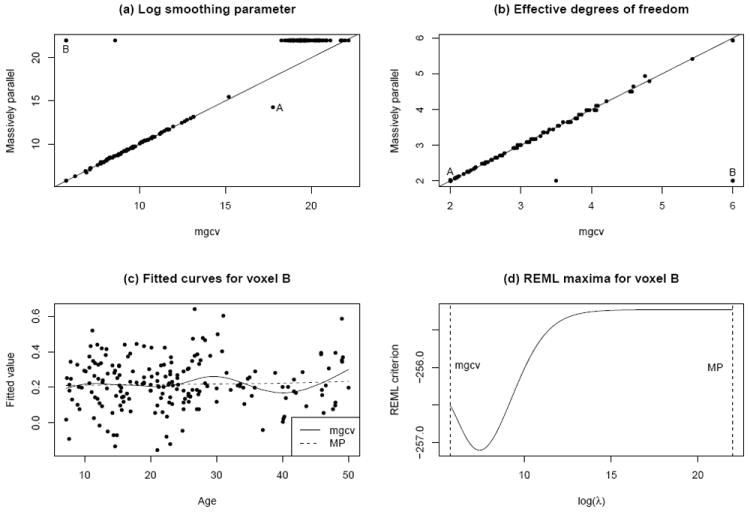
(a) Log smoothing parameter λ and (b) effective degrees of freedom, obtained by the MP method vs. by the mgcv implementation of Wood (2006, 2011), for 200 randomly selected voxels. (c) Fitted curves by the two methods for a voxel indicated by “B” in subfigures (a) and (b). As shown in (d), the discrepancy occurs because mgcv and MP choose λ values representing local and global maxima, respectively, of the REML criterion.

In Fig. 4(a), almost all of the 200 voxels fall into one of two distinct groups. For the 93 voxels for which both methods choose log λ < 14, the λ value chosen by MP smoothing for these voxels is approximately the mgcv-chosen value, rounded to the nearest grid point. For the 105 voxels for which the MP method chose the maximum value log λ = 22, the story is a bit more complicated. The smoothing parameter chosen by mgcv is usually somewhat smaller (see the horizontal cluster of points in the top right corner of Fig. 4(a)), but this makes no practical difference since either method yields an essentially linear fit—and hence the corresponding points in Fig. 4(b) are all at (2,2). (Similarly, for the voxel marked “A” in the figure, mgcv chooses a higher smoothing parameter, but the two methods produce virtually identical near-linear fits.) There are, however, three voxels for which log λ = 22 according to the MP method but mgcv chooses a much smaller value; these appear in the upper left corner of Fig. 4(a), but two of the three points (near the “B”) are indistinguishable.

The smooths by each method for one of these two points (voxels) are shown in Fig. 4(c). The mgcv-based smooth is implausibly bumpy, and the reason for this is revealed in Fig. 4(d): mgcv has settled on a local maximum of the REML criterion, whereas the much smoother fit by MP reflects the global maximum (within the range of values considered). The other two voxels for which mgcv chose much lower smoothing parameters than MP are also attributable to local maxima. See Welham and Thompson (2009) for a careful study of bimodality of the REML criterion. In summary, we have found that smoothing parameter selection generally produces a fast approximation to the mgcv result, and in some cases can give a seemingly better result, i.e. a global rather than local maximum of the REML criterion. In fairness, it should be noted that mgcv is designed for state-of-the-art multiple smoothing parameter selection in generalized additive models, for which a grid search would be highly inefficient and hence iterative maximization (by a form of Newton’s method) is needed. But in the single smoothing parameter case considered here, the grid search implemented in MP smoothing can sometimes avoid a local maximum attained by the “gold standard” iterative approach of mgcv.

6.4 Clustering

We applied the clustering procedure of Section 5 to the estimated developmental trajectories for the 1648 voxels for which the RLRT yielded FDR< 0.1. A detailed study of optimal choice of the number of functional principal components, and the number of clusters, lies beyond the scope of this paper. For this preliminary application, we used 6 FPCs, which explain 98% of the variance in the fitted curves, and took k = 6, at which the R² criterion (Tarpey et al., 2010) appears to stabilize. Fig. 5 illustrates the six resulting clusters, with mean curves representing the distinct patterns found in the data. Since we clustered based on the first derivative, curves in the same cluster tend to have similar shape but may be at very different levels with respect to the vertical axis. The two largest clusters (shown in green and purple) are characterized by a decline in mean homotopic connectivity during the adolescent years; the mean connectivity subsequently continues its gradual decline in one cluster, whereas in the other it increases somewhat in middle age. Within the z = 8 slice shown in Fig. 5, all voxels in the thalamus with a significant age effect (the red cluster) share a similar developmental pattern, marked by increasing homotopic connectivity with age. In contrast, the significant voxels in the frontal operculum seem to be divided into three clusters: the largest exhibits decreasing connectivity throughout the age range (purple), while the other two (green and orange) seem to follow a pattern of decreasing connectivity until age 20, followed by a relatively flat trajectory.

Prior to the analyses of this section, all participants’ data had been registered to standard space using the MNI152 brain atlas, a template image derived from adult brains only. Our sample’s wide age range may therefore magnify the effect of registration error on the results, since the registration of the children’s brains to the adult-based MNI152 space may be inferior to that of the adults. There is currently no standard procedure for dealing with such disparities (Wilke et al., 2008; Fonov et al., 2011; Evans et al., 2012). In addition, it may be that differences introduced by registration are so subtle as to be negligible in the context of the smoothing of the functional images during preprocessing.

7 Discussion

The proposed MP methodology has numerous potential applications, especially to neuroimaging data. Y can represent any functional or structural quantity measured at a large set of brain locations, and x can be a continuous variable other than age. Moreover, B need not represent a B-spline basis: for instance, high angular resolution diffusion imaging (HARDI) can be formulated as a penalized smoothing problem with a modified spherical harmonic basis (Descoteaux et al., 2006, 2007), for which MP smoothing makes it feasible to select an optimal smoothing parameter separately at each voxel.

Beyond the basic nonparametric regression model (2.2), MP methodology can be applied to any set of L instances of model (2.7), (2.8) with common X, Z and varying y, λ, σ². For example:

• MP semiparametric models, incorporating covariates on which y depends linearly, can be fitted by simply adding appropriate columns to X in (2.7).

• As emphasized by Ruppert et al. (2003) and Reiss et al. (2010), varying coefficient models can be formulated as minimizing a penalized least squares criterion much like (2.6); hence MP varying coefficient models can be implemented within our framework.

• Alternatively, the parallel instances of model (2.7), (2.8) may not be derived from a non-or semiparametric model at all; they may be linear mixed models in the conventional sense. In this case the methods of Section 3 would perform MP testing for a zero random effects variance, while the methods of Section 4 would perform MP mixed model estimation (cf. the related approach of Lippert et al., 2011, for genome-wide association studies). Wood (2011, p. 27) notes that his more general REML-based smoothing parameter selection methodology could serve as an approach to generalized linear mixed model estimation, but not necessarily the most efficient one. But in the setting of MP linear mixed models, our approach could sometimes be much faster than fitting all L models in turn.

We are also studying extensions of the proposed methods to more complex designs and models, including generalized linear models and problems with multiple smoothing parameters.

Much further work is needed to refine the functional data clustering procedure of Section 5, including optimal choice of the number of FPCs and the number of clusters, and incorporating spatial information to make each cluster more nearly contiguous.

In the neuroimaging literature, MP analyses that treat each voxel separately are referred to (and sometimes derided) as “mass-univariate” models. Ordinarily the residuals are correlated across voxels. In principle, confidence interval accuracy and the operating characteristics of hypothesis tests could be improved by taking this spatial dependence into account; but implementation is very challenging in high-dimensional settings. Our ongoing research is exploring ways to improve estimation by borrowing strength across voxels (e.g., Derado et al., 2010; Li et al., 2011; cf. Staicu et al., 2010). We believe that the combination of our techniques with new approaches to spatial dependence holds great potential for more sophisticated analyses of neuroimaging data.

An R package called vows implementing the methods of the article, including some of the extensions sketched earlier in this section, is available on the CRAN repository at http://cran.r-project.org/web/packages/vows/.