A Tri-Factor Model for Integrating Ratings Across Multiple Informants

Abstract

Psychologists often obtain ratings for target individuals from multiple informants such as parents or peers. In this paper we propose a tri-factor model for multiple informant data that separates target-level variability from informant-level variability and item-level variability. By leveraging item-level data, the tri-factor model allows for examination of a single trait rated on a single target. In contrast to many psychometric models developed for multitrait-multimethod data, the tri-factor model is predominantly a measurement model. It is used to evaluate item quality in scale development, test hypotheses about sources of target variability (e.g., sources of trait differences) versus informant variability (e.g., sources of rater bias), and generate integrative scores that are purged of the subjective biases of single informants.

When measuring social, emotional, and behavioral characteristics, collecting ratings from multiple informants (e.g., self, parent, teacher, peer) is widely regarded as methodological best practice (Achenbach, McConaughy & Howell, 1987; Achenbach et al., 2005; Renk, 2005). Similarly, the use of multisource performance ratings (e.g., by supervisors, peers, and subordinates, a.k.a., 360-degree assessment) is considered an optimal method for evaluating job performance (Conway & Huffcutt, 1997; Lance et al., 2008). Because each informant observes the target within a specific relationship and context, it is desirable to obtain ratings from multiple informants privy to different settings to obtain a comprehensive assessment, particularly when behavior may vary over contexts. Further, any one informant’s ratings may be compromised by subjective bias. For instance, depressed mothers tend to rate their children higher on psychopathology than do unimpaired observers, in part because of their own impairment and in part because of an overly negative perspective on their children’s behavior (Boyle & Pickles, 1997; Fergusson, Lunskey & Horwood, 1993; Najman, 2000; Youngstrom, Izard & Ackerman, 1999). In principle, researchers can better triangulate on the true level of the trait or behavior of interest from the ratings of several informants. The idea is to abstract the common element across informants’ ratings while isolating the unique perspectives and potential biases of the individual reporters.

Although there is widespread agreement that collecting ratings from multiple informants has important advantages, less agreement exists on how best to use these ratings once collected. The drawbacks of relatively simple analysis approaches, such as selecting an optimal informant, conducting separate analyses by informant, or averaging informant ratings, have been discussed at some length (e.g., Horton & Fitmaurice, 2004; Kraemer, Measelle, Ablow, Essex, Boyce & Kupfer, 2003; van Dulmen & Egeland, 2011). In contrast to these approaches, psychometric models offer a more principled alternative wherein the sources of variance that contribute to informant ratings can be specified and quantified explicitly.

Several psychometric modeling approaches have already been proposed for analyzing multiple informant data. Reviewing these approaches, we identify the need for a new approach that is more expressly focused on issues of measurement. We then propose a new measurement model for multiple informant data, which we refer to as the tri-factor model (an adaptation and extension of the bi-factor model of Holzinger and Swineford, 1937). The tri-factor model stipulates that informant ratings reflect three separate sources of variability, namely the common (i.e., consensus) view of the target, the unique (i.e., independent) perspectives of each informant, and specific variance associated with each particular item. Correlated (non-unique) perspectives can also be accommodated by the model when some informants overlap more than others in their views of the target, albeit at some cost to interpretability. We demonstrate the advantages of the tri-factor model via an analysis of parent reports of childrens’ negative affect. Finally, we close by discussing directions for future research.

Psychometric Models for Multiple Informant Data

A number of different psychometric models for multiple informant data have appeared in the literature. As noted by Achenbach (2011), most of these models represent adaptations of models originally developed for the analysis of multitrait-multimethod (MTMM) data (Campbell & Fiske, 1959). Such data are often collected with the goal of assessing convergent and discriminant validity, as evidenced by the magnitude of inter-trait correlations after accounting for potential method-halo effects which could otherwise distort these correlations (Marsh & Hocevar, 1988). Quite often, the “methods” are informants, and the goal is then to isolate trait variability from rater effects and measurement error (e.g., Alessandri, Vecchione, Tisak, & Barbaranelli, 2011; Barbaranelli, Fida, Paciello, Di Giunta, & Caprara, 2008; Biesanz & West, 2004; Eid, 2000; Pohl & Steyer, 2010; Woehr, Sheehan, & Bennett, 2005).¹

One of the earliest proposed psychometric models for MTMM data is the Correlated Trait/Correlated Method model (CTCM; Marsh & Grayson, 1995; Kenny, 1979; Widaman, 1985). Given multiple trait ratings from each of multiple informants, the CTCM model is structured so that each rating loads on one trait factor and one method (i.e., informant) factor. Across methods, all ratings of the same trait load on the same trait factor and, across traits, all ratings made by the same method load on the same method factor. Trait factors are permitted to correlate, as are method factors, but trait and method factors are specified to be independent of one another.

Although the CTCM structure nicely embodies many of the ideas of Campbell and Fiske (1959), it has proven difficult to use in practice. In particular, the CTCM model often fails to converge (Marsh & Bailey, 1991), and suffers from potential empirical under-identification (Kenny & Kashy, 1992). As a more stable alternative, Marsh (1989) advocated use of the Correlated Trait/Correlated Uniqueness model (CTCU; see also Kenny, 1979). The CTCU model maintains correlated trait factors; however, method factors are removed from the model. To account for the dependence of ratings made by the same informant, the uniquenesses (i.e., residuals) of the measured variables are intercorrelated within informant.

Due to the lack of explicit method factors, the CTCU model has been criticized for failing to separate method variance from error variance, potentially leading to underestimation of the reliability of the measured variables (Eid, 2000; Lance et al., 2002; Pohl & Steyer, 2010). Additionally, whereas the CTCM model permits correlated method factors, in the CTCU model uniquenesses are not permitted to correlate across methods. This feature of the CTCU model has been considered both a strength and a limitation. Marsh (1989) argued that if a general trait factor (i.e, higher order factor) influenced all trait ratings then correlated method factors might actually contain common trait variance. By not including across-method correlations, the CTCU model removes this potential ambiguity from the model. Yet this also implies that if methods are truly correlated (e.g., informants are not independent) then the trait variance may be inflated by excluding these correlations from the model (Conway et al., 2004; Kenny & Kashy, 1992; Lance et al., 2002).

Several additional criticisms are shared by the CTCM and CTCU models. Marsh and Hocevar (1988) and Marsh (1993) noted that CTCM and CTCU models are typically fit to scale-level data (i.e., total scores) with unfortunate implications. First, the uniqueness of each manifest variable contains both measurement error and specific factor variance, yet because only one measure is available for each trait-rater pair there is no ability to separate these two sources of variance. Thus the factor loadings may underestimate the reliability of the manifest variables to the extent that the specific factor variance is large. Second, when specific factors are correlated, as might occur when informants rate the same items, this could artificially inflate the trait variances obtained by analyzing the scale-level data. Marsh and Hocevar (1988) and Marsh (1993) thus advocated using second-order CTCM and CTCU models in which the traditional scale-level manifest variables are replaced with multiple indicator latent factors defined from the individual scale items or item parcels.

At a more fundamental level, Eid (2000) and Pohl, Steyer and Kraus (2008) critiqued the CTCM and CTCU models for being based largely on intuition, incorporating arbitrary restrictions, and having ambiguously defined latent variables. To address these shortcomings, Eid (2000) proposed the CTC(M-1) model. This model is defined similarly to the CTCM model except that the method factor is omitted for a “reference method” chosen by the analyst (e.g., self-reports). The remaining method factors (e.g., parent- and peer-report factors) are then conceptualized as residuals relative to the reference method. The notion is that there is a true score underlying any given trait rating and when this true score is regressed on the corresponding trait rating from the reference method the residual constitutes the method effect (with an implied mean of zero and zero correlation with the reference method trait ratings). Eid et al (2003) also extended the CTC(M-1) model to allow for multiple indicators for each method-trait pair, and to allow for trait-specific method effects. This latter extension is important in relaxing the assumption that method effects will be similar across heterogeneous traits.

The CTC(M-1) model has the virtue of having well-defined factors and a clear conceptual foundation. It has, however, been criticized on the grounds that the traits must be defined with respect to a reference method and the fit and estimates obtained from the model are neither invariant nor symmetric with respect to the choice of reference method (Pohl & Steyer, 2010; Pohl, Steyer & Kraus, 2008). Eschewing the definition of method effects as residuals, Pohl et al. (2008) argued that it is better to conceptualize method factors as having causal effects on the underlying true scores of the trait ratings. As causal predictors, method factors would neither be implied to have means of zero nor to have zero correlation with the trait factors (also construed to be causal predictors). The MEcom model of Pohl and Steyer (2010) thus permits method factor means and method-trait correlations to be estimated. The MEcom model also obviates the need to select a reference method, thus allowing traits to be defined as what is common to all raters. Finally, given multiple indicators for each trait-method pair, the MEcom model retains the advantage that trait-specific method factors can be specified.

Despite these many advantages, the MEcom model also has potential limitations. First, method effects are defined as contrasts between informants (imposed through restrictions on the method factor loadings), not as the effect of a given informant. Thus the unique effects of the informants are not separated, complicating the assessment of specific sources of rater bias. Second, some of the common variance across informant trait ratings will be accounted for by the method factors. That is, trait ratings made by disparate informants will correlate not only due to the common influence of the underlying trait but also due to the fact that they are influenced by correlated methods. Although Pohl and Steyer (2010) regard such a specification as more realistic, it runs counter to the argument made by Marsh (1989) that trait factors should exclusively account for the correlations among trait ratings across different methods. Third, due to the inclusion of trait-method correlations (unique to this model), the variances of the trait ratings cannot be additively decomposed into trait, method, and error components.

In sum, a variety of psychometric models have been developed with the goal of separating trait and method variability in informant ratings, and each of these models has specific advantages and limitations. The common goal of all of these developments has been to improve the analysis of MTMM data for evaluating convergent and discriminant validity. Yet many researchers do not collect multiple informant data with the intent of examining construct validity. Often, the primary goal is simply to improve construct measurement. That is, researchers seek to generate integrated scores of the construct of interest that optimally pool information across informants who have unique access to and perspectives on the target individuals. There is then less concern with estimating inter-trait correlations and greater concern with scale development and the estimation of scores for use in substantive hypothesis testing.

The psychometric modeling approach we develop in this paper is thus designed for the situation in which one wishes to evaluate and measure a single construct for a single target based on the ratings of multiple informants, and to extract integrated scale scores for use in subsequent analysis. This situation clearly does not parallel the usual MTMM design and hence models initially developed for MTMM data are not readily applicable.² Bollen and Paxton (1998) demonstrated, however, that one can often decompose informant ratings into variation due to targets (reflected in all informants’ ratings, such as trait variation) and variation due to informants (reflecting informants’ unique perspectives, contexts of observation, and subjective biases) even when data do not conform to the traditional structure of an MTMM design. Bollen and Paxton noted that this endeavor is greatly facilitated by the availability of multiple observed indicator variables for the trait. In the present paper, we draw upon and extend this idea to present a novel model for evaluating common and unique sources of variation in informant ratings.

Taking advantage of recent advances in item factor analysis, our model is specified at the item level, leveraging the individual item responses as multiple indicators of the trait. We stipulate a tri-factor model for item responses that includes a common factor to represent the consensus view of the target, perspective factors to represent the unique views (and biases) of the informants, and specific factors for each item. It is conceptually advantageous to assume these factors are independent contributors to informants’ ratings. After introducing the model, however, we shall describe instances in which one might find it useful or practically necessary to introduce correlations between subsets of factors. It is also notable that the tri-factor model does not require that a specific informant be designated as a reference (as required by the CTC(M-1) model), permitting the common factor to be interpreted as what is common to all informants. Nor does the tri-factor model represent informant effects via contrasts between informants (as required by the MEcom model), thus enabling the evaluation of putative sources of bias for specific informants’ ratings.

The tri-factor model has three primary strengths. First, with the tri-factor model we can evaluate the extent to which individual items reflect the common factor, perspective factors, and item-specific factors. This information can be quite useful in determining which items are the most valid indicators of the trait versus those that are most influenced by the idiosyncratic views of the rater. In contrast, scale-level data do not provide any information on the validity of individual items. Further, many scales were developed through item-level factor analyses conducted separately by informant, yet such analyses cannot distinguish common factor versus perspective factor variability. Thus an item may appear to factor well with other items due to perspective effects alone even if it carries little or no information about the trait. The tri-factor model separates these sources of variability to provide a more refined psychometric evaluation of the items and scale.

A second strength of the tri-factor model is that we can include external predictors to understand the processes that influence informants’ ratings. In particular, we can regress the common, perspective, and specific factors on predictor variables to evaluate systematic sources of variability in trait levels, observer effects, and specific item responses. For instance, we might expect the child of a depressed parent to have a higher level of negative affect, represented in the effect of parental depression on the common factor. In addition, a parent who is depressed may be a biased rater of his or her child’s negative affect. The latter effect would be captured in the effect of parental depression on the perspective factor of the depressed parent.

Finally, a third strength of the tri-factor model is that it is expressly designed to be used as a measurement model. That is, a primary goal in fitting a tri-factor model is to obtain scores on the common factor. These scores provide an integrative measure of the characteristic of interest that is purged of both known and unknown sources of rater bias. Scores for the perspective factors may also be of interest, for instance when research focuses on why informants evaluate targets differently. In this sense, the purpose in fitting a tri-factor model is quite different from the purpose of fitting MTMM models, which are more typically aimed at evaluating construct validity.

In sum, the tri-factor model contributes to a strong tradition of psychometric models for analyzing multiple informant data. It is designed for the purpose of generating integrated scores from item-level data across multiple informants and it enables researchers to evaluate processes that influence both the common and unique components of informant ratings. In what follows we further explicate the tri-factor model and we discuss model estimation and scoring. We then show how the model can be applied through a real-data example.

The Tri-Factor Model for Multiple Informant Data

We begin by describing the decomposition of variability in item responses that is the basis of the tri-factor model. We then describe how the model can be extended to incorporate predictors. Following our description of the model we discuss estimation and scoring.

Unconditional Tri-Factor Model

The unconditional tri-factor model consists of a set of observed ratings from each informant, which we shall refer to as item responses, and three types of latent variables. We assume that the items all measure a single, unidimensional trait (an assumption that, in practice, can be evaluated by goodness of fit testing). We designate a given item response as y_irt and its expected value as μ_irt, where i indicates the item (i = 1, 2, … I), r indicates the rater type (e.g., self, teacher, mother; r = 1, 2, … R), and t indicates the target (t = 1, 2, … N). The item set and rater types are taken to be fixed, whereas targets are assumed to be sampled randomly from a broader population of interest. We shall initially assume parallel item sets across raters, but later describe the application of the model to differential item sets. The rater types may be structurally different (e.g., co-worker versus supervisor) or interchangeable (e.g., two randomly chosen co-workers), a distinction made by Eid et al. (2008) for MTMM models (see also Nussbeck et al., 2009, and the related concept of “distinguishability” as defined by Gonzalez & Griffin, 1999, and Kenny, Kashy & Cook, 2006). Latent variables represent sources of variability in the item responses across targets. The three types of latent variables are C_t, P_rt, and S_it, representing, respectively, a common factor, R unique perspective factors (one for each informant), and I specific factors (one for each item). The latent variables are assumed to be normally distributed and independent.

The structure of the tri-factor model is

$$g_i\left({\mu }_{\mathit{irt}}\right)={\nu }_{ir}+{\lambda }_{ir}^{(C)}{C}_t+{\lambda }_{ir}^{(P)}{P}_{rt}+{\lambda }_{ir}^{(S)}{S}_{it}$$ (1)

Focusing first on the left side of the equation, g_i(·) is a link function chosen to suit the scale of y_irt, such as the identity link for a continuous item or the logit or probit link for a binary item. The link function can vary across items, allowing for items of mixed scales types (Bartholomew & Knott, 1999; Bauer & Hussong, 2009; Skrondal & Rabe-Hesketh, 2004). The inverse of the link function, or $g_i^{-1}(·)$ returns the expected value of the item response. For a continuous item response the expected value would be a conditional mean and for a binary item response it would be a conditional probability of endorsement (conditional on the levels of the factors).

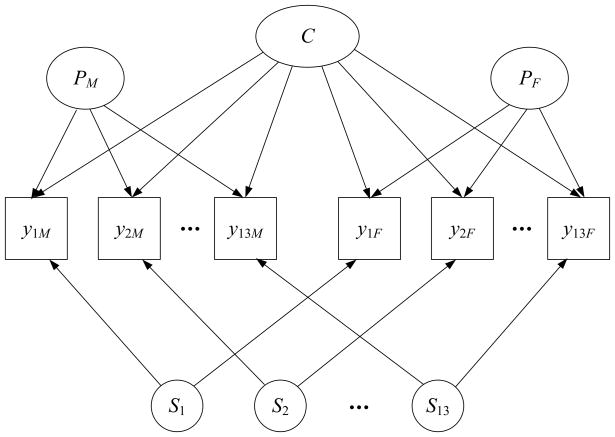
Turning now to the right side of the equation we see the usual set up for a factor analytic model with an intercept ν_ir and factor loadings ${\lambda }_{ir}^{(C)},{\lambda }_{ir}^{(P)}$, and ${\lambda }_{ir}^{(S)}$ for the three types of factors. Conditional on the factors, item responses are assumed to be locally independent. An example tri-factor model for 13 items rated by two informants, mothers and fathers, is shown in path diagram form in Figure 1. Note that each item loads on one of each type of factor: the common factor, a unique perspective factor for the informant, and a specific factor for the item.

Figure 1.

Unconditional tri-factor model for parent-report ratings on 13 items. The observed ratings are numbered by item; M and F subscripts differentiate ratings of the mother and father, respectively. Intercepts and random error terms are not shown in the diagram.

The factors are conceptually defined and analytically identified by imposing constraints on the factor loadings and factor correlations. To start, all informant ratings are allowed to load on the common factor C_t. This factor thus reflects shared variability in the item responses across informants. It is considered to represent the consensus view of the target across informants. This consensus will reflect trait variability as well as other sources of shared variability (Kenny, 1991). Informants may observe the target in the same context, may relate to the target in similar ways, or may directly share information with one another. For instance, mothers and fathers both serve the role of parent and both observe their child’s behavior principally within the home environment. Parents may also communicate with each other about their children’s problem behavior. Given data from both parents, as in Figure 1, C_t would represent the common parental view of the child’s behavior, whatever its sources (trait, context, common perspective, mutual influence). If the goal of fitting the model is to isolate general trait variability within C_t then other sources of shared variability should be minimized in the research design phase, for instance by selecting dissimilar informants who observe the child in different contexts (e.g., teacher and parent; Kraemer et al, 2002).

The unique perspective factors, P_1t, P_2t,…, P_Rt, each affect only a single informant’s ratings and are assumed to be orthogonal to C_t and to each other. By imposing the constraint that the factors are orthogonal, we ensure that each factor P captures variance that is unique to a specific informant and that is not shared (i.e., does not covary) with other informants (in contrast to C_t which represents shared variability across sets of ratings, including shared perspectives). Independent sources of variation across informants might include distinct contexts of observation, differences in the opportunity to observe behaviors, differences in informants’ roles (e.g., mother, father, teacher), and subjective biases.

Finally, when the same item is rated by multiple informants, we anticipate that the item responses will be dependent not only due to the influence of the common factor but also due to the influence of a factor specific to that item. For instance, if the item “cries often” was administered as part of an assessment of negative affect, we would expect informant ratings on this item to reflect not just negative affect, globally defined across items, but also something specific to the behavior crying. The specific factors, S_1t, S_2t,…, S_It account for this extra dependence. A given specific factor, S_it, is defined to affect the responses of all informants to item i but to no other items. The specific factors are also assumed to be orthogonal to one another and all other factors in the model. With these constraints, the specific factors capture covariation that is unique to a particular item. As noted by Marsh (1993), modeling specific factors for items rated by multiple informants is essential to avoid inflating the common factor variance.

Further restrictions on the model parameters should be imposed when some or all informants are interchangeable (Eid et al., 2008; Nussbeck et al., 2009). For example, suppose that a researcher has obtained self-ratings as well as the ratings from two randomly chosen peers for each target. The self-ratings are structurally different from the peer-ratings whereas the peers are interchangeable. The tri-factor model should be specified so that all parameters (e.g., item intercepts, factor loadings, and perspective factor means and variances) are constrained to equality across interchangeable informants but allowed to differ across structurally different informants (Nussbeck et al., 2009).

For structurally different informants, the question may be raised whether all parameters should differ across informant types. For instance, mothers and fathers are structurally different, yet it may be that both parents engage in a similar process when rating their children. As in the broader literatures on measurement and structural invariance, similarity may be seen as a matter of degree, and this can be assessed empirically within the model through the imposition and testing of equality constraints (see, e.g., Gonzalez & Griffin, 1999; Kenny, Kashy & Cook, 2006, for tests of distinguishability among dyad members). Equal item intercepts and factor loadings would imply that informants interpret and respond to the items in the same way. If, additionally, perspective factor variances are equal then this would imply that the decomposition of variance in the item responses is identical across informants. Finally, if the perspective factor means are also equal, this would imply that there are no systematic differences across informants in their levels of endorsement of the items. Indeed, if all of these equality constraints can be imposed then the informants neither interpret the items differently nor does one type of informant provide systematically higher or more variable ratings than another, and the model obtains the same form as the model for interchangeable raters. In contrast, when some but not all equality constraints are tenable, this may elucidate important differences between informants. For instance, compared to mothers, fathers may be less likely to rate their children as displaying negative affect (Seiffge-Krenke & Kollmar, 1998), resulting in a mean difference between the unique perspective factors for mothers and fathers. As such, empirical tests of equality constraints across informants may provide substantively important information on whether and how the ratings of structurally different informants actually differ.

As with all latent variable models, some additional constraints are necessary to set the scale of the latent variables. We prefer to set the means and variances of the common and specific factors to zero and one, respectively. For interchangeable informants, we similarly standardize the scale of the perspective factors. In contrast, for structurally different informants, we standardize the scale of one perspective factor, while estimating the means and variances of the other perspective factors.³ To set the scale of the remaining perspective factors, the intercept and factor loading for at least one item must be equated across informants. Last, when only two informants are present, the factor loadings for the specific factors must be equated across informants, in which case the specific factor essentially represents a residual covariance.

Standardizing the scale of the latent factors has the advantage that all non-zero factor loadings can be estimated and compared in terms of relative magnitude. Comparing ${\lambda }_{ir}^{(C)}$ to ${\lambda }_{ir}^{(P)}$ sheds light on the subjectivity of the item ratings. A high value for ${\lambda }_{ir}^{(P)}$ indicates that responses to this item largely reflect the idiosyncratic views of the informants, whereas a high value for ${\lambda }_{ir}^{(C)}$ indicates that the item responses largely reflect common opinions of the target’s trait level. Similarly, if ${\lambda }_{ir}^{(S)}$ is large relative to ${\lambda }_{ir}^{(C)}$ and ${\lambda }_{ir}^{(P)}$ then this suggests that the item is not a particularly good indicator of the general construct of interest (as most of the variability in item responses is driven by the specific factor). Inspection of the relative magnitude of the factor loadings can thus aid in scale evaluation and development.

Conditional Tri-Factor Model

The conditional tri-factor model extends the model described above by including predictors of the different factors. Adding predictors to the model serves at least two potential purposes. First, by incorporating predictors we bring additional information into the model by which to improve our score estimates, a topic we will explore in greater detail in the next section. Second, we can evaluate specific hypotheses concerning sources of systematic variability in the factors. For instance, if we think that a given predictor influences trait levels, then we can regress the common factor on that predictor. Alternatively, if we think that informants with a particular background are more likely to rate a target’s behavior in a specific direction, then we can use this background characteristic to predict the perspective factors. We might also regress perspective factors on contextual variables that vary within informant type, such as amount of time spent with the target. Finally, if we think that some items are more likely to be endorsed for certain targets than others (irrespective of their global trait levels) then we can regress the specific factors of these items on the relevant target characteristics.

It is conceptually useful to distinguish between predictors that vary only across targets versus predictors that vary across informants for a given target. For instance, if parental ratings of negative affect were collected, predictors of interest might include the child’s gender, whether the mother has a lifetime history of depression and whether the father has a lifetime history of depression. Child gender is a target characteristic whereas history of depression is informant-specific. Designating target characteristics by the vector w_t and informant-specific characteristics by the vectors x_rt (one for each rater r), regression models for the factors can be specified as follows:

$$C_t={\alpha }^{(C)}+{\mathbf{w}}_t^{\prime }{\mathbf{\beta }}^{(C)}+\sum _{r=1}^R{\mathbf{x}}_{rt}^{\prime }{\mathbf{\gamma }}_r^{(C)}+{\zeta }_t^{(C)}$$ (2)

$$P_{rt}={\alpha }_r^{(P)}+{\mathbf{x}}_{rt}^{\prime }{\mathbf{\gamma }}_r^{(P)}+{\zeta }_{rt}^{(P)}$$ (3)

$$S_{it}={\alpha }_i^{(S)}+{\mathbf{w}}_t^{\prime }{\mathbf{\beta }}_i^{(S)}+{\zeta }_{it}^{(S)}$$ (4)

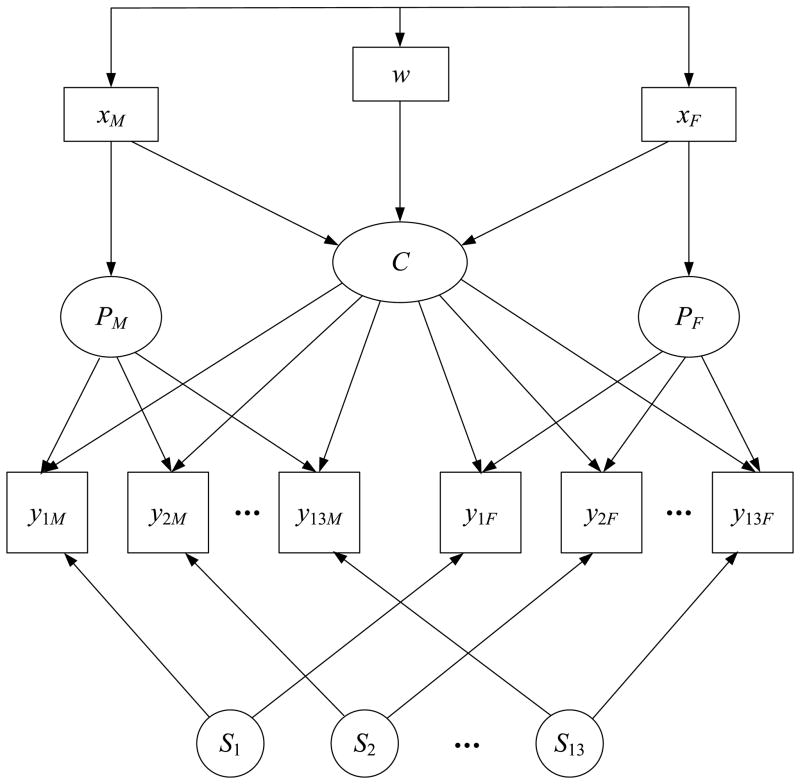
where α designates an intercept term, β designates a vector of target effects, γ designates a vector of informant-specific effects, ζ designates unexplained variability in a factor, and parenthetical superscripts are again used to differentiate types of factors. The tri-factor model previously illustrated in Figure 1 is extended in Figure 2 to include target and informant-specific effects on the common factor and perspective factors. Specific factors can also be regressed on target characteristics but these paths are not included in Figure 2 to minimize clutter. For interchangeable informants, all parameters should again be equated across raters, including the effects contained in the vectors ${\mathbf{\gamma }}_r^{(C)}$ and ${\mathbf{\gamma }}_r^{(P)}$ in Equations (2) and (3), and the intercepts and residual variances of the perspective factors. For structurally different raters, these parameters may be permitted to differ, or may be tested for equality.

Figure 2.

Conditional tri-factor model for parent-report ratings on 13 items. The observed ratings are numbered by item; M and F subscripts differentiate ratings of the mother and father, respectively. The predictor w is a target characteristic and the predictors x_M and x_F are informant-specific predictors. Intercepts and error terms/disturbances are not shown in the diagram.

In Equation (2) the common factor is affected by both target and informant characteristics. Continuing our example, girls may be higher in negative affect than boys – a target effect. Having a depressed mother and/or father may also predict higher negative affect – an informant-specific effect. These effects on the common factor are shown as directed arrows in Figure 2 (child gender would be w and parental history of depression would be x_M and x_F for mothers and fathers, respectively). In contrast, for perspective factors, the focus is exclusively on informant-specific predictors. Equation (3) shows that the perspective factor of a given informant is predicted by his or her own characteristics but not the characteristics of other informants. For instance, an informant with a history of depression might provide positively biased ratings of target negative affect. A history of depression for one parent does not, however, necessarily bias the ratings of the other parent. Thus, in Figure 2, x_M exerts an effect on the perspective factor for the mother and x_F exerts an effect on the perspective factor for the father. Last, the regression model for the specific factors includes only target effects. For instance, child gender could be allowed to influence the item “cries often” if this symptom was more likely to be expressed by girls than boys even when equating on levels of negative affect. The model shown in Figure 2 would then be extended to include a path from w to the specific factor for “cries often.”

With the incorporation of these predictors, the assumptions previously made on the factors in the unconditional tri-factor model now shift to the residuals. Specifically, each residual ζ in Equations (2) to (4) is assumed to be normally distributed and orthogonal to all other residuals. Conditional normality and independence assumptions for the factors may be easier to justify in practice. For instance, suppose that parents with a lifetime history of depression provide positively biased ratings of their children’s negative affect. This bias is detectable when one parent and not the other has experienced depression, but suppose that both parents have experienced depression. In the unconditional tri-factor model, this would result in a higher score for the child on the common factor for negative affect, because the bias is shared across both parents’ ratings. The conditional tri-factor model, in contrast, would account for this shared source of bias, removing its contribution to the common factor and making the assumption of conditional independence for the perspective factors more reasonable.

Similarly, the constraints needed to identify the model shift from the factor means and variances in the unconditional model to the factor intercepts and residual variances in the conditional model. For the conditional model, we generally prefer to set the intercepts and residual variances of the common factor and specific factors to zero and one. For interchangeable raters, the same constraints are placed on the perspective factor intercepts and residual variances. In contrast, for structurally different raters, we prefer to standardize the scale of one perspective factor while freely estimating the intercepts and residual variances of the remaining factors. This choice requires the intercept and factor loading of at least one item to be set equal across informants (see Footnote 3).

These scaling choices are convenient but not equivalent to setting the marginal means and variances of the factors to zero and one, as we recommended for the unconditional model. Two implications of this scaling difference are noteworthy. First, the raw intercept and factor loading estimates for the items are not directly comparable between the unconditional and conditional models. Second, unlike the unconditional model in which the marginal variances of the factors were equated (except possibly for some perspective factors) the marginal variances of the factors will generally differ within the conditional model. For this reason, one cannot directly compare the magnitudes of the raw factor loading estimates across types of factors in the conditional model. In both instances, however, such comparisons can be made when using the conditional model by computing standardized estimates.

Potential Modifications to the Model Structure

In both the unconditional and conditional tri-factor model structures, we imposed certain assumptions to improve the clarity of the model and its interpretation. Not all of these assumptions are strictly necessary to identify the model and, in certain cases, some may be viewed as theoretically unrealistic or inconsistent with the data. These assumptions may then be relaxed, albeit with the risk of muddying the conceptual interpretation of the factors. We revisit two of these assumptions here, beginning with the assumption that all factors are uncorrelated.

Within the unconditional model, the assumption of orthogonality enables us to define the perspective factors as the non-shared, unique components of variability in the item responses of the informants. It also allows us to state that the common and specific factors alone account for the shared variability across informants, with the common factor representing the broader construct of interest (as defined by the full item set) and the specific factors representing narrower constructs (as defined by single items). Within the conditional model, these same definitions of the factors pertain after controlling for the predictors (which may also account for some common variability across items and/or informants).

In some cases, however, a researcher may have a theoretical rationale for permitting correlations among a subset of factors in the model. For instance, if the content of two items overlapped, such as “often feels lonely” and “feels lonely even when with others,” then one might allow the specific factors for the two items to correlate. In effect, the correlation between these specific factors would account for the influence of a minor factor (loneliness) that jointly affects both items but that is narrower than the major factor of interest (negative affect). Failing to account for local dependence due to minor factors can lead to the locally dependent items “hijacking” the major factor, as evidenced by much higher factor loadings for these items relative to other items. For the tri-factor model, in particular, failing to account for local dependence among the specific factors would be expected to distort the factor loadings for the common factor, as this is the only other factor in the model that spans between informants. Introducing correlated specific factors may thus aid in avoiding model misspecifications that would otherwise adversely impact the estimation of the common factor. The trade off, however, is that the conceptual distinctions between the factors become blurred: the common factor no longer reflects all common variability across raters other than that unique to particular items, since some common variability is now accounted for by the correlations among specific factors. More cynically, the introduction of many correlated specific factors could be motivated solely by a desire to improve model fit, and might occlude a more profound misspecification of the model (e.g., a multidimensional common factor structure). The inclusion of correlated specifics should thus be justified conceptually (not only empirically).

As with the specific factors, the perspectives of some informants may be more similar than others. For instance, research on employee evaluations suggests that an average of 22% of the variance in job performance ratings can be attributed to common rater “source” effects (i.e., informants originating from the same context), over and above variance attributable to idiosyncratic rater characteristics (Hoffman, Lance, Bynum, & Gentry, 2010; see also Mount, Judge, Scullen, Sytzma, & Hezlett, 1998; Scullen, Mount, & Goff, 2000). Similarly, if the informants were mothers, fathers, and teachers, one might expect mother and father ratings to be more similar to one another than to teacher ratings. We might then find much higher factor loadings for the parental ratings than the teacher ratings, as the common factor would be required to account for the higher similarity of the parent ratings. Introducing a correlation between the parent perspective factors would account for overlapping role and context effects for mothers and fathers, enabling the common factor to integrate the across-role, across-context ratings of teachers and parents more equitably. It is important to recognize, however, that introducing correlated perspective factors for informants originating from a common setting or context changes the definition of the common factor, in effect reweighting how information is integrated across informants. The conceptual definition of the common factor is then determined predominantly by which perspective factors remain uncorrelated.

The other assumption that we shall revisit concerns which types of predictors are allowed to affect which types of factors. Equations (2) to (4) included only a subset of theoretically plausible associations between known characteristics of the targets and informants and the latent factors that underlie informant ratings. Specifically, we allowed both target and informant characteristics to affect the common factor, but we restricted the predictors of the perspective factors to informant characteristics and the predictors of the specific factors to target characteristics. These restrictions are not strictly necessary and could be relaxed if there was a conceptual motivation or an empirical imperative to do so. For instance, if mothers rate girls as higher than boys on negative affect but fathers do not, then the perspective factor for one or the other parent could be regressed on child gender by adding target characteristic effects to Equation (3). Cross-informant effects could potentially also be added to Equation (3). Similarly, Equation (4) could be expanded to include informant characteristics or item-specific predictors (e.g., a predictor differentiating whether an item is positively or negatively worded). We regard the simpler specifications in Equations (2) to (4) to be conceptually and practically useful for a wide variety of potential applications of the tri-factor model, but decisions about which predictors to include should be driven by the theoretical underpinnings of a given application.

Aside from these two assumptions of the model, we shall also reconsider one assumption we have made concerning the data. To this point, we have assumed for simplicity that item sets are parallel across informants, i.e., that all informants provide ratings on the same set of items. This parallelism is theoretically desirable because it allows for the estimation of the specific factors and the separation of specific factor variance from random error. But the use of parallel items may not always be feasible, particularly when informants observe the target in different contexts with different affordances for behavior (e.g., behaviors at school or work versus behaviors at home). The tri-factor model is still applicable with non-parallel item sets; however, for items rated by only one informant the specific factors must be omitted from the model specification. For these items, the analyst must be mindful that specific factor variance is conflated with random error. One implication is that the reliability of the item may be under-estimated. Nevertheless, perspective and common factor loadings can be estimated and compared for these items. For structurally different informants, equivalence tests should be restricted to the subset of parallel items (if any).

Estimation

Estimation of the tri-factor model is straightforward if all ratings are made on a continuous scale. The model can then be fit by maximum likelihood in any of a variety of structural equation modeling (SEM) software programs (or by other standard linear SEM estimators). When items are binary or ordinal, however, estimation is more challenging. We provide a cursory review of this issue here; for a more extensive discussion of estimation in item-level factor analysis see Wirth and Edwards (2007).

Maximum likelihood estimation with binary or ordinal items is complicated by the fact that the marginal likelihood contains an integral that does not resolve analytically and must instead be approximated numerically. Unfortunately, the computing time associated with the most common method of numerical approximation, quadrature, increases exponentially with the number of dimensions of integration. As typically implemented, the dimensions of integration equal the number of factors in the model. Given the large number of factors in the tri-factor model (1 + R + I), this approach would seem to be computationally infeasible. Cai (2010a), however, noted that for certain types of factor analytic models, termed two-tier models, the dimensions of integration can be reduced. The tri-factor model can be viewed as a two-tier model where the common and perspective factors make up the first tier and the specific factors make up the second tier. Using Cai’s (2010a) approach, the dimensions of integration for the tri-factor model can then be reduced to a more manageable number and computationally efficient estimates can be obtained by maximum likelihood using quadrature. Another option is to implement a different method of numerical approximation, for instance Monte Carlo methods. In particular, the Robbins-Monro Metropolis-Hastings maximum likelihood algorithm developed by Cai (2010b, 2010c) is also a computationally efficient method for fitting the tri-factor model. Similarly, Bayesian estimation by Markov Chain Monte Carlo (MCMC) approximates maximum likelihood when priors are selected to be non-informative (Edwards, 2010).

An alternative way to fit the tri-factor model is to use a traditional, limited-information method of estimation that is somewhat less optimal statistically but quite efficient computationally. Motivating this approach is the notion that binary and ordinal responses can be viewed as coarsened versions of underlying continuous variables (Christoffersson, 1975; Muthén, 1978; Olsson, 1979). For instance, the binary item “lonely” reflects an underlying continuous variable “loneliness.” Assuming the underlying continuous variable to be normally distributed corresponds to a probit model formulation (e.g., choosing g in Equation (1) to be the probit link function). Based on this assumption and the observed bivariate item response frequencies, polychoric correlations can be estimated for the underlying continuous variables. Finally, the model is fit to the polychoric correlation matrix using a weighted least squares estimator. The theoretically optimal weight matrix is the asymptotic covariance matrix of the polychoric correlations but this weight matrix is unstable except in extremely large samples (Browne, 1984; Muthén, du Toit & Spisic, 1997). In practice, a diagonal weight matrix is often employed as a more stable alternative (Muthén et al, 1997). Simulation studies have demonstrated that this Diagonally Weighted Least Squares (DWLS) estimator performs well even at relatively modest sample sizes (Flora & Curran, 2004; Nussbeck et al., 2006).

Several issues beyond computational efficiency may also influence estimator selection. Practically, weighted least squares and DWLS are widely accessible and easily implemented in a variety of SEM software programs. Further, analysts using these estimators have access to well-developed tests of model fit and goodness of fit criteria from which to judge the suitability of the model for the data. ML and Bayesian MCMC estimation approaches, however, more favorably accommodate missing data. In this context, missing data is most likely to occur due to informant non-response, such that all items for a given informant are missing. Both ML and MCMC estimation include cases with partial data under the assumption that the missing data are missing at random. In contrast, weighted least squares estimators are often implemented under the assumption of complete data, requiring listwise deletion and implicitly assuming missing data are missing completely at random. Within some software (e.g., Mplus), partially missing data is permitted with weighted least squares or DWLS under the assumption that the missing data process may be covariate-dependent (Asparouhov & Muthén, 2010).⁴

Another issue that may influence estimation is factor loading reflection (Loken, 2005). Specifically, an equivalent fit to the data can be obtained by reversing the polarity of a factor (e.g., multiplying all factor loadings for a factor by negative one). In practice this problem is most likely to affect doublet specific factors (occurring when only two informants rate each item). For maximum likelihood and weighted least squares estimation factor loading reflection is largely a nuisance that can be avoided by providing positive start values for the factor loadings or by judiciously implementing positivity constraints. With MCMC estimation, however, factor loading reflection can be a more serious problem as the iterative process constructs a bimodal posterior distribution by sampling positive and negative values for the factor loadings, but “converging” on neither estimate. Informative priors, particularly for doublet specific factor loadings, can help to mitigate this problem.

Scoring

After fitting the model it will often be of interest to obtain score estimates for the sample that can be used in later data analyses. For instance, the primary goal behind our development of the tri-factor model was to obtain negative affect scores that we could subsequently use in longitudinal analyses to predict the onset of substance use disorders (Hussong et al., 2011). Rather than include the mother’s ratings and father’s ratings of the child as separate measures, we wished to obtain a single, integrated, multi-informant measure that would be purged of the idiosyncratic views of the specific informants, including potential rater bias. Thus our focus was on obtaining valid and reliable common factor scores. In other applications, however, the perspective factor score estimates may be of equal or greater interest. For instance, Lance et al. (2008) and De Los Reyes (2011) argue that rating discrepancies across informants are substantively meaningful and should not be regarded simply as a type of measurement error.

Score estimates for the factors are obtained similarly regardless of the method of estimation used to fit the tri-factor model. Specifically, score estimates are computed as either the mean or the mode of the posterior distribution of the factor for the individual given his or her observed item responses and the parameter estimates for the model (see Skrondal & Rabe-Hesketh, 2004, sections 7.2–7.4). With continuous items, the mean and mode coincide and can be computed via the regression method (Bartholomew & Knott, 1999; Thomson, 1936, 1951; Thurstone, 1935). With binary or ordinal items the mean and mode are not equal but tend to be highly correlated. In the literature on item response theory the mean is usually referred to as the Expected a Posteriori (EAP) estimate and the mode is usually referred to as the Modal a Posteriori (MAP) estimate, with the latter being somewhat easier to compute (Thissen & Orlando, 2001).⁵

Both EAPs and MAPs are “shrunken” estimates, meaning that the scores generated for the target will be closer to the factor mean (across targets) as the amount of information available for the target (e.g., number of items rated) decreases. Conceptually, we are using what we know about the population in general to improve our score estimates for each specific individual. In the unconditional tri-factor model, all scores for a given factor are shrunken toward the same marginal mean. In contrast, in the conditional tri-factor model, scores are shrunken toward the conditional mean of the factor given the values of the predictors (Bauer & Hussong, 2009). In other words, rather than use the overall average to improve our score estimate for the target, we can use the average for people who are similar to the target with respect to the predictors. For example, if the common factor is regressed on the sex of the target, then scores for girls will be shrunken toward the conditional mean for girls and scores for boys will be shrunken toward the conditional mean for boys. In this sense, the scores obtained from a conditional tri-factor analysis are “tuned” to the characteristics of the target and informants.

Summary

In total, the tri-factor model provides a number of key advantages for modeling multi-informant data. First, the model does not require ratings on multiple traits or multiple targets, as the focus is not on construct validity but on construct measurement. Second, because the model is fit to item-level data from multiple informants, it is possible to evaluate item quality in a way that is not possible when analyzing scale-level data or single-informant item-level data. Third, the conditional formulation of the tri-factor model permits tests of hypotheses about putative sources of trait variability, informant differences, and item properties. Finally, the model can be used to create and evaluate scores for the factors for use in subsequent analyses. When generated from the conditional tri-factor model these scores are tuned to the specific characteristics of the targets and informants.

Let us now turn to an empirical application of the tri-factor model to illustrate these advantages of the model.

Example: Parent-Reported Negative Affect

Our demonstration derives from an integrative data analysis of two longitudinal studies of children of alcoholic parents and matched controls (children of non-alcoholic parents): the Michigan Longitudinal Study (MLS; Zucker et al., 1996, 2000) and the Adolescent and Family Development Project (AFDP; Chassin, Rogosch & Barrera, 1991). As noted by Curran et al. (2008), a major challenge in conducting integrative data analysis is measurement (see also Bauer & Hussong, 2009; Curran & Hussong, 2009). In combining longitudinal studies, in particular, one must be sensitive to age-related changes in the construct and the age-appropriateness of the items. In the present case, we sought to obtain a measure of negative affect for children between 2 and 18 years of age based on ratings provided by both mothers and fathers. In fitting the tri-factor model to this data our aims were threefold. First, we sought to explicate the sources of variance, both random and systematic, that underlie parent ratings of negative affect. Second, we wished to evaluate potential study, age, familial risk, and gender differences in negative affect, both as broadly defined across the item set and as narrowly measured by specific items. Third, we sought to generate valid and reliable negative affect scores that would account for potential rater biases, for instance due to parental depression.

Sample

Like many psychometric models, the tri-factor model assumes independence of observations. This assumption would be violated if we applied the model directly to the full set of longitudinal data. We thus pursued the strategy recommended by Curran et al. (2008) to select ratings randomly from a single age for each participant for inclusion in the tri-factor analysis. We refer to this cross-sectional draw from the data as the calibration sample (N=1080). It is this sample that is used to fit, evaluate, and refine the model. Once the optimal model has been determined, however, the estimates obtained from the calibration sample can be used to generate factor score estimates for the full set of observations, facilitating subsequent longitudinal analyses.

To check the stability of our results, we also randomly selected a second set of ratings for each target (excluding the ages selected for the calibration sample) and refit the final model. We shall refer to this second cross-sectional sample as the cross-validation sample (N=975). More ideally, we would cross-validate the model on a truly independent sample; nevertheless, this second sample provided an opportunity to evaluate the stability of the parameter estimates and scores obtained from the model.

Table 1 shows the number of observations at each age from each study present in the original longitudinal sample, the calibration sample, and the cross-validation sample.

Table 1.

Number of observations by age and study

Age	Full Longitudinal Sample		Calibration Sample		Cross-Validation Sample
	MLS	AFDP	MLS	AFDP	MLS	AFDP
2	11	-	2	-	2	-
3	137	-	45	-	24	-
4	111	-	27	-	27	-
5	91	-	30	-	20	-
6	127	-	29	-	29	-
7	122	-	31	-	29	-
8	107	-	25	-	30	-
9	160	-	41	-	42	-
10	150	32	43	9	38	12
11	131	107	36	42	31	27
12	172	191	55	55	55	73
13	154	266	45	96	48	82
14	149	294	48	89	43	103
15	159	247	54	84	33	87
16	146	150	54	64	32	42
17	139	54	50	15	35	19
18	25	4	9	0	8	4
N	2091	1345	626	454	526	449

Measures

Thirteen binary items present in both the MLS and AFDP studies (originating from the Child Behavior Checklist; Achenbach & Edelbrock, 1981) were identified as indicators of negative affect for inclusion in the tri-factor analysis, as shown in Table 2. For conditional models, target-specific characteristics of interest were study (58% from MLS), gender (64% male), and age (range 2–18; M=12.07, SD=3.84). Informant-specific characteristics of interest were lifetime history of an alcohol use disorder (AUD; 24% of mothers, 65% of fathers), depression or dysthymia (14% of mothers, 9% of fathers), or antisocial personality disorder (ASP; 1% of mothers, 12% of fathers). ASP almost always co-occurred with an AUD, thus impairment was assessed via three binary parental impairment variables indicating: (1) history of depression or dysthymia, (2) history of an AUD without ASP, and (3) history of an AUD with ASP.

Table 2.

Numbers of non-missing values (N) and endorsement rates for negative affect items in the calibration sample.

Item	Mother		Father
	N	endorse	N	endorse
1. lonely	1048	0.17	905	0.18
2. cries a lot	1048	0.17	906	0.14
3. fears do something bad	1047	0.16	904	0.20
4. has to be perfect	1049	0.41	905	0.39
5. no one loves him/her	1048	0.23	906	0.18
6. worthless or inferior	1049	0.22	904	0.16
7. nervous/tense	1049	0.21	906	0.22
8. fearful/anxious	1048	0.18	906	0.16
9. feels guilty	1049	0.11	906	0.09
10. sulks a lot	1047	0.27	907	0.25
11. sad/depressed	1048	0.23	907	0.19
12. worries	1048	0.38	905	0.29
13. others out to get him/her	1048	0.10	906	0.10

Fitting the tri-factor model

Unconditional model

We fit the model shown in Figure 1 to the calibration sample data using the WLSMV (DWLS) estimator in Mplus version 6.1 (Muthén & Muthén, 1998–2010).⁶ Because mothers and fathers are structurally different informants, the underlying process by which they rate the negative affect of their child may differ. As such, we initially allowed the model parameters to differ across the two informants. Each factor was scaled to have a mean of zero and variance of one with the exception that the father perspective factor mean and variance were freely estimated. Identification constraints were imposed to equate the intercepts and factor loadings of one item across mothers and fathers. Since the specific factors were doublets, we avoided the factor loading reflection problem by imposing boundary constraints on the loadings of these factors. Overall, this model provided good fit to the data, χ²(261) = 550.69, p < .0001; RMSEA = .03 (90% CI = .028–.036); CFI = .96; TLI = .95.

We next evaluated the degree of structural similarity between mothers’ and fathers’ ratings. We began by imposing equality constraints only on the item intercepts and factor loadings (i.e., factorial invariance). The fit of this model was still good, χ²(297) = 569.73, p < 0001; RMSEA = .03 (90% CI = .026–.033); CFI = .96; TLI = .96, but significantly worse than the unrestricted model, Δχ²(36)= 62.50, p=.004.⁷ Because the chi-square difference test is sensitive to sample size, potentially having power to detect even trivial differences between parameter values, Cheung and Rensvold (2002) suggested retaining invariance constraints that do not lead to a meaningful decrement in goodness of fit indices (i.e., RMSEA, CFI, TLI). More recently, however, Fan and Sivo (2009) argued that changes in goodness of fit indices are insensitive to misspecification of the mean structure, particularly in large models. Consistent with the latter observation, further inspection of the results suggested that, all else being equal, fathers were more likely to endorse Item 3, and mothers were more likely to endorse Items 5, 6, and 12 (see Table 2). Allowing only the intercepts of these four items to differ across informants resulted in a non-significant chi-square difference relative to the unrestricted model, Δχ²(32)= 45.02, p=.06.

Given this partial invariance of the factor structure across mothers and fathers, we proceeded to test whether the perspective factor means and variances differed between the two informants. Equating these parameters (i.e., setting the perspective factor mean and variance to zero and one, respectively, for both informants) did not significantly worsen the fit of the model, Δχ²(2) = 1.34, p=.51, and the absolute fit of this model was also good, χ²(295) = 511.16, p < 0001; RMSEA = .03 (90% CI = .022–.030); CFI = .97; TLI = .97. Thus, mothers and fathers functioned similarly to interchangeable raters, with the important exception that they differentially endorsed four out of thirteen items.

Conditional model

In extending to the conditional tri-factor model we adopted the scaling convention to set the intercept and residual variance of the factors to zero and one, respectively. The model was then fit in a sequence of steps, ordered by theoretical priority. First, we regressed the common factor on potential sources of target variability. We evaluated target effects of study, gender, age (including linear, quadratic and cubic trends), and all two-way interactions between these predictors, trimming non-significant interactions from the final model.⁸ Referencing Figure 2, this block of predictors replaces the single predictor w. Simultaneously, we included informant-specific effects of parental impairment on the common factor.⁹ The parental impairment variables thus replace x_M and x_F in Figure 2, with paths included from these predictors to the common factor. The effects of the parental impairment variables were initially allowed to differ over informants, and this model provided good fit to the data, χ²(596) = 876.41, p < 0001; RMSEA = .02 (90% CI = .019–.025); CFI = .95; TLI = .95. Constraining these effects to be equal did not significantly worsen model fit, Δχ²(3) = 2.10, p=.55; χ²(599) = 860.60, p < 0001; RMSEA = .02 (90% CI = .018–.025); CFI = .96; TLI = .95. We thus retained these equality constraints.

Second, we regressed each perspective factor on the impairment indicators for the corresponding informant. Referring again to Figure 2, we added the paths from x_M and x_F to P_M and P_F, where each x stands for a set of impairment variables. Here it is important to differentiate the two effects of the parental impairment variables. The regression of the common factor on the impairment variables captures the potentially real elevation of negative affect of children with one or more impaired parents. To the extent that the negative affect of children of impaired parents is actually higher than that of other children, this should be reflected in the ratings of both parents, as transmitted by the common factor, irrespective of which parent might be impaired. Prior literature suggests, however, that impaired parents may also provide artificially elevated ratings of negative affect. The regression of the perspective factors on the impairment variables captures this possible source of rater bias, which should be observed only in the ratings of the impaired parent and not an unimpaired co-parent. We again initially allowed these effects to differ by informant, χ²(593) = 846.54, p < 0001; RMSEA = .02 (90% CI = .018–.024); CFI = .96; TLI = .95, and then constrained them to be equal, χ²(596) = 838.79, p < 0001; RMSEA = .02 (90% CI = .017–.024); CFI = .96; TLI = .96. As the chi-square difference test (Δχ²(3) = 2.37, p=.50) was not significant, we retained the more parsimonious structure with equal effects across informants.

The fit of the conditional tri-factor model at this step was already quite good; nevertheless, to be conservative, we proceeded to evaluate potential target effects on the specific factors that, if falsely excluded from the model, might distort the pattern of effects observed for the common factor (akin to the assessment of differential item functioning in item response theory). Because we had no theoretical predictions concerning the specific factors, we identified these effects using an empirical approach. Specifically, we examined modification indices to identify items for which target-specific effects might explain systematic variation. The mechanical use of modification indices in structural equation models has been criticized (appropriately) for failing to identify model misspecifications accurately (MacCallum, Roznowski and Necowitz, 1992), but more targeted uses of modification indices in measurement models have proven beneficial (Glas, 1998; Yoon & Millsap, 2007). Additionally, to reduce the likelihood of capitalizing on chance, we adopted a conservative criterion for effect inclusion: a modification index exceeding 6.64, the critical value for a single degree-of-freedom chi-square test with an alpha level of .01. Predictors of the specific factors were added to the model one at a time, beginning with the effect displaying the largest modification index. Using this approach we detected target effects for the specific factors of Items 1, 2, 3, 4, 8, 9 and 12 (see Table 2). The fit of the final model including these effects was excellent, χ²(586) = 718.34, p = .0001; RMSEA = .015 (90% CI = .011–.019); CFI = .98; TLI = .98.

Interpretation

Raw and standardized intercept and factor loading estimates for the final tri-factor model are presented in Table 3. The standardized solution is particularly informative as the magnitudes of the standardized factor loadings are directly comparable and indicate the relative effects of the common, perspective, and specific factors on the items. Comparing columns of Table 3, we can see that the common factor loadings are often lower than the perspective and specific factor loadings. Thus the negative affect common factor often contributes less to the item ratings than variation uniquely associated with the informant or that is specific to a given item. Comparing rows of Table 3, we can see which items most reflect the common factor and are least susceptible to perspective differences. At the extreme, we can see that the item “has to be perfect” has a very small loading on the common factor. Endorsement of this item co-occurs with other items almost exclusively due to unique perspective effects, something that would not be revealed in a factor analysis of a single informant’s ratings. It is encouraging to note, however, that the items that might be considered core features of negative affect also tend to have the highest common factor loadings (e.g., Items 1, 5, 6, 10, 11, and 13).

Table 3.

Raw and standardized intercept and factor loading estimates from the conditional tri-factor model fit to the calibration sample (final model).

Raw Estimates
Item	Intercept	Factor Loading
		Common	Perspective	Specificity
1. lonely	−0.85	0.73	0.62	0.49
2. cries a lot	−0.60	0.65	0.59	0.81
3. fears do something bad	−0.82 (M), −0.76 (F)	0.41	0.70	0.59
4. has to be perfect	0.45	0.11	0.78	0.80
5. no one loves him/her	−0.42 (M), −1.08 (F)	0.97	0.71	0.40
6. worthless or inferior	−1.18 (M), −1.61 (F)	1.06	1.00	0.67
7. nervous/tense	−2.34	0.66	1.60	1.85
8. fearful/anxious	−1.18	0.37	1.16	0.65
9. feels guilty	−2.49	0.87	1.52	1.11
10. sulks a lot	−0.50	0.66	0.70	0.00
11. sad/depressed	−1.22	0.99	0.87	0.01
12. worries	0.26 (M), −0.24 (F)	0.58	1.18	0.76
13. others out to get him/her	−2.05	0.76	0.67	0.40

Standardized Solution
Item	Intercept	Factor Loading
		Common	Perspective	Specificity
1. lonely	−0.53	0.52	0.39	0.50
2. cries a lot	−0.33	0.41	0.33	0.69
3. fears do something bad	−0.55 (M), −0.51 (F)	0.31	0.48	0.43
4. has to be perfect	0.28	0.08	0.50	0.58
5. no one loves him/her	−0.24 (M), −0.64 (F)	0.65	0.42	0.23
6. worthless or inferior	−0.59 (M), −0.81 (F)	0.60	0.51	0.34
7. nervous/tense	−0.84	0.27	0.59	0.67
8. fearful/anxious	−0.62	0.22	0.62	0.50
9. feels guilty	−1.00	0.40	0.62	0.49
10. sulks a lot	−0.35	0.52	0.49	0.00
11. sad/depressed	−0.69	0.64	0.51	0.00
12. worries	0.14 (M), −0.12 (F)	0.35	0.63	0.43
13. others out to get him/her	−1.33	0.56	0.44	0.26

Note: Intercepts that differed between mothers and fathers are labeled (M) or (F), respectively, to specify the informant. Standardized factor loading estimates differ slightly between mothers and fathers (never exceeding a difference of .04). Values for mothers are reported.

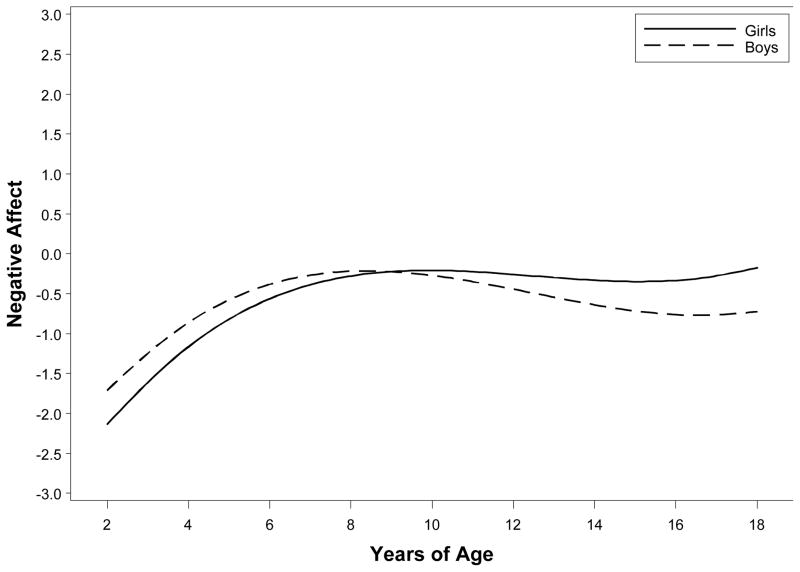
Table 4 presents raw and partially standardized estimates for the effects of the regressors on the factors. The partially standardized estimates are computed by standardizing the factors but leaving the regressors in their raw scales, and are particularly useful when predictors are binary (e.g., study, gender, and impairment) or have a meaningful metric (e.g., age). Sex-specific patterns of developmental change were detected for the common factor, as depicted in Figure 3. A study difference was also observed for the common factor: targets from MLS displayed lower levels of negative affect than targets from AFDP. In addition, parental impairment effects on the common and perspective factors indicate that depressed or ASP parents indeed have children with higher negative affect levels, but depressed parents in particular perceive the negative affect of their children to be even greater than it is commonly perceived to be (i.e., their ratings are biased).

Table 4.

Effects obtained from the regression of common, perspective, and specific factors on age, gender (male), study (MLS) and parental impairment.

Effect	Estimate	SE	Partially Standardized Estimate
Common Factor
Age	−0.003	0.042	−0.003
Age2	−0.015	0.003	−0.013
Age3	0.002	0.001	0.002
MLS	−0.764	0.131	−0.669
Male	−0.063	0.128	−0.055
Male*Age	−0.061	0.031	−0.054
Parent alcoholism	0.095	0.088	0.083
Parent alcoholism + ASP	0.582	0.174	0.510
Parent depression	0.369	0.130	0.323
Perspective Factors
Parent alcoholism	0.061	0.096	0.060
Parent alcoholism + ASP	−0.145	0.179	−0.143
Parent depression	0.538	0.126	0.528
Specific Factors
1. Lonely
Age	−0.313	0.119	−0.196
2. Cries a lot
Age	−0.295	0.079	−0.191
Male	−0.633	0.197	−0.411
3. Fears do something bad
MLS	−0.860	0.289	−0.796
4. Has to be perfect
Age	0.047	0.049	0.041
Age2	−0.019	0.005	−0.017
MLS	−0.771	0.191	−0.672
8. Fearful/anxious
MLS	−2.210	0.597	−1.522
9. Feels guilty
MLS	−0.912	0.285	−0.836
12. Worries
MLS	−0.847	0.239	−0.786

Note. Bold entries are significant at p < .05. Partially standardized estimates are computed by standardizing the factors but leaving regressors in their raw scales. Age was centered at 10 years. All binary predictors are named to indicate the presence of the characteristic (e.g., MLS is scored 1 for targets from the MLS study, 0 for targets from the AFDP study).

Figure 3.

Age trends in the common factor for negative affect for girls and boys (averaging over other predictors).

The last effects listed in Table 4 are for the specific factors. Most of these effects are for study, with some items being endorsed less frequently in the MLS sample than would be expected due to study differences on the common factor alone. Age trends are observed for several items as well. In particular, “lonely” and “cries a lot” show steeper declines with age than the common factor. “Has to be perfect” also follows a distinct age trend, but this is not terribly surprising given that this item did not load on the common factor. Finally, there is a gender difference on the item “cries a lot.” This item is more likely to be endorsed for girls than boys even after accounting for gender differences in the common factor of negative affect.

Sensitivity Analysis

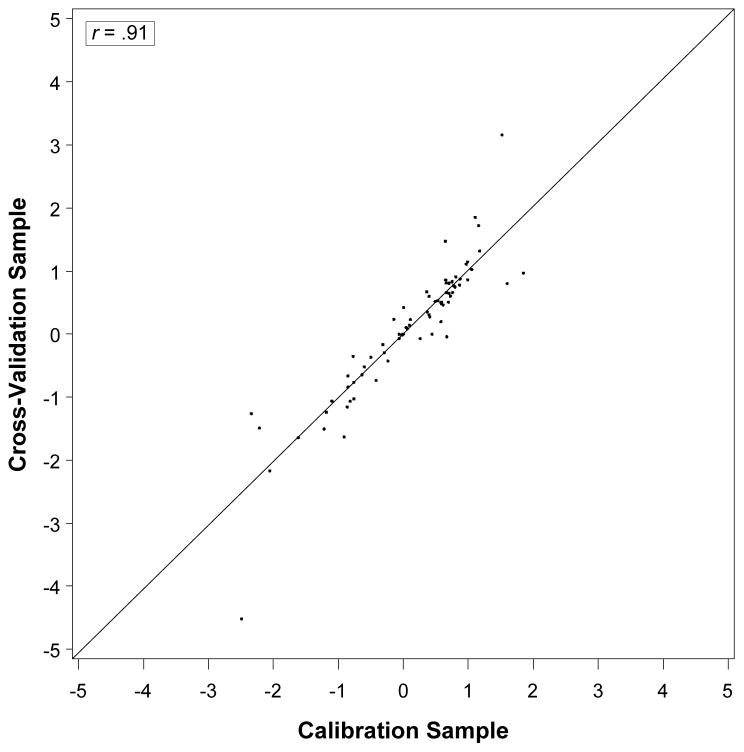
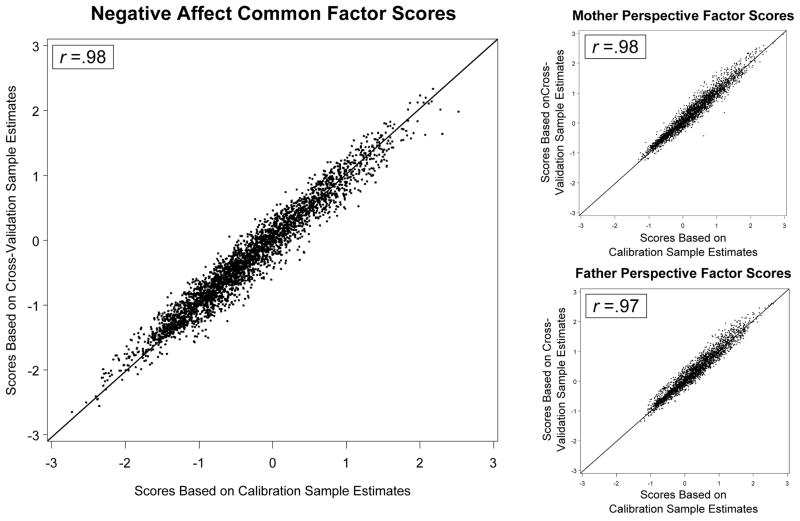
To examine the stability of the final model we refit the final conditional tri-factor model to the cross-validation sample, once again obtaining excellent fit, χ² (586) = 782.42, p < .0001; RMSEA = .02 (90% CI = .016–.023); CFI = .97; TLI = .96. The intercepts, loadings, and factor regression parameter estimates obtained from the two samples are compared in Figure 4. Although some discrepancies were observed for more extreme estimates, the two sets of estimates were generally quite similar and were correlated at .91. We also examined the stability of the scores obtained from the final model. Specifically, we generated both common factor and perspective MAP factor scores for the full longitudinal data based on each set of estimates. The correlations between the two sets of scores were between .97 and .98, as shown in the scatterplots in Figure 5, indicating a high level of stability.

Figure 4.

Plot illustrating stability of parameter estimates across two cross-sectional draws from the pooled longitudinal data.

Figure 5.

Scatterplots illustrating the stability of MAP scores generated from estimates obtained from two non-overlapping cross-sectional draws from the longitudinal data.

Comparison to Usual Practice

We also considered whether the scores generated by the tri-factor model differed meaningfully from what might be obtained using more conventional strategies. The alternative scoring strategies we implemented ranged from simple to complex. The simplest approach was to average the proportion of items endorsed by the mother with the proportion of items endorsed by the father. The next simplest approach was to compute the proportion of items endorsed by either the mother or the father. The more complex approaches we considered both involved factor analyzing the item responses of mothers and fathers separately, obtaining factor scores for each reporter and then an average factor score. In the first variant of this approach we obtained the factor scores from a standard two-parameter logistic item response theory model (without differential item functioning). In the second variant, we implemented a moderated nonlinear factor analysis model to allow for predictor effects on the factor as well as potential differential item functioning (Bauer & Hussong, 2009). In contrast to the tri-factor model, the appropriate application of these alternative scoring approaches is less clear when data is missing for an informant. In those instances scores were based solely on the ratings of the available informant.

The relations among the scores, as observed within the calibration sample, are summarized in correlation form in Table 5. Squaring the correlations, we can see that the common factor scores obtained from the tri-factor model share approximately 60% to 70% of their variance with the scores obtained from more conventional approaches. By contrast, it is interesting that the conventional scores are much more highly correlated, sharing between 86% and 94% of their variance, despite considerable differences in the complexity of the methods by which they were obtained.

Table 5.

Correlations between tri-factor analysis common factor scores, the average proportion of items endorsed by mothers and fathers, the proportion of items endorsed by either mothers or fathers, and the average of factor score estimates obtained separately for mothers and fathers.

	TriFS	AvgProp	OrProp	AvgFS1	AvgFS2
Tri-factor common factor scores (TriFS)	1.00
Average proportion of items endorsed by mothers and fathers (AvgProp)	0.79	1.00
Proportion of items endorsed by either mothers or fathers (OrProp)	0.79	0.95	1.00
Average of factor scores estimates obtained separately for mothers and fathers from a 2PL-IRT model (AvgFS1)	0.82	0.97	0.93	1.00
Average of factor scores estimates obtained separately for mothers and fathers from a MNLFA model (AvgFS2)	0.84	0.97	0.93	0.99	1.00

Note. 2PL-IRT = two-parameter logistic item response theory model, MNLFA model = moderated nonlinear factor analysis model

It is clear from these results that the common factor scores generated from the tri-factor analysis overlap with but are distinct from the scores provided by other approaches. The shared variance between the scores reflects the fact that each approach taps into the consensus view of the target to some extent. We would argue, however, that the tri-factor model provides a more interpretable measure of the target because it formally separates the unique perspective factor variance from the common factor variance. With ad hoc scoring approaches perspective effects (including rater bias) will often contaminate the combined scores, particularly when there are relatively few informants and these effects are unlikely to “average out.” Indeed, when we examined the correlations between the ad hoc measures and the perspective factor scores obtained from the tri-factor analysis, we found these correlations to be substantial (r = .47–.54).

Conclusions

Relative to simpler approaches for aggregating multiple informant data, psychometric models offer an important advantage: they embody an explicit theoretical model of the sources of variation in informant ratings. The tri-factor model proposed here stipulates that the observed item responses reflect three sources of variation: a common factor, a perspective factor for the informant, and a specific factor for the item. In contrast to models developed for MTMM data, which largely focus on issues of construct validation, the tri-factor model is principally intended to serve as a measurement model. The tri-factor model provides information on the quality of the items; that is, the extent to which the responses to each item reflect the common factor versus perspective factors or specific factors. Additionally, predictors may be incorporated into the model to test putative sources of underlying target differences and/or rater bias. Finally, we can obtain scores from the tri-factor model that separate the common view of the target from the unique views of the individual informants, and that reflect the specific characteristics of the target and informants.

Our development of the tri-factor model draws upon a 100-year tradition in factor analysis of defining and interpreting factors in terms of the patterns of dependence they induce among the manifest indicators (beginning with Spearman, 1904). The tri-factor model also represents a straightforward extension of the bi-factor model originally developed by Holzinger and Swineford (1937), with a novel application to multiple informant data (for other recent extensions and applications of the bi-factor model within psychological research see Cai, Yung and Hansen, 2011; Gibbons and Hedecker, 1992; Gibbons et al, 2007; Reininghaus et al, 2011; Reise et al, 2011). In this sense, the tri-factor model is fully consistent with factor analytic theory. It is important to recognize, however, that the conventional approach to specifying and interpreting factor analytic models has sometimes been criticized. Two specific concerns are that model restrictions (e.g., independence of factors) sometimes appear arbitrary and that the meaning of the latent variables is inferred from intuition rather than formal psychometric theory (e.g., true score/classical test theory). These issues are discussed in detail for MTMM model specifications in Eid (2000), Pohl and Steyer (2010) and Pohl, Steyer & Kraus (2008), and with respect to closely related latent state-trait models in Steyer (1989), Steyer, Ferring and Schmitt (1992), and Geiser and Lockhart, (2012). The tri-factor model is potentially open to similar critiques. Yet we are of the opinion that there are many different and useful ways to define and interpret latent variables (see Bollen, 2002) and that a broad, inclusive approach enables the development of models that are both conceptually appealing and practically useful. In this sense, the ultimate utility of the tri-factor model will be borne out through empirical applications, similar to our analysis of parent-reported negative affect.

There are, of course, many potential directions for future research on the tri-factor model. For instance, the data analytic conditions under which the tri-factor model can be usefully applied are presently unclear. Simulations examining parameter recovery across variations in sample size, number of items, item type (continuous versus binary or ordinal), number of informants, extent of missing data, number of predictors, and methods of estimation would be informative in this regard, but lie outside of the scope of the present study. The stability of our empirical results and the face validity of our findings are suggestive that the model will generally perform well with reasonably large samples. Another interesting avenue of research would be to apply the model in an experimental setting in which some informants are intentionally manipulated to provide biased ratings, to determine the extent to which the model can adequately detect this bias and remove it from the common factor score estimates.

Additionally, because the tri-factor model is a type of SEM, there are many potential ways that the model could be extended. For instance, one could include latent predictors to estimate regressor effects without biases due to measurement error. Alternatively, one could include criterion variables predicted by the common factor or perspective factors. Given the challenges of estimating these models, however, we believe that the greatest utility of the tri-factor model is as a measurement model for evaluating item quality and for generating scores. In most cases an investigator will wish to generate scores for the common factor, and perhaps also for perspective factors, for use in subsequent analyses. For instance, the motivation behind our example analysis was to generate negative affect scores so that we could examine whether trajectories of negative affect over childhood and adolescence could be used to predict substance use disorders in adulthood. The tri-factor model provided us with a way to generate an integrated negative affect measure based on ratings from both the mother and father while also controlling for possible rater biases. It is our hope that other investigators will similarly find the tri-factor model useful for understanding and summarizing the information provided by multiple informants in their own research.