A model of subjective report and objective discrimination as categorical decisions in a vast representational space

Abstract

Subliminal perception studies have shown that one can objectively discriminate a stimulus without subjectively perceiving it. We show how a minimalist framework based on Signal Detection Theory and Bayesian inference can account for this dissociation, by describing subjective and objective tasks with similar decision-theoretic mechanisms. Each of these tasks relies on distinct response classes, and therefore distinct priors and decision boundaries. As a result, they may reach different conclusions. By formalizing, within the same framework, forced-choice discrimination responses, subjective visibility reports and confidence ratings, we show that this decision model suffices to account for several classical characteristics of conscious and unconscious perception. Furthermore, the model provides a set of original predictions on the nonlinear profiles of discrimination performance obtained at various levels of visibility. We successfully test one such prediction in a novel experiment: when varying continuously the degree of perceptual ambiguity between two visual symbols presented at perceptual threshold, identification performance varies quasi-linearly when the stimulus is unseen and in an ‘all-or-none’ manner when it is seen. The present model highlights how conscious and non-conscious decisions may correspond to distinct categorizations of the same stimulus encoded by a high-dimensional neuronal population vector.

1. Introduction

Since Helmholtz's (1867–1910) proposal of perception as unconscious inference, several computational models have been put forward to describe the mechanisms of this process [1,2]. The hypothesis that perception corresponds to an inferential decision on sensory data has received support from neurophysiological recordings during perceptual tasks [3,4]. For instance, intracranial [5] and scalp recordings [6,7] have revealed a neural response seemingly reflecting the accumulation of sensory evidence following the presentation of a stimulus and which may predict how subjects perceive the stimulus [8].

Nevertheless, superficially at least, conscious perception does not always seem to obey the logic of optimal perceptual inference. For instance, one can objectively discriminate a stimulus at above-chance level while subjectively claiming not to have seen it [9,10]. This paradoxical dissociation, referred to as ‘subliminal perception’, has nourished a vast body of philosophical and scientific proposals on the nature of conscious and unconscious perception. For instance, Tononi & Edelman [11] have argued that conscious processes are quantitatively more complex, integrated and differentiated than unconscious processes. Lau [12] and Rosenthal [13] claim that conscious perception is qualitatively different from unconscious perception, as it relies on higher order metacognitive representations. Recent empirical studies challenge these accounts, however. First, subliminal stimuli can recruit complex semantic and integrative processes [14–16]. Second, even second-order metacognitive inferences can apparently be performed above chance on unseen stimuli [17,18].

Here, building upon earlier proposals [8,12], we explore a simple theoretical idea: objective and subjective tasks rely on the same inference principles, but they differ in the nature and size of the decision space. Our proposal stems from Signal Detection Theory (SDT) and outlines how a minimal extension of the classic unidimensional depiction of SDT to multiple dimensions provides geometrical intuitions on several empirical findings in conscious and unconscious perception.

Specifically, we identified six major sets of empirical findings that should be accounted for:

• — Stimuli which are subjectively reported as ‘unseen’ can nevertheless be objectively discriminated above chance in a two-alternative forced-choice task [9,16,19–22].

• — Discrimination performance is typically better on seen than on unseen trials, even when sensory stimuli are physically identical [23–25].

• — Experimental paradigms can be designed in which objective discrimination performance is identical, while subjective visibility differs [12,24,26].

• — Subjective reports vary nonlinearly as a function of sensory strength. For instance, brief or faint visual stimuli are generally reported as ‘completely unseen’, but once their duration or contrast reaches a threshold level, subjects tend to report items as ‘clearly seen’ [23,25,27–29].

• — Prior knowledge increases the subjective visibility of physically identical stimuli [29–32].

• — Attention generally increases subjective visibility but has also been found to decrease it [9,26].

2. Model

(a). General assumptions

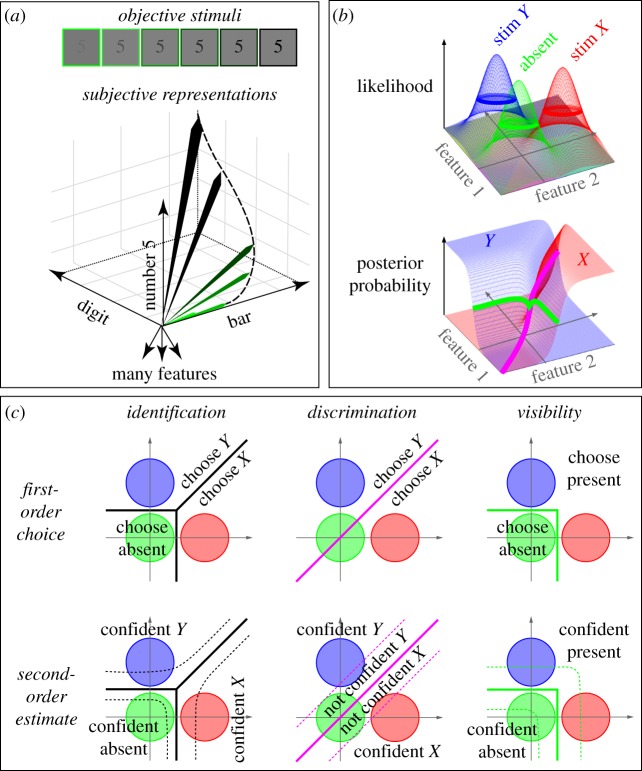
Our first assumption is that incoming stimuli are encoded as continuous vectors in a vast representational space. In the visual domain, for instance, a hierarchy of specialized visual processors decompose any visual scene into a broad variety of features that range from low-level (line orientation, contrast, colour, etc.) to higher level attributes (face/non-face, etc.). Each of these features may be encoded by the firing rate of a group of neurons. Mathematically, each stimulus is therefore encoded by a set of coordinates, one for each feature dimension (figure 1a).

Figure 1.

A multi-dimensional decision-theory framework for objective discrimination and subjective reports. (a) Stimulus information is represented in a vast vector space, in which each dimension encodes the evidence about a particular feature. Each sensory stimulus thus corresponds to an input vector whose length and direction change depending on the quality of the stimulus. (b) When considering binary decisions (e.g. perceiving stimuli X or Y), the huge dimensionality of the representational space can be approximated by a two-dimensional feature space. In this space, assuming that the true stimulus distributions are known, the likelihood (top), the prior and the posterior probability (bottom) of belonging to a given class (‘absent’ trial in green, stimulus X in red, or stimulus Y in blue) can be computed for each input vector (here, the posterior probabilities of the absent class have been removed for readability.) (c) Posteriors can be used to perform different tasks. In each case, the regions of the problem space corresponding to a fixed decision are delineated by a boundary. Identification consists in finding the MAP across all classes (absent, X or Y; black lines). Discrimination consists in determining the MAP among a restricted set of classes (X or Y; purple line). Visibility judgement consists in determining whether the absent class is the most likely among all classes (‘absent’ or not ‘absent’; green line). Each of these first-order decisions can be supplemented by a second-order confidence judgement task, which is modelled as the estimation of the likelihood of a correct response in the primary task. Samples far away from the decision border are associated with higher posterior probabilities of the corresponding class and can thus be classified as more ‘confident’ than samples close to the border. This geometrical representation makes it clear that each confidence judgement is always attached to a specific task and is thus not necessarily identical to visibility judgement. Note that the present colour coding (classes, tasks, etc.) will be used throughout the figures.

Second, stimulus strength is assumed to be directly reflected in the length (i.e. the norm) of the input vector. This assumption corresponds to the observation that the depth of sensory encoding varies with the quality of the incoming stimulus: a briefly flashed and masked stimulus only evokes modest activity in higher visual cortices [25,28], and thus its internal vector has a small projection, particularly on high-level dimensions. Conversely, an unmasked high-contrasted image results in a long internal vector (figure 1a).

Our third assumption is that each behavioural task imposes, in a top-down manner, a categorical structure of classes to this continuous vector space (e.g. ‘click left for faces and right for non-faces’). Performing the task consists in identifying, on every trial, the class in which the input vector falls. Formally, this is a statistical inference problem: in order to perform optimally, given a sensory input and prior knowledge, subjects should attempt to compute the posterior probability of each of the classes in order to select the class with the maximum a posteriori (MAP) choice, which is the one most likely to be correct. Each task imposes distinct, possibly overlapping response classes, and may therefore lead to different answers.

Our fourth assumption is that the content of conscious perception, which can be reported verbally, is the outcome of such an inferential decision process, but with the specific characteristic of having a very rich set of classes. While simple binary decisions may be performed non-consciously (e.g. press right or press left [14]), the inference system that underlies conscious perception must remain constantly open to myriads of possible contents, including unexpected ones (e.g. a fire alarm). We propose that what the subject experiences as a conscious percept is the class with the highest posterior probability, among all possible classes. As we shall see, ‘negative’ classes, for example ‘I didn't see anything’, must also be considered.

(b). Geometrical approximation in two dimensions

The vast number of input features, classes and tasks makes the present proposal difficult to apprehend in its full generality. However, most of its properties can be approximately captured by projecting the large vector space onto a plane defined by the two main axes of interest (figure 1b,c). These axes are chosen to be two features or feature bundles that are most relevant to the task under consideration (e.g. the mean vectors of neuronal activity evoked by face and by non-face stimuli, if the task is face/non-face discrimination). Each circle represents the top of the distribution of a particular class of stimuli (i.e. likelihood function, given sensory and internal noise). The lines delimit the regions of space where response decisions change. Although one should not forget that this is just a considerable simplification of the underlying multi-dimensional space and stimuli distribution, this two-dimensional representation brings the present model closer to the classic two-class problem of SDT. Indeed, although SDT is not limited to a single dimension, it is often depicted as a binary problem with two Gaussian distributions plotted along a single axis. We argue that this classic diagram fails to capture the interaction between multiple features, classes and tasks, whereas a two-dimensional depiction fulfils these requirements (see [33–35] for similar proposals using two-dimensional representations to dissociate tasks such as discrimination and detection).

(c). Mathematical formulation

Bayesian theory describes the optimal way of selecting the most likely model of the environment, referred to as ‘hypothesis’ (H, here the response class), in the presence of sensory evidence (E), here the input vector. Each class is characterized by a likelihood function P(E|H) and a prior probability P(H). P(E|H) indicates the probability that the evidence E was generated by the class H, and therefore captures how sensory samples from a given class are distributed within the vector space. The prior probability P(H) defines the probability of H to occur independently of any evidence. Bayes' theorem stipulates that the posterior probability of H is a function of its prior probability and of its likelihood: P(H|E) = P(E|H) × P(H)/P(E). Finally, decisions result from the selection of the class that has the MAP probability. This MAP criterion results in the segregation of representational space into distinct regions separated by sharp decision boundaries (importantly, the placement of these boundaries does not constitute an additional hypothesis of the model, but derives directly from the hypothesis that decisions are based on a MAP criterion).

In the following simulations, we use a series of computational simplifications. First, we neglect the cost function associated with each decision—sometimes referred to as ‘loss’ or ‘utility’ function. In the presence of costs, the optimal decision is the one which minimizes the expected loss and may differ from the MAP. Mathematically, however, priors and costs play a similar role and were thus merged in the present paper for simplicity. Second, the present model assumes that priors are fixed in a given context, rather than continuously updated after each decision. Assuming modifiable priors would lead to important new predictions, but would also increase the number of ad-hoc parameters in the models (e.g. learning rate, estimated world volatility, creation or deletion of classes). Third, we assume Gaussian distributions in order to facilitate the computations. Fourth, importantly, we assume that subjects have an accurate estimate of stimulus distributions—although following Lau [12,35], we will discuss the important consequences that ensue when subjects’ priors and likelihood functions are inappropriately calibrated. Fifth, we assume that, on a given trial, the same input vector enters into different tasks, thus neglecting the possibility that the internal evidence evoked by a fixed stimulus may vary with the task, owing, for instance, to decay [15,36], noise level [25], attention [37] or other top-down changes. Finally, we treat stimulus evidence on a given trial as a single discrete point in the n-dimensional space. In the discussion, we briefly examine the additional properties that arise if these simplifying assumptions are relaxed.

(d). The fundamental three-class problem

Given these assumptions, binary decision experiments can be simplified to a stereotypical three-class problem: either nothing is presented (‘Absent’ trial), or one of two stimuli X or Y is displayed (figure 1b). Absent trials are assumed to correspond to a null vector whose likelihood function peaks at the origin of vector space. X and Y trials are represented by two base vectors, which are chosen as the axes of the two-dimensional representation.

In this typical set-up, three different tasks can be performed (figure 1c):

• (i) Identification consists in determining which hypothesis has the highest posterior probability (absent, X or Y?).

• (ii) Forced-choice discrimination consists in restricting the responses to a subset of classes (e.g. X or Y, excluding the absent class).

• (iii) Visibility judgement consists in reporting whether the stimulus is seen or unseen. We assume that this instruction is interpreted as a decision, whether the stimulus is most likely to be absent or present (i.e. absent or not absent?).

Formally, these are all first-order tasks, because they all ask a simple question: which class (or set of classes) could have led to the observed input vector? For each of them, the second-order ‘confidence’ judgement can also be performed by setting additional response classes, corresponding to whether the first-order decision has a high or low probability of being correct. As shown graphically in figure 1c, there is a distinct confidence judgement associated with each primary task. At the expense of Persaud et al. [38] and Lau et al. [12], we note that the second-order tasks need not coincide with visibility judgement. Also, note that, for both the first- and second-order decisions, the decision boundaries can be derived directly from the definition of the task, the priors and the likelihood functions for each class, and therefore do not constitute additional assumptions of the model.

3. Empirical consequences of the decision framework

We shall now see how this framework accounts for the six fundamental empirical properties listed earlier.

(a). Above-chance discrimination of stimuli reported as ‘unseen’

Empirical finding 1 is that perceptual decisions can be performed at above-chance level even when subjects report not seeing any stimulus [21,22,38–40]. For example, blindsight patients can perform simple discriminations on visual stimuli they report not seeing [19]. This paradoxical ability also exists in healthy subjects whose discrimination performances have been repeatedly shown to be dissociated from subjective reports (see reviews in [16,41]).

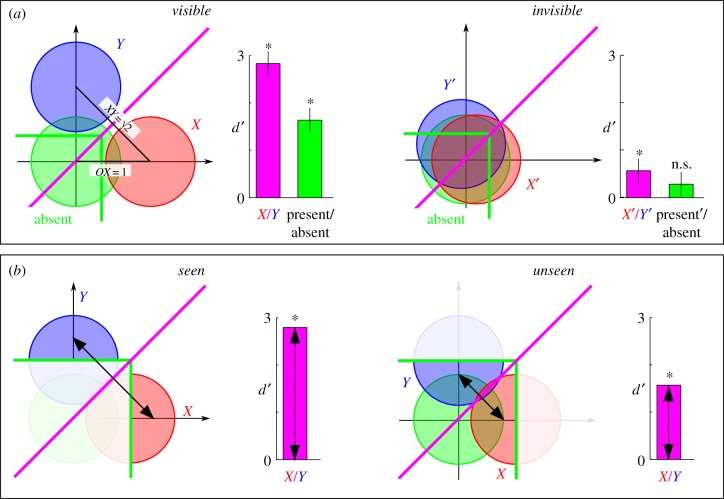
For simplicity, we only consider here the case in which two stimuli (X and Y) become undetectable when they are visually degraded (X’ and Y’). We assume that the degraded stimuli are generated from the same class as X and Y, yet with lower evidence (i.e. shorter vector length). As shown in figure 2a, it is quite possible for degraded stimuli X’ and Y’ to fall in the region reported as unseen during visibility judgement (i.e. the most likely class is absent), and yet to yield above-chance performance in a forced-choice task when discrimination is restricted to classes X and Y. This finding could be trivial if the visibility judgement was systematically biased towards the unseen response (and indeed such response bias has often been proposed as an interpretation of subliminal perception experiments [42]). However, our simulations assume a Bayes-optimal inference process. Thus, we show that there are conditions under which the absent or unseen response is the most probable one, and yet X versus Y can still be discriminated.

Figure 2.

An account of unconscious and conscious discrimination performance in two types of experimental designs. (a) In the stimulus degradation design, stimuli are made invisible by reducing the evidence (e.g. lowered contrast, masking, inattention). This manipulation makes the stimuli more similar to the absent class (right). As the XY distance can be longer than the distances separating the absent class and the stimuli classes (OX, OY), discrimination performance (purple) can remain significant while detection sensitivity (green) is not detectable better than chance. (b) In the fixed-stimulus design, near-threshold stimuli are sorted as a function of whether they are reported as seen or unseen. Unseen stimuli can be discriminated at above-chance levels, but discrimination performance improves drastically on seen trials.

The geometry of the two-dimensional model reveals why discrimination performance (i.e. d’ of X/Y discrimination) can be higher than detection sensitivity (i.e. d’ of absent/not-absent judgement): the distance separating the X and Y vectors is larger than that separating them from the absent class. In the two-dimensional case, discrimination performance is √2 higher than detection performance (figure 2a). Consequently, given adequate statistical power, discrimination may be significantly above chance when detection sensitivity is not.

The above account can also be extended to the second-order judgements, such as confidence rating and post-decision wagering on the first-order forced-choice X/Y discrimination task. Because such second-order judgements rely on similar decisional principles as the first-order tasks (figure 1c), confidence in discrimination can be above chance on unseen trials and confidence in visibility can be lower than that in discrimination. This conclusion fits with two recent experiments in which subjects performed above chance in their confidence judgements, even on trials reported as unseen [17,18].

(b). Discrimination performance generally improves with subjective visibility

Empirical finding 2 is that, although objective discrimination can be above chance with subjectively invisible stimuli, such unconscious performance is generally mediocre. In many studies, objective discrimination performance improves dramatically when the stimuli are reported as ‘seen’ compared with unseen, even when sensory stimulation is identical [23,25,27].

How does the model account for these findings? In experiments that compare highly contrasted and visible stimuli with degraded and invisible stimuli, the improvement in discrimination performance with subjective visibility is trivial (figure 2a): stimulus degradation diminishes the evidence for X and Y and thus worsens both visibility judgement and X/Y discrimination. The two tasks are thus necessarily correlated [12,24]. Less trivially, however, the model predicts the same effect for fixed stimuli presented at perceptual threshold. Even when the stimuli are physically identical, internal variability can explain why approximately 50% of them are reported as unseen (those which are most similar to the absent class). As a consequence of this variability, sensory inputs reported as unseen are associated with a shorter input vector and are therefore closer to the X/Y discrimination border than samples reported as seen (figure 2b). The simple hypothesis of a noisy input vector, together with non-orthogonal discrimination and detection tasks, suffices to explain why unseen trials generally exhibit a lower discrimination performance than seen trials.

(c). Discrimination performance can be equated on ‘seen’ and ‘unseen’ trials

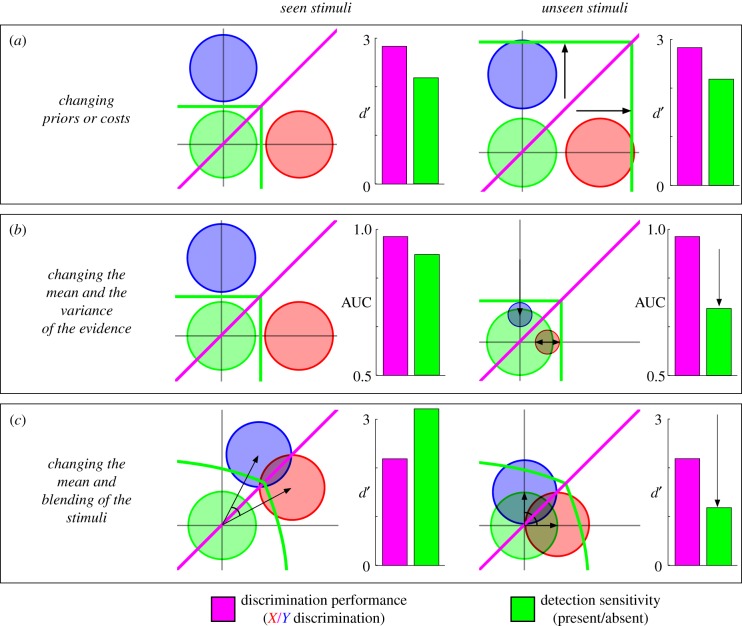
Empirical finding 3 is that it is possible to find experimental conditions in which discrimination performance is equated while visibility varies. For instance, blindsight patients do not always show different discrimination performance in their blind and healthy visual fields [20,35,43]. In healthy subjects, using meta-contrast masking and inattention, stimuli have been created that differ in visibility but are equated for objective discrimination performance [24,26,44].

In the model, three major circumstances (and mixtures of them) may lead to identical discrimination performance for seen and unseen stimuli:

• — first, for fixed stimuli X and Y, an increase in the prior probability (or cost) of the absent class may lead to an increase in unseen responses while leaving X/Y discrimination unaffected (figure 3a). This account formalizes the hypothesis that blindsight patients have an inappropriate ‘criterion’ for visibility judgement (e.g. [12,35,43]). Note, however, that the concept of criterion can be misleading because it incorrectly suggests a single scalar value. In the present framework, the ‘criterion’ emerges as a set of decisional boundaries that delimit the categorical regions in the representational space, and that are specific to the selected task. A change in the task or in the priors may thus impose a different division of space, and hence a shift in decision boundaries;

• — second, consider experiments in which, within each class, the experimenter presents two visible targets X and Y and two invisible targets X’ and Y’. If both the length and the variance of the input vectors X’ and Y’ are reduced compared with X and Y, their visibility can drop without affecting discrimination performance (figure 3b). This case could correspond to a simultaneous manipulation of stimulus strength (length of input vector) and of attention (variance of the input vector) as proposed by Rahnev et al. [26]; and

• — third, if both the amplitude and the angle of the input vectors X’ and Y’ are decreased compared with X and Y, then X/Y discrimination performance could be manipulated independently of visibility (figure 3c). This case could correspond to a simultaneous change in contrast and in stimulus ambiguity, for instance using morphing or blending to reduce the difference between X and Y stimuli.

The present account provides no less than three mechanisms by which blindsight, meta-contrast and inattention could produce their effects. Each mechanism could be explicitly tested by experimentally manipulating the contrast, the variance and/or the blending of sensory stimuli as well as the prior probability associated with each class.

Figure 3.

Three ways in which stimulus visibility can be manipulated independently of stimulus discriminability. (a) Changing the prior (or the cost) of the absent class affects the placement of the criterion for subjective visibility reports and can thus lead to a systematic report of invisibility, without affecting objective discrimination performance (purple) or detection sensitivity (green). (b) Simultaneously changing the length and the variance of the input vectors jointly affects detection sensitivity and subjective visibility reports while preserving objective discrimination performance. (The area under the curve (AUC) is an equivalent of d’ for continuous measures.) (c) Simultaneously changing the length (e.g. contrast) and the angle (e.g. ambiguity) of the input vectors can lead to a similar pattern of results.

(d). Subjective reports are often nonlinearly related to sensory strength

Empirical finding 4 is that a nonlinear curve often relates the strength of sensory stimulation and visibility ratings [25,27,29]. For example, when the stimulus onset asynchrony (SOA) separating a briefly flashed digit and its subsequent mask is varied linearly, a sharp transition in visibility occurs around an SOA of 50 ms: below this duration, subjects tend to report the stimulus as completely unseen, whereas above it, stimuli are reported as clearly visible [25,27]. However, this all-or-none visibility pattern does not characterize all types of subjective reports [27,41,45,46]. For example, Sergent & Dehaene [27] showed that the attentional blink leads to a much sharper nonlinear pattern than backward masking.

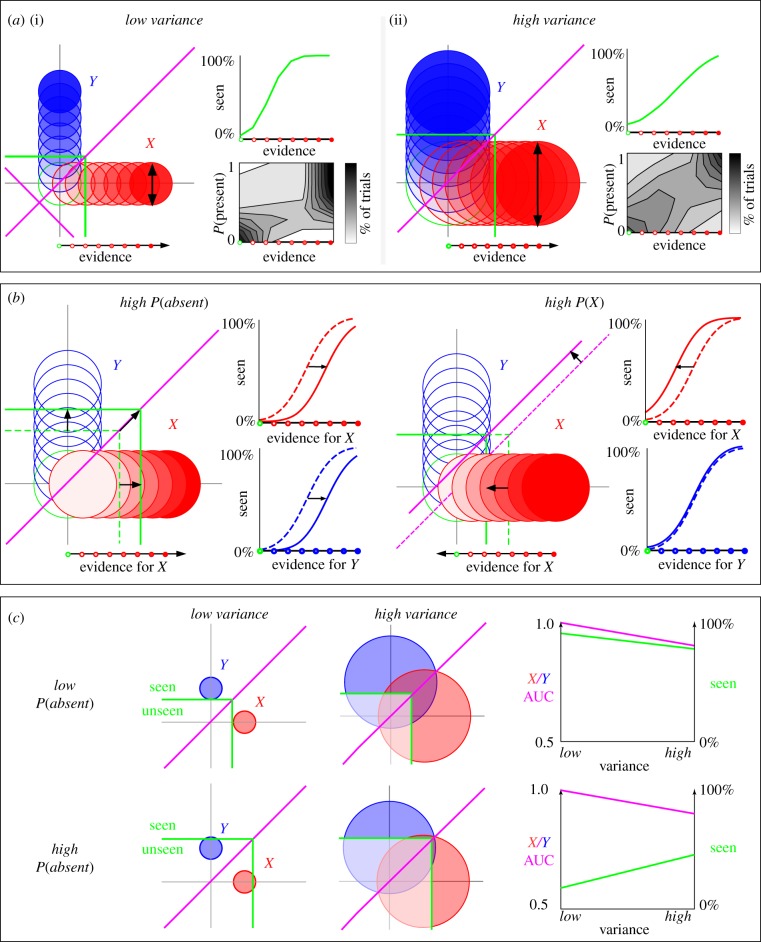
We consider two classes X and Y, within which the stimuli can vary parametrically in strength from trial to trial (figure 4a). This parametric variation is assumed to have a linear effect on the amount of sensory evidence in favour of the corresponding stimulus (i.e. the length of the input vector). In such cases, the model predicts that visibility responses are nonlinearly related to stimulus evidence, as the MAP criterion imposes a decision boundary that sharply delineates the regions of space respectively responded with the seen and unseen labels. Interestingly, although the fraction of seen responses is always a sigmoid, its slope may vary from a stepwise ‘all-or-none’ pattern to a shallow and near-linear function. The parameter driving this change in sigmoid slope is the variance in representational space. With higher variance, visibility becomes more linearly related to sensory evidence (figure 4a(ii)). This is because when variance increases, a greater number of absent samples fall outside the region responded classified as absent, and, analogously, a greater number of present trials (X or Y) fall outside their respective regions—ultimately leading to a flat relationship between stimulus evidence and discrimination performance. This change is also accompanied by an increased proportion of unseen responses. Contrarily, the sigmoid becomes sharper and the number of seen responses increases when the variance of the stimulus diminishes (figure 4a(i)).

Figure 4.

Input variance and prior knowledge can affect the nonlinearity and the threshold of subjective visibility reports. (a) Parametrically varying stimulus strength directly changes the amplitude of the input vector and leads to a nonlinear pattern of subjective visibility reports. The slope and intercept of the resulting sigmoid depend on stimulus variance: low variance leads to an all-or-none relationship between the evidence and the visibility reports (i), whereas high variance leads to a more linear relationship as well as an increase in the visibility threshold (ii). (b) Prior knowledge can also affect the visibility threshold. Increasing the prior probability of the absent class increases the visibility threshold for all stimuli, thus lowering subjective visibility reports. When only the prior probability of X is increased (capturing ‘hysteresis’ experiments where subjects come to expect the next stimulus), then the visibility threshold is lowered for X alone, while the visibility threshold for Y barely changes. (c) Visibility and discrimination interact when both priors and stimuli variance are varied. If the probability of the absent class is relatively low (or similarly if the evidence is relatively high), increasing the variance reduces both visibility ratings and discrimination performance. However, when P(absent) is high (or similarly, if the evidence is low), increasing the variance can diminish discrimination performance while increasing visibility ratings. This diagram captures the paradoxical finding that increased attention can lead to reduced visibility [26].

The present model thus shows how both near-linear and nonlinear visibility patterns can be produced by a single type of decision. The model also predicts that unseen trials should tend to be characterized by linear patterns and seen trials with all-or-none patterns—an empirically verified phenomenon [7,25,27,29,47]. Because there is no unequivocal way of determining the internal variance of sensory inputs in existing experiments, the present account remains speculative. Nevertheless, stimulus variance could be explicitly manipulated in future experiments.

(e). Prior knowledge can lower the visibility threshold

Empirical finding 5 is that the subjective visibility threshold is affected by prior knowledge [29,30,32,48–50]. Prior exposure to a given word increases its objective identification and subjective visibility when the same word is later presented under stronger masking [30]. Similarly, Melloni et al. [29] recently used a hysteresis paradigm in which letters were embedded in white noise. Across a series of trials, the identity of the letter was fixed while its signal-to-noise ratio gradually increased and then gradually decreased. Subjects reported seeing the letter better in the descending than in the ascending condition (i.e. once they knew the identity of the letter), even for identical physical stimulation.

In the present model, these effects arise from changes in the priors for classes X and Y. At the beginning of the ascending condition, stimulus evidence is low, and the X and Y classes are equally likely. Once the stimulus has been identified, at the beginning of the descending condition, its prior probability P(X) is increased, and consequently P(absent) and P(Y) are decreased. Because the decision boundary for the seen response is partly determined by P(X), the seen response is more likely in the descending sequence than in the ascending one (figure 4b).

Although this account captures the influence of prior knowledge on visibility reports [30], it oversimplifies the hysteresis paradigm [29]. Indeed, subjects are also likely to learn the structure of the ascending and descending sequences and expect a higher frequency of absent trials towards the beginning of the ascending sequence and towards the end of the descending sequence. This expectation, if present, would again increase the prior probability of the unseen response, thus leading to increased reports of invisibility for these stimuli compared with physically identical stimuli presented in a random sequence. The model further predicts that X/Y discrimination should remain identical in ascending and descending sequences. During the descending sequence, subjects should exhibit a bias towards X reports, owing to the increased prior for X, but no change in d’. These predictions offer a way to test the validity of the present model.

(f). Attention can either increase or decrease visibility

Empirical finding 6 is that attention and visibility can be paradoxically decorrelated. In many studies, attention increases detection sensitivity and subjective visibility (e.g. [26,37,51]). However, attention can also lead to decreased subjective visibility [26]. In Rahnev et al.'s study [26], subjects performed a basic detection task on a target whose location was validly cued on 70% of trials. Crucially, the contrast of the unattended target was adjusted to yield the same level of objective performance as the attended target. Remarkably, subjects reported that unattended trials were more visible than the attended ones.

If we assume that attention affects the variance of the input vector, the present model predicts that attention can lead to opposite visibility effects depending on the proportion of trials reported as seen or unseen (figure 4c). If P(absent) is low, so that most trials are reported as seen, then increasing the variance diminishes both discrimination performance and visibility, because it increases the proportion of input vectors that fall close to the absent class. This captures the classical effect that inattention increases noise and thus reduces both objective performance and subjective visibility. Importantly, however, if P(absent) is high, so that most trials are reported as unseen, then increasing the stimulus variance still diminishes discrimination performance, but may paradoxically increase visibility ratings. This is because with higher variance, a greater number of samples fall outside the region responded as unseen and thus become subjectively visible (figure 4c).

The model therefore predicts that attention can induce opposite effects on visibility and discrimination performance even when the mean evidence is unchanged. Contrary to Rahnev et al. [26], who argue that attention induces a conservative visibility bias by changing the inter-trial variance of the stimulus, we predict that visibility ratings are influenced by an interaction between the variance and initial visibility threshold (determined by prior knowledge or stimulus evidence). Once again, this prediction could be tested in an experiment explicitly manipulating stimulus variance, contrast and priors.

4. Experimental test of the model

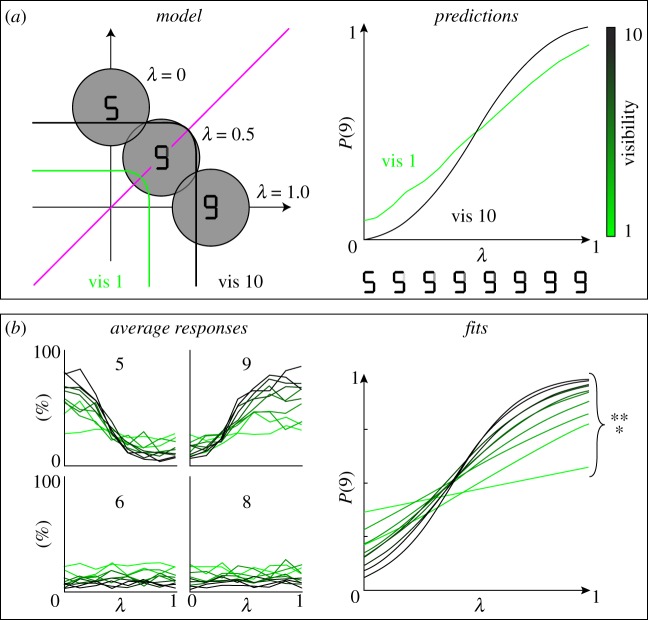
Most the above arguments account for empirical observations only in retrospect. We thus opted to confront the present model to a novel experimental set-up. The model critically predicts that linear and nonlinear profiles of behavioural responses arise from the same decision mechanism. In particular, it predicts that the discrimination profile of physically identical stimuli will increasingly become nonlinear as visibility increases (figures 2b and 4a).

We tested this prediction by linearly varying a parameter λ to create a continuum between two perceptual classes X and Y (figure 5). For λ = 0, the stimulus is X, for λ = 1, the stimulus is Y, but we can create an arbitrary series of intermediate stimuli S(λ) = λX + (1 – λ)Y. Whereas de Gardelle et al. [47] used a linear morph between two faces, here we varied the contrast of a single line to create a continuum between two different digits (e.g. ). Geometrically, such a continuum can be represented as a line joining the prototypical vectors of each class (figure 6a). We presented the stimuli at perceptual threshold, such that for a fixed stimulus, there were a large number of both seen and unseen subjective reports.

Figure 5.

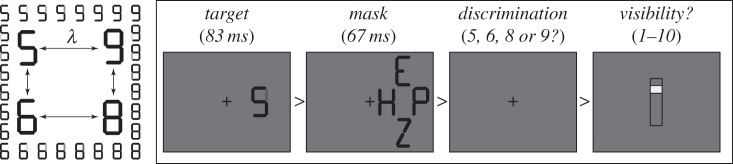
Experimental design. To test whether linear and nonlinear subjective reports could be accounted by a single type of decision, we parametrically varied the evidence (λ) favouring four different stimuli (5, 6, 8, 9) by creating morphs between pairs of these digits (left). For each morph, on each trial, subjects performed a forced-choice identification task and provided a subjective visibility report (right).

Figure 6.

Empirical test of the predicted variation in nonlinear categorization as a function of visibility. (a) The present framework predicts that the steepness of the sigmoid characterizing discrimination performance as a function of λ should increase with visibility reports. In particular, the discrimination performance of unseen stimuli should follow a quasi-linear trend. (b) The results (n = 17) confirm that (i) stimuli could be identified above chance even at the lowest visibility ratings (ii) discrimination performance correlated with visibility ratings and (iii) increasingly steeper sigmoids indicated that, unlike unseen stimuli, visible stimuli were associated with a nearly all-or-none identification performance.

The model predicts that the steepness of discrimination performance should increase as subjective visibility increases. Stimuli rated as unseen could be categorized better than chance (figure 2b), but with a shallow slope because such stimuli are necessarily close to the ‘absent’ class (figure 6a). Conversely, highly visible stimuli should yield a steeper sigmoidal function. Thus, we expected significantly better identification performance on seen compared with unseen trials (figure 2b), and an increasingly ‘all-or-none’ response pattern as a function of stimulus ambiguity λ (figure 6a).

(a). Method

Nineteen healthy volunteers, with normal or corrected-to-normal vision, participated after giving informed consent (29% males, age: 25 ± 5 years old, 88% right handed). Each trial began with the presentation of an ambiguous digit (target) presented for 83 ms and subsequently masked by pseudo-random black surrounding letters displayed for 67 ms (figure 5). Subjects were asked to identify in less than 2 s which of four digits was presented (5, 6, 8 or 9), using their left and right index and middle fingers. Visual feedback was given for non-ambiguous trials (morphs at 0 or 100%): misidentifications were followed by a 100 ms red fixation-cross, whereas correct identifications were followed by 100 ms green fixation-cross. Subjects subsequently reported subjective visibility using a 10-point vertical rating scale (bottom: not seen, top: clearly visible). Subjects used the two middle fingers to change the location of the randomly placed visibility cursor and pressed the space bar with their thumb to validate the visibility rating. The inter-trial interval was fixed at 300 ms. Subjects performed a total of 1000 trials divided into 25 blocks, at the end of which their median reaction times and their accuracy were displayed. The experiment lasted approximately one hour.

Prior to the main experiment, subject performed a staircase procedure similar to the main task (100 trials with unambiguous targets, no visibility ratings and no time limit). The contrast was lowered to reach an accuracy of approximately 70% [52]. Target contrast then remained fixed throughout the main experiment. The staircase procedure was repeated up to five times in case of an unstable perceptual threshold. Two subjects who failed to converge to a stable threshold were excluded.

All stimuli were generated on a computer using INKSCAPE, MATLAB 2009b and the Psychophysics Toolbox and were displayed on a 17’ computer cathode ray tube screen (1600 × 900 refreshed at 60 Hz). The screen background colour was 50% grey throughout the whole experiment and a black fixation-cross was constantly presented in the middle of the screen. Targets were morphs between two digits (5–6, 5–9, 6–8, 9–8), each made of 5–7 black bars (figure 5). In each pair, a single bar varied between grey (background colour) to maximal contrast in eight linear steps (parameter λ varying from 0 to 1 in steps of 0.143). Masks were composed of four pseudo-random capital letters constructed from the same basic visual features as the digits and were located at the top (E, O, U, Z), at the bottom (A, F, P Z), to the left (A, H, O, U) and to the right (E, F, P H) of the target digit. Symbols subtended 0.45° × 0.85° and were presented to the left or right side of the fixation (2.12°). Masks were centred on the previously presented target (1.23° × 2.27°). Targets, masks and their respective location were randomly selected at each trial. On 15% of trials, the target was absent and replaced by a grey background.

(b). Results

Unambiguous targets were accurately identified on 67.7% of trials (s.d. = 14.1%, t₁₆ = 5.00, p < 0.001) confirming that the staircase procedure was efficient (targeted accuracy: 70%). Subjects used the visibility scale appropriately, as indicated by their more frequent use of the 0% visibility response on target-absent trials than on target-present trials (36.7 versus 16.9% of trials, t₁₆ = 4.867, p ≤ 0.001). Subjects used the entire visibility scale on target-present trials, from 0% (16.9% of trials) up to 100% visibility (18.7% of trials).

We sorted trials as a function of reported visibility (10 levels), and within each level examined how identification responses varied as a function of bar contrast (parameter λ). We only focused on the two adequate responses to a given morph (e.g. response 5 or 9 for the 5–9 morph) and computed the fraction of these responses that corresponded to reporting the presence of a bar. We used R software to fit a binomial distribution as a function of bar intensity, separately for each subject and each visibility level. As seen in figure 6b, subjects’ choices varied significantly as a function of bar contrast at all visibility ratings (all p < 0.001). Thus, subjects discriminated digits at above-chance level even on trials when they reported no subjective perception. Furthermore, as predicted, the slope of the sigmoid function increased significantly with visibility ratings (r²(15) = 0.79, p = 0.004). Thus, discrimination performance improved with subjective visibility ratings. Trials rated as invisible had such a shallow slope that the response proportion was nearly linearly related to the intensity of the bar, while trials rated as highly visible resulted in a nearly stepwise, ‘all-or-none’ response function.

(c). Discussion of the experiment

Although subjects were presented with identical stimuli, subjective reports varied considerably from trial to trial, from total invisibility to maximal visibility. Furthermore, three predictions were verified: (i) identification scores were always higher than the chance level; (ii) they increased with visibility and (iii) when varying the degree of ambiguity λ, objective identification became increasingly nonlinear, as subjective visibility increased. These results confirm that, for physically identical stimuli, visibility is associated with a greater degree of ‘all-or-none’ perception, a finding that the framework can explain without any additional assumption (i.e. no need to postulate a qualitative difference between conscious and unconscious processing).

Our results extend a previous study by de Gardelle et al. [47], which examined the amount of masked repetition priming elicited by a morphed face when the prime was unmasked (SOA = 300 ms) or heavily masked stimuli (SOA = 43 ms). As in the present experiment, they observed linearly increasing priming for invisible morphs and categorical priming for visible morphs. Although the authors proposed that this dissociation reflected two distinct processes (unconscious analogue versus conscious discrete), the present model suggests that this interpretation is unnecessary: even within a single decision process, response patterns may vary in their degree of nonlinearity depending on the mean and variance of the stimulus evidence.

The model further predicts that, when conscious perception occurs, subjects perceive the stimuli strictly categorically (digit 5 or 9, but no intermediate percept). According to Harnad's definition [53], categorical perception is defined by ‘within-category compression and between-category separation’. In a companion paper in preparation, we will present additional evidence that the conscious experience of our morphs follows Harnad's definition of categorical perception [53]. First, discriminability is indeed enhanced for pairs of digits presented near the perceptual boundary. Second, when presented with two identical ambiguous morphs, subjects frequently judge that the stimuli differ, as predicted if each has an approximately 50% chance of falling in either of two discrete perceptual categories. Third, when the present identification task is replicated using a continuous response scale, subjects respond bimodally and barely use the intermediate levels to report perceiving a mixture of two digits. Thus, at least for this type of stimuli, and as postulated in our theoretical premises, what we consciously perceive seems to result from a categorical decision among a limited number of classes (see also [54,55]).

5. General discussion

We have shown how a simple geometrical framework for subjective report and objective discrimination tasks, based on signal detection and Bayesian theories, can account for six fundamental findings in behavioural studies of conscious and unconscious perception. The present model subsumes a series of frameworks describing both conscious and unconscious perception as statistical inferences [1,2,8,12,56–58]. The core of our hypothesis is that, during perception, the brain is faced with a massive classification problem. Each task, including conscious identification and subjective report, imposes, in a top-down manner, a set of classes along which the stimuli can be classified. Contrary to most laboratory tasks, open-ended subjective reports are typically based on numerous features and classes. A picture-naming task, for instance, typically involves tens of thousands of classes. Like others before us [33–35], we thus insist on the necessity to conceptualize decisions within a multi-dimensional framework. This conceptualization leads to several important methodological and theoretical consequences.

Firstly, the present model goes against the idea that subjective reports of ‘not seeing’ are necessarily unreliable because they can be affected by conservative response biases [33,42,59,60] and that objective measures, for example detection sensitivity (d’), should be favoured (see review in [16]). On the contrary, we show that subjective reports cannot be reduced to objective measures [42,59,60] nor to the second-order measures such as confidence rating and post-decision wagering [12,24,26,38]. In particular, the present model predicts that visibility and confidence should be partially correlated (figure 1c) but experimentally dissociable. This prediction is well supported by recent empirical findings showing that second-order judgements can be performed above chance on unseen stimuli [17,18,41,45]. In the present model, subjective visibility reports reflect a legitimate decision process whose details (including response bias) can and should be accounted for. As recently demonstrated [29,30,61], a shift in visibility criterion reflects the underlying prior probabilities and cost functions of the subjects’ internal model of the world, and, consequently, should not be disregarded as an experimental confound. What we call a ‘subjective’ report may simply be the brain's best attempt at solving a difficult perceptual decision problem with myriads of potential classes, each with different costs and prior probabilities that depend on the subject's prior experience.

Secondly, the model shows, in a principled manner, how experimental conditions can be designed to equate discrimination performance between seen and unseen trials (figure 3). In a series of behavioural experiments, Lau and collaborators have equated objective discrimination performance between seen and unseen responses, in an attempt to isolate conscious processing independently of other pre- or post-perceptual increases in information processing [12,24,26]. The present geometrical analysis suggests that Lau's experiments have adopted only a subset of the possible solutions: both masking the stimuli at different levels [24] and changing the amount of attention they receive [26] may change the signal-to-noise ratio of the incoming evidence. However, under such conditions, discrimination performance is equated at the expense of introducing physical differences between the visible and invisible stimuli. It is therefore unclear whether contrasting the two reflects an effect of visibility or of the stimulus’ physical properties. Consequently, it may be preferable to use physically identical stimuli and alter subjective visibility by changing the priors (figure 3a)—a solution indeed adopted in several recent studies [29,30,61].

The empirical finding of a nonlinear sigmoidal relationship between subjective visibility reports and the physical properties of a stimulus [7,9,16,47,62–64] has led to the notion that conscious perception is an all-or-none phenomenon [25,27,29]. The present model readily reproduces this nonlinear pattern (figure 4a) but it also predicts exceptions in cases of high stimulus variance or low signal-to-noise ratio. These predictions remain untested, but may offer potential explanations to studies revealing a continuous relationship between stimulus evidence and subjective reports [27,41,45,46]. In the future, directly manipulating the mean and the variance of stimulus evidence could clarify the role of each of these factors in linear and nonlinear response patterns to sensory manipulations.

According to the present model, the reason why unconscious responses tend to be linearly related to stimulus evidence is simple: when perceptual evidence is low enough to be categorized as unseen, the evidence necessarily lies close to the origin of the multi-dimensional space and therefore leads to shallow (though above-chance) forced-choice curves. We tested this idea in an original experiment, and the results confirmed that fixed stimuli presented at threshold lead to quasi-linear discrimination when reported as unseen, but to a sharp sigmoidal discrimination curve when reported as seen. Contrary to previous proposals [17,25,47], the present model accounts for these findings without having to postulate that distinct processes operate below and above the threshold for conscious perception.

(a). Limits of the model and possible extensions

For simplicity, we postulated that the very same representational vector is used for different tasks. The idea is that the same input vector is ‘resampled’ several times with different response classes (e.g. a discrimination task followed by a visibility task on the same trial). This resampling assumption is supported by a recent experiment [65] in which, within a rapid stream of letters, subjects were asked to identify the one that was circled by a visual cue. On each trial, subjects provided as many as four mutually exclusive guesses about the target letter. The results showed that all guesses were sampled from an identical distribution centred on the position and/or the time of the cue. This experiment suggests that the posterior probability of each letter was computed once and for all and that successive guesses corresponded to the MAP after excluding the previous answers, exactly as expected from the present model.

Nevertheless, in other contexts, the hypothesis that the input vector remains unchanged and identically available for a series of successive judgements may turn out to be simplistic. Temporal decay may affect the quality of decisions made after a delay [66], particularly for unconscious stimuli [15,36]. A recent study suggests that an attentional cue presented after a sensory stimulus can retroactively improve its visibility [37]. The task set imposed by the first task may also change the quality of the evidence available for the second task [67]. Similarly, the order in which two questions are presented may influence the subject's answers [68]. Busemeyer et al. [69] have proposed accounting for the latter phenomenon with a computational principle inspired from quantum mechanics, according to which each successive judgement alters the input vector by projecting it onto a subspace defined by the task. As projections are not commutative, the order of successive questions can change the successive decisions. It remains to be seen whether such non-commutativity is a fundamental principle that should be added to the present model.

Another limit of the present model lies in its assumption, shared with SDT, that decisions are based on a single input vector. A natural extension of the model would represent a sensory input as a series of samples, i.e. a trajectory in multi-dimensional space. Indeed, SDT has been superseded by sequential sampling models [70–72], according to which each decision is based on an accumulation of noisy samples arising from the stimulus. Whichever accumulator first reaches a fixed threshold is selected as the winner of the perceptual decision. Models of this kind are supported by a large set of empirical findings, [1,8,73–75] and account, not only for response proportions, but also for response times and their distributions [70,73,76]. Extending the present model in this direction, as attempted by Del Cul et al. [25], would lead to precise predictions about subjects’ reaction times in objective and subjective tasks.

In the tradition of ‘ideal observer’ analyses, we also assumed that the decision system is fully informed of the stimulus distributions and uses optimal priors and likelihood functions to compute the posterior probability of each response class. This is undoubtedly an idealization. A dynamic model in which the likelihood functions, priors and costs would be learned by updating them after each trial, and may therefore be ill estimated, may go a long way towards explaining a variety of human deviations from optimality. For instance, using a model similar to the present one, Ko & Lau [35] proposed an account of blindsight as an inadequate revision of priors following the radical decrease in visual input strength caused by a lesion to area V1 (similar to figure 3a). Confidence judgements and visibility ratings would be particularly affected by inadequate priors and likelihoods, because the present model assumes that these tasks require a quantitative estimation of the posterior probabilities (figure 1). In agreement with this idea, Rahnev et al. [26,44] performed a series of experiments in which human observers deviated radically from optimality in their confidence judgements. Their findings could be explained by assuming that subjects used a single estimate of input variance for distinct experimental conditions (e.g. for attended versus unattended trials). This interpretation is compatible with the present model and with the general idea that there are sharp limits to the number of decision criteria that subjects may deploy on a given trial [77,78].

(b). Neural mechanisms

The present model was framed at an abstract mathematical level of description. While this approach provides useful geometrical intuitions and a simple testable framework, an important future endeavour will be to flesh it out at the neural level. The vast representational space may correspond to the function of posterior unimodal and multimodal sensory areas, where many neurons render explicit dimensions of the stimuli that are only encoded implicitly and in a distributed form in the sensory periphery. Their role may be to augment the dimensionality of sensory inputs and therefore facilitate decision-making by turning decisions into linearly separable problems [79]. The categorical decision system, in turn, could be subserved by areas of the dorsolateral and inferior prefrontal cortices as well as anterior temporal and superior parietal cortices. These areas have been proposed to form a ‘global workspace’ where conscious information is maintained and broadcast to additional processes [10]. They receive the necessary convergence of multimodal inputs and are known to contribute to both decision-making and to all-or-none conscious perception [10,80,81]. Explicit simulations of such recurrent networks with winner-take-all dynamics show how they tend to quickly converge to a discrete stable attractor [82] which approximates the maximum-likelihood estimate [83,84]. The dynamics of such networks may therefore account for perceptual categorizations, which the present model considers as inherent to conscious perception.

Funding statement

This work was supported by a DGA grant to J.R.K., by INSERM, CEA, a European Research Council senior grant ‘NeuroConsc’ to S.D., and the European Union Seventh Framework Programme (FP7/2007: 2013) under grant agreement no. 604102 (Human Brain Project).