On the (f)utility of measuring the lead equivalence of protective garments

Abstract

Purpose: Protective garments incorporating lead (Pb) or other moderate to high atomic number elements are a necessary radiation protection tool. However, as lead has been replaced by other elements, verifying manufacturers’ claims regarding the lead equivalence of such garments has become nearly impossible, and current standards only require measurement of attenuation or lead equivalence at a single beam quality. A garment may provide a high degree of protection at the specified beam quality, but underperform at others. The authors sought to measure the lead equivalence of several protective garments and propose a better method for quantifying the protective value of garments.

Methods: The authors measured the penetration of primary and scattered radiation through lead sheets and three protective garments of nominal 0.5 mm Pb equivalence, one lead and two lead-free. Penetration was measured using beams of nominal 60, 80, 100, and 120 kVp. Primary penetration through protective garments at 70 kVp was also measured. A lead-lined enclosure was constructed for measuring scatter penetration, as instruments must be protected from stray radiation when measuring low-level penetration of scattered radiation. Using polynomial least-squares fits to the measured data of penetration through lead sheets, the authors determined the lead equivalence of the protective garments across a range of beam qualities.

Results: The lead garment was 0.5 mm Pb equivalent across all beam qualities evaluated. While the maximum lead equivalence of the lead-free garments did occur at the manufacturer-specified beam quality, neither garment was 0.5 mm Pb equivalent at the specified beam quality. The lead equivalence of the lead-free garments was a strong function of beam quality and nature of the radiation, i.e., primary or scattered. The lead equivalence of the lead-free garments in primary beams ranged from 0.40 to 0.47 mm Pb equivalent and in scattered beams ranged from 0.37 to 0.46 mm Pb equivalent. The penetration through one lead-free garment at 60 kVp was 478% higher than the penetration through the lead garment. The authors have also provided linear fits of radiation penetration through lead as a function of half-value layer. It is likely that assessment of protective value can be performed using primary beams matched to the spectra of scattered beams. The authors propose the diagnostic radiation index of protection (DRIP), a weighted sum of the percentage of radiation penetration across a range of beam qualities, as a more robust method for specifying the protective value of garments.

Conclusions: The protective value of garments from both primary and scattered radiation is a strong function of beam quality. Assessment of the protective value should be performed across a range of beam qualities. Methods for performing such assessment must be developed and must specify beam qualities, measurement geometry, and the appropriate weighting across the beam quality range for different applications.

INTRODUCTION

Protective garments incorporating lead or other moderate to high atomic number elements are a key radiation protection tool, along with distance and time. The protection provided by garments that use only lead can be empirically calculated and the variation in protection as a function of x-ray energy is well-understood. However, lead garments must be treated as hazardous waste for disposal and are heavy, causing back strain and other orthopedic problems for those who must wear them for long periods of time.^{1, 2, 3} The problems of weight and disposal have been mitigated by creating proprietary combinations of moderate atomic number elements to replace all or portions of the lead at a fraction of the weight.^{4, 5, 6} Tin, antimony, yttrium, copper, barium, and tungsten are elements commonly used for this application. These new “lightweight” aprons exploit K-edge photoelectric interactions to attenuate radiation, and may incorporate other materials of lower atomic number to attenuate fluorescence x rays resulting from these K-edge interactions. These lightweight aprons may be lead-composite, including both lead and other elements, or lead-free. While such aprons may provide sufficient protection in diagnostic radiology, they do not provide the same protection as lead.⁷ It is commonly known that the protection provided by lead-free garments is a strong function of beam quality. Therefore, the specification of “lead equivalence” at a single beam quality (or worse, a single kVp) is inadequate for determining the amount of protection provided by such a garment.

Previous investigations have focused on the performance of lead, lead-composite, and lead-free garments in primary x-ray beams.^{8, 9, 10, 11, 12, 13, 14, 15} Most investigators have declined to measure the transmission of scattered radiation owing to concerns about x-ray tube loading and difficulties associated with measuring scattered radiation. One study did examine the performance of lead-composite aprons using scattered radiation from a 110 kVp fluoroscopy beam,¹⁶ finding lead-composite garments to provide protection comparable to lead garments. Investigators have recognized the importance of using broad-beam geometries when evaluating lead-composite or lead-free garments as the elements used in their constructions may emit fluorescence x rays after K-edge interactions,^{9, 10, 15} and one study has reported that for some lead-free materials the relative biological effectiveness (RBE) of transmitted and secondary radiations can be a factor of 2 greater than for other materials or lead aprons.¹⁵ The International Electrotechnical Commission (IEC) has published a standard (IEC 61331-1) for the evaluation of materials used in protective garments, including both narrow beam and broad-beam geometries and defining the attenuation ratio, buildup factor, attenuation equivalent, and lead equivalent.¹⁷ ASTM International has published a standard for measurement of attenuation in a narrow beam geometry (ASTM F2547-06).¹⁸ However, IEC 61331-1 and ASTM F2547-06 do not require specification at more than one beam quality chosen from a list of possibilities.

The purpose of our study was to compare the performance of lead and lead-free garments to sheet lead in (1) a broad-beam geometry using scattered radiation of different qualities and (2) a narrow beam geometry using primary radiation of different qualities.

MATERIALS AND METHODS

X-ray beam characterization and measurement equipment

Four dosimeters and two electrometers (Radcal Corp., Monrovia, CA) were used in the course of the experiments—one 1800 cm³ ionization chamber (Model 10 × 5-1800), one 180 cm³ ionization chamber (Model 10 × 5-180), one 6 cm³ ionization chamber (Model 10 × 5-6), one solid state dosimeter (model AGMS-D), one Model 9015 electrometer, and one Accu-Dose electrometer. All measurements were performed using a Definium 6500 digital radiography system (GE Healthcare, Waukesha, WI). A tube current of 500 mA was used for all measurements, including beam quality characterization. Primary radiation transmission was measured using x-ray beams of 60, 70, 80, 100, and 120 kVp. Scattered radiation transmission was measured at 60, 80, 100, and 120 kVp. Beam quality was characterized for each of these peak tube potentials using the 6 cm³ ionization chamber and sheets of Type 1100 aluminum. Beams were characterized by their nominal kVp and their first and second half-value layers (HVL).

Protective garments

Three garments were evaluated in this investigation. The first was a lead apron from American Medical Sales (AMD Technologies, Inc., Los Angeles, CA). The specifications listed on the tag of this apron (Garment A) were: “0.5 mm Pb equivalent.” The second was a Greenlite lead-free wraparound skirt (Infab Corporation, Camarillo, CA). The specifications listed on the tag of this apron (Garment B) were: “Minimum 0.5 mm lead equivalent, 98.2% direct beam attenuation at 80 kVp.” The third was a Xenolite-TB lead-free apron (Lite Tech, Inc., Norristown, PA). The specifications listed on the tag of this apron (Garment C) were: “0.5 mm Pb equivalent at 100 kVp.” The tag of Garment B stated compliance with ASTM F2547-06, which specified a HVL of 4.0 mm Al at 80 kVp.

Lead sheets

Three lead sheets (Rotometals, Inc., San Leandro, CA) of 0.40 mm (1/64 in.) nominal thickness were used for measuring the penetration of scattered radiation through pure lead. This thickness was selected as it was the closest thickness to 0.35 and 0.5 mm, the standard recommended lead-equivalent thicknesses of protective garments.¹⁹ The thicknesses of the lead sheets were calculated by dividing the mass per unit area of each sheet by the physical density of lead. The nominal dimensions of each sheet were 91 × 122 cm (3 × 4 ft) and each was approximately rectangular in shape. Each sheet was carefully spread and flattened onto a flat floor. Slight deviations from a true rectangular shape were factored into the determination of the area using geometric formulae to calculate the area of a four-sided convex quadrilateral.

The mass of each sheet was measured using three different hospital-grade digital scales. This was accomplished by weighing two average adults and then weighing each adult while holding one rolled sheet of lead to determine the combined weight of the lead sheet and the adult. The mass of the rolled lead sheet was determined by subtraction of the results. This was repeated three times for each scale and for each adult. A total of 18 measurements per sheet were acquired.

Attenuation of scattered radiation

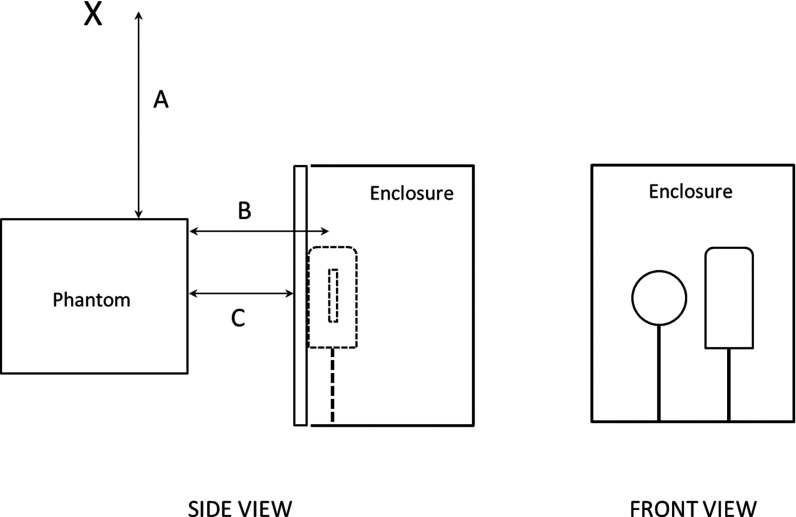
The broad-beam experimental geometry for measuring the transmission of scattered radiation is illustrated in Fig. 1. A five-sided box-like enclosure was constructed to shield the ionization chambers from stray radiation. It was constructed from wood and lined with 1.59 mm (1/16 in.) sheet lead and 0.5 mm lead aprons. The box was open to radiation scattered from the phantom at the front. This setup is critical when measuring low levels of scattered radiation with sensitive instruments. During preliminary testing, we noticed that measurements were contaminated by stray radiation scattered by the walls, floor, and ceiling of the room and objects within the room. Shielding the chambers from stray radiation proved essential to the experiment.

Figure 1.

Experimental setup for measurement of attenuation of scattered radiation. “X” marks the location of the x-ray tube focal spot. The circular object in the enclosure is the 180 cm³ ionization chamber, the oblong object is the 1800 cm³ ionization chamber. Distances: A = 70, B = 47, C = 40 cm. “C” represents the distance from the phantom to the lead or garment being tested.

The lead sheets and garments to be tested were suspended in front of the open face of the box, assuring there were no wrinkles or folds in garments when so placed. The ionization chambers were directly behind the tested materials and fully inside the box. The lead sheet or garment being tested was positioned and secured to ensure that no gaps existed between the tested device and the enclosure and the cables from the chambers to the electrometers were carefully shielded at the point of entry into the box. Garment B, a wraparound skirt, was hung such that the two front panels overlapped in the fashion they would when worn to provide the stated 0.5 mm Pb equivalence. A 25.4 cm thick polymethyl methacrylate (PMMA) phantom of area 35 × 35 cm was used to simulate a scatter-generating patient. The x-ray field was collimated to dimensions of 35 × 35 cm at the surface of the phantom. The solid state dosimeter was used as a monitor to measure radiation output during the scattered radiation experiment. It was placed on the corner of the phantom at the edge of the x-ray field, on the side away from the enclosure. Both the 1800 and 180 cm³ ionization chambers were used to measure the transmitted exposure. The exposure time was adjusted as necessary to produce sufficient signal in the electrometer while managing x-ray tube loading. All measurements were normalized to the radiation output measured with the monitor.

Three measurements were made with each garment and without any garment in place at 60, 80, 100, and 120 kVp. Three measurements were also made using four different thicknesses of lead sheet. These combinations provided the widest range of lead thicknesses possible and are detailed in Sec. 3.

Attenuation of primary radiation

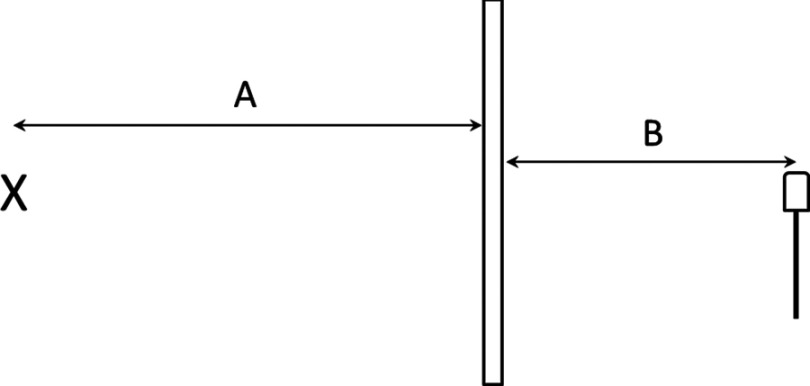
The narrow-beam experimental geometry for measuring the transmission of primary radiation is illustrated in Fig. 2. The x-ray field was collimated to dimensions of 5.2 × 5.9 cm at a distance of 103 cm from the x-ray source, where the lead sheets or garments were located. The exposure time was adjusted as necessary to produce sufficient signal in the electrometer while managing x-ray tube loading, and all measurements were normalized to mAs as necessary. No beam monitor was used, as the scattered radiation experiment had demonstrated that the output from the x-ray system was constant to within 1.5%, and the monitor chamber would have cast a shadow on the measurement chamber owing to the narrow-beam geometry.

Figure 2.

Experimental setup for measurement of attenuation of primary radiation. “X” marks the location of the x-ray tube focal spot. The small oblong object at location B is the 6 cm³ ionization chamber. Distances: A = 103, B = 67 cm.

The garments tested were suspended from a rack such that they hung straight with no wrinkles or folds. Garment B, the wraparound skirt, was hung such that the two front panels overlapped in the fashion they would when worn to provide the stated 0.5 mm Pb equivalence. The 6 cm³ ionization chamber was used to measure exposure during the primary radiation experiment. Measurements of the unattenuated exposure were made by removing the lead sheet or garment from the beam path. Three measurements were made with each garment and without any garment in place at 60, 70, 80, 100, and 120 kVp. Three measurements were made with two lead thicknesses at 80, 100, and 120 kVp. Measurements with two lead sheets at 60 kVp were not feasible owing to the small signal measured in the 6 cm³ chamber, therefore, results for attenuation of primary radiation by lead sheets are presented for only three beam qualities.

RESULTS

Results are provided in Figs. 34 and Tables 1 through 6.

Figure 3.

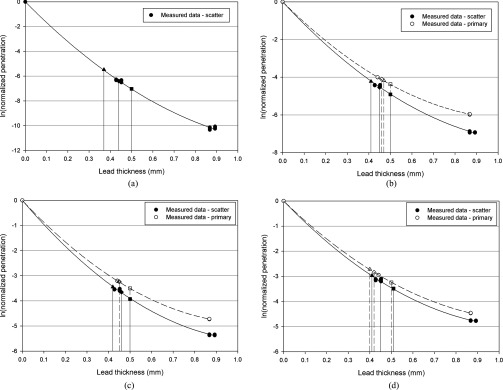
(a) Penetration of scattered radiation from 60 kVp beam through lead sheets (solid circles: ●), Garment A (solid square: ■), Garment B (solid diamond: ♦), and Garment C (solid triangle: ▲). The polynomial least-squares fit was anchored at (0,0) and the fit was used to calculate lead-equivalent thicknesses of tested garments. The drop lines mark the lead equivalence of the Garments A, B, and C. (b) Penetration of primary and scattered radiation from 80 kVp beam through lead sheets (primary, open circles: ○ and scattered, solid circles: ●), Garment A (primary, open square: □ and scattered, solid square: ■), Garment B (primary, open diamond: ◊ and scattered, solid diamond: ♦), and Garment C (primary, open triangle: △ and scattered, solid triangle: ▲). The polynomial least-squares fit was anchored at (0,0) and the fit was used to calculate lead-equivalent thicknesses of tested garments. The drop lines mark the lead equivalence of the Garments A, B, and C for primary (dashed) and scattered (solid) radiation. (c) Penetration of primary and scattered radiation from 100 kVp beam through lead sheets (primary, open circles: ○ and scattered, solid circles: ●), Garment A (primary, open square: □ and scattered, solid square: ■), Garment B (primary, open diamond: ◊ and scattered, solid diamond: ♦), and Garment C (primary, open triangle: △ and scattered, solid triangle: ▲). The polynomial least-squares fit was anchored at (0,0) and the fit was used to calculate lead-equivalent thicknesses of tested garments. The drop lines mark the lead equivalence of the Garments A, B, and C for primary (dashed) and scattered (solid) radiation. Note that the drop lines for Garments B and C (primary) lie on top of one another. (d) Penetration of primary and scattered radiation from 120 kVp beam through lead sheets (primary, open circles: ○ and scattered, solid circles: ●), Garment A (primary, open square: □ and scattered, solid square: ■), Garment B (primary, open diamond: ◊ and scattered, solid diamond: ♦), and Garment C (primary, open triangle: △ and scattered, solid triangle: ▲). The polynomial least-squares fit was anchored at (0,0) and the fit was used to calculate lead-equivalent thicknesses of tested garments. The drop lines mark the lead equivalence of the Garments A, B, and C for primary (dashed) and scattered (solid) radiation.

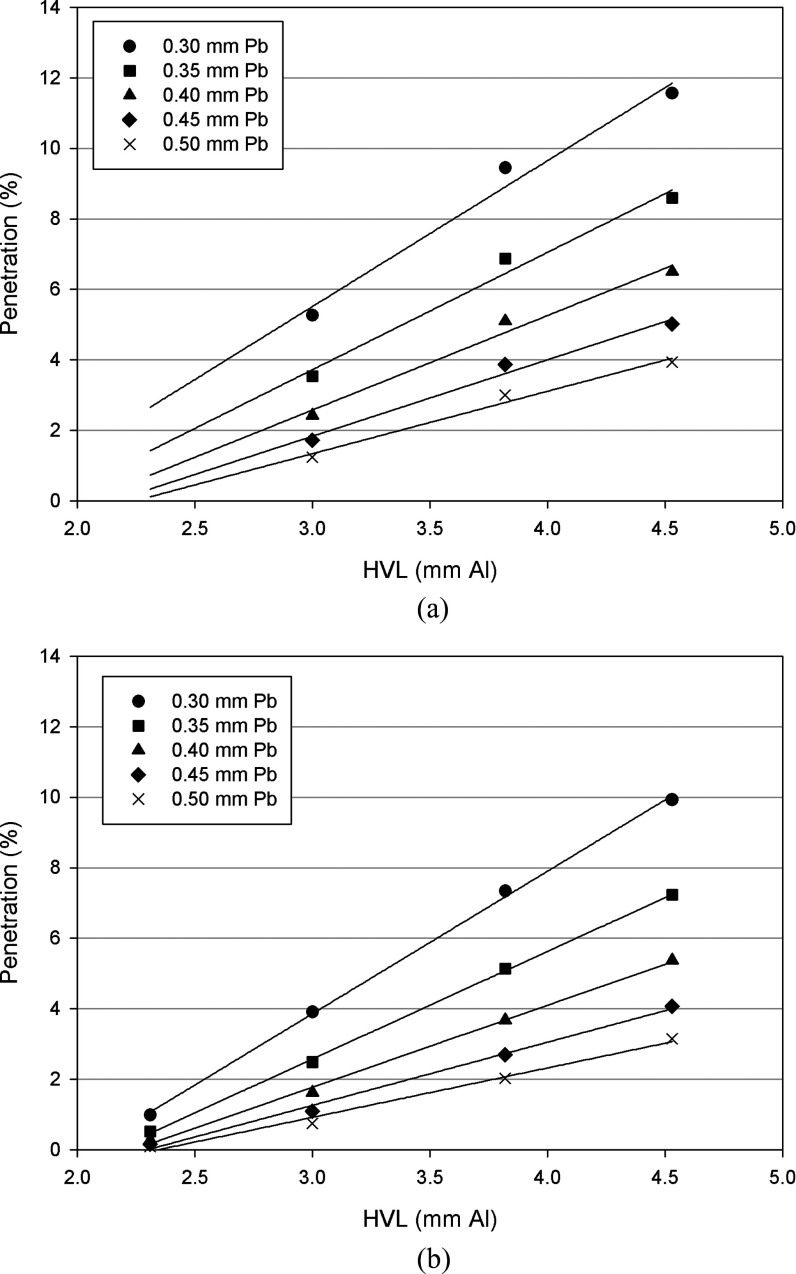
Figure 4.

(a) Penetration of primary radiation through lead for various thicknesses of lead as a function of first half-value layer, (b) Penetration of scattered radiation through lead for various thicknesses of lead as a function of first half-value layer. The data points for these lines are derived from the polynomial least-squares fits to the data of Figs. 3a, 3b, 3c, 3d. Linear fit parameters are listed in Table 6.

Table 1.

Beam qualities used in this experiment.

Nominal kVp	First HVL1 (mm Al)	Second HVL (mm Al)	Homogeneity coefficient
60	2.31	3.06	0.753
70	2.65	3.78	0.700
80	3.00	4.42	0.678
100	3.82	5.76	0.663
120	4.53	7.03	0.645

¹HVL = half-value layer. All HVL were measured with Type 1100 aluminum.

Table 6.

Results of linear least-squares fits of percent penetration versus half-value layer in Fig. 4.

	0.30 mm Pb		0.35 mm Pb		0.40 mm Pb		0.45 mm Pb
Fit parameter1	P2	S	P	S	P	S	P	S
a	4.1379	4.0423	3.3287	3.0510	2.6795	2.3230	2.1685	1.7910
b	−6.9008	−8.2676	−6.2649	−6.5778	−5.4607	−5.1950	−4.6721	−4.1135
			0.50 mm Pb
Fit parameter1			P				S
a			1.7698				1.4015
b			−3.9705				−3.2846

¹y = ax + b.

²P = primary [Fig. 4a], S = scattered [Fig. 4b].

X-ray beam characterization

X-ray beams were characterized by their nominal kVp and their first and second HVL. The thicknesses of the aluminum attenuators used were measured using digital calipers, and HVL are quoted to three significant figures. Beam qualities are given in Table 1.

Lead sheet thicknesses

The physical properties, including calculated thicknesses, of the lead sheets are given in Table 2. With one exception, the measurements of the mass of each lead sheet were within 1% of each other and the coefficient of variation (CV) of the measurements was less than 0.75%.

Table 2.

Properties of lead sheets used for attenuation measurements.

Lead sheet identifier	Area (cm2)	Mass (g)	Thickness (mm)1
Lead 1	11 302	5480	0.43
Lead 2	11 117	5558	0.44
Lead 3	11 174	5730	0.45
Manufacturer's specification	11 148	n/a	0.40

¹Density of lead = 11.342 g/cm³.

The physical density of lead was taken to be 11.342 g/cm³. Dividing the mass per unit area of each sheet by the physical density of lead yielded the average thickness of each lead sheet. Table 2 also provides the manufacturer's specifications for the lead sheets. The results of our measurements agree well with the specifications. It is important to keep in mind that these are average results for an entire sheet. Sheets of lead should not be expected to be perfectly flat over the entire area. The slight variations in average thickness noted among the sheets are no doubt a product of the manufacturing process and indicative of expected variations produced by this process. After all measurements were completed, we evaluated the uniformity of a single lead sheet (Lead 2) by cutting it into an 8 × 6 matrix of 15 × 15-cm sections, resulting in 48 sections. The overall mean thickness was 0.44 mm, which matched our calculated bulk thickness. The CV of thickness was 0.027, approximately 0.01 mm of lead. The outer columns were approximately 0.015 mm thinner than the columns in the center. Differences between the top row and center rows were negligible while the bottom row was thinner by about 0.01 mm. Considering these variations, any systematic error introduced in the results, expressed as a deviation from the average thickness, was small, i.e., less than 0.015 mm.

Precision of radiation measurements

Radiation measurements were repeated three times each. Reproducibility was excellent and not a substantial contributor to experimental error. For a total of 93 series of three measurements, the CV was less than 0.5% for 78% of the measurements. It was between 0.5% and 1.0% for 13% of the measurements. For the remaining 9% of the measurement series, the CV was less than 2.6% except for one measurement of scattered radiation penetration through 0.893 mm of lead at 60 kVp, for which the CV was 7.2%. Indeed, most of the measurements for which the CV was greater than 1% were of very weakly penetrating beams of 60 kVp, more than 0.8 mm of lead attenuation, or both.

Attenuation of scattered and primary radiation by lead

Measurements with ionization chambers shielded by the enclosure and measurements without the chambers shielded from stray radiation indicated that the signal from stray radiation constituted anywhere from about 30% of the penetration signal for one sheet of lead at 120 kVp to 250% of the penetration signal at 60 kVp and two sheets of lead. Thus, careful attention was paid to constructing the enclosure to avoid even small gaps or voids.

Figures 3a, 3b, 3c, 3d illustrate the penetration of scattered and primary beams through the lead sheets. These figures plot the logarithm of the normalized signal (i.e., normalized to the unattenuated measurement) versus lead thickness. Data points corresponding to measurements made with each ionization chamber are plotted separately, providing an idea of the variation attributable to factors including slight variations in lead sheet or garment thickness and variations in the intensity of scattered radiation along the anode-cathode axis of the simulated patient. Lead 1, Lead 3, Lead 1 + Lead 2, and Lead 2 + Lead 3 (Table 2) were used for scatter penetration measurements, corresponding to lead thicknesses of 0.43, 0.45, 0.87, and 0.89 mm, respectively. Lead 2 and Lead 1 + Lead 2 were used for primary penetration measurements, corresponding to lead thicknesses of 0.44 and 0.87 mm, respectively. The error bars representing the statistical precision of the measured penetration for the three measurements are smaller than the data points. A second order polynomial fixed at the origin was fitted to the data for each beam quality (Table 3). The penetration of the various beams through lead was interpolated from these fits and is presented in Table 4.

Table 3.

Results of polynomial least-squares fits of the logarithm of normalized penetration versus lead thickness. Results listed as “fit parameter (standard error).”

	60 kVp		80 kVp		100 kVp		120 kVp
Fit parameter1	P2	S	P	S	P	S	P	S
a	…	6.5392	5.1823	5.0837	4.2665	4.5214	3.6106	3.9349
		(0.1964)	(0.0388)	(0.1030)	(0.0144)	(0.0827)	(0.0203)	(0.0863)
b	…	−17.3547	−11.3690	−12.3351	−9.1465	−10.0647	−8.2763	−8.8824
		(0.1538)	(0.0310)	(0.0836)	(0.0115)	(0.0672)	(0.0168)	(0.0713)
c	…	0	0	0	0	0	0	0

¹y = ax² + bx + c.

²P = primary, S = scattered.

Table 4.

Penetration through protective garments and lead sheets as a percentage of initial intensity.

	60 kVp		70 kVp		80 kVp		100 kVp		120 kVp
Lead (mm)1	P2	S2	P	S	P	S	P	S	P	S
0.30	…	0.99	…	…	5.3	3.9	9.4	7.3	11.6	9.9
0.35	…	0.51	…	…	3.5	2.5	6.9	5.1	8.6	7.2
0.40	…	0.28	…	…	2.4	1.6	5.1	3.7	6.5	5.4
0.45	…	0.15	…	…	1.7	1.1	3.9	2.7	5.0	4.1
0.50	…	0.10	…	…	1.2	0.75	3.0	2.0	3.9	3.2
Garment	P	S	P	S	P	S	P	S	P	S
A (lead)	0.17	0.090	0.57	…	1.3	0.7	3.0	2.0	3.9	3.1
B (lead-free)	0.24	0.17	0.68	…	1.6	1.1	3.9	2.6	5.8	4.2
C (lead-free)	0.40	0.43	0.88	…	1.5	1.5	3.9	3.2	6.6	5.1

¹Penetration calculated from polynomial fits listed in Table 3.

²P = primary, S = scattered.

Attenuation of scattered and primary radiation by protective garments

The penetration of the various beams through the protective garments tested is presented in Table 4. The measured penetration, along with the polynomial fits described in Sec. 3D., was used to calculate the lead-equivalent thicknesses of the protective garments. Calculated lead-equivalent thicknesses are shown in Figs. 3a, 3b, 3c, 3d as square, triangular, or diamond-shaped data points, and are listed in Table 5 as a function of beam quality.

Table 5.

Lead equivalence of protective garments in millimeters lead.¹

	60 kVp		80 kVp		100 kVp		120 kVp
Garment	P2	S2	P	S	P	S	P	S
A (lead)	…	0.50	0.50	0.50	0.50	0.50	0.50	0.51
B (lead-free)	…	0.45	0.46	0.45	0.45	0.46	0.42	0.45
C (lead-free)	…	0.37	0.47	0.42	0.45	0.42	0.40	0.41

¹The maximum error in these measurements was calculated to be ≤ 0.02 mm.

²P = primary, S = scattered.

DISCUSSION

Attenuation of scattered and primary radiation by lead

Measurements of penetration of scattered radiation through the lead sheets using the 180 and 1800 cm³ ionization chambers were expected to systematically differ slightly owing to various factors. The chambers differed in geometric shape, the 180 cm³ chamber was pancake-shaped with the flat surface facing the scatter source and the 1800 cm³ chamber was cylindrical with a curved surface facing the scatter source. Thus, the chambers did not sample similar geometric volumes of air. The chambers were positioned adjacent to one another but the 1800 cm³ chamber was located on the side nearer the anode of the x-ray tube and the 180 cm³ chamber was nearer the cathode. Therefore, the intensity and spectrum of scattered radiation was different at the positions of the chambers. These spectral differences, combined with any difference in the energy dependence of the two chambers, may have contributed to minor differences in measurements. As previously discussed, the lead itself was not perfectly uniform and slight differences in attenuation measurements owing to such variations in thickness were expected. Finally, the exposure rates changed markedly between the unattenuated and fully attenuated beams. Any differences in exposure rate dependence between the two chambers would result in slight differences in measurements.

Despite the aforementioned potential systematic errors, differences in the measurements of attenuation by the two chambers were small, as evidenced by Figs. 3a, 3b, 3c, 3d. The circular data points representing the two chambers overlap at each of the four lead thicknesses for which measurements were made. The overlapping points appear as slightly oval data points as opposed to distinctly different circular data points. Because of the high consistency in the measurements of the two chambers, the data from the two chambers were combined to yield one least-squares fit of a second-order polynomial that represented the attenuation curve for penetration of primary or scattered radiation through lead at each beam quality.

Lead equivalence of protective garments

The data in Table 5 indicated that the lead garment was indeed 0.5 mm lead-equivalent across all beam qualities tested. Such consistency was no surprise, considering that the material was lead.

The measured lead equivalence of both lead-free garments was consistently less than the manufacturers’ specification of 0.5 mm by more than our maximum error of measurement of 0.02 mm. The maximum lead equivalence of Garment B was 0.46 mm at 80 kVp as measured in the primary beam, less than the manufacturer's specification of 0.5 mm lead-equivalent. The lead equivalence of Garment B was consistent across the range of tested beam qualities. The fact that this garment consistently measured as 10% less lead-equivalent than the lead garment indicates that Garment B would be 10% lighter than lead by this factor alone. The maximum lead equivalence of Garment C was 0.47 mm at 80 kVp as measured in the primary beam, and was 0.45 mm at 100 kVp, less than the manufacturer's specification of 0.5-mm lead equivalent at 100 kVp. A large contributor to the reduced weight of this garment compared to lead was the reduced lead equivalence at beam qualities other than 80 kVp (Table 5, Fig. 3). Garment C clearly incorporates one or more materials with a K-edge that peaks in attenuation for a primary beam near 80 kVp.

Lead-free garments compared to lead garments

Across the range of beam qualities evaluated, lead-free garments consistently allowed more penetration of primary radiation than the lead garment (Table 4). The penetration ranged from 15% to 69% greater for Garment C for primary beams of nominal energy from 70 to 120 kVp. At 60 kVp, the penetration was 235% greater. The penetration for Garment B ranged from 19% to 49% higher for primary beams of nominal energy from 70 to 120 kVp and was 41% greater at 60 kVp.

Lead-free garments fared even worse when compared to the lead garment for penetration of scattered radiation (Table 4). The penetration ranged from 61% to 241% greater for Garment C for scattered beams of initial energy from 120 to 80 kVp and was 478% greater for the initial 60 kVp beam. The penetration for Garment B ranged from 30% to 57% greater for scattered beams of initial energy from 120 to 80 kVp and was 89% greater for the initial 60 kVp beam. The trend was reversed for scattered radiation compared to primary radiation, i.e., lead-free garments provided more protection from scattered beams of higher initial energy than those of lower initial energy. This is easy to understand when one considers that more of the scattered radiation from a 120 kVp beam lies near the K-edge of the materials used in the construction of lead-free aprons.

These observations are not meant to imply that the protection provided by Garments B and C is inadequate. The National Council on Radiation Protection and Measurements has indicated that a more appropriate lead-equivalent thickness for protective garments might be 0.35 mm of lead, rather than the 0.5-mm that is currently typical in the United States.¹⁹ A 0.35-mm lead apron would be 30% lighter than a 0.5-mm lead apron simply by virtue of its reduced thickness. It would also provide less protection. Figures 4a, 4b plot the penetration of radiation through various thicknesses of lead for the beam qualities evaluated in this investigation. It can be seen from these figures that at higher beam qualities a 0.35-mm lead apron allows about 2–2.5 times more radiation to penetrate than does a 0.5-mm lead apron. Figure 4 also demonstrates that, across the range of primary beam qualities commonly encountered in diagnostic radiology, the penetration of primary and scattered radiation through lead changes by large factors as the HVL increases from 2.3 to 4.5 mm Al.

How should protection be specified?

Protective garment specifications in terms of lead equivalence are not easy to verify for several reasons. The first problem with lead equivalence is that it requires the use of lead as a reference material, and the lead must be accurately calibrated for thickness. While this can be accomplished, it is cumbersome. Further, there is nothing special about lead that makes it ideal as a reference shielding material. Second, standards for measuring attenuation or lead equivalence do not require measurement at more than one beam quality.^{17, 18} The data presented in this work clearly demonstrate that measurement of attenuation or lead equivalence at a single beam quality is inadequate. Finally, measurement of lead equivalence using scattered radiation is difficult and requires careful attention to experimental design in order to avoid errors caused by stray radiation.

These factors make verification of the claims of manufacturers regarding the lead equivalence of protective garments highly problematic, and allow manufacturers to overstate the lead equivalence of their products through specification at the single beam quality at which their product provides maximum attenuation. Specifications of the protective value of protective garments should accurately reflect the protection provided across the range of beam qualities for which it will be used, and these specifications should be relatively easy to verify by the end users.

Our data suggest that evaluation of protective garments under full scatter conditions may be unnecessary. Primary beams can be specified to adequately simulate scattered radiation beams. Making measurements in primary beams is simpler and not prone to errors caused by stray radiation. Standardization of such measurements of penetration requires that standard beam qualities be specified a priori. These beam qualities should reflect the radiation qualities against which protective garments are to be used for protection. For example, if a protective garment is to be used during interventional procedures, the beam qualities used for measuring protective value should be similar to those encountered in the interventional laboratory. Specifying these beam qualities presents challenges that must be surmounted before such a technique can be implemented, including accurately determining the workload distribution as a function of beam quality for different imaging scenarios.

Developing a method by which users can reproduce beam quality characteristics is a challenge. Specifying the beam quality in terms of kVp and HVL in millimeters of Type 1100 aluminum is prone to inaccuracies because of the 0.5% impurity allowance for Type 1100 aluminum and owing to the inability to accurately define the waveform specified as “kVp.” Penetration of radiation through lead changes by about 1%–4% for every millimeter change in HVL measured in aluminum (Fig. 4), depending on the thickness of a lead shield. Therefore, an uncertainly of 0.1 mm in HVL measurement would result in an error of approximately 0.35% in a measurement of penetration. For example, if the specification for a garment was that the penetration at 120 kVp was 5%, then a measurement of 5.35% might be the result of error in the beam quality measurement, not a property of the shield. Thus, a measurement of 5.35% would have to be accepted as within the bounds of measurement, even though 5.35% could potentially mean that the shielding is 7% outside specification. It is possible that alternative methods to specify beam qualities used in protective garment evaluation can be developed, including methods that do not rely on small thicknesses of aluminum.

The diagnostic radiation index for protection (DRIP)

Building on a similar concept originally hinted at by Yaffe et al.⁵ when lead composite materials were initially introduced, we propose the DRIP. We propose that about four standard beam qualities be selected and the penetration through protective garments be measured for these beam qualities, with the garment configured as it would be for clinical use. The results of these measurements, as penetration percentages, would then be weighted by the distribution of workload for which the garment will be used across the four beam qualities at which the garment was evaluated. For example, if the nominal primary beams were specified as 60, 80, 100, and 120 kVp, penetration measurements of garments used for complex fluoroscopically guided interventions in the abdomens of adult patients might be heavily weighted toward beams in the range of 80–100 kVp. For complex interventions in children, the weighting might favor 60–80 kVp. Weighting factors would therefore change according to garment use. The sum of the weighted percentages would be the DRIP

$$\mathrm{DRIP}=\sum _{i=1}^n{a}_i\left[\frac{I_{T,i}}{I_{0,i}}\times 100\right],$$ (1)

where a_i is the weighting factor for beam quality i (∑_ia_i = 1), I_T,i is the transmitted primary beam exposure with the garment present, I_0,i is the initial primary beam exposure without the garment present, and n is the number of beam qualities for which penetration is measured. The DRIP would ensure protection across all relevant beam qualities, would not be subject to overestimation owing to K-edge effects, and would be measureable and verifiable by users.

Future work includes matching primary to scattered radiation spectra, determining workload distribution across the necessary primary spectra (i.e., beam qualities), and determining the optimum measurement geometry and method for specifying beam qualities.

CONCLUSION

Existing methods and ASTM standards for measuring the lead equivalence of protective garments are inadequate, and measuring lead equivalence under full scatter conditions is difficult, requires special enclosures to block stray radiation, and requires the use of a set of calibrated reference lead materials. These factors make it difficult for users to verify claims of manufacturers regarding the protective value of their garments. In fact, IEC 61331-1 prohibits specification of lead equivalence for garments containing little or no lead. We have demonstrated that measurement of penetration properties across a wide range of beam qualities better characterizes protective value for the full range of uses of x rays in medicine. Our data also suggest that measurements under full scatter conditions are not clearly more beneficial than measurements made in primary beams. The critical factors for determining the protective value of garments are the specification of the characteristics of the radiation beams used to measure the protective value and the weighting of measurements made at different beam qualities to reflect the environments in which the garment is used. We have proposed the DRIP as a garment-independent quantity for specifying protective value. However, work remains to be done to mature the DRIP into a user-friendly method for specifying protective value.