Optimal Co-segmentation of Tumor in PET-CT Images with Context Information

Abstract

PET-CT images have been widely used in clinical practice for radiotherapy treatment planning of the radiotherapy. Many existing segmentation approaches only work for a single imaging modality, which suffer from the low spatial resolution in PET or low contrast in CT. In this work we propose a novel method for the co-segmentation of the tumor in both PET and CT images, which makes use of advantages from each modality: the functionality information from PET and the anatomical structure information from CT. The approach formulates the segmentation problem as a minimization problem of a Markov Random Field (MRF) model, which encodes the information from both modalities. The optimization is solved using a graph-cut based method. Two sub-graphs are constructed for the segmentation of the PET and the CT images, respectively. To achieve consistent results in two modalities, an adaptive context cost is enforced by adding context arcs between the two subgraphs. An optimal solution can be obtained by solving a single maximum flow problem, which leads to simultaneous segmentation of the tumor volumes in both modalities. The proposed algorithm was validated in robust delineation of lung tumors on 23 PET-CT datasets and two head-and-neck cancer subjects. Both qualitative and quantitative results show significant improvement compared to the graph cut methods solely using PET or CT.

I. Introduction

Accurate target delineation plays an increasingly important role in image-guided radiation therapy due to the high dose gradients achievable with the technology. Inaccurate delineation of target volumes by a small amount can result in either overdose of the surrounding tissues, dangerous underdose of the tumor, or both [1], [2]. For effective assessment of target volumes in cancer treatment, medical imaging modalities like Computed Tomography (CT) and Positron Emission Tomography (PET) are widely used. CT images usually have high resolution and provide detailed anatomical information. However, limited physiological information can be captured by CT imaging. Fig. 1(a) shows one typical example. Studies show that a large inter-observer variability has been observed for many tumor sites because the tumors usually have a very similar intensity distribution with surrounding soft tissues [3], [4] in CT images. To improve the visualization of tumor tissues, Positron Emission Tomography (PET) imaging with the metabolic tracer ¹⁸F-FDG (Fluoro Deoxy Glucose) was introduced. In PET, target tumors generally have high standardized uptake values (SUVs), which helps to distinguish normal tissues from malignant tumors. However, due to the physically limited spatial resolution of PET and the method of visualization, the boundary of a lesion in PET can appear fuzzy and indistinct (see Fig. 1(b)). Thus accurate segmentation of tumors using only PET is still problematic. A number of studies have demonstrated that combining PET and CT information results in more consistent delineation of the tumor volumes [5], [6], [7], [8], [9]. The integrated PET-CT has recently become a standard method of imaging for radiation therapy treatment planning and has been increasingly used for tumor delineation.

Fig. 1.

The PET-CT images. (a) One slice of a CT image for treatment planning of lung tumor (red line). (b) The corresponding PET image.

Though PET-CT images have been routinely used in clinic, target delineation is still typically performed manually by the oncologist on a slice-by-slice basis with very limited support of automated segmentation tools. Many existing automated segmentation algorithms only work for single modality. Automated segmentation from co-registered PET-CT images remains challenging. In this work, we propose a novel method for co-segmentation of tumor in PET and CT images, which makes use of the advantages from both modalities: the superior contrast of PET and the superior anatomical resolution of CT. Our method strives to compute simultaneously, the tumor volume defined on CT as well as that defined on PET, which are not necessarily identical. The rationale is that PET and CT convey different information, which is not always complementary, but sometimes contradictory; so the tumor volumes defined on PET and on CT could be different. Our method is based on Boykov’s graph cut method [10]. The basic idea of the graph cut method is to formulate the segmentation problem as an energy minimization problem. The energy encodes both boundary and region information, which can be minimized in the discrete space using the graph-based method. In this paper, we propose a novel energy representation, which incorporates the region and boundary information from both PET and CT images. To achieve consistent segmentation results between two modalities, a novel context term is introduced into the energy function. The co-segmentation of PET and CT images is achieved by solving a single maximum flow problem, which leads to a globally optimal solution in low-order polynomial time.

The rest of the paper is organized as follows. In Section II, we give a brief review of the related work on tumor segmentation using PET-CT images, as well as the graph-based segmentation methods. In Section III, we introduce the proposed graph model, including the formulation of the energy and the corresponding graph construction. Section IV gives the detailed description of the lung tumor segmentation using the proposed graph model. Section VII discusses the novelty of the approach as well as its limitations. Finally, Section VIII draws the conclusion.

II. Related Work

A. Tumor Segmentation on PET-CT images

The usage of both PET and CT images for accurate target delineation in radiotherapy has attracted considerable attention in recent years. The most widely used PET segmentation method in clinical practice is thresholding based on SUVs, such as using an absolute SUV value [11], [12], a percentage of the maximum SUV [13], [14], [15], [16], [17] and many other variants [18], [19], [20], [21]. Among the thresholding methods, the signal-to-background ratio (SBR) algorithms are most commonly used [22], [18], [23], in which the threshold value is calculated depending on mean background accumulation and the signal of the lesion. Such a method requires an estimate of the lesion volume of interest before segmentation, which may not be easy at all. Recently, many more segmentation algorithms are brought in PET oncology from the field of Computer Vision [24]. Some of these approaches have been well known for other medical image modalities including the use of image gradients [25], [26], deformable contour models [27], [28], [29], mutual information in hybrid [30], [31], [32], [33], [34] and histogram mixture models for heterogeneous regions [35], [36], [37], [38]. However, almost all these methods can segment tumor either only on PET images or on the fused PET-CT images [29], [30], [39]. Wojak et al. developed a joint variational segmentation method which incorporates the PET information into the fuzzy segmentation model [40]. The method only computes a contour in CT, which is driven by the PET information. No precise segmentation is performed on PET data. Gribben et al. considered PET and CT as vectorial components with a covariance matrix linking two modalities, and solved the resulting MAP estimation problem using the Iterated Conditional Modes (ICM) algorithm [31]. The proposed approach aims to compute an identical tumor contour for PET-CT images. This may compromise the segmentation quality since PET and CT may convey different information, resulting a disagreement of the tumor volume defined on PET from that on CT.

The most closely related work is Han et al. [39]. In both our method and Han et al.’s, the PET/CT segmentation is formulated as an MRF optimization problem and is solved by computing a single maximum flow in the constructed graph. The key novelty of our method is the recognition of possible differences of tumor volume defined in PET from that defined in CT, which result in the delineation of true tumor boundaries in both modalities, rather than a compromised identical one. The introduction of the context term in the energy function provides a mechanism penalizing the contour difference in PET and CT while enabling the contour to follow the salient features in each modality to obtain a difference contour. To the best of our knowledge, no previous method is able to simultaneously delineate the tumor contours from PET and CT while allowing such differences. In Han et al.’s method, if PET and CT convey contradictory information, an arbitration term in the energy function is used to produce a compromised contour for both PET and CT, that is, their method strives to compute a single compromised tumor volume from PET and CT. Thus, their method is also more sensitive to registration errors. To implement the arbitration mechanism, the size of the graph constructed from the input PET/CT images in Han et al.’s method is about three times the CT image size; while in our method, the graph size is just about two times the CT image size.

B. Graph-based Segmentation

Graph-based methods have been widely used for image segmentation. The main idea is to formulate the segmentation problem as a discrete energy minimization problem. Image features are incorporated by designing proper cost functions for energy terms. Felzenswalb et al. [41] used pairwise region comparison for image segmentation based on minimum spanning tree (MST) algorithm. Grady et al. [42] showed how to extend the shortest method for 3-D surface segmentation. Xu et al. [43] proposed a novel approach using shortest-path algorithm for multiple surfaces segmentation in 3-D. Wu and Chen [44] developed an optimal surface detection method based on maximum flow. Li et al. [45] extended the work for multiple interacting surfaces segmentation. A generalized version of the framework dubbed LOGISMOS was reported in [46], which allows simultaneous segmentation of multiple objects and surfaces. Most recently, Song et al. [47]’s method incorporates both shape and context prior knowledge for multiple surface segmentation.

Our work is inspired by the multiple surface detection method [45], [47] and the multi-region segmentation method [48] based on the graph theoretical framework. A separate appearance model is employed for each spatially distinct region in an image. Geometric interactions are incorporated between region boundaries. In our work, we extend the idea for co-segmenting objects in multiple images with different modalities. The tumor volumes defined on PET and on CT are viewed as two mutually interacting regions, which are segmented simultaneously. An adaptive context term is employed to encourage consistent segmentation in PET and CT.

III. Graph Model

The main idea of the proposed method is to formulate the segmentation problem as an energy minimization problem in the discrete space, which can be solved using a graph-based method. Two subgraphs are constructed, one for PET and one for CT. The weight of arcs in the subgraph encodes the boundary and region information from the corresponding image. The key point is the incorporation of context information between the PET and CT images, which is enforced by adding inter-subgraph arcs between correspondent nodes of two subgraphs. The node correspondence between the two subgraphs (i.e., the voxel correspondence between the PET and the CT images) can be established, for example, using image registration if necessary. It can be either one-to-one or multiple-to-one correspondence, in which one PET voxel may correspond to a set of CT voxels.

A. Energy Function

Consider a PET-CT image pair ( , ), where denotes an input CT image and denotes the registered PET image. For each voxel v ∈ , we have a correspondent voxel v′ ∈ . Let l_v and l_v′ denote the binary labels assigned to each voxel v ∈ and v′ ∈ , respectively. In our notation, l_v = 1 (l_v′ = 1) means that the voxel v (v′) belongs to the target object. If l_v = 0 (l_v′ = 0), then the voxel v (v′) is considered to be in the background. The set of voxels whose label are 1 in (resp., ) defines the tumor region in the CT (resp., PET) image.

To express our energy function, we start with the energy term E_CT for the segmentation of CT, which consists of two similar terms as in the well-known binary graph cut method [10]: a region term and a boundary term. For each voxel v ∈ , a region cost D_v(l_v) is assigned, which measures how well the voxel v with a label l_v fits into a given intensity model. Let defines the neighboring relationship between voxels in . Then the boundary cost V_uv(l_u, l_v) can be expressed as

$$V_{uv}(l_u,l_v)=\{\begin{array}{ll}{B}_{uv}\hfill & \text{if}{l}_u\ne l_v\hfill \\ 0\hfill & \text{if}{l}_u=l_v\hfill \end{array},$$ (1)

where B_uv is the penalty of assigning different labels l_u and l_v to two neighboring voxels (u, v) ∈ . Our energy term for CT segmentation takes the form:

$$E_{CT}(l)=\sum _{v\in \mathcal{I}}{D}_v(l_v)+\sum _{(u,v)\in {\mathcal{N}}_{CT}}{V}_{uv}(l_u,l_v),$$ (2)

The energy term E_PET for the segmentation of PET image has the same form as that used for CT. Let $D_{v^{\prime }}(l_v^{\prime })$ denote the region cost for voxel v′ ∈ , V_u′v′(l_u′, l_v′) denote the boundary cost between two neighboring voxels (u′, v′) ∈ , where defines the neighboring relationship between voxels in . Then the energy term E_PET can be expressed as

$$E_{\mathit{PET}}(l)=\sum _{v^{\prime }\in {\mathcal{I}}^{\prime }}{D}_{v^{\prime }}(l_{v^{\prime }})+\sum _{(u^{\prime },v^{\prime })\in {\mathcal{N}}_{\mathit{PET}}}{V}_{u^{\prime }{v}^{\prime }}(l_{u^{\prime }},l_{v^{\prime }}),$$ (3)

As described above, the key to a successful segmentation is to make use of information from both PET and CT images. To incorporate context information between the modalities, a context term is added into the energy, which penalizes the segmentation difference between the two image datasets. Let (v, v′) denote a pair of corresponding voxels in the CT image and the PET image . The context cost W_vv′(l_v, l_v′) is defined, as follows.

$$W_{{vv}^{\prime }}(l_v,l_{v^{\prime }})=\{\begin{array}{ll}{C}_{{vv}^{\prime }}\hfill & \text{if}{l}_v\ne l_{v^{\prime }}\hfill \\ 0\hfill & \text{if}{l}_v=l_{v^{\prime }}\hfill \end{array},$$ (4)

where C_vv′ is employed to penalize the disagreement between labels of corresponding voxels v and v′. Our context energy term takes the form:

$$E_{\mathit{context}}(l)=\sum _{(v,v^{\prime })}{W}_{{vv}^{\prime }}(l_{v^{\prime }},l_{v^{\prime }}).$$ (5)

The energy function of our co-segmentation is defined in the following way.

$$E(l)=E_{CT}(l)+E_{\mathit{PET}}(l)+E_{\mathit{context}}(l),$$ (6)

Our goal is to compute an optimal set l^* of labels such that the total energy is minimized. The label set l^* defines an optimal co-segmentation of PET-CT images.

Most previous co-segmentation algorithms in computer vision [49], [50], [51] work on a pair of images with similar (or nearly identical) foregrounds and unrelated backgrounds, and explicitly make use of histogram matching, which makes the models computationally intractable. Batra et al. recently applied the graph cut method for co-segmentation [52], in which a common appearance model is assumed across all the segmented images. However, the PET and CT images may not have such a common appearance model. We propose a more flexible PET-CT context term E_context to make use of the dual modality information.

B. Graph Construction

Our energy is minimized by solving a maximum flow problem in a corresponding graph, which admits a globally optimal solution in low-order polynomial time. In this section, we show how to encode our proposed energy terms through proper graph construction.

For energy terms E_CT and E_PET, a directed graph G is defined, which contains two node-disjoint subgraphs G_CT (N, A) and G_PET (N′, A′) for E_CT and E_PET (see Fig. 2), respectively. Note that two subgraphs use exactly the same structure to incorporate the region and boundary terms in the corresponding energy function. For the construction of G_CT (N, A), every voxel v ∈ has a corresponding node n_v ∈ N in G_CT. Two dummy nodes, a source s and a sink t, are added into the graph. To encode the region term D_v(l_v), we put a t-link arc from source s to each node n_v with the weight D_v(l_v = 0) and a t-link arc from each node n_v to the sink t with the weight D_v(l_v = 1). The boundary term V_uv(l_u, l_v) is enforced by adding n-links as follows. For each pair of neighboring voxels (u, v) ∈ , two n-link arcs are introduced, one from n_u to n_v and the other in the opposite direction from n_v to n_u. The weight of each arc is set as B_uv. The subgraph G_PET (N′, A′) can be built using the same way to encode the region term D_v′(l_v′) and the boundary term V_u′v′(l_u′, l_v′) for the energy term E_PET. To solve them in a single maximum flow, two subgraphs share the same source s and sink t.

Fig. 2.

Illustrating the graph construction of G with two sub-graphs G_CT and G_PET for the co-segmentation of PET-CT images. Three types of arcs are introduced. The t-link arcs (brown), n-link arcs (orange), and d-link arcs (green) encode the region costs, boundary costs, and the context penalties, respectively.

To enforce the context term E_context(l), additional inter-graph arcs are added between G_CT and G_PET, named as “d-link” arcs. For every pair of corresponding voxels (v, v′), where v belongs to the CT image and v′ is the corresponding voxel in the PET image , two d-link arcs are added between corresponding nodes of two subgraphs, one from n_v to n_v′ and the other from n_v′ to n_v. The weight of arcs is set as C_vv′, which is the context cost penalizing the segmentation difference between two images (see the definition in Section III-A).

We thus finish the construction of the graph. Fig. 2 shows one example. Here the constructed graph G can be considered as a graph constructed for a 4-D image segmentation problem, where the 4-D image = { , } contains all voxels from the CT image and the PET image . The neighboring setting between and is defined by their correspondence relation. The regional cost for each voxel v ∈ and v′ ∈ is enforced by two t-link arcs, and the boundary costs between two neighboring voxels (u, v) ∈ and (u′, v′) ∈ are enforced by the n-link arcs. Furthermore, the context term is encoded as the summation of the boundary costs enforced by the d-link arcs between corresponding voxel pairs (v, v′), where v ∈ and v′ ∈ . Intuitively, these d-link arcs can be viewed as the n-link arcs between the two subgraphs associated with the two 3-D sub-images in the 4D image . We thus transform the optimization problem as a 4-D segmentation problem, which is solvable by the minimum s-t cut method [10]. Specifically, a minimum s-t cut = (A^*, Ā^*) is found, which separates the graph G into two parts, the source set A^* and the sink set Ā^* with s ∈ A^* and t ∈ Ā^*, and A^* ∪ Ā^* = N ∪ N′ ∪ {s, t}. This minimum s-t cut, which can be obtained by solving a maximum flow problem in low-order polynomial time, defines an optimal segmentation minimizing the objective energy function Eq. (6). The target tumor volume on the CT image is defined by those voxels whose corresponding nodes in G_CT belong to the source set A^*. Similarly, the segmented tumor volume on the PET image is given by those voxels whose associated nodes in G_PET belong to the source set A^*.

IV. Lung Tumor Segmentation Methods

In this section, we apply the proposed graph model for a challenging task: lung tumor segmentation in PET-CT images. The tumor may invade into the adjacent area of the lung, including the chest wall, the mediastinal structure or the diaphragm, which increases the difficulty of tumor detection with anatomical imaging. The incorporation of PET information is necessary for a successful tumor delineation. Here our algorithm is applied for co-segmentation of PET-CT images, which can be divided into two steps. In the pre-processing step, the PET image is registered with the CT image. Then, our graph-based co-segmentation is conducted based on PET and CT images.

A. Registration

As a pre-processing, the PET image is registered with the CT image using rigid transformation based on the Elastix toolbox [53], which allows rotation and translation transformations. The PET image is upsampled using a cubic B-spline interpolator during registration to obtain a one-to-one voxel correspondence between the CT and the registered PET images. Note that the one-to-one correspondence may not be necessary. Our method can handle the case in which one PET voxel corresponds to a set of CT voxels.

We are aware that deformations due to breathing often require non-linear registration. However, affine registration is frequently used by physicians for PET-CT delineation of tumor volumes (e.g., Refs. [6], [54], [55]), for simplicity, we choose to use affine transformation in this study. In addition, our method allows differences between the tumor contours on PET and those on CT, which extensively alleviates the stringent requirement on registration. We will conduct experiments to demonstrate the feasibility of affine registration in this study.

B. Initialization

Initial seed points are required for our graph-based co-segmentation. In our application, one center point and two radii are given by the user for each target tumor based on the fused PET-CT image, from which two spheres are generated in an approximate tumor area. We require that the small one have to be completely inside the tumor and the large one have to be completely outside the tumor (see Fig. 3). In this way, all voxels inside the small sphere are taken as the seed set of the object for both CT and PET images, denoted by in the CT image and by in the PET image ; all voxels outside the large sphere are considered to be the seeds for the background, denoted by (resp., ) in (resp., ). If there exists more than one tumor site in the dataset, then for each possible location, one center point as well as two radii are required as the initial input. Suppose we have M possible tumor locations in the image. Let (resp., ${\mathcal{F}}_i^{\prime }$) and (resp., ${\mathcal{B}}_i^{\prime }$) denote the seed sets associated with the location i in CT (resp., PET) for i = 1, …, M. Then the overall seed set of the object can be expressed as = ∪ ∪ … ∪ (resp., ${\mathcal{F}}^{\prime }={\mathcal{F}}_1^{\prime }\cup {\mathcal{F}}_2^{\prime }\cup \dots \cup {\mathcal{F}}_M^{\prime }$). The overall seed set of the background has the form: = ∩ ∩ … ∩ (resp., ${\mathcal{B}}^{\prime }={\mathcal{B}}_1^{\prime }\cap {\mathcal{B}}_2^{\prime }\cap \dots \cap {\mathcal{B}}_M^{\prime }$). Note that in this application, the CT and PET images share the same seed spheres.

Fig. 3.

Example slices of the initialization step in the fused image of CT (colored red) and PET (colored green). The orange sphere completely lies inside the tumor and the blue sphere completely contains the tumor. The center point is given by the cross point of two red lines.

C. Graph-based Co-segmentation

The graph is constructed following the method described in Section III-B. Two sub-graphs G_CT and G_PET are constructed for the segmentation of the CT and PET images, respectively. The cost functions are designed, as follows.

1) Cost functions for G_CT

For every voxel inside the small sphere (v ∈ ), which is identified as a tumor seed by the user, its hard region costs are set as D_v(l_v = 1) = 0 and D_v(l_v = 0) = +∞. This makes sure that those voxels in will be labeled as the object. Similarly, for every voxel outside the large sphere (v ∈ ), which is identified as the background seed, D_v(l_v = 1) = +∞ and D_v(l_v = 0) = 0. Thus these voxels must be included in the background.

For any voxel lying between the two spheres (v ∈ – – ), the region costs are designed based on how the intensity of voxel v fits into given intensity models. The image intensity of the tumor in CT roughly follows a gaussian distribution. Thus the region costs can be assigned according to the intensity distribution learned from the seed set of the object. Let i_v denote the intensity value for voxel v. The mean intensity value of all voxels in is denoted by ī and the corresponding standard deviation is σ. Then for any voxel v ∈ – – , the region term takes the form:

$$\begin{array}{l}{D}_v(l_v=1)=-{\lambda }_{1}log\mathit{Pr}(i_v\mid l_v=1)\\ \propto \frac{{(i_v-\overline{i})}^2}{{\sigma }^2}\end{array}$$ (7)

$$\begin{array}{l}{D}_v(l_v=0)=-{\lambda }_{2}log(1-Pr(i_v\mid l_v=1))\\ \propto -log(1-exp(-\frac{{(i_v-\overline{i})}^2}{{\sigma }^2})),\end{array}$$ (8)

where λ₁ and λ₂ are two given scaling constants. Fig. 4(a) shows one typical slice of the cost image for the region term in CT.

Fig. 4.

One typical slice of a cost image for the region term in (a) CT and (b) PET images. The target tumor boundary is labeled by the red contour. A larger intensity value indicates that the voxel is of the tumor in a higher probability.

For the cost design of the boundary term, a gradient-based cost is employed, which has a similar form as the well-known graph cut method in [10]. As described in Section III-A, B_uv denotes the penalty of assigning different labels to neighboring voxels (u, v) ∈ . B_uv can be expressed as

$$B_{uv}=-{\lambda }_{3}log(1-exp(\frac{-{\mid \nabla \mathcal{I}\mid }^2(u,v)}{2{\sigma }_g^2})),$$ (9)

where |∇ |²(u, v) denotes the squared gradient magnitude between u and v, σ_g is a given Gaussian parameter, and λ₃ is the scaling constant.

2) Cost functions for G_PET

For every voxel v′ ∈ or v′ ∈ , its hard region costs are set using the same form as we do for the CT image: D_v′(l_v′ = 1) = 0 and D_v′(l_v′ = 0) = +∞ for v′ ∈ , and D_v′(l_v′ = 1) = +∞ and D_v′(l_v′ = 0) = 0 for for v′ ∈ . For all other voxels v′ ∈ – – between two spheres, the region costs are computed based on the SUV values. As described in [56], the typical threshold value for tumor used in clinic application ranges from 15% to 50% of the maximum SUV in the image. Let S(v′) denote the SUV value for voxel v′. S_max denote the maximum SUV value in the image. Then for every voxel with a higher SUV value than 50% of S_max, it has a high likelihood to belong to a tumor. Similarly, for every voxel with a lower SUV value than 15% of S_max, it most likely belongs to the background. Based on this prior knowledge, our region cost functions take the form:

$$D_{v^{\prime }}(l_{v^{\prime }}=1)=\{\begin{array}{ll}0\hfill & \text{if}S(v^{\prime })>S_U\hfill \\ {\lambda }_4{C}_{\mathit{max}}·(1-\frac{1}{1+e^{-(\frac{S(v^{\prime })-S_L}{S_U-S_L}-\alpha )/\beta }})\hfill & \text{if}{S}_L\le S(v^{\prime })\le S_U\hfill \\ {\lambda }_4{C}_{\mathit{max}}\hfill & \text{if}S(v^{\prime })<S_L\hfill \end{array}$$ (10)

$$D_{v^{\prime }}(l_{v^{\prime }}=0)={\lambda }_4{C}_{\mathit{max}}-D_{v^{\prime }}(l_{v^{\prime }}=1)$$ (11)

where C_max is the maximum region cost allowed; S_U = 50% · S_max and S_L = 15% · S_max are the upper and lower threshold values for the possible tumor region. A sigmoid function is employed to assign a high cost for a voxel with a low SUV value between S_L and S_U. Parameter a controls the curvature of the function and parameter β controls the center point of the function. λ₄ is a given coefficient. One typical slice of the cost image for the region term in PET is shown in Fig. 4(b).

The boundary term takes the same form as we have used in the CT images. The penalty B_u′v′ of assigning different labels to neighboring voxels (u′, v′) ∈ can be expressed as

$$B_{u^{\prime }{v}^{\prime }}=-{\lambda }_{5}log(1-exp(\frac{-{\mid \nabla {\mathcal{I}}^{\prime }\mid }^2(u^{\prime },v^{\prime })}{2{\sigma }_g^{\prime 2}})),$$ (12)

where |∇ |²(u′, v′) denotes the squared gradient magnitude between u′ and v′. ${\sigma }_g^{\prime }$ and λ₅ are given parameters.

3) Cost functions for the context term

The context term in the energy function is designed to make use of the complementary information of PET and CT to improve the tumor boundary in the other modality. The segmentation difference between PET and CT should be penalized appropriately. To formulate the context cost functions, the region costs D_v(l_v = 1) in the CT image and D_v′(l_v′ = 1) in the PET image are normalized between [0, 1], denoted by N_v and N_v′, respectively. The normalization is to make sure that if two corresponding voxels have the same label (object or background), they will have similar region costs, that is, D_v(l_v = 1) (D_v(l_v = 0)) approximately equals to D_v′(l_v′ = 1) (D_v′(l_v′ = 0)). This allows us using different ways to design the region cost functions for CT and for PET. In our setting, a voxel with a higher region cost N_v or N_v′ is more likely to be the object, and a voxel with a lower cost is more likely to be in the background. Our context cost term C_vv′ (l_v ≠ l_v′) can be described as follows:

$$C_{{vv}^{\prime }}=\theta (1-\mid N_v-N_{v^{\prime }}\mid )+K,$$ (13)

where θ is a scaling constant, K is the minimum penalty for an inconsistent segmentation. Intuitively, if two corresponding voxels have the same label (object or background), they will have similar region costs and a larger context cost will be assigned to penalize the inconsistent segmentation between CT and PET. Note that the soft context cost term enables our method to follow the prominently salient features in each modality to obtain difference tumor volumes for PET and CT images.

V. Experimental Methods

Our method computes the tumor volume defined in CT as well as that defined in PET simultaneously. Two contours are generated, one on CT and one on PET. Ideally, we should validate both tumor volumes against manual delineation using the same set of PET-CT data. However, due to the clinical protocol in the application domain from which our PET-CT datasets were obtained, the manual contours are either available on CT or on PET, but not on both. We thus used two different sets of PET-CT data to validate the CT segmentation and PET segmentation, separately.

A. Lung cancer datasets for validation of CT segmentation

23 sets of 3-D FDG PET-CT images are obtained from different patients with lung tumors. Each set of images contains one CT image and one corresponding PET image acquired during the treatment planning of the radiotherapy. Images are acquired with a dual Positron Emission Tomography (PET) and Computed Tomography (CT) scanner developed by Siemens Medical Solutions USA, Molecular Imaging (Hoffman Estates, IL). The specific PET/CT scanner system used in this proposal is a Biograph 40. The PET system specifications include 6 mm spatial resolution (NEMA 2001), an 162 mm axial and 605 mm trans-axial field of view, 2 mm plane spacing, 500 psec coincidence time resolution, 4.4 cps/kBq, and ≤ 5% variation in uniformity. Standard imaging protocols utilize 3 minutes per bed position and 90 minutes post-injection, reconstructed as 4 × 4 × 4 mm³ voxels. CT scans are typically 1 × 1 × 2 mm³ voxels acquired with 0.6 mm spatial resolution and 250 mAs, with and without contrast. The reconstructed matrix size for each CT slice is 512 × 512, with a voxel size ranging from 0.98 × 0.98 × 2.00 mm³ to 1.37 × 1.37 × 2.00 mm³. For the PET images, the reconstructed matrix size ranges from 128 × 128 to 168 × 168. The voxel size ranges from 3.39 × 3.39 × 2.02 mm³ to 4.07 × 4.07 × 4.00 mm³. As described in Section IV-A, the PET images were co-registered to the CT images in the pre-processing step and the experiments were conducted on the CT and the registered PET images, which have exactly the same size as the corresponding CT images.

The gross tumor volume (GTV) for each of the PET-CT datasets was traced by three independent experienced radiation oncologists on the CT images with the guidance of the corresponding PET images using the Pinnacle treatment planning system (Philips ADAC Pinnacle³). The PET image is either fused with the CT dataset or displayed side by side with CT for the delineation. The reference standard is generated by applying the Simultaneous Truth and Performance Level Estimation (STAPLE) algorithm [57] to the three manual delineations. Unfortunately, manual contours on PET alone for those lung cancer subjects were not available due to our current clinical practice standard. We thus did not validate the PET segmentation on these datasets.

The tumor size was roughly quantified by the longest diameter of the manual segmentation in the axial image plane, as suggested in the Response Evaluation Criteria in Solid Tumors (RECIST) [58]. For our datasets, 15.78 mm ≤ ≤ 150.99 mm. The average tumor size is 81.65 mm³. The tumor sizes are estimated from the reference standard.

B. Head-and-neck cancer datasets for validation of PET segmentation

Two clinical PET-CT image pairs of different head-and-neck cancer patients, which contain 3 volumes of interests (VOI) in total, were used to validate the PET segmentation of our method. These datasets were used in the PET Contouring Grand Challenge in XII Turku PET Symposium (http://www.turkupetcentre.net/PET symposium XII software session/ContouringChallengeResults/index.php) for evaluating 33 PET-CT segmentation methods [59]. The images are obtained using the metabolic tracer ¹⁸F-Fluorodeoxyglucose (FDG) and a hybrid PET/CT scanner (GE Discovery). Three VOIs, including two tumor volumes and one lymph node volume, are manually delineated by 3 experts on 2 occasions with at least a week in between. A series of union masks are generated using the 6 manual delineations. The one with the closest absolute volume of the mean of all 6 expert manual delineations is used as reference standard. Detailed information about the data and how the reference standard is defined can be found in [59]. For these datasets, only manual contours on PET were available. So we only validate our method on PET segmentation with these datasets.

C. Parameter setting

In our CT contour validation experiments, the following parameter setting was empirically employed for all analyzed lung cancer datasets. For the segmentation of tumor in CT, boundary term provides a more important information compared with the region term. Thus we set coefficients as λ₁ = λ₂ = 1 for the regional term and λ₃ = 5, σ_g = 0.5 for the boundary term. For the segmentation in PET, regional information based on the SUV thresholding plays a key role. Thus we set coefficients as λ₄ = 1 for the regional term and λ₅ = 0.1, ${\sigma }_g^{\prime }=0.5$ for the boundary term. The scaling constant θ for the context term is set as 0.2. The minimum context penalty K is set as 0.1.

In our PET contour validation experiments on the head-and-neck cancer subjects, all parameters are kept the same as the CT contour validation on the lung cancer subjects, except that the upper SUV threshold for PET region cost $S_U^{\prime }=40\%·S_{\mathit{max}}$ instead of S_U = 50% · S_max in the lung cancer case.

D. Validation of CT segmentation on lung cancer subjects

The proposed algorithm was carried out on all 23 sets of PET-CT images for validation. For quantitative measurement, the segmentation performance on CT images was evaluated by comparing the computed results against the reference standard. Here we only use the segmentation results on CT for quantitative validation.

1) Evaluation measures

For volumetric error measurement, the Dice similarity coefficient (DSC) was computed, with

$$\mathit{DSC}=2\mid V_m\cap V_c\mid /(\mid V_m\mid +\mid V_c\mid ),$$ (14)

where V_m denotes the volume of the reference standard and V_c denotes the computed result. All DSC values were computed in 3-D. For the boundary surface distance error, the average symmetric surface distance (ASSD) with the form

$$\mathit{ASSD}=\frac{{\sum }_{a\in A}{min}_{b\in B}d(a,b)+{\sum }_{b\in B}{min}_{a\in A}d(a,b)}{N_A+N_B}$$ (15)

was used [60], where A denotes the boundary surface of the reference stand and B denotes the computed surface. a and b are mesh points on the reference surface and the computed surface, respectively. d(a, b) represents the distance between a and b. N_A and N_B are the number of points on A and B, respectively.

2) Comparison with graph cut method solely using CT or PET

To determine the performance of our novel co-segmentation approach in comparison with the graph cut approach of solely using CT or PET, these three methods were applied to all 23 datasets with identical initialization and the same cost functions for the boundary term and the regional term in the corresponding image modalities. The computed scores of DSC and ASSD were computed for all three methods. Statistical significance of the observed differences was determined using Student t-tests for which p-value of 0.05 was considered significant.

3) Comparison with graph cut method using fused PET-CT images

As described in Section IV-C3, our method employs a soft context cost term, which allows different segmented tumor volumes in PET and in CT. It is of interest to compare our co-segmentation method with the graph cut method on fused PET-CT images, which only produce an identical segmentation result on both modalities. The underlying assumption of the graph cut method on fused images is that the tumor volume defined in PET is the same as that defined in CT. However, the literature shows that PET and CT do not convey the same type of information, which is not necessarily complementary, but sometimes contradictory. Thus, the tumor volume defined in PET may not be identical to that defined in CT. In addition, the registration between PET and CT may not be perfect. The registration errors may also lead to tumor volume disagreement between PET and CT spatially.

For the fused PET-CT segmentation with graph cuts, each node in the graph is associated with a pair of corresponding voxels: one in PET and the other in CT. The region boundary costs are set as the sum of the original separate costs in PET and CT. To show the effectiveness of the proposed soft context costs, both methods were applied to all 23 datasets with identical initialization. The computed scores of DSC and ASSD were compared between the two methods.

4) Sensitivity to registration errors

Allowing different tumor contours defined on PET and on CT enables our method to be more tolerant to inaccurate registration. To demonstrate this, artificial registration errors were added to the transformation matrix computed with the Elastix toolbox. The resulting transformation matrix was used for registration between PET and CT. Then the proposed method was applied on the registered PET and CT images with the artificial transformation matrix. More specifically, we add 10% perturbation to the X, Y and Z components of the translation transformation between PET and CT. Separately, we add 10% perturbation to the three rotation angles between PET and CT to simulate errors in the rotation component of the transformation. The signs of the perturbation are randomly selected. The DSC and ASSD scores were computed and compared between before and after the artificial registration errors added.

5) Robustness to seed initialization

The observer who initialized the center point and two radii was asked to do the initialization again after over six months. The 2nd initialization was conducted without providing any information from the 1st initialization. The experiments on 23 lung cancer datasets were conducted again using the 2nd initialization. Accuracy scores including Dice Similarity Coefficient (DSC) and Average Symmetric Surface Distance (ASSD) were computed for the segmentation from the 2nd initialization.

E. Validation of PET segmentation on head-and-neck cancer subjects

Our method was used to segment the three VOIs of two head-and-neck PET-CT image datasets. For quantitative measurement, the segmentation performance on PET images was evaluated by computing the Dice similarity coefficient (DSC) scores against the reference standard. The DSC scores were compared with the 33 PET-CT segmentation methods [59] that were registered to the PET Contouring Grand Challenge. Our CT segmentation results were not used in this validation experiment.

VI. Results

A. Quantitative validation of CT segmentation

The computed Dice similarity coefficient (DSC) and average symmetric surface distance (ASSD) of segmented lung tumors are summarized in Table. I. Since the size of the target tumor has serious influence on the final quantitative value, e.g., the larger tumor tends to have a larger surface distance error, the results are presented as three groups according to the tumor size. In both evaluation metrics, the proposed approach combining information from both PET and CT achieved a significant improvement in comparison with three other graph cut based methods: the graph cut method using only CT, the graph cut method using only PET, and the graph cut method using fused PET-CT images (p < 0.05).

TABLE I.

Quantitative scores of segmented lung tumors using the proposed co-segmentation method in comparison with three other methods: the graph cut methods solely using CT, solely using PET and the graph cut method using fused PET-CT. The tumors are divided into three groups according to their sizes. All results are reported as mean±standard deviation.

Tumor size S (mm)	Num of datasets	DSC				ASSD (mm)
		Proposed	CT Only	PET Only	fused PET-CT	Proposed	CT Only	PET Only	fused PET-CT
S < 50	5	0.82 ± 0.07	0.81 ± 0.07	0.59 ± 0.15	0.78 ± 0.08	0.77 ± 0.43	1.05 ± 1.07	3.40 ± 0.84	1.12 ± 0.77
50 ≤ S < 100	11	0.82 ± 0.08	0.42 ± 0.25	0.68 ± 0.14	0.81 ± 0.08	2.06 ± 0.95	19.83 ± 14.58	9.56 ± 15.66	2.28 ± 1.15
S ≥ 100	7	0.78 ± 0.07	0.34 ± 0.17	0.68 ± 0.06	0.76 ± 0.08	3.36 ± 1.48	25.00 ± 11.03	5.79 ± 0.94	3.98 ± 1.74
Overall	23	0.81 ± 0.08	0.48 ± 0.27	0.66 ± 0.13	0.79 ± 0.08	2.17 ± 1.42	17.32 ± 14.75	7.07 ± 11.14	2.54 ± 1.67

Fig. 5 shows the performance comparison for all 23 lung datasets among the proposed algorithm and three other graph cut based methods ordered according to the tumor size. Generally speaking, our method not only shows an overall improvement of the segmentation, but also has a consistent segmentation performance for all tumors in the entire set of the 23 images. In contrary, the performance of the method using only CT or only PET is very uneven. For the CT-only method, the uneven performance is mainly caused by the leaking problem due to the less contrast of intensity between tumor and its surrounding tissues; while for the PET-only method, the blurring boundary is the major contribution to the uneven performance. Fig. 8(g)–(i) shows the segmentation performed on CT only, in which a serious leaking problem happens. In comparison with the method using fused PET-CT images, the proposed approach provides a more flexible control, which results in more accurate segmentation results.

Fig. 5.

Quantitative and comparative performance evaluation based on computed (a) DSC values and (b) ASSD values on 23 PET-CT lung cancer images, ordered according to the size of the tumor. Our method (blue) showed a relatively consistent results over all datasets compared to three other graph cut based methods: the graph cut method solely using CT (red), solely using PET (green), and the graph cut method using fused PET-CT images (orange).

Fig. 8.

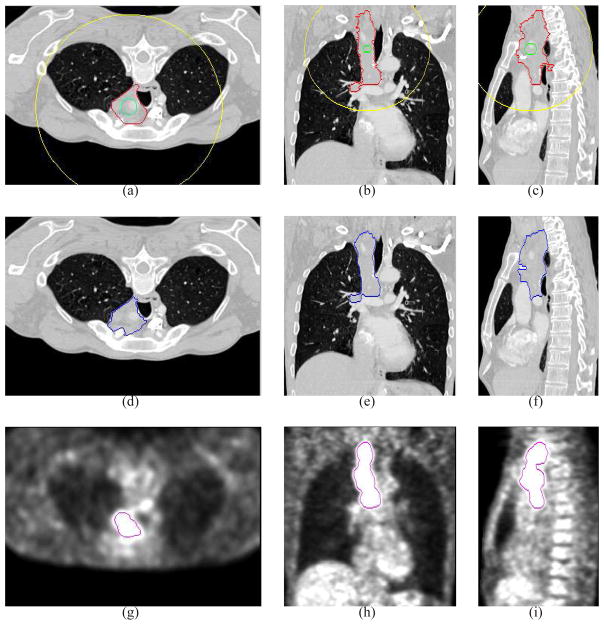
Comparative segmentation results in the transverse (left), coronal (middle) and sagittal (right) views. (a)–(c) The manual segmentation results. (d)–(f) Our proposed co-segmentation results in the CT image. (g)–(i) The segmentation results by the graph cut method solely using the CT image. (j)–(l) The segmentation results by the graph cut method solely using the PET image. (m)–(o) The segmentation results by the graph cut method on the fused PET-CT image. The typical improvements of the proposed method in comparison with those three other methods are indicated by arrows.

Table. II shows the Dice similarity coefficient (DSC) and average symmetric surface distance (ASSD) of segmented results with three different registrations: registration computed with the Elastix toolbox, registration added 10% artificial translation errors to the Elastix registration, registration added 10% artificial rotation errors to the Elastix registration. The scores demonstrate the robustness of our method to registration errors within a certain range.

TABLE II.

Quantitative performance scores of the proposed method with three different registrations between PET and CT. All results are reported as mean±standard deviation.

Metric	Elastix reg	10% translation err	10% rotation err
DSC	0.81 ± 0.08	0.80 ± 0.08	0.80 ± 0.08
ASSD (mm)	2.17 ± 1.42	2.39 ± 1.70	2.32 ± 1.42

As to the robustness of our method with respect to the seed initialization, Figure 6 shows the Dice similarity coefficient (DSC) and average symmetric surface distance (ASSD) of the segmented results with two different initializations. We can observe that our method achieved highly comparable results over those two initializations.

Fig. 6.

Quantitative results for the proposed method using different initializations.

B. Quantitative validation of PET segmentation

Table III shows the DSC scores of our segmentation results on the three head-and-neck cancer VOIs, comparing against the top 7 methods in the PET Contouring Grand Challenge [59]. Manual delineation methods (MD) use a computer mouse to contour a VOI slice-by-slice. MD^b is performed by two independent, experienced physicians viewing only PET image data ( ${\text{MD}}_1^b$ and ${\text{MD}}_2^b$ in Table III). MD^c performed on the PET images by a nuclear medicine physicist who used visual aids derived from the original PET. Pipeline methods (PL) are complex, multistep algorithms combining thresholding, region growing, watershed, morphological operations and other techniques. Method PL^b is a variant of the ‘Smart Opening’ algorithm, adapted for PET from the tool in [61]. Method PL^g is a new fuzzy segmentation technique for noisy and low resolution oncological PET images [37]. Watershed methods (WS) use variants of the classical algorithm in [62]. Method WS^b uses viscosity and markers to overcome the local minima problems in image gradient [63]. The thresholding methods were not among the top ranking ones. In fact, only one automated segmentation method outperformed the proposed method according to the DSC metric.

TABLE III.

Comparison of the proposed method against the top methods in the PET Contouring Grand Challenge [59] according to the DSC metric on the head-and-neck datasets

Rank	Methods	DSC
1	MDc	0.813 ± 0.093
2	${\text{MD}}_2^b$	0.805 ± 0.035
3	PLb	0.771 ± 0.105
4	our method	0.761 ± 0.106
5	PLg	0.749 ± 0.039
6	${\text{MD}}_1^b$	0.739 ± 0.040
7	PLc	0.723 ± 0.091
8	WSb	0.687 ± 0.108

C. Illustrative results

Illustrative results of the experiments on the lung cancer subjects are shown in Fig. 8 for three views. From all views, our co-segmentation works quite well in both CT and PET images. Fig. 8 shows the segmentation results obtained using four compared methods. Our approach makes use of the advantages from both CT and PET images, exhibiting expected improvement in comparison with three other graph-cut methods.

Illustrative results of the experiments on the head-and-neck cancer subjects are shown in Fig. 9. Our approach achieved highly accurate PET segmentation results.

Fig. 9.

Illustrative results of PET segmentation on head-and-neck cancer subjects.

D. Execution time

Our algorithm was implemented in C++ on a Linux workstation (3GHz, 32GB memory). Current non-optimized implementation required about 6 minutes for each dataset. The execution time for the registration was about 60s.

Our graph-based co-segmentation took about 3 minutes.

VII. Discussion

Our proposed method makes use of advantages of both PET and CT to co-segment tumor from the dual modalities simultaneously. The novel feature lies on its global optimality for the PET-CT tumor segmentation with respect to the problem-specific objective function.

A. Importance of co-segmentation

Although PET-CT images have been routinely used in clinic qualitatively by physicians, many existing PET-CT segmentation algorithms only work for a single modality. The introduction of integrated PET-CT scanners has provided new opportunities to develop co-segmentation methods for tumor delineation by combining physiological information from PET with anatomical information from CT. Though utilizing both PET and CT information, the segmentation methods [29], [30], [31] are potentially more dependent on accurate registration than the proposed approach since they do not allow disagreement of tumor volumes on PET and on CT. First, image registration itself remains very challenging; even with the integrated PET-CT scanners, the acquired PET and CT images may not be well aligned due to the substantially longer acquisition time for PET. In addition, the tumor boundary defined in PET may not be identical to that defined in CT because of the different imaging mechanisms, even with perfect registration. Therefore, simultaneously segmenting tumor from both PET and CT while admitting the (subtle) difference of the boundaries defined in the two different modalities is more reasonable than those previous methods on fused PET-CT images, in which identical tumor boundaries are assumed. Our method is able to co-segment tumor using both PET and CT to accommodate the uncertainties in imaging and registration. Co-segmentation makes use of the high tumor contrast in PET and the exquisite anatomical structures provided by CT scans, enabling the identification and characterization of more lesions than either modality alone. A big challenge in PET segmentation is that pathological and physiological uptakes of the tracer cannot be distinguished; while the pathology and physiology changes are differentiable in CT. This further provides the rationale for the idea of co-segmentation.

B. Possible improvement

The initialization of the object and the background seed sets can potentially be automated or largely automated by using an approach similar to the one used in [64]. The approach proposed in [64] sets a threshold for the PET SUV value to define the object seeds first. Then starting from the object seeds, nearby voxels are searched to find voxels with SUV values lower than another threshold. Those voxels are defined as background seeds. These threshold parameters can be learned from training datasets, thus alleviating the human burden in specifying the object and background seed sets.

The context term in the energy function of our method is designed to make use of the complementary information of PET and CT to improve the tumor boundary in the opposite modality. Of course, the segmentation difference should be penalized appropriately. For example, if the weights of inter-subgraph arcs are all set +∞, then the tumor contours in PET and in CT are forced to be identical; while if those weights are all set 0, then it is equivalent to segmenting the two contours separately. Although in this study the parameters for those arc weight assignment were determined empirically, in the future we plan to apply machine-learning techniques to find appropriate parameter settings based on training datasets. In addition, a joint probabilistic models learned from both CT and PET for context cost design may also help. However, it may still pose a great challenge to determine appropriate parameters if the structural/anatomical and functional target volumes vary a lot. For the cases that PET and CT cannot provide enough complementary information to each other, our method may not be able to use the information of the other modality to improve the segmentation results.

Our method can be viewed as a general multi-modality co-segmentation framework. The low-level image features for a specific modality can be incorporated in the cost function design. The cost function design, in fact, is critically important for improving the performance of our method. In this study, we do not well utilize the PET uptake heterogeneity for the cost function design (i.e., D_v′(·)). In the future, we will investigate a better way to design the cost functions D_v′(·) by making use of the SUV heterogeneity, and the new cost functions should be easy to be integrated in our framework.

In many cases, tumor grows adjacently to the boundary of its host. For instance, lung tumor may be in touch with lung parenchyma or close to the diaphragm; esophageal cancer attaches to the esophagus walls. The delineation of such a tumor from PET could be much more challenging due to the artifacts induced by the spill-over of signal from intensely avid lesions into adjacent normal structures. In that setting, however, the boundary surfaces of the tumor’s adjacent structures can serve as valuable prior information to help separate the tumor from those structures. In the future, we plan to simultaneously segment those boundary surfaces from the CT scan as well as the tumor from both PET and CT datasets by integrating the graph searching method [44], [45], [65] with the graph cut method [10]. The integration of those two methods into one single optimization process, yet still admitting globally optimal solutions, will certainly become a more powerful tool for medical image analysis.

VIII. Conclusion

In this article, we propose a novel approach for the co-segmentation of the PET-CT images, which makes use of the strength from both modalities: the functionality information of PET and the anatomical structure information of CT. The target tumor volumes in PET and in CT are concurrently segmented with the help of the information acquired from the other modality. Our method was validated on a challenging task of segmenting lung tumor from 23 patient datasets and the challenging head-and-neck tumor from 2 patient subjects. The results clearly demonstrated the applicability and the improved performance of the proposed approach in comparison with the segmentation methods solely using PET or CT.

Fig. 7.

Typical tumor segmentation in the transverse (left), coronal (middle) and sagittal (right) views. (a)–(c) 2-D slices of a 3-D CT image with the reference standard (red) and outlines of spherical initialization (green and yellow). (d)–(f) Proposed co-segmentation results in the CT image. (g)–(i) Co-segmentation results in the PET image.