A Comparison of Two Methods for Estimating DCE-MRI Parameters via Individual and Cohort Based AIFs in Prostate Cancer: A Step Towards Practical Implementation

Abstract

Multi-parametric Magnetic Resonance Imaging, and specifically Dynamic Contrast Enhanced (DCE) MRI, play increasingly important roles in detection and staging of prostate cancer (PCa). One of the actively investigated approaches to DCE MRI analysis involves pharmacokinetic (PK) modeling to extract quantitative parameters that may be related to microvascular properties of the tissue. It is well-known that the prescribed arterial blood plasma concentration (or Arterial Input Function, AIF) input can have significant effects on the parameters estimated by PK modeling. The purpose of our study was to investigate such effects in DCE MRI data acquired in a typical clinical PCa setting. First, we investigated how the choice of a semi-automated or fully automated image-based individualized AIF (iAIF) estimation method affects the PK parameter values; and second, we examined the use of method-specific averaged AIF (cohort-based, or cAIF) as a means to attenuate the differences between the two AIF estimation methods.

Two methods for automated image-based estimation of individualized (patient-specific) AIFs, one of which was previously validated for brain and the other for breast MRI, were compared. cAIFs were constructed by averaging the iAIF curves over the individual patients for each of the two methods. Pharmacokinetic analysis using the Generalized kinetic model and each of the four AIF choices (iAIF and cAIF for each of the two image-based AIF estimation approaches) was applied to derive the volume transfer rate (K^trans) and extravascular extracellular volume fraction (v_e) in the areas of prostate tumor. Differences between the parameters obtained using iAIF and cAIF for a given method (intra-method comparison) as well as inter-method differences were quantified.

The study utilized DCE MRI data collected in 17 patients with histologically confirmed PCa. Comparison at the level of the tumor region of interest (ROI) showed that the two automated methods resulted in significantly different (p<0.05) mean estimates of v_e, but not of K^trans. Comparing cAIF, different estimates for both v_e, and K^trans were obtained. Intra-method comparison between the iAIF- and cAIF-driven analyses showed the lack of effect on v_e, while K^trans values were significantly different for one of the methods.

Our results indicate that the choice of the algorithm used for automated image-based AIF determination can lead to significant differences in the values of the estimated PK parameters. K^trans estimates are more sensitive to the choice between cAIF/iAIF as compared to v_e, leading to potentially significant differences depending on the AIF method. These observations may have practical consequences in evaluating the PK analysis results obtained in a multi-site setting.

Introduction

Prostate cancer (PCa) is the second most frequently diagnosed cancer and the sixth leading cause of cancer death in males worldwide [1]. Diffusion weighted magnetic resonance imaging [2] and dynamic contrast enhanced MRI (DCE MRI) [3] play increasingly important roles in detection and staging of prostate cancer [4]. In addition, roles for multi-parametric prostate MRI (which includes DCE MRI) in stratifying patients for specific therapies [5], and for assessing response to therapy [6–8] are continuously evolving [9,10]. In particular, much effort has focused on the development of quantitative DCE MRI methods to better characterize the microvascular properties associated with prostate cancer [11–13]. As with tumors in many other organs, prostate cancer demonstrates earlier and more pronounced enhancement than normal surrounding tissue, thought to be related to angiogenesis. These newly formed vessels demonstrate higher permeability than the walls of normal vessels, and it has been suggested that a worse prognosis is associated with a greater number of abnormal vessels in prostate cancer [14], and microvessel density (a measure of angiogenesis) can predict disease progression [15]. Due to such histological findings, there is much interest in DCE MRI as a non-invasive tool in prostate cancer detection, and as a measure of tumor aggressiveness and response to therapy.

DCE MRI involves serial acquisition of T₁-weighted images before and after the injection of paramagnetic contrast agent (CA). As the CA enters the region of interest (ROI) under investigation, it changes the tissue’s native T₁ and T₂ relaxation times to a degree based on the accumulated concentration of the CA. When the CA leaves the tissue, the relaxation rates return to their native values. If the signal intensity time course of the tissue as well as that of a feeding vessel (the so-called arterial input function, or AIF) can be measured, then the data can be analyzed with an appropriate pharmacokinetic (PK) model to extract parameters related to, for example, vessel perfusion and permeability, and tissue volume fractions. Although the value of such parameters in assessing the disease has been suggested by individual studies [3,12], it is widely recognized that PK parameters are sensitive to acquisition and processing techniques [3,13], potentially limiting their reproducibility and practical value in multi-site clinical trials and, eventually, in the standard-of-care setting. The effect of different AIF estimation methods on PK values obtained for PCa characterization is unknown. It is known, however, that patient-specific physical factors, such as cardiac output, blood flow distribution and kidney function all affect the AIF dynamics [16]. Therefore, since different approaches exist to deriving individualized AIF, quantification of their effect on the PK modeling and their comparisons are critical for assessing the results obtained by different analysis tools and for establishing the value of PK parameters from DCE MRI as a PCa imaging biomarker.

In general, there are three groups of approaches for defining AIF. Firstly, model-based AIF (mAIF) approaches rely on assuming either an a priori functional form of the AIF that is designed to capture the “characteristic” shape of the AIF, or an AIF obtained from population studies (see, for example, references [17,18]). A second approach is patient-specific, and utilizes individualized AIFs (iAIFs), which are typically defined based on the signal intensity changes observed in the voxels corresponding to a major feeding vessel [19]. Although the evidence is rather limited, some studies suggest that the use of an iAIF leads to more accurate fitting of the model, allow capturing of patient-specific variability and, subsequently, more accurate parameter estimation [20–22]. Estimation of patient-specific AIFs based on the manual contouring of a feeding vessel requires operator time, potentially introducing inter-rater variability into the subsequent PK analysis. Therefore, a number of approaches have been proposed for automatically determining an image derived iAIF on a patient-specific basis [19,23,24]. In practice, individualized estimation of the AIF may not always be possible due to the presence of acquisition artifacts or difficulties in identifying representative voxels in the feeding vessel. This leads to the third AIF estimation approach, which is based on averaging the iAIFs estimated from a representative group of patients (cohort AIF, or cAIF), where iAIF estimation is feasible (e.g., see [23]). Unlike the model-based AIF approach [18], the cAIF may allow capturing of AIF features common across the selected patient cohort related to the disease site, acquisition parameters, or clinical characteristics of the patients.

In this contribution, we report on the effects of individualized (iAIF) and cohort-specific AIFs (cAIF) obtained using automated image-based methods on PK parameters estimated from the Generalized Kinetic model [25] applied to DCE MRI data collected in men with known prostate cancer. More specifically, we compare two automated methodologies for AIF estimation that were previously developed and evaluated by two independent research groups [23,24], and apply them to prostate DCE 3T MRI data that was collected using standard clinical imaging protocols.

Our long-term goal is to develop a practical approach for prescribing the AIF for quantitative PK analysis of DCE MRI data of prostate cancer in typical clinical imaging conditions. Towards this end, in this work we aim to address two fundamental questions: 1) does the choice of the automated methodology for both iAIF and cAIF affect the values of PK parameters, and 2) given an automated AIF determination method, is there a significant variability in the results between iAIF- and cAIF-based estimation?

Methods

Patient characteristics

The study was HIPAA compliant and approved by the Institutional Review Board at Brigham and Women’s Hospital. Informed written consent was obtained from the patients participating in the study. The study cohort consisted of 17 patients with histologically confirmed PCa that underwent a staging multi-parametric prostate 3T MRI exam. Pathology revealed these patients to have a Gleason score of 4+5 (n=3), 4+4 (n=1), 4+3 (n=5), 3+4 (n=6) and 3+3 (n=2). The mean age of our cohort was 58 years (range 42–74).

MR imaging

MR imaging exam was performed on a GE Signa HDx 3.0T magnet (GE Healthcare, Waukesha, WI) using a combination of 8-channel abdominal array and endorectal coil (Medrad, Pittsburgh, PA). The MR sequences included T₁- and T₂-weighted imaging, diffusion weighted (DW) imaging, and DCE MRI [26]. T₁-weighted imaging was performed with a spoiled gradient recalled echo (SPGR) sequence with TR/TE/α = 385 ms/6.2 ms/65° over a (16 cm)² field of view (FOV). T₂-weighted imaging was performed with a FRFSE (Fast Recovery Fast Spin Echo) sequence with TR/TE = 3500/102 ms, FOV = (16 cm)². A DW echo planar imaging sequence with trace diffusion sensitization and b-values of 0 and 500 s/mm², and TR/TE = 2500/65 ms provided data for an Apparent Diffusion Coefficient (ADC) map. Finally, DCE MRI utilized a 3D SPGR sequence with TR/TE/α = 3.6 ms/1.3 ms/15°, FOV = (26 cm)², with full gland coverage and reconstructed image voxel size of 1 × 1 × 6 mm (interpolated to 256 × 256 matrix). DCE MRI frames were acquired at approximately 5 s intervals (the number of frames varied between 12 and 16 slices resulting in the time resolution between 4.4 and 5.3 seconds) to achieve a clinically appropriate compromise between spatial and temporal resolutions. Gadopentetate dimeglumine (Magnevist, Berlex Laboratories, Wayne, New Jersey) was injected intravenously using a syringe pump (0.15 mmol/kg) at the rate of 3 ml/s followed by 20 ml saline flush at the same rate. The protocol included ~5 baseline scans prior to contrast injection for estimation of baseline tissue properties.

Cancer-suspicious regions of interest (ROIs) were located and outlined on axial MR images using 3D Slicer software [27] by an abdominal radiologist (FF) with over 10 years of experience in interpretation of the prostate MRI. ROI localization was based on the pathology report of the prostatectomy and/or biopsy specimen and concomitant MR findings suspicious for PCa (reduced signal on T₂-weighted MRI, reduced ADC, and rapid enhancement and washout of the contrast agent on DCE MRI).

AIF Estimation Methods

Two previously published and evaluated approaches to AIF estimation were utilized in this study.

Method 1

The first AIF estimation method incorporates a priori knowledge of anatomy (i.e., the likely location of major vessels in the field of view) and the characteristics of a typical AIF uptake curve shape [24]. This method does not require any user involvement. Therefore, we will refer to it as fully automatic, or FA-AIF. The method first selects the middle slices of the time-resolved DCE MRI multi-slice image volume that are less likely to be affected by wraparound and inflow artifacts. For the slices selected in the first step, a mask is generated to locate the enhancing regions of the image. The generation of this mask is based on the intensity difference between the first time frame and the time frame with the maximum intensity value, yielding the regions where candidate AIF voxels exist. These candidate voxels are then ranked based on the expected characteristics of AIF curve shape, such as short bolus arrival time, short time to peak and high upslope. The top ranking voxels are selected from the enhancing mask and their signal intensity curve is averaged to determine the final AIF. It was found that selecting the best 5 voxels as candidates for AIF produced robust and accurate results, and is a compromise between selecting too few voxels (making the resulting AIF prone to noise and motion errors), and selecting too many voxels (making the resulting AIF prone to saturation and flow effects). Details can be found in ref. [24]. The method is implemented in a research tool used for PK analysis of the DCE MRI (OncoQuant, GE Global Research, Niskayuna, NY).

Method 2

This method employs a voxel tracking algorithm with a manually defined seed point. Since this approach requires user initialization, we will refer to it as semi-automatic, or SA-AIF method. The method first averages, for each slice in the imaging volume, all the time frames in the dynamic scan to yield a high SNR image stack from which the two femoral arteries are readily identified in a central slice. One seed point is then placed at the center of each artery and a 5 × 5 region of interest (ROI) is then automatically generated around each seed point and the voxels within this ROI are added to an AIF search pool. This ROI is then transferred to an adjacent slice and new seed points (again, one for each artery) are selected from the adjacent slice based on the ROI. The new seed points are selected automatically by calculating the correlation coefficient (CC) between the intensity values of the ROI in the original slice and a 5 × 5 ROI centered on each of the points identified in the adjacent slice. The center points for the ROI in the new slice with the highest CC become the seed points for this slice, and the process is repeated for all slices. Once the AIF search pool has been defined, voxels are added to the AIF mask if they meet the following empirically determined criteria: 1) the maximum of the signal curve for the voxel occurs in the first 45 seconds following contrast injection; 2) the maximum of the signal curve is at least 20 times greater than the standard deviation of the signal curve over the pre-contrast frames; and 3) the mean of the final 45 seconds of data is less than 50% of the maximum signal. The final AIF is calculated as the median time-resolved signal from all voxels in the AIF mask. Details can be found in ref. [23]. The method was implemented as a Matlab tool (MathWorks, Natick, MA).

Given the AIF masks produced by each of the two methods, the signal intensity time courses for each voxel in the mask is converted to contrast agent concentration using Eq. [1]:

$$R_1(t)=r_{1}C(t)+R_{10},$$ [1]

where R₁(t) = 1/T₁(t), r₁ is the longitudinal relaxation rate of the contrast agent. The relaxivity was set to 4.9 mM⁻¹s⁻¹, appropriate for Magnevist at 3T [28]. We note that the value used does not have any impact on quantitative results being compared, since all concentration curves are scaled in the same fashion. C(t) is the concentration of the contrast agent, and R₁₀ = 1/T₁₀ where T₁₀ is the pre-contrast longitudinal relaxation time of blood. Patient-specific estimation of T₁₀ prostate values was not performed, as the appropriate imaging sequence was not included as part of the standard clinical protocol. Therefore, prostate tissue T₁₀ of 1597 ms was assumed [29,30], and blood T₁₀ was set at 1600 ms [31]. T₁(t) is the T₁ of the blood estimated from the imaging at each time point derived from the SPGR signal intensity equation:

$$SI=M_0\frac{\mathit{sin}(\alpha )·[1-exp(-TR/T_1)]}{1-cos(\alpha )·exp(-TR/T_1)},$$ [2]

where M₀ is a combination of proton density and scanner gain, and we have assumed TE≪T₂^*. Signal intensity time curves were converted into whole blood concentration assuming a hematocrit value of 0.4. To obtain the cohort-specific AIFs, individual AIF curves were first normalized by aligning the temporal position of the peak concentration, followed by extracting the median concentration value at each time point.

Image Analysis

PK analysis of the DCE-MRI data was based on the Generalized Kinetic Model (Equation 8 in [25]) implemented in a custom research software tool (OncoQuant, GE Global Research, Niskayuna, NY). We chose the 2-parameter model without explicit plasma volume fraction term because of the instability in PK analysis and model fitting at the temporal resolution of the prostate DCE MRI data (~5 s). Prior to use in this study, the PK analysis software was validated using a digital phantom¹ to confirm the ability of the software to recover the true parameter values from the synthetically generated uptake curves in the absence of noise. Four maps for each of the studied parameters (K^trans and v_e) were generated for each patient: one map each using the iAIF produced by FA-AIF and SA-AIF methods, and one map each from the corresponding averaged AIFs (cAIFs). The PK maps were further post-processed to discard voxels that showed poor quality of fit (i.e., a coefficient of determination R² < 0.75) or non-physiological estimates for PK parameters (i.e., values outside of the following ranges: 0< K^trans < 5 min⁻¹, or 0 < v_e < 1).

Evaluation methodology

The results of the automated AIF detection methods were inspected visually using 3D Slicer research platform [27] to confirm that the AIF voxels identified were located within the femoral artery. Quantitative analysis was then applied to evaluate the differences between the two automated methods for AIF estimation, as well as the effect of the choice between the iAIF and cAIF for a given method. As there is no “gold-standard” available for such a study, our goal was to determine 1) what effect the method of AIF estimation has on DCE MRI analysis of the prostate, and 2) what effect substituting a cAIF for an iAIF has on DCE MRI analysis. We explore these two questions with the inter- and intra-method comparison, as follows.

Inter-method comparison

Lesion means of the parameters obtained using individual and cohort-specific AIFs were compared by method of estimation (FA-AIF vs SA-AIF) using the mixed models analysis of variance (MMANOVA) analog of the paired t-test. The pairing factor was estimation type. These models included a random effect for patient and lesion within patient as determined by Akaike Information Criterion (AIC) [32]. The distributions of lesion means by group were depicted in boxplots with annotated p-values from MMANOVA paired t-test. Bland-Altman type plots were used to illustrate differences in mean lesion parameters versus the average of the pairs. Lower 95% confidence intervals estimated for the mean difference that exclude the zero (horizontal gray) line identify the cases where the two methods are statistically different (p<0.05).

Intra-method comparison

The goal of intra-method comparison was to determine the interchangeability of individual and cohort-based pharmacokinetic parameters. Scatter plots of cohort versus individual parameters with linear regression lines were created as patient-level descriptive summaries of voxel data for each lesion (selected examples are shown in Fig. 4). To synthesize the relationships between cohort and individual measures over all patients, we modeled these data using a random coefficient mixed models regression analysis separately for SA-AIF and FA-AIF. This voxel-wise comparison approach estimates an overall (fixed effect) regression line as an average of patient-specific (random effect) regression lines to estimate the overall relationship between cohort ( $K_{\mathit{cAIF}}^{\mathit{trans}}$) and individual ( $K_{\mathit{iAIF}}^{\mathit{trans}}$) estimators of K^trans, and v_e (v_e,cAIF and v_e,iAIF, respectively). This modeling approach allowed us to account, in some measure, for the intra-patient correlation among voxels within a lesion and for lesions within subjects, providing a more appropriate variance estimates for test statistics. All analyses were conducted in SAS (version 9.2) and graphics constructed using R (version 2.15).

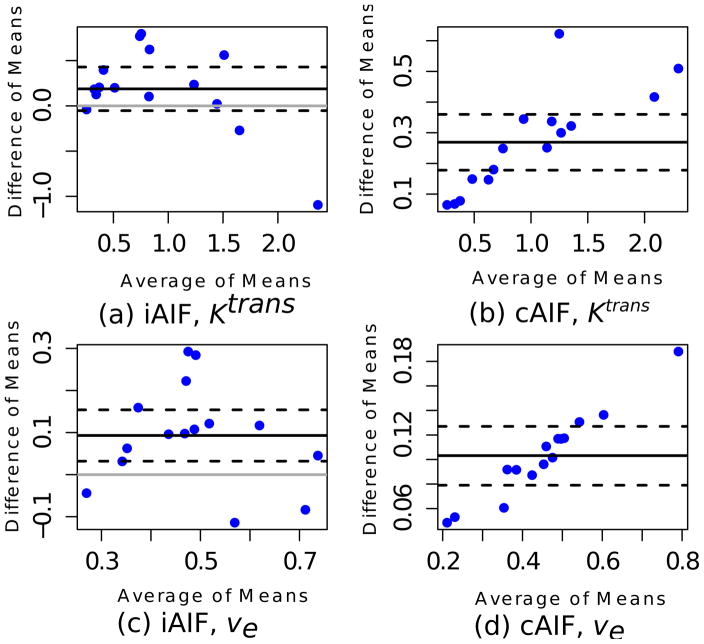
Figure 4.

Bland-Altman plots show the difference (SA-AIF minus FA-AIF) of means for K^trans and v_e against their average. Solid black lines represent the average difference of the means and dotted black lines are 95% confidence intervals for the average mean difference based on the MMANOVA model. Cases where the lower 95% confidence interval lines (dotted black lines) lie above the gray, horizontal (zero effect) line are statistically significant.

Results

DCE-MRI data for 17 patients with pathologically confirmed PCa were initially included in the analysis, and AIF masks were estimated using each of the two AIF methods. Upon examination of the AIF concentration curves, four of the datasets had the peak concentration of iAIF for at least one of the two methods outside the range of +/− 2 standard deviations (SD) from the mean peak concentration. As the goal of our study was to compare the two AIF methods rather than to characterize the disease in the patient cohort, we chose to define those AIF measurements as outliers, so that our comparison is not affected by the extreme values and the test cohort is more uniform.

Application of FA-AIF resulted in the selection of five voxels for constructing the AIF for each patient. In 11 patients, all of these voxels were located in the area of the patient’s left femoral artery, while in the remaining two patients, AIF voxels were identified in both left and right femoral arteries. SA-AIF selected a much larger number of voxels to construct the AIF (a mean of 203 voxels, with a range of 56 to 471 voxels), with voxels identified in both left and right femoral arteries in all 13 patients. In 7 out of 13 cases there was no spatial overlap between the AIF voxels identified by the two methods. The resulting individual AIFs from the two methods were then used to construct the method-specific cohort AIFs shown in Fig. 1.

Figure 1.

cAIF for FA-AIF (left) and SA-AIF (right) methods (solid line). Dashed lines correspond to +/− 1 standard deviation observed in the iAIFs estimated using these two methods. FA-AIF method resulted in a sharper and higher estimate of the peak concentration, as well as larger variability across the cases.

PK modeling using either the cAIF or the iAIF as estimated by both methods resulted in an acceptable fit (i.e., an R² ≥ 0.75, 0 < v_e < 1 and 0 < K^trans < 5 min⁻¹) in 80% of the voxels located within the tumor ROIs. In one case, estimated values for v_e were physiologically unrealistic (v_e=1) for all ROI pixels using one of the AIF estimation methods. Therefore, this case was completely excluded from the analysis as it resulted in physiologically unrealistic parameters of the model for all ROI voxels. The remaining 12 cases that had acceptable fit and physiologically realistic parameter values were used in the subsequent comparison. For three patients there were two cancer-suspicious areas in each gland, resulting in a total of 15 ROIs available for analysis. The number of voxels per lesion ranged from 10 to 169. Depending on the selected AIF, the means of the estimated values of K^trans ranged from 0.64 to 1.01 min⁻¹ and the means of v_e were in the range from 0.39 to 0.51. An illustrative example of the effect of the AIF selection for one of the patients is shown in Fig. 2.

Figure 2.

Illustration of the effect of the AIF choice on the conspicuity of a PCa lesion. (a) Image-based AIF curves extracted using FA-AIF and SA-AIF, and the method- and cohort-specific averaged AIFs. Arrows highlight the peak values for each AIF curve. (b,c,d,e): pixel-wise color maps of the Ktrans parameter estimated using the General Kinetic model using the different choices of AIF. The visual appearance of the lesion region (white arrow) varies dramatically depending on the AIF selection. Note that sub-figures (b–e) do not allow assessment of the true voxel size due to the interpolation applied by the visualization software (3D Slicer).

Inter-method comparison

The estimates of the pharmacokinetic parameters obtained using SA-AIF were consistently and significantly higher (p<0.05) than those that were generated using FA-AIF. One exception to this was K^trans estimation, which was not significantly different between the automatic methods for iAIF. The boxplots in Fig. 3 depict the disributions of K^trans and v_e by estimation method side by side. The medians of the means (wide solid bars in boxes) are consistently lower for FA-AIF than for SA-AIF by the paired t-test excepting individual K^trans estimation. The Bland-Altman plots in Fig. 4 show the difference (SA-AIF vs FA-AIF) of mean ROI values of PK parameters against their average values. Solid black lines representing the average difference of the means are consistently numerically greater than zero. Cases where the lower 95% confidence interval lines (dotted black lines) lie above the gray, horizontal (zero effect) line are statistically significant.

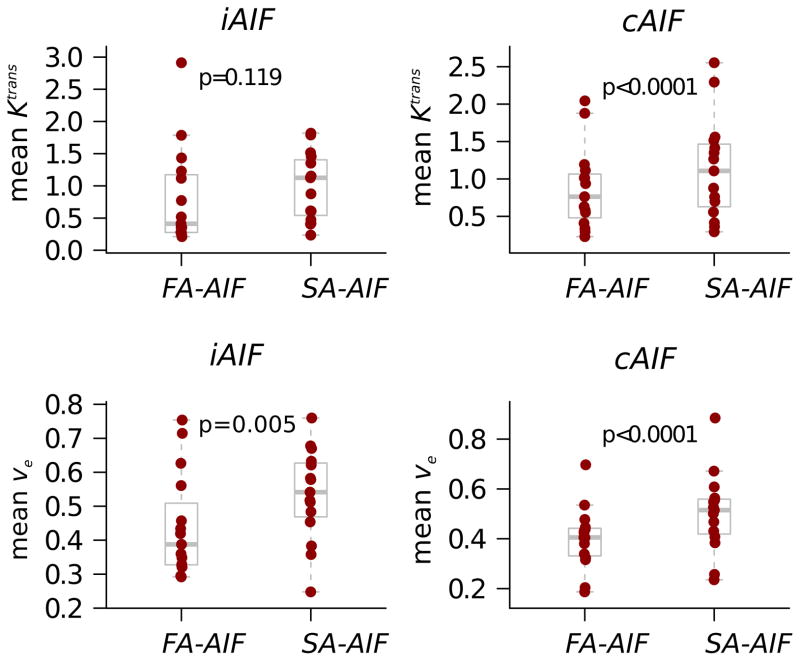
Figure 3.

Box-and-whisker plots compare mean K^trans and v_e estimated using iAIF and using FA-AIF and SA-AIF methods. Dots represent lesion mean values and the gray box outlines depict summary measures. The median line (wide horizontal line) and 25th, and 75th percentile box ends show relatively symmetric data by group. P values reflect the MMANOVA paired t-test comparison of groups. SA-AIF method estimation yields significantly higher estimates of imaging metrics in all comparisons, except for the mean K^trans values estimated with iAIF.

The primary conclusion from the lesion means analysis is that FA-AIF and SA-AIF estimation methods may result in statistically significant differences in estimated mean pharmacokinetic parameters.

Intra-method comparison

Fig. 5 contains scatter plots of cohort versus individual estimates on the natural log scale of pharmacokinetic measures at the voxel level for representative lesions. The correlation (squared root of R²) was high (>0.8) in all of the lesions for both FA-AIF and SA-AIF estimates. In many plots, slopes are approximately 1 but the y-intercepts are generally less than 0, with individual values predicting lower cohort values. To best determine the relationship between cohort and individual pharmacokinetic parameters, we estimated the overall intercept and slope by method predicting cohort measures from individual measures. In Table 1, we report the overall intercept and slope for the data. While v_e was analyzed on its original scale, K^trans required a log transformation to meet normality assumptions of the model. In this table, the confidence intervals are the most important summary measures of effects. Despite the significant variability in individual graphs shown above, all of the confidence intervals for the intercepts contain zero. Similarly, there is insufficient evidence to conclude that the slopes are different from 1. An exception is the comparison of the FA-AIF based estimates of K^trans (see Table 1), where the differences are significant. The SA-AIF method has better agreement between individual and cohort measures for K^trans. No significant difference was observed between the individualized and cohort-based v_e estimates for either of the two methods.

Figure 5.

Illustrative scatter plots of the cohort vs individual estimates on the natural logarithm scale of pharmacokinetic measures at the voxel level for individual lesions. The coefficient of determination (R²-measures of the strength of the linear relationship) and slope estimates for the red linear regression lines are listed in each plot. Also placed are the perfect agreement lines (dashed black lines) representing a y-intercept of zero and slope of 1. In these plots, S is the subject identifier and L is the lesion number. Left to right shown are cases of (a) excellent agreement (FA-AIF, v_e, subject 17, lesion 1); (b) relatively poor agreement (FA-AIF, v_e, subject 29) and (c) typical agreement (SA-AIF, K^trans, subject 17).

Table 1.

Results of mixed models regression (random coefficient model) predicting cohort measures from individual pharmacokinetic measures for K^trans and v_e by estimation method (intra-method analysis). A 95% CI that excludes 1 is sufficient evidence to conclude that the slope is greater than 1 with a type I error rate of 5% (highlighted in bold).

Model	Method	Parameter	Estimate	95% CI
$\mathit{log}(K_{\mathit{cAIF}}^{\mathit{trans}})=\mathit{log}(K_{\mathit{iAIF}}^{\mathit{trans}})$	FA-AIF	Intercept	0.206	[−0.453, 0.862]
		Slope	1.116	[1.031, 1.200]
	SA-AIF	Intercept	0.089	[−0.129, 0.306]
		Slope	1.031	[0.969, 1.094]
ve,cAIF=ve,iAIF	FA-AIF	Intercept	0	[−0.043, 0.024]
		Slope	0.935	[0.738, 1.132]
	SA-AIF	Intercept	−0.011	[−0.042, 0.020]
		Slope	0.955	[0.830, 1.080]

Discussion

Our study was motivated by the practical need of studying the effect of AIF determination method on PK modeling. We therefore compared two methodologies for automated AIF estimation, and applied them to prostate DCE MRI data that was collected using standard clinical 3T MR imaging protocols. Our results indicate that automated image-based methods for AIF determination can lead to significantly different AIF curves, which subsequently can have strong effect on the visual appearance of the lesion in the quantitative maps. We have attempted to statistically assess the effects of the AIF choice. Our quantitative analysis led us to conclude that for the studied MRI dataset of biopsy-confirmed PCa patients, the choice of the method used for individualized AIF determination is important. Both for cohort and individualized AIFs determined using FA-AIF and SA-AIF methods, the mean values of the PK parameters are significantly different at the lesion level. One exception to this is that no statistically significant differences between the two methods were observed for K^trans when iAIF was used. Our intra-method comparison of the iAIF- and cAIF-based parameter values showed that overall estimates of the relationship for cohort and individual parameters are consistent with an intercept of 0 and slope of 1. Again, a notable exception is the K^trans parameter estimated with the FA-AIF method, where significant differences were observed.

The differences in the estimated parameters can be explained by the differences in the shape and peak values of the AIF curves produced by the two methods. FA-AIF method selects 5 pixels, the final AIF shape being obtained by averaging the 5 curves observed at each of the voxels. The AIF curve produced by the SA-AIF method is generated using a larger number of pixels. As a result, the concentration values of the AIF estimated by FA-AIF method can be higher (as can be seen in Fig. 1 and Fig. 2), leading to lower K^trans and v_e estimates. Based on the formulation of the PK model, K^trans is sensitive to the scale of the AIF, while AIF curve shape can influence v_e estimation. The observation that no significant differences in K^trans were observed for inter-method comparison may indicate that in our population the differences in AIF scales between the individual methods are not large. However, all other choices of parameters and iAIF/cAIF combinations led to significant differences in our inter-method comparison. This result underscores the conclusion that the values of the PK parameters obtained using different AIF methods may not be directly comparable, and the AIF approaches cannot be exchanged freely. At the same time, the choice between the cohort-specific and individualized AIF for a given method does not lead to significant differences in most cases.

The spatial analysis of the arterial voxels identified by FA-AIF and SA-AIF methods shows that in over half of the cases the voxels selected by the two algorithms do not overlap. This result is not completely unexpected. FA-AIF method employs a hard-coded selection of just 5 voxels that have the best fit consistent with the expected appearance of the AIF signal [24]. The SA-AIF method is based on a different heuristic and is initialized manually by placing the seed on the center slice in the dataset [23]. Starting from the seed point, the algorithm follows contiguous path, and cannot “jump” across slices: if no voxels are identified in a given slice, the algorithm stops. Finally, being initialized manually, the SA-AIF algorithm can follow either the left or right artery path, based on the observer choice of the seed, while FA-AIF method appears to prefer the artery on the left side of the patient in most cases.

Comparison of the different PK modeling methodologies should ideally consider the discriminating power of the estimated PK parameters in differentiating between cancer and normal tissue, or the relevance to the true characteristics of tumor angiogenesis. In practice, due to the diffuse nature of prostate cancer and partial volume effects, reliable localization of the normal areas was often not feasible in our data. This is consistent with the experience reported in a recent study by Barrett et al., where normal tissue could be identified only in 10 out of 36 analyzed cases [11]. Although validation approaches are proposed based on phantoms [33] or using alternative imaging modalities [34], determination of the ground truth values for the estimated parameters (K^trans and v_e) in clinical patients is typically not possible. Similarly, the estimation of the “gold standard” AIF is not feasible, since our study utilized not research, but standard of care prostate MRI sequences used at Brigham and Women’s Hospital. High temporal sampling of 1 s, as suggested by Henderson et al. may be required for AIF sampling based on simulations [35], but is not yet feasible in the clinical setting at 3T without significantly sacrificing spatial resolution and signal. Our study investigates the impact of AIF choice under the typical imaging conditions currently employed in the clinic, which may be different from the research protocols employed elsewhere.

We recognize that the comparison approach we used may not be sufficient for making recommendations regarding the preferred AIF methodology. Our goal was rather to emphasize and quantify the issues related to the difficulties in reproducible, quantitative characterization of the prostatic tissue from DCE MRI based on PK modeling. In the future, we plan to attempt a similar comparison for a population of PCa patients followed over the course of treatment. Correlation of the estimated dynamics in the PK parameters with the clinical outcomes and comparison of the parameters obtained for repeated imaging exams may provide useful insight into the validity of the processing technique.

Our study has several limitations. We focused on only two automated approaches to estimating individualized AIF. Moreover, the results are specific to the imaging protocol employed, as difference in DCE MRI temporal resolution will affect the accuracy of AIF estimation. Currently, there is no consensus on whether individualized AIF estimated either manually or automatically offers any benefits for PK modeling. Sparse and sometimes contradictory evidence exists in the literature regarding the utility of the individualized AIF estimation [18,20,36,37]. We intentionally did not include generic population AIF or manual individualized AIF in this comparison to limit the scope of the study. Our PK modeling approach uses Generalized Kinetic model [25]. While this model is dependent on the temporal resolution of the data, its use is appropriate and recommended for temporal resolution better than 20 seconds [38]. The rationale for using the 2-parameter model instead of the more complete 3-parameter extended Tofts model can be justified by the very small vascular fraction (~1%) of prostate tissue [39]. Sensitivity of the alternative models to the choice of AIF may be different. Though we were able to account for correlation among voxels within a lesion, and for lesions within subjects, we have not explored the correlation between the neighboring image voxels in our data. Finally, we used histopathology information obtained as part of the routine clinical processing to localize the tumor ROI in the images. Although significantly more sophisticated alternatives exist [40], such approaches are complex logistically and are rarely implemented as part of the routine clinical workflows. In our study we focused on a cohort of patients whose management was based on the standard of care adopted by our institution.

In summary, our conclusion is that detailed validation of the individualized AIF estimation methodology is warranted when the purpose of the PK maps is quantitative assessment of the PCa and characterization of perfusion parameters. Without such validation, direct comparison of the quantitative parameters estimated by PK models may be compromised by differences in the processing techniques. The validation of PK methodology applied to clinical data requires solving numerous technical challenges, including high quality data acquisition, correlation with the histopathology and/or clinical outcomes, and localization of the cancer and normal tissue in the MR images. Availability of the annotated repositories of relevant clinical imaging data, accompanied by the clinical information, enables focused analyses of individual processing steps, such as the automatic AIF determination method. As a step towards quantitative image methodology evaluation and reproducible research, we are making the de-identified MRI data used in this study publicly available to facilitate further research efforts in robust DCE-MRI analysis².