Abstract
19F magnetic resonance spectroscopy (MRS) studies of 2-fluoro-2-deoxy-D-glucose (FDG) and 2-fluoro-2-deoxy-D-glucose-6-phosphate (FDG-6P) can be used for directly assessing total glucose metabolism in vivo. To date, 19F MRS measurements of FDG phosphorylation in the brain have either been achieved ex vivo from extracted tissue or in vivo by unusually long acquisition times. Electrophysiological and functional magnetic resonance imaging (fMRI) measurements indicate that FDG doses up to 500mg/kg can be tolerated with minimal side effects on cerebral physiology and evoked fMRI-BOLD responses to forepaw stimulation. In halothane-anesthetized rats, we report localized in vivo detection and separation of FDG and FDG-6P MRS signals with 19F 2D chemical shift imaging (CSI) at 11.7T. A metabolic model based on reversible transport between plasma and brain tissue, which included a non-saturable plasma to tissue component, was used to calculate spatial distribution of FDG and FDG-6P concentrations in rat brain. In addition, spatial distribution of rate constants and metabolic fluxes of FDG to FDG-6P conversion were estimated. Mapping the rate of FDG to FDG-6P conversion by 19F CSI provides an MR methodology that could impact other in vivo applications such as characterization of tumor pathophysiology.
Keywords: FDG, FDG-6P, brain metabolism, 19F MRS
Introduction
Glucose represents brain’s main energy source and therefore measurement of glucose metabolism in vivo provides a direct measurement of brain activity. Previous 19F magnetic resonance spectroscopy (MRS) studies of 2-fluoro-2-deoxy-D-glucose (FDG) and 2-fluoro-2-deoxy-D-glucose-6-phosphate (FDG-6P) have shown promise for assessing total glucose metabolism in the brain [1–4], as a complementary method to oxidative glucose metabolism measured by 1H-[13C] MRS [5, 6]. However, most of 19F MRS measurements of FDG phosphorylation have either been achieved ex vivo from extracted tissue [7, 8] or in vivo by unusually long acquisition times (e.g., 5 hours) [2]. 19F MRS spectra of FDG were acquired also with short acquisition times (5 minutes) but these spectra represent non-localized FDG signal from the entire brain [1]. Furthermore, some of these studies fell short of routine applications because of the high dose of FDG used and/or long acquisition times [2–4, 9].
Although positron emission tomography (PET) can also measure FDG phosphorylation in vivo using the [18F]-FDG tracer, this method cannot distinguish between the FDG and FDG-6P moieties and therefore requires a waiting period of 30–45 minutes before the PET scan to allow clearance of the FDG precursor. A typical voxel size for whole-body acquisition mode of a PET scan is 4×4×4mm3, acquired in 20 to 30 minutes. In the present work, we demonstrate that similar spatiotemporal resolution can be achieved by chemical shift imaging (CSI) with [19F]-FDG and therefore, 19F CSI could be viewed as a complementary method to PET, each with their distinct advantages and/or disadvantages.
In the past two decades 19F MRS has demonstrated great potential across a variety of disciplines and applications [10, 11]. In vivo 19F MRS with FDG studies in real-time (i.e., within the first half hour of start of FDG infusion) are lacking primarily because of low concentrations of FDG and FDG-6P in the brain. The low FDG concentration in the brain is due to competition of FDG and glucose in the blood for glucose transporter (GLUT). In addition, after entering the brain, FDG competes with glucose for hexokinase. Therefore, increasing the FDG dose to higher values would result in an undesired decrease of glucose concentration and metabolism in the brain with potentially adverse effects on systemic physiology. In this study electroencephalography (EEG) and functional magnetic resonance imaging (fMRI) measurements were used as correlates of brain function/activity, which when minimally affected by FDG presence will enable a measurable protocol to optimize the FDG dose needed to achieve maximum SNR for the 19F CSI experiments without compromising animal’s systemic physiology. In the present work we report mapping of 19F FDG and FDG-6P signals in rat brain. Then the detection of FDG and FDG-6P by 19F 2D CSI within minutes of FDG infusion was used for mapping the rate of FDG phosphorylation.
Materials and Methods
In vitro 19F MRS
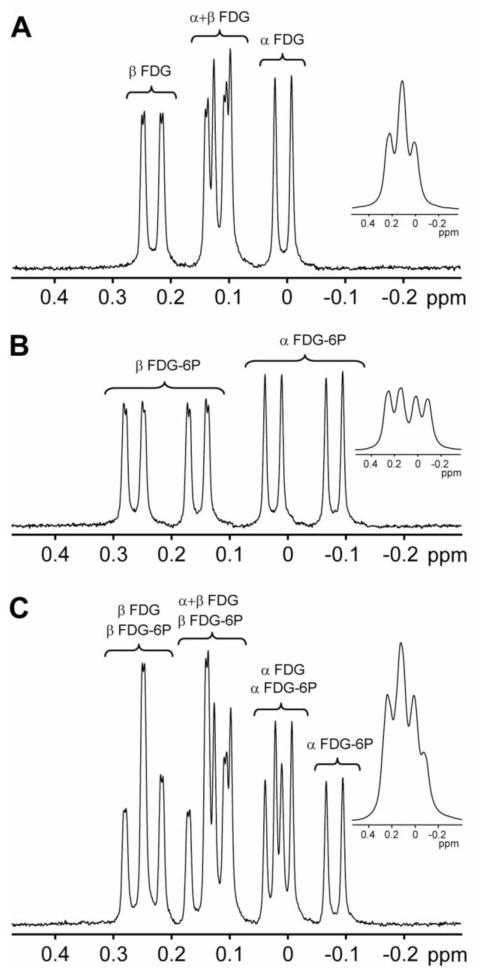
The salt forms of FDG and FDG-6P were purchased from Sigma-Aldrich (Sigma-Aldrich Co, St. Louis, MO). 19F spectra without 1H decoupling of samples containing 5mM FDG (Fig. 1A), 5mM FDG-6P (Fig. 1B) and both 5mM FDG and 5mM FDG-6P (Fig. 1C) in 20% D2O and at pH 7.4 were acquired at 35 °C on an 11.7T Bruker vertical-bore spectrometer (Bruker, Billerica, MA) using a simple pulse-acquire sequence with a spectral window of 938 Hz. Both FDG and FDG-6P exist in solution as a mixture of two conformations, α and β. The 19F splitting pattern of α and β resonances (Fig. 1A, 1B and 1C) is due to the presence of several adjacent non-equivalent 1H nuclei. We did not apply 1H decoupling because of several reasons: (i) small separation between the 1H and 19F frequencies [1]; (ii) tissue heating induced by large RF decoupling power required at high field; (iii) possible noise injection. Longitudinal (T1) and transverse (T2) relaxation times were measured using conventional inversion recovery and spin echo methods, respectively (Tab. 1) with the corresponding intensities fitted to a single exponential function. We are not aware of any T1 and/or T2 measurements of 19F FDG or FDG-6P in vivo. This could be due to the fact that the FDG or FDG-6P signals in vivo are also affected by the concurrent cellular metabolism.
Figure 1. 19F NMR of FDG and FDG-6P.
The 19F spectra of 5mM FDG (A), 5mM FDG-6P (B) and a sample containing 5mM of both FDG and FDG-6P (C) acquired at 11.7T and 35 °C. The insets represent the same spectra obtained using 25Hz exponential apodization of the original FID. Apodization of the in vitro FID by 25Hz results in a similar 19F spectrum as for in vivo situation (where the intrinsic line-broadening was estimated to be 25Hz). The result of the apodization is the collapse of the 19F resonances into 3 signals for FDG (A, inset) and 4 signals for FDG-6P (B, inset) and FDG/FDG-6P (C, inset) samples. Because there is no other 19F signal in the spectra except those of FDG and FDG-6P, the 0ppm reference was assigned to transmitter frequency.
Separation of FDG and FDG-6P 19F signals
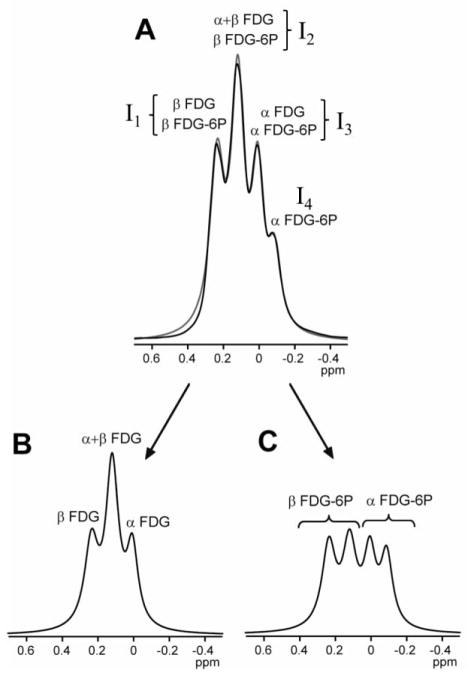
Up on phosphorylation of FDG in vivo, the broadened FDG and FDG-6P 19F signals overlap to generate four 19F resonances (Fig. 2A). The intensities of these resonances, I1 to I4, are given by:
| (1) |
| (2) |
| (3) |
| (4) |
where is the resonance intensity for molecule m (m = FDG or FDG-6P) and conformation i (i = α or β). Because recycle time TR used is short (0.2s), the longitudinal magnetization is not completely recovered by T1 relaxation and the measured intensity is related to the fully relaxed intensity :
| (5) |
where the relaxation factor represents the fraction of intensity recovered after TR=0.2s and depends on the flip angle θ and the longitudinal relaxation time (Tab. 1):
| (6) |
Figure 2. In vitro separation of FDG and FDG-6P signals.
Any 19F spectrum at 25Hz apodization containing FDG and FDG-6P resonances (A) can be separated into FDG (B) and FDG-6P (C) signals by fitting the FDG/FDG-6P spectrum to a sum of FDG and FDG-6P signals. The gray curve in (A) represents the result of the fit of the four overlapping resonances (labeled I1 to I4) with a sum of four Lorentzian functions. The result of the fit provides the intensities I1 to I4, which can be used to estimate the FDG and FDG-6P signals, according to Eqs. (8–12), with relative uncertainties of about 15% estimated from the in vitro measurements with known concentrations. The 0ppm reference was assigned to transmitter frequency.
The value of θ used in our 2D CSI experiments was 28°. The optimum (Euler) flip angle for each resonance can be estimated from Eq. (5) to obtain maximum signal per unit time (Tab. 1):
| (7) |
Our in vitro MRS measurements indicate that for both FDG and FDG-6P, 43% of the molecules are in the α conformation and 57% in the β conformation. These conformation measurements are in good agreement with those obtained from rat brain extracts, 48% and 47% for α FDG and α FDG-6P, respectively [8]. The small difference observed when compared these measurements to our measurements might be due to acquisition of the 19F spectra at different temperatures. Thus, the ratio R0 between the β and α conformations is the same for both molecules:
| (8) |
Therefore, in Eqs. (1–4), the intensities I1 and I2 (α and β anomers) are dependent on the intensities I3 and I4 (α anomer only) as:
| (9) |
| (10) |
Solving Eqs. (3–4) we can separate the FDG and FDG-6P signals for the α conformation:
| (11) |
| (12) |
Similarly, the intensities of the FDG and FDG-6P β conformations can be calculated from those of α conformations using Eq. (8).
Animal preparation
All animal experimental procedures were performed in accordance with protocols approved by the Yale Institutional Animal Care and Use Committee (IACUC) and in agreement with the National Institute of Health Guide for the Care and Use of Laboratory Animals. All animals used in this study were fasted overnight for 12–16 hours to increase the FDG to glucose ratio for higher FDG uptake in the brain. The animal preparation was the same for the MRS, fMRI and electrophysiological experiments. The experiments were conducted on artificially ventilated (70% N2O/30% O2) adult Lewis rats (Charles River, Wilmington, MA). The rats were initially anesthetized with halothane (2–3%) during the surgical preparation. After all the surgical procedures, halothane anesthesia was maintained at 1–2 % during the experiments. A femoral artery was cannulated (PE-50) for monitoring physiological parameters (pCO2, pO2, pH, blood pressure) and for extracting arterial blood samples during FDG infusion to obtain the arterial input function. A femoral vein was cannulated (PE-10) to administer D-tubocurarine chloride (initial 0.5 mg/kg; supplemental 0.25 mg/kg/h) or FDG (60 to 800 mg/kg). The FDG infusion rate and total volume infused were calculated for each animal based on its weight to obtain the targeted dose (60 to 800 mg/kg). Ventilation parameters were adjusted to maintain normal physiology. Adequate analgesia was ensured by monitoring the pain response in blood pressure to an automated electrical tail-pinch (5 mA, 0.3 ms, 10 Hz, 1 s) every hour, except during data acquisition. The animal’s core temperature, blood pressure, and breathing rate were monitored. The systemic temperature, measured with a rectal probe, was maintained at 37±0.5°C with homeothermic blankets. Four rats (230–240 g) were used for MRS experiments, five rats (200 – 240 g) for fMRI experiments and eight rats (250–300 g) for EEG measurements. Each group of rats received a one-time exposure of FDG. The MRS, fMRI and electrophysiological measurements were done in separate group of animals.
Forepaw stimulation
Two subcutaneously placed copper needles were inserted into the contralateral forepaw (between the second and fourth digits) and all snout whiskers were shaved to avoid contaminating somatosensory signals. Stimulus presentation was controlled by a μ-1401 analog-to-digital converter unit (CED, Cambridge, UK) running custom-written script to provide 0.3 ms duration pulses with 2 mA amplitude and 3 Hz frequency with 30s “off” followed by 30s “on” block design by an isolation unit (WPI, Sarasota, FL). The same forepaw stimulation protocol was used for both electrophysiological and fMRI measurements.
Electrophysiological recordings (n=8)
EEG measurements were obtained at various FDG doses (60, 80, 200, 500 and 800 mg/kg) using various infusion times (2 to 8 minutes). For the EEG measurements, the animals were placed in a stereotaxic holder on a vibration-free table inside a Faraday cage. The EEG signals were recorded using a pair of steel electrodes placed laterally between the scalp and the outside surface of the skull in the right frontal and occipital areas [12]. The wires were secured using tissue glue. The EEG signals were amplified and filtered (1–100 Hz) using a Grass Data Recording System Model 79D (Grass Instruments Co., Quincy, MA). EEG signals were digitized and recorded (sampling rate 1000 Hz) using a CED Micro 1401 and Spike 2 software (Cambridge Electronic Design, Cambridge, UK). EEG and physiology during FDG infusion were compared with the animal physiology before the FDG infusion using two-tailed Student’s t-test analysis (Tab. 2). The EEG data were processed in terms of root mean square to reflect the power.
Functional MRI studies (n=5)
The fMRI data were obtained on an 11.74T Bruker horizontal-bore spectrometer (Bruker, Billerica, MA) using a 1H surface coil (1.4 cm). The fMRI data were collected with sequential sampling echo planar imaging sequence: field of view of 2.56 × 2.56 cm2; image matrix of 64×64; slice thickness of 2 mm; repetition delay of 1000 ms, and echo time of 13 ms; and voxel size of 400×400×2000 μm3. Sixteen dummy scans were carried out before fMRI data acquisition [13]. Neuroanatomy was imaged using a gradient echo pulse sequence. The data were subjected to a translational movement criterion using a center-of-mass analysis [14]. After masking of non-brain tissues by thresholding each image within a series, the masked raw images were converted into binary maps (i.e., brain vs. background). Removal of image intensity information (i.e., binary maps) assured that the analysis was not biased by stimulation-induced effects. For each binary map in the series two center-of-mass values were calculated, one for each in-plane direction. If either center-of-mass value in a series deviated by more than ¼ of a pixel, the entire dataset was discarded from further analysis. Data which did not pass the movement analysis test were not analyzed further. Single run data were used to create activation maps (30s rest vs. 30s stimulation). We calculated the relative responses for every individual trial (i.e. the percentage change or ΔS/S maps of response compared to the pre-stimulus state) and calculated t-maps to identify the localization of functional responses. We calculated the probability (p-value) from the t-statistic of Student’s t-test where the activated voxels were defined on the basis of p ≤ 0.001. Then the activation map was overlaid on the corresponding anatomical image and we generated time courses of BOLD responses.
In vivo 19F CSI (n=4)
All 19F CSI experiments were acquired with the same FDG dose (500mg/kg). The 400mM FDG solution was continuously infused for 8 minutes using a constant infusion rate. The FDG infusion rate and total volume infused were calculated for each animal based on its weight to obtain a total dose of 500mg/kg. No forepaw stimulation was applied during the 19F CSI acquisition. The arterial input function was measured by extracting arterial blood samples at different time points during FDG infusion. The 19F 2D CSI data were obtained on a modified 11.7 T Bruker horizontal-bore spectrometer (Bruker, Billerica, MA) using a 1H/19F resonator/surface probe using the following parameters: spectral window = 20161Hz, 8 × 8 encoding steps, TR = 0.2 s, number of averages = 128, field of view = 3.2 cm × 3.2 cm, total acquisition time = 27 min. A 500 μs gaussian pulse was used for selective excitation of a 6mm slice. The duration of the phase encoding gradients was 100μs. The 19F spectrum in each voxel was line broadened (10 Hz), baseline (first order) and phase (zero order) corrected. The nominal voxel volume was 96 μL while the effective voxel volume, calculated from the point-spread function [15], was 112μL, which was only 14% larger than the nominal voxel volume.
Modeling of FDG phosphorylation
FDG transport and phosphorylation were described by a model consisting of three metabolite pools, FDG in blood plasma (FDGp), FDG in brain tissue (FDGt) and FDG-6P, present only in brain tissue. The coupled differential equations that describe the FDG kinetics between the three pools are:
| (13) |
| (14) |
| (15) |
where Vpt(t) and Vtp(t) are the saturable plasma to tissue and saturable tissue to plasma fluxes, VD(t) is the non-saturable plasma to tissue flux, Vout(t) represents the blood clearance flux and Vm(t) the rate of FDG-6P synthesis, respectively. These fluxes are defined as [16]:
| (16) |
| (17) |
| (18) |
| (19) |
| (20) |
Here, [FDGp] is expressed in mM while FDGt and FDG-6P are expressed in μmol/g. To calculate the FDGt and FDG-6P concentrations in mM, we divided the corresponding values in μmol/g with the brain water space volume, Vb = 0.77 mL/g [16]. FDG is transported across the blood-brain barrier by GLUT’s, for which the transport is governed by Michaelis-Menten kinetics with Vmax = 1.7 μmol min−1 g−1 and [16]. For GLUT proteins, involved in the transport of both glucose and FDG, a competitive inhibition mechanism was demonstrated in rat brain [16]. Therefore, the apparent Michaelis-Menten constant Kapp is given by Eq. (20), where [16]. The glucose concentration in the plasma was measured for each animal before the FDG infusion and the average value was [Glc] = 4.7 ± 0.6 mM. Using Eq. (20) we calculated an apparent Michaelis-Menten constant Kapp = 9.8 mM. KD = 0.022 mL min−1 g−1 is the non-saturable transport coefficient [16] and km is the rate constant for the FDG-6P synthesis.
The time dependence of the FDGt and FDG-6P concentrations was obtained by numerical integration of Eqs. (13–14). The method involves the division of time in N=104 small intervals and calculation of FDGt and FDG-6P concentrations for each intermediate step. During each small time interval Δt (Δt=0.01 min), the concentration was assumed to change linearly with time. For any step n, using Eqs. (13–20), [FDGt](tn+1) and [FDG-6P](tn+1) can be calculated from the [FDGp](tn), [FDGt](tn) and [FDG-6P](tn) values as follows:
| (21) |
| (22) |
The average concentration for FDGp, FDGt or FDG-6P during the experiment was determined by integration of the time-dependent FDG or FDG-6P concentrations:
| (23) |
where texp=27 min is the CSI experiment duration and X represents FDGp, FDGt or FDG-6P.
Results
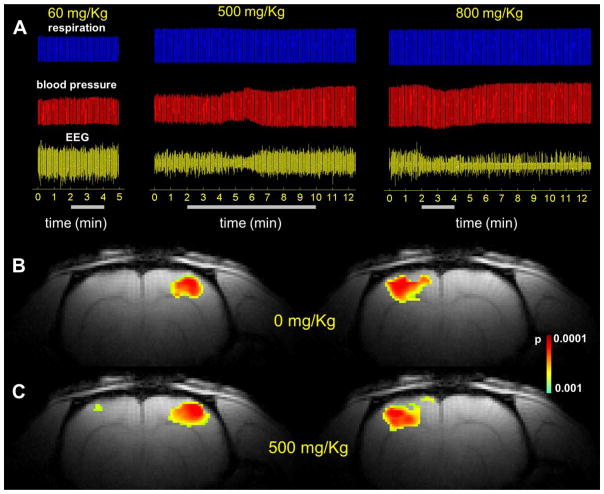
The relaxation measurements of both conformations for FDG and FDG-6P were measured in vitro (Tab. 1) to determine the optimal pulse sequence parameters for high SNR 19F spectral data acquisition. EEG and fMRI measurements during infusion of various FDG doses were compared with those before infusion (Fig. 3 and Tab. 2). The goal was to achieve the highest FDG concentration in the brain (required for the 19F CSI experiments) without compromising brain activity as measured by EEG (for basal activity) and by fMRI (for functional activity). Thus, we started with the lowest dose of 60mg/kg and then increased the FDG dose (e.g., 80, 200, 500, 800 mg/kg) until the EEG measurements suggested adverse effects on brain function as indicated by reduction in the EEG power following the FDG infusion. Electrophysiological measurements indicate that at high FDG doses (800mg/kg) the amplitude of the EEG signal is significantly reduced (p<0.001) and it does not recover to the same levels as before the FDG infusion (Fig. 3A). A significant effect on blood pressure (p=0.002) was also observed at 800mg/kg (Tab. 2). Moreover, fMRI responses during forepaw stimulation were suppressed (data not shown) indicating that doses of 800mg/kg have negative effects on animal physiology and its responses to stimulations (Tab. 2). At 500mg/kg, the EEG recovers after several minutes to the same levels as before the infusion (p=0.22; Fig. 3A), while the evoked responses to forepaw stimulation are similar to those obtained before FDG infusion (Fig. 3B, C), indicating that doses of 500mg/kg do not significantly affect the physiology of the animal. Moreover, the LD50 for FDG is 600 mg/kg/day delivered i.p. for five consecutive days [17]. Based on the LD50 and our results we decided to use a dose of 500mg/kg for the 19F CSI experiments, infused continuously for 8 minutes. During the course of all experiments obtained at this dose, the systemic physiological parameters (blood pressure, core body temperature, pH, pO2, pCO2) were within the physiological range. The FDG dose of 500mg/kg necessary for 19F CSI is similar to doses employed in more commonly [1,6-13C2]-glucose infusion protocols for 1H[13C]MRS (e.g., 1350 mg/kg over 110min of infusion, with an initial bolus of 170 mg/kg infused in first 15 seconds), which are used to measure oxidative glucose metabolism in rat and human brain [5, 18–20].
Figure 3. Effect of various FDG doses on animal physiology.
Measurements of respiration (A, top), blood pressure (A, middle) and EEG (A, bottom) show minimum effects of FDG for doses up to 500 mg/Kg, while doses higher than 500 mg/Kg result in adverse effects on physiology, monitored by EEG signal. Left and right forepaw stimulations (2 mA, 0.3ms, 3Hz) before (B) and after infusion of 500 mg/Kg FDG (C). The results show that the activated areas before and after FDG infusion are very similar, which indicates that the brain activity is not affected by the infusion of 500 mg/Kg FDG. The FDG total dose is indicated in each case at the top of the respiration signal, while the bars below the EEG signal represent the duration of the FDG infusion.
Table 2.
EEG and physiology during FDG infusion compared with animal physiology before FDG infusion. Data represent average of 4 recordings using two tailed Student’s t-test analysis. EEG data were processed in terms of root mean square to reflect the power. fMRI activation for each dose is indicated.
| FDG dose (mg/kg) | parameter measured | no FDG infusion | with FDG infusion | p value | fMRI activation |
|---|---|---|---|---|---|
| 60 | blood pressure | 90±14 | 92±14 | 0.42 | observed, data not shown |
| respiration rate | 2.6±0.1 | 2.6±0.1 | 0.92 | observed, data not shown | |
| EEG | 0.28±0.04 | 0.26±0.04 | 0.09 | observed, data not shown | |
| 500 | blood pressure | 97±15 | 98±19 | 0.57 | observed, see Fig. 3 |
| respiration rate | 2.6±0.1 | 2.6±0.1 | 0.99 | observed, see Fig. 3 | |
| EEG | 0.17±0.04 | 0.19±0.04 | 0.22 | observed, see Fig. 3 | |
| 800 | blood pressure | 98±21 | 90±20 | 0.002 | not observed, data not shown |
| respiration rate | 2.6±0.1 | 2.6±0.1 | 0.19 | not observed, data not shown | |
| EEG | 0.20±0.04 | 0.14±0.04 | <0.001 | not observed, data not shown |
Measurement of T1 and T2 relaxation times (Tab. 1) indicate that a full relaxation of all 19F FDG and FDG-6P resonances requires a TR of more than 5s. Under these conditions, obtaining a reasonable SNR value for the 19F CSI experiments requires more than one hour acquisition. Thus, the TR was optimized to a value of 0.2s that results in a maximum SNR for a 2D CSI experiment duration of 27 minutes.
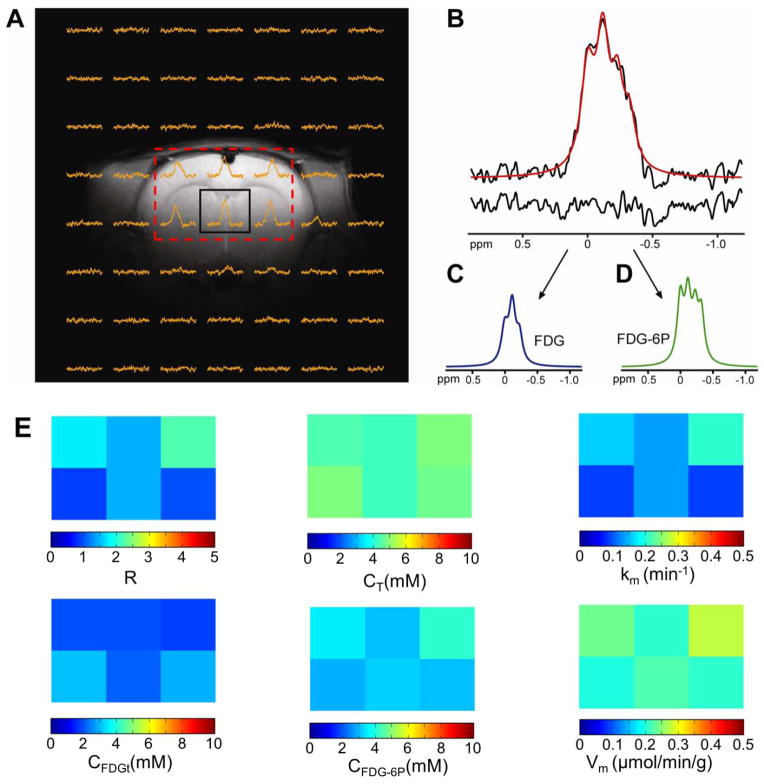
19F 2D CSI was used to obtain localized in vivo 19F spectra of FDG and FDG-6P (Fig. 4A). However, determination of metabolic rate of FDG utilization in the brain tissue relies on the successful separation of the FDG and FDG-6P 19F signals. For a homogenous and well shimmed in vitro sample, the 19F resonances are well separated (Fig. 1C). However, a significant increase in the linewidths of the 19F resonances for in vivo experiments at 11.7T by an additional 20 to 30 Hz was observed, due to the inherent inhomogeneities of the brain tissue (Fig 4A and B). Our results indicate that an additional line broadening of 25 Hz results in the partial or sometimes total overlap of FDG and FDG-6P signals, giving rise to four partial overlapping resonances (Fig. 1C, inset). However, separation and measurement of FDG and FDG-6P in vivo 19F CSI signals is possible (Fig. 4C and D) and the ratio R between the FDG-6P and FDG signals can be calculated in each voxel (Fig. 4E, top left). Since R represents also the ratio between the FDG-6P and FDG concentrations in a voxel, it can be used to calculate the rate of FDG to FDG-6P conversion, providing that we know the total 19F signal, CT, represented by the sum of FDG and FDG-6P concentrations per tissue volume. CT was estimated for each CSI voxel (Fig. 4E, top middle) by comparing the total 19F signal with that of a CSI voxel from an in vitro sample containing only FDG (10mM), acquired under the same experimental conditions as for the in vivo 19F CSI. Moreover, metabolic modeling that includes a reversible transport between plasma and tissue and a non-saturable plasma to tissue component [16] can be used to estimate the FDG and FDG-6P concentrations in the brain tissue, provided that the rate constant, km, for the FDG to FDG-6P conversion is known. The method involves measurement of FDG concentration in the blood plasma, FDGp (measured separately by 19F MRS of blood extracts) at various time-points (Fig 5A, open symbols), and provides a numerical relationship between R and the rate constant km, which is required to express the ratio R into a rate of FDG to FDG-6P conversion. In addition, the FDG and FDG-6P concentrations calculated using the metabolic modeling method can be used as validation for concentration measurements obtained from the comparison with the 19 F CSI of the in vitro sample under identical conditions as the in vivo experiment.
Figure 4. Separation of FDG and FDG-6P signals in rat brain during FDG infusion.
Acquisition of a 2D CSI dataset allows measurement of 19F signals from 6 voxels (A). The 19F spectrum of the central voxel, indicated by the black box in Fig. 4A contains the sum of both FDG and FDG-6P signals (B, top). This signal can be separated into FDG (C) and FDG-6P (D) signals. The red line in (B) represents the sum of the FDG and FDG-6P signals. The goodness of the fit can be visualized by calculating the difference (B, bottom) between the measured spectrum (black) and the fitted spectrum (red). The spatial distribution of the ratio R (E, top left) and the total FDG + FDG-6P concentration CT (E, top middle) were used to calculate the distributions of metabolic rate constant km (E, top right), FDGt (E, bottom left), FDG-6P (E, bottom middle) and metabolic flux of FDG to FDG-6P conversion, Vm (E, bottom right). The 0ppm reference in (B–D) was assigned to transmitter frequency.
Figure 5. Determination of metabolic rate of FDG consumption in rat brain.
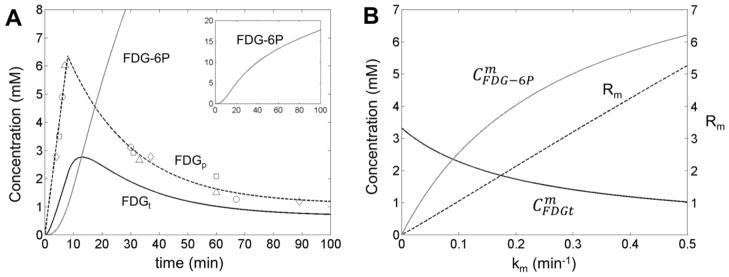
The time dependence of FDG in plasma (FDGp, open symbols), combined with the ratio R between FDG-6P and FDG 19F signals measured in each CSI voxel, can be used to calculate the FDG and FDG-6P concentrations in the brain tissue (A). The metabolic model is based on a reversible transport between plasma and tissue plus a non-saturable plasma to tissue contribution. The model includes also the conversion of FDG to FDG-6P, described by the metabolic rate km. The time dependence of the FDGp was assumed linear for the entire duration of the FDG infusion (8 minutes) followed by an exponential decay of the FDG in the plasma after FDG infusion was stopped. The average FDGt and FDG-6P concentrations, and were calculated by integration of time-dependent FDGt and FDG-6P concentrations according to Eq. (23), for various km values between 0 to 0.5 min−1 (B). The ratio Rm was calculated for various km values and shows a strong linear dependence on km (B, dashed line) with a slope SR= 10.596 ± 0.002 min. This linear dependence can be used to calculate the km value in each CSI voxel using the experimentally measured ratio R. As an example for the central (boxed) voxel shown in Fig. 4A, the ratio R is 1.48, which corresponds to a metabolic rate constant km= 0.14 min−1. The time dependencies for FDG and FDG-6P concentrations in the brain tissue for this voxel are shown in (A) with continuous black and gray lines, respectively. The various open symbols in (A) correspond to blood samples extracted from different animals. The scale for R is shown on the right side of Figure 5B.
The FDG-6P synthesis takes place only in the tissue and there is no FDG-6P tissue to plasma flux. During the FDG infusion (first 8 minutes), the FDGp shows a linear increase with time, followed by an exponential decrease after the FDG infusion was stopped (Fig. 5A, dashed line). The average FDGt and FDG-6P concentrations, (Fig. 5B, solid black line) and (Fig. 5B, solid grey line), respectively, were calculated for various km values by integration over the entire duration of the 19F CSI experiment (27 minutes) according to Eq. (23).
The available brain space occupied by the FDG and FDG-6P is Vb = 0.77 mL/g [16, 21]. Using a brain tissue density of 1.04 g/mL [22] we estimated the fraction of space available to FDG and FDG-6P to be ft = 0.80. Therefore, the FDG signal in a voxel is given by , where fp=0.03 represents the fraction of brain space occupied by the blood [23] and was calculated by integration according to Eq. (23). The FDG-6P signal in a voxel is given only by one term, , since there is no FDG-6P component in the blood plasma. Thus, the ratio Rm between the FDG-6P and FDG concentrations in a voxel was calculated as:
| (24) |
Interestingly, although both and dependencies on km are not linear, the ratio Rm shows a strong linear dependence on km (Fig 5B, dashed black line):
| (25) |
with SR = 10.596 ± 0.002 min. Therefore, the spatial distribution of the metabolic rate constant km can be simply calculated from the ratio R measured in each voxel using Eq. (25)(Fig. 4E, top right). Note that the ratio Rm in Eq. (24) is different than the ratio R determined from the 19F CSI measurements. Thus, Rm is calculated using the modeling of FDG and FDG-6P concentrations in the blood and tissue, based on FDG transport kinetics (Fig. 5), while R represents the ratio between the FDG-6P and FDG signals measured in each voxel (Fig. 4E, top left). In addition, the spatial distributions of FDGt and FDG-6P concentrations (Fig. 4E, bottom left and middle, respectively) were also determined from the CT value in each voxel combined with Eq. (24). The distribution of the metabolic flux of FDG to FDG-6P conversion, Vm, was estimated using Eq. (19) (Fig. 4E, bottom right).
As an example, the ratio R in the central (black box) voxel in Fig. 4A is 1.48. According to Eq. (25), this ratio corresponds to a metabolic rate constant km = 0.14 min−1. Using this value, the time dependencies of FDGt and FDG-6P, shown in Fig. 5A in solid black and gray lines, respectively, were calculated. The results show that the FDG concentration in the brain tissue increases during the infusion period and decreases after the infusion was stopped (Fig. 5A, solid black line). The decrease in the FDG concentration is due to conversion of FDG to FDG-6P and perhaps some due to back transport into the blood plasma. The time dependence of the FDG-6P concentration shows a continuous increase due to accumulation of the FDG-6P (Fig. 5A, solid gray line and inset). The average FDGt and FDG-6P concentrations for the same voxel, calculated by integration of time dependent concentration using Eq. (23), are and . Thus, the average metabolic flux in this voxel, calculated for the entire duration of the experiment (27 minutes) is Vm = 0.22 μmol min−1 g−1. This value is in good agreement with measurements of oxidative glucose metabolic flux (CMRglc(ox)) by 1H-[13C] MRS obtained under halothane anesthesia. For example, a value of 0.26 ± 0.02 μmol min−1g −1 was measured in the rat brain under physiological conditions [24], while in general values ranging from 0.10 ± 0.06 μmol min−1g −1in white matter to 0.40 ± 0.08 μmol min−1g −1 in gray matter were reported [ 6]. It should be noted that the range of Vm values measured here (i.e., 0.2–0.3 μmol min−1g −1)is in ageement with prior values of CMRglc(ox)measured by 1H-[13C] MRS for halothane anesthesia which ranged from 0.1–0.4 μmol min−1g −1with variable partial volume arising from white matter. In order to test the accuracy of and determination using the blood-brain transport kinetics, these values were compared with those obtained from the in vivo 19F CSI measurements (Fig. 4E). For this voxel, the total 19F signal corresponds to a concentration of CT = 4.4 ± 0.4 mM (where the error represents the standard deviation over the four animals investigated). Using the measured R value of 1.48, we calculated that CFDGt = 2.1 mM and CFDG-6P = 3.3 mM, values that are in excellent agreement with the FDGt and FDG-6P concentrations calculated above using the blood-brain transport kinetics.
Discussion
19F MRS measurements were obtained using a surface 1H/19F RF coil for which the B1 field is non-homogenous across different brain regions. However, this did not affect the determination of the FDG phosphorylation rates because the modeling (Fig. 5) requires measurement of ratio R (Fig. 4E, top left), indicating the relative FDG-6P and FDG signals in a voxel rather than the absolute FDG and FDG-6P concentrations. The spatial distribution of the ratio R between the FDG-6P and FDG 19F signals, is relatively inhomogeneous with values ranging from 0.92 to 2.21 (Fig. 4E, top left). This relatively large range of values might be caused by imperfect separation of FDG and FDG-6P signals, incomplete separation of blood and tissue signals, and/or gray vs. white matter partial volume in different voxels. As a consequence, the spatial distribution of the metabolic rate constants km shows also a relatively large range of values, from 0.09 to 0.21 min−1(Fig. 4E, top right). In contrast, the spatial distribution of CT, given by the sum of FDG and FDG-6P concentrations per tissue volume, is within the range of 4.2 to 4.9 mM (Fig. 4E, top middle). This indicates a relatively uniform presence of 19F labeled substrate (FDG + FDG-6P) in the brain tissue, although the FDG phosphorylation rate varies across regions. The spatial distribution of FDG in the brain tissue ranges from 1.74 to 3.02 mM (Fig. 4E, bottom left), while for FDG-6P the concentration ranges from 2.92 to 4.18 mM (Fig. 4E, bottom middle). Interestingly, the results indicate that the FDGt concentration is higher in voxels with lower FDG-6P, suggesting a lower metabolic rate in these voxels. Indeed, a strong correlation (r2=0.9162) was observed between km and FDG-6P concentrations, which supports this hypothesis. However, the values of the metabolic flux (defined by the product of km and FDG concentration) span a relatively narrow range, from 0.20 to 0.28 μmol min−1 g−1 (Fig. 4E, bottom right), due to inverse correlation between km and the FDG concentration in these voxels. Moreover, Eq. (19) represents a linear approximation which holds at low FDG concentrations and may need to be amended for concentrations higher than the K of hexokinase. Since the endpoint of FDG and FDG-6P concentrations are not required for our kinetic model, the animal brain was not extracted at the end of the study.
Although it is generally believed that the FDG phosphorylation to FDG-6P is the final step in the FDG metabolic pathway, there are reports of possible metabolites beyond FDG-6P (e.g., in tumors), such as fluorodeoxymannose (FDM) or fluorodeoxymannose-6-phosphate (FDM-6P)[8, 25]. However, during our in vivo 19F CSI experiments, no additional 19F metabolites except for FDG and FDG-6P were observed within the timespan of the data acquisition. The bandwidth of the 500μs Gaussian pulse used for excitation was 5420Hz which corresponds to 10.8ppm at 500MHz, or 5.4ppm on each side of the transmitter frequency, centered on the FDG signal. The α-anomers of FDM and FDM-6P resonate at about 6 ppm away from the FDG signal [8, 25] and therefore we expect that their intensities will be greatly reduced due to decreased excitation efficiency of the Gaussian pulse at this shift. Moreover, the intensities of FDM and FDM-6P signals are in general smaller than that of FDG [8, 25]. Together, these two factors might make the FDM and/or FDM-6P signals undetectable. Another possible explanation for the absence of FDM or FDM-6P signals could be that the synthesis rate of these metabolites is very slow in normal tissue (vs. in tumors, where were detected) and their 19F signal is not observable within first 30 minutes of FDG infusion. Thus our metabolic modeling includes only FDG, present in blood and brain tissue and FDG-6P, present only in the brain tissue.
Our in vitro experiments indicate that 1H decoupling of 19F MRS signals improves SNR less than theoretically expected, by about 30% (data not shown), but to achieve 1H decoupling without additional noise injected we need incorporation of advanced RF circuit design than those available on our current scanner. In addition, 1H decoupling of 19F MRS signals is somewhat challenging because of small separation in frequency between the 1H and 19F nuclei [1] and 1H decoupling at 11.7T requires relatively large RF power which could result in significant tissue heating. Therefore, we chose to acquire the 19F 2D CSI datasets without 1H decoupling.
EEG and fMRI measurements indicate that FDG doses up to 500mg/kg can be tolerated with minimal side effects on cerebral physiology and evoked functional responses to forepaw stimulation (LD50 for FDG is 600mg/kg). Because EEG signals represent the global brain activity and the evoked responses indicate local brain activities, these results suggest that both global and local brain activities are not significantly nor permanently affected at FDG doses up to 500mg/kg.
Measurement of localized FDG and FDG-6P 19F signals could become an important tool for tumor diagnosis. A prolonged retention of FDG and its metabolites for 2 days was observed in mice tumor cells, while in other healthy organs the metabolites were almost cleared after one day [9]. Moreover, the change in the rate of FDM synthesis, but not of the FDG signal was reported to correlate well with the response to 5-fluorouracil chemotherapy, suggesting that the measurement of in vivo FDM production could be used to predict tumor response to treatments [25]. Our results provide an early step towards these future goals for use of 19F MRS in vivo. Moreover further examinations of fixed tissues with 19F MRS and/or histology could provide additional information needed for further quantification and testing of the present metabolic modeling.
The duration of a typical PET scan is 20 to 30 minutes, which is comparable with the acquisition time of 27 minutes used in the present work. The spatial resolution of a PET scan is limited by physical parameters such as detector array geometry, acquisition protocol, patient motion, scatter, counting statistics or positron range [26]. For a whole-body 2D acquisition, the spatial resolution of 128×128 PET images is usually 4×4mm2, with 4–5 mm slice thickness, resulting in a typical voxel volume of 64 to 80 μL [26]. Thus, the voxel size of a PET scan is similar to that of 19F CSI voxels used in the present work (nominal and effective volume of 96 μL and 112μL, respectively). However, new reconstruction techniques for PET imaging could provide a way to generate super-resolution images of 1×1×1mm3 voxels, from a series of low-resolution images of 4×4×4.25mm3 voxels, acquired from different points of view, without increasing the total scan time [26, 27].
In summary, in the present work we report in vivo separation and mapping of FDG and FDG-6P signals with 19F CSI in halothane-anesthetized rat brain. The FDG and FDG-6P concentrations were calculated using a metabolic model based on reversible transport between plasma and brain tissue. In addition, this model provides also the spatial distribution of rate constants and metabolic fluxes of FDG to FDG-6P conversion. Future efforts will be directed towards increasing the FDG/FDG-6P SNR by optimizing the infusion protocol using a time-dependent infusion rate (to achieve a near-uniform FDG blood concentration for the whole duration of the experiment) and by collecting 1H decoupled and/or NOE enhanced 19F spectra, which may in turn allow lowering the FDG dose necessary for translational studies.
Table 1.
Longitudinal (T1) and transverse (T2) relaxation times, the relaxation factor f and the Euler angle θ for α and β conformations of FDG and FDG-6P. The T1 and T2 were measured at 35°C and 11.7T. The relaxation factor f and the Euler angle θ were calculated using Eq. (6) and Eq. (7), respectively.
| Molecule | T1 (s) | T2 (s) | f | θ |
|---|---|---|---|---|
| αFDG | 1.90 ± 0.04 | 0.72 ± 0.02 | 0.229 ± 0.003 | 25.8 ± 0.3 |
| βFDG | 1.49 ± 0.03 | 0.85 ± 0.02 | 0.259 ± 0.002 | 29.0 ± 0.3 |
| αFDG-6P | 1.21 ± 0.02 | 0.45 ± 0.01 | 0.284 ± 0.002 | 32.1 ± 0.3 |
| βFDG-6P | 1.02 ± 0.02 | 0.53 ± 0.01 | 0.305 ± 0.002 | 34.7 ± 0.3 |
Acknowledgments
The authors thank scientists and engineers at MRRC (mrrc.yale.edu) and Core Center for QNMR (qnmr.yale.edu). This work was supported by grants from National Institutes of Health (R01 MH-067528, P30 NS-52519, R01 CA-140102 and R01 EB-011968).
Footnotes
Disclosure/Conflict of Interest: The authors declare no conflict of interest.
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- 1.Berkowitz BA, Ackerman JJ. Proton decoupled fluorine nuclear magnetic resonance spectroscopy in situ. Biophys J. 1987;51:681–5. doi: 10.1016/S0006-3495(87)83393-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Nakada T, Kwee IL. Heterogeneity of regional cerebral glucose metabolism demonstrated in situ in rat brain by 19F NMR rotating frame zeugmatography: one dimensional chemical shift imaging of normal and gliosarcoma implanted brain. Magn Reson Imaging. 1987;5:259–66. doi: 10.1016/0730-725x(87)90002-6. [DOI] [PubMed] [Google Scholar]
- 3.Nakada T, Kwee IL, Card PJ, Matwiyoff NA, Griffey BV, Griffey RH. Fluorine-19 NMR imaging of glucose metabolism. Magn Reson Med. 1988;6:307–13. doi: 10.1002/mrm.1910060309. [DOI] [PubMed] [Google Scholar]
- 4.Nakada T, Kwee IL, Griffey BV, Griffey RH. 19F 2-FDG NMR imaging of the brain in rat. Magn Reson Imaging. 1988;6:633–5. doi: 10.1016/0730-725x(88)90085-9. [DOI] [PubMed] [Google Scholar]
- 5.de Graaf RA, Brown PB, Mason GF, Rothman DL, Behar KL. Detection of [1,6-13C2]-glucose metabolism in rat brain by in vivo 1H-[13C]-NMR spectroscopy. Magn Reson Med. 2003;49:37–46. doi: 10.1002/mrm.10348. [DOI] [PubMed] [Google Scholar]
- 6.Hyder F, Patel AB, Gjedde A, Rothman DL, Behar KL, Shulman RG. Neuronal-glial glucose oxidation and glutamatergic-GABAergic function. J Cereb Blood Flow Metab. 2006;26:865–77. doi: 10.1038/sj.jcbfm.9600263. [DOI] [PubMed] [Google Scholar]
- 7.Shinohara S, Kanazawa Y, Kojima M. Evaluation of energy metabolism in brain using epimerization of 2-deoxy-2-fluoro-D-glucose by 19F NMR: the effect of anesthesia. Magn Reson Med. 1991;21:191–6. doi: 10.1002/mrm.1910210204. [DOI] [PubMed] [Google Scholar]
- 8.Southworth R, Parry CR, Parkes HG, Medina RA, Garlick PB. Tissue-specific differences in 2-fluoro-2-deoxyglucose metabolism beyond FDG-6-P: a 19F NMR spectroscopy study in the rat. NMR Biomed. 2003;16:494–502. doi: 10.1002/nbm.856. [DOI] [PubMed] [Google Scholar]
- 9.Kanazawa Y, Umayahara K, Shimmura T, Yamashita T. 19F NMR of 2-deoxy-2-fluoro-D-glucose for tumor diagnosis in mice. An NDP-bound hexose analog as a new NMR target for imaging. NMR Biomed. 1997;10:35–41. doi: 10.1002/(sici)1099-1492(199701)10:1<35::aid-nbm447>3.0.co;2-f. [DOI] [PubMed] [Google Scholar]
- 10.Lanza GM, Winter PM, Neubauer AM, Caruthers SD, Hockett FD, Wickline SA. 1H/19F magnetic resonance molecular imaging with perfluorocarbon nanoparticles. Curr Top Dev Biol. 2005;70:57–76. doi: 10.1016/S0070-2153(05)70003-X. [DOI] [PubMed] [Google Scholar]
- 11.Yu JX, Kodibagkar VD, Cui W, Mason RP. 19F: a versatile reporter for non-invasive physiology and pharmacology using magnetic resonance. Curr Med Chem. 2005;12:819–48. doi: 10.2174/0929867053507342. [DOI] [PubMed] [Google Scholar]
- 12.Nersesyan H, Hyder F, Rothman DL, Blumenfeld H. Dynamic fMRI and EEG recordings during spike-wave seizures and generalized tonic-clonic seizures in WAG/Rij rats. J Cereb Blood Flow Metab. 2004;24:589–99. doi: 10.1097/01.WCB.0000117688.98763.23. [DOI] [PubMed] [Google Scholar]
- 13.Sanganahalli BG, Herman P, Hyder F. Frequency-dependent tactile responses in rat brain measured by functional MRI. NMR Biomed. 2008;21:410–6. doi: 10.1002/nbm.1259. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Chahboune H, Ment LR, Stewart WB, Ma X, Rothman DL, Hyder F. Neurodevelopment of C57B/L6 mouse brain assessed by in vivo diffusion tensor imaging. NMR Biomed. 2007;20:375–82. doi: 10.1002/nbm.1130. [DOI] [PubMed] [Google Scholar]
- 15.Coman D, de Graaf RA, Rothman DL, Hyder F. In vivo 3D molecular imaging with BIRDS at high spatiotemporal resolution. NMR Biomed. 2013 doi: 10.1002/nbm.2995. (in press) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Crane PD, Pardridge WM, Braun LD, Oldendorf WH. Kinetics of transport and phosphorylation of 2-fluoro-2-deoxy-D-glucose in rat brain. J Neurochem. 1983;40:160–7. doi: 10.1111/j.1471-4159.1983.tb12666.x. [DOI] [PubMed] [Google Scholar]
- 17.Bessell EM, Courtenay VD, Foster AB, Jones M, Westwood JH. Some in vivo and in vitro antitumour effects of the deoxyfluoro-D-glucopyranoses. Eur J Cancer. 1973;9:463–70. doi: 10.1016/0014-2964(73)90128-x. [DOI] [PubMed] [Google Scholar]
- 18.de Graaf RA, Mason GF, Patel AB, Behar KL, Rothman DL. In vivo 1H-[13C]-NMR spectroscopy of cerebral metabolism. NMR Biomed. 2003;16:339–57. doi: 10.1002/nbm.847. [DOI] [PubMed] [Google Scholar]
- 19.de Graaf RA, Rothman DL, Behar KL. State of the art direct 13C and indirect 1H-[13C] NMR spectroscopy in vivo. A practical guide. NMR Biomed. 2011;24:958–72. doi: 10.1002/nbm.1761. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Rothman DL, De Feyter HM, de Graaf RA, Mason GF, Behar KL. 13C MRS studies of neuroenergetics and neurotransmitter cycling in humans. NMR Biomed. 2011;24:943–57. doi: 10.1002/nbm.1772. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Crane PD, Braun LD, Cornford EM, Cremer JE, Glass JM, Oldendorf WH. Dose dependent reduction of glucose utilization by pentobarbital in rat brain. Stroke. 1978;9:12–8. doi: 10.1161/01.str.9.1.12. [DOI] [PubMed] [Google Scholar]
- 22.Gredell JA, Turnquist PA, Maciver MB, Pearce RA. Determination of diffusion and partition coefficients of propofol in rat brain tissue: implications for studies of drug action in vitro. Br J Anaesth. 2004;93:810–7. doi: 10.1093/bja/aeh272. [DOI] [PubMed] [Google Scholar]
- 23.Bereczki D, Wei L, Otsuka T, Hans FJ, Acuff V, Patlak C, Fenstermacher J. Hypercapnia slightly raises blood volume and sizably elevates flow velocity in brain microvessels. Am J Physiol. 1993;264:H1360–9. doi: 10.1152/ajpheart.1993.264.5.H1360. [DOI] [PubMed] [Google Scholar]
- 24.Patel AB, de Graaf RA, Mason GF, Kanamatsu T, Rothman DL, Shulman RG, Behar KL. Glutamatergic neurotransmission and neuronal glucose oxidation are coupled during intense neuronal activation. J Cereb Blood Flow Metab. 2004;24:972–85. doi: 10.1097/01.WCB.0000126234.16188.71. [DOI] [PubMed] [Google Scholar]
- 25.McSheehy PM, Leach MO, Judson IR, Griffiths JR. Metabolites of 2′-fluoro-2′-deoxy-D-glucose detected by 19F magnetic resonance spectroscopy in vivo predict response of murine RIF-1 tumors to 5-fluorouracil. Cancer Res. 2000;60:2122–7. [PubMed] [Google Scholar]
- 26.Kennedy JA, Israel O, Frenkel A, Bar-Shalom R, Azhari H. Super-resolution in PET imaging. Medical Imaging. IEEE Transactions on. 2006;25:137–147. doi: 10.1109/TMI.2005.861705. [DOI] [PubMed] [Google Scholar]
- 27.Irani M, Peleg S. Motion Analysis for Image Enhancement: Resolution, Occlusion, and Transparency. Journal of Visual Communication and Image Representation. 1993;4:324–335. [Google Scholar]