Skip to main content
NCBI home page
NIHPA Author Manuscripts logoLink to NIHPA Author Manuscripts
. Author manuscript; available in PMC: 2015 May 1.
Published in final edited form as: Neuroimage. 2014 Jan 15;91:177–186. doi: 10.1016/j.neuroimage.2014.01.009

Development of a High Angular Resolution Diffusion Imaging Human Brain Template

Anna Varentsova a, Shengwei Zhang b, Konstantinos Arfanakis b,c,d
PMCID: PMC3965645  NIHMSID: NIHMS556506  PMID: 24440528

Abstract

Brain diffusion templates contain rich information about the microstructure of the brain, and are used as references in spatial normalization or in the development of brain atlases. The accuracy of diffusion templates constructed based on the diffusion tensor (DT) model is limited in regions with complex neuronal micro-architecture. High angular resolution diffusion imaging (HARDI) overcomes limitations of the DT model and is capable of resolving intravoxel heterogeneity. However, when HARDI is combined with multiple-shot sequences to minimize image artifacts, the scan time becomes inappropriate for human brain imaging. In this work, an artifact-free HARDI template of the human brain was developed from low angular resolution multiple-shot diffusion data. The resulting HARDI template was produced in ICBM-152 space based on Turboprop diffusion data, was shown to resolve complex neuronal micro-architecture in regions with intravoxel heterogeneity, and contained fiber orientation information consistent with known human brain anatomy.

Keywords: high angular resolution diffusion imaging, HARDI, brain, template, Turboprop, fiber orientation distribution

Introduction

Diffusion MRI allows investigation of the brain’s microstructure by examining the 3D displacement profile of water molecules in tissue (LeBihan and Breton, 1985; Merboldt et al., 1985). Diffusion templates representative of the microstructure of the average human brain can be constructed by combining diffusion information from multiple human subjects, and are used as reference for comparisons of the micro-architecture of the brain across populations, as well as to generate digital brain atlases. Conventional diffusion tensor imaging (DTI) data (Basser et al., 1994; Basser and Pierpaoli, 1996) have been used for the development of several brain templates and atlases (Mori et al., 2008; Van Hecke et al., 2008; Peng et al., 2009; Zhang et al., 2011). However, DTI assumes Gaussian diffusion, and therefore a single fiber orientation, in each voxel (Basser et al., 1994), which is an inappropriate assumption for more than 90% of human brain white matter (Jeurissen et al., 2012). This oversimplification of the DT model limits the accuracy of DTI-based brain templates. High angular resolution diffusion imaging (HARDI) (Alexander et al., 2002; Tuch et al., 2002) collects diffusion-weighted (DW) signals along a higher number of directions than the minimum required in DTI, and has the potential to describe non-Gaussian diffusion and resolve multiple fiber orientations within a voxel. Moreover, scalar quantities that describe diffusion anisotropy in voxels with multiple fiber orientations more accurately than the tensor-derived fractional anisotropy (FA), have been introduced for use with HARDI (Tuch, 2004). Therefore, a HARDI template and atlas may represent the average human brain micro-architecture more accurately than those based on DTI.

One of the key factors contributing to the accuracy of a brain template is the image quality of the data used for its development (Zhang et al., 2011). High quality data with minimal artifacts are necessary in order to produce a high quality HARDI template. For DTI, it has been shown that, multiple-shot pulse sequences minimize image artifacts in regions with magnetic field inhomogeneities at the cost of long scan times (Gui et al., 2008). However, HARDI is characterized by lower scanning efficiency than DTI. When combining HARDI with multiple-shot sequences, the scan time becomes inappropriate for human imaging.

The present work addressed the aforementioned limitations by constructing a HARDI template of the human brain from multiple-shot low angular resolution diffusion data from multiple subjects. This was accomplished by extending the work by Caan et al., 2009, according to which, spatially co-registered low angular resolution DTI datasets from multiple subjects can be treated as a single diffusion dataset of higher angular resolution than that of its individual parts. More specifically, differences in brain shape and head positioning across human subjects lead to different local rotations during spatial normalization, which means that the combined dataset contains diffusion-weighted (DW) signals corresponding to a large number of unique diffusion directions (equal to the product of the number of diffusion directions per subject and the number of subjects). This approach is in essence an application of the well-established super-resolution concept in angular sampling (Borman and Stevenson, 1998; Elad and Feuer, 1997; Park et al., 2003). Caan et al., 2009, demonstrated this approach by fitting dual tensors in each voxel of a composite dataset constructed from conventional single-shot echo-planar DTI data from 11 subjects (contaminated by echo-planar image artifacts). In the present work, low angular resolution Turboprop-DTI datasets from 72 subjects, relatively free of distortions and other artifacts (Arfanakis et al., 2005; Pipe and Zwart, 2006; Gui et al., 2008), were combined into a single high angular resolution diffusion dataset, and constrained spherical deconvolution (CSD) (Tournier et al., 2007) with up to sixth order spherical harmonics was employed to construct a human brain HARDI template in ICBM-152 space (Mazziotta et al., 1995). The resulting HARDI template was shown to resolve complex neuronal micro-architecture in regions with intravoxel inhomogeneity and contained fiber orientation information consistent with known human brain anatomy.

Material and Methods

MRI Data

Turboprop-DTI data from 72 healthy human subjects (forty-two female: 26.6±4.8 years of age, 20–39 years age range; thirty male: 31.9±4.9 years of age, 22–40 years age range), originally acquired for the development of the previously published IIT and IIT2 DTI templates (Peng et al., 2009; Zhang et al., 2011), were used in this study. The diffusion properties are shown to be relatively similar across subjects in this age group (Sullivan and Pfefferbaum, 2006; Hasan et al., 2008). Written informed consent was provided by all participants according to procedures approved by the institutional committee for the protection of human subjects. All datasets were collected on a 3 Tesla General Electric MRI scanner (GE, Waukesha, WI) with the following parameters: TR=5800 ms, TE=94 ms, 8 spin-echoes per TR, 5 k-space lines per spin-echo, 128 samples per line, 16 blades per image, field of view 24 cm × 24 cm, 45 contiguous oblique axial slices, 3 mm slice thickness, 256×256 final image matrix, b=900 s/mm2 for 12 diffusion directions uniformly distributed in 3D space (minimum energy scheme) (Hasan et al., 2001), and two b=0 s/mm2 images for each slice. The scan time for this sequence was 21 min and 57 s.

High-resolution T1-weighted data were also obtained for each subject, using the 3D magnetization-prepared rapid acquisition gradient echo (MP-RAGE) sequence with the following parameters: TE=3.2 ms, TR=8 ms, preparation time=725 ms, flip angle 6º, field of view 24 cm × 24 cm, 124 slices, 1.5 mm slice thickness, 192×256 k-space matrix reconstructed to 256×256. The scan time for this sequence was 9 min and 58 s.

Generation of a High Angular Resolution Diffusion Dataset from Low Angular Resolution Data

Brain extraction, motion correction, b-matrix reorientation and diffusion tensor estimation were performed for each subject, using TORTOISE (http://www.tortoisedti.org) (Pierpaoli et al., 2010). Turboprop-DTI is relatively immune to eddy-currents and magnetic field non-uniformities, and therefore corresponding corrections were not conducted (Gui et al., 2008). The mean b=0 s/mm2 image volume was obtained for each subject. The mean b=0 s/mm2 and DW data (after preprocessing) were then transformed to ICBM-152 space, as follows. All 72 DTI datasets were registered to the IIT2 DTI template (Zhang et al., 2011) using deformable registration of diffusion tensors with explicit orientation optimization (DTITK) (Zhang et al., 2006), and averaged to construct a temporary DTI template. The 72 original DTI datasets were then registered to the temporary template, and the results were averaged to obtain an updated template. This process was repeated 6 times, eventually transforming all datasets to population space. The resulting transformations were applied to the mean b=0 s/mm2 image volumes of all datasets. The mean b=0 s/mm2 image volumes in population-space were then non-linearly registered to the ICBM-152 T2-weighted template using the Automatic Registration Toolbox (ART) (Ardekani et al., 2005). The resulting ART transformations were averaged across subjects. Finally, for each subject, the transformation from subject space to population space was combined with the average ART transformation from population space to ICBM-152 space, and then applied to the original mean b=0 s/mm2 and DW image volumes (after preprocessing). The voxel size used in ICBM-152 space was 1 mm × 1 mm × 1 mm.

Since the final transformation applied to the preprocessed mean b=0 s/mm2 and DW image volumes of each subject included rotations that varied throughout the brain, diffusion gradient directions that corresponded to the transformed DW volumes were estimated for each voxel separately from the local applied rotation. That local rotation matrix, R, was computed from the local Jacobian matrix of the final transformation using singular value decomposition:

J=U·W·VT, [1]
R=U·VT, [2]

where J is the local Jacobian matrix, W is a diagonal matrix with singular values in the diagonal elements, and U and V contain the left- and right-singular vectors, respectively. Due to differences in brain shape and head positioning across subjects, the applied rotations in each brain location were different for each subject (Fig. 1). Consequently, each voxel of the combined dataset in ICBM-152 space contained a total of 864 DW signals (72 subjects × 12 diffusion directions), corresponding to 864 unique diffusion directions (i.e. 864 unique samples on a hemisphere of 3D space). To assess the angular sampling resolution in the combined dataset, gaps in angular sampling were estimated in each white matter voxel, and for each (θ,φ), by calculating the maximum opening angle a cone can have if it: i) originates from the center of the unit sphere, ii) is centered at (θ,φ) and iii) does not include any of the samples in the combined dataset (Fig.2A). In the following, this cone is referred to as the local sampling gap cone. For each (θ, φ) of a voxel of the combined dataset, the opening angle of the local sampling gap cone was translated into the number of diffusion directions of a uniform sampling scheme with a largest sampling gap cone of the same size as the local sampling gap cone of that voxel (Fig.2B). Furthermore, the minimum angular sampling resolution in a voxel of the combined dataset was evaluated by means of the opening angle of the largest sampling gap cone in that voxel, which was again translated into the number of diffusion directions of a uniform sampling scheme with a largest sampling gap cone of the same size.

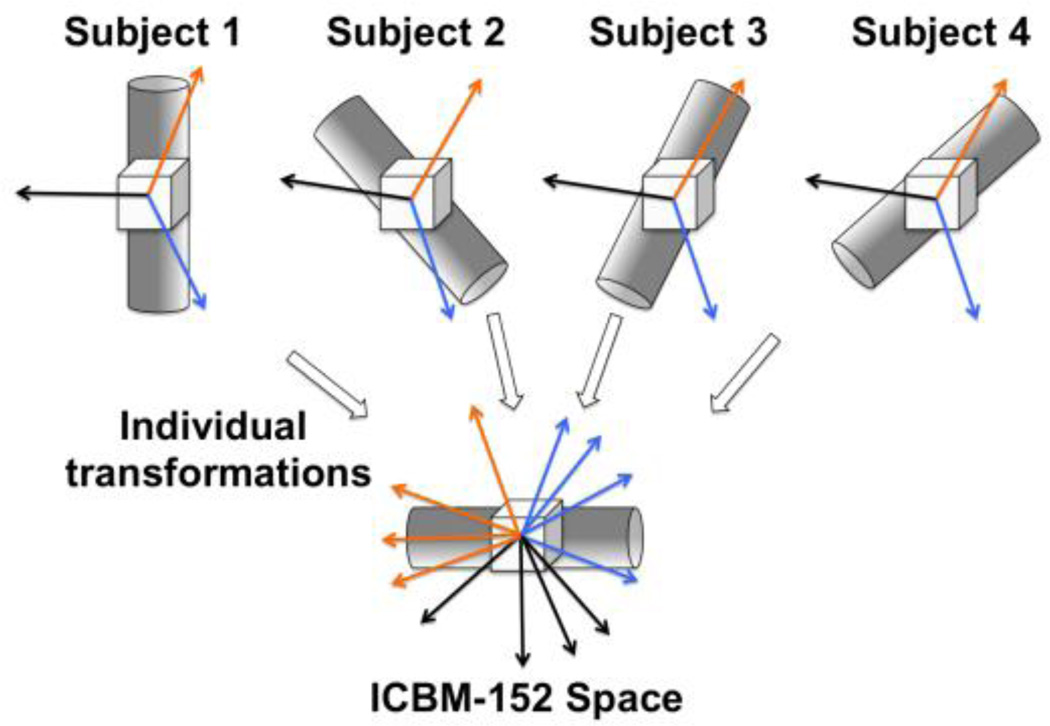
Figure 1.

Figure 1

Open in a new tab

An example of how combining low angular resolution DW data from multiple subjects leads to a single dataset with a large number of DW signals along unique diffusion directions. The cylindrical tubes represent the same fiber bundle in four different subjects, the cubes represent image voxels, and the arrows represent three diffusion gradient vectors. In the first row, the fiber bundle is at different orientations in the scanner’s reference frame, due to differences in brain shape and head positioning across subjects. (Note: the differences in orientation of the fiber bundle due to brain shape and head positioning have been exaggerated to improve visualization). In contrast, the three diffusion gradient vectors have the same orientation in the scanner’s frame for all subjects, since all subjects were scanned using the same scanner, pulse sequence and set of diffusion directions. Spatial transformation of each subject’s tissue to ICBM-152 space requires a different rotation of the fiber bundle across subjects. The diffusion gradients that correspond to the DW signals after transformation to ICBM-152 space are obtained by applying the corresponding rotations to the original diffusion gradient vectors, and are shown in the second row. In this example, appropriate combination of three DW signals from four subjects results in a single dataset containing twelve DW signals along unique diffusion directions.

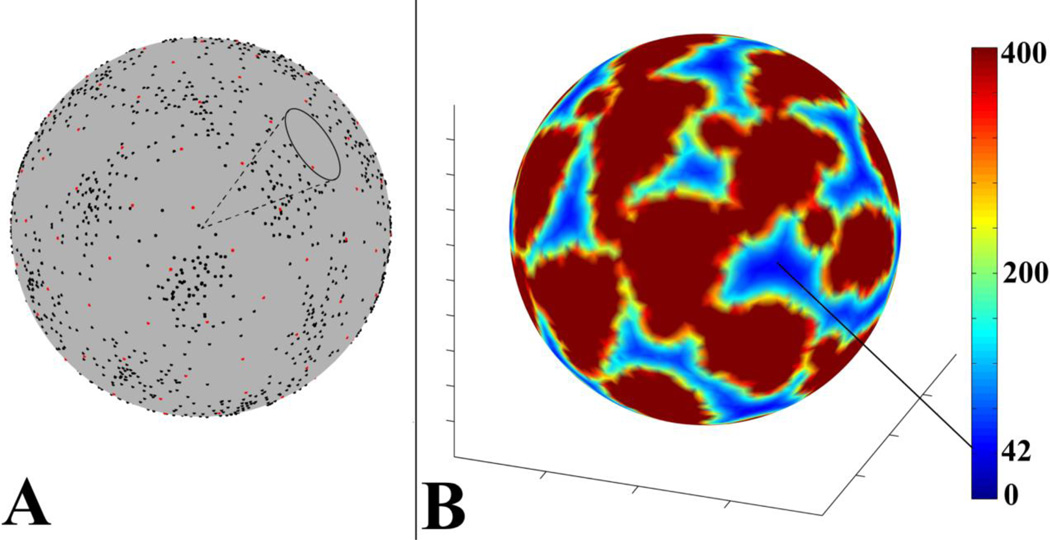
Figure 2.

Figure 2

Open in a new tab

A) An example of a local sampling gap cone. Black dots represent samples in a voxel of the combined dataset, and red dots represent samples of a uniform sampling scheme with 60 diffusion gradients. B) An example of expressing the opening angle of local sampling gap cones in terms of the number of gradients of uniform sampling schemes (color scale) with a largest sampling gap cone of the same size as the local sampling gap cone. For the voxel in this example, the sparsest angular sampling was equivalent to that of a uniform sampling scheme with 42 gradients. However, for the same voxel, angular sampling resolution was substantially higher along other directions in 3D space.

To address differences in acquisition gain factors across subjects, the DW signals from each subject were divided by the corresponding mean b=0 s/mm2 signal. In the following, we will use the notation Sij for the normalized DW signals of the combined dataset, where i indicates the subject (from 1 to 72) and j indicates the diffusion direction (from 1 to 12).

Corrections in the High Angular Resolution Diffusion Dataset

Despite normalization of the DW signals with the corresponding mean b=0 s/mm2 signal, the mean per subject normalized DW signal:

meani(Sij)=∑j=112Sij12, [3]

was expected to vary across subjects in each voxel of the combined dataset (seen as “steps” in Fig. 3A) due to the following reasons. First, different positioning of homologous fibers relative to the diffusion gradients, leads to different DW signals across subjects for the same set of diffusion directions, and inevitably to a small variation in meani(Sij) across subjects. Second, for each subject, all DW signals in a voxel are divided by the same b=0 s/mm2 signal, and therefore, noise in b=0 s/mm2 introduces a variation of meani(Sij) across subjects. Third, residual spatial mismatch leads to substantial variation in the meani(Sij) across subjects. For example, assigning cerebrospinal fluid signals from one subject and white matter signals from another to the same voxel leads to substantially lower normalized DW signals for the former subject compared to the latter. Variation of the meani(Sij) across subjects due to the second and third reasons mentioned above is an artifact of the process used to construct the combined dataset, and may introduce errors in HARDI reconstruction.

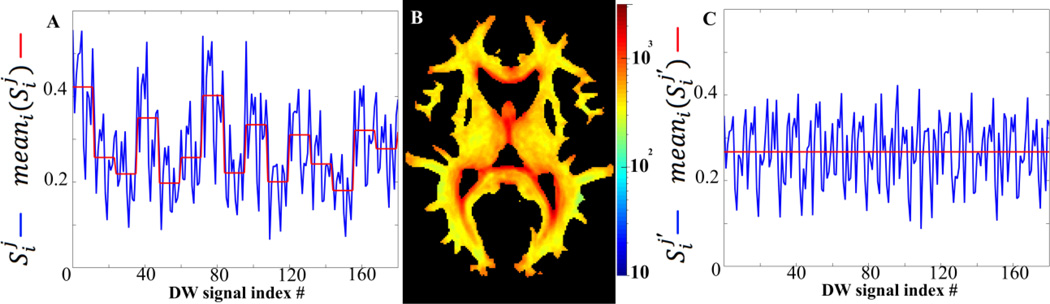
Figure 3.

Figure 3

Open in a new tab

(A) Typical normalized DW signals (Sij) in a white matter voxel of the combined dataset, originating from 15 of the 72 subjects (blue curve; signals are plotted in series, i.e. all signals from subject 1, followed by all signals from subject 2, etc.), and mean normalized DW signal (mean(Sij)) per subject (red curve). (B) Axial map of the ratio of CVDW values for the combined over the simulated dataset in white matter (logarithmic color scale). (C) Corrected normalized DW signals (Sij') (blue curve) and mean normalized DW signal per subject after correction (red curve).

A simulation was used to assess the importance of the above sources of error in the combined dataset. The highest true variation in meani(Sij) across subjects (due to the first reason described above) occurs in the case of single fiber orientation. Therefore, a dataset containing a single fiber diffusion profile was simulated in the same space as the combined dataset, using in each voxel the tensor model with eigenvalues λ1=1.8×10−3, λ2= λ3=0.15×10−3 mm2/s (Papadakis et al., 2000), and the actual diffusion gradient vectors of the combined dataset. The coefficient of variation of meani(Sij) was calculated in each voxel of the combined and simulated datasets, separately, as follows:

CVDW=std(meani(Sij))mean(meani(Sij)), [4]

where mean(meani(Sij)) and std(meani(Sij)) are the mean and standard deviation of the meani(Sij) over all subjects. The ratio of CVDW values for the combined over the simulated dataset was calculated in each voxel (Fig.3B). It was demonstrated that the CVDW values in the combined dataset were substantially higher than those in the simulated dataset. This finding suggested that the second and third sources of variation in meani(Sij) across subjects had substantial effect on the combined dataset, and therefore, a correction was necessary to reduce errors in HARDI reconstruction. The approach that was selected for that purpose was to divide the normalized DW signals from each subject by the subject’s meani(Sij):

Sij′=Sijmeani(Sij). [5]

Consequently, any difference in meani(Sij) across subjects was eliminated (Fig.3C). It should be noted that this process also eliminated the small but true variation in meani(Sij) across subjects (caused by different positioning of homologous fibers relative to the diffusion gradients). However, this was considered acceptable since the true variation in meani(Sij) was very small (CVDW of the simulated dataset was 3.23×10−4 ± 1.16×10−4 on average over all white matter), and the variation that was an artifact of the process used to construct the combined dataset was much more substantial than the true variation, as shown in Fig.3B. Therefore, the process described above was used to generate the final signals of the combined dataset, Sij′.

Construction of a HARDI Template

Signals Sij′ of the combined dataset were used to estimate fiber orientation distribution (FOD) functions by performing constrained spherical deconvolution (CSD) (Tournier et al., 2007) with up to lmax=6 order modified real spherical harmonics (SH) basis. The same process was repeated for all voxels of the combined dataset. All the information generated above constituted the final HARDI template. A conventional DTI coloring scheme was used when mapping fiber orientation information, with red color corresponding to fibers oriented left-right, green for anterior-posterior, and blue for superior-inferior.

Evaluation of the Information Captured in the HARDI Template

FODs of the template were compared to those of previously published studies, in brain regions known to consist of fibers with relatively similar orientation, as well as in regions containing multiple fiber orientations. The ability to resolve crossing fibers in the HARDI template was evaluated by tracing pathways through known regions of fiber intersection. For this purpose, each fiber bundle involved in a crossing was mapped using the MRtrix toolbox (Tournier et al., 2012) with tracking step size = 0.2 mm, radius of curvature = 1 mm, minimum tract length = 10 mm, and two ROIs positioned on opposite sides of the crossing.

To evaluate the consistency of FOD reconstruction in neighboring voxels, for each voxel of the combined dataset, the correlation between the FOD in that voxel and the FOD in each of its 6 nearest neighbors was calculated (Anderson, 2005):

ri,j,ki′,j′,k′=∑l=06∑m=−llulm(i,j,k)ulm(i′,j′,k′)[∑l′=06∑m′=−l′l′|ul′m′(i,j,k)|2]12[∑l″=06∑m″=−l″l″|ul″m″(i′,j′,k′)|2]12 [6]

where i, j, k are the coordinates of the voxel of interest, i′, j′, k′ are the coordinates of a neighboring voxel, ri,j,ki′,j′,k′ is the correlation between the FOD at i, j, k and the FOD at i′, j′, k′, ulm is the spherical harmonic coefficient representation of a FOD, and then averaged over all 6 neighbors:

A(i,j,k)=16(ri,j,ki−1,j,k+ri,j,ki+1,j,k+ri,j,ki,j−1,k+ri,j,ki,j+1,k+ri,j,ki,j,k−1+ri,j,ki,j,k+1), [7]

where A(i, j,k) is the average correlation of neighboring FODs at voxel i, j, k. Maps of the average correlation of neighboring FODs were generated for the resulting HARDI template.

The effect that angular sampling resolution varying in spherical coordinates may have on FOD reconstruction was also evaluated. In each white matter voxel of the combined dataset, the opening angle of the local sampling gap cone centered at the direction corresponding to the maximum of the FOD was estimated. The consistency of FOD reconstruction was then compared in neighboring voxels with different opening angle of the local sampling gap cone centered at the main fiber orientation.

Finally, the resulting HARDI template was compared to NTU-90 (Yeh and Tseng, 2011), which, to our knowledge, is the only other HARDI template that is publicly available. Only qualitative comparisons of sharpness and level of artifacts were conducted, since a detailed quantitative comparison of FODs and derived quantities is complicated by differences in FOD reconstruction, voxel dimensions, demographic characteristics of the subjects, and publicly available output.

Results

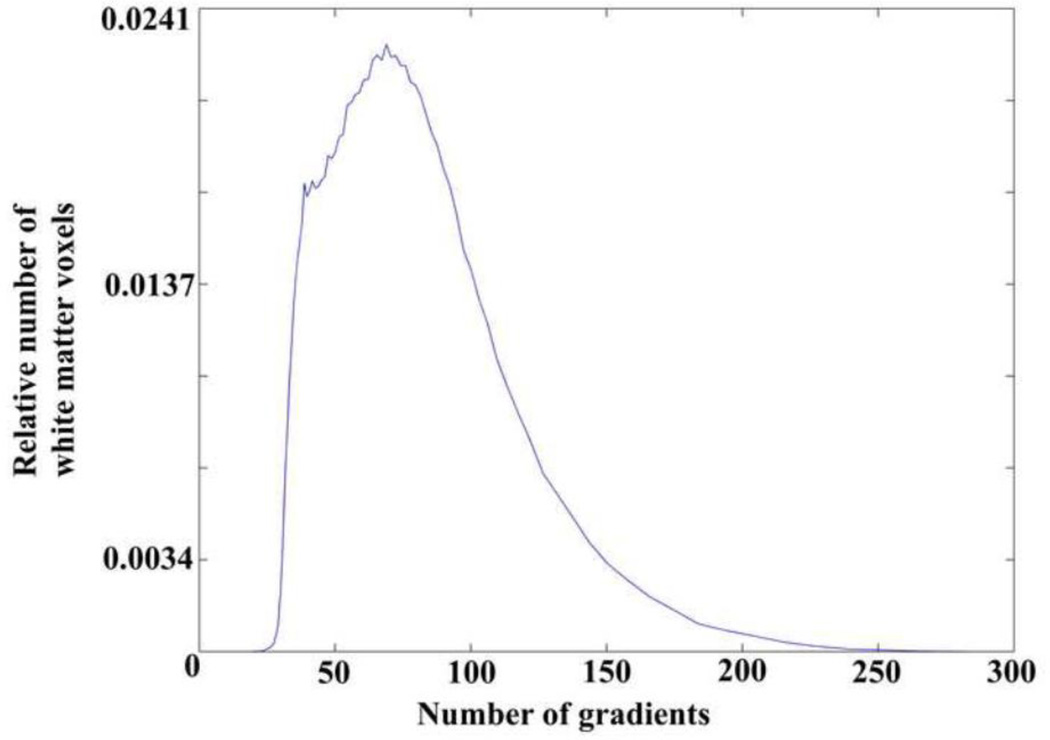
The angular sampling resolution varied over (θ,φ) in voxels of the combined dataset (Fig.2A). Different voxels of the combined dataset exhibited different opening angles of the largest sampling gap cone. Figure 4 shows a histogram of the relative number of white matter voxels that have an opening angle of the largest sampling gap cone equal to that of a uniform sampling scheme with the number of directions shown on the horizontal axis. The peak of the histogram is at 67 gradients. It should be stressed that the histogram refers to the opening angle of the largest sampling gap cone in voxels of the combined dataset. The angular sampling resolution is higher in other parts of 3D space for the same voxels.

Figure 4.

Figure 4

Open in a new tab

Histogram of the relative number of white matter voxels that have an opening angle of the largest sampling gap cone equal to that of a uniform sampling scheme with the number of directions shown on the horizontal axis. The peak of the histogram is at 67 gradients. This histogram refers to the opening angle of the largest sampling gap cone (lowest angular sampling resolution) in voxels of the combined dataset. The same voxels have higher angular sampling resolution in other parts of 3D space.

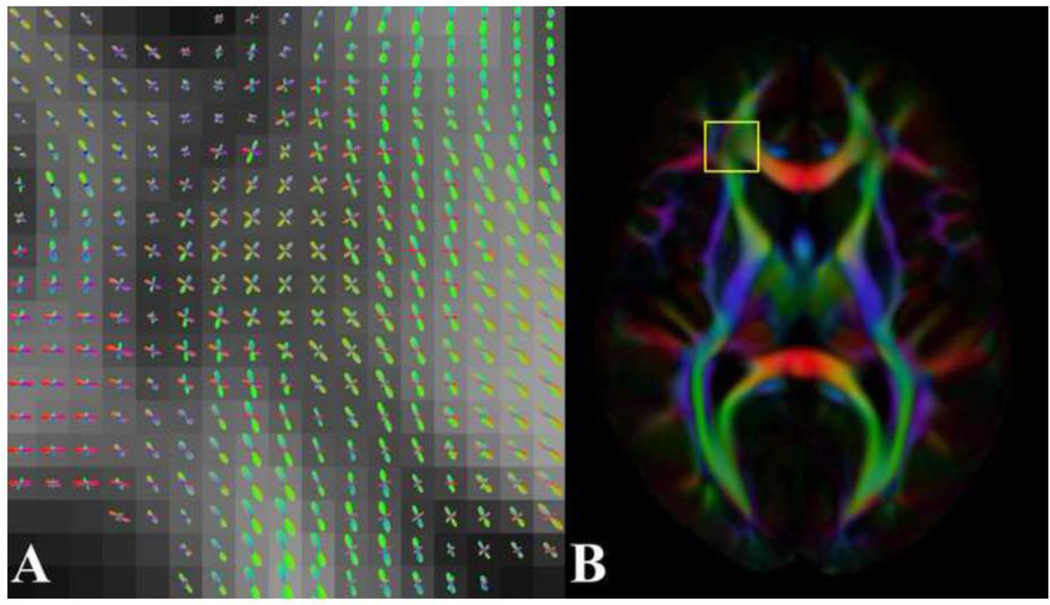
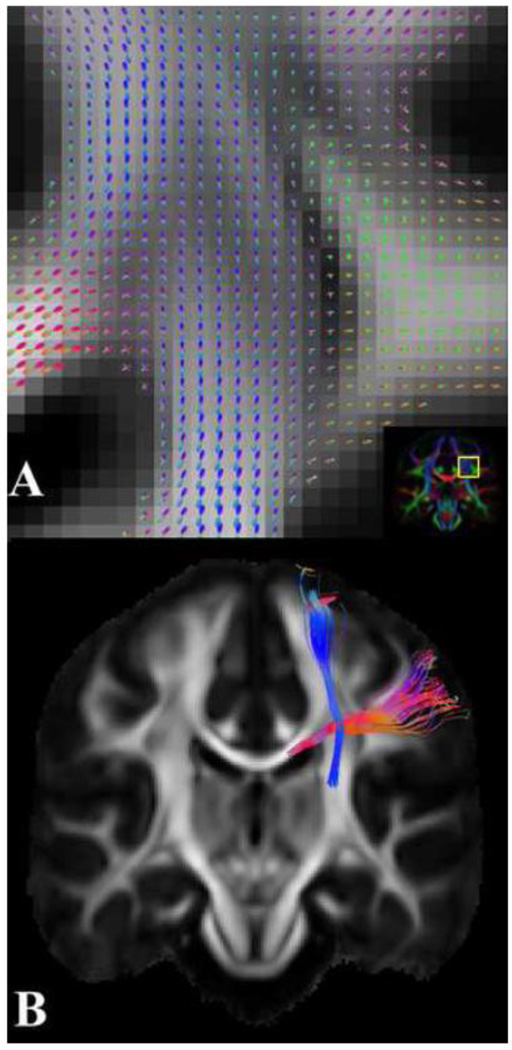
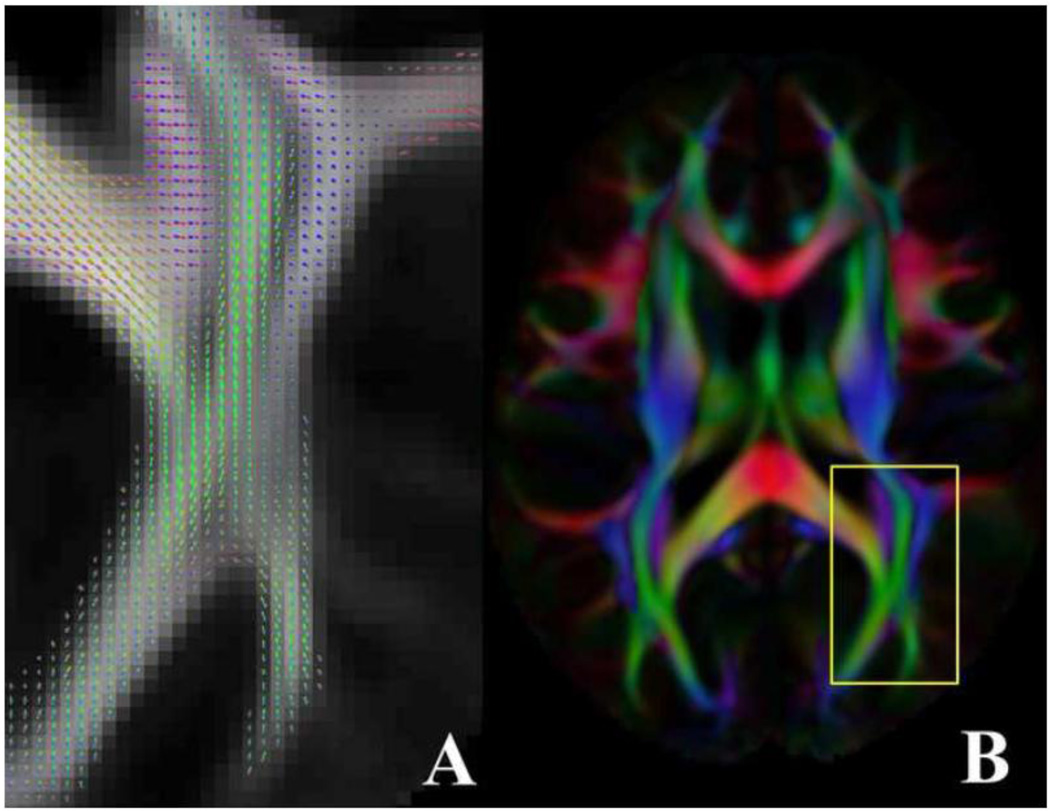
In voxels known to contain white matter fibers with relatively similar orientation, such as those in portions of the corpus callosum and the corticospinal tracts, FODs of the HARDI template suggested the presence of a well-defined fiber orientation (Fig.5). In contrast, in frontal lobe regions known to have complex fiber organization, FODs suggested fiber crossing or fanning (Fig.6), in agreement with findings of HARDI studies on single subjects (Descoteaux et al., 2011; Tuch, 2004). Multimodal FOD profiles implying fiber crossings were also observed at the intersections between fibers of the corpus callosum, corticospinal tract, and superior longitudinal fasciculus (Figs.7,8), similar to what was previously demonstrated in single subjects (Descoteaux et al., 2011; Hess et al., 2006; Patel et al., 2010b; Tournier et al., 2007). Tractography targeting only two tracts in these regions resolved two-way crossings (Fig.7B) (Jeurissen et al., 2011; Kaden et al., 2007), while targeting three tracts resolved three-way crossings between commissural projections of the corpus callosum, the corticospinal tract, and superior longitudinal fasciculus (Fig.9) (Wedeen et al., 2008), in agreement with studies on HARDI datasets from individual subjects. In addition, cross-shaped FODs were detected in other brain regions known to be characterized by fiber orientation inhomogeneity: at the decussation of the superior cerebellar peduncle (Fig.10) (Tuch, 2004); at the regions where fibers of the ventral tegmental areas and substantia nigra meet the oculomotor nerves (Fig.10) (Gray, 1918); at the intersection of optic radiations with fibers of the tapetum (Fig.11) (Tuch, 2004).

Figure 5.

Figure 5

Open in a new tab

Highly coherent FODs in voxels of the corpus callosum (A) and corticospinal tract (B) of the generated HARDI template. The outlines of the magnified regions in (A, B) are overlaid on the corresponding FA-weighted orientation color maps.

Figure 6.

Figure 6

Open in a new tab

(A) Axial map of FODs in right frontal lobe white matter of the HARDI template, demonstrating fiber crossing and fanning. (B) The outline of the magnified region in (A) is overlaid on the corresponding FA-weighted orientation color map.

Figure 7.

Figure 7

Open in a new tab

(A) Coronal FOD map suggesting fiber crossing at the intersection of the corpus callosum (red) and corticospinal tract (blue) of the HARDI template (the outline of the magnified region is overlaid on the corresponding FA-weighted orientation color map). (B) Coronal view of fibers crossing at the region shown in (A). Each bundle was mapped using the HARDI template, two spherical ROIs positioned on opposite sides of the fiber crossing, and the AND logical operator.

Figure 8.

Figure 8

Open in a new tab

(A) Axial FOD map through the left centrum semiovale of the HARDI template, where fibers of the superior longitudinal fasciculus coexist with commissural projections of the corpus callosum. (B) The outline of the magnified region in (A) is overlaid on the corresponding FA-weighted orientation color map.

Figure 9.

Figure 9

Open in a new tab

Tractography result at the crossing between commissural projections of the corpus callosum (red), the corticospinal tract (blue), and superior longitudinal fasciculus (green). Each bundle was mapped using the HARDI template, two spherical ROIs positioned on opposite sides of the fiber crossing, and the AND logical operator.

Figure 10.

Figure 10

Open in a new tab

Axial FOD map through the brainstem of the HARDI template, demonstrating fiber crossings at the decussation of the superior cerebellar peduncle, and the regions where fibers of the ventral tegmental areas and substantia nigra meet the oculomotor nerves (the outline of the magnified region is overlaid on the corresponding FA-weighted orientation color map).

Figure 11.

Figure 11

Open in a new tab

(A) Axial FOD map of the HARDI template showing fiber crossing at the intersection of optic radiations with fibers of the tapetum. (B) The outline of the magnified region in (A) is overlaid on the corresponding FA-weighted orientation color map.

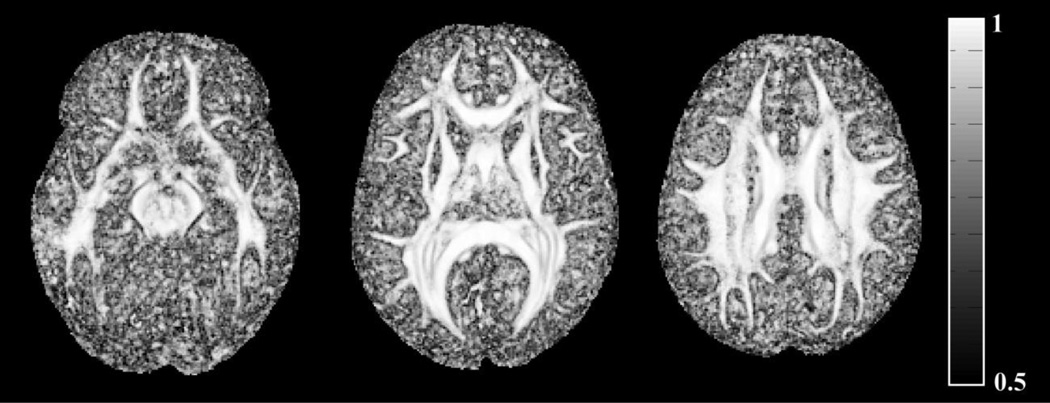
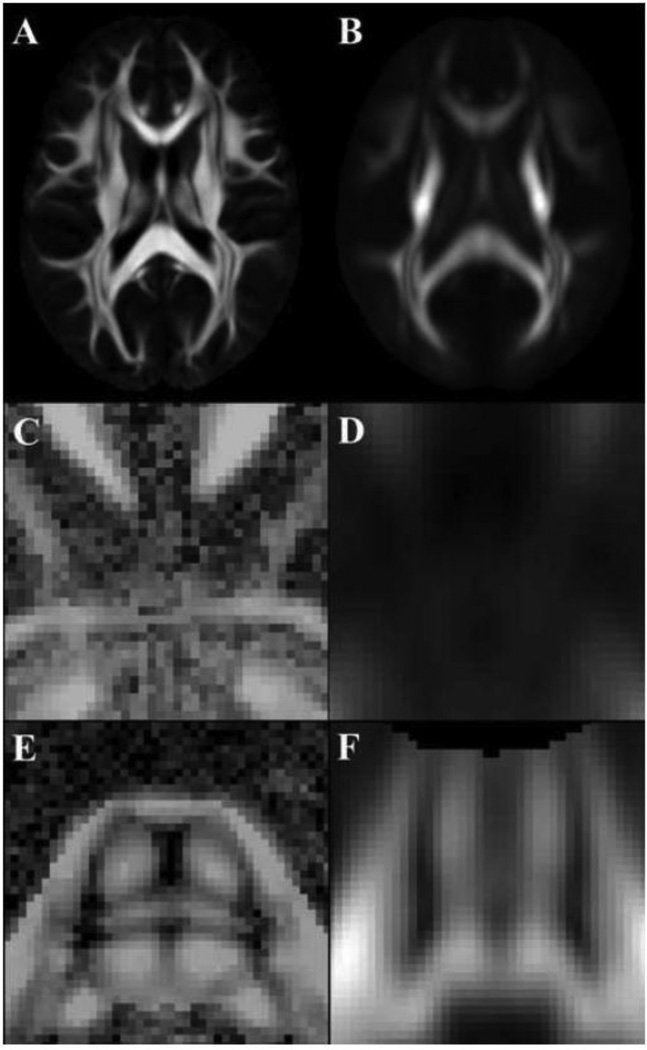
Maps of the mean correlation of neighboring FODs in the generated HARDI template demonstrated higher correlation in white matter compared to gray matter and cerebrospinal fluid (Fig.12). Also, FODs were shown to be independent of the opening angle of the local sampling gap cone centered at the main fiber orientation (Fig.13). Finally, the HARDI template generated here was characterized by higher image sharpness, provided the ability to distinguish smaller white matter fiber bundles such as the anterior commissure and transverse pontine fibers, and contained fewer image artifacts than NTU-90 (Fig.14).

Figure 12.

Figure 12

Open in a new tab

Maps of the mean correlation of neighboring FODs in the generated HARDI template.

Figure 13.

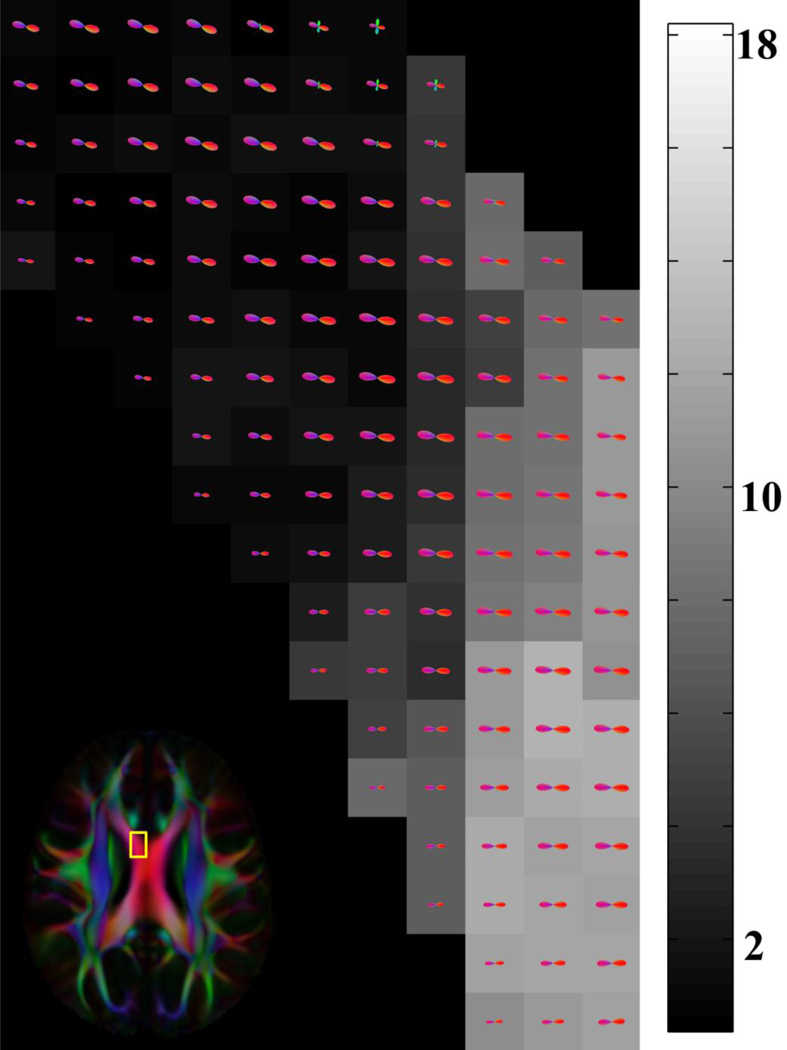
Figure 13

Open in a new tab

FODs in the corpus callosum (in color) overlaid on a grayscale map of the opening angle of the local sampling gap cone centered at the main fiber orientation. The numbers next to the grayscale bar correspond to the opening angle of the local sampling gap cone in degrees. The outline of the magnified region is overlaid on the corresponding FA-weighted orientation color map.

Figure 14.

Figure 14

Open in a new tab

Axial FA map of the (A) HARDI template generated here and (B) NTU-90 (FA of primary fiber bundle is shown for NTU-90). Axial GFA map through the (C, D) anterior commissure and (E, F) pons of (C, E) the HARDI template generated here and (D, F) NTU-90.

Discussion

A HARDI template of the human brain may be more representative of the average brain micro-architecture than available DTI templates. Therefore, development of a high-quality HARDI template of the human brain is particularly important to the neuroimaging community. The high image quality achieved with multiple-shot diffusion imaging techniques is well-documented (Gui et al., 2008; Peng et al., 2009). However, the scan time of multiple-shot HARDI acquisitions is inappropriate for human brain imaging. The purpose of this work was to develop a high-quality HARDI template of the human brain from low angular resolution multiple-shot diffusion data. This was accomplished by extending the work by Caan et al., 2009, and exploiting the fundamental assumption of template development, namely that the information combined into a template originated from the same distribution. The resulting HARDI template was produced in ICBM-152 space based on Turboprop diffusion data from 72 human subjects, was shown to resolve complex neuronal micro-architecture in regions with intravoxel heterogeneity, and contained fiber orientation information consistent with known human brain anatomy.

The FOD information contained in the generated HARDI template was in agreement with published HARDI results from individual subjects in voxels known to contain white matter fibers with similar orientation, as well as in voxels with documented fiber fanning or crossing (Figs.5–8,10,11). The latter was true despite the fact that fiber fanning or crossing was not detectable in the original 12 diffusion-direction DTI datasets from individual subjects. The ability to resolve complex neuronal micro-architecture in the generated HARDI template allowed mapping of fibers in brain regions with known fiber crossings (Figs.7B, 9) (Varentsova et al., 2013).

FOD maps were characterized by relatively high consistency of FOD shapes in white matter (Figs.5–8,10–12). Neighboring FODs were highly consistent even in regions with large variations in the opening angle of the local sampling gap cone centered at the main fiber orientation (Fig.13). This was probably due to the fact that the minimum angular sampling resolution was sufficiently high throughout white matter (Fig.4).

Other HARDI templates of the human brain have recently been developed (Bouix S, 2010; Patel et al., 2010a; Raffelt et al., 2011; Yeh and Tseng, 2011). The main differences in methodology used for their construction compared to the present work are discussed here. First, all previous studies performed HARDI reconstruction for each subject prior to averaging across subjects (Bouix S, 2010; Patel et al., 2010a; Raffelt et al., 2011; Yeh and Tseng, 2011), in contrast to HARDI reconstruction on a combined DW dataset. The two approaches are expected to be equivalent for the same product of the number of subjects and number of diffusion directions per subject, however, a detailed comparison using the same raw data for both approaches is needed. Both approaches are vulnerable to misregistration. In this work, all datasets were spatially normalized using deformable registration of diffusion tensors with explicit orientation optimization, accomplished with one of the leading techniques for DTI registration (Wang et al., 2011; Zhang et al., 2006). Although, registration was not based on FODs since such information was not available for individual datasets, the diffusion tensors contain sufficiently rich information to achieve relatively high spatial normalization accuracy for the development of a HARDI template. Previous studies used image registration algorithms based on a single scalar quantity (Bouix S, 2010; Patel et al., 2010a; Raffelt et al., 2011; Yeh and Tseng, 2011) and/or affine transformations (Bouix S, 2010; Patel et al., 2010a), which are expected to result in lower registration accuracy than that achieved here. Furthermore, all previous studies used conventional echo-planar imaging, thereby limiting the quality of the information captured in the template, primarily in the frontal and temporal lobes (Patel et al., 2010a; Yeh and Tseng, 2011). Examples of the above limitations of previously published templates were demonstrated in a qualitative comparison of the HARDI template generated here and NTU-90 (Yeh and Tseng, 2011) (Fig.14). The HARDI template generated here was characterized by higher image sharpness, provided the ability to distinguish smaller white matter fiber bundles, and contained fewer image artifacts than NTU-90 (Fig.14). More comprehensive quantitative comparisons across HARDI templates are currently problematic, due to one or more of the following reasons: differences in a) FOD reconstruction methods, b) reference space, c) demographic characteristics of the subjects, d) voxel-size, as well as e) the fact that most previously published HARDI templates or important information about these templates is not publicly available. Advances in hardware and image processing methodology have recently allowed collection of high quality HARDI data in reasonable scan times (Setsompop et al., 2013; Sotiropoulos et al., 2013). Further improvements in HARDI templates may be achieved through these efforts in the future.

The generated HARDI template may have the following potential applications. First, it may be used as a reference for spatial normalization of HARDI datasets from different subjects for the purpose of comparisons of the microstructural integrity of white matter across populations. Spatial normalization could be achieved using newly developed FOD-based registration techniques (Raffelt et al., 2011; Yap et al., 2011), or tensor-based methods such as DTI-TK, which has been successfully applied to both DTI (Adluru et al., 2012; Wang et al., 2011; Zhang et al., 2009) and HARDI studies (Duclap et al., 2013; Schmitt et al., 2013). Second, the presented HARDI template may be combined with probabilistic fiber-tracking to develop a probabilistic atlas of human brain white matter (Varentsova et al., 2013). Third, the generated template may be used as a digital phantom in the evaluation of tractography algorithms. Finally, the approach used in the present work for the development of a HARDI template may potentially be used to repurpose numerous DTI datasets collected by clinical studies on groups of patients and healthy controls for the purpose of performing inter-group comparisons. In most such studies, HARDI reconstruction is not ideal due to the relatively low number of diffusion directions used. However, a HARDI dataset can be constructed per group and comparison of HARDI characteristics, or HARDI-based tractography results, across groups may be informative. Certainly, extensive research on the statistical methods and biomedical applications of the above potential directions is required.

Although the generated HARDI template resolved known fiber crossings and contained orientation information consistent with known human brain anatomy, the present study has certain limitations. First, typical HARDI acquisition schemes include diffusion gradient vectors uniformly distributed in 3D space. In the combined dataset, the distribution of diffusion gradients was not uniform and therefore the effective number of gradient directions was lower than 864. Nevertheless, it was demonstrated that the large number of subjects used and the differences in brain shape and head positioning across subjects provided sufficiently high angular sampling resolution (Figs.2,4). A more uniform distribution of the diffusion vectors of the combined dataset may be achieved by systematically rotating the original set of diffusion directions to be used on individual subjects. Another possible limitation of the present study is that the b-value was lower than that of typical HARDI acquisitions. Higher b-values have been shown to introduce more orientational contrast (Tournier et al., 2007). Lower b-values can also be used for CSD restoration with some restrictions on the maximum achievable angular resolution of restoration (lmax) (Tournier et al., 2007). But b-values should not be treated in isolation. Instead, factors such as signal to noise ratio and numbers of signals in the dataset should also be considered. Crossing fibers have successfully been resolved in a number of recent HARDI studies based on data acquired with low b-values (Bouix S, 2010; Patel et al., 2010b; Tournier et al., 2007).

Conclusion

In this work, an artifact-free HARDI template of the human brain was developed from low angular resolution multiple-shot diffusion data. The resulting HARDI template was produced in ICBM-152 space, was shown to resolve complex neuronal micro-architecture in regions with intravoxel heterogeneity, and contained fiber orientation information consistent with known human brain anatomy. This template is available for download at www.iit.edu/~mri.

Acknowledgements

This work was supported by grants from the National Institute of Biomedical Imaging and Bioengineering (NIBIB) (R21EB006525), and the National Institute of Neurological Disorders and Stroke (NINDS) (R21NS076827).

Footnotes

Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.

References

  1. Adluru N, Zhang H, Fox AS, Shelton SE, Ennis CM, Bartosic AM, Oler JA, Tromp do PM, Zakszewski E, Gee JC, Kalin NH, Alexander AL. A diffusion tensor brain template for rhesus macaques. Neuroimage. 2012;59(1):306–318. doi: 10.1016/j.neuroimage.2011.07.029. [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Alexander DC, Barker GJ, Arridge SR. Detection and modeling of non-Gaussian apparent diffusion coefficient profiles in human brain data. Magn Reson Med. 2002;48:331–340. doi: 10.1002/mrm.10209. [DOI] [PubMed] [Google Scholar]
  3. Anderson AW. Measurement of fiber orientation distributions using high angular resolution diffusion imaging. Magn Reson Med. 2005;54:1194–1206. doi: 10.1002/mrm.20667. [DOI] [PubMed] [Google Scholar]
  4. Ardekani BA, Guckemus S, Bachman A, Hoptman MJ, Wojtaszek M, Nierenberg J. Quantitative comparison of algorithms for inter-subject registration of 3D volumetric brain MRI scans. J Neurosci Methods. 2005;42:67–76. doi: 10.1016/j.jneumeth.2004.07.014. [DOI] [PubMed] [Google Scholar]
  5. Arfanakis K, Gui MZ, Lazar M. White matter tractography by means of turboprop diffusion tensor imaging. Ann N Y Acad Sci. 2005;1064:78–87. doi: 10.1196/annals.1340.014. [DOI] [PubMed] [Google Scholar]
  6. Basser PJ, Mattiello J, Lebihan D. Estimation of the effective self-diffusion tensor from the NMR spin-echo. J Magn Reson B. 1994;103:247–254. doi: 10.1006/jmrb.1994.1037. [DOI] [PubMed] [Google Scholar]
  7. Basser PJ, Pierpaoli C. Microstructural and physiological features of tissues elucidated by quantitative-diffusion-tensor MRI. J Magn Reson B. 1996;111:209–219. doi: 10.1006/jmrb.1996.0086. [DOI] [PubMed] [Google Scholar]
  8. Borman S, Stevenson RL. Technical report. Notre Dame, Indiana, USA: Department of Electrical Engineering, University of Notre Dame; 1998. Spatial resolution enhancement of low-resolution image sequences: a comprehensive review with directions for future research. [Google Scholar]
  9. Bouix SRY, Sabuncu M. Med Image Comput Comput Assist Interv. Proc of the Workshop on Computational Diffusion MRI; 2010. Building an average population HARDI atlas. [Google Scholar]
  10. Caan M, Sage C, van der Graaf M, Grimbergen C, Sunaert S, van Vliet L, Vos F. Dual tensor atlas generation based on a cohort of coregistered non-HARDI datasets. Med Image Comput Comput Assist Interv. 2009;12:869–876. doi: 10.1007/978-3-642-04268-3_107. [DOI] [PubMed] [Google Scholar]
  11. Descoteaux M, Deriche R, Le Bihan D, Mangin JF, Poupon C. Multiple q-shell diffusion propagator imaging. Med Image Anal. 2011;15:603–621. doi: 10.1016/j.media.2010.07.001. [DOI] [PubMed] [Google Scholar]
  12. Duclap D, Schmitt B, Lebois A, Guevara P, Zhang H, Longo Dos Santos C, Le Bihan D, Mangin J, Poupon C. Proc Int Soc Magn Reson Med. Salt Lake City: Utah; 2013. Towards a super-resolution CONNECT/ARCHI atlas of the white matter connectivity; p. 3153. [Google Scholar]
  13. Elad M, Feuer A. Restoration of a single superresolution image from several blurred, noisy, and undersampled measured images. IEEE Trans Image Process. 1997;6:1646–1658. doi: 10.1109/83.650118. [DOI] [PubMed] [Google Scholar]
  14. Gray H. Anatomy of the human body. Philadelphia, PA: Lea & Febiger; 1918. [Google Scholar]
  15. Gui MZ, Peng HL, Carew JD, Lesniak MS, Arfanakis K. A tractography comparison between turboprop and spin-echo echo-planar diffusion tensor imaging. Neuroimage. 2008;42:1451–1462. doi: 10.1016/j.neuroimage.2008.05.066. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Hasan KM, Ewing-Cobbs L, Kramer LA, Fletcher JM, Narayana PA. Diffusion tensor quantification of the macrostructure and microstructure of human midsagittal corpus callosum across the lifespan. NMR in Biomedicine. 2008;21:1094–1101. doi: 10.1002/nbm.1286. [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Hasan KM, Parker DL, Alexander AL. Comparison of gradient encoding schemes for diffusion-tensor MRI. J Magn Reson Imaging. 2001;13:769–780. doi: 10.1002/jmri.1107. [DOI] [PubMed] [Google Scholar]
  18. Hess CP, Mukherjee P, Han ET, Xu D, Vigneron DB. Q-ball reconstruction of multimodal fiber orientations using the spherical harmonic basis. Magn Reson Med. 2006;56:104–117. doi: 10.1002/mrm.20931. [DOI] [PubMed] [Google Scholar]
  19. Jeurissen B, Leemans A, Jones DK, Tournier JD, Sijbers J. Probabilistic Fiber Tracking Using the Residual Bootstrap with Constrained Spherical Deconvolution. Hum Brain Mapp. 2011;32:461–479. doi: 10.1002/hbm.21032. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Jeurissen B, Leemans A, Tournier JD, Jones DK, Sijbers J. Investigating the prevalence of complex fiber configurations in white matter tissue with diffusion magnetic resonance imaging. Hum Brain Mapp (in print) 2012 doi: 10.1002/hbm.22099. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Kaden E, Knosche TR, Anwander A. Parametric spherical deconvolution: Inferring anatomical connectivity using diffusion MR imaging. Neuroimage. 2007;37:474–488. doi: 10.1016/j.neuroimage.2007.05.012. [DOI] [PubMed] [Google Scholar]
  22. Le Bihan D, Breton E. C. R. Acad. Sci. Vol. 15. Paris: 1985. In vivo magnetic-resonance imaging of diffusion; pp. 1109–1112. [Google Scholar]
  23. Mazziotta JC, Toga AW, Evans A, Fox P, Lancaster J. A Probabilistic Atlas of the Human Brain - Theory and Rationale for Its Development. Neuroimage. 1995;2:89–101. doi: 10.1006/nimg.1995.1012. [DOI] [PubMed] [Google Scholar]
  24. Merboldt KD, Hanicke W, Frahm J. Self-diffusion NMR imaging using stimulated echoes. J Magn Reson. 1985;64:479–486. [Google Scholar]
  25. Mori S, Oishi K, Jiang H, Jiang L, Li X, Akhter K, Hua K, Faria AV, Mahmood A, Woods R, Toga AW, Pike GB, Neto PR, Evans A, Zhang J, Huang H, Miller MI, van Zijl P, Mazziotta J. Stereotaxic white matter atlas based on diffusion tensor imaging in an ICBM template. Neuroimage. 2008;40:570–582. doi: 10.1016/j.neuroimage.2007.12.035. [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Papadakis NG, Murrills CD, Hall LD, Huang CL, Adrian Carpenter T. Minimal gradient encoding for robust estimation of diffusion anisotropy. Magn Reson Imaging. 2000;18:671–679. doi: 10.1016/s0730-725x(00)00151-x. [DOI] [PubMed] [Google Scholar]
  27. Park S, Park M, Kang M. Super-resolution image reconstruction: a technical overview. IEEE Signal Process Mag. 2003;20:21–36. [Google Scholar]
  28. Patel V, Dinov ID, Van Horn JD, Thompson PM, Toga AW. LONI MiND: metadata in NIfTI for DWI. Neuroimage. 2010a;51:665–676. doi: 10.1016/j.neuroimage.2010.02.069. [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Patel V, Shi Y, Thompson PM, Toga AW. Mesh-based spherical deconvolution: a flexible approach to reconstruction of non-negative fiber orientation distributions. Neuroimage. 2010b;51:1071–1081. doi: 10.1016/j.neuroimage.2010.02.060. [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Peng H, Orlichenko A, Dawe RJ, Agam G, Zhang S, Arfanakis K. Development of a human brain diffusion tensor template. Neuroimage. 2009;46:967–980. doi: 10.1016/j.neuroimage.2009.03.046. [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Pierpaoli C, Walker L, Irfanoglu MO, Barnett A, Basser P, Chang LC, Koay C, Pajevic S, Rohde G, Sarlls J, Wu M. Proc Int Soc Magn Reson Med. Stockholm, Sweden: 2010. TORTOISE: an integrated software package for processing of diffusion MRI data; p. 1597. [Google Scholar]
  32. Pipe JG, Zwart N. Turboprop: Improved PROPELLER imaging. Magn Reson Med. 2006;55:380–385. doi: 10.1002/mrm.20768. [DOI] [PubMed] [Google Scholar]
  33. Raffelt D, Tournier JD, Fripp J, Crozier S, Connelly A, Salvado O. Symmetric diffeomorphic registration of fibre orientation distributions. Neuroimage. 2011;56:1171–1180. doi: 10.1016/j.neuroimage.2011.02.014. [DOI] [PubMed] [Google Scholar]
  34. Schmitt B, Duclap D, Lebois A, Guevara P, Zhang H, Assaf Y, Poupon F, Riviere D, Cointepas Y, Mangin J, Poupon C. Proc Int Soc Magn Reson Med. Salt Lake City: Utah; 2013. A novel probabilistic connectivity atlas for the human connectome : the CONNECT/ARCHI atlas; p. 3155. [Google Scholar]
  35. Setsompop K, Kimmlingen R, Eberlein E, Witzel T, Cohen-Adad J, McNab JA, Keil B, Tisdall MD, Hoecht P, Dietz P, Cauley SF, Tountcheva V, Matschl V, Lenz VH, Heberlein K, Potthast A, Thein H, Van Horn J, Toga A, Schmitt F, Lehne D, Rosen BR, Wedeen V, Wald LL. Pushing the limits of in vivo diffusion MRI for the Human Connectome Project. Neuroimage. 2013;80:220–230. doi: 10.1016/j.neuroimage.2013.05.078. [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Sotiropoulos SN, Jbabdi S, Xu J, Andersson JL, Moeller S, Auerbach EJ, Glasser MF, Hernandez M, Sapiro G, Jenkinson M, Feinberg DA, Yacoub E, Lenglet C, Van Essen DC, Ugurbil K, Behrens TE. Advances in diffusion MRI acquisition and processing in the Human Connectome Project. Neuroimage. 2013;80:125–143. doi: 10.1016/j.neuroimage.2013.05.057. [DOI] [PMC free article] [PubMed] [Google Scholar]
  37. Sullivan EV, Pfefferbaum A. Diffusion tensor imaging and aging. Neurosci Biobehav Rev. 2006;30:749–761. doi: 10.1016/j.neubiorev.2006.06.002. [DOI] [PubMed] [Google Scholar]
  38. Tournier JD, Calamante F, Connelly A. Robust determination of the fibre orientation distribution in diffusion MRI: non-negativity constrained super-resolved spherical deconvolution. Neuroimage. 2007;35:1459–1472. doi: 10.1016/j.neuroimage.2007.02.016. [DOI] [PubMed] [Google Scholar]
  39. Tournier JD, Calamante F, Connelly A. MRtrix: Diffusion tractography in crossing fiber regions. Int J Imaging Syst Technol. 2012;22:53–66. [Google Scholar]
  40. Tuch DS. Q-Ball imaging. Magn Reson Med. 2004;52:1358–1372. doi: 10.1002/mrm.20279. [DOI] [PubMed] [Google Scholar]
  41. Tuch DS, Reese TG, Wiegell MR, Makris N, Belliveau JW, Wedeen VJ. High angular resolution diffusion imaging reveals intravoxel white matter fiber heterogeneity. Magn Reson Med. 2002;48:577–582. doi: 10.1002/mrm.10268. [DOI] [PubMed] [Google Scholar]
  42. Van Hecke W, Sijbers J, D'Agostino E, Maes F, De Backer S, Vandervliet E, Parizel PM, Leemans A. On the construction of an inter-subject diffusion tensor magnetic resonance atlas of the healthy human brain. Neuroimage. 2008;43:69–80. doi: 10.1016/j.neuroimage.2008.07.006. [DOI] [PubMed] [Google Scholar]
  43. Varentsova A, Zhang S, Arfanakis K. Proc Int Soc Magn Reson Med. Salt Lake City: Utah; 2013. Probabilistic Atlas of the Adult Human Brain White Matter; p. 2128. [Google Scholar]
  44. Wang Y, Gupta A, Liu Z, Zhang H, Escolar ML, Gilmore JH, Gouttard S, Fillard P, Maltbie E, Gerig G, Styner M. DTI registration in atlas based fiber analysis of infantile Krabbe disease. Neuroimage. 2011;55:1577–1586. doi: 10.1016/j.neuroimage.2011.01.038. [DOI] [PMC free article] [PubMed] [Google Scholar]
  45. Wedeen VJ, Wang RP, Schmahmann JD, Benner T, Tseng WY, Dai G, Pandya DN, Hagmann P, D'Arceuil H, de Crespigny AJ. Diffusion spectrum magnetic resonance imaging (DSI) tractography of crossing fibers. Neuroimage. 2008;41:1267–1277. doi: 10.1016/j.neuroimage.2008.03.036. [DOI] [PubMed] [Google Scholar]
  46. Yap PT, Chen Y, An H, Yang Y, Gilmore JH, Lin W, Shen D. SPHERE: SPherical Harmonic Elastic REgistration of HARDI data. Neuroimage. 2011;55:545–556. doi: 10.1016/j.neuroimage.2010.12.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
  47. Yeh FC, Tseng WY. NTU 90: a high angular resolution brain atlas constructed by q-space diffeomorphic reconstruction. Neuroimage. 2011;58:91–99. doi: 10.1016/j.neuroimage.2011.06.021. [DOI] [PubMed] [Google Scholar]
  48. Zhang H, Yushkevich PA, Alexander DC, Gee JC. Deformable registration of diffusion tensor MR images with explicit orientation optimization. Med Image Anal. 2006;10:764–785. doi: 10.1016/j.media.2006.06.004. [DOI] [PubMed] [Google Scholar]
  49. Zhang H, Yushkevich P, Rurckert D, Gee J. Proc Int Soc Magn Reson Med. Honolulu, Hawaii; 2009. A computational DTI template for aging studies; p. 3230. [Google Scholar]
  50. Zhang S, Peng H, Dawe RJ, Arfanakis K. Enhanced ICBM diffusion tensor template of the human brain. Neuroimage. 2011;54:974–984. doi: 10.1016/j.neuroimage.2010.09.008. [DOI] [PMC free article] [PubMed] [Google Scholar]

RESOURCES