Inference of the Genetic Architecture Underlying BMI and Height with the Use of 20,240 Sibling Pairs

Abstract

Evidence that complex traits are highly polygenic has been presented by population-based genome-wide association studies (GWASs) through the identification of many significant variants, as well as by family-based de novo sequencing studies indicating that several traits have a large mutational target size. Here, using a third study design, we show results consistent with extreme polygenicity for body mass index (BMI) and height. On a sample of 20,240 siblings (from 9,570 nuclear families), we used a within-family method to obtain narrow-sense heritability estimates of 0.42 (SE = 0.17, p = 0.01) and 0.69 (SE = 0.14, p = 6 × 10⁻⁷) for BMI and height, respectively, after adjusting for covariates. The genomic inflation factors from locus-specific linkage analysis were 1.69 (SE = 0.21, p = 0.04) for BMI and 2.18 (SE = 0.21, p = 2 × 10⁻¹⁰) for height. This inflation is free of confounding and congruent with polygenicity, consistent with observations of ever-increasing genomic-inflation factors from GWASs with large sample sizes, implying that those signals are due to true genetic signals across the genome rather than population stratification. We also demonstrate that the distribution of the observed test statistics is consistent with both rare and common variants underlying a polygenic architecture and that previous reports of linkage signals in complex traits are probably a consequence of polygenic architecture rather than the segregation of variants with large effects. The convergent empirical evidence from GWASs, de novo studies, and within-family segregation implies that family-based sequencing studies for complex traits require very large sample sizes because the effects of causal variants are small on average.

Introduction

Widely regarded as a growing epidemic,¹ obesity is known to be a precursor to social^2,3 and psychological⁴ problems, as well as a plethora of physiological conditions.⁵ Managing such a problem requires knowledge of the genetic and environmental contributors to the disease. Body mass index (BMI), a commonly used proxy for quantifying obesity, predicts the risk of consequential etiology.⁶ In addition to accurately estimating the heritability $\left(h^2\right)$ of BMI, understanding the genetic architecture that belies genetic variation is also of major importance for gene-mapping strategies, drug development, epidemiology, and the future of genomic medicine. In this paper, we infer the genetic architecture of BMI and height through calculating heritability, the relative contribution of rare and common variants, and the extent to which these traits are polygenic. Crucially, we make inferences by using within-family identity-by-descent (IBD) estimation because methods using this framework are neither prone to confounding due to population stratification nor dependent upon strong modeling assumptions.

One reason that knowledge of a trait’s underlying genetic architecture is important is that it might dictate the optimal study design for detecting genetic variants. Clues about the relative contribution of rare and common variants can be leveraged from information between estimates of $h^2$ and the estimation of “chip heritability” ($h_C^2$, the proportion of phenotypic variation captured by SNPs on a SNP chip). The chip heritability of BMI is estimated to be much lower for BMI $\left(h_C^2=0.17\right)$ ⁷ than for height $\left(h_C^2=0.45\right)$.^7–10 Supposing that BMI and height had similarly large true heritabilities (as is often shown from twin studies),^11,12 given that SNP chips capture the effects of common variants better than the effects of rare variants,⁸ we might infer a larger contribution of rare variants influencing BMI. However, previous heritability estimates for BMI have varied enormously.¹³ Indeed, based on a recent review,¹¹ a meta-analysis of 81 twin studies led to an estimate of 0.75, whereas a meta-analysis of 25 non-twin family-based studies, performed on sample sizes in the low thousands, gave an estimate of 0.46. Conversely, with estimates typically in the range of 0.7–0.9, pedigree studies on the heritability of height are more consistent with twin-based studies.^12,14

To date, far more variants have been discovered to be robustly associated with height than with BMI, even though similar samples size have been used.^15,16 One possible explanation for this is a difference in heritability. For example, if we assume the same number of genetic variants for both traits, the average effect size will be smaller in BMI if its heritability is lower, and therefore power will be reduced for the same sample size. Power is proportional to the square of the effect size, so if effect sizes are on average halved, then four times the sample size is required for detection. Alternatively, causal variants for BMI could be at lower frequencies in the population than those for height, also leading to decreased power in genome-wide association studies (GWASs) as a result of reduced linkage disequilibrium (LD) between causal variants and genotyped SNPs. It is important to distinguish between these hypotheses because it quantifies how much variation has not yet been accounted for by past experimental designs.

Here, using a method developed to avoid dependence on modeling assumptions regarding between-family variance by using the realized genetic sharing between siblings¹⁷ to estimate heritability, we report heritability estimates of 0.42 for BMI and 0.69 for height on a sample of 20,240 quasi-independent sibling pairs (QISPs). This is at the lower end of the scale of previous estimates and is consistent with estimates resulting from family-based studies. Using within-family IBD methods, we also demonstrate, while being agnostic about allele frequencies, that there is strong evidence of extreme polygenicity in BMI and height. We demonstrate how the consequence of this finding can explain why linkage analyses of complex traits over the past two decades seldom replicate.^18,19 Finally, we use these data to provide empirical evidence that genomic inflation (the overall elevation of test statistics across all loci) increases with increased sample size as a result of polygenic variation. This is an important finding that forecasts that, even after adequate correction for population stratification, genomic inflation in very large association studies is likely to occur when real genetic signals are enriched as a result of increasing power with increasing sample size.¹⁵

Material and Methods

Genotyping and Phenotyping

From five separate cohorts, we collected 20,240 QISPs who had data on dense (minimum 300,000) SNP genotypes, height measurements, weight measurements, age at time of measurements, and gender. The term “quasi-independent” refers to the fact that although there was often more than one sibling pair per family, each sibling pair was treated as independent. Extensive descriptions of each cohort have been provided previously, and they are summarized in Table S1, available online. In brief, we obtained 9,585 QISPs from the Queensland Institute of Medical Research (QIMR),²⁰ 4,607 from the Framingham Heart Study,²¹ 2,722 from the Swedish Twin Registry’s TWINGENE data set,^22,23 1,819 from the Netherland Twin Registry,^24,25 and 1,507 from the UK Twin Registry’s TWINSUK data set.²⁶

All individuals in the study were of European ancestry and over the age of 18 years old. BMI and height were adjusted with a linear model for a number of covariates (see Table S2). BMI was also adjusted for between-sex variance. Clinical or self-reported measurements of height and weight were used for calculating BMI by means of the standard formula of raw weight values (kg) over the square of raw height values (m). The data-collection procedures followed were in accordance with the ethical standards of the respective responsible committees on human experimentation (institutional and national), and proper informed consent was obtained.

Heritability Estimates

Marker-level IBD was calculated for each QISP with the Merlin software package²⁷ (see volta plots, Figure S1). For each of the five cohorts, we selected full siblings and dizygotic twins and pruned SNPs so that LD was constrained to r² < 0.05 to ensure that markers used for estimating IBD were in linkage equilibrium. Minor allele frequency was greater than 0.2 for maximizing information from the retained SNPs, leaving approximately 20,000 SNPs per cohort (Table S1). As can be seen in Figure S1, this SNP density was sufficiently high to produce accurate estimates of IBD. Subsequently, chromosome-wide IBD was calculated by approximate integration over the marker-wise IBD status for all markers across a chromosome on the basis of their genetic position:

$${\hat{\theta }}_j=\sum _{i\le m}^{i=1}\frac{1}{2}{d}_{i,i+1}\left(x_i+x_{i+1}\right),$$

where $d_{i,i+1}$ is the genetic distance between marker $i$ and $i+1$ and $x_i$ is the estimate of IBD status at marker $i$.

Subsequently, genome-wide IBD, $\hat{\theta }$, was estimated as

$$\hat{\theta }=\frac{1}{L}\sum _{j\le 22}^{j=1}{l}_j{\hat{\theta }}_j,$$

where $l_j$ is the genetic length of chromosome $j$ and $L=\sum l_j$. The genome-wide IBD matrix between QISPs was constructed as a block diagonal $2n\times 2n$ matrix (A), where $n$ is the number of QISPs, and each block was a $2\times 2$ diagonal matrix with off-diagonal elements being ${\text{θ}}_i$ coefficients for the $i^{\text{th}}$ QISP. The common-environment matrix (C) was also $2n\times 2n$ with $2\times 2$ diagonal blocks whose off-diagonal elements fixed to 1. The phenotype was then modeled with linear mixed models of the form

$$y=\text{Xβ}+g+w+e,$$

where y is the vector of phenotypes, X is the design matrix of fixed effects, β is the estimate of fixed effects, $g$ is the vector of genetic values, $w$ is the vector of common environmental effects, and $e$ is the vector of residual values. The genetic variance was calculated as ${\text{σ}}_{\text{A}}^2=\text{var}\left(g\right)$ and $h^2={\text{σ}}_{\text{A}}^2/{\text{σ}}_P^2$, where ${\text{σ}}_P^2$ is the phenotypic variance. The partitioning of heritability estimates across chromosomes was achieved by the construction of genetic-relationship matrices $\left({\text{A}}_j\right)$ for each chromosome $\left(j\right)$ from chromosome-wide IBD estimates $\left({\hat{\theta }}_j\right)$ and then via a joint analysis of the form

$$y=\text{Xβ}+\sum _{j\le 22}^{j=1}{g}_j+w+e.$$

These variance components can be calculated in 22 separate models or in a single model comprising 22 components (each model also fits C). The correlation between the $h^2$ estimates of each chromosome from these two approaches was high (r = 0.98), as would be expected given that the chromosome-wide IBD values were uncorrelated. All restricted maximum likelihood (REML) estimates were performed with the GCTA software package.²⁸

Simplifying the sibling relationship structure into QISPs instead of having a block diagonal structure where each block represents the siblings in one family is computationally more efficient with the use of very large sample sizes and has now been implemented as an option (–reml-wfam) in GCTA. Using simulation, we showed that the estimates remain unbiased (Figure S2).

Linkage Analysis

IBD estimates at a 0.1 cM grid were obtained for each sibling pair with the Merlin software package,²⁷ and linkage analysis was performed directly from these estimates. We used the Visscher-Hopper (VH) method^29,30 to regress IBD estimates because it is a good approximation of the maximum-likelihood variance-component method implemented in Merlin (Figure S3). In brief, the VH method performs a within-locus meta-analysis for linkage tests performed with two orthogonal similarity metrics, the sum of squares of the difference in phenotypes, and the sum of squares of the sum of phenotypes between the siblings. Because it has been demonstrated to improve power in linkage analysis,³¹ 246 and 254 QISPs were excluded for having $p_D>{\overline{p}}_D+4\text{SD}\left(p_D\right)$, where $p_D$ is the squared difference of the sibling phenotypes, for BMI and height, respectively.

Meta-analysis

The linkage analysis can be performed as described above with the use of all 20,240 QISPs or via a meta-analysis from the summary statistics of linkage analyses performed on each cohort separately. For a particular genetic position, the effect can be calculated as

$${\mathrm{\beta }}_M=\frac{\sum \frac{{\mathrm{\beta }}_k}{s_k^2}}{\sum \frac{1}{s_k^2}},$$

for which the SE is

$$s_M=\frac{1}{\sum \frac{1}{s_k}},$$

where $k=\left\{1\dots 5\right\}$ represents each cohort. The strong correlation between the meta-analysis and the combined analysis (Figure S4) is evidence that linkage signals are of genetic origin.

Permutations

Permutation analysis is a useful approach for developing a threshold that allows for nonindependence between multiple tests.³² In this instance, we performed permutations for each trait to generate thresholds to demonstrate that LOD scores from the linkage analysis were more extreme than expected under the null model of no genetic variation. For each permutation, pairwise elements of the arrays of $y_1$ and $y_2$ were shuffled together, such that the pairs of sibling phenotypes remained the same but no longer corresponded to their IBD values. Then the entire linkage analysis was performed with the permuted phenotypes, where we no longer expected a biological link between genotype and phenotype. This was performed 500 times for each trait.

Simulations

The outcome of the linkage analysis showed that there were LOD scores exceeding traditional thresholds, as well as elevated LOD scores across the genome. We performed simulations to understand what kind of genetic architecture might manifest such a result, whereby we used the genotypes used for calculating IBD in the 20,240 siblings to simulate phenotypes representative of a range of different architectures.

By changing the distribution of effects of common SNPs across the genome, we generated different models. The simulations were performed with all LD-pruned SNPs. Phenotypes were simulated such that every SNP had a background effect sampled from either distribution A, ${\mathrm{\beta }}_{\text{A}}\sim N\left({\mathrm{\mu }}_{\text{A}},{\mathrm{\sigma }}_{\text{A}}^2\right)$, or distribution B, ${\mathrm{\beta }}_{\text{B}}\sim N\left({\mathrm{\mu }}_{\text{B}},{\mathrm{\sigma }}_{\text{B}}^2\right)$. For example, using this framework, if we were to simulate one quantitative trait locus (QTL) per chromosome, then ${\mathrm{\sigma }}_{\text{A}}=0$ and ${\mathrm{\sigma }}_{\text{B}}=1$, where one SNP is selected at random from each chromosome to be a QTL and has an effect sampled from distribution B. For simulating a uniform polygenic effect, ${\mathrm{\sigma }}_{\text{A}}=1$ and ${\mathrm{\sigma }}_{\text{B}}=0$ such that each SNP has an effect. For simulating clustering of effects, ${\mathrm{\sigma }}_{\text{A}}=0$ and ${\mathrm{\sigma }}_{\text{B}}=1$, and SNPs falling under distribution B are chosen such that there are on average p cM between regions for an effect drawn from distribution B and each region is $q$ cM in length. In this case, p = 50 and q = 5 (results of the simulations are insensitive to the values chosen for parameters p and q [data not shown]). An example of the distribution of SNP effects can be seen in Figure S5. From the $n\times m$ dimensional matrix X, where $n$ is the number of individuals, $m$ is the number of SNPs with an effect, and each element ${\text{X}}_{ij}\in \left\{0,1,2\right\}$ represents the number of minor alleles for individual i at SNP j, genetic scores were produced for each individual i as

$$G_i=\sum {\mathrm{\beta }}_j{\text{X}}_{ij}.$$

The rare-effect models assumed that a single SNP was responsible for the entire genetic variance within a family without occurring in any other individuals in the population. Thus, for each SNP, $E\left(V_G\right)=h^2/20,240$. For simulating a uniform polygenic model, a SNP $j$ was chosen at random from the panel of ∼20,000 SNPs for each of the 20,240 QISPs, and thus for an individual in QISP $i^{\ast }$, his or her genetic score was defined simply as

$$G_{i^{\ast }}={\mathrm{\beta }}_{i^{\ast }}\left({\text{X}}_{i^{\ast }j}-{\overline{\text{X}}}_j\right)/{\text{σ}}_j.$$

For simulating a rare model with clustered genetic effects, SNPs across the genome were sampled with nonuniform probabilities, such that there were on average $p$ cM between regions with length $q$ cM and these regions were given a 10× higher probability of being sampled than any other regions. In this case, the values were set to p = 50 and q = 5.

Genetic scores were generated within cohorts, and then final phenotypes were produced after individuals from all cohorts were combined. Nongenetic variance was simulated by the sampling of $e_i\sim N\left(0,V_E\right)$, where $V_E=\left(V_G/h^2\right)-V_G$.

For each model detailed above, simulations were performed for $h^2=\left\{0.42,0.69\right\}$. Simulations were performed for each of the five cohorts and for the combined sample. Each model × h² × n combination was repeated 500 times.

A Note on Within-Family Analysis

Full details on the use of within-family analysis and its advantages are outlined elsewhere,^17,33 but a brief explanation follows. Given that siblings are phenotypically correlated, one can ask, “Of the phenotypic similarity of two siblings, what proportion is attributed to the actual genomic proportion that they share by descent”? If a trait is heritable, then sibling pairs who have higher-than-average genome-wide IBD will be phenotypically more similar to each other. This is in essence equivalent to a linkage analysis, but in this case we use genome-wide IBD instead of IBD at a particular locus. We obtain a realized estimate of the total amount of genetic similarity between siblings through direct calculation of genome-wide IBD. Thus, in our ACE model, the phenotypic similarity between siblings is partitioned into a proportion of this covariance that is captured by the realized genome-wide IBD between siblings (in the A component) and a proportion that is not (C). In the extreme case that none of the sibling phenotypic correlation can be explained by genome sharing by descent, the A component would be zero and the C component would reflect the observed phenotypic similarity. Conversely, if all phenotypic correlation between siblings can be explained by how much of their genome is shared by descent, then the C component would be zero.

The only information that can contribute to the A component is the realized genome-wide IBD between siblings, and because this is simply determined by random recombination events at meiosis, it is immune to confounding from population stratification. Unlike other experimental designs, this approach requires no assumptions regarding the common environmental structure of complex pedigrees, and cohort-specific effects will be uncorrelated with realized genome-wide IBD estimates. We performed two simulations to demonstrate this.

The purpose of the first simulation was to demonstrate that, unlike association studies, within-family linkage analysis is immune to population stratification. We simulated an extreme case of population stratification in 20,000 QISPs from our five different cohorts; h² was set to 0 (no genetic effects), sibling correlation was set to r = 0.3, and a large cohort effect was simulated, which explained 20% of phenotypic variance. We then performed genome-wide linkage analysis as previously described. In association studies, any ancestry-informative loci between cohorts would be correlated with the cohort effect, leading to spurious association signals and therefore a genomic-inflation factor (also known as a genomic-control [GC] factor, λ_GC) significantly greater than 1. However, because the cohort effect was uncorrelated with the sibling IBD estimate, we observed no genomic inflation with the within-family linkage design (100 replicates, mean(λ_GC) = 1.02, SE(λ_GC) = 0.015, p = 0.11, Figure S6).

The purpose of the second simulation was to demonstrate that genetic heterogeneity between cohorts does not lead to biased heritability estimates, nor does it lead to genomic inflation in a within-family linkage analysis. Using 20,000 QISPs from five different cohorts and ∼20,000 LD-pruned SNPs, we simulated phenotypes such that each genetic effect was present in only one cohort. To do this, we constructed the phenotypes by simulating genetic effects at every SNP on chromosomes 1, 6, 11, 16, and 21 for individuals in the Framingham cohort, on chromosomes 2, 7, 12, 17, and 22 for the TWINGENE cohort, on chromosomes 3, 8, 13, and 18 for the TwinsUK cohort, on chromosomes 4, 9, 14, and 19 for the Netherlands Twin Registry cohort, and on chromosomes 5, 10, 15, and 20 for the QIMR cohort. Genetic effects were then scaled such that the phenotypes for each cohort had the same heritability. This simulation represents the most extreme form of genetic heterogeneity through genotype-cohort interaction. Empirical heritability estimates of the simulated phenotypes were obtained for 100 replicates for each simulated value of h² = {0, 0.25, 0.5, 0.75, 1}. We observed unbiased estimates from these simulations (Figure S7), as expected from a within-family design. We also performed a linkage analysis for each simulated phenotype for each individual cohort and also for the cohorts combined. Because there was no overlap of genetic effects between cohorts, combining the data did not lead to increased genomic inflation (Figure S8).

Despite its advantages for genetic analysis, it is important to note that the main drawback of using a within-family design is its dependence on very large sample sizes. This is because the SD of IBD sharing is relatively small (e.g., ∼0.037 for full siblings), and therefore large sample sizes are required for obtaining precise estimates.

Results

Heritability Estimates for Height and BMI

Theory predicts that the expected proportion of alleles shared identically by descent between siblings has a mean of 0.5 and a SD of 0.039.¹⁷ We used ∼20,000 SNPs in linkage equilibrium to estimate IBD for 20,240 sibling pairs from 9,577 nuclear families and obtained a SD of 0.037 (Figure S9). Because there is variation around the expected value of 0.5, we could relate the proportion of phenotypic similarity to the amount of genetic similarity between siblings. We partitioned phenotypic variance of BMI and height in additive genetic (A), common environment (C), and specific environment (E) variance components to apportion phenotypic variance into genetic and nongenetic causes. Considering that the variance for BMI is larger in females than in males, we adjusted BMI for a number of covariates (Table S2) in two gender groups separately. Height was also adjusted for the covariates in Table S2. Heritability was then estimated with REML,²⁸ giving h² = 0.42 (SE 0.17) for BMI and 0.69 (SE 0.14) for height (Table 1). Because age of measurement has a significant effect on BMI, the inclusion of siblings who were measured at different ages might have reduced the heritability estimate because they had a lower correlation (Figure S10). We calculated the heritability for BMI on 17,039 QISPs who were measured within 10 years of each other, resulting in h² = 0.35 (SE 0.18), demonstrating that a possible age by genotype interaction does not cause a deflation of h².

Table 1.

Summary of Estimates of BMI and Height Heritabilities from Realized Relationships for All Cohorts

Cohort	QISPs	r	h2(SE)	c2(SE)	ra	h2(SE)b	c2(SE)c
QIMR	9,585	0.26	0.76 (0.20)	0.00 (0.10)	0.39	0.80 (0.22)	0.00 (0.10)
Framingham Heart study	4,607	0.30	0.00 (0.34)	0.27 (0.17)	0.47	0.72 (0.28)	0.10 (0.14)
TWINGENE	2,722	0.24	0.00 (0.47)	0.24 (0.24)	0.50	0.75 (0.35)	0.12 (0.18)
Netherlands Twin Registry	1,819	0.37	0.78 (0.47)	0.00 (0.23)	0.48	0.00 (0.42)	0.49 (0.22)
TwinsUK	1,507	0.41	0.31 (0.55)	0.25 (0.28)	0.54	0.56 (0.46)	0.26 (0.23)
Total	20,240	0.29	0.42 (0.17)	0.10 (0.08)	0.44	0.69 (0.14)	0.08 (0.07)

^aCorrelation between phenotypes of QISPs after adjustment for fixed effects.

^bHeritability estimates.

^cProportion of the phenotypic variance attributed to common environmental variance.

Under a polygenic model of genetic architecture, we expect the heritability contribution of a chromosome to be proportional to its size.^7,33 We quantified this by partitioning the genetic variation, such that for each chromosome, a variance component was composed from the respective chromosome-wide coefficients of IBD sharing. Figure S11 shows a positive relationship between chromosome size and genetic variance for height (r = 0.38, p = 0.049) and BMI (r = 0.08, p = 0.469). The lack of statistical significance for BMI is expected even under the assumption that the association is real because a lower heritability combined with larger sampling variance of IBD coefficients for individual chromosomes entails larger SEs.¹⁷

Polygenic Variation Causes Genomic Inflation in Linkage Studies

Using these data, we were able to perform a linkage study on both height and BMI. We constructed quantile-quantile (Q-Q) plots of the test statistics for BMI and height and observed increasing genomic-inflation factors (λ_GC) as sample size increased (Figure 1, Figure 2, and Figure S12). For the combined analysis, λ_GC = 1.65 and 2.18 for BMI and height, respectively. The lower inflation of test statistics for BMI than for height is consistent with the fact that BMI has a lower heritability. The inflation of test statistics in population-based studies such as GWASs could arise from either truly associated variants or population stratification.³⁴ However, because within-family analysis depends only on the degree of genetic sharing among siblings, all signals from this linkage analysis must necessarily be of genetic origin. We also observed that the linkage results from the combined data set shown here were consistent with a meta-analysis performed on separate linkage analyses of the five independent cohorts (Figure S4), ruling out variance heterogeneity between cohorts as a source of test-statistic inflation.

Figure 1.

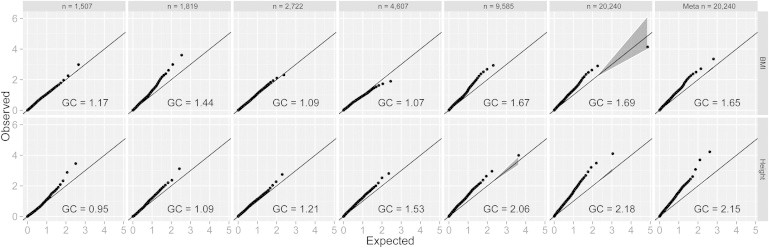
Q-Q Plots of Linkage Analyses

For each cohort (left five panels), as well as the combined data set and the p values from the meta-analysis (the two right-most panels), Q-Q plots were produced for both BMI (top) and height (bottom) to demonstrate overall genomic inflation as being a departure from the expectation (x = y line). 95% confidence intervals are shaded in gray, and GC values for each cell represent genomic inflation. Markers are pruned to be 20 cM apart for reducing correlations between tests (for Q-Q plots on all markers, see Figure S12). From left to right, cohorts are TwinsUK, Netherlands Twin Registry, TWINGENE, Framingham, and QIMR. The sixth panel (n = 20,240) shows the results from the combined analysis, and the seventh panel represents the meta-analysis of all five cohorts.

Figure 2.

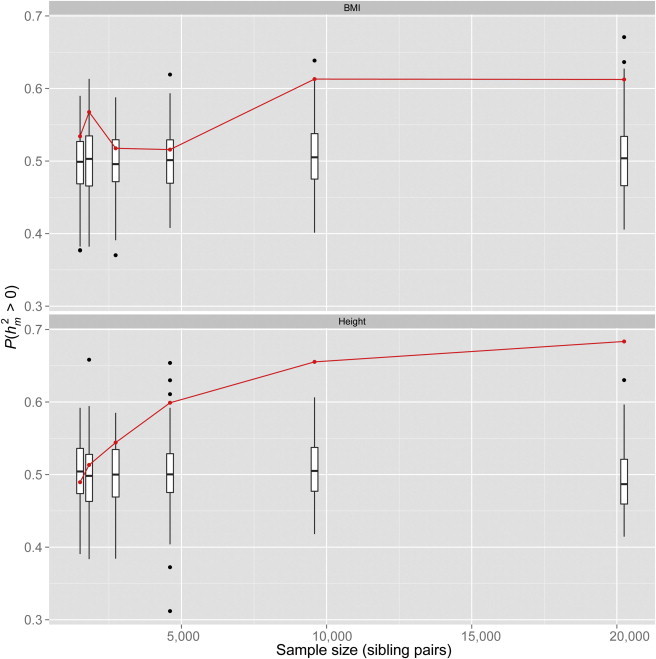
Proportion of Markers with Positive Heritability Estimates $P\left(h_m^2>0\right)$

For each cohort (five bars to the left) and for the combined sample set (bar furthest to the right), an independent permutation analysis was performed such that the entire family of tests was rerun with QISP phenotypes randomly relabeled from QISP genomic IBD scores. Thus, each box-and-whisker plot represents the distribution of $P\left(h_m^2>0\right)$ values from the 100 permutations per cohort; red points represent the $P\left(h_m^2>0\right)$ achieved in the true linkage scans.

To explore the possible genetic architecture behind this genomic inflation, we used the genetic data from the 20,240 QISPs to simulate phenotypes by using different underlying models of genetic architecture. Polygenic models of evenly distributed variants or clustered variants, as well as an oligogenic model (one QTL per chromosome), were tested and generated with the use of either common or rare variants (Figure S5). We recorded two measurements per simulation, the proportion of loci with heritability estimates greater than zero, $P\left(h_m^2>0\right)$, and the maximum LOD score from each simulation. Under the null hypothesis of no genetic variation, we expect $P\left(h_m^2>0\right)=0.5$ because the sampling variance of $h_m^2$ estimates about zero is symmetric. Our original linkage scan gave results of 0.61 (empirical SE = 0.04, p = 0.006) for BMI and 0.68 (SE = 0.04, p = 1.6 × 10⁻⁵) for height (Figure 2 and Figure S13). The results from the simulation study, shown in Figure 3, demonstrate that these values are consistent with expectations from polygenic models when sample size gets sufficiently large. We observed no difference between linkage results for different simulated polygenic models and those from the actual linkage analysis on BMI and height.

Figure 3.

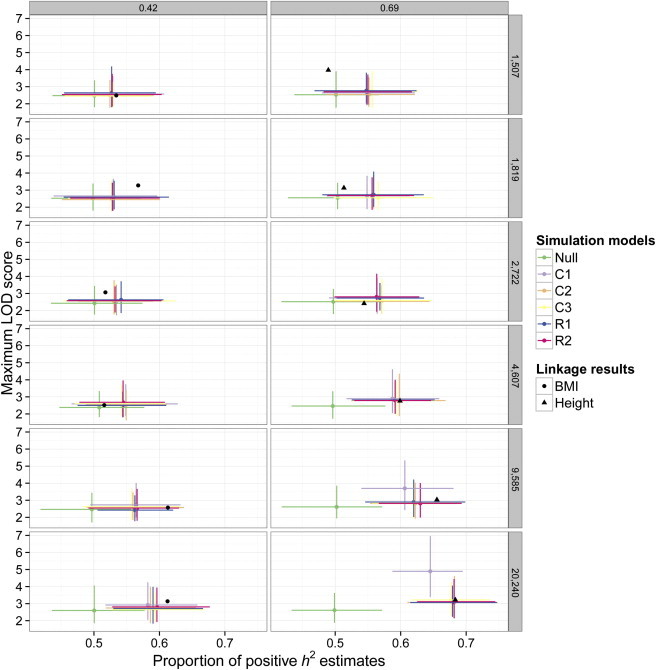
Simulations of Genetic Effect Models

Expected results for various polygenic models are compared to observed results from true linkage analyses. Maximum LOD scores (y axis) from linkage scans are plotted against $P\left(h_m^2>0\right)$ (x axis). Rows of panels correspond to sample sizes, representing different cohort sizes (top five rows) and the combined data set (bottom row). Columns of panels correspond to simulated h²; the left column represents BMI, and the right column represents height. Each model × sample size × heritability combination was replicated 100 times, and error bars represent 95% confidence intervals. Genetic models are as follows: Null, no genetic effects; C1, oligogenic where a single common QTL exists per chromosome; C2, polygenic with common SNPs uniformly distributed throughout the genome; C3, polygenic with common SNPs clustering across the genome; R1, polygenic with rare SNPs uniformly distributed throughout the genome; and R2, polygenic with rare SNPs clustering across the genome. It is shown that different polygenic architectures have nearly identical properties in linkage analysis and that they are consistent with the results for BMI and height.

Polygenic Variation Creates the Illusion of Large Effects in Linkage Studies

QTLs discovered for complex traits through linkage studies have a long history of poor replication rates in independent samples,¹⁸ and this might provide evidence of an underlying polygenic architecture. Using the traditional genome-wide threshold of LOD = 3.0, our linkage analysis detected one significant region for BMI (chromosome 20) and two for height (chromosomes 5 and 15), but these were not significant at the more stringent threshold of LOD = 3.3³⁵ (Figure 4 and Figure S14). We confirmed by permutation analysis³² that these linkage peaks were genome-wide significant when tested against the null model of no genetic variation anywhere in the genome (p < 0.05) (Figure S15). Using the polygenic simulation results, we then derived empirical significance thresholds under the null model of underlying polygenic variation (Figure S16). At these thresholds, the linkage peaks were not significant at the experiment-wide level (p = 0.21 for BMI and 0.18 for height, Figure 4).

Figure 4.

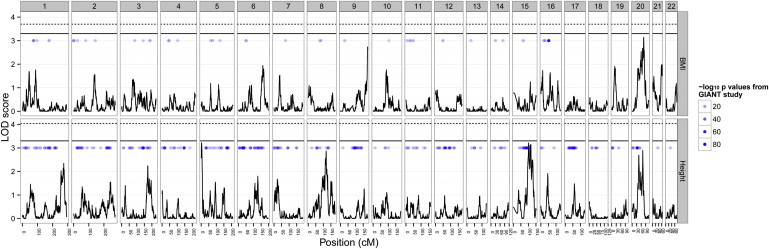
Linkage Analysis for BMI and Height

LOD scores for BMI across all autosomes are shown on the top row, and height is shown on the bottom row. The traditional threshold of LOD = 3.3 is depicted by solid lines, and the more stringent empirical threshold based on simulations of polygenic models is shown by dotted lines (α = 0.05, see Figure S16). Blue points represent GWAS hits from the GIANT study (different shades of blue correspond to different log₁₀ p values). There is no correlation between linkage signals and GWAS signals (Figure S18).

Association studies have not previously reported significant signals on chromosome 20 for BMI,³⁶ whereas numerous reports of weak signals from linkage studies have implicated almost the entire genome³⁷ (including chromosome 20³⁸) to have some involvement (Figure S17). Our simulations indicate that under a polygenic model of genetic architecture, where no large effect exists, we expect to find signals of LOD > 3.3 at experiment-wide error levels of α = 0.12 and α = 0.20 for BMI and height, respectively. Moreover, at the more traditionally used threshold of LOD = 3.0, we expect error levels of α = 0.20 and α = 0.32 for BMI and height, respectively. This is evidence that the observation of seemingly large effects in linkage studies is actually more likely to be a property of a highly polygenic underlying architecture.

Discussion

How we design future studies to uncover genetic variants will depend on the underlying genetic architecture of the trait in question.³⁹ There is mounting evidence that many of the traits that we call complex are highly polygenic. One example is from GWASs, where robustly associated common variants are increasingly found for BMI and height as the sample size increases, suggesting that there exist many variants of small effect for these traits.^15,16 It is possible to use results from such studies to estimate the total number of variants contributing to the trait’s genetic variance.^40–42 Another line of evidence comes from sequencing studies, where it has been shown that an increase in de novo mutations leads to an increased risk of schizophrenia and autism, indicating a large mutational target across the genome.^43,44 In this study, we present evidence of polygenicity from the observed genome-wide inflation of BMI and height test statistics that are free from confounding.

Heritability estimates for height are relatively consistent across studies and between different experimental designs. However, the estimates of heritability for BMI vary widely; on average, they are reported to be 0.75 in twin-based studies and 0.46 in non-twin pedigree studies.¹¹ All pedigree designs rely on inference from the resemblance between relatives and therefore depend on modeling assumptions,^45–47 such as the extent of shared environmental factors between different types of relatives. Here, we used a method that utilizes the realized sharing of genetic variation between siblings to avoid any dependence on modeling assumptions¹⁷ to estimate heritability of BMI and height from 20,240 QISPs at 0.42 (SE = 0.17, p = 0.01) and 0.69 (SE = 0.14, p = 6 × 10⁻⁷), respectively. A recent study using IBD estimates derived from long-range phased genotype data in an extended genealogy also reported estimates of h² = 0.42 for BMI and 0.69 for height, further supporting that h² for BMI and height was likely to be overestimated in previous twin and family studies.⁴⁸

From these results, we can make some inference on the relative contribution of rare and common variants to BMI. “Chip heritability” estimates $\left(h_c^2\right)$, the proportion of phenotypic variance explained by common SNPs, are typically much lower in BMI than in height. The discrepancy between $h_c^2$ and $h^2$ is likely to arise when causal variants and observed SNPs are in insufficient LD, hypothesized to be caused in part by the difference in allele-frequency distributions between the causal variants and the observed SNPs.⁸ For example, from our estimate of heritability for height, the ratio $h_c^2/h^2=0.46/0.69=0.67$ suggests that rare variants contribute relatively little to the genetic variance for height,⁸ given that only one-third of heritability is missing. However, $h_c^2=0.17$ ⁷ for BMI, and because previous $h^2$ estimates have been variable,^11,13 the variance proportion that is said to be missing is not easily determined. Under the assumption that the heritability of BMI is approximately the same as that of height, then a substantial proportion $\left(1-\left(0.17/0.69\right)=0.75\right)$ of the genetic variance is not captured by common SNPs. However, in this study we report an estimate of $h^2=0.42$ for BMI, which falls at the lower end of the range of previous estimates. This suggests that the role of rare variants might be of lesser importance for BMI than was previously suggested⁷ (i.e., $\left(0.17/0.42\right)=0.40$ of the variance is captured by common SNPs). An important consequence of this finding is that association studies for BMI are likely to have lower power to identify causal variants than are equally sized studies for height where the heritability is higher. Recent results from large-scale meta-analyses support this conclusion (32 associations in BMI versus 180 in height in similarly sized studies⁴⁹).

Our study also provides an interpretation of the past two decades of linkage studies. Linkage analysis has a long history of reporting significant signals (given traditional thresholds of LOD = 3.0⁵⁰ or 3.3³⁵) that mostly fail to replicate in independent studies.^18,37,51 This might be caused by a variety of phenomena, for example, rare variants with large effects that are unique to a single family will not be replicated in other cohorts.³⁹ However, we have demonstrated that when there is no such large effect, one can still observe significant signals given a polygenic model of genetic architecture. Thus, a parsimonious explanation for linkage signals that cannot be replicated is that the thresholds cited above are not sufficiently stringent because they assume a null model of no genetic effects.⁵² One way that nonreplicating linkage signals could arise from a highly polygenic architecture is that through random sampling, a chromosomal region can have multiple alleles of small effect shared identically by descent across families on one sample by chance, and this stochastic occurrence is unlikely to be repeated in an independent sample. Through our simulation studies, we have shown that under the null model of genome-wide polygenic variation, the traditionally used thresholds are too low to detect a region with a large effect and should be set dependent upon trait heritability (e.g., LOD = 3.7 for h² = 0.42 and LOD = 4.1 for h² = 0.69). We also suggest that using the term “false positive” is not strictly accurate when discussing previously reported signals that failed to replicate because they are indeed likely to be caused by genetic variation. However, they are unlikely to signify the presence of a genomic region with a single large effect, which is often the goal of linkage analysis.

In summary, using results from our large SNP-based linkage study to date, we have provided evidence that BMI and height are highly polygenic, that heritability of BMI might have been previously overestimated, and that the failure of most linkage studies to replicate or lead to identified causal variants can be reconciled by the polygenic nature of complex traits.