Dynamic self-assembly of motile bacteria in liquid crystals

Abstract

This paper reports an investigation of dynamical behaviors of motile rod-shaped bacteria within anisotropic viscoelastic environments defined by lyotropic liquid crystals (LCs). In contrast to passive microparticles (including non-motile bacteria) that associate irreversibly in LCs via elasticity-mediated forces, we report that motile Proteus mirabilis bacteria form dynamic and reversible multi-cellular assemblies when dispersed in a lyotropic LC. By measuring the velocity of the bacteria through the LC (8.8 +/− 0.2 μm/s) and by characterizing the ordering of the LC about the rod-shaped bacteria (tangential anchoring), we conclude that the reversibility of the inter-bacterial interaction emerges from the interplay of forces generated by the flagella of the bacteria and the elasticity of the LC, both of which are comparable in magnitude (tens of pN) for motile Proteus mirabilis cells. We also measured the dissociation process, which occurs in a direction determined by the LC, to bias the size distribution of multi-cellular bacterial complexes in a population of motile Proteus mirabilis relative to a population of non-motile cells. Overall, these observations and others reported in this paper provide insight into the fundamental dynamical behaviors of bacteria in complex anisotropic environments and suggest that motile bacteria in LCs are an exciting model system for exploration of principles for the design of active materials.

Introduction

Bacteria adapt to a broad range of microenvironments with varied physical and chemical properties. Aspects of these microenvironments can impact the motility and viability of the microorganisms.¹ While bacteria most commonly inhabit isotropic microenvironments which possess direction-independent physical properties, some specialized bacteria including Staphylococcus aureus, Neisseria gonorrhoeae, Beta-hemolytic strains of Streptococcus, Mycobacterium tuberculosis, and Pseudomonas aeruginosa have been previously shown to colonize microenvironments possessing anisotropic properties (e.g., optical, mechanical, and diffusional), including those enriched in collagen, cellulose, chitin, synovial fluid, and the matrix of extracellular polymeric substances associated with bacterial biofilms.^2–5 How the anisotropy of these environments influences dynamic behaviors of bacteria, and in particular, intercellular interactions remains poorly understood.

In this paper, we address this topic by studying bacteria in model liquid crystalline materials. Liquid crystals (LCs) encompass a state of soft matter in which properties are typically anisotropic.⁵ Unlike isotropic liquids, LCs exhibit long-range order and elasticity that enables energy to be stored at rest in strained states, and they form topological defects in confined systems.^5–8 These properties significantly influence the behavior of micrometer-sized synthetic particles (e.g., polystyrene or silica) when dispersed within a LC. For example, individual elongated microparticles are spontaneously oriented within nematic LC to minimize local elastic distortions that arise due to the preferential alignment of LC mesogens at the particle surface (so called “surface anchoring”).^7,9 The specific orientation assumed by the particles relative to the far-field director, which defines the average alignment of LC mesogens in the bulk, depends on the type of anchoring (e.g., tangential or perpendicular) at the particle surface. In addition, a series of recent studies have revealed that the elasticity of LCs can generate direction-dependent interparticle forces that lead to formation of complex, self-assembled structures of micrometer-sized particles in LCs including linear chains and two-dimensional arrays.^7–11 Such LC-mediated elastic forces can be very strong, commonly producing pair interaction potentials on the order of 10² – 10³ kT and lead to the irreversible association of microparticles. Although interest exists in harnessing these forces to create self-assembled colloidal structures for use in photonics or in the design of metamaterials,¹² the strength of the anisotropic interparticle interactions often leads to the irreversible association of particles and kinetic traps (particle configurations which produce local free energy minima) and thus optical tweezers or other techniques are typically needed to guide the assembly process.

While the self-organization of ‘passive’ colloids in LCs has been well characterized, much less is known about the behaviors of ‘active’ particles^13,14 that propel themselves within LCs. Such an investigation is of particular interest because active particles may be able to generate forces of sufficient magnitude to overcome the irreversibility of many LC-mediated interparticle interactions (see above). Bacteria can be viewed as a promising class of active particles for these types of fundamental studies because, as we demonstrate, they can be genetically engineered to manipulate the magnitude of the propulsive force that they generate in LCs. Additionally, focusing on bacteria provides an opportunity to gain insight into the influence of elasticity of LCs on intracellular bacterial organization in anisotropic microenvironments.

Past studies have reported that the elasticity of anisotropic microenvironments can impact the orientation and motility of the bacteria. Smalyukh et al. observed that the long axes of rod-shaped P. aeruginosa cells oriented parallel to the direction of DNA alignment in a concentrated solution of aligned DNA chains. They also found that cell motion was biased in this direction.¹⁵ These phenomena were hypothesized to arise from minimization of energy associated with elastic deformation of the nematic-like DNA biopolymer matrix. More recently, Kumar et al. have reported that elastic forces similarly induce Escherichia coli to move anisotropically when suspended in a nematic LC.¹⁶ In this paper, we move beyond these past studies of isolated bacteria (i.e., single particles) by focusing instead upon the interplay of elasticity-mediated inter-bacterial forces and flagella-derived dissociative forces on the self-organization of multiple bacteria dispersed in a LC.

To investigate the above-described fundamental issues, we studied the behavior of Proteus mirabilis cells suspended in a lyotropic LC that creates an anisotropic viscoelastic microenvironment. P. mirabilis is a Gram-negative, rod-shaped γ-proteobacterium 2 – 3 μm in length that is commonly associated with urinary tract infections and the biofouling of catheters. Guided by environmental cues, P. mirabilis cells differentiate into long (~ 20 μm) swarmer cells having a characteristically high density of flagella that generate sufficient propulsive forces to enable movement through high viscosity fluids (μ ≤ 8.34 Pa·s), which is a phenotype that is thought to play a role in pathogenesis.¹⁷ We hypothesized that these large propulsive forces might also permit the emergence of complex inter-bacterial behaviors in viscoelastic media such as LCs. Rather than working with swarmer cells per se, we studied P. mirabilis cells overexpressing the flhDC operon, which encodes the master regulator of flagellum biosynthesis, FlhD₄C₂. Overexpressing flhDC produces vegetative P. mirabilis cells (P. mirabilis-flhDC) that have a high density of flagella that resembles swarmer cells, and enables them to move through viscous fluids.¹⁷ Focusing our studies on P. mirabilis-flhDC enabled us to recapitulate the dominant phenotype of swarmers—movement through viscous environments—without the technical complexities of isolating and working with isogenic populations of these differentiated cells.

For our studies of P. mirabilis-flhDC in anisotropic environments, we used aqueous solutions of disodium cromoglycate (DSCG). DSCG (also known as cromolyn) is an example of a lyotropic LC. Aqueous DSCG solutions exhibit nematic LC phases within a particular range of compositions and temperatures due to formation of aggregates of stacked DSCG molecules.^18,19 Our choice of DSCG for these studies was primarily guided by its known biocompatibility with several types of cells and bacteria.^20,21 DSCG has also been characterized extensively, including the determination of its phase diagram,^18,22 birefringence,²³ and elastic constants.²⁴ In addition, synthetic LCs are particularly attractive model anisotropic fluids because it is possible to exert spatiotemporal control of the local LC alignment, e.g. through changes in boundary conditions or application of external fields.

Experimental

Bacterial strains and cell culture

P. mirabilis strain HI4320 was transformed with plasmid pflhDC to create P. mirabilis-flhDC. The plasmid pflhDC contained the flhDC genes from P. mirabilis inserted into pACYC184 (which contains a gene for chloramphenicol resistance). Empty vector pACYC184 (without flhDC) was transformed into HI4320 to obtain wild type vegetative P. mirabilis. Both strains were grown in chloramphenicol-resistance nutrient medium consisting of 1% (wt/vol) peptone (Becton, Dickinson, Sparks, MD), 0.5% (wt/vol) yeast extract (Becton, Dickinson), and 1% (wt/vol) NaCl (Fisher Scientific, Fairlawn, NJ) at 30°C in a shaking incubator.¹⁷ Saturated overnight cultures were diluted 100-fold in 10 mL of fresh nutrient medium and grown in 150 mL Erlenmeyer flasks at 30°C in a shaking incubator at 200 rpm. We observed that the highest swimming velocity of P. mirabilis cells occurred during stationary phase, hence we harvested cells at an absorbance (λ=600 nm) of ~3.2 and centrifuged. The cells were then washed three times with an aqueous buffer for bacterial motility (0.01 M KPO₄, 0.067 M NaCl, 10⁻⁴ M EDTA, 0.1 M glucose, and 0.001% Brig-35, pH 7.0). To obtain non-motile P. mirabilis cells, the cells were treated 4% glutaraldehyde for 3 h at 25°C after harvesting.

E. coli K-12 strain MG1655 (CGSC #8237) was grown in Luria-Bertani media (LB) (1% tryptone w/v, 0.5% yeast extract w/v, 1% NaCl w/v) at 37°C in a shaker incubator. Saturated overnight cultures were diluted 100-fold in 10 mL of fresh nutrient medium and grown in 150 mL Erlenmeyer flasks at 37°C in a shaking incubator at 200 rpm for 2 hours. After harvesting, these cells were washed as described above for P. mirabilis.

Lyotropic LC preparation

Disodium cromoglycate (DSCG) was purchased from Sigma-Aldrich (Milwaukee, WI) and used as received. Lyotropic LCs containing DSCG were prepared by mixing 15.3 wt% of DSCG with 84.7 wt% of aqueous motility buffer. The mixture was shaken for at least 12 h to ensure complete solubility and homogeneity. Prior to experimentation, the DSCG solution was heated at 65°C for 10 min to avoid possible time dependence of the properties of the mixture.^25,26 After cooling the solution to 25°C, a small volume of motility buffer containing bacteria was added to the DSCG mixture producing a final concentration of ~10⁴ cells/μL. The final concentration of DSCG was 15.0 wt% in all experiments. At this concentration, DSCG forms a nematic LC phase below ~ 27°C and an isotropic phase above ~ 40°C with two-phase coexistence observed within the range of intermediate temperatures.^18,22

Microscopy

We optically imaged cells using a Nikon Eclipse Ti inverted microscope equipped with crossed polarizers and a Photometics CoolSNAP HQ2 CCD camera (Tucson, AZ) using a Nikon Plan Apo λ, 100X/1.45 oil objective lens. Videos consisting of 400 frames were collected with the EM gain off and with a 100 ms exposure time (10 frames/sec). Images of cells were collected using Nikon NIS Elements software. For non-motile cells, bright field and crossed polar images were collected for the same field of view. A thermoplate (Tokai Hit, Japan) and 100X objective heater (Bioptichs, PA) were used to control the temperature of the samples during experiments. An Olympus BX60 microscope equipped with crossed polarizers was also used to analyze the imaging chambers. Images were captured using a digital camera (Olympus C-2040 Zoom) mounted on the microscope and set to an f-stop of 2.8 and a shutter speed of 1/125 sec.

Bacterial motility data analysis

Microscopy data for motile cells was analyzed using the MATLAB computing environment (MathWorks, Natick, MA, USA) by identifying the centroid of each bacterium in successive frames and grouping those points together to create a cell trajectory. We combined the position of the cell at each interval in a cell track with the CCD frame rate to determine cell velocity. Using this script, we determined the length and position of each cell and the average cell velocity over the entire track. Tracks that were shorter than 25 frames were discarded. ImageJ software was used to calculate the angular dispersion of non-motile cell populations relative to the direction of rubbing, the distance between associated non-motile cells, and the angle with respect to the far-field director of multicellular complexes.

Rheology

An Advanced Rheometric Expansion System (ARES) (TA Instruments, Rheometric Scientific, Piscataway, NJ) with cone and plate type geometry (cone diameter 50 mm; cone angle 0.04 rad) was used to measure the effective viscosity of the DSCG solution. Steady shear rate sweeps were performed at room temperature at shear rates between 10⁻³ and 10³ s⁻¹. A gap of 0.0508 mm between the plate and the center of the cone was used such that DSCG solution fully filled the space between the plates, with excess material extended beyond the plates.

Statistical analysis

All experimentally determined values have been reported in the text and figures with associated standard errors.

Results

Anisotropic motion and orientation of P. mirabilis-flhDC cells in nematic DSCG

We first sought to confirm that the elasticity of the nematic LC phase of DSCG solutions (15 wt%) in aqueous motility buffer induced bacteria to move anisotropically, as has been reported previously for E. coli.¹⁵ At this concentration, DSCG forms a nematic LC phase below ~ 27°C and an isotropic phase above ~ 40°C with coexistence of two phases at intermediate temperatures.^18,22 All of the experiments described in this manuscript were performed in 15 wt% DSCG. To prepare optical chambers for imaging bacterial cells suspended in DSCG solutions, we first rubbed a glass slide and a glass cover slip unidirectionally multiple times with tissue paper (Kimwipe). A small volume (~1 μL) of DSCG solution containing bacteria was subsequently confined between the two rubbed glass substrates in a cavity created using 6 μm-thick Mylar film (Fig. S1). Epoxy was used to seal the chamber and prevent water evaporation. The imaging chamber was prepared so the rubbed surfaces of the glass substrates were both in contact with the DSCG solution and oriented such that the rubbing directions on the two substrates were antiparallel. The sample was briefly (~10 s) heated to 42°C into the isotropic phase of DSCG to mitigate any flow-induced alignment of the nematic LC before cooling back to room temperature. Using this technique, large regions (in excess of 100 μm × 100 μm) of the LC phase of DSCG (at 25°C) exhibited an orientation that was parallel to the surface with an azimuthal alignment in the direction of rubbing (Fig. S1). We confirmed that the alignment of the nematic LC in these regions was parallel to the direction of rubbing by inserting a quarter wave plate into the optical path of a microscope and analyzing the appearance of the sample between crossed polars.²⁷ Each imaging chamber was used within 3 h of its preparation.

Initial experiments with E. coli strain MG1655 revealed limited motility in nematic phases of DSCG (average velocity V̄ ~ 1.2 +/− 0.4 μm/s), which made it challenging to differentiate between motile and non-motile cells. With few exceptions, past studies have demonstrated that many types of bacteria are unable to generate sufficient propulsive forces to move through fluids with μ > 0.06 Pa·s (e.g. the motility of Escherichia coli strain KL227 ceases at μ = 0.06 Pa·s).²⁸ Since E. coli MG1665 cells do not generate a large propulsive force in fluids of high viscosity such as lyotropic liquid crystals (and thus, we expected, would irreversibly aggregate in LCs), we instead investigated motile strains of P. mirabilis that were engineered to overexpress flhDC and enable cell motility in isotropic fluids with a dynamic viscosity, μ ≤ 8.34 Pa·s.¹⁷ The aspect ratio of the engineered cells (k = L/2R) was ~ 3, closely matching vegetative P. mirabilis cells that did not overexpress flhDC. We measured the P. mirabilis-flhDC cells to move through DSCG solutions with a much higher velocity (V̄ = 8.8 +/− 0.2 μm/s) than both E. coli cells and vegetative P. mirabilis cells that did not overexpress flhDC (V̄ = 0.2 +/− 0.1 μm/s) (Fig. 1A). When we analyzed the motion of P. mirabilis-flhDC cells dispersed in nematic DSCG solution (Video S1), we observed cells moving preferentially along the direction of LC alignment,^15,16 as illustrated by the offset representative trajectories shown in Fig. 1B. The mean-square displacement for P. mirabilis-flhDC cells parallel to the nematic LC director (x-direction) was approximately two orders of magnitude greater than in the perpendicular direction (Fig. 1D). In contrast, P. mirabilis-flhDC cells suspended in an isotropic DSCG solution (achieved by equilibrating the solution at 42°C) exhibited a comparable velocity of V̄ = 8.1 +/− 0.3 μm/s without a directional bias (Fig. 1C and D; Video S2).

Fig. 1.

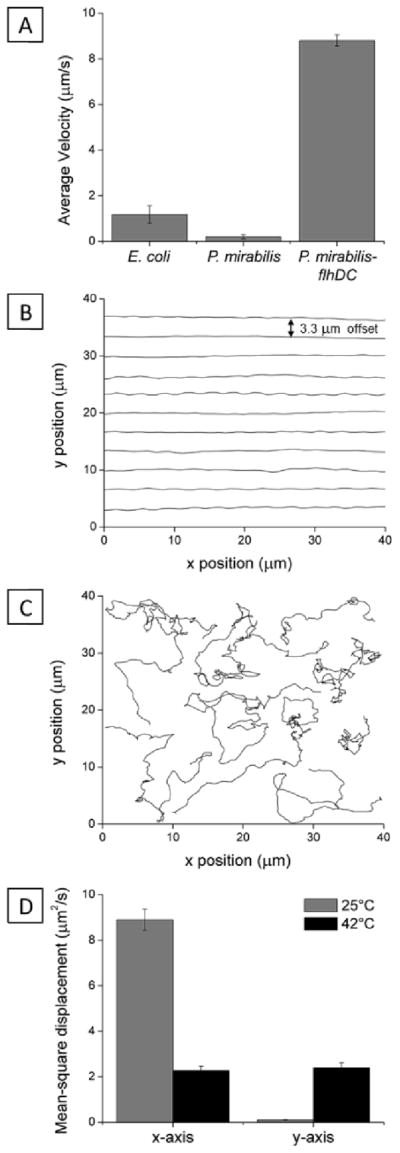
Anisotropic motion of bacteria in nematic LC. (A) Average velocities of P. mirabilis-flhDC cells in nematic DSCG solutions (15 wt%) at 25°C. (B) Superimposed trajectories (offset from one another by 3.3 um) of P. mirabilis-flhDC in nematic DSCG solutions at 25°C. The LC director was oriented along the x-axis (in the direction of rubbing of the glass slides). (C) Superimposed representative trajectories of P. mirabilis-flhDC in isotropic phases of DSCG at 42°C. (D) Plot of the mean-square displacement of P. mirabilis-flhDC calculated from analysis of 139 trajectories (25°C) and 75 trajectories (42°C). The velocities of P. mirabilis-flhDC cells in DSCG solution were comparable in magnitude at 25°C (V̄ = 8.8 +/− 0.2 μm/s) and 42°C (V̄ = 8.1 +/− 0.3 μm/s). Values are reported with associated standard errors.

To estimate the flagella-derived forces generated by the motile P. mirabilis-flhDC in nematic DSCG, we sought to determine the viscous drag force (F_d = 6πμRV̄) which balances the propulsive force. Nematic LCs possess direction-dependent (Miesowicz) shear viscosities with the direction of lowest viscosity being parallel to the director.^29–31 In common thermotropic liquid crystals, the Miesowicz viscosity corresponding to shear flow with velocity perpendicular to the director is often ~10× larger than the viscosity parallel to the director.²⁹ Because experimental determination of Miesowicz viscosities of lyotropic LCs is difficult as general and facile methods to manipulate the surface anchoring of lyotropic LC phases do not exist, we estimated the apparent viscosity experienced by the motile P. mirabilis-flhDC in nematic DSCG to be μ~ 0.7 Pa·s by comparing the average velocity in nematic DSCG to previous measurements of P. mirabilis-flhDC motility in solutions of known viscosity.¹⁷ (We note that we also performed rheological measurements of the DSCG solution at 25°C and measured an effective viscosity of μ~ 1 Pa·s.) Employing μ = 0.7 Pa·s as an approximation of the Miesowicz viscosity along the director, we estimate that F_d ~ 60 pN for the rod-shaped P. mirabilis-flhDC (R = 0.5 μm) cells moving at V̄ = 8.8 μm/s in nematic DSCG. Below we compare the magnitude of these flagella-derived propulsive forces to inter-bacterial forces generated by the elasticity of the LC.

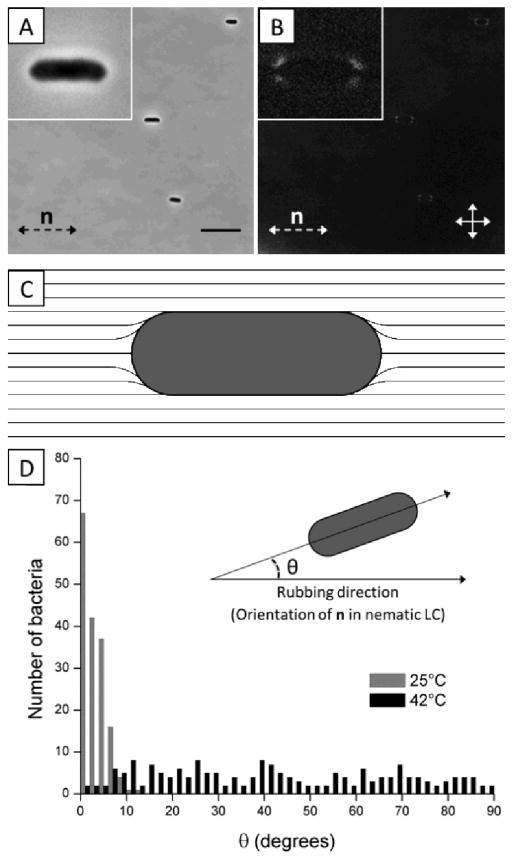
Because the interactions between P. mirabilis-flhDC cells mediated by the elasticity of the LC are dependent on the anchoring of the LC on the surface of the bacteria and the resulting strain in the LC, we first characterized the anchoring of the LC on individual cells. To determine the anchoring of the LC on the bacteria, we characterized the distribution of orientations of non-motile P. mirabilis-flhDC cells in both the nematic and isotropic phases of DSCG solutions and characterized the ordering of nematic LC near the cells using polarized light microscopy. Treating P. mirabilis-flhDC cells with 4% glutaraldehyde rendered them non-motile. Non-motile P. mirabilis-flhDC cells suspended in an isotropic DSCG solution exhibited no preferential orientational alignment (Fig. S2). In contrast, we measured the long axes of non-motile P. mirabilis-flhDC cells to preferentially align parallel to the far-field LC director in nematic DSCG (Fig. 2A and D) and we observed four small regions with a bright optical appearance near the poles of each bacterium (Fig. 2B), both which are consistent with tangential anchoring of the LC at the bacterial surface (Fig. 2C). We also calculated that shear forces generated by motile bacteria should not perturb this local ordering of LC because the Ericksen number (Er = ηV̄R/K) for the motion of P. mirabilis-flhDC cells in DSCG is < 1.²⁹ If the tangential surface anchoring of the LC on the surface of P. mirabilis-flhDC was strong, the orientation-dependent energy of interaction of the LC and the rod-shaped bacterium (length L = 3 μm, radius R = 0.5 μm) would be:^6,15,34,35

Fig. 2.

Configuration of LC around bacteria and resulting bacterial alignment. (A, B) Bright field and crossed polars images, respectively of non-motile P. mirabilis-flhDC cells dispersed in nematic DSCG solution at 25°C. The double-headed solid arrows in B indicate the positions of the polarizers while the double-headed dotted arrows depict the orientation of the LC director (n). (C) Schematic representation of the LC director profile that results from weak, tangential anchoring of the LC on the surface of P. mirabilis-flhDC cells. (D) Distribution of angles between the rubbing direction of the glass slides and the long axis of P. mirabilis-flhDC cells in DSCG solution at 25°C (nematic) and 42°C (isotropic). The scale bar in A is 10 μm. Values are reported with associated standard errors.

$$U_{\mathit{elastic}}=2\pi K{\theta }^{2}L/ln(2L/R),$$ (1)

where θ is the angle (in radians) between the director of the LC and long-axis of the bacterium and K is the elastic constant of the LC (K = 10 pN)²⁴, where for simplicity the elastic constants for splay, twist, and bend are assumed to be equal in magnitude allowing the strain of the LC to be described by a single elastic constant. This analysis leads to the prediction that even slight deviations of the bacterial long axis from the nematic director would be highly unfavorable (e.g., U_elastic ~ 90kT for θ = 4°). In contrast, we measured a significant number of bacteria to be oriented away from the far-field director (35% of cells in nematic DSCG were recorded with θ ≥ 4°), suggesting that the tangential anchoring of the LC on the surface of the bacteria is likely weak [a conclusion which receives support from additional observations reported below; we note also that weak, tangential anchoring of DSCG at surfaces has been reported elsewhere^36,37].

Interactions of bacteria mediated by LC

As noted above, past studies have demonstrated that the elasticity of LCs, and topological defects that form about passive particles in LCs, mediate particle-particle interactions that result in self-assembly of the particles.^7–11 For example, it has been demonstrated that spherical and ellipsoidal colloids with tangential surface anchoring form well-defined chains – for spherical colloids the vector that joins the particle centers is offset 30° from the far-field director.³⁸ We observed the above-described strain induced in the LC by non-motile and motile P. mirabilis-flhDC cells similarly leads to inter-bacterial forces that result in the formation of multi-cellular complexes. Fig. 3A provides a sequence of snapshots which demonstrates the formation of a linear chain of two motile P. mirabilis-flhDC cells (Video S3). At t = 3.7 s, the two bacteria, which had previously been swimming towards one another, associate together into a chain. This chain-like assembly then continues to move with a velocity similar to that of the faster individual component cell prior to the association event (Fig. 3B). At later time points, the bacteria move within the LC together, retaining this state of association. We only observed the end-on-end association of P. mirabilis-flhDC cells in the nematic phase of the DSCG solution (they do not form within the isotropic phase). We also found that a small space remained between associated motile bacteria indicating the existence of a short-range repulsion. Limited by the resolution of our optical microscope, we estimate that the closest approach of the surfaces of the bacteria is approximately 0.3 μm. Although the origin of the repulsive interaction leading to this separation is unknown, it may arise from steric and/or electrostatic interactions between cells due to the presence of the lipopolysaccharide that decorates the outer leaflet of the bacterial membrane.

Fig. 3.

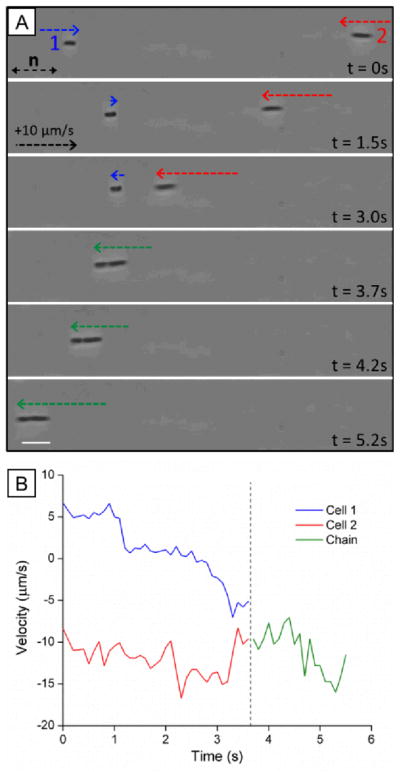
Dynamic association of motile bacteria in nematic LC. (A) Sequence of images (bright field) showing end-on-end association of two motile P. mirabilis-flhDC cells in nematic DSCG solution (15 wt%) at 25°C. Dotted arrows indicate the velocity of the bacterial cells (see calibration in t = 1.5s). (B) Plot of the velocities of the P. mirabilis-flhDC cells shown in A before and after association into the chain. The scale bar in A is 5 μm.

The role of the elasticity of the LC in mediating the inter-bacterial interactions was confirmed by measurement of the relative orientations of the centroids of non-motile bacterial cells within chains (Fig. 4A). An angle of 5.5 +/− 0.8° with respect to the far-field LC director was measured for chains of non-motile P. mirabilis-flhDC cells, consistent with theoretical predictions for elasticity-mediated interactions of ellipsoidal microparticles with tangential anchoring and aspect ratios matching P. mirabilis-flhDC cells.⁹ We found that linear chains of motile P. mirabilis-flhDC cells were instead oriented at an angle of 3.3 +/− 0.5° from the far-field director, an observation which likely reflects the drag forces generated by the motion of the swimming bacteria. Crossed-polar images confirm the quadrupolar symmetry of the nematic director near the surface of the non-motile bacteria within these chains (Fig. 4B).

Fig. 4.

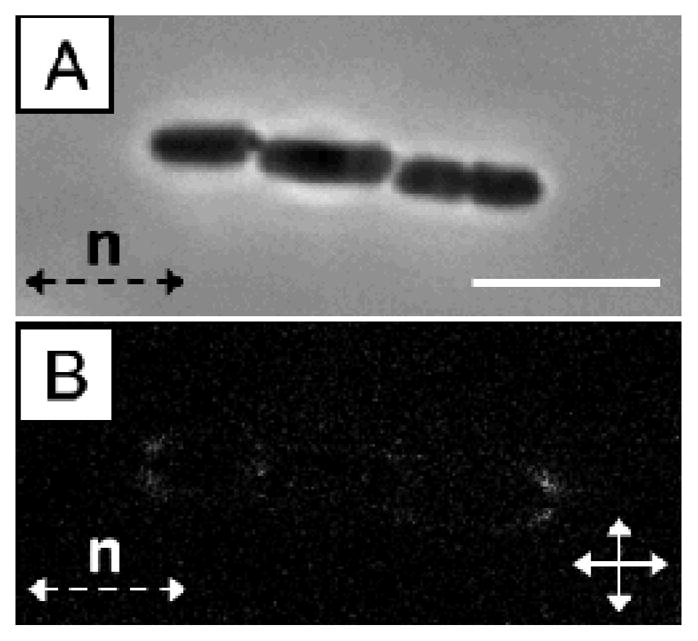
(A) Bright field and (B) crossed polars images of a non-motile P. mirabilis-flhDC multi-cellular complex (trimer) in nematic DSCG solution (15 wt%) at 25°C. The scale bar in A is 5 μm.

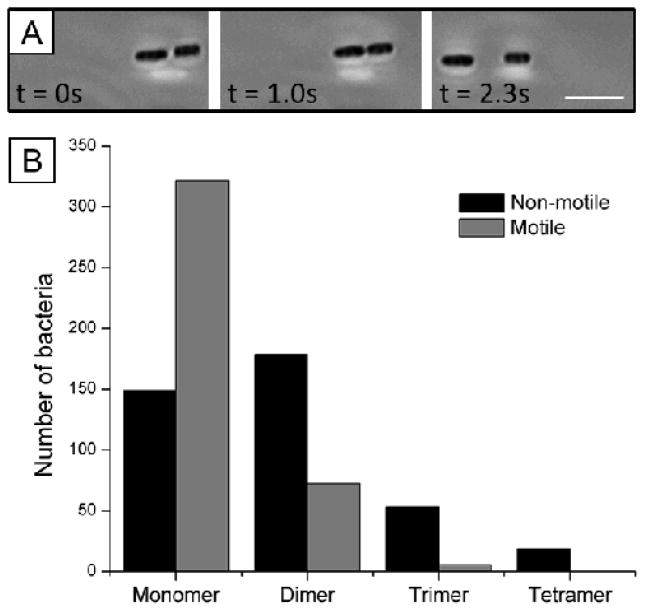
Consistent with past studies of assemblies of passive particles, non-motile bacteria associated irreversibly in nematic DSCG solutions. In contrast, however, we frequently observed motile bacteria within multi-cellular assemblies to separate from each other with trajectories that followed the LC director (Fig. 5A; Videos S4 and S5). We hypothesized that this dissociation of motile P. mirabilis-flhDC bacteria via flagella-derived forces would decrease the populations of multi-cellular assemblies (dimers, trimers, and tetramers) found in LC suspensions of motile cells relative to non-motile cells. To test this idea, we prepared dispersions of both motile and non-motile P. mirabilis-flhDC cells in parallel at equal cell densities. Approximately 30 minutes after the addition of the concentrated bacteria solutions to DSCG and preparation of imaging chambers, we acquired images of more than 400 motile and non-motile bacteria. We quantified the number of single cells and cells within multi-cellular assemblies for each population (motile and non-motile) and scaled the final numbers to a population of 400 total cells. As seen in Fig. 5B, we found that the population of motile monomers is higher by a factor of two relative to non-motile monomers, whereas the population of non-motile dimers is enriched relative to motile dimers. The role of flagella-derived forces in biasing the size-distribution of multi-cellular bacterial complexes is evidenced further in the populations of motile and non-motile trimers and tetramers in Fig. 5B.

Fig. 5.

Reversible assembly of motile bacteria within LCs. (A) Sequence of images (bright field) showing both the association and dissociation of two motile bacteria in nematic DSCG solution at 25°C. (B) Populations of bacteria in multi-cellular complexes formed in nematic DSCG solution by non-motile (black) and motile (gray) bacteria. (See text for experimental details.) The total number of cells in both populations is 400. The scalebar in A is 5 μm.

We estimated the magnitude of the LC-mediated attractive force acting between bacteria with surface anchoring energy W and quadrupolar distortions of the director as

$$F_{\mathit{elastic}}\propto C(W^2{R}^2/K){(2R/d)}^6$$ (2)

where d is the distance between the surfaces of the two rod-shaped bacteria (0.3 μm, see above), and C is a coefficient of order one.^15,39,40 The parameter W (so-called “anchoring strength”) quantifies how strongly LCs are held in a particular orientation at a surface. Guided by observations reported above indicating weak anchoring (WR/K~1) of LCs on the surfaces of the bacteria [and reports of weak anchoring of DSCG at other interfaces^34,35], we used W ~10⁻⁵ J/m² to calculate F_elastic ~ 10 pN at d = 0.3 μm. Our observation that F_elastic is comparable to our estimate of the propulsive forces generated by the flagella of P. mirabilis-flhDC cells [~ 60 pN, see above] provides additional support for the conclusion that the population of multi-cellular assemblies shown in Fig. 5B (for motile bacteria) belong to non-equilibrium states of the system that arise from the interplay of flagella-derived dissociative forces and elasticity-mediated attractive forces in the LC.

Discussion

Our results suggest that the elasticity of a nematic LC significantly influences both bacterial dynamics and organization. Not only do elasticity-mediated forces orient and direct the motion of isolated bacteria parallel to the director, as has been reported previously,^15,16 but additionally we find they induce the assembly of P. mirabilis-flhDC cells into linear chains. The force (~ 60 pN) produced by motile P. mirabilis-flhDC cells to move within the viscous LC solution at V̄ = 8.8 +/− 0.2 μm/s is comparable in order of magnitude to the attractive LC inter-bacterial force (~ 10 pN), which facilitates the dissociation of multi-cellular complexes. Specifically, from our estimates of the magnitudes of these forces, we conclude that a P. mirabilis-flhDC cell can escape from elasticity-mediated interaction with another cell when a significant component of its flagella-derived propulsive force is directed opposite to the attractive elastic force. An unresolved question that emerges from our study is the extent to which the flagella-derived forces are changed when the bacteria are assembled into multi-bacterial complexes (as a consequence of the LC-mediated attractions). It is possible that the close proximity of bacteria within multi-cellular complexes (~ 0.3 μm spacing) may restrict the motion of flagella bundles (and propulsive forces) when bacterial motion is directed in opposition to the attractive elastic force. We note, for example, that following the formation of a linear chain of bacteria (Fig. 3A), the cells continue to move at a speed and in a direction consistent with the fastest individual cell prior to the association event (Fig. 3B). This observation may indicate that little propulsive force is generated by the second component cell in the direction of motion, which is opposite to the elastic attraction force.

We observed that the dissociation of motile P. mirabilis-flhDC cells using flagella-derived forces significantly influenced the population of individual cells and multi-cellular assemblies dispersed within LC (Fig 5). Specifically, the reversibility of the elasticity-mediated inter-bacterial interaction for motile cells enriches monomers and depletes multi-cellular assemblies with respect to non-motile cells, which irreversibly associate with one another. We predict that the size distributions measured for motile bacteria suspended within the LC for longer periods will evolve, likely heightening the differences that we observed between the populations of motile and non-motile cells. Alternatively, the relative abundance of multi-cellular complexes of motile bacteria can likely be tuned by manipulating the magnitude of the propulsive force they generate or by altering their size and shape (thus influencing the strength of the elastic attraction forces) using different species of bacteria or genetic engineering.

Finally, the results in this paper suggest several additional directions for research using motile bacteria suspended in LCs. Future investigations could focus on elastic interactions acting on bacteria at interfaces of LCs, interactions of bacteria with LC defects, and the use of external electric and magnetic fields to manipulate LCs and actively control bacterial behavior (e.g., to dynamically focus bacteria to a specific location in a system for analysis). In additional to producing fundamental information about the behavior of bacteria in anisotropic viscoelastic environments, these studies also may generate novel insight into the influence of anisotropy on bacteria in biological microenvironments.

Conclusions

In summary, this paper reports that motile P. mirabilis-flhDC cells form dynamic, reversible multi-cellular assemblies within the nematic phase of a lyotropic LC due to the interplay of elasticity-mediated forces and flagella-derived forces. While passive synthetic particles^7–11 as well as non-motile bacteria aggregate irreversibly when dispersed in a LC, we find the propulsive forces generated by the flagella of the P. mirabilis-flhDC cells are comparable in magnitude to LC-mediated attractive inter-bacterial forces (tens of pN) and can be used to overcome them. We observe that flagella-mediated dissociation significantly reduces the population of motile bacteria found in multi-cellular complexes relative to a population of non-motile cells. Overall, our observations provide new insight into the manner in which elastic forces may also influence bacteria organization and dynamics within biological anisotropic viscoelastic microenvironments. In addition, our studies reveal that motile bacteria in LCs are a versatile system for investigations of self-organization that result from dissipative processes, for elucidation of general design principles for active soft matter (including systems containing synthetic particles driven by catalytic reactions^13,14), and potentially for studies of the emergence of cooperative behaviors of populations of bacteria at high concentrations. In particular, we demonstrate that bacteria can be genetically engineered to manipulate the magnitude of the propulsive force that they generate in LCs to control, for example, the frequency with which they can escape elasticity-mediated inter-bacterial interactions. Based on our results, we envision that bacteria are well suited to serve as model “active” particles with which to unmask dynamic phenomena that emerge from the interplay of local propulsive forces and anisotropic viscoelastic environments in LCs.