Optimal matching with minimal deviation from fine balance in a study of obesity and surgical outcomes

Summary

In multivariate matching, fine balance constrains the marginal distributions of a nominal variable in treated and matched control groups to be identical without constraining who is matched to whom. In this way, a fine balance constraint can balance a nominal variable with many levels while focusing efforts on other more important variables when pairing individuals to minimize the total covariate distance within pairs. Fine balance is not always possible; that is, it is a constraint on an optimization problem, but the constraint is not always feasible. We propose a new algorithm which returns a minimum distance finely balanced match when one is feasible, and otherwise minimizes the total distance among all matched samples that minimize the deviation from fine balance. Perhaps we can come very close to fine balance when fine balance is not attainable; moreover, in any event, because our algorithm is guaranteed to come as close as possible to fine balance, the investigator may perform one match and on that basis judge whether the best attainable balance is adequate or not. We also show how to incorporate an additional constraint. The algorithm is implemented in two similar ways, first as an optimal assignment problem with an augmented distance matrix, second as a minimum cost flow problem in a network. The case of knee surgery in the Obesity and Surgical Outcomes Study motivated the development of this algorithm and is used as an illustration. In that example, two of 47 hospitals had too few nonobese patients to permit fine balance for the nominal variable with 47 levels representing the hospital, but our new algorithm came very close to fine balance. Moreover, in that example, there was a shortage of nonobese diabetic patients, and incorporation of an additional constraint forced the match to include all of these nonobese diabetic patients, thereby coming as close as possible to balance for this important but recalcitrant covariate.

1. Introduction

1.1 Motivating example: surgical outcomes in the severely obese

There are reasons to be concerned about surgical care for severely obese patients, those with a body mass index (BMI) of 35 or more. In part, their health problems may affect their surgical outcomes. In part, Medicare pays surgeons an essentially flat fee for performing a particular type of operation, but time and effort required from a surgeon in certain operations is affected by the sheer mass of the patient, the amount of cutting and repair required. This flat fee entails, in effect, a lower hourly rate of payment for operations on severely obese patients, with the possible consequence that market forces yield inferior care for the severely obese. Building upon the Surgical Outcomes Study (e.g., Silber, et al. 2001, 2005), the Obesity and Surgical Outcomes Study (OBSOS) is designed to compare severely obese (BMI ≥ 35) and non-obese (20 ≤ BMI < 30) surgical patients in Medicare with respect to survival, complications, length of stay in the hospital, readmission rates, surgical time which implicitly determines the surgeon’s hourly rate of compensation, and access to surgical care. The OBSOS study focuses on five types of surgery, thoracotomy, colectomy without cancer, colectomy with cancer, hip replacement without fracture, and knee replacement.

Forty seven hospitals, j = 1, 2, …, 47 = J, in Illinois, New York and Texas participated in OBSOS by performing chart abstractions for selected surgical patients. In addition, we had Medicare claims data, including mortality, for these hospitals and for all other hospitals in Illinois, New York and Texas. Because BMI is not in Medicare claims and had to be determined using chart abstraction, the Medicare claims data from all hospitals except the 47 participating hospitals was of limited use; however, an independent “risk score” was estimated from these hospitals. The “risk score” used a logit regression for the probability of death within thirty days of surgery from conditions such as prior heart attacks or a history of cancer. Because the risk score is estimated using outcomes, it must come from an independent sample. See Hansen (2008) for discussion of risk scores and, in particular, of estimating them from an independent sample.

The study design called for matching of severely obese patients to non-obese patients with ‘fine balance’ for J = 47 hospitals and control for various subsets of prognostic factors. For instance, diabetes is more common among the obese and may complicate surgery, but among many questions, one question is whether obesity matters apart from its relationship with diabetes. Among the clinical covariates were: (i) age, (ii) sex, (iii) diabetes, (iv) a modification of the acute physiology (Apache) score (Knaus et al. 1991), (v) a binary indicator of a missing Apache score, (vi) the risk-of-death score described above, and (vii) a propensity score estimating the probability of severe obesity from other covariates. A matching algorithm is said to match optimally subject to a fine balance constraint if the match (i) minimizes the total covariate distance within matched pairs, (ii) subject to the additional requirement that the marginal distribution of a nominal variable is exactly balanced; see Rosenbaum, Ross and Silber (2007) and Rosenbaum (1989, §3.2; 2010, Chapter 10).

Why is fine balance useful? Randomization in experiments and propensity scores in observational studies balance observed covariates stochastically, and randomization also balances unobserved covariates, but neither has much success in balancing many small strata because of imbalances that occur in small strata by chance. If a completely randomized trial had 20 strata with 5 patients per stratum, then the binomial distribution yields a 73% chance that at least one stratum will have maximal imbalance, that is, only treated subjects or only controls, so that stratum provides no direct information about treatment effects. Matching with fine balance does not leave the matter to chance, instead forcing balance on a nominal variable with many categories without constraining who is matched to whom.

Fine balance was possible for thoracotomy, colectomy with or without cancer, and hip replacement, but not for knee replacement. Severe obesity is a strain on the knees, and knee surgery is common among the severely obese. In two of the 47 hospitals, namely hospitals #3 and #23, there were more severely obese patients having knee surgery than there were non-obese patients having knee surgery; see Table 1.

Table 1.

Frequencies of knee surgeries by hospital for the obese, all of the nonobese, and the near-fine match. Fine balance is not quite possible for knee surgery because, in hospitals 3 and 23 there are more obese than nonobese patients.

	Hospital ID
Hospital ID j	1	2	3	4	5	6	7	8	9	10	11	12
All Not Obese Mj	102	77	75	37	34	107	49	73	47	56	54	37
Obese nj	59	43	94	30	19	70	25	22	37	30	35	14
Matched Not Obese mμj	59	43	75	30	19	70	25	22	37	30	35	14
Hospital ID j	13	14	15	16	17	18	19	20	21	22	23	24
All Not Obese Mj	51	36	52	31	32	60	35	52	91	41	0	37
Obese nj	34	29	35	30	20	19	30	26	40	12	2	15
Matched Not Obese mμj	34	29	35	30	20	19	30	26	40	16	0	15
Hospital ID j	25	26	27	28	29	30	31	32	33	34	35	36
All Not Obese Mj	57	48	138	91	57	28	62	55	52	35	48	54
Obese nj	19	47	41	50	16	13	32	15	23	23	9	15
Matched Not Obese mμj	19	47	41	50	17	13	32	23	23	23	14	18
Hospital ID j	37	38	39	40	41	42	43	44	45	46	47
All Not Obese Mj	92	121	28	50	59	22	66	72	92	91	12
Obese nj	43	66	15	16	34	16	23	48	47	42	7
Matched Not Obese mμj	43	66	15	16	34	16	23	48	47	42	7

How can one match to minimize the total covariate distance subject to the constraint that a nominal variable is as close as possible to fine balance?

1.2 Goal: close individual matches that minimize deviations from fine balance

We develop a new algorithm that minimizes the total covariate distance within matched pairs while coming ‘as close as possible to fine balance.’ As is typically done in combinatorial optimization (e.g., Papadimitriou and Steiglitz 1982), the new problem is solved by reducing it to another problem for which a fast algorithm exists. One version of the algorithm in §3 uses the optimal assignment algorithm in a new way with an augmented distance matrix and Proposition 1 proves that this reduction to the assignment problem does indeed solve the optimal near-fine matching problem. A second version of the algorithm in the Web-Appendix uses minimum cost flow in a network. See §1.3 for brief review, references and availability of software for optimal assignment and minimum cost flow.

Actually, ‘as close as possible to fine balance’ is not a well-defined notion, and the algorithm permits the user to choose among several alternative definitions. For instance, one definition distributes the excess from hospitals 3 and 23 among other hospitals to minimize the total covariate distance. Another definition minimizes the total covariate distance while distributing the excess from hospitals 3 and 23 as uniformly as possible among the other hospitals. A third option minimizes a chi-square-like statistic; see (4) below.

Our algorithm comes ‘as close as possible to fine balance,’ but how close that is will depend upon the data at hand. The investigator will need to examine the degree of balance produced by coming ‘as close as possible to fine balance,’ as in Table 1 for the OBSOS study. In OBSOS, a near-fine match is very close to fine balance. If ‘as close as possible to fine balance’ is not close enough, the investigator may need to abandon pair matching of the entire treated group in favor of some more flexible design, such as optimal full matching or optimal subset matching (Rosenbaum 1991, 2011; Hansen and Klopfer 2006). In any event, by coming ‘as close as possible to fine balance,’ the results produced by the algorithm will provide a clear basis for a decision about this aspect of study design.

1.3 Review: optimal assignment algorithms and network optimization

Among combinatorial optimization algorithms, the assignment algorithm is one of the most widely available and studied; see Dell’Amico and Toth (2000). Bertsekas (1981) provides Fortran code for his auction algorithm which is available in R in the pairmatch function of Hansen’s (2007) optmatch package. Bergstralh et al. (1996) discuss optimal matching in SAS. Papadimitriou and Steiglitz (1982) provide a worst-case time bound of O(I³) for one assignment algorithm, where I is the number of subjects available for matching. For comparison, if you multiply two I × I matrices in the usual way, the time required is O(I³). A different class of algorithms for optimal matching in statistics is discussed by Lu et al. (2011). For a survey of matching in observational studies, see Stuart (2010).

The alternative formulation of the problem in the Web-Appendix in terms of network optimization requires specialized programming in currently available statistical packages. The first author has created an R package called finebalance that implements the network formulation. This solves the implementation problem for R users. In light of this, we discuss the solution using the assignment algorithm in §3 and briefly the solution using network optimization in the Web-Appendix.

For discussion of some other applications of optimal multivariate matching in various fields, see Ahmed et al. (2006), Apel et al. (2010), Guan et al. (2009), Heller et al. (2009), Marcus et al. (2008), and Stuart and Green (2007). Matching is one form of adjustment for observed covariates relevant to nonparametric identification; see, for instance Tan (2006) or Imai et al. (2010).

1.4 Outline

The paper is organized as follows. Section 2 develops notation and defines the optimization problem. Intuition is built up in §3.1 and §3.2 by considering two tiny examples, and then a general procedure and proof is given in §3.3 using the assignment algorithm. Extensions to matching with L ≥ 1 controls are straightforward and are discussed in §2.2 and the Web-Appendix. The OBSOS study faced an additional problem not mentioned in §1.1, namely a severe shortage of non-obese diabetics for use as controls, and a modification of the procedure in §3.3 is described in §4 that additionally constrains the match so that every one of the rare and therefore highly informative, non-obese diabetics is included in the matched sample. In §5, the near-fine matched sample is constructed for the example in §1.1, and in §5.2 the near-fine match is contrasted with a conventional match for the same data. An alternative but equivalent formulation in terms of network optimization is described in the Web-Appendix; it can be more efficient in its use of computer memory. Finally, §6 discusses other related matching problems that can be solved with the same approach.

2. Notation, Definitions, and Statement of the Problem

2.1 Minimum distance pair matching

There are T treated subjects, 𝘛 = {τ₁, …, τ_T} and C ≥ T potential controls, 𝘊 = {γ₁, …, γ_C} with a nonnegative, possibly infinite, distance δ_τtγc ≥ 0 between τ_t and γ_c. In effect, an infinite distance, δ_τt,γc = ∞, will forbid matching τ_t to γ_c. Write Δ for the T × C matrix of δ_τt,γc. In modern practice, δ_tc is some form of robust Mahalanobis distance with a caliper based on a propensity score; see Rosenbaum (2010, Part II) for review of these standard devices. For a finite set A write |A| for the number of elements of A, so |𝘛| = T.

A pair matching is a function μ : 𝘛 → 𝘊 such that $\mu ({\tau }_t)\ne \mu ({\tau }_t^{\prime })$ whenever ${\tau }_t\ne {\tau }_t^{\prime }$, that is, each treated subject τ_t is matched to a different control, μ(τ_t). Without further constraints, an optimal pair matching is one that minimizes the total distance within the T matched pairs, that is, μ(·) minimizes Σ_τt∈𝘛 δ_τt,μ(τt). Although there are C!/(C − T)! possible matchings μ(·), it is possible to find an optimal assignment in at most O{(T + C)³} arithmetic operations using the optimal assignment algorithm; see Papadimitriou and Steiglitz (1982).

There is a nominal variable ν with J integer values, that is, ν : 𝘛 ∪ 𝘊 → {1, 2, …, J}. In §1, J = 47 and ν(τ_t) is the hospital that performed surgery on obese patient τ_t. A match μ(·) is finely balanced if the T treated subjects in 𝘛 and their T matched controls in μ(𝘛) = {μ(τ_t), t ∈ 𝘛} ⊆ 𝘊 have the same number of individuals with each value of the nominal variable, that is if

$$\mid \{{\tau }_t\in 𝘛:\nu ({\tau }_t)=j\}\mid =\mid \{{\tau }_t\in 𝘛:\nu \{\mu ({\tau }_t)\}=j\}\mid ,j=1,\dots ,J.$$ (1)

Importantly, (1) is a constraint on the marginal distributions of ν(·), not on who is matched to whom, that is, not on the joint distribution of ν(τ_t) and ν{μ(τ_t)}. An optimal finely balanced match satisfies (1) and minimizes the total covariate distance Σ_τt∈𝘛 δ_τtμ(τt) among all matches μ that satisfy (1).

The constraint (1) is not always feasible: there may be no match μ such that (1) is true. Write n_j = |{τ_t ∈ 𝘛 : ν(τ_t) = j}|, M_j = |{γ_c ∈ 𝘊 : ν(γ_c) = j}|, and m_μj = |{τ_t ∈ 𝘛 : ν{μ(τ_t)} = j}|, so (1) says n_j = m_μj, but of necessity m_μj ≤ M_j for every μ, so no matching μ can satisfy (1) if n_j > M_j. In Table 1, n₃ = 94 > 75 = M₃, so no finely balanced match exists.

A near-fine optimal match is one that minimizes the total distance Σ_τt∈𝘛 δ_τt,μ(τt) among all matches μ that make the m_μj as close as possible to the n_j. Because there are J differences n_j − m_μj, there are actually several senses in which they may be made as close as possible. For a function f : A → B, the constraint f = min means that a feasible solution must be in the set {a ∈ A : f(a) = min_a′∈A f(a′)}.

For instance, ${\sum }_{j=1}^J\mid n_j-m_{\mu j}\mid =min$ if the total of the absolute differences |n_j − m_μj| is minimized. For any pair-match, the total number of treated subjects equals the total number of controls, $0={\sum }_{j=1}^J{n}_j-m_{\mu j}$, so positive n_j − m_μj must counterbalance negative n_j − m_μj. In §1, there are n₃ − M₃ = 94 − 75 = 19 extra obese knee surgeries from hospital j = 3 and n₂₃ − M₂₃ = 2 −0 = 2 extra obese knee surgeries from hospital j = 23, or 19 + 2 = 21 extra patients in total; these 21 extra patients must be distributed among the other 47 − 2 = 45 hospitals. In Table 1, the minimum value of ${\sum }_{j=1}^J\mid n_j-m_{\mu j}\mid$ for a match is 42, because n₃ − m_μ3 ≥ 19 and n₂₃ − m_μ,23 ≥ 2 with $0={\sum }_{j=1}^J{n}_j-m_{\mu j}$, so the minimum value of ${\sum }_{j=1}^J\mid n_j-m_{\mu j}\mid$ is 2 × (19 + 2) = 42, and the constraint ${\sum }_{j=1}^J\mid n_j-m_{\mu j}\mid =min$ is the same as the constraint ${\sum }_{j=1}^J\mid n_j-m_{\mu j}\mid =42$.

Write d_μ(j) for the j^th largest |n_j − m_μj|, so d_μ(1) ≤ ··· ≤ d_μ(J), and d_μ = {d_μ(1), …, d_μ(J)}^T. By d_μ = min we mean: d_μ(J) = min, and subject to this condition d_μ(J−1) = min, and so on. In Table 1, d_μ = min entails d_μ(47) = 19 because of hospital j = 3, d_μ(46) = 2 because of hospital j = 23, d_μ(45) = ··· = d_μ(25) = 1 and d_μ(24) = ··· = d_μ(1) = 0; then the 21 control patients not available from hospitals 3 and 23 are drawn instead from 21 other hospitals taking one patient per hospital.

Three of the many possible precise definitions of near-fine optimal match follow:

$$\text{Total}:\text{minimize}\sum _{{\tau }_t\in 𝘛}{\delta }_{{\tau }_t,\mu ({\tau }_t)}\text{subject}\text{to}\sum _{j=1}^J\mid n_j-m_{\mu j}\mid =min,$$ (2)

$$\text{Minimax}:\text{minimize}\sum _{{\tau }_t\in 𝘛}{\delta }_{{\tau }_t,\mu ({\tau }_t)}\text{subject}\text{to}{\mathbf{d}}_{\mu }=min,$$ (3)

and

$$\text{Chi}-\text{square}:\text{minimize}\sum _{{\tau }_t\in 𝘛}{\delta }_{{\tau }_t,\mu ({\tau }_t)}\text{subject}\text{to}\sum _{j=1}^J\frac{{(n_j-m_{\mu j})}^2}{n_j}=min.$$ (4)

The version (4) is equivalent to minimizing the one-sample chi-square statistic in which the n_j act as the “expected counts.” One can impose other sorts of constraints, such as max_1≤j≤J |n_j − m_μj| ≤ β or max_1≤j≤J |n_j − m_μj|/n_j ≤ β instead of the constraints in (2)–(4) or in addition to these constraints, and the finebalance function in the R package finebalance permits a wide variety of combinations.

Our suggestion is to begin with the constraint (2), check the resulting (n_j, m_μj)’s, and consider alternative constraints only if some of the (n_j, m_μj) seem unacceptably discrepant.

2.2 Matching with L ≥ 1 controls per treated subject

With many more potential controls than treated subjects, T ≪ C, one may wish to match each treated subject to L ≥ 1 controls, where C/T ≥ L. Optimal near-fine matching with L ≥ 1 may be solved as a special case of optimal near-fine pair matching. To match with L = 2 controls, duplicate the treated group, find the optimal match, then ‘remember’ that the two copies of each treated subject are actually the same person yielding a 1-to-2 match. Specifically, to match with L = 2 ≤ C/T controls, replace 𝘛 = {τ₁, …, τ_T} by ${𝘛}^{\ast }=\{{\tau }_1,\dots ,{\tau }_T,{\tau }_1^{\ast },\dots ,{\tau }_T^{\ast }\}$ with ${\delta }_{{\tau }_t,{\gamma }_c}={\delta }_{{\tau }_t^{\ast },{\gamma }_c}$ for each t, c, and with τ_t and ${\tau }_t^{\ast }$ having the same value for the nominal covariate, $\nu ({\tau }_t)=\nu ({\tau }_t^{\ast })$. Then a minimum distance near-fine pair match of 𝘛^* with 𝘊 is a minimum distance near-fine match of 𝘛 to L = 2 controls in 𝘊. The case of L ≥ 3 is similar. An alternative but equivalent approach is described in the Web-Appendix.

3. Near-Fine Balance Using the Assignment Algorithm

3.1 A small example

In the current section, we discuss augmenting the distance matrix Δ so that the assignment algorithm solves (2). For instance, this could be done in SAS using proc assign or in R using the pairmatch function of Hansen’s (2007) optmatch package.

Before describing the general procedure in §3.3, a toy example is presented in Table 2 and another in Table 3. It has T = 5 treated subjects, with τ₁, τ₂, and τ₃ in hospital ν(τ_t) = 1, τ₄ in hospital ν(τ₄) = 2, and τ₅ in hospital ν(τ₅) = 3. Fine balance is not possible because there are only two controls in hospital 1, namely γ₁ and γ₂, but there are three treated subjects in hospital 1. Table 2 augments the distance matrix Δ by adding two rows, labeled ε₂₁ and ε₃₁ and one column ξ₁ to produce a 7 × 7 = K × K matrix ϒ; that is, Table 2 is ϒ. Write υ_kℓ for the element of ϒ in row k and column ℓ. Assume each δ_τt,γc in Δ satisfies 0 ≤ δ_τt,γc ≤ ∞. Consider any assignment α(·) in ϒ with finite distance ${\sum }_{k=1}^K{\upsilon }_{k,\alpha (k)}<\infty$. In this assignment, no treated subject τ_t will be assigned to ξ₁ because the total distance ${\sum }_{k=1}^K{\upsilon }_{k,\alpha (k)}$ would then be ∞; so α(τ_t) ≠ ξ₁ for t = 1, …, T. For the same reason, α(ε₂₁) must equal γ₃ or γ₄ or ξ₁, and α(ε₃₁) must equal γ₅ or γ₆ or ξ₁. Finally, either α(ε₂₁) = ξ₁ or α(ε₃₁) = ξ₁; otherwise, α(τ_t) = ξ₁ for some t, and, as just noted, this cannot happen. Define the match μ(τ_t) = α(τ_t) for t = 1, …, T. It is easy to see that any match μ(·) built in this way from an assignment α(·) in ϒ with finite distance ${\sum }_{k=1}^K{\upsilon }_{k,\alpha (k)}<\infty$ satisfies the constraint in (2): μ(·) has m_μ1 = 2 and either (m_μ2, m_μ3) = (2, 1) or (m_μ2, m_μ3) = (1, 2), whereas n₁ = 3, n₂ = 1, n₃ = 1, so ${\sum }_{j=1}^J\mid n_j-m_{\mu j}\mid =min=2$. Moreover, for any assignment α(·) in ϒ with finite distance, we have ${\sum }_{k=1}^K{\upsilon }_{k,\alpha (k)}={\sum }_{{\tau }_t\in 𝘛}{\delta }_{{\tau }_t,\mu ({\tau }_t)}$ because υ_6,α(6) = υ_7,α(7) = 0. Conversely, every match μ(·) with ${\sum }_{j=1}^J\mid n_j-m_{\mu j}\mid =min=2$ corresponds with an assignment α(·) such that υ_6,α(6) = υ_7,α(7) = 0 and υ_t,α(t) ≠ ξ₁ for t = 1, …, 5. Finally, if α(·) is an optimal assignment with finite distance, that is, if it minimizes ${\sum }_{k=1}^K{\upsilon }_{k,\alpha (k)}$ and the minimum value is finite, then μ(·) solves (2) with ${\sum }_{k=1}^K{\upsilon }_{k,\alpha (k)}={\sum }_{{\tau }_t\in 𝘛}{\delta }_{{\tau }_t,\mu ({\tau }_t)}$. Indeed, in this very special case, the solution also solves (3) and (4).

Table 2.

Augmenting the distance matrix to minimize the total distance while minimizing the total deviation from fine balance.

	𝘊	γ1	γ2	γ3	γ4	γ5	δ6	ξ1
𝘛	ν	1	1	2	2	3	3	—
τ1	1	δ11	δ12	δ13	δ14	δ15	δ16	∞
τ2	1	δ21	δ22	δ23	δ24	δ25	δ26	∞
τ3	1	δ31	δ32	δ33	δ34	δ35	δ36	∞
τ4	2	δ41	δ42	δ43	δ44	δ45	δ46	∞
τ5	3	δ51	δ52	δ53	δ54	δ55	δ56	∞
ε21	—	∞	∞	0	0	∞	∞	0
ε31	—	∞	∞	∞	∞	0	0	0

Table 3.

An augmented distance matrix that distributes the deviations from fine balance as uniformly as possible.

	𝘊	γ1	γ2	γ3	γ4	γ5	γ6	γ7	γ8	γ9	γ10	ξ1
𝘛	ν	1	1	2	2	2	2	3	3	3	3	—
τ1	1	δ11	δ12	δ13	δ14	δ15	δ16	δ17	δ18	δ19	δ1,10	∞
τ2	1	δ21	δ22	δ23	δ24	δ25	δ26	δ27	δ28	δ29	δ2,10	∞
τ3	1	δ31	δ32	δ33	δ34	δ35	δ36	δ37	δ38	δ39	δ3,10	∞
τ4	1	δ41	δ42	δ43	δ44	δ45	δ46	δ47	δ48	δ49	δ4,10	∞
τ5	1	δ51	δ52	δ53	δ54	δ55	δ56	δ57	δ58	δ59	δ5,10	∞
τ6	2	δ61	δ62	δ63	δ64	δ65	δ66	δ67	δ68	δ69	δ6,10	∞
τ7	3	δ71	δ72	δ73	δ74	δ75	δ76	δ77	δ78	δ79	δ7,10	∞
ε21	—	∞	∞	0	0	0	0	∞	∞	∞	∞	0
ε31	—	∞	∞	∞	∞	∞	∞	0	0	0	0	0
ζ21	—	∞	∞	0	0	0	0	∞	∞	∞	∞	∞
ζ31	—	∞	∞	∞	∞	∞	∞	0	0	0	0	∞

3.2 A second small example

The procedure in §3.1 augments the distance matrix Δ so that the assignment algorithm solves (2), but that approach does not generally solve problems of the form (3) or (4). Problem (2) is concerned only with the total, ${\sum }_{j=1}^J\mid n_j-m_{\mu j}\mid$, whereas problem (3) is concerned to make individual |n_j − m_μj| as small as possible.

Consider the small example in Table 3 which has the seven treated subjects τ_t and ten controls γ_c. Fine balance is infeasible: there are five treated subject and two controls with ν = 1, so |n₁ − m_μ1| ≥ 3 for every match and the minimum value of ${\sum }_{j=1}^J\mid n_j-m_{\mu j}\mid$ is 6. Problem (2) would allow seven controls to be selected so that |n₁ − m_μ1| = 3, |n₂ − m_μ2| = 3, |n₃ − m_μ3| = 0 with ${\sum }_{j=1}^J\mid n_j-m_{\mu j}\mid =6$, but problems (3) and (4) would each insist that |n₁ − m_μ1| = 3, |n₂ − m_μ2| = 2, |n₃ − m_μ3| = 1 or |n₁ − m_μ1| = 3, |n₂ − m_μ2| = 1, |n₃ − m_μ3| = 2 with ${\sum }_{j=1}^J\mid n_j-m_{\mu j}\mid =6$. In other words, problem (2) would permit the use of 1, 2, 3 or 4 controls with ν(γ_c) = 2 (and similarly for ν(γ_c) = 3), but problems (3) and (4) would each insist that d_μ = {d_μ(1), d_μ(2), d_μ(3)}^T = (1, 2, 3)^T.

In Table 3, the 7 × 10 distance matrix Δ is augmented into an 11 × 11 = K × K matrix ϒ in a manner similar to but slightly different from Table 2. In Table 3, two rows, ε₂₁ and ε₃₁, resemble the augmenting rows in Table 2. Two additional rows, ζ₂₁ and ζ₃₁, are almost the same except in the ξ₁ column where the ε’s have a 0 and the ζ’s have an ∞.

An assignment α(·) in ϒ with finite total distance ${\sum }_{k=1}^K{\upsilon }_{k,\alpha (k)}<\infty$ is easily seen to satisfy d_μ = {d_μ(1), d_μ(2), d_μ(3)}^T = (1, 2, 3)^T by reasoning as follows. To have ${\sum }_{k=1}^K{\upsilon }_{k,\alpha (k)}<\infty$, the assignment α(·) must avoid the ∞’s, so one of γ₃, γ₄, γ₅, γ₆ must be assigned to ζ₂₁ and one of γ₇, γ₈, γ₉, γ₁₀ must be assigned to ζ₃₁. Also, if ${\sum }_{k=1}^K{\upsilon }_{k,\alpha (k)}<\infty$ then either ε₂₁ is paired with one of γ₃, γ₄, γ₅, γ₆ and ε₃₁ is paired with ξ₁ or else ε₃₁ is paired with one of γ₇, γ₈, γ₉, γ₁₀ and ε₂₁ is paired with ξ₁. In consequence, the match μ(·) formed by restricting the assignment α(·) to 𝘛 uses both γ₁ and γ₂ and two or three of γ₃, γ₄, γ₅, γ₆ and two or three of γ₇, γ₈, γ₉, γ₁₀ so d_μ = {d_μ(1), d_μ(2), d_μ(3)}^T = (1, 2, 3)^T.

3.3 A general procedure

Problems (2)–(4) are each special cases of a more general problem, namely

$$\text{minimize}\sum _{{\tau }_t\in 𝘛}{\delta }_{{\tau }_t,\mu ({\tau }_t)}\text{subject}\text{to}{\underset{\_}{\kappa }}_j\le m_{\mu j}\le {\overline{\kappa }}_j,j=1,\dots ,J,$$ (5)

where κ_j ≤ κ̄_j are numbers that are determined by the n_j’s and M_j’s. In problem (2), κ_j = min (n_j, M_j) and κ̄_j = M_j.

The general procedure for (5) is as follows.

• Add rows. Augment the T × C distance matrix Δ by appending $R={\sum }_{j=1}^{J}max(0,M_j-n_j)$ rows defined as follows. For j = 1, …, J, append κ̄_j − κ_j rows ε_jp, p = 1, …, κ̄_j − κ_j, with the distance between ε_jp and γ_c equal to 0 if ν(γ_c) = j and equal to ∞ otherwise. For j = 1, …, J, append M_j − κ̄_j rows ζ_jp, p = 1, …, M_j − κ_j, with the distance between ζ_jp and γ_c equal to 0 if ν(γ_c) = j and equal to ∞ otherwise. Call this matrix Λ.

• Add columns. Augment the (T + R) × C matrix Λ by appending T + R − C columns ξ_q, q = 1, …, T + R − C defined as follows. The distance between τ_t and ξ_q is ∞ for all t, q, the distance between ε_jp and ξ_q is zero for all jp, q, and the distance between ζ_jp and ξ_q is ∞ for all jp, q. Write K = T + R and call this K × K matrix ϒ.

• Find an optimal assignment. Find an optimal assignment α(·) in ϒ.

• Remove extraneous material. Define the match μ(τ_t) = α(τ_t) for t = 1, …, T.

If M_j ≥ n_j for j = 1, …, J, then: (i) exact fine balance is feasible, (ii) R = C − T and K = C so no columns ξ_q are appended, and (iii) the algorithm reduces to the procedure in Rosenbaum, Ross and Silber (2007). The proof of Proposition 1 is in the Appendix.

Proposition 1

If this optimal assignment α(·) produced by the above procedure has infinite total distance, ${\sum }_{k=1}^K{\upsilon }_{k,\alpha (k)}=\infty$, then there is no solution to (5) having finite total distance. Conversely, if ${\sum }_{k=1}^K{\upsilon }_{k,\alpha (k)}<\infty$ then μ(τ_t) = α(τ_t) for t = 1, …, T solves (5). In the worst case, the solution runs in polynomial time, specifically in O(K³) = O{(T + C)³} arithmetic operations.

4. Forcing the use of certain controls

In §1.1, an additional issue concerns diabetes. Diabetes is more common among the obese, and indeed among the 1430 severely obese patients undergoing knee surgery, there were 510 diabetics, whereas among the 2696 non-obese knee surgeries there were only 467 diabetics. Even if all of the 467 non-obese diabetes were included as matched controls, there would be a small deficit, and nothing in the procedure in §3.3 ensures that all 467 diabetic controls will be included in the matched sample. There is a simple adjustment to the procedure in §3.3 that adds an additional constraint to the one in (5), namely that all 467 diabetic controls be included in the match, and then minimizes the total distance subject to both constraints. Let 𝘚 ⊂ 𝘊 be the subset of potential controls who are diabetic. To force a subset 𝘚 ⊂ 𝘊 of controls to be included in the match: if γ_c ∈ 𝘚 and ν(γ_c) = j then (i) change the entry in ϒ for row ε_jp and γ_c from 0 to ∞, (ii) change the entry in ϒ for row ζ_jp and γ_c from 0 to ∞, and (iii) call the result ϒ_𝘚. Reasoning parallel to the proof of Proposition 1 shows that a finite minimum distance assignment in this adjusted matrix ϒ_𝘚 is a minimum distance match subject to the two constraints that all γ_c ∈ 𝘚 be matched and κ_j ≤ m_μj ≤ κ̄_j, j = 1, …, J. Conversely, if δ_τt,γc < ∞ for all τ_t, γ_c, then an infinite minimum distance assignment in ϒ_𝘚 indicates that there is no match μ that uses all controls γ_c ∈ 𝘚 and satisfies κ_j ≤ m_μj ≤ κ̄_j, j = 1, …, J. For instance, in Table 3, if all δ_τt,γc < ∞ and 𝘚 = {γ₃, γ₄, γ₅}, then a minimum distance assignment α(·) with finite distance exists having α(ζ₂₁) = γ₆ and α(ε₂₁) = ξ₁. However, if 𝘚 = {γ₃, γ₄, γ₅, γ₇, γ₈, γ₉} then an optimal assignment α(·) in ϒ_𝘚 must have infinite total distance, and if all δ_τt,γc < ∞ this signifies the infeasibility of joint requirements γ_c ∈ 𝘚 and κ_j ≤ m_μj ≤ κ̄_j, j = 1, …, J.

The procedure above forces the use of a subset 𝘚 ⊂ 𝘊 of controls when constructing a match with near-fine balance for a nominal variable such as the 47 hospitals. In some other context, one might wish to force the use of all 467 diabetic controls without fine balance. To force the use of a subset 𝘚 ⊂ 𝘊 of controls in optimal matching without fine balance, begin with the T ×C matrix Δ of distances, and append C – T rows having C columns with ∞ in columns for γ_c ∈ 𝘚 and 0 in columns for γ_c ∉ 𝘚, calling the resulting C×C matrix Ψ with ψ_kℓ in row k and column ℓ. An assignment α (·) in Ψ defines a match as μ (τ_t) = α (τ_t) ∈ 𝘊, t = 1, …, T. A minimum distance assignment α (·) in Ψ with finite total distance ${\sum }_{k=1}^C{\psi }_{k,\alpha (k)}<\infty$ is a minimum distance match with $\infty >{\sum }_{k=1}^T{\psi }_{k,\alpha (k)}={\sum }_{t=1}^T{\delta }_{{\tau }_t,\mu ({\tau }_t)}$ subject to the constraint that for each γ_c ∈ 𝘚 there is a τ_t ∈ 𝘛 such that γ_c = μ (τ_t).

5. Matching in the Study of Obesity and Surgical Outcomes

5.1 A near-fine match

As noted in §1, fine balance was not achievable for knee surgery in Table 1 because two hospitals performed more knee surgeries on the severely obese with a BMI of 35 or more than among the non-obese with a BMI between 20 and 30. The matching will solve (2), coming as close to fine balance on the hospital as possible, with the additional constraint in §4 that all 467 diabetic controls be included in the match.

In addition to the seven covariates mentioned in §1 and an indicator for a missing Apache score (Rosenbaum 2010, §13), the match will use an analog of the propensity score, namely an estimated probability of obesity given these five covariates, making seven covariate in total; see Rosenbaum and Rubin (1985) for discussion of the propensity score in matching. The distance δ_τt,γc used a caliper on the obesity probability implemented using a penalty function together with a robust version of the Mahalanobis distance; see Rosenbaum (2010, Part II) for specifics of these standard matching techniques.

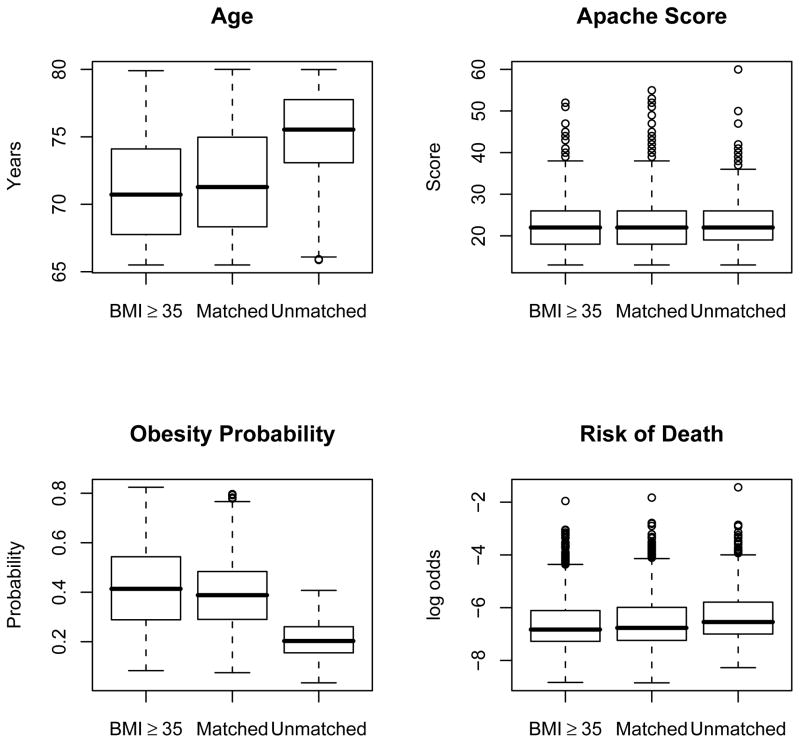
Figure 1 depicts the distribution of the four continuous covariates among the 1430 severely obese patients undergoing knee surgery, their 1430 matched controls, and the 1266 unmatched potential controls. The unmatched potential controls are older, have lower estimated obesity probabilities and slightly higher but still very low estimated log-odds of death. For the four variables in Figure 1, the Spearman rank correlation between the severely obese patient and the matched control was 0.93 for age, 0.81 for the Apache Score, 0.91 for the obesity probability, and 0.82 for the risk score. All 467 diabetic controls were included in the match, but this was still somewhat less than the 510 diabetics among the severely obese. In total, 84% of pairs were matched for diabetes and 91% were matched for sex.

Figure 1.

Baseline comparison of 1430 severely obese knee surgery patients, 1430 matched non-obese knee surgery patients, and 1266 unmatched non-obese knee surgery patients. Severe obesity is a body mass index (BMI) of at least 35, whereas non-obese refers to a body mass index between 20 and 30.

Table 1 shows the distribution of matched patients m_μj by hospital. Hospitals 3 and 23 had too few non-obese controls to permit fine balance, and their deficit of 19 + 2 = 21 controls is made up by other hospitals, for instance, hospital 22 which contributed 4 extra controls and hospital 29 which contributed 1 extra control. Recall that (2) seeks to minimize the total covariate distance within matched pairs subject to the constraint that the total deviation from fine balance is as small as possible. This is a constraint on the marginal distribution of hospital variable, but no attempt is made to match patients to other patients in the same hospital; rather, the pairing emphasizes clinically important variables such as diabetes, age and the Apache and risk scores. In particular, only 45 of 1430 pairs or 3% contain two patients from the same hospital. In Table 1, the Pearson chi-square statistic for the 47 × 2 table hospital × obese-vs-matched-control is 7.8 which is expected to equal its degrees of freedom of 46 in a completely randomized experiment, so the marginal distributions are much closer than they would be in a completely randomized experiment.

5.2 Comparison of the near-fine match with two conventional matches

The near-fine match in §5.1 will now be compared to two conventional optimal matches, called μ₁ and μ₂. Both μ₁ and μ₂ are minimum distance matches using the robust Mahalanobis distance with penalty function calipers on the propensity score, but without the augmentation in §3.3 to force near-fine balance on the hospital indicators and without the forced use of all nonobese diabetics. In μ₁ the hospitals are ignored in the matching. In μ₂, the hospitals are included in both the propensity score and the robust Mahalanobis distance.

Before matching, in the obese group, there were 510 diabetics, or 35.7% = 510/1430, whereas in the nonobese group there were only 467 diabetics or 17.3% = 467/2696, and exact balance for diabetes is not possible. Consider the 2 × 2 table recording obesity by diabetes in the matched samples and its associated chi-square test for independence. In §5.1, the match came as close as possible to balance using all 467 diabetic controls, the matched controls were 32.7% = 467/1430 diabetic, and the chi-square P-value was 0.098, so the balance is imperfect but an imbalance of this magnitude would not be extremely unusual under complete randomization of 2 × 1430 patients to two unmatched groups of equal size. In contrast, the μ₁ match tried to match for diabetes, including it in both the propensity score and the robust Mahalanobis distance, but it picked as matched controls only 374/467 available diabetics, so its control group was 26.2% = 374/1430 diabetic, with a p-value of 4.7×10⁻⁸. The μ₂ match also tried to match for diabetes, but it picked as matched controls only 368/467 available diabetics, so its matched control group was 25.7% = 368/1430 diabetic, with a p-value of 1.1×10⁻⁸. In brief, in §5.1, it was helpful to use the augmentation of the distance matrix in §4 to force the use of all diabetic controls in the marginal distribution separate from the attempt to match individual diabetics to diabetics.

Consider now the absolute difference in the number of obese and nonobese patients in each of the 47 hospitals, that is, 47 absolute differences. For the near-fine match in §5.1, all of the quartiles of these absolute differences were zero patients, the mean absolute difference was 0.89 patients and the maximum absolute difference was 19 patients for hospital #3 which could not have an absolute difference less than 19. For the μ₁ match, the three quartiles of the absolute differences were 3, 9, and 14.5, the mean difference was 10.0 patients, with a maximum difference of 53 patients in hospital #3. For the μ₂ match, the three quartiles of the absolute differences were 1, 3, and 5, the mean difference was 4.0 patients, with a maximum difference of 27 patients in hospital #3. Consider the 2 × 47 table recording obesity by hospital. In this table, the P-value from the chi-square test of independence is 1.00 for the near-fine match in §5.1, is 1.2 × 10⁻⁸ for the μ₁ match which ignored the hospitals, and is 0.998 for the μ₂ match. In brief, the best balance on hospitals is from the near-fine match, though the μ₂ match exhibits better balance than expected from complete randomization of 2 × 1430 patients; however, the μ₁ match is not usable.

Finally, the cross-match test in Heller et al. (2010 or the crossmatch package in R) was used to examine the multivariate balance on the seven covariates. That method takes the matched pairs, forgets for a moment who is matched to whom, rematches subjects using their covariates alone (using optimal nonbipartite matching), and counts the number of times a treated subject was rematched to a control. If the cross-match test were applied to data from a completely randomized experiment with treated and control groups of equal size, the cross-match-probability that a rematched pair contains one treated subject and one control is 1/2. When applied to the near-fine match in §5.1, the P-value from the cross-match test was 0.52, and the estimate of the cross-match-probability was 0.50, so this method judges the multivariate imbalance on the seven covariates to be not unlike the imbalance produced by complete randomization of 2×1430 patients. In contrast, the same test applied to the μ₁ match yields a P -value of 1.00 and an estimate of the cross-match-probability of 0.59, so the balance on the seven covariates is much better than expected from complete randomization. For the μ₂ match, the crossmatch P -value is 0.31 and an estimate of the cross-match-probability is 0.49. Judged by this standard, the balance on the seven covariates is best for μ₁ which ignored the hospitals, but is acceptable for all three matches.

In brief, the near-fine match in §5.1 had reasonable balance for the 7 covariates, for diabetes in particular, and excellent balance for the 47 hospitals. The other two matches, μ₁ and μ₂, were unacceptable for diabetes, and μ₁ was unacceptable for the hospitals.

6. Discussion: interactions, extensions

Minimum distance fine or near-fine matching may address interactions among covariates in several ways. First, the nominal variable ν (·) may itself be an interaction, for instance not 47 hospitals but 47 × 3 = 141 categories from the 47 hospitals and three 5-year age categories, (66, 70], (70, 75], (75, 80]. Second, concerning interactions between the nominal variable ν(·) and other covariates, the distance δ_τt,γc may include an added penalty for matching a patient in one hospital to a patient in another hospital; then, the algorithm will prefer to match patients with similar covariates in the same hospital recognizing that this is not always possible. Alternatively or additionally, the distance δ_τt,γc may include covariates that describe the hospital, such as hospital volume or teaching status; then, the algorithm will prefer to match similar patients in similar hospitals. Finally, a propensity score can include covariates that describe the hospital as well as the patient and can include interaction terms; then, a caliper on the propensity incorporated in δ_τt,γc will tend to balance hospital as well as patient characteristics and also their interactions. See Rosenbaum (2010, Part II) for discussion of the use of penalties and calipers in minimum distance matching.

When fine balance is not feasible, the algorithms in §3.3 and the Web-Appendix minimize the total covariate distance Σ_τt∈𝘛 δ_τt,μ(τt) within matched pairs among all matched samples with minimal deviation from fine balance. In fact, these algorithms can be used in other ways. The algorithms create a family of methods with exact fine balance at one extreme and with no attempt at fine balance at the other extreme.

Specifically, by a suitable choice of (κ_j, κ̄_j), j = 1, …, J, the algorithms in §3.3 and the Web-Appendix may be used to minimize Σ_τt∈𝘛 δ_τt,μ(τt) while producing a controlled rather than minimal deviation from fine balance. For example, suppose that fine balance is feasible because M_j > n_j ≥ 1 for every j. In this case, if one set (κ_j, κ̄_j) = (n_j − 1, n_j + 1), j = 1, …, J, then the resulting match would deviate from fine balance by at most 1 in each hospital, but because the constraint is less constraining, the minimum value of the total covariate distance Σ_τt∈𝘛 δ_τt,μ(τt) will be no larger than before and is very likely to be smaller. Setting κ_j = max(0, n_j − λ) and κ̄_j = min (M_j, n_j + λ) for an integer λ ≥ 0 will limit the maximum deviation from fine balance to at most λ. For λ = 0, this yields fine balance. For sufficiently large λ this yields a conventional minimum distance match that makes no effort to balance the nominal variable. By varying λ, the investigator can control the relative emphasis placed on balancing the nominal variable versus finding pairs that are close in terms of the covariate distance.

Appendix. The proof of Proposition 1

The proof of Proposition 1 parallels the discussion of Tables 2 and 3. Because each υ_kℓ ≥ 0, if ${\sum }_{k=T+1}^K{\upsilon }_{k,\alpha (k)}=\infty$ then ${\sum }_{k=1}^K{\upsilon }_{k,\alpha (k)}=\infty$. The first step is to show that ${\sum }_{k=T+1}^K{\upsilon }_{k,\alpha (k)}<\infty$ if and only if κ_j ≤ m_μj ≤ κ̄_j for j = 1, …, J, where m_μj = |{τ_t ∈ 𝘛 : ν {μ (τ_t)} = j}|. Now ${\sum }_{k=T+1}^K{\upsilon }_{k,\alpha (k)}<\infty$ if and only if the M_j − κ̄_j rows ζ_jp are assigned to different columns γ_c with ν (γ_c) = j, and at most κ̄_j − κ_j rows ε_jp are assigned to other columns γ_c with ν (γ_c) = j; therefore, of the M_j columns γ_c with ν (γ_c) = j, at least M_j − κ̄_j are not paired with τ_t’s and at most M_j − κ_j are not paired with τ_t’s, so at least κ_j and at most κ̄_j columns γ_c with ν (γ_c) = j are paired with τ_t’s. The second step is to note that if ${\sum }_{k=T+1}^K{\upsilon }_{k,\alpha (k)}<\infty$ then ${\sum }_{k=T+1}^K{\upsilon }_{k,\alpha (k)}=0$ and

$$\sum _{k=1}^K{\upsilon }_{k,\alpha (k)}=\sum _{k=1}^T{\upsilon }_{k,\alpha (k)}=\sum _{{\tau }_t\in 𝘛}{\delta }_{{\tau }_t,\alpha ({\tau }_t)}=\sum _{{\tau }_t\in 𝘛}{\delta }_{{\tau }_t,\mu ({\tau }_t)},$$

so an optimal assignment α (·) in ϒ with ${\sum }_{k=T+1}^K{\upsilon }_{k,\alpha (k)}<\infty$ minimizes the total distance in matched pairs Σ_τt∈𝘛 δ_τt,μ(τt) subject to the constraint κ_j ≤ m_μj ≤ κ̄_j for j = 1, …, J. The time bound is for the Hungarian method applied to a K × K assignment problem; see Papadimitriou and Steiglitz (1982, Theorem 11.1).