RESTING STATE INTER AND INTRA HEMISPHERIC HUMAN BRAIN FUNCTIONAL CONNECTIVITY

Abstract

Resting-state functional connectivity between neuroanatomical regions has attracted significant attention in recent years. In the process of obtaining the resting-state functional connectivity map of the human brain from blood-oxygen-level-dependent fMRI signals, it is common to average the signals from left and right hemispheres. This averaging can introduce unappreciated complexities and unintended consequences not related to the research question of interest. In this paper, we mathematically demonstrate that measures of functional connectivity obtained by averaging homologous regions from the both hemispheres become undesirably dependent on four inter-hemispheric connectivity measures. We explore this finding in real-world fMRI data from 25 healthy young participants. We show that inter-hemispheric averaging has a mixed effect on the results and may introduce correlation artifacts to the connectivity map. Furthermore, we show mathematically and demonstrate with Monte Carlo simulations of null data that inter-hemispheric averaging will not alter human brain connectivity map at rest only and if only there are no inter-hemispheric correlations.

1. INTRODUCTION

Recent advances in functional Neuroimaging technology have revealed that spontaneous low-frequency (<0.1 Hz) fluctuations in the resting-state fMRI signal are correlated between areas believed to be functionally related [1]. Strong homologous-region inter-hemispheric functional connectivity is reported in animal and human brains with a variety of non-neuroimaging tools [2]. Neuroimaging findings also present strong homologous-region inter-hemispheric correlations [1], [3], often interpreted as inter-hemispheric synchrony. Based on this interpretation, inter-hemispheric averaging of the resting-state fMRI signals, especially for lateralized regions (i.e. Lateral Parietal, Supra Marginal, and etc), has become a common practice in the field of Neuroimaging [4–6]. Averaging is further justified because it can increase statistical power for detecting functional connectivity, and it circumvents issues associated with lack of localization accuracy in regions close to the medial plane (i.e. Posterior Cingulate). In fact, when regions are identified using seed locations these seeds are often placed exactly on the medial plane to cover both hemispheres which makes the segregation of the two hemispheres impossible.

In this paper, we first mathematically examine the effects of inter-hemispheric averaging on the functional connectivity map of the brain at rest. We then validate the mathematical findings with simulations and with resting state fMRI data from 25 healthy young participants.

2. ARITHMATIC AVERAGING

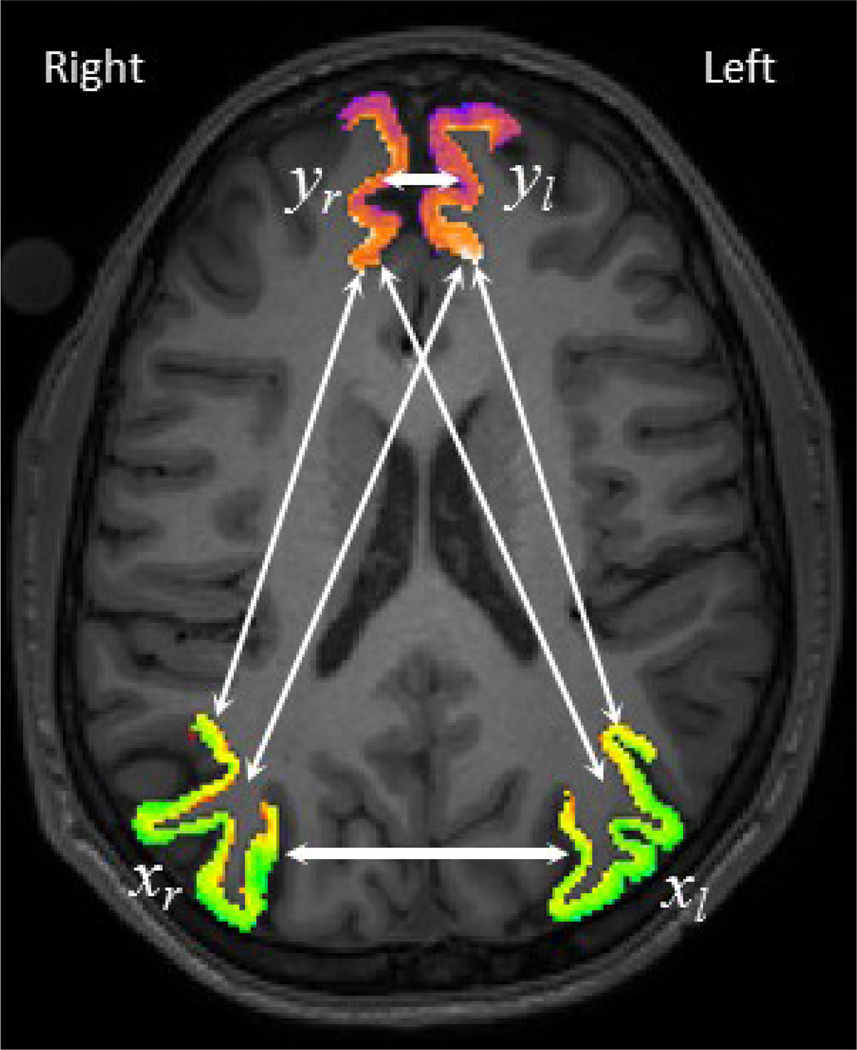
In this section we illustrate the mathematical relationship between the correlation coefficients of two pairs of regional signals and their correlation coefficient after pair-wise inter-hemispheric averaging. Fig. 1 shows two sample pairs of regions (Inferior Parietal (x_r, x_l), and Superior Frontal (y_r, y_l)) on the right and left hemispheres overlaid on a sample MRI image. In neuroscience research we are often interested in studying intra-hemispheric functional connectivity (correlations: _ρxr,yr, ρ_xl,yl) while being aware of strong homologous-region inter-hemispheric functional connectivity (Correlations: ρ_xr,xl, ρ_yr,yl). However, there is also cross-region inter-hemispheric functional connectivity (correlations: ρ_xr,yl, ρ_xl,yr), which is often paid less attention in this field. Thus there are two intra and four inter-hemispheric functional connectivities that can be computed between two pairs of regions in both hemispheres. The goal of this section is to demonstrate the mathematical relationship between the functional connectivity after inter-hemispheric averaging, ρ_{(xr+xl),(yr+yl)}¹ and the six aforementioned inter and intra-hemispheric functional connectivities. If we define x = x_r + x_l, y = y_r + y_l, then correlation of two averaged signals is:

$${\rho }_{x,y}={\sigma }_{x,y}/\sqrt{{\sigma }_x^2{\sigma }_y^2}=\frac{{\rho }_{x_r,y_r}{\sigma }_{x_r}{\sigma }_{y_r}+{\rho }_{x_r,y_l}{\sigma }_{x_r}{\sigma }_{y_l}+{\rho }_{x_l,y_r}{\sigma }_{x_l}{\sigma }_{y_r}+{\rho }_{x_l,y_l}{\sigma }_{x_l}{\sigma }_{y_l}}{\sqrt{({\sigma }_{x_r}^2+{\sigma }_{x_l}^2+2{\rho }_{x_r,x_l}{\sigma }_{x_r}{\sigma }_{x_l})({\sigma }_{y_r}^2+{\sigma }_{y_l}^2+2{\rho }_{y_r,y_l}{\sigma }_{y_r}{\sigma }_{y_l})}}$$ (1)

where ρ_a,b is the correlation coefficient between the signals a and b, ${\sigma }_a^2$ is the variance of signal a, and σ_a,b is the covariance of signals a and b. Equation (1) demonstrates that the correlation between averaged signals is not only a function of intra-hemispheric correlations, but also depends on homologous and cross-region inter-hemispheric correlations. Most striking is the denominator: since it is only a function of the homologous inter-hemispheric connectivities and increases for positive values, which makes the overall connectivity of averaged signals smaller, against conventional wisdom. When the homologous-regions inter-hemispheric correlation is very high, ρ_xr,xl = ρ_yr,yl ≈ 1, the averaged signals correlation become equal to:

$${\rho }_{x,y}\approx {\lambda }_1{\rho }_{x_r,y_r}+{\lambda }_2{\rho }_{x_r,y_l}+{\lambda }_3{\rho }_{x_l,y_r}+{\lambda }_4{\rho }_{x_l,y_r}$$ (2)

where λ₁ = σ_xrσ_yr/ϑ, λ₂ = σ_xrσ_yl/ϑ, λ₃ = σ_xlσ_yr/ϑ, λ₄ = σ_xlσ_yl/ϑ, and ϑ = σ_xr σ_yr + σ_xr σ_yl + σ_xl σ_yr + σ_xl σ_yl. The Lambdas are the weighting factors in the range of [0,1) that control the influence of each of the four correlations in equation (2) and λ₁ + λ₂ + λ₃ + λ₄ = 1. As it seen in this equation, the cross-region inter-hemispheric correlations (ρ_xr,yl, ρ_xl,yr) are as important as the intra-hemispheric correlations (ρ_xr,yr, ρ_xl,yl) in the computation of the correlation between the averaged signals. Next we examine a case in which no homologous-regions inter-hemispheric correlations exist (ρ_xr,xl = ρ_yr,yl ≈ 0). Surprisingly, equation (2) still holds for this special case as well, with differences only in the normalization factor ϑ. Therefore, in the absence of homologous inter-hemispheric dependency

$${\rho }_{x,y}\approx {\lambda }_1^{\prime }{\rho }_{x_r,y_r}+{\lambda }_2^{\prime }{\rho }_{x_r,y_l}+{\lambda }_3^{\prime }{\rho }_{x_l,y_r}+{\lambda }_4^{\prime }{\rho }_{x_l,y_l}$$ (3)

where ${\lambda }_1^{\prime }={\sigma }_{x_r}{\sigma }_{y_r}/\vartheta \prime ,{\lambda }_2^{\prime }={\sigma }_{x_r}{\sigma }_{y_l}/\vartheta \prime ,{\lambda }_3^{\prime }={\sigma }_{x_l}{\sigma }_{y_r}/\vartheta \prime ,{\lambda }_4^{\prime }={\sigma }_{x_l}{\sigma }_{y_l}/\vartheta \prime$, and $\vartheta \prime =\sqrt{{\sigma }_{x_r}^2{\sigma }_{y_r}^2+{\sigma }_{x_r}^2{\sigma }_{y_l}^2+{\sigma }_{x_l}^2{\sigma }_{y_r}^2+{\sigma }_{x_l}^2{\sigma }_{y_l}^2}$. Again Lambdas are the weighting factors in the range of [0,1) that control the influence of each of the four correlations in equation (3) and ${\lambda \prime }_1^2+{\lambda \prime }_2^2+{\lambda \prime }_3^2+{\lambda \prime }_4^2=1$. Since $a+b\ge \sqrt{a^2+b^2}$, then ϑ ≥ ϑ′, and eventually ${\lambda }_i\le {\lambda }_i^{\prime }$, ∀i ∈ {1,2,3,4}. This result shows that stronger homologous inter-hemispheric correlations make the correlation of averaged signals weaker. This is at first surprising because averaging is often justified on the grounds that high homologous inter-hemispheric functional connectivity increases the signal-to-noise ratio of the averaged signal. On the other hand, cross-region inter-hemispheric correlations differently affect the averaged signals correlation depending on the sign of the correlations. However, we will show in the next section that inter-hemispheric correlations are often highly positive and negative cases are rare or extremely small. In that case, one can conclude; the effect of homologous and cross-region inter-hemispheric correlations on the averaged signals correlation is opposite. While an increase in homologous correlations cause reductions in the average signal correlation, the increase in cross-region inter-hemispheric correlations causes the averaged signals correlation to increase.

Fig. 1.

Illustration of all six different correlations involved when inter-hemispheric averaging preformed.

Finally, if one normalizes the temporal signals to zero mean and unit variance, meaning σ_xr = σ_yr = σ_xl = σ_yl = 1, it is easy to show that λ_i = 1/4, ${\lambda }_i^{\prime }=1/2$, ∀i ∈ {1,2,3,4}. Therefore the correlation of averaged signals is equal to the average of two corresponding intra-hemispheric correlations only when all four inter-hemispheric correlations are zero (ρ_xr,xl = ρ_yr,yl = ρ_xr,yl = ρ_xl,yr ≈ 0). In the next section, we show that this is not the case in real data. Thus inter-hemispheric averaging can both increase or reduce the correlation magnitude.

3. EXPERIMENTAL RESULTS

In this section, we use real and simulated fMRI data to validate the findings in the previous section. We start with a small dataset of resting BOLD fMRI data and then perform a Monte Carlo simulation of null data.

3.1. fMRI Data Examination

The prevailing method of fMRI data analysis has poor localization accuracy due to its spatial normalization and smoothing steps. Analyzing fMRI data in a subject’s native space instead gives the highest level of localization accuracy. Native space analysis circumvents the necessity of spatial normalization and smoothing by assigning a single temporal signal to each neuroanatomical region in the brain. This makes the computation of inter-regional correlations much easier where at the same time maximizes localization accuracy.

In this study we only consider ten neuroanatomical regions that have repeatedly been reported to be part of human brain default network. These regions and their abbreviation are: Hippocampus (Hi), Entorhinal (En), Inferior-Parietal (IP), Isthmus-Cingulate (IC), Medial-Orbito-Frontal (MOF), Para-Hippocampal (PHi), Posterior-Cingulate (PoC), Pre-Cuneus (PCu), Superior-Frontal (SF), Supra-Marginal (SM). Please note that any region can be selected for this analysis, as the primary aim of this paper is not to detect the human brain default network.

3.2.1. Subject’s Data and Acquisition

We used a small pilot dataset to examine the effect of inter-hemispheric averaging on resting-state functional connectivity map. Twenty five young and healthy participants (11 M, 14 F, mean age: 25.4 Y, STD age: 2.74 Y) were recruited through a random market mailing from within 10 miles of the Columbia University Medical Center. Participants were screened to exclude individuals with a history of neurologic or psychiatric conditions and those using psychoactive medications.

Structural images were acquired using a 3.0 Tesla magnetic resonance scanner (Philips). The structural image obtained with T1-weighted turbo field echo sequence with TE/TR = 2.98ms/6.57ms; flip angle = 8 degrees; 256×256 matrix; in-plane voxel size = 1.0 mm ×1.0 mm; slice thickness = 1.0mm (no gap), and 165 slices. Functional images were acquired using the same scanner with a field echo echo-planar imaging (FE-EPI) sequence (TE/TR = 20ms/2000ms; flip angle = 72 degrees; 112×112 matrix; in-plane voxel size = 2.0 mm × 2.0 mm; slice thickness = 3.0 mm (no gap); 37 transverse slices per volume), and 6:1 Philips interleaved, in ascending order. Participants were scanned for 9.5 minutes, with instructions to rest and to keep their eyes open for the duration of the scan; and not to think of any one thing in particular and not to fall asleep.

3.2.2. fMRI Localization and Preprocessing

The structural T1 images were segmented and parcellated using FreeSurfer software [7]. The regional masks were transferred to the subject’s fMRI space using FSL rigid body registration tool, flirt [8] and used to generate a single temporal signal for each region by spatial averaging of the voxels at each time point.

The 6:1 slice interleaving of Philips scanner was corrected using Sinc interpolation. As is reported in recent publications, resting bold signals are extremely sensitive to motion [9], so additional processes of motion removal have been taken into account here. First, we used mcflirt to register all the volumes to a reference image (averaged fMRI image). Second, we used the method described in [10] to create frame-wise displacement (FD) and root mean square differences (RMSD) of the bold percentage signal. Third, the contaminated volumes were detected (FD>0.5mm or RMSD>0.3%) and replaced with the new volumes generated by linear interpolation of adjacent volumes. Volume replacements were done before band-pass filtering [11]. Finally, we residualized the temporal signals by regressing out the FD, White Matter and Ventricles signals.

The motion corrected signals were band-pass filtered with cut off frequencies of 0.01 and 0.08 Hz using the tool flsmaths –bptf. After filtering, the first 10 volumes were discarded due to the initial lag of the FIR filter. Next we computed the inter-regional correlation by masking out the contaminated volumes due to motions (FD>0.5mm or RMSD>0.3%) [10]. The mean correlation values are plotted as a cross-correlogram of Fig. 2 (upper triangular). The upper triangular in Fig. 2 is divided into three sections by two white lines. The section on the left/right gives the intra-hemispheric correlations in the left/right hemisphere, and the middle section gives the inter-hemispheric correlations. From the middle section it is evident that homologous-regions have the strongest correlations. However, the cross-region inter-hemispheric correlations are also as strong as the intra-hemispheric correlations.

Fig. 2.

Cross-Correlogram of the default network before and after inter-hemispheric averaging in upper and lower triangular, respectively.

Next, we averaged the signals from the corresponding left and right hemisphere regions and plot their correlation values in a separate cross-correlogram in Fig. 2 (lower triangular). As seen in Fig. 2, inter-hemispheric averaging generates a different set of results. In many cases, the correlation magnitudes increase, which was shown to be indicative of significantly high cross-region inter-hemispheric correlations. In other cases, averaging reduces the correlation, which is the result of a strong inter-hemispheric correlation for the corresponding regions. These results clearly show that averaging has a mixed and surprisingly complex effect on the final correlation map, as seen in Fig. 2. This finding is in contrast to the commonly held belief that strong inter-hemispheric correlations justify inter-hemispheric averaging and call for greater nuance. In the next subsection we show that only in the absence of inter-hemispheric correlations, averaging does not change the distribution of the induced correlations.

3.2. Monte Carlo Simulation

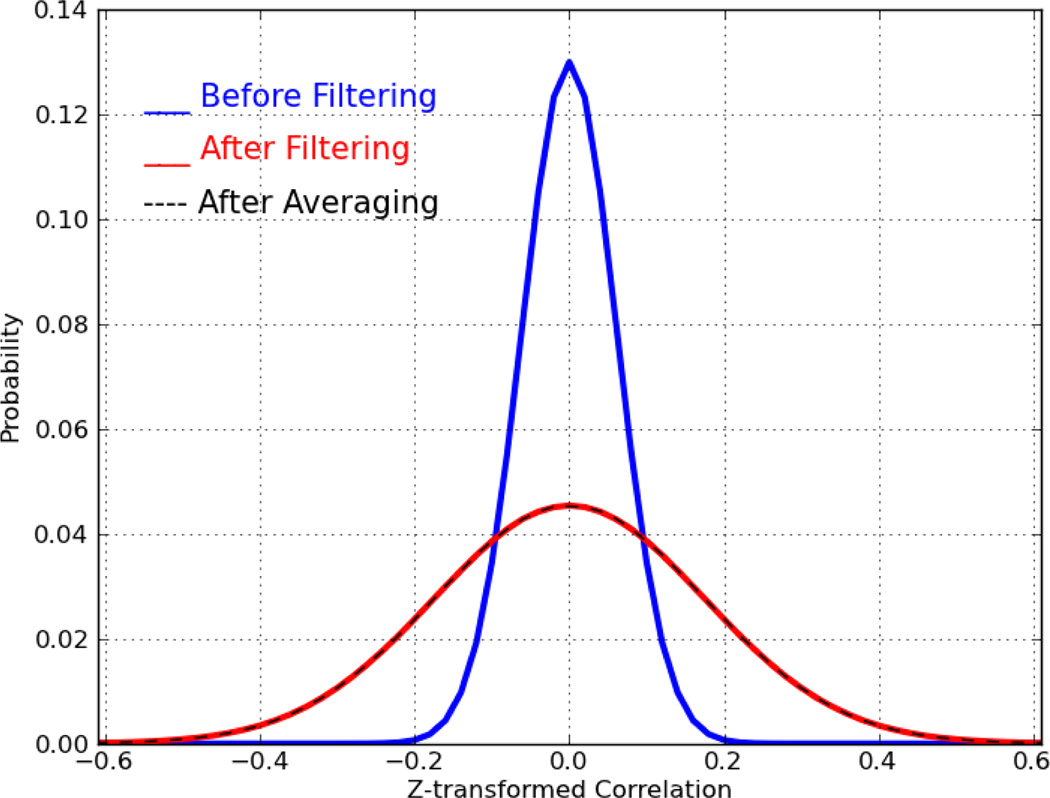
We generated 10⁴ sequences of Gaussian random numbers (mean=0, std=1), all with equal length of 285 points (this is the same length as our real data). Then we computed every possible pair-wise correlation within the generated sequences. Next, we band-pass filtered these signals (with the same filter used in real data) and recomputed all pair-wise correlations. Fig. 3 shows the distributions of all possible pair-wise correlations before (blue) and after (red) band-pass filtering. As demonstrated, the temporal band-pass filtering induces correlations up to 0.5. Even without filtering, purely random signals can generate correlations up to 0.2. This simulation shows that for a pair of limited length filtered random signals (285 points), the probability of generating non-zero correlations is significantly high, which violates any zero correlation assumptions.

Fig. 3.

Distribution of pair-wise correlation computed for Gaussian random sequence of length 280 points, before filtering (blue), after filtering (red), after averaging (black)

Finally, we examined the effect of random signal averaging on the final distribution of the pair-wise correlations. We randomly averaged half of the 10⁴ random sequences with the other half yielding 5,000 new random sequences. Distribution of all of their possible pair-wised correlations is shown in Fig. 3 by black dashed line curve. As the figure shows, averaging does not introduce any extra correlations. This clearly validates the results of inter-hemispheric independence, meaning if the inter-hemispheric time-series are independent of one another, averaging will not have a significant effect on the distribution of the final correlations.

4. CONCLUSION

The analysis of the current study suggests that the inter-regional correlation map can be measured by hemispherically averaged signals only when there is no inter-hemispheric correlation. This result is confirmed with Monte Carlo simulations of null data. However, analysis of real data shows that there exist strong inter-hemispheric correlations in human brain regions. In fact, homologous inter-hemispheric correlations are shown to be particularly strong (ρ_xr,xl = ρ_yr,yl ≈ 1) between certain regions. More interesting is the effect that homologous and cross-region inter-hemispheric correlations have on the correlation between the inter-hemispherically averaged signals: the theoretical formula shows that homologous and cross-region inter-hemispheric functional connectivity have opposite effects; most surprisingly, positive homologous inter-hemispheric functional connectivity acts to decrease the functional connectivity between inter-hemispherically averaged signals, in direct contrast to a commonly held view in the Neuroimaging community at large. This is also confirmed with real data examination. While there are many pair-wise correlations which will be increased by inter-hemispheric averaging, there also exist pairs of regions whose functional connectivity is decreased by inter-hemispheric averaging. Therefore, inter-hemispheric averaging of the fMRI signals seems to be problematic and, because of the complex and unintended consequences demonstrated in this paper, should best be avoided.