Abstract
Nanoparticle shape can improve drug delivery, based in part on recent findings that flexible, worm-like nanocarriers (Worms) increase the amount of drug delivered to tumors and shrink the tumors more effectively than spherical micelles (Spheres). Here, all-atom molecular dynamics (MD) simulations are used to build a rational coarse grain (rCG) model that helps clarify shape-dependent effects in delivery of the widely used anticancer drug Taxol by block copolymer micelles. Potentials for rCG-MD were developed to examine the partitioning of this hydrophobic-aromatic drug into Worms and Spheres that self-assemble in water from poly(ethyleneglycol)-poly(caprolactone) (PEG-PCL), a weakly segregating amphiphile. PCL is a biodegradable, hydrophobic polymer widely used in biomaterials and accurately modeled here. Thermodynamic integration of the force to pull a single Taxol molecule from the micelles into solvent shows that twice as much drug loads into Worms than Spheres, fully consistent with experiments. Diffusivity of drug in the hydrated PEG corona is surprisingly slow compared to that in the core, indicative of strong but transient drug-polymer interactions. The distinctly distended corona of the Worms enhances such interactions and reflects the same balance of molecular forces that underlie an experimentally-validated phase diagram for simulated Spheres, Worms, and Bilayers. Moreover, with realistic drug loadings in micro-second simulations, Taxol is seen to draw PEG chains into the PCL core, dispersing the drug while localizing it near the interface—thus providing a molecular explanation for a measurable burst release of drug as well as the enhanced delivery seen with Worms.
Cancer is diagnosed today in about 50% of the population over the average lifetime of a person, with nearly all therapies pushed from bench to bedside based solely on trial-and-error experimentation, particularly when it comes to formulation. Current treatments generally include chemotherapy, and many of the top anticancer drugs in the clinic have a hydrophobic and/or aromatic character that allows them to permeate cell membranes but also motivates packaging into nanoparticles of various types[1]. In solubilizing a drug to increase the injectable dose, nanoparticles generally improve pharmacokinetics compared to free drug as they limit rapid excretion through the kidney and increase the drug delivered to a disease site such as a tumor.[2] Paclitaxel or “Taxol” is prototypical and one of the first anti-cancer drugs discovered (in the bark of the Pacific yew tree). It is now one of the most common anti-cancer drugs in the clinic as it binds and stabilizes microtubules to frustrate cell division,[3] and for similar reasons Taxol is also used in numerous polymer coatings on drug-eluting stents to help prevent restenosis.[4] Nanoparticles of various materials have been designed for delivery of such hydrophobic-aromatic drugs plus other therapeutics and are now widely investigated, with recent discoveries including the surprising advantages of filament- shaped particles on circulation, delivery, and even tumor shrinkage.[5–8] Filamentous viruses that include several strains of influenza are of course natural assemblies, some of which can circulate, are physically flexible, and can carry multiple copies of the virus’ genome. Synthetic amphiphiles that also self-assemble into filaments or other micelles and vesicles in water are attractive for delivery applications, especially when biocompatible and degradable, but the interplay between drug partitioning, interfacial effects, and morphology is generally a resource-intensive process of experimentation. At high drug concentrations, perturbations to nanoparticle structure, properties, and/or drug aggregation can be perplexing and potentially contribute to mechanisms such as a burst release in which drug is lost shortly after loading. Here we address such issues with rational coarse grain molecular dynamics (rCG-MD) simulations that tie closely to the physical chemistry of polymer-based micelles and drugs.
Block copolymer amphiphiles are simply too large to simulate atomistically, but rCG-MD models that maintain specific chemical properties show great promise in clarifying physical properties such as amphiphile phase behavior in water. Our approach to modeling in a chemically exacting manner begins by accurately capturing solubilities and flexibilities of each polymer chain.[9,10] Poly(ethylene glycol) (PEG) is a widely used biocompatible polymer and so are polyesters such as the polycaprolactone (PCL), which is attractive for drug delivery systems and other biomaterial applications such as stents[11] due to its gradual hydrolysis to monomers.[12] The phase behavior of PEG-PCL block copolymers can depend on the method of preparing the micelle, bilayered vesicle, or nanoparticle[13,14] and can be complex because PCL is semi-crystalline.[15] A hydrophobic anti-cancer drug such as Taxol adds an additional level of complexity to self-assembly as well as controlled release. Nonetheless, it is clear from wide-ranging experiments of Taxol-loaded, PEG-PCL based Wormlike filomicelles (‘Worms’) that– compared to Sphere micelles of the same composition–Worms load about twice as much drug, deliver almost two-fold more drug to mouse tumors, and can also sustainably shrink tumors that are untreatable with Taxol-Spheres.[16,17] Here, we utilize a novel set of rCG-MD approaches to examine the morphological dependence of Taxol delivery with PEG-PCL micelles. Thermodynamic integration together with other methods of analysis quantify drug partitioning and characterize drug dispersion. First we show that Taxol partitions two-fold more in the cores of Worms versus Spheres, and we ultimately provide an explanation for the sudden and generally inefficient ‘burst release’ seen with many types of drug delivery systems.[17]
Computational Experiments: Enhanced Taxol loading is in Worm Micelles
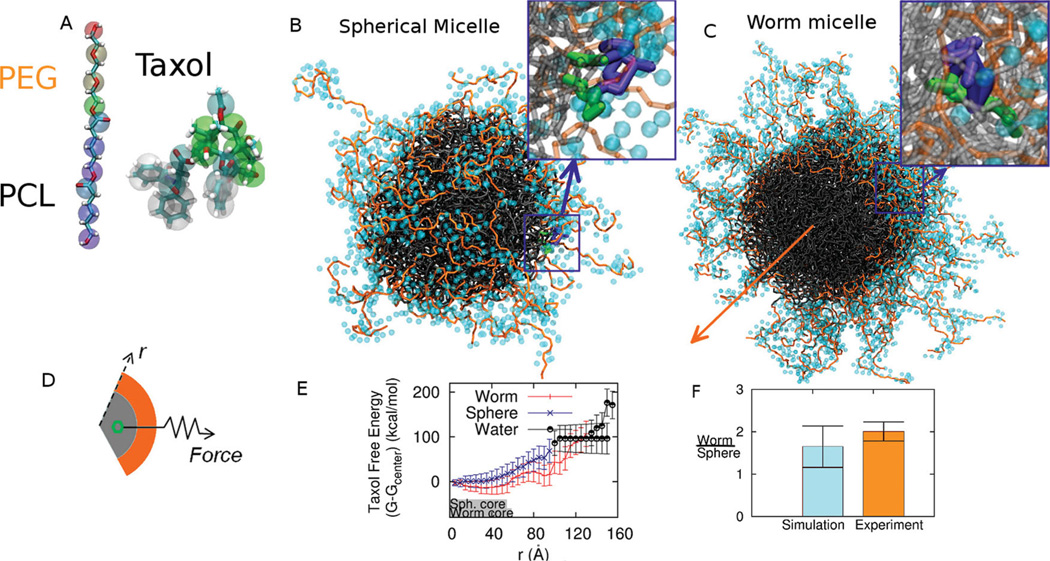
While our rCG-MD models of strongly segregating but relatively short block copolymer amphiphiles of ~1 kg/mol or less have been shown to assemble into the expected bilayers and micelles in water,[18,19] drug delivery applications often use longer chains (≫ 1 kg/mol) and weakly segregating amphiphiles such as PEGx–PCLy (x and y in g/mol). Achieving the proper but subtle balance between solubilities and chain flexibilities is critical to self-assembly as well as experimentally relevant integration of Taxol within a rCG-MD model (Figure 1A). All-atom simulations of a melt of PCL oligomers at 1 Atm and 300K (Figure S1) are used at the start to obtain the flexibility parameters of the rCG model, while all-atom simulations of Taxol partitioning in 3-octanol and water are likewise needed to parameterize bonds and angles for realistic flexibility and solubility. The rCG models break-up each molecule into 2–5 heavy atoms per bead (Table S1, Table S2), depending on the specific chemistry and symmetry of the underlying chemical structure, thus decomposing the intermolecular potentials into chemical components[20] and optimizing intramolecular potentials based an all-atomistic simulations[21,22] (see Experimental Section). Stable, Taxol-integrating micelles of PEG2000–PCL5000 form in water in both spherical (Figure 1B) and worm micelle morphologies (Figure 1C). As might be expected, where Taxol locates near the interface (50 Å), it orients with aromatic portions facing the PCL core (insets in Figure 1B,C). Full quantitation of drug loading is shown below to be well within the capabilities of modern rCG computations and can put all of these models to the test against experimental results for drug delivery.
Figure 1.
Rational Coarse Grain Models of PEG-PCL and Taxol with Free Energy Calculations. A. Based on all-atom computations, the diblock copolymer is modeled with one CG bead per ethylene glycol monomer and three CG beads per caprolactone monomer plus one interfacial CG bead between the two blocks. Taxol’s CG model maps 3–5 heavy atoms into each CG bead. Supplemental Tables 1 and 2 provide mapping details. B, C. Spherical micelle and Worm micelle cross-section used for thermodynamic integration with Taxol constrained near the interface. The block copolymer is PEG2000–PCL5000,and PEG in orange is shown with its hydration layer of CG water. Taxol’s aromatic groups orient toward the core. The orange arrow indicates the symmetry axis of the worm micelle. D, E. Thermodynamic integration constrains Taxol at a radial position r from the center of mass of a micelle and measures the constraint Force vs r. The core dimensions of Sphere and Worm micelles at 0.05% PCL density are indicated schematically with gray bars, and the transition to water is taken at 0.01% PEG density, which is also close to the plateau density for bulk water. The change in Taxol free energy ΔG(r) is determined relative to the center of the micelle, although the minimum free energy for the Worm is close to the PEG-PCL interface. F. The partition coefficient for Taxol transferred into water from each micelle is calculated, and the partition ratio (Worm/ Sphere) agrees with experiments.
First we calculate the free energy profile of the drug dragged through micelles of the same molecular weight copolymer by utilizing thermodynamic integration along a radial path from the center of mass of the given micelle, through the PEG corona, and into the bulk water. The drug’s center of mass is fixed at a radius r within a spherical or cylindrical shell with a constraint force F (Figure 1D), and the change in Taxol Free Energy, ΔG(r), is calculated as
| (1) |
where Fr is the radial component of the local constraint force of the spring which is ensemble averaged 〈…〉. The resulting ΔG(r) are clearly distinct for the Worms and Spheres (Figure 1E).
Within the core of each micelle–denoted schematically by a grey bar out to a PCL density of 0.05%–Taxol’s free energy is seen to be more negative for the Worms than for the Spheres. The minimum energy for Taxol in the Worm is also close to the interface, whereas the minimum in the Sphere is at the center of the core. Upon pulling the drug across either micelle’s interface, the Worm shows a distinct local minimum (near 90 Å) that is not seen with the Sphere. This is indicative of particularly strong interactions of Taxol with PEG chains that are more extended by packing constraints in the Worm (out to 130 Å) than the Sphere (out to 100 Å). The difference is in some sense surprising because PEG molecular weights are the same, but simple ideas of surfactant packing in micelles seem consistent with this. Out to the edge of this hydrated polymer corona (defined at 0.01% PEG density without drug), drug interaction with PEG remains strong with ΔG < 0, even though drug interactions with the PCL core are stronger. Moreover, Taxol interacts sufficiently strongly with PEG in the Worm (less so in the Sphere) that pulling on the drug with force F stretches PEG into bulk water.
Experiments had shown Worms load about twice as much Taxol as Spheres, and so we calculated the mean change in free energy from the minimum in each PCL core to the PCL interface as 35.1 kBT (20.9 kcal/mol) for the Sphere and 34.8 kBT (21.3 kcal/mol) for the Worm (Table 1). These energies relate to the partition coefficients through logn K, and for Taxol in lipid vs. water the reported logn Klipid/w = 13.1 kBT[23] appears considerably smaller than for PCL-based micelles–a fact which had been noted previously in studies of PEG-PCL vesicles.[24] More importantly, the relative partitioning of Taxol into Worms versus Spheres4
| (2) |
agrees remarkably well with experimental results (Figure 1F) for a similar molecular weight copolymer[25] that also shows more drug in worm micelles by a factor of 2.01 (± 0.22). A morphology change from worm to sphere thus decreases drug loading. Importantly, a slight degradation of PCL will drive a Worm-to-Sphere transition–as clarified in simulations below of the PEG-PCL phase diagram, and this will tend to release drug and thus contribute to the enhanced anti-cancer effects of Taxol-loaded Worms.[25]
Table 1.
Thermodynamic integration results for single molecule Taxol partitioning into Water from Octanol as well as Sphere and Worm micelles composed of PEG2000–PCL5000. ΔG is taken from the minimum in the PCL core.
| Taxol Partitioning | Octanol | Sphere Micelle | Worm micelle |
|---|---|---|---|
| ΔG (kcal/mol) | 1.9 (+/−0.1) | 20.9 (+/−8.1) | 21.1 (+/−6.6) |
| logn K (kBT) | 3.16 (2.49–4.4)a) | 34.8 | 35.1 |
Experimental range cited in text.
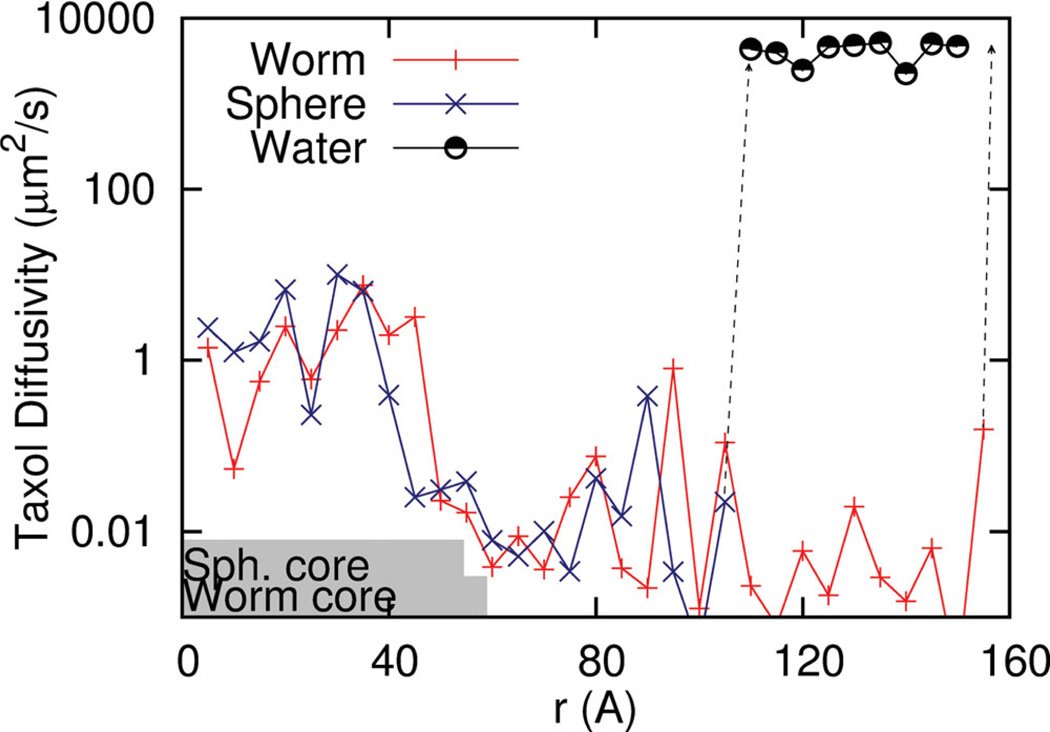
As part of the same simulations, the local diffusion coefficient of Taxol is calculated from the variation of local forces on the solute and a force auto-correlation function (FACF) analysis.[26] The slow diffusion in this system and the position dependent diffusivity make this a useful method:
| (3) |
D(r) ranges from about 0.1 to 1 µm2/s in the hydrophobic PCL core (Figure 2), which is slower than the typical diffusivity of a lipid in a bilayer (~1 µm2/s) but slightly faster than diffusivities of Taxol in PCL as deduced from drug release studies.[27] Surprisingly, within the PEG corona, diffusion of Taxol decreases significantly to 0.001 µm2/s, and this appears due to strong but transient interactions with PEG chains, which are sufficiently long to be entangled (with 46 monomers). In bulk water, Taxol diffusion jumps to 4000 µm2/s, which is 4-fold larger than experiment,[28] but the small difference almost certainly reflects the effects of the larger solvent molecules. This transition to diffusion in bulk occurs at longer length scales for the Worm than the Sphere because the PEG brush of the Worm is significantly extended as noted before. Most important in these analyses, the strong but transient interactions with the PEG corona do impede Taxol diffusion but do not define a free energy minimum for either type of micelle (Figure 1F). Taxol that loads into the PEG corona is thus predicted to be lost more rapidly, consistent with a burst release process (e.g., Figure S2).
Figure 2.
Taxol diffusivity derived from force auto-correlation function (FACF) analysis of drug pulled from the center of mass of the micelle into water. Core dimensions of Sphere and Worm micelles down to 0.05% PCL density are indicated with gray bars. The transition to water is indicated by a dashed line and shows the expected rapid increase in drug diffusivity. Between the core and water, Taxol interacts strongly with the PEG corona, which impedes diffusion.
Phase Diagram and Density Profiles of PEG-PCL reveal Weak Segregation
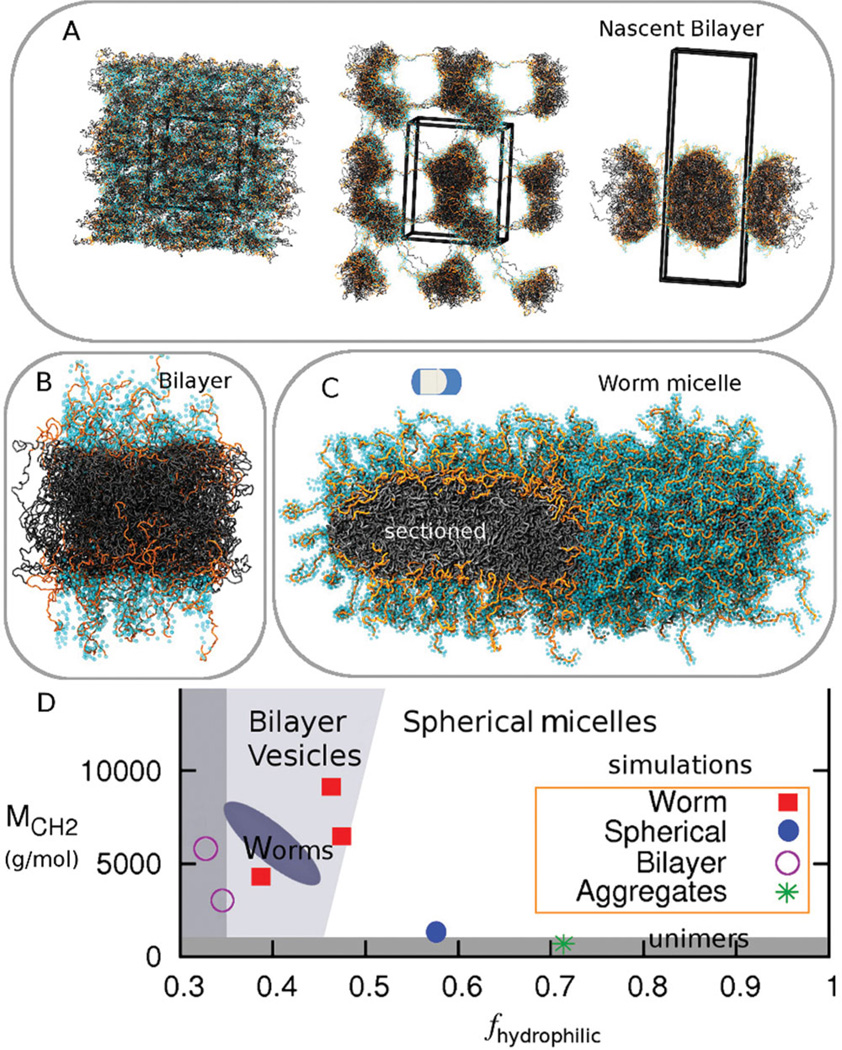
To ensure that our modeled polymers possess the correct physical properties, we simulated seven PEG-PCL copolymers with different hydrophilic fractions (fhydrophilic) and different molecular weights (Table S3) and compared to the recent experimental phase diagram based on over 30 different PEG-PCL polymers.[15] We perform rCG-MD simulations with the LAMMPS code[29] and we find–consistent with experiments– that the stable morphology in solution ranges from polymer vesicle bilayers to worm micelles to spherical micelles with transitions achieved primarily by increasing fhydrophilic (Figure 3,Table S3). At low fhydrophilic the model is consistent with bilayer formation as shown in Figure 3A: random fluctuations in a homogeneous mixture of copolymer and water are soon followed by segregation with both hydrophobic and hydrophilic entanglements throughout the periodic box, and then complete segregation of water and polymer into a bicelle (30 ns), that over long times reveals a bilayer. Figure 3C shows such a PEG2000–PCL7700 bilayer patch of a ‘polymersome’, while Figure 3 B shows a stable worm micelle of PEG2000–PCL5000,which has a much lower fhydrophilic. Likewise, PEG2000–PCL1000 generates a spherical micelle while PEG2000–PCL500 is too short to assemble (Figure 3D) even though many diacyl lipids that readily assemble have a molecular weight in the range of just 500 g/mol. Long established arguments of Israelachvili[30] predict the curvature trends in curved assemblies here and do apply in a straightforward fashion to strongly segregating block copolymers such as PEG-polybutadiene (PEG-PBD),[31] but PCL is a weakly segregating block. Oxygen in PCL contributes to fhydrophilic in the estimations here and in recent work,[15] and this important contribution quantitatively aligns the phase diagram of PEG-PCL (Figure 3D) to that of other, more strongly segregating block copolymers such as PEG-PBD.[31] Orange chains of PEG in the sectioned bilayer and worm micelle (Figure 3B,C) are indeed seen to interact with the PCL core in addition to generating the expected corona hydrated with light blue waters.
Figure 3.
Coarse Grain self-assembly of PEG-PCL with comparison to experimental phase diagram. A. Homogeneous dispersion of PEG1000–PCL3000 that assembles into a Bilayer. PEG is orange with cyan CG water forming a hydration layer (≤ 5 Å). Fluctuations in the random mixture are followed by segregation with extensive polymer entanglements in the periodic box, and then formation of a bicelle-like frustrated bilayer (at 30 ns). B, C. Bilayer of PEG2000–PCL7700,and Worm of PEG2000–PCL5000 are both stable morphologies. D. Phase diagram for CG simulations fit within a recent experimental phase diagram of the dominant phases.
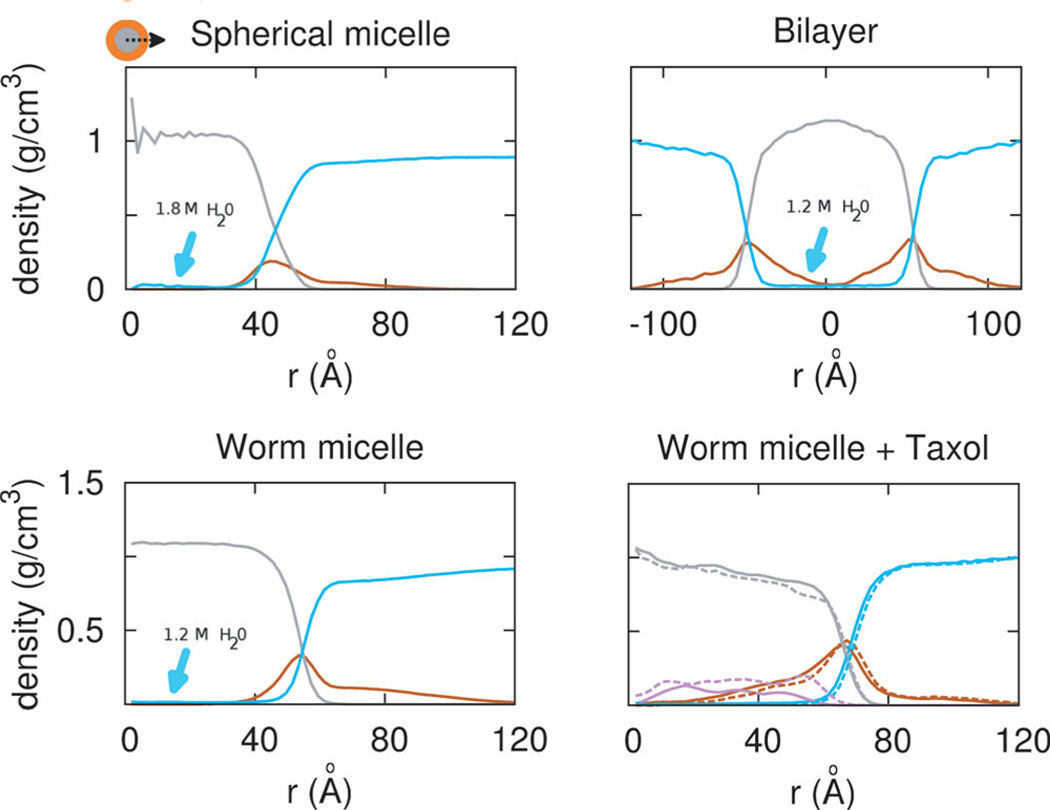
Density profiles of the same molecular weight polymers in worm or sphere micelle morphologies (Figure 4) and also a similar molecular weight polymer bilayer quantify the extent of PEG penetration into the core as well as other key features. PEG penetrates into the core of the worm micelle more so than in the spherical micelle, and as clarified below this effectively increases the loading capacity at the interface and results in the additional free energy well noted earlier in Figure 1E. With the spherical micelle, the interfacial region allows water penetration to nearly all occupied PEG corona regions, and slightly into the PCL core, while the worm micelle case does not allow water penetration as deep into the PEG corona region. Water is seen in the core at about 0.02 wt% loading per nanocarrier, which is much lower than typical Taxol loading (see below), and the center of the Sphere has 50% more water (~1.8 M) compared to the Worm and Bilayer (~1.2 M). The core of the Worm is nonetheless larger in diameter, by about 5 Å, due to stretching of the chains, consistent with mean field theories.[32] The worm and bilayer morphology also possesses a denser PEG corona (orange) (0.4 g/cm3) than the spherical micelle, even though PCL density in the core (grey) is comparable to a bulk melt (1.2 g/cm3) in all three morphologies. All of these contributing factors result in a larger loading volume for Taxol in worm micelle and the low free energy state.
Figure 4.
Morphology dependent density profiles. (from left to right, top to bottom) Sphere of PEG2000–PCL5000,Worm of PEG2000–PCL5000 without and with taxol, and Bilayer of PEG2000–PCL7700. Water (cyan) penetrates into the core of the Sphere moreso than other morphologies. Worm and Bilayer morphology possess a denser PEG corona (orange) at 0.4 g/cm3 than the Sphere. Density in the core (grey) approaches that of a bulk melt of PCL, 1.2 g/cm3. With 3 or 9 wt% Taxol, PEG shifts into the core, and core density decreases. Increasing drug load shifts drug towards the interface.
As 3 wt% Taxol or 9 wt% Taxol are added to micelles of PEG2000–PCL5000, the density profiles change and prove revealing. PEG shifts into the core, decreasing the PCL core density by a remarkable 33%, to 0.8 g/cm3. With increasing drug concentration, Taxol shifts towards the interface from 40 Å to 60 Å. Drug partitioning towards the interface and strong interactions with the hydrophilic component have long been thought to contribute to burst release,[33] and this is the clearest molecular evidence of such polymer rearrangement. Molecular dynamics is a crucial component to the design of drug delivery vehicles, and can depict a molecular view of the drug loading, and the degree of drug-vehicle interactions.
As a further check on the polymer physics of these assemblies, the radius of the hydrophobic core, Rcore, is shown to depend on the PCL tail length, Mh, with the form Rcore ~ Mh0.50, indicating a weakly segregated interface dominated by chain entropy (see Figure S3). This is in surprising contrast to the growth of the core with the molecular weight of the tail with a strongly segregating block copolymer such as PEG-PBD, which scales as ~Mh0.6 and is close to the strong segregation theory (SST) of ~Mh0.66.[9] Likewise, from the interaction parameter χcalculated from short chain atomistic simulations of polymers in the melt phase, the interfacial width in SST can be estimated to be 10 Å (see Suppl. Results), but here we see a much larger width of ~20 Å in the Worm. The difference demonstrates the weak segregation, consistent with significant penetration of PEG into the PCL core, with implications for Taxol partitioning. The increased hydration at the interface, could also play a role in the noted suppression of crystallization in PEG-PCL worm-like micelles,[15] promoting a melt that is more likely to integrate Taxol than a crystal.
Taxol aggregation in Water versus Taxol dispersion within PEGPCL Worm Micelles
Taxol’s poor solubility is well-documented with partitioning between octanol and water that ranges experimentally from logn Ko/w = 2.5 to 4.4[13,34] (Table 1). Simulations here of rCG Taxol in octanol-water mixtures as well as in pure water (Figure 5 A,B) show Taxol molecules in pure water aggregate within nanoseconds (<10 ns). Taxol reportedly exhibits a head-to-tail packing in its crystalline phase in polar solvents, and head-to-head packing in non-polar solvents due to hydrogen bonding.[35] In our short simulations, head-to-tail crystallization in the aggregate was not evident, but the obvious close packing clearly minimizes contact with water. In contrast and as detailed below, Taxol molecules remain homogeneously dispersed within the PCL core of micelles, with some notable local correlations.
Figure 5.
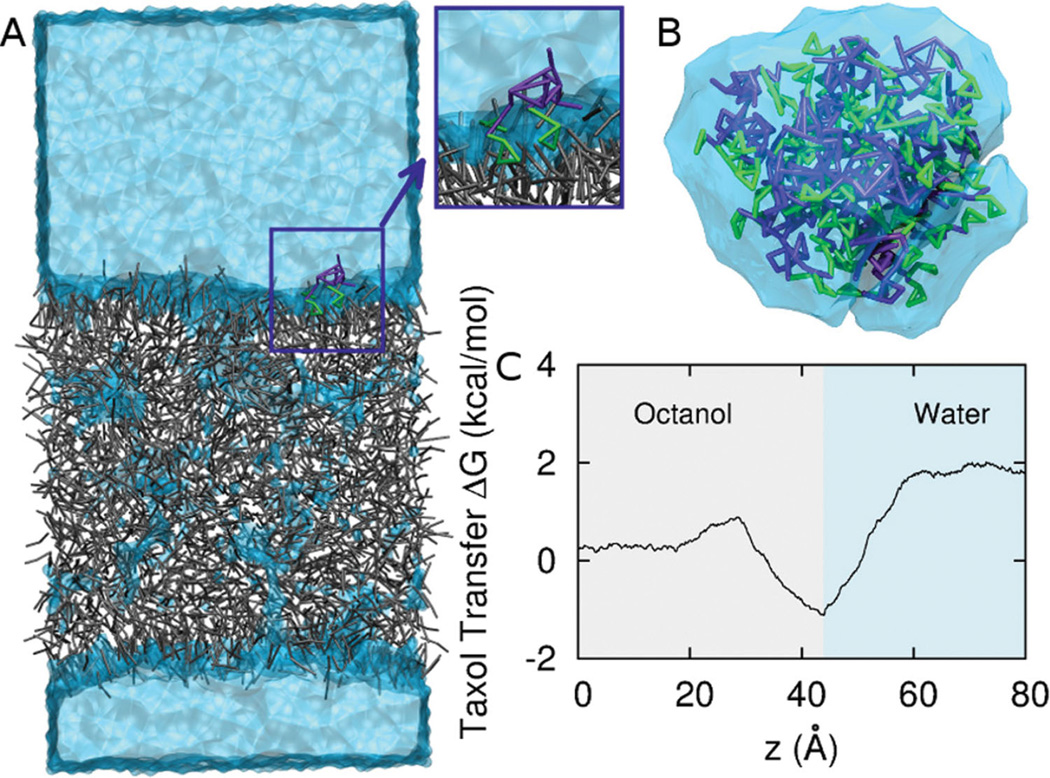
Taxol in bulk water and at the Octanol water interface. A. Steered molecular dynamics of drug across a CG octanol-water interface. Octanol is grey, CG water is light blue, and Taxol is purple and green (benzene groups). B. Taxol aggregates in CG water in tens of nsec due to hydrophobicity. C. ΔG vs. z across the octanol-water interface. Interfacial adsorption near z = 40 Å is followed by an increase in free energy in the water phase with a net change of 1.9 kcal/mol.
Jarzinsky’s equality,[36] a special case of Crook’s theorem,[37] tells us that the work, W,relates to the free energy change, ΔG, between the two phases: From this we can calculate an octanol/water partition coefficient, logn Ko/w, where Ko/w = e−ΔG/kT by measuring the work in pulling Taxol across an octanol-water interface. Taxol is pulled at constant velocity, and the force is averaged over many pulls. Figure 5C shows Taxol has a preference for the interface of an octanol-water mixture, as is evident in the local minimum of the free energy profile. Indeed, the orientation of Taxol close to the interface (Figure 5B, inset) shows the more hydrophobic and aromatic portions buried in octanol, which is reminiscent of orientations in PEG-PCL micelles (Figure 1B–C) and is typical of the interfacial activity of aromatic compounds at lipid membranes. Importantly, far from the interface, the total free energy change of −1.9 kcal/mol corresponds to a partition coefficient of 3.16 which is in the middle of the experimental range (Table 1).
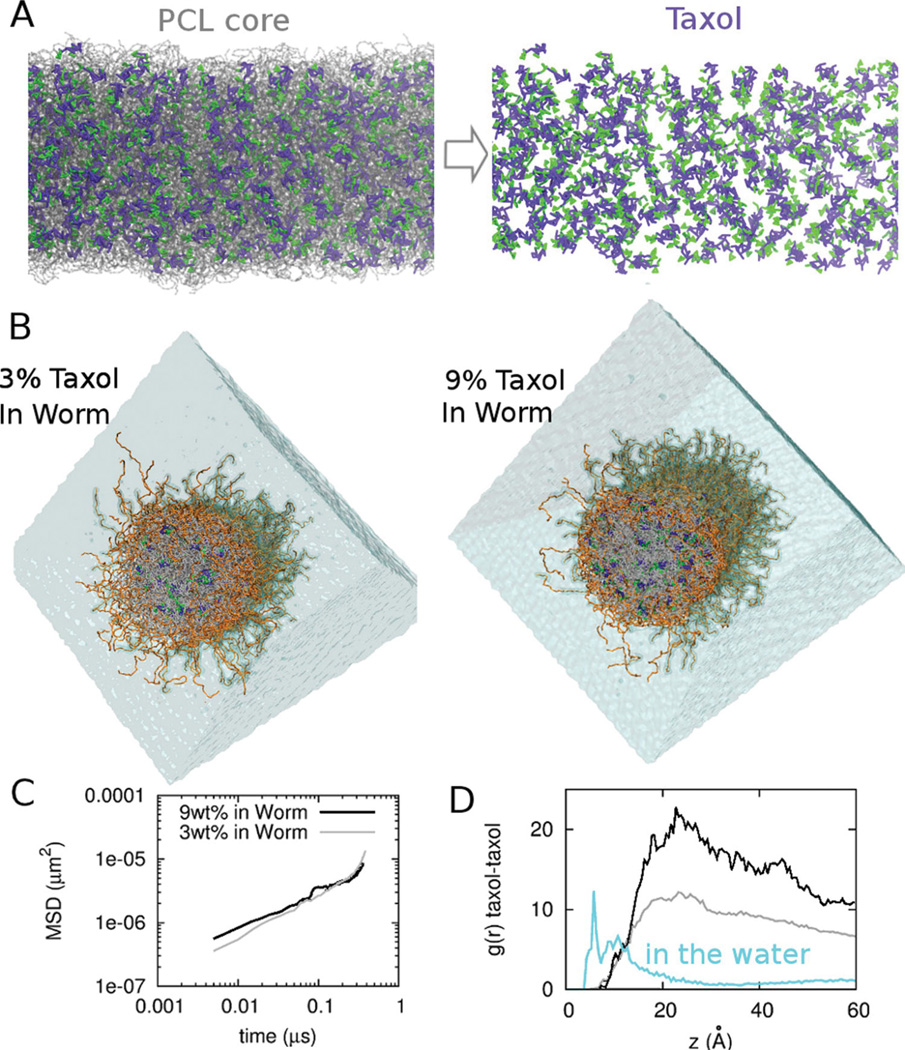
To test the drug-drug-polymer interactions and perturbations to assemblies, we set up worm micelles at different concentrations of Taxol loading, and at the higher load of 9 wt% Taxol, which is at the high end of experimental loadings[38],drug molecules appear dispersed as quantified below (Figure 6A). After very long simulations that approach ~µsec’s, the micellar structure also remains stable at both 3 wt% and 9 wt% Taxol (Figure 6A,B), and mean squared displacements versus time (Figure 6C) further allow us to estimate the diffusion constant as: . At 300 nsec, 3 wt% Taxol gave DTax/PCL ~ 3 µm2/s whereas 9 wt% gave slightly lower DTax/PCL ~ 1 µm2/s, which suggests enhanced drug-drug interactions at high loading. Mean diffusivity speeds up on longer times and likely reflects more equilibrated interactions within the core, such as with PEG permeating the interface (Figure 3C). Regardless, the values for DTax/PCL here are within the range of values calculated above by pulling Taxol through the core using the FACF method (Figure 2).
Figure 6.
Taxol dispersion at realistic drug concentrations within a Worm micelle. A. CG Taxol at 9 wt% in a PEG2000–PCL5000 Worm micelle core, with Taxol in purple and green and PCL chains as transparent grey. B. CG Taxol at 3 wt% loading (left) and 9 wt% loading (right), with the Worm’s end-cap removed to reveal the radial distribution of Taxol. C. Mean-squared displacement (MSD) of Taxol diffusing over 0.5 ms in 3 wt% and 9 wt% loaded Worms. D. Radial distribution function g(r) for taxol-taxol interactions in bulk water, and in the two drug-loaded Worms.
Importantly, after the very long simulations (450 ns), the Taxol-Taxol radial distribution function g(r) shows aggregation in water but dispersion of the drug in the PCL core (Figure 6D). In bulk water, the Taxol-Taxol peak is at ~5 Å and is consistent with a local head-to-tail stacking as cited above. Within the micelle, Taxol perturbs the interface and interacts strongly with interfacial PEG, while also setting up a Taxol-Taxol network, the periodicity of which is denoted by the peak in the g(r) at 20 Å and appears consistent with a locally correlated head-to-head stacking. Deeper examination of g(r) shows that increased drug load decreases the correlations, due perhaps to the increased interaction with PEG. Loading of the drug near the interface, towards the micellar corona as an explanation of ‘burst release’ has been in discussion in drug delivery community for many decades[33] and is now clearly demonstrated here in a nanoparticle.
Accounting for morphology-dependent drug loading requires accurate modeling of the subtly distinct contributions to the aggregate free energy — namely the entropies of hydrophilic and hydrophobic blocks, the various interaction energies near and far from the interface, the solvent, and the drug. The solubility of simple aliphatic and aromatic compounds has been shown to depend on the state of the polymer molecule and the underlying micellar morphology in Flory-type mean field theory.[39] We show here that an ideal way to capture such complexity for advanced delivery systems while maintaining a strong connection with the underlying chemistry and experimental properties is to use a multi-scale rCG-MD approach.
Others have used Dissipative Particle Dynamics with highly simplified potentials to study integration of Taxol into self-assemblies of PEG-poly(lactic acid) (i.e. PEG-PLA, another type of polyester copolymer) and concluded that the drug acts as a template for self-assembly.[40] However, experiments show that including Taxol during the PEG-PCL micellization process prevents worm formation entirely.[41] Here we demonstrate that the collective behavior of the drug at higher loading can influence the packing and interfacial profile in the Worms: in particular, increases in Taxol concentration shift the drug towards the interface, increasing drug-drug interactions and drug-PEG interactions. Higher concentrations of drug should therefore exhibit greater burst release. Controlled supression of burst release should increase plasma residence time of drug and, in combination with passive targeting to tumors (via Enhanced Permeation and Retention), improve drug delivery to tumors.[42] Doubtless, these drug concentration effects may depend on the specific drug and nanoparticle, but the results nonetheless suggest a practical means to harnessing the relative immisciblity of polymers to understand and control burst release from physically loaded nanocarriers. In general, the core polymer (PCL here) is thought to dominate drug release, but here we show that the corona (PEG) and the interface (between PEG and PCL) also play a significant role. Consistent with this picture, particles made with PEG-PLA modified by the hydrophilic polymer glycolic acid also exhibit strong burst release,[42] with increased burst release found with increasing glycolic acid. Moreover, modifications of Taxol to make the drug more soluble in PEG-polyesters generally increases loading and exhibits a more sustained release profile,[13] predictably shifting the solute towards the core. On the other hand, Worms made from strongly segregating, highly hydrophobic copolymers such as PEG-PBD do not stably retain much Taxol compared to Worms of PEGPCL,[25] which is consistent with an important role for the intermediate solubility of PCL. Likewise, increasing the molecular weight of PEG generally promotes loading with shorter PCL lengths,[43] most likely due to the additional interaction of Taxol with the PEG.
Several key considerations in the choice of a nanoparticle system for delivery are highlighted here with shape of the nanocarrier itself as important perhaps as miscibility of components with themselves, water, and drug. Similarly detailed investigations could help clarify interactions of drug-laden micelles with cell membranes, particularly in promoting diffusion of drug from the micellar interface and corona into and across the cell membrane. It has been speculated by various groups that permeation is a central mechanism in drug delivery, preceding endocytosis,[44] and such hypotheses seem increasingly within the realm of simulation: namely, diffusion in water of a nano-carrier with drug partitioned from its target (eg. Microtubule for Taxol) by a tumor cell membrane. Detailed insights into the various barriers to delivery can and should be increasingly computed to transcend the dominating empiricism of drug delivery and maximize the impact of nanoparticle science on human health and disease.
Supplementary Material
Acknowledgements
We gratefully acknowledge an NIH NRSA postdoctoral fellowship (to S. M. Loverde) and NIH grants (NIH R01-EB007049 to D.E.D; NSF DMR- 0520020 to M.L.K.). We had helpful discussions with Wataru Shinoda, Russell DeVane, and Axel Kohlmeyer. Support was provided in part by the NSF through TeraGrid resources provided by National Institute for Computational Sciences (NICS) at the University of Tennessee under grant number TG-MCA93S020.
Footnotes
Supporting Information
Supporting Information is available from the Wiley Online Library or from the author.
Contributor Information
Sharon M. Loverde, Email: sloverde@seas.upenn.edu, Chemical and Biomolecular Engineering, University of Pennsylvania, 129 Towne Building, 220 South 33rd St., University of Pennsylvania, Philadelphia, PA 19104, USA.
Michael L. Klein, Department of Chemistry, Temple University, Beury Hall 130, 1901 N. 13th St., Philadelphia, PA 19122, USA
Dennis E. Discher, Email: discher@seas.upenn.edu, Chemical and Biomolecular Engineering, University of Pennsylvania, 129 Towne Building, 220 South 33rd St., University of Pennsylvania, Philadelphia, PA 19104, USA.
References
- 1.Peer D, Karp JM, Hong S, Farokhzad OC, Margalit R, Langer R. Nat. Nanotechnol. 2007;2:751. doi: 10.1038/nnano.2007.387. [DOI] [PubMed] [Google Scholar]
- 2.Kwon G, Kataoka K. Adv. Drug Delivery Rev. 1995;16:295. [Google Scholar]
- 3.De Brabander M, Geuens G, Nuydens R, Willebrords R, De Mey J. Proc. Natl. Acad. Sci. USA. 1981;78:5608. doi: 10.1073/pnas.78.9.5608. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Stone GW, Ellis SG, Cox DA, Hermiller J, O’Shaughnessy C, Mann JT, Turco M, Caputo R, Bergin P, Greenberg J, Popma JJ, Russell ME. N. Engl. J. Med. 2004;350:221. doi: 10.1056/NEJMoa032441. [DOI] [PubMed] [Google Scholar]
- 5.Champion JA, Mitragotri S. Proc. Natl. Acad. Sci. USA. 2006;103:4930. doi: 10.1073/pnas.0600997103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Geng Y, Dalhaimer P, Cai S, Tsai R, Tewari M, Minko T, Discher DE. Nat. Nanotechnol. 2007;2:249. doi: 10.1038/nnano.2007.70. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Gratton SE, Ropp PA, Pohlhaus PD, Luft JC, Madden VJ, Napier ME, DeSimone JM. Proc. Natl. Acad. Sci. USA. 2008;105:11613. doi: 10.1073/pnas.0801763105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Park JH, von Maltzahn G, Xu MJ, Fogal V, Kotamraju VR, Ruoslahti E, Bhatia SN, Sailor MJ. Proc. Natl. Acad. Sci. USA. 2010;107:981. doi: 10.1073/pnas.0909565107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Loverde SM, Ortiz V, Kamien RD, Klein ML, Discher DE. Soft Matter. 2010;6:1419. doi: 10.1039/b919581e. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Srinivas G, Discher DE, Klein ML. Nat. Mater. 2004;3:638. doi: 10.1038/nmat1185. [DOI] [PubMed] [Google Scholar]
- 11.Liu SJ, Chiang FJ, Hsiao CY, Kau YC, Liu KS. Ann. Biomed. Eng. 2010;38:3185. doi: 10.1007/s10439-010-0075-6. [DOI] [PubMed] [Google Scholar]
- 12.Jeong B, Bae YH, Lee DS, Kim SW. Nature. 1997;388:860. doi: 10.1038/42218. [DOI] [PubMed] [Google Scholar]
- 13.Forrest ML, Yanez JA, Remsberg CM, Ohgami Y, Kwon GS, Davies NM. Pharm. Res. 2008;25:194. doi: 10.1007/s11095-007-9451-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Shum HC, Kim JW, Weitz DA. J. Am. Chem. Soc. 2008;130:9543. doi: 10.1021/ja802157y. [DOI] [PubMed] [Google Scholar]
- 15.Rajagopal K, Mahmud A, Christian DA, Pajerowski JD, Brown AEX, Loverde SM, Discher DE. Macromolecules. 2010;2010:9736. doi: 10.1021/ma101316w. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Christian DA, Cai S, Garbuzenko OB, Harada T, Zajac AL, Minko T, Discher DE. Mol. Pharm. 2009;6:1343. doi: 10.1021/mp900022m. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Geng Y, Discher DE. Polymer. 2006;47:2519. [Google Scholar]
- 18.Shinoda W, DeVane R, Klein ML. Molecular Simulation. 2007;33:27. [Google Scholar]
- 19.Shinoda W, DeVane R, Klein ML. Self-assembly of surfactants in bulk phases and at interfaces using coarse-grain models. In: Voth GA, editor. Coarse-graining of condensed phase and biomolecular systems. CRC Press; 2008. p. 329. [Google Scholar]
- 20.Siepmann JI, Karaborni S, Smit B. Nature. 1993;365:330. [Google Scholar]
- 21.Noid WG, Chu J, Ayton GS, Shrishna V, Izvekov S, Voth GA, Das A, Anderson HC. J. Chem. Phys. 2008;128:244114. doi: 10.1063/1.2938860. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Shelley JC, Shelley MY, Reeder RC, Bandyopadhyay S, Klein ML. J. phys. Chem. B. 2001;105:4464. [Google Scholar]
- 23.Wenk MR, Fahr A, Reszka R, Seelig J. J. Pharm. Sci. 1996;85:228. doi: 10.1021/js950120i. [DOI] [PubMed] [Google Scholar]
- 24.Ahmed F, Pakunlu RI, Srinivas G, Brannan A, Bates F, Klein ML, Minko T, Discher DE. Mol. Pharm. 2006;3:340. doi: 10.1021/mp050103u. [DOI] [PubMed] [Google Scholar]
- 25.Cai S, Vijayan K, Cheng D, Lima EM, Discher DE. Pharm Res. 2007;24:2099. doi: 10.1007/s11095-007-9335-z. [DOI] [PubMed] [Google Scholar]
- 26.Marrink SJ, Berendsen HJC. J. phys. Chem. 1994;98:4155. [Google Scholar]
- 27.Lao LL, Venkatraman SS, Peppas NA. Eur. J. Pharm. Biopharm. 2008;70:796. doi: 10.1016/j.ejpb.2008.05.024. [DOI] [PubMed] [Google Scholar]
- 28.Ross JL, Santangelo CD, Makrides V, Fygenson DK. Proc. Natl. Acad. Sci. USA. 2004;101:12910. doi: 10.1073/pnas.0402928101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Plimpton S. J. Comp. Phys. 1995;117:1. [Google Scholar]
- 30.Israelachvili JN. Intermolecular and Surface Forces. London: Academic Press; 2011. [Google Scholar]
- 31.Jain S, Bates FS. Science. 2003;300:460. doi: 10.1126/science.1082193. [DOI] [PubMed] [Google Scholar]
- 32.Noolandi J, Hong KM. Macromolecules. 1983;16:1443. [Google Scholar]
- 33.Teng Y, Morrison ME, Munk P, Webber SE, Prochazka K. Macro molecules. 1998;31:3578. [Google Scholar]
- 34.Stella VJ, Borchardt RT, Hageman MJ, Oliyai R, Maag H, Tilley J. Prodrugs: Challenges and Rewards. AAPS Press/Springer; 2007. [Google Scholar]
- 35.Mastropaolo. Proc. Natl. Acad. Sci. USA. 1995;92:6920. doi: 10.1073/pnas.92.15.6920. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Jarzynski C. Phys. Rev. Lett. 1997;78:2690. [Google Scholar]
- 37.Crooks G. Phys. Rev. E. 1999;60:2721. doi: 10.1103/physreve.60.2721. [DOI] [PubMed] [Google Scholar]
- 38.Soo PL, Luo L, Maysinger D, Eisenberg A. Langmuir. 2002;18:9996. [Google Scholar]
- 39.Nagarajan R. Polym. Adv. Technol. 2001;12:23. [Google Scholar]
- 40.Guo XD, Tan JP, Kim SH, Zhang LJ, Zhang Y, Hedrick JL, Yang YY, Qian Y. Biomaterials. 2009;30:6556. doi: 10.1016/j.biomaterials.2009.08.022. [DOI] [PubMed] [Google Scholar]
- 41.Mahmud A. 2011 [Google Scholar]
- 42.Gaucher G, Marchessault RH, Leroux JC. J. Controlled Release. 2010;143:2. doi: 10.1016/j.jconrel.2009.11.012. [DOI] [PubMed] [Google Scholar]
- 43.Letchford K, Liggins R, Burt H. Pharmaceutics, Preformulation and Drug Delivery. 2007;97:1179. [Google Scholar]
- 44.Chen H, Kim S, Li L, Wang S, Park K, Cheng JX. Proc. Natl. Acad. Sci. USA. 2008;105:6596. doi: 10.1073/pnas.0707046105. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.