Abstract
The purpose of this paper is to extend the single-subject Eve atlas from Johns Hopkins University, which currently contains diffusion tensor and T1-weighted anatomical maps, by including contrast based on quantitative susceptibility mapping. The new atlas combines a “deep gray matter parcellation map” (DGMPM) derived from a single-subject quantitative susceptibility map with the previously established “white matter parcellation map” (WMPM) from the same subject’s T1-weighted and diffusion tensor imaging data into an MNI coordinate map named the “Everything Parcellation Map in Eve Space,” also known as the “EvePM.” It allows automated segmentation of gray matter and white matter structures. Quantitative susceptibility maps from five healthy male volunteers (30 to 33 years of age) were coregistered to the Eve Atlas with AIR and Large Deformation Diffeomorphic Metric Mapping (LDDMM), and the transformation matrices were applied to the EvePM to produce automated parcellation in subject space. Parcellation accuracy was measured with a kappa analysis for the left and right structures of six deep gray matter regions. For multi-orientation QSM images, the Kappa statistic was 0.85 between automated and manual segmentation, with the inter-rater reproducibility Kappa being 0.89 for the human raters, suggesting “almost perfect” agreement between all segmentation methods. Segmentation seemed slightly more difficult for human raters on single-orientation QSM images, with the Kappa statistic being 0.88 between automated and manual segmentation, and 0.85 and 0.86 between human raters. Overall, this atlas provides a time-efficient tool for automated coregistration and segmentation of quantitative susceptibility data to analyze many regions of interest. These data were used to establish a baseline for normal magnetic susceptibility measurements for over 60 brain structures of 30- to 33-year-old males. Correlating the average susceptibility with age-based iron concentrations in gray matter structures measured by Hallgren and Sourander (1958) allowed interpolation of the average iron concentration of several deep gray matter regions delineated in the EvePM.
Keywords: quantitative magnetic susceptibility mapping, stereotaxic atlas, segmentation, iron, brain, deep gray matter
1. Introduction
Stereotaxic atlases provide a useful frame of reference when analyzing subject data, especially when automated coregistration between subject and atlas allows for efficient segmentation of the subject brain into regions of interest from the atlas. The most commonly used atlases for MRI research contain information that is based mainly on cytoarchitectural features derived from T1-weighted contrast. For example, the Talairach and Tournoux atlas (Talairach and Tournoux, 1988) showcases Brodmann’s areas, while the International Consortium of Brain Mapping (ICBM) provides a target template for normalization-based group analyses (Mazziotta et al., 2001; Mazziotta et al., 1995).
The Eve atlas from Johns Hopkins University is a single-subject female brain at 1mm3 isotropic resolution, in standard Montreal Neurological Institute (MNI) coordinates (Mori et al., 2009; Mori et al., 2008; Oishi et al., 2009). Regions of interest in the White Matter Parcellation Map (WMPM) based on this atlas contain information about white matter orientation and tract structures that is derived from Diffusion Tensor Imaging. However, they provide limited detail on gray matter structures, which have a very low fractional anisotropy (Mori et al., 2008). The resolution from DTI is relatively low at 3T, with large 2.2mm3 isotropic voxels (10.6 μL). Previously, these gray matter structures were delineated using T1-weighted anatomical scans (Oishi et al., 2009); however, several gray matter structures, such as the red nucleus, substantia nigra, and dentate nucleus, were not easily visible on T1-weighted images.
With the recent advent of high-field imaging, quantitative susceptibility mapping (QSM) provides a novel contrast, particularly in deep gray matter regions (de Rochefort et al., 2010; Deistung et al., 2008; Duyn et al., 2007; Li et al., 2012b; Liu, 2010; Liu et al., 2012; Liu et al., 2009; Schweser et al., 2011; Shmueli et al., 2009; Wharton and Bowtell, 2010). Magnetic susceptibility is the intrinsic property of a substance to affect an applied magnetic field (Kuchel et al., 2003; Schenck, 1996; Yablonskiy, 1998). This susceptibility can be calculated using a map of the resonance frequency in each voxel, which traditionally utilizes the MR phase signal from gradient-recalled echo (GRE) imaging. The origin of contrast in QSM images has been attributed to iron-containing structures in the deep gray matter nuclei and myelin-containing structures in white matter, the latter being orientation-dependent (Fukunaga et al., 2010; Haacke et al., 2010; Lee et al., 2009; Lee et al., 2010; Li et al., 2012a; Li et al., 2011; Li et al., 2012b; Liu, 2010; Schweser et al., 2011). While all susceptibilities in tissue are diamagnetic due to the large water content (Schenck, 1996), iron-rich structures such as the red nucleus and globus pallidus appear bright in a quantitative susceptibility map referenced to CSF, indicating that they are more paramagnetic with respect to CSF, whereas white matter structures appear dark, indicating relative diamagnetism with respect to CSF.
Here, we used high resolution multi-orientation QSM images (1.7 μL voxels) to create a new deep gray matter parcellation map (DGMPM), which is expected to be useful as a template for automated group analyses that can anatomically identify iron-rich structures in the brain. We then combined this map with the white matter regions from the previously established White Matter Parcellation Map (WMPM) from the Eve Atlas to create the EvePM, the “Everything Parcellation Map in Eve Space.” Our goal is to provide a normal baseline of mean susceptibility for each region, which can be correlated with brain iron concentration, and, when such data are or become available, can be compared with various neurodegenerative diseases, in hopes of finding a biomarker (Bilgic et al., 2011; Schenck and Zimmerman, 2004). The Eve atlas, complete with different T1-weighted, diffusion-based, susceptibility contrast, and parcellation maps can be freely obtained from the MRI Studio website (https://www.mristudio.org), with additional information on the website for the National Research Resource for Functional Brain Imaging (http://www.mri-resource.kennedykrieger.org).
2. Methods
2.1 MRI acquisition
After IRB approval and written informed consent, five healthy male volunteers (aged 30 to 33 years old) were studied at 3T (Philips Medical Systems, Best, The Netherlands) using dual-channel body-coil excitation and 32-channel head coil receive. In order to generate high-quality quantitative susceptibility maps, we acquired a multi-orientation dataset from each subject (Li et al., 2012b; Liu et al., 2009; Wharton and Bowtell, 2010). Each volunteer was scanned with the brain positioned in four separate orientations with respect to the scanner’s B0 field: in the supine position, with the head parallel to the direction of the scanner’s B0 field; tilted to the right, with the subject’s right ear towards the right shoulder; tilted back, with cushions under the subject’s neck so that the chin was tilted up; and tilted to the left and slightly forward, with the subject’s left ear towards the left shoulder and the chin tilted forward towards the chest. When positioning the imaging volume, the midline of the sagittal plane was placed parallel to an imaginary line connecting the anterior (AC) and posterior commissures (PC) of the corpus callosum, and the midlines of the coronal and axial planes were positioned along the medial longitudinal interhemispheric fissure.
Each orientation data set consisted of one survey scan, a reference scan for SENSE reconstruction (Pruessmann et al., 1999), a T1-weighted MPRAGE (Mugler III and Brookeman, 1990), and a 3D gradient-recalled echo. The MPRAGE scan was acquired to display structural detail, using a 3D gradient-recalled echo with a turbo-field echo readout (TFE factor = 184, TFE shot interval = 3500ms, TI = 1000ms, SENSE = 1 × 1 × 2, TE = 3.2ms, TR = 7.0ms, α = 8°) with an acquired isotropic resolution of 1.2mm3 (FOV = 220mm × 220mm × 144mm, reconstructed to 224mm × 224mm). Phase images were acquired using a 3D ten-echo gradient-recalled echo sequence (SENSE = 2×1×2, TR = 70ms, TE1 = 6ms, ΔTE = 6ms, α = 20°, Scan Duration = 9:19min), with a nominal resolution of 1.2mm3 isotropic, covering the entire brain (120 slices, FOV = 220mm × 220mm × 144mm, reconstructed resolution = 0.98mm × 0.98mm × 1.2mm). Fat suppression was accomplished using a water-selective ProSet 121 excitation pulse and one 60mm-wide REST slab positioned inferior and parallel to the acquired volume. Complex images from the 32 coils were combined using standard SENSE reconstruction on the system. Single-orientation QSM images were calculated using the GRE images acquired in the supine position.
2.2 Analysis of multi-orientation and single-orientation quantitative susceptibility maps
We followed a protocol to derive quantitative susceptibility maps using multiple orientations described previously by (Li et al., 2012b). For each subject, the fourth-echo magnitude images acquired at all orientations were coregistered to the fourth-echo magnitude image acquired in the supine position, using the Oxford FMRIB Software Library (FSL) Linear Image Registration Tool (FLIRT) (Jenkinson and Smith, 2001; Smith et al., 2004; Woolrich et al., 2009), with rigid-body linear transformation with a cost ratio determined by a normalized mutual information algorithm. In principle, any magnitude image acquired at any of the echo times can be used to coregister the images from the orientations; in this particular case, the fourth-echo magnitude images (acquired at TE = 24ms) were used because they exhibited excellent contrast between brain structures and the area outside the brain, while maintaining sufficient signal. The coregistration transformation matrix was applied to the real and imaginary data from every echo time (TE) to generate coregistered real and imaginary images, which were subsequently converted to magnitude and phase images. Therefore, the data from all of the orientations were placed in the same frame of reference with respect to the subject, particularly with respect to the imaginary line drawn between the anterior and posterior commissures of the corpus callosum. The direction of the main magnetic field in the subject frame of reference, defined by (Li et al., 2012b), could then be calculated based on the scanner’s angulation parameters for each position and the coregistration transformation matrix.
The phase signal from each echo was processed with Laplacian-based phase unwrapping (Li et al., 2011; Schofield and Zhu, 2003) and the frequency shift Δf in Hertz was calculated as the linear slope of the phase as a function of TE using eight echoes. Dividing Δf by the frequency of the main magnetic field (f = γB0 = 128MHz at 3T) and multiplying it by 106 produced the relative magnetic field shift in units of ppm. The linear fitting of the frequency shift also provided an estimate of the initial phase φ0, the intercept. Our threshold was π/8, meaning that voxels with an intercept larger than this threshold were considered unreliable. This was used to exclude voxels with an unreliable phase measurement, which may be due to turbulent flow, partial volume effects, or an unusually high frequency shift (Schweser et al., 2011).
Once a map of the frequency shift has been calculated, the slowly-varying background gradients from the B0 field inhomogeneities and interfaces of structures with vastly different susceptibilities (e.g., the sinuses) need to be removed in order to gauge the effects from the small susceptibility differences between gray and white matter structures. Some methods for removing these background gradients include polynomial fitting (Duyn et al., 2007), dipole fitting (de Rochefort et al., 2010; Wharton and Bowtell, 2010), and the sophisticated harmonic artifact reduction for phase data (SHARP) (Schweser et al., 2011). For this project, we used the dipole fitting method to model the background gradient field for each position, by calculating the susceptibility sources outside the brain that would produce the most similar background gradient field to the experimentally measured field. This was accomplished by solving the following minimization problem:
| 1 |
where is the unit vector in the direction of the main magnetic field in the subject frame at the ith head orientation, is the spatial frequency vector in the subject frame, and Wi is a chosen weighting matrix for the ith orientation. M is a brain mask and β is a regularization parameter. In the present study, for each head orientation, we used the mean normalized GRE magnitude image at the first echo (TE = 6ms) as the weighting matrix. The brain mask was calculated using the FSL Brain Extraction Tool (BET) (Smith, 2002; Smith et al., 2004; Woolrich et al., 2009), and assigned a value of one inside the brain and zero outside the brain. For the dipole fitting, the regularization parameter β was set to be 1000, which makes the fitted susceptibility source inside the brain very small (less than 1 * 10−6 ppm) and emphasizes the susceptibility sources outside the brain. An iterative conjugate gradient-based solver was developed for solving this minimization problem using MATLAB R2011b (The MathWorks, Natick, MA). The magnetic field shift distribution calculated by these fitted susceptibility sources was then subtracted from the measured field shift map, and the residual magnetic field shift was used for calculating susceptibility.
The quantitative susceptibility map for each subject was calculated by using the multiple orientation method COSMOS (Liu et al., 2009; Wharton and Bowtell, 2010), which among existing QSM methods gives the best inverse conditioning and the best image quality. In the subject frame of reference, with phase/frequency data collected at N independent head orientations, the quantitative susceptibility χ was obtained by solving the minimization problem:
| 2 |
where
| 3 |
and α is a regularization parameter. Mout is a complementary mask of the brain mask M used in the dipole fitting procedure with zero inside the brain area and one outside the brain. Similar to the dipole fitting procedure we used the mean normalized GRE magnitude image at the first echo (TE = 6ms) as the weighting matrix for each head orientation. The regularization parameter α was set to 20 and a convergence tolerance of 10−5 was used in the developed LSQR solver for solving the minimization problem as in Eq. (2). For the COSMOS calculation, a very low convergence tolerance may be used, because the inverse calculation is well-conditioned and very stable. With α set to 20, the resulting susceptibility outside the brain is fairly small (less than 1 * 10−5 ppm), which emphasizes the susceptibility contributions within the brain. The choice of the α and β regularization parameters are related to the residual signal power inside and outside the brain, and the output QSM results are not very sensitive to their selection. Within a relatively large range, the results are not significantly different. More information on these parameters can be found in previous work (Li et al., 2012b).
To calculate a susceptibility map based on a single-orientation dataset, Eq. (2) retains only the term O1 instead of O1 through ON. For our single-orientation QSM images, we used a maximum relative residual of 0.08 as the stopping criterion. These single-orientation LQSR calculations were calibrated using the COSMOS calculation (Li et al., 2011).
The multi-orientation susceptibility calculations with COSMOS, as well as the single-orientation calculations with LSQR, were each processed in approximately 20 minutes. Dipole fitting was completed in approximately 30 minutes. Fitting the linear slope in each voxel per orientation took less than a minute per subject. We processed several subjects simultaneously on separate desktops running MATLAB (The MathWorks, Natick, MA).
2.3 Creating the single-subject atlas in MNI coordinates
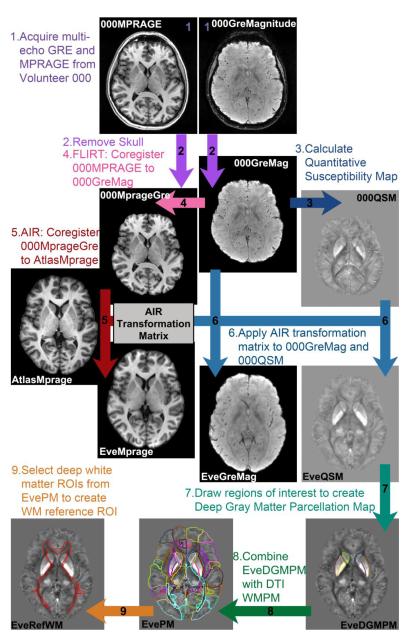
The process for creating our single-subject “Everything Parcellation Map” (EvePM) for automated parcellation analysis is outlined in Figure 1. The JHU MNI single-subject Eve atlas consists of one subject, a 33-year-old white female, with many different brain images in MNI coordinates, including images weighted according to diffusion, T2, and T1 (Mori et al., 2008; Oishi et al., 2009). We acquired a series of multi-echo GRE images and a T1-weighted MPRAGE scan on this subject (Volunteer 000). The data were processed using MATLAB, which employs FSL-FLIRT for motion correction, and MRI Studio (https://www.mristudio.org), which employs AIR for motion correction. More information about MRI Studio (Jiang et al., 2006) is also available from the National Research Resource for Functional MRI (http://www.mriresource.kennedykrieger.org/). The EvePM was created with the following steps:
A series of multi-echo GRE images was acquired at four orientations. One magnitude image (“000GreMagnitude ”) at TE = 24ms from the supine orientation, with the subject lying along the same directly as the B0 field, was used to create a reference for future magnitude images from other volunteers. Using MATLAB, the corresponding fourth echo magnitude images from the other orientations were coregistered to this supine magnitude image with FSL FLIRT (Jenkinson et al., 2002; Jenkinson and Smith, 2001). A T1-weighted MPRAGE (“000Mprage”) was acquired at the same resolution as the GRE acquisition. The JHU MNI Eve atlas contains a T1-weighted MPRAGE image in Eve MNI coordinates (“AtlasMprage”, downloadable from the website as “JHU_MNI_T1”).
The skull was removed from the 000MPRAGE image using FSL BET (Smith, 2002; Smith et al., 2004; Woolrich et al., 2009). Skull-stripping was also performed with FSL BET on the reference echo of the GRE magnitude image in the supine position. The brain mask was applied to the other echoes, which are automatically coregistered as a result of the multi-echo GRE acquisition method. Then the brain mask was applied to the other orientations after they were coregistered.
The skull-stripped GRE images (“000GreMag”) from four head orientations were processed to yield quantitative susceptibility maps for Volunteer 000 (“000QSM”), providing a template for coregistering QSM images from other volunteers.
Using FSL FLIRT in MATLAB, we coregistered the 000Mprage to the 000GreMag, resulting in an MPRAGE image in the GRE coordinates (“000MprageGre”).
The coregistered T1-weighted 000MprageGre was coregistered to the original T1-weighted image in the pre-existing Eve atlas (“AtlasMprage”) with Automated Image Registration (AIR) (Woods et al., 1998a; Woods et al., 1998b) in the DiffeoMap module of the MRI Studio platform (Li, X.; Jiang, H.; and Mori, S.; Johns Hopkins University, http://www.mristudio.org), transforming the MPRAGE image in the volunteer’s original GRE coordinates to match the AtlasMprage in MNI coordinates.
The resulting AIR transformation matrix was then applied to the fourth echo of the GRE magnitude (000GreMag) and the multi-orientation quantitative susceptibility map (000QSM), transforming these images to MNI coordinates, with a field of view at 181 × 217 × 181 mm3, image dimensions 181 × 217 × 181 mm3, and 1mm3 isotropic resolution. These GRE magnitude and QSM images in the MNI coordinates of the Eve atlas were named “EveGreMag” and “EveQSM”. Because the single-subject atlas was formed from this particular subject, the internal structures did not need any additional warping steps for coregistration. The EveGreMag was used to coregister the outer surface of the brain between the atlas and other subjects; therefore, the specific echo time chosen for aligning these magnitude images is not very important as long as the contrast between the “inside” and “outside” of the brain is always clear.
Gray matter regions of interest (dentate nucleus, red nucleus, substantia nigra, caudate nucleus, putamen, globus pallidus) were drawn on the new EveQSM by an experienced neuroradiologist (AF); these became the Deep Gray Matter Parcellation Map in Eve space and MNI coordinates (“EveDGMPM”, also shown in Fig. 3c). This DGMPM contained the ROIs for testing the rater agreement.
The DGMPM was combined with the White Matter Parcellation Map from DTI fractional anisotropy analysis (Fig. 3a) to create the “Everything Parcellation Map” (“EvePM”, shown in Fig. 3d).
To analyze each subject on the same reference scale, several of the deep white matter regions were grouped into one “reference ROI” (described in the section below on “2.7 Creating a reference region for magnetic susceptibility measurements”), denoted as “EveRefWM.” The average susceptibility within this white matter ROI was assigned to be −0.03 ppm in the QSM, which results in the average susceptibility of the CSF in the ventricles to be approximately 0 ppm. The final QSM map for Eve is called “EveRefQSM,” downloadable from the MRI Studio website in the “Images” folder of the individual software packages as “JHU_MNI_SS_QSM_ss.” The EveGreMag is called “JHU_MNI_SS_GreMag_ss.”
Figure 1.
Flowchart for creating EvePM and atlas templates.
Figure 3.
Regions of interest overlaid on QSM images in the axial, sagittal, and coronal planes. (a) The deep gray matter regions from the WMPM (an ROI atlas created with T1-weighted and DTI images) showed poor agreement with the deep gray matter structures within QSM images, most notably misalignment with the substantia nigra, which is difficult to delineate on T1-weighted images. (b) These deep gray matter regions were redrawn using the QSM contrast, creating the DGMPM. (c) Combining the WMPM and DGMPM produced the EvePM.
2.4 Coregistering subjects to atlas space
A flowchart showing the analysis steps for each dataset is exemplified in Figure 2 for “Volunteer 001.”
Figure 2.
Flowchart showing analysis steps for each dataset.
Magnitude and phase data were acquired with a multi-echo GRE.
Skull removal was performed using FSL BET (Smith, 2002; Smith et al., 2004; Woolrich et al., 2009) on the first echo of the GRE magnitude images (“001GreMagnitude”). The brain mask was then applied to the other echoes, which are automatically coregistered as a result of the multi-echo GRE acquisition method.
A quantitative susceptibility map (“001QSM”) was calculated using the GRE signal phase from multiple orientations, as described above in Section 2.2.
Using AIR (Woods et al., 1998a; Woods et al., 1998b) in the MRI Studio platform, the magnitude image from the fourth echo of the GRE scan (“001GreMag”) was coregistered using affine rigid body registration and trilinear interpolation to the magnitude image from the fourth echo of the GRE scan of the Eve atlas (“EveGreMag”), resulting in “001GreAIR” in MNI coordinates.
The resulting AIR transformation matrix was applied to the subject QSM, resulting in “001QSMAIR”. To facilitate processing for these QSM images, which had not been referenced for absolute susceptibility, the 001GreAIR and 001QSMAIR images were transformed from float to byte format and intensity-corrected using automated histogram matching with their respective templates, EveGreMag and EveRefQSM. The automated histogram matching places the contrast for regions of interest on the same relative scale.
To coregister the internal structures, the atlas GRE magnitude image (“EveGreMag”) and the associated quantitative susceptibility map (“EveQSM”) were used as templates to coregister the affine-coregistered subject GRE magnitude (“001GreAIR”) and QSM (“001QSMAIR”) simultaneously using dual-channel Large Deformation Diffeomorphic Metric Mapping (LDDMM) (Beg et al., 2005; Cao et al., 2005; Miller et al., 2002), resulting in “001GreLDDMM” and “001QSMLDDMM.”
The inverse AIR and LDDMM transformation matrices were applied to the “Everything Parcellation Map in Eve Space” (“EvePM”), transforming these regions of interest into subject coordinates (“001PM”).
Deep white matter regions from this transformed parcellation map were selected as a reference ROI (“001RefWM”), as defined in volunteer 000, in order to analyze the subjects on the same reference scale.
The subject QSM maps (“001QSM”) were normalized so that the average susceptibility of the white matter reference region of interest in 001RefWM was −0.03ppm, resulting in referenced QSM maps (“001QSMRefWM”). The regions of interest delineated in the transformed subject parcellation map (“001PM”) were applied to this referenced QSM map.
Coregistration of one subject to the atlas in MRI Studio took less than half an hour. All of the coregistration processes between atlas and subjects using MRI Studio were finished within two hours, after which the data were sent to the server at the Center for Imaging Science (http://cis.jhu.edu) to undergo LDDMM processing. All of these data were processed within twelve hours.
The same analysis was repeated for a single-orientation quantitative susceptibility map from each subject, which took approximately the same time to process.
2.5 Applying EvePM to subject susceptibility maps
The combined AIR and LDDMM transformation matrices from coregistration were applied with nearest-neighbor interpolation to the Everything Parcellation Map (EvePM), thereby transforming the EvePM into the subject’s frame of reference and creating an automated personalized region of interest map per subject. The regions of interest for the transformed EvePM were overlaid per subject using MATLAB (The MathWorks, Natick, MA). These ROIs were visually checked using ROIEditor, part of the MRI Studio toolbox (X. Li, H. Jiang, S. Mori; Johns Hopkins University, http://www.mristudio.org), by overlaying the ROI masks onto the QSM images and searching for gross alignment errors across structures. The mean susceptibility and standard deviation were calculated for the left and right structures for over 60 regions of interest. Because a mask of the brain was used to calculate the quantitative susceptibility map, regions outside of this mask were excluded from the calculations. The amount of time needed to apply the transformation matrices in MRI Studio and calculating the mean and standard deviations within each ROI using MATLAB across all subjects was less than two hours.
2.6 Gauging accuracy of transformation-based segmentation
The current gold standard for drawing regions of interest is to have an expert rater manually demarcate regions that are visually discernible. We first coregistered all of the subjects with twelve-channel affine nonlinear registration using AIR to transform the GRE magnitude and QSM images into atlas space, namely with image dimensions of 181 × 217 × 181 mm3 at 1mm3 isotropic resolution. Using the QSM images, each rater was asked to draw regions of interest in the deep gray matter within four to eight specified axial slices per brain structure. The affine registration guaranteed consistence in the level of ROI delineation among subjects and ensured that each rater would draw their regions of interest in agreeing slices, allowing a thorough comparison of inter-rater reliability (Mori et al., 2008).
The “truth” (T) set consisted of one expert rater (Rater A) delineating the regions of interest on all of our subjects using the affine-coregistered multi-orientation quantitative susceptibility maps. To assess inter-rater reliability, we asked two more colleagues (Raters B, C) to draw regions of interest using the multi-orientation quantitative susceptibility map for each subject. To assess intra-rater reliability, the expert rater drew the regions of interest on each subject two times, with one week in between sessions. A few months later, the raters also drew regions of interest on affine-coregistered single-orientation susceptibility maps: Rater B delineated the “gold standard” on these single-orientation QSM images and performed the intra-rater analysis. To assess the accuracy of segmentation, we compared these easily discernible selected regions using our atlas coregistration with LDDMM (automated reliability) with the regions drawn by two raters (inter-rater reliability) and the regions drawn two times by one rater (intra-rater reliability). Each rater and the automated algorithm saved each region of interest as an individual binary map. We compared these binary maps using MATLAB (The MathWorks, Natick, MA, USA), excluding voxels outside the brain and gauging the regions with no overlap, partial overlap, and complete overlap. The reliability analysis provided estimates of Kappa statistics, sensitivity, specificity, false positive and negative rates, positive and negative predictive values, Jaccard similarity metrics, and the Dice coefficient (Bartko and Carpenter, 1976; Dice, 1945; Jaccard, 1912; Landis and Koch, 1977; Shattuck et al., 2009; Zijdenbos et al., 1994; Zou et al., 2004). We also measured the volumetric and boundary-based agreements (Zhang et al., 2010). Full calculation approaches are explained in Appendix 1.
2.7 Creating a reference region for magnetic susceptibility measurements
Magnetic susceptibility measurements are relative, and in order to be reproducibly reported, must be referenced to the mean susceptibility of a particular tissue or structure. It is common to reference to the cerebrospinal fluid (CSF) by assigning a value of 0.00ppm as the mean susceptibility in the ventricles (Li et al., 2011; Yao et al., 2009). However, the CSF showed a large range of susceptibility values, possibly due to partial volume or flow effects, proximity to iron-rich gray matter structures, etc. In line with others (Li et al., 2012b; Wharton and Bowtell, 2010), we found that the white matter structures had a much more reproducible average susceptibility over a narrower range of values. Therefore, we created a “reference region of interest” consisting of multiple white matter areas within the atlas transformed into subject space with LDDMM. This reference ROI consists of the following structures, defined as “deep white matter” (Faria et al., 2012): cerebral peduncles, internal capsule, posterior thalamic radiations (including the optic radiations), corona radiata, centrum semiovale, superior longitudinal fasciculi, fronto-occipital fasciculi (including inferior longitudinal fasciculi), and corpus callosum. This large region of interest became our “Reference ROI,” and the average susceptibility of this white matter region was set to −0.03 ppm. This particular value was chosen because it leads to an average susceptibility of approximately 0.00 ppm in the ventricles, allowing each subject to be analyzed on the same reference scale as others referencing with respect to CSF. Referencing the susceptibility maps in this manner produced reproducible measurements of average susceptibility between subjects. More details can be found in Appendix 2.
2.8 Correlating susceptibility measurements with brain iron concentration
In 1958, Hallgren and Sourander measured iron concentration of several brain structures from 81 cadavers ranging from 30 to 100 years of age (Hallgren and Sourander, 1958). They calculated regression lines according to the method of least squares to obtain the following equations describing the concentration of non-heme iron in mg per 100g of fresh weight of tissue (y) for these structures as a function of age (x):
| Caudate Nucleus: | y =9.66[1−exp(−0.05x)]+0.33 | [5] |
| Putamen: | y =14.62[1−exp(−0.04x)]+0.46 | [6] |
| Globus Pallidus: | y = 21.41[1−exp(−0.09x)]+0.37 | [7] |
Using the multi-orientation quantitative susceptibility maps, we plotted the brain iron concentration as a function of average susceptibility for these three regions at our subject’s average age of 31-years-old. Then, we linearly interpolated this correlation and placed the average susceptibility values for the other deep gray matter regions on this line. This was then used to predict the mean brain iron concentration for these structures in the EvePM. Not included in this prediction were the gyral areas, which encompass both gray and white matter, and the white matter structures, which contain contributions from myelin and orientation with respect to the main magnetic field.
3. Results
3.1 Region of interest analysis
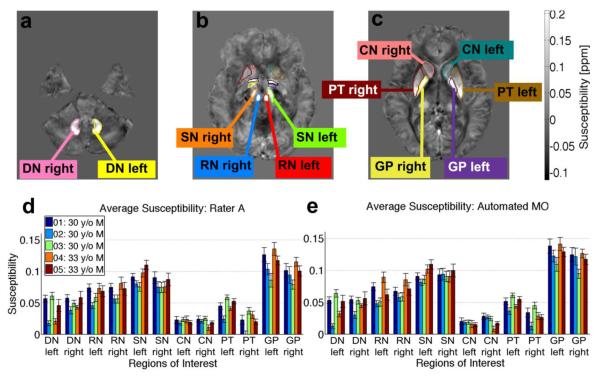
Figure 3a shows that the gray matter regions from the WMPM created from T1-weighted and DTI contrast are poorly aligned with gray matter structures seen in the QSM images, most notably in the substantia nigra, which is a difficult structure to delineate on T1-weighted images. The gray matter regions were redrawn using the new QSM contrast, producing the DGMPM (Fig. 3b). Figure 3c shows regions of interest delineated by automated segmentation with the EvePM in the axial, sagittal, and coronal planes, with gray matter from the DGMPM and white matter adjusted from the WMPM. The subset of regions used for testing the accuracy of automated and manual segmentation, which were uniformly selected across four to eight slices of subject brains in MNI coordinates, are shown in Figure 4, at the levels of the (a) dentate nucleus, (b) red nucleus and substantia nigra, and (c) the basal ganglia. The average and standard deviation of the susceptibility in regions of interest are also displayed per volunteer for each region of interest, as delineated by the gold standard Rater 1 (Fig. 4d) and by LDDMM (Fig. 4e).
Figure 4.
Regions of interest for assessing accuracy of segmentation: dentate nucleus (DN), substantia nigra (SN), red nucleus (RN), caudate nucleus (CN), putamen (PT), globus pallidus (GP). Regions of interest were drawn by the raters to analyze accuracy of segmentation at the level of (a) the cerebellum, (b) the brain stem, and (c) the basal ganglia. (d) The bar plot shows the average susceptibility calculated from the referenced multi-orientation QSM images in these regions of interest for each volunteer as delineated by (d) Rater A, the “gold standard” and (e) automated segmentation of the multi-orientation QSM images with the LDDMM algorithm.
3.2 Accuracy of brain segmentation
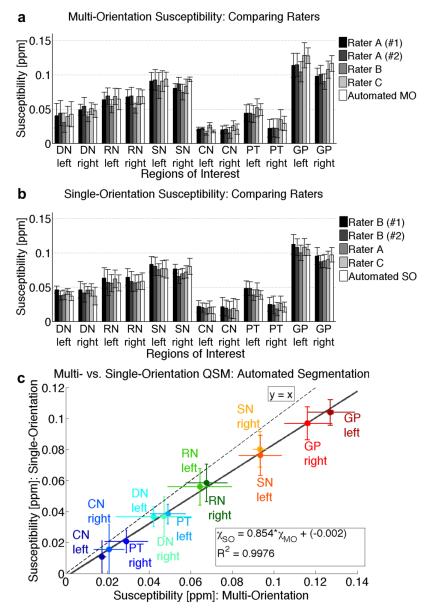
The average and standard deviation for the susceptibility measurements for each of the accuracy-assessment ROIs over all of the subjects and for all analysis approaches are shown in the bar graph in Figure 5, analyzed using (a) multi-orientation QSM and (b) single-orientation QSM, which are (c) highly correlated (R2 = 0.998). However, the single-orientation susceptibility values show a systematic reduction to about 85% of the corresponding multi-orientation susceptibilities. One dataset delineated by Rater A was established as the “gold standard” for comparing the segmentation methods using the multi-orientation QSM images, and one dataset delineated by Rater B was established as the “gold standard” for comparing segmentation methods using the single-orientation QSM images. Statistics characterizing the accuracy of segmentation for multi-orientation QSM are shown in Tables 1 and 2, and Figure 6, and for single-orientation QSM in Tables 3 and 4, and Figure 7. These results show that most of the measurements by the raters and automated LDDMM are within a standard deviation of variation.
Figure 5.
Deep gray matter magnetic susceptibility values averaged across subjects (n = 5), as determined by the different raters and automated (LDDMM) analysis for susceptibility maps calculated with (a) multi-orientation QSM and (b) single-orientation QSM. (c) Plot of multi-orientation vs. single-orientation susceptibility values shows a linear correlation (inset equation), with the single-orientation LSQR underestimating values from COSMOS, as compared to the line of identity (y = x).
Table 1.
Overall average statistics comparing the accuracy of segmentation using multi-orientation QSM
| Overall Average Statistics: Multi-Orientation QSM |
||||
|---|---|---|---|---|
| Intra-rater | Inter-rater | Inter-rater | ||
| (Rater A, | (Raters | (Raters | ||
| Auto vs. Manual | #1 & #2) | A2 & B) | A2 & C) | |
| Kappa | 0.85 ± 0.00 | 0.94 ± 0.01 | 0.89 ± 0.02 | 0.89 ± 0.02 |
| Sensitivity | 0.80 ± 0.06 | 0.92 ± 0.02 | 0.94 ± 0.04 | 0.85 ± 0.05 |
| Specificity | 1.00 ± 0.00 | 1.00 ± 0.00 | 1.00 ± 0.00 | 1.00 ± 0.00 |
| PPV | 0.91 ± 0.03 | 0.96 ± 0.02 | 0.85 ± 0.05 | 0.95 ± 0.03 |
| NPV | 1.00 ± 0.00 | 1.00 ± 0.00 | 1.00 ± 0.00 | 1.00 ± 0.00 |
| FPR | 0.00 ± 0.00 | 0.00 ± 0.00 | 0.00 ± 0.00 | 0.00 ± 0.00 |
| FNR | 0.20 ± 0.06 | 0.08 ± 0.02 | 0.06 ± 0.04 | 0.15 ± 0.05 |
| Jaccard | 0.74 ± 0.04 | 0.88 ± 0.02 | 0.81 ± 0.04 | 0.81 ± 0.04 |
| Dice | 0.85 ± 0.03 | 0.94 ± 0.01 | 0.89 ± 0.02 | 0.90 ± 0.02 |
| Boundary-based | 0.29 ± 0.12 | 0.16 ± 0.07 | 0.27 ± 0.08 | 0.29 ± 0.10 |
Abbreviations: PPV: positive predictive value; NPV: negative predictive value; FPR: false positive rate; FNR: false negative rate
Table 2.
Volumetric analysis using Multi-Orientation QSM
| Volume (mm3) for Segmentation using Multi-Orientation QSM |
|||||
|---|---|---|---|---|---|
| Rater A, | Rater A, | ||||
| first trial | second trial | Rater B | Rater C | Automated | |
| DN left | 461.8±43 | 499.2±72.2 | 494±83.7 | 602.8±100.8 | 449±60.2 |
| DN right | 225.2±34.7 | 250.6±12.6 | 222.2±18.7 | 284.2±17.5 | 243.6±23.7 |
| RN left | 564.8±36.9 | 574±36.3 | 554.2±65.2 | 603.4±124.5 | 522.2±30.3 |
| RN right | 899±98.2 | 946.8±55 | 776.4±82.2 | 1079.8±63.4 | 859.4±42.3 |
| SN left | 2404.8±160.6 | 2423.8±162.2 | 2064.2±136.9 | 2275±142.3 | 2295.8±158.3 |
| SN right | 1317.2±149.1 | 1327.4±117.6 | 1173±69.9 | 1515.2±129.4 | 1085.4±209.5 |
| CN left | 498±59.7 | 537.2±49.5 | 518.4±48.7 | 646±86.3 | 534.6±55.6 |
| CN right | 230±42.2 | 235.6±8.1 | 226.6±21.9 | 304±27.2 | 229.2±9.2 |
| PT left | 542.8±70.4 | 579.8±60.6 | 537.6±79.7 | 528.8±301.7 | 495.2±148.9 |
| PT right | 924.4±88.3 | 969.8±76 | 779.2±72 | 1047.6±42.9 | 829.8±43.7 |
| GP left | 2400.2±217.9 | 2420.6±236 | 1919.6±172.8 | 2321.4±207.1 | 2119.8±218.8 |
| GP right | 1371.2±171.4 | 1391.4±112.7 | 1223.8±132.2 | 1529.4±125.8 | 1081.8±241.8 |
Abbreviations: DN: dentate nucleus; RN: red nucleus; SN: substantia nigra; CN: caudate nucleus; PT: putamen; GP: globus pallidus
Figure 6.
Statistics showing the accuracy of segmentation between raters using multi-orientation susceptibility maps. Comparing the regions of interest to the second time point of Rater A showed intra-rater reliability between Rater A’s two time points (“Intra-Rater”), reliability between human and automated delineation with multi-orientation QSM (“Automated MO”), and inter-rater reliability between Raters A and B (“Inter-Rater A and B”), as well as between Raters A and C (“Inter-Rater A and C”), through the following statistics: (a) the Kappa statistic, (b) the Dice coefficient, (c) the Jaccard similarity metric, (d) the positive predictive value, (e) the sensitivity, (f) the specificity, (g) correlation between volumes with the coefficients of linear fitting, and (h) boundary-based metric.
Table 3.
Overall average statistics comparing the accuracy of segmentation using single-orientation QSM
| Overall Average Statistics: Single-Orientation QSM |
||||
|---|---|---|---|---|
| Intra-rater | Inter-rater | Inter-rater | ||
| (Rater B, | (Raters | (Raters | ||
| Auto vs. Manual | #1 & #2) | B2 & A) | B2 & C) | |
| Kappa | 0.88 ± 0.03 | 0.86 ± 0.02 | 0.85 ± 0.02 | 0.86 ± 0.02 |
| Sensitivity | 0.94 ± 0.05 | 0.90 ± 0.02 | 0.93 ± 0.03 | 0.90 ± 0.02 |
| Specificity | 1.00 ± 0.00 | 1.00 ± 0.00 | 1.00 ± 0.00 | 1.00 ± 0.00 |
| PPV | 0.84 ± 0.05 | 0.83 ± 0.04 | 0.80 ± 0.03 | 0.83 ± 0.04 |
| NPV | 1.00 ± 0.00 | 1.00 ± 0.00 | 1.00 ± 0.00 | 1.00 ± 0.00 |
| FPR | 0.00 ± 0.00 | 0.00 ± 0.00 | 0.00 ± 0.00 | 0.00 ± 0.00 |
| FNR | 0.06 ± 0.05 | 0.10 ± 0.02 | 0.07 ± 0.03 | 0.10 ± 0.02 |
| Jaccard | 0.79 ± 0.04 | 0.76 ± 0.04 | 0.75 ± 0.02 | 0.76 ± 0.03 |
| Dice | 0.88 ± 0.03 | 0.86 ± 0.02 | 0.85 ± 0.02 | 0.86 ± 0.02 |
| Boundary-based | 0.28 ± 0.13 | 0.19 ± 0.07 | 0.28 ± 0.08 | 0.23 ± 0.08 |
Abbreviations: PPV: positive predictive value; NPV: negative predictive value; FPR: false positive rate; FNR: false negative rate
Table 4.
Volumetric analysis using Single-Orientation QSM
| Volume (mm3) for Segmentation using Single-Orientation QSM |
|||||
|---|---|---|---|---|---|
| Rater B, | Rater B, | ||||
| first trial | second trial | Rater A | Rater C | Automated | |
| DN left | 478.2±96.3 | 403±80.7 | 492.2±92.1 | 433.2±60.8 | 485±45.7 |
| DN right | 222±11.1 | 193.2±15.7 | 253.6±25.5 | 218.2±23.1 | 238.8±21.2 |
| RN left | 480±42.5 | 460.6±48.3 | 520.4±56.7 | 518.8±64.8 | 534±28 |
| RN right | 783.2±90.4 | 713.4±123.5 | 792.8±125.1 | 755.8±53.3 | 823.8±22.7 |
| SN left | 2003±200.5 | 1982.2±217 | 2302±219.6 | 2128.6±96.6 | 2340.2±198.1 |
| SN right | 1091.8±99.8 | 1040.2±114 | 1325.4±73 | 1163.2±43.2 | 1203.2±164.6 |
| CN left | 471.4±103.8 | 450.4±91.3 | 480.6±158.7 | 464.8±125.4 | 553.2±34.4 |
| CN right | 221.8±16 | 194.8±16.4 | 249.4±11.3 | 454.8±477.6 | 216.8±19.6 |
| PT left | 544.6±40.2 | 487±79.6 | 538±51.3 | 479.6±158.1 | 429.8±40.4 |
| PT right | 780.4±118.5 | 740.6±126.2 | 820.8±160.5 | 673.2±110.3 | 833.2±39.1 |
| GP left | 1961.4±192.9 | 1951.4±193 | 2289.8±237.8 | 1925±527.3 | 2162.8±213.9 |
| GP right | 1236.6±51.1 | 1153.4±180.4 | 1330±142.1 | 1413.4±429.1 | 1145.8±262.3 |
Abbreviations: DN: dentate nucleus; RN: red nucleus; SN: substantia nigra; CN: caudate nucleus; PT: putamen; GP: globus pallidus
Figure 7.
Statistics showing the accuracy of segmentation between raters using single-orientation susceptibility maps. Comparing the regions of interest to the second time point of Rater B showed intra-rater reliability between Rater B’s two time points (“Intra-Rater”), reliability between human and automated delineation with single-orientation QSM (“Automated SO”), and inter-rater reliability between Raters B and A (“Inter-Rater B and A”), as well as between Raters B and C (“Inter-Rater B and C”), through the following statistics: (a) the Kappa statistic, (b) the Dice coefficient, (c) the Jaccard similarity metric, (d) the positive predictive value, (e) the sensitivity, (f) the specificity, (g) correlation between volumes with the coefficients of linear fitting, and (h) boundary-based metric.
For segmentation using multi-orientation QSM, the overall average Kappa for “manual vs. automated” delineation for the twelve ROIs was 0.85 (Table 1, Fig. 6a), which signifies excellent agreement according to the Landis and Koch criteria, in which a Kappa statistic of 0.61-0.80 denotes “substantial” and 0.81-1.00 denotes “almost perfect” agreement (Landis and Koch, 1977). The left portion of the substantia nigra, a generally small and difficult structure to segment, had the smallest index of agreement (Kappa = 0.79, still within a range of substantial agreement), while the left red nucleus had the largest index of agreement (Kappa = 0.90). Generally, the Kappa statistic was higher for large paramagnetic structures, with QSM contrast sufficient for both manual and automated segmentation. The inter-rater reliability was found to be Kappa = 0.89 for both Raters B and C, as compared with the gold standard from Rater A. The Kappa statistics for the automated method were fairly close to the inter-rater Kappa statistics, indicating that the automated approach has accuracy similar to manual segmentation performed by multiple raters. The intra-rater reliability was found to have a Kappa = 0.94, which was, as expected, higher than the “manual vs. automated” or inter-rater Kappa values for most regions. The Dice coefficients (Fig. 6b) were very similar to the Kappa statistics, namely 0.94 for the intra-rater, 0.85 for “manual vs. automated,” 0.89 for inter-rater A and B, and 0.90 for inter-rater A and C segmentation. The overall Jaccard similarity metric (Fig. 6c) was 0.74 for the “manual vs. automated” method, 0.88 for the intra-rater reliability, 0.81 between Raters A and B, and 0.81 between Raters A and C. The overall positive predictive value (PPV, Fig. 6d) was 0.91 for the “manual vs. automated” method, which reflects how well areas that were delineated in the automated method predicted a matching area in the manual gold standard. The PPV for “manual vs. automated” was lower than the intra-rater PPV of 0.96 and one inter-rater PPV of 0.95 between Raters A and C, but higher than the inter-rater PPV of 0.85 between Raters A and B. The negative predictive value (NPV) was close to 1.0 for all methods, mainly because the “true negatives” for these samples consisted of the entire brain mask, which was much larger than the individual regions of interest. The overall false negative rate (FNR) between automated and the manual gold standard was 0.2, which was a little higher than the intra-rater FNR of 0.08 and the inter-rater FNRs of 0.06 (Rater B) and 0.15 (Rater C). The false positive rate (FPR), or the probability of a positive value from the method corresponding with a negative value of the gold standard, was extremely low (approximately 0%) for all of the methods. The overall sensitivity of the “manual vs. automated” method, which measures how many of the automated “positives” matched the “true positives” of the manual method, was 80% (Fig. 6e). This was a little less than intra-rater measurements and those of Rater B and Rater C (92%, 88%, and 85%, respectively). The specificity (Fig. 6f), which measures the proportion of negative values in the gold standard that were correctly identified by the tested method, was extremely high (greater than 99%) for all methods. The volumetric analysis (Fig. 6g) revealed high correlations between all of the metrics. The R2 ranged from 0.9923 to 0.9998 and the slopes ranged from 0.803 (inter-rater A and B) to 1.003 (intra-rater). The R2 of the second delineation by Rater A (“gold standard”) vs. the automated method (R2 = 0.9941) was higher than the R2 from Rater A vs. Rater C (R2 = 0.9923), and the slope of Rater A vs. the automated method (0.890) was higher than Rater A vs. Rater B (0.803). The agreement between the boundaries (Fig. 6h) was also comparable between all of the delineations. The highest disagreement (high boundary-based metric), both in manual vs. automated and inter-raters, occurred in the left globus pallidus.
For segmentation using single-orientation QSM, with a gold standard using the second set of ROIs delineated by Rater B, the overall average Kappa for “manual vs. automated” delineation for the twelve ROIs was 0.88 (Table 3, Fig. 7a), whereas the intra-rater (between the two ROI maps created by Rater B) and inter-rater (between Raters B and A, as well as between Raters B and C) Kappa statistics (0.86, 0.85, and 0.86, respectively) were somewhat lower than the statistics from segmentation with multi-orientation QSM. The susceptibility calculations for these single-orientation QSM maps are less well-conditioned than the multi-orientation method, resulting in noisier maps that are more difficult for human raters to delineate manually. Still, the Kappa statistics denote “almost perfect” agreement based upon the Landis and Koch criteria. Among the individual regions, the lowest Kappa statistic was once again found in the left substantia nigra, with an intra-rater Kappa statistic of 0.81, but a higher “manual vs. automated” Kappa of 0.88. The lowest “manual vs. automated” Kappa statistic was found in the right caudate nucleus (0.82), with the highest Kappa statistic in the left putamen (0.92); however, this range is still well within “almost perfect” agreement. The Dice coefficients (Fig. 7b) were once again similar to the Kappa statistics, with 0.86 for the intra-rater, 0.88 for “manual vs. automated,” 0.85 for inter-rater B and A, and 0.86 for inter-rater B and C segmentation. Compared to the multi-orientation QSM, the Jaccard similarity metric (Fig. 7c) was higher for the “manual vs. automated” method (0.79), while metrics for the intra-rater (0.76), inter-rater B and A (0.75), and inter-rater B and C (0.76) were lower. The overall positive predictive value (PPV, Fig. 7d) was 0.84 for the “manual vs. automated” method, with lower values for the human rater delineation (intra-rater = 0.83, inter-rater B and A = 0.80, inter-rater B and C = 0.83), showing that the human raters had more variation from the manual gold standard. The negative predictive value (NPV) was once again approximately 1.0 for all methods. The overall false negative rate (FNR) between automated and the manual gold standard was 0.06, which was a little lower than the intra-rater FNR of 0.10 and the inter-rater FNRs of 0.07 (Raters B and A) and 0.10 (Raters B and C), indicating that the automated method is less likely to include voxels that are not truly part of the region of interest. The false positive rate (FPR) was once again extremely low (approximately 0%) for all of the methods, most likely because the brain mask region of true negatives was again much larger than each individual region of interest. The overall sensitivity of the “manual vs. automated” method was 94% (Fig. 7e), indicating that the automated method matched the regions of interest in the gold standard very well, even better than the intra-rater and inter-rater measurements (90%, 93%, 90%, respectively). The specificity (Fig. 7f) was extremely high (greater than 99%) for all methods. The volumetric analysis (Fig. 7g) once again exhibited high correlations between all of the metrics, though slightly lower correlations than the linear fitting of the multi-orientation data. The R2 ranged from 0.9859 to 0.9992 and the slopes ranged from 0.992 to 1.172. The R2 and slope comparing the automated method to Rater B (“gold standard”) at 0.9949 and 1.134, respectively, fell between the two inter-rater agreements between Raters B and C (R2 = 0.9859, slope = 1.011) and Raters B and A (R2 = 0.9981, slope = 1.172), showing that coregistration of single-orientation QSM images with the automated method is very comparable to human delineation of these single-orientation QSM images. The agreement between the boundaries (Fig. 7h) was also comparable between segmentation methods, with the highest disagreement once again in the left globus pallidus.
3.3 Average magnetic susceptibility across brain regions
The mean and standard deviation of the magnetic susceptibility from automated segmentation with multi-orientation QSM for each three-dimensional structure in the EvePM, as referenced to the multi-structure white matter reference ROI, are listed in Table 5 across all subjects (n = 5). Overall, for coregistration and segmentation with multi-orientation QSM, the globus pallidus had the highest average susceptibility at 0.105 +/− 0.010ppm relative to CSF, while the values for other gray matter structures were generally also positive, likely due to the presence of iron within these structures. The lowest susceptibility was found in the posterior thalamic radiations, with an average susceptibility of −0.043 +/− 0.001ppm. Such low susceptibility values were generally seen in white matter tracts oriented perpendicular to the main magnetic field.
Table 5.
Average susceptibility measurements and standard deviation per region of interest from atlas-based segmentation
| Region of Interest | Average Susceptibility [ppm] |
Standard Deviation |
|---|---|---|
| White Matter (Reference) | −0.030 | 0 |
| Superior Parietal Region | −0.009 | 0.002 |
| Cingulate Region | −0.007 | 0.003 |
| Superior Frontal Region | −0.014 | 0.002 |
| Middle Frontal Region | −0.010 | 0.002 |
| Inferior Frontal Region | −0.012 | 0.002 |
| Precentral Region | −0.022 | 0.003 |
| Postcentral Region | −0.016 | 0.003 |
| Angular Region | −0.006 | 0.003 |
| Precuneus | −0.002 | 0.002 |
| Cuneus | −0.012 | 0.003 |
| Lingual Region | −0.004 | 0.004 |
| Fusiform Region | −0.014 | 0.001 |
| Parahippocampal Region | −0.013 | 0.007 |
| Superior Occipital Region | −0.024 | 0.003 |
| Inferior Occipital Region | −0.010 | 0.002 |
| Middle Occipital Region | −0.014 | 0.003 |
| Entorhinal Region | −0.021 | 0.014 |
| Superior Temporal Region | −0.012 | 0.002 |
| Inferior Temporal Region | −0.005 | 0.003 |
| Middle Temporal Region | −0.013 | 0.003 |
| Supramarginal Region | −0.007 | 0.002 |
| Insula | −0.021 | 0.004 |
| Amygdala | 0.002 | 0.008 |
| Hippocampus | −0.015 | 0.004 |
| Cerebellum | −0.023 | 0.003 |
| Corticospinal Tract | −0.013 | 0.007 |
| Cerebral Peduncle | −0.030 | 0.010 |
| Anterior Limb of Internal Capsule | −0.022 | 0.004 |
| Posterior Limb of Internal Capsule | −0.033 | 0.005 |
| Posterior Thalamic Radiation | −0.043 | 0.001 |
| Anterior Corona Radiata | −0.035 | 0.003 |
| Superior Corona Radiata | −0.029 | 0.003 |
| Posterior Corona Radiata | −0.040 | 0.004 |
| Cingulum (Cingulate Gyrus) | −0.023 | 0.002 |
| Cingulum (Hippocampus) | −0.013 | 0.005 |
| Fornix (Cres) / Stria Terminalis | −0.025 | 0.004 |
| Superior Longitudinal Fasciculus | −0.014 | 0.002 |
| Superior Fronto-Occipital Fasciculus | −0.038 | 0.003 |
| Inferior Fronto-Occipital Fasciculus | −0.023 | 0.005 |
| Sagittal Stratum | −0.030 | 0.002 |
| External Capsule | −0.032 | 0.005 |
| Uncinate Fasciculus | −0.009 | 0.007 |
| Pontine Crossing Tract | −0.014 | 0.003 |
| Middle Cerebellar Peduncle | −0.019 | 0.003 |
| Fornix (Column and Body) | −0.014 | 0.007 |
| Corpus Callosum (Genu) | −0.033 | 0.004 |
| Corpus Callosum (Body) | −0.029 | 0.002 |
| Corpus Callosum (Splenium) | −0.030 | 0.005 |
| Retrolenticular Portion of Internal Capsule | −0.030 | 0.005 |
| Red Nucleus | 0.064 | 0.012 |
| Substantia Nigra | 0.093 | 0.004 |
| Tapetum | −0.015 | 0.007 |
| Caudate Nucleus | 0.016 | 0.006 |
| Putamen | 0.030 | 0.008 |
| Thalamus | −0.008 | 0.004 |
| Globus Pallidus | 0.105 | 0.010 |
| Lateral Ventricle (Frontal) | −0.022 | 0.008 |
| Lateral Ventricle (Body) | 0.018 | 0.004 |
| Lateral Ventricle (Atrium) | −0.008 | 0.010 |
| Lateral Ventricle (Occipital) | −0.026 | 0.007 |
| Lateral Ventricle (Temporal) | −0.008 | 0.003 |
| Dentate Nucleus | 0.030 | 0.011 |
Our automated segmentation also separates left and right structures within a region of interest. The statistics characterizing the accuracy of segmentation showed no significant differences between these lateralized portions of one structure. Most of the average susceptibility values for these structures were within a standard deviation, showing no statistically significant differences between the two hemispheres. In the putamen, however, the left structure consistently exhibited a higher average susceptibility than the right across all volunteers (Fig. 4d,e) and all segmentation methods (Fig. 5), a trend also visible in the globus pallidus, but less significant. Table 6 and Figure 8 show a comparison of the average susceptibility for regions of interest delineated by our atlas analysis with multi-orientation QSM images to values from the literature, for regions of interest in the deep gray matter and several white matter fiber bundles (Li et al., 2011; Li et al., 2012b; Liu et al., 2011; Schweser et al., 2011; Wharton and Bowtell, 2010).
Table 6.
Comparison of measured gray matter quantitative magnetic susceptibility values with literature and with iron concentration measured for these structures. All susceptibility values have been referenced to CSF by setting the reported susceptibility value for CSF to 0 ppm
| Average | Subject | Field | Susceptibility Calculation Method |
|---|---|---|---|
| Susceptibility | Demographics | Strength | (Source Cited) |
| [ppm] | (M: Male, | Acquired | |
| (Ref to CSF) | F: Female) | ||
| Globus Pallidus | |||
| 0.11 +/− 0.01 a | 30-33 y/o (5M) | 3T Philips | COSMOS |
| 0.16 +/− 0.02 b | 25-30 y/o (5M) | 7T Philips | COSMOS (Wharton and Bowtell, 2010) |
| 0.16 +/− 0.02 b | 25-30 y/o (5M) | 7T Philips | L2 RSO (Wharton and Bowtell, 2010) |
| 0.11 +/− 0.01 b | 25-30 y/o (5M) | 7T Philips | TKD (Wharton and Bowtell, 2010) |
| 0.09 +/− 0.03 c | 3T GE | WKD (Li et al., 2011) | |
| 0.16 +/− 0.02 d | 22-29 y/o (4F, 5M) | 3T GE | COSMOS (Liu et al., 2011) |
| 0.16 +/− 0.02 d | 22-29 y/o (4F, 5m) | 3T GE | MEDI (Liu et al., 2011) |
| 0.20 +/− 0.04 e | 26 y/o (1M) | 3T Siemens | COSMOS (Schweser et al., 2011) |
| 0.22 +/− 0.07 e | 26 y/o (1M) | 3T Siemens | LSQR (Schweser et al., 2011) |
| 0.20 +/− 0.07 e | 21-26 y/o (3F, 2M) | 3T Siemens | LSQR (Schweser et al., 2011) |
| 0.14 +/− 0.02 f | 21-29 y/o (6F, 5M) | 1.5T GE | MEDI (Bilgic et al., 2011) |
| 0.11 +/− 0.02 f | 21-29 y/o (6F, 5M) | 1.5T GE | L2 RSO (Bilgic et al., 2011) |
| Substantia Nigra | |||
| 0.09 +/− 0.01 a | 30-33 y/o (5M) | 3T Philips | COSMOS |
| 0.14 +/− 0.02 b | 25-30 y/o (5M) | 7T Philips | COSMOS (Wharton and Bowtell, 2010) |
| 0.13 +/− 0.03 b | 25-30 y/o (5M) | 7T Philips | L2 RSO (Wharton and Bowtell, 2010) |
| 0.08 +/− 0.01 b | 25-30 y/o (5M) | 7T Philips | TKD (Wharton and Bowtell, 2010) |
| 0.05 +/− 0.03 c | 3T GE | WKD (Li et al., 2011) | |
| 0.10 +/− 0.03 d | 22-29 y/o (4F, 5M) | 3T GE | COSMOS (Liu et al., 2011) |
| 0.09 +/− 0.03 d | 22-29 y/o (4F, 5M) | 3T GE | MEDI (Liu et al., 2011) |
| 0.20 +/− 0.06 e | 26 y/o (1M) | 3T Siemens | COSMOS (Schweser et al., 2011) |
| 0.18 +/− 0.07 e | 26 y/o (1M) | 3T Siemens | LSQR (Schweser et al., 2011) |
| 0.17 +/− 0.06 e | 21-26 y/o (3F, 2M) | 3T Siemens | LSQR (Schweser et al., 2011) |
| 0.18 +/− 0.07 f | 21-29 y/o (6F, 5M) | 1.5T GE | MEDI (Bilgic et al., 2011) |
| 0.17 +/− 0.03 f | 21-29 y/o (6F, 5M) | 1.5T GE | L2 RSO (Bilgic et al., 2011) |
| Red Nucleus | |||
| 0.06 +/− 0.00 a | 30-33 y/o (5M) | 3T Philips | COSMOS |
| 0.11 +/− 0.02 b | 25-30 y/o (5M) | 7T Philips | COSMOS (Wharton and Bowtell, 2010) |
| 0.10 +/− 0.02 b | 25-30 y/o (5M) | 7T Philips | L2 RSO (Wharton and Bowtell, 2010) |
| 0.06 +/− 0.01 b | 25-30 y/o (5M) | 7T Philips | TKD (Wharton and Bowtell, 2010) |
| 0.03 +/− 0.02 c | 3T GE | WKD (Li et al., 2011) | |
| 0.06 +/− 0.02 d | 22-29 y/o (4F, 5M) | 3T GE | COSMOS (Liu et al., 2011) |
| 0.05 +/− 0.05 d | 22-29 y/o (4F, 5M) | 3T GE | MEDI (Liu et al., 2011) |
| 0.09 +/− 0.03 e | 26 y/o (1M) | 3T Siemens | COSMOS (Schweser et al., 2011) |
| 0.15 +/− 0.06 e | 26 y/o (1M) | 3T Siemens | LSQR (Schweser et al., 2011) |
| 0.12 +/− 0.04 e | 21-26 y/o (3F, 2M) | 3T Siemens | LSQR (Schweser et al., 2011) |
| 0.11 +/− 0.04 f | 21-29 y/o (6F, 5M) | 1.5T GE | MEDI (Bilgic et al., 2011) |
| 0.08 +/− 0.03 f | 21-29 y/o (6F, 5m) | 1.5T GE | L2 RSO (Bilgic et al., 2011) |
| Dentate Nucleus | |||
| 0.03 +/− 0.01 a | 30-33 y/o (5M) | 3T Philips | COSMOS |
| 0.06 +/− 0.03 c | 3T GE | WKD (Li et al., 2011) | |
| 0.09 +/− 0.02 f | 21-29 y/o (6F, 5M) | 1.5T GE | MEDI (Bilgic et al., 2011) |
| 0.06 +/− 0.01 f | 21-29 y/o (6F, 5m) | 1.5T GE | L2 RSO (Bilgic et al., 2011) |
| Putamen | |||
| 0.03 +/− 0.01 a | 30-33 y/o (5M) | 3T Philips | COSMOS |
| 0.07 +/− 0.01 b | 25-30 y/o (5M) | 7T Philips | COSMOS (Wharton and Bowtell, 2010) |
| 0.06 +/− 0.01 b | 25-30 y/o (5M) | 7T Philips | L2 RSO (Wharton and Bowtell, 2010) |
| 0.05 +/− 0.01 b | 25-30 y/o (5M) | 7T Philips | TKD (Wharton and Bowtell, 2010) |
| 0.04 +/− 0.02 c | 3T GE | WKD (Li et al., 2011) | |
| 0.06 +/− 0.04 d | 22-29 y/o (4F, 5M) | 3T GE | COSMOS (Liu et al., 2011) |
| 0.05 +/− 0.02 d | 22-29 y/o (4F, 5m) | 3T GE | MEDI (Liu et al., 2011) |
| 0.07 +/− 0.02 e | 26 y/o (1M) | 3T Siemens | COSMOS (Schweser et al., 2011) |
| 0.10 +/− 0.04 e | 26 y/o (1M) | 3T Siemens | LSQR (Schweser et al., 2011) |
| 0.09 +/− 0.01 e | 21-26 y/o (3F, 2M) | 3T Siemens | LSQR (Schweser et al., 2011) |
| 0.10 +/− 0.02 f | 21-29 y/o (6F, 5M) | 1.5T GE | MEDI (Bilgic et al., 2011) |
| 0.08 +/− 0.02 f | 21-29 y/o (6F, 5M) | 1.5T GE | L2 RSO (Bilgic et al., 2011) |
| Caudate Nucleus | |||
| 0.02 +/− 0.00 a | 30-33 y/o (5M) | 3T Philips | COSMOS |
| 0.06 +/− 0.02 b | 25-30 y/o (5M) | 7T Philips | COSMOS (Wharton and Bowtell, 2010) |
| 0.06 +/− 0.01 b | 25-30 y/o (5M) | 7T Philips | L2 RSO (Wharton and Bowtell, 2010) |
| 0.05 +/− 0.01 b | 25-30 y/o (5M) | 7T Philips | TKD (Wharton and Bowtell, 2010) |
| 0.02 +/− 0.01 c | 3T GE | WKD (Li et al., 2011) | |
| 0.05 +/− 0.02 d | 22-29 y/o (4F, 5M) | 3T GE | COSMOS (Liu et al., 2011) |
| 0.06 +/− 0.02 d | 22-29 y/o (4F, 5M) | 3T GE | MEDI (Liu et al., 2011) |
| 0.11 +/− 0.02 f | 21-29 y/o (6F, 5M) | 1.5T GE | MEDI (Bilgic et al., 2011) |
| 0.09 +/− 0.02 f | 21-29 y/o (6F, 5M) | 1.5T GE | L2 RSO (Bilgic et al., 2011) |
| Thalamus | |||
| −0.01 +/ − 0.00 a | 30-33 y/o (5M) | 3T Philips | COSMOS |
| 0.02 +/− 0.01 b | 25-30 y/o (5M) | 7T Philips | COSMOS (Wharton and Bowtell, 2010) |
| 0.02 +/− 0.01 b | 25-30 y/o (5M) | 7T Philips | L2 RSO (Wharton and Bowtell, 2010) |
| −0.01 +/− 0.01 b | 25-30 y/o (5M) | 7T Philips | TKD (Wharton and Bowtell, 2010) |
| 0.06 +/− 0.02 f | 22-29 y/o (4F, 5M) | 1.5T GE | MEDI (Bilgic et al., 2011) |
| 0.05 +/− 0.02 f | 22-29 y/o (4F, 5M) | 1.5T GE | L2 RSO (Bilgic et al., 2011) |
| Corpus Callosum (Genu) | |||
| −0.03 +/− 0.00 a −0.03 +/− 0.01 c −0.04 +/− 0.01 g |
30-33 y/o (5M) 30-36 y/o (5M) |
3T Philips 3T GE 7T Philips |
COSMOS WKD (Li et al., 2011) COSMOS (Li et al., 2012b) |
| Corpus Callosum (Body) | |||
| −0.03 +/− 0.00 a −0.04 +/− 0.04 g |
30-33 y/o (5M) 30-36 y/o (5M) |
3T Philips 7T Philips |
COSMOS COSMOS (Li et al., 2012b) |
| Corpus Callosum (Splenium) | |||
| −0.03 +/− 0.01 a −0.04 +/− 0.01 c −0.04 +/− 0.01 g |
30-33 y/o (5M) 30-36 y/o (5M) |
3T Philips 3T GE 7T Philips |
COSMOS WKD (Li et al., 2011) COSMOS (Li et al., 2012b) |
| Internal Capsule | |||
| −0.03 +/− 0.00 (ALIC,PLIC) a −0.04 +/− 0.01 b −0.04 +/− 0.01 b −0.06 +/− 0.00 b −0.07 +/− 0.01 c |
30-33 y/o (5M) 25-30 y/o (5M) 25-30 y/o (5M) 25-30 y/o (5M) |
3T Philips 7T Philips 7T Philips 7T Philips 3T GE |
COSMOS COSMOS (Wharton and Bowtell, 2010) L2 RSO (Wharton and Bowtell, 2010) TKD (Wharton and Bowtell, 2010) WKD (Li et al., 2011) |
| Sagittal Stratum | |||
| −0.03 +/− 0.00 a −0.08 +/− 0.02 c |
30-33 y/o (5M) | 3T Philips 3T GE |
COSMOS WKD (Li et al., 2011) |
| Posterior Thalamic Radiations | |||
| −0.04 +/− 0.00 a −0.05 +/− 0.00 g |
30-33 y/o (5M) 30-36 y/o (5M) |
3T Philips 7T Philips |
COSMOS COSMOS (Li et al., 2012b) |
This current manuscript
COSMOS (Calculation of Susceptibility through Multiple Orientation Sampling), RSO (Regularized Single Orientation), and TKD (Thresholded K-Space Division) (Wharton and Bowtell, 2010)
WKD (Weighted K-space partial Derivatives) (Li et al., 2011)
COSMOS, MEDI (Morphology Enabled Dipole Inversion), (Liu et al., 2011)
COSMOS, LSQR (Algorithm for sparse linear equations and sparse least squares) (Schweser et al., 2011)
MEDI, L2 RSO (12 norm Regularized Single Orientation) (Bilgic et al, 2012)
COSMOS (Li et al., 2012b)
Figure 8.
Comparison of atlas-based average susceptibility values with values from different approaches in the literature for (a) gray matter and (b) white matter. All numbers have been referenced to CSF = 0ppm (Table 6). Abbreviations: GP = globus pallidus, SN = substantia nigra, RN = red nucleus, DN = dentate nucleus, PT = putamen, CN = caudate nucleus, TH = thalamus, CCg = genu of the corpus callosum, CCb = body of the corpus callosum, CCs = splenium of the corpus callosum, IC = internal capsule, SS = sagittal stratum, TR = posterior thalamic radiations, W&B 2010 = Wharton and Bowtell 2010.
3.4 Correlating iron concentration with mean susceptibility
Figure 9a shows the magnetic susceptibility measured for nine deep gray matter structures in our five 30- to 33-year-old volunteers using multi-orientation QSM. It would be useful to correlate these to tissue iron concentration values reported in the literature. However, brain iron concentration changes with age. Based on histology-based brain iron extracted from 81 subjects aged 30- to 100-years-old, Hallgren and Sourander reported the iron concentration as a function of age for only three of the structures in our atlas, namely the globus pallidus, putamen, and caudate nucleus (Hallgren and Sourander, 1958). In an effort to deduce the iron concentration for our volunteers in the other regions, we plotted the concentrations for the three known regions calculated for age 31 as a function of measured quantitative magnetic susceptibility (black circles in Fig. 9b) and fitted them to a straight line, thereby generating a plot of the brain iron concentration as a function of average susceptibility with respect to CSF:
Figure 9.
Interpolating iron concentration for deep gray matter regions. (a) The average susceptibility per volunteer for regions of interest in the deep gray matter, calculated from multi-orientation QSM images. (b) A line correlating susceptibility and iron concentration was calculated using the age-based iron concentration per region according to the Hallgren and Sourander paper of 1958. Then the average susceptibility for the gray matter regions was used to calculate corresponding iron concentrations according to this line, also shown in the bar graph in (c).
Overall, the Pearson’s correlation coefficient for the interpolated iron concentration versus the age-based calculations from the Hallgren and Sourander paper (Hallgren and Sourander, 1958) was R2 = 0.997, indicating a very good correlation. We subsequently placed the susceptibilities of other regions (gray squares) on this line connecting these points. The iron concentration of these other regions can then be calculated from the average susceptibility according to the equation for the fitted line. Table 7 lists the predicted iron concentration for each of these gray matter regions and compares them to average iron concentration values for similar age groups, as taken from the literature.
Table 7.
Iron concentrations interpolated from average susceptibility measurements from automated atlas segmentation, as compared to iron concentrations from the literature for deep gray matter regions
| Region of Interest |
Average [Iron] [mg Iron per 100g tissue] |
Subject Demographics |
|---|---|---|
| Globus Pallidus |
20.4+/− 1.3 a 20.5 +/− 0.2 A 21.3 +/− 3.5 B 20.5 +/− 3.2 C |
30-33 y/o (5 males, interpolated atlas, QSM) 31-100 y/o (81 subjects, linear regression, colorimetry) 31-100 y/o (81 subjects, averaged, colorimetry) 38-81 y/o (7 males, mass spectrometry) |
| Substantia Nigra |
18.8 +/− 0.6 a 18.5 +/− 6.5 B 15.3 +/− 2.5 E |
30-33 y/o (5 males, interpolated atlas, QSM) 31-100 y/o (81 subjects, averaged, colorimetry) 29-35 y/o (5 subjects, ETAAS) |
| Red Nucleus | 14.8 +/− 1.7 a 19.5 +/− 6.9 B |
30-33 y/o (5 males, interpolated atlas, QSM) 31-100y/o (81 subjects, averaged, colorimetry) |
| Dentate Nucleus |
10.2 +/− 1.5 a 10.4 +/− 4.9 B |
30-33y/o (5 males, interpolated atlas, QSM) 31-100 y/o (81 subjects, averaged, colorimetry) |
| Putamen | 10.2 +/− 1.0 a 10.9 +/− 0.2 A 13.3 +/− 3.4 B 15.3 +/− 2.9 C |
30-33y/o (5 males, interpolated atlas, QSM) 31-100y/o (81 subjects, linear regression, colorimetry) 31-100 y/o (81 subjects, averaged, colorimetry) 38-81 y/o (7 males, mass spectrometry) |
| Caudate Nucleus |
8.3 +/− 0.8 a 8.0 +/− 0.2 A 9.3 +/− 2.1 B 9.2 +/− 1.5 C |
30-33y/o (5 males, interpolated atlas, QSM) 31-100y/o (81 subjects, linear regression, colorimetry) 31-100 y/o (81 subjects, averaged, colorimetry) 38-81 y/o (7 males, mass spectrometry) |
| Amygdala | 6.3 +/− 1.1 a 4.9 D |
30-33 y/o (5 males, interpolated atlas, QSM) 81.7 y/o (11 subjects, INAA) |
| Thalamus | 4.9 +/− 0.6 a 4.8 +/− 1.2 B 4.9 +/− 1.1 C |
30-33 y/o (5 males, interpolated atlas, QSM) 31-100 y/o (81 subjects, averaged, colorimetry) 38-81 y/o (7 males, mass spectrometry) |
| Hippocampus | 4.0 +/− 0.6 a 4.3 D |
30-33 y/o (5 males, interpolated atlas, QSM) 81.7 y/o (11 subjects, INAA) |
From the current manuscript, interpolated iron concentrations from quantitative susceptibility values for five 30-33 y/o males
Calculations for our five 30-33 y/o males based on linear-regression equations for [mg iron per 100g of fresh tissue] as a function of age for 81 subjects between the ages of 31 to 100 years of age, analyzed with colorimetry, from (Hallgren and Sourander, 1958)
Average [mg iron per 100g of fresh tissue] for all 81 subjects between the ages of 31 to 100 years of age, analyzed with colorimetry, from (Hallgren and Sourander, 1958)
Average [mg iron per kg wet mass of tissue] for seven deceased males between 38 to 81 years old, with a mean age of 52.3 years, analyzed with inductively coupled plasma mass spectrometry, from (Langkammer et al., 2010)
Average [μg iron per g of dry weight] for eleven control subjects (8 females, 3 males) at a mean age of 81.7 years, analyzed with instrumental neutron activation analysis (INAA), from (Deibel et al., 1996) and calculated to [μg iron per g of wet weight] in a review by (Haacke et al., 2005)
Average [ng iron per mg wet tissue] for five substantia nigra autopsied samples from five subjects aged approximately 29 to 35 years old, analyzed with instrumental neutron activation analysis (INAA) and electro-thermal atomic absorption spectroscopy (ETAAS), taken from Figure 1 of (Zecca et al., 2005)
4. Discussion
The white matter parcellation map from the Eve atlas is based on the standard DTI resolution of 2.2 × 2.2 × 2.2 mm3 isotropic voxels, with gray matter mainly delineated on a coregistered T1-weighted MPRAGE with 1mm3 isotropic voxels. Due to possible partial voluming effects and insufficient contrast for several gray matter regions like the dentate nucleus, red nucleus, and substantia nigra, the boundaries of the white matter parcellation map do not perfectly agree with deep gray matter structures that can be easily seen on QSM images, as shown in Figure 3a. The increase in contrast provided by the quantitative susceptibility images improved the definition of these deep gray matter regions (Fig. 3b,c), allowing the magnetic susceptibility of deep gray matter structures to be automatically and reproducibly quantified for a group of 30- to 33-year-old volunteers. In addition, using literature data for the age-dependent iron content of three regions, a calibration plot correlating magnetic susceptibility with iron content could be generated that was used to determine the iron concentrations of six other deep gray matter structures.
4.1 Quantification of magnetic susceptibilities
We compared our multi-orientation magnetic susceptibility numbers to data reported in the recent QSM literature by recalculating all of these values with respect to CSF (0.00 ppm) as a reference (Table 6, Fig. 8). This was needed because various referencing approaches have been used to normalize the relative susceptibility numbers between subjects. Most groups choose reference regions of interest in some CSF-containing structure and assign this to 0 ppm (Bilgic et al., 2011; Schweser et al., 2011). However, many of the structures containing CSF are fairly inhomogeneous and small, making them difficult to delineate accurately. Other groups reference to the average susceptibility of white matter set to 0 ppm (Wharton and Bowtell, 2010), which provides more reproducible results, but a slightly skewed frame of reference from the natural demarcation of gray matter tending to be more paramagnetic and white matter tending to be more diamagnetic than CSF. Our referencing approach (Li et al., 2012b) is a compromise between the two methods in which the region is chosen in easily delineated deep white matter and assigned an average susceptibility of −0.03 ppm, so that the average susceptibility of CSF is approximately 0.00pm. For example, examination of the histograms for susceptibility in the CSF between the frontal portion and body of the lateral ventricle shows substantial differences both within and between volunteers, whereas the histograms for the white matter reference region show consistent average susceptibilities and standard deviations across all volunteers (for more details, see Appendix 2). Note that using white matter as a reference region of interest may not be appropriate for all subject populations (e.g., comparing normal controls to multiple sclerosis patients, who may have white matter lesions). However, a large ROI in the white matter has been shown to be a consistent choice for normal control populations, as previously shown by others (Deistung et al., 2013; Li et al., 2012b; Wharton and Bowtell, 2010).
The QSM template in the current Eve atlas is a high-end standard meant to show what can be achieved for this resolution using multiple orientations. When using other approaches, the relationship between this standard and other approaches should be established first. With respect to inter-subject coregistration, steps 1-5 in Figure 2 should be independent of the QSM analysis method because these use only use the magnitude images. From step 6 on (LDDMM on magnitude + QSM), differences in analysis may change the structure definition. However, while the single brain orientation images have some artifacts, the size and relative contrast of the deep gray matter structures are expected to be similar to those on multi-orientation QSM images and the atlas remains useful. Of course, the value of the susceptibility may be affected by the particular method used to calculate the single orientation susceptibilities.
Figure 5 shows a comparison between the average and standard deviations of susceptibility values from (a) multi-orientation QSM and (b) single-orientation QSM images across all of our 30- to 33-year-old subjects for each rater. Overall, the average susceptibility values per region of interest fall within a standard deviation per rater and method. Generally, when using the single-orientation QSM images, the statistics for segmentation accuracy for “manual vs. automated” delineation were higher than intra-rater and inter-rater delineation. Single-orientation QSM images tend to be noisier than multi-orientation QSM images, which, according to our human raters, makes manual ROI delineation particularly difficult. Thus, the automated segmentation method may improve delineation, especially when much variation exists between human raters. Figure 5c shows a correlation plot of the multi- and single orientation susceptibility values. They are highly correlated, but the slope shows that the single-orientation susceptibilities calculated with dipole fitting and the LSQR method consistently underestimate the susceptibility by about 85%. This does not reduce the value of the atlas, but indicates that in use it for absolute determinations of susceptibilities for subjects in clinical studies, researchers should first compare their particular single-orientation approach with the multi-orientation gold standard for their controls. QSM is an approach that is especially sensitive to the acquisition and processing methods as well as, for certain structures, to the age of the subjects. Coregistration using the QSM contrast in the Eve atlas, however, should be sufficient to put the uniformly calculated regions of interest from the EvePM into subject space for comparison in these clinical studies.
Generally, as shown by Table 6 and Figure 8, the relative shifts between the average susceptibility of structures measured with multi-orientation QSM in this work showed trends similar to measurements at 3T and 7T by other investigators (Li et al., 2011; Li et al., 2012b; Liu et al., 2011; Schweser et al., 2011; Wharton and Bowtell, 2010). However, the actual values still show some variation between groups. This is not unexpected in view of the age and gender differences between the subjects analyzed, as well as the many different analysis approaches used and the continuous development of new approaches. Currently, there are multiple methods of phase unwrapping to derive the resonance frequency map and several approaches for removal of the background gradient fields and the calculation of susceptibility from the resonance frequency. The latter part of the calculation may especially induce great differences as the magnitude of the susceptibility and its accuracy depends on threshold settings for the inverse analysis, the use of one versus multiple brain orientations, and the use of different types of regularization. The referencing method will also affect the susceptibility measurements, especially if the reference region shows wide variations in average susceptibility within and across volunteers, as previously discussed for referencing to CSF.
The papers cited in Table 6 and Figure 8 utilized manual delineation, with only two dimensional, usually transverse, images showing the regions of interest, and no uniform mention of the percentage of each structure that was segmented; therefore, the “average susceptibility” of a particular region could possibly denote a few brain slices across that structure or many slices across the entire structure, resulting in more heterogeneity between projects. For example, the SHARP method with susceptibilities calculated using COSMOS for one male, LSQR for one male, and LQSR for males and females showed consistently higher average susceptibilities in the globus pallidus (Schweser et al., 2011), with very little description on how the ROIs were drawn. Region of interest selection was thoroughly described in (Bilgic et al., 2011), with ten 1mm slices encompassing the basal ganglia, white matter, and thalamus; in this group, the bright rims around the globus pallidus and putamen were excluded, leading to lower average susceptibility values in the globus pallidus, but surprisingly higher values in the putamen. White matter was used as a reference ROI in (Wharton and Bowtell, 2010), with regions of interest drawn on the left and right sides of four to five slices per brain level; however, the reference ROI is not shown in the paper, only listed as “WM throughout the brain for each subject.” The COSMOS and MEDI calculations in (Liu et al., 2011) were referenced to one white matter ROI (above the corpus callosum), with deep gray matter regions drawn manually on magnitude images, and cortical regions drawn on the COSMOS images; the average susceptibility values in the substantia nigra seem lower compared to the globus pallidus for these methods. Our method seemed to correlate within rounding error with Weighted K-space partial Derivatives (Li et al., 2011) conducted at 3T, with similar susceptibilities in the globus pallidus, putamen, caudate nucleus, and corpus callosum. These similarities could be due to both groups processing the phase images with Laplacian-based phase unwrapping, which partially removes the background field, resulting in smoother frequency maps. Interestingly, this was the only group who reported substantially higher values in the dentate nucleus than the putamen, but do not describe the age range of their subjects or the structure containing their CSF reference. Previous work at 7T from our group (Li et al., 2012b) showed close agreement in the white matter structures, especially the corpus callosum and posterior thalamic radiations, most likely due to the close age range across all-male subjects (30 to 33 years old versus 30 to 36 years old) and utilizing similar processing with multi-orientation GRE acquisition, Laplacian-based phase unwrapping for background removal, and COSMOS for susceptibility calculation. Our current work shows consistently lower standard deviations than most other groups, which we mainly attribute to uniformity of segmentation and similarity between the age and gender of our subjects. Substantial agreement between all methods was especially seen in the putamen, a relatively straightforward structure to delineate, in which iron accumulation is relatively constant between the ages of 20 and 60 years old.
Future research comparing the susceptibility values from uniformly-drawn 3D regions of interest for the various methods across specific age groups, scanner types, field strengths, referencing, and sequence parameters would be useful to assess the reproducibility or calculable differences between the methods.
4.2 Iron concentrations
Comparing iron concentrations per region of interest is complicated by the age-dependence of iron in the brain. For example, while iron in the globus pallidus levels off around twenty years of age, the iron in the putamen increases significantly between 60 to 70 years of age (Brass et al., 2006; Drayer et al., 1986). Therefore, the iron calculated in the putamen for our set of volunteers between 30-to 33-years-old may differ from the average iron in the putamen across volunteers of many different ages, but it is still a good value to use for the linear calibration curve for the age group of our volunteers. Based on the available data from Hallgren and Sourander (Hallgren and Sourander, 1958), we were limited to three points for linear fitting, which may have limited accuracy. However, as Table 7 shows, our estimates of the average iron concentration in deep gray matter regions correspond fairly well with the existing literature. Overall, the values shown for the nine different deep gray matter structures seem to reinforce our age-based calibration of brain iron concentration as a function of average susceptibility per region of interest.
Most of the literature data are based on the combined average susceptibility for left and right portions of various structures. Our atlas-based analysis automatically separates left and right regions. When comparing these, the average susceptibility for most of them was within a standard deviation of difference. Interestingly, in our study, for all of the different methods of segmentation, the left and right portions of the putamen showed similar statistical measurements, but heterogeneity in average susceptibility. That is, the left putamen consistently showed a higher average susceptibility than the right putamen (when conducting a paired t-test comparing the left and right structures for all volunteers per rater, the p-value ranged from 0.001 to 0.02). This behavior was also mirrored by the average susceptibility in the left and right portions of the globus pallidus (p-value ranging from 0.002 to 0.01). Our previous work for five male subjects in the same age range at 7T also showed a higher average susceptibility in the left putamen when compared to the right, but within a standard deviation (Li et al., 2012b). Because the QSM images were created with multi-orientation multi-echo gradient-recalled echo images, we do not believe that these differences are due to any technological errors in the acquisition or analysis. However, these datasets only assessed five right-handed male scientist and engineer volunteers, and a larger population is needed to merit scientifically sound observations. Closer examination of the basal ganglia at higher resolution or higher field may pinpoint the source of the heterogeneity seen in these quantitative susceptibility images.
4.3 Technical details
In this study, we utilized affine transformation for brain normalization, which is a valid procedure but does produce some errors. Therefore, the standard deviations shown do not only demonstrate variations in average susceptibility measurements between volunteers, but also possible errors from registration. This is especially possible in small regions of interest, which are less likely to be accurately coregistered. That said, by comparing the rater segmentation across affine-coregistered images and specifying the slices through which each region of interest was delineated, we ensured a controlled environment for analyzing the accuracy of segmentation for coregistration with either multi-orientation QSM or single-orientation QSM.
Due to the large variation in the peripheral cortical areas between subjects, the cortex was segmented into various regions containing both white and gray matter. Because we erode the superficial cortex while processing the quantitative susceptibility maps, these cortical areas may actually contain more white matter, and only provide a general measurement of the susceptibility in the periphery of the brain. In the future, an analysis using the subject MPRAGE to assess the percentage of gray and white matter in the cortical areas may provide a closer examination of differences between these outer regions of the brain.
Generally, automated processing with LDDMM provides segmentation at an accuracy that is comparable to manual delineation by multiple raters (Faria et al., 2011; Faria et al., 2010; Oishi et al., 2009). The specificity was particularly high and the false positive rate was particularly low; this is most likely due to the area of “negative” agreement being the entire brain, which was large in size compared to the regions that were delineated. Because of the intrinsic ability of the human eye to differentiate between structures of different intensities, manual delineation is held as the gold standard of ROI segmentation; however, drawing these regions by hand can be time-consuming: the human raters on average spent several days drawing ten ROIs on five volunteers, whereas the automated algorithm delineated left and right regions for over sixty structures in less than 24 hours.
Manual delineation is also prone to human error; for example, one of the raters initially demarcated only the outline of a region, which had to be corrected. Also, as seen with the single-orientation QSM images, several smaller structures may be particularly difficult for researchers to manually delineate, resulting in more variation due to human error. The average statistical metrics showed “almost perfect” agreement between all of the segmentation processes for both multi-orientation and single-orientation QSM. Using boundary-based metrics, we confirmed that the disagreement between manual and automated delineation was not significantly higher than the disagreement between delineation by human raters; in fact, the automated segmentation seemed to perform better than human raters when delineating single-orientation QSM images. Finally, the correlations between volumes measured manually or with the automated method were very close to 1, for coregistration and segmentation using either multi-orientation or single-orientation QSM. Note that a correlation of 1 would be an absolutely perfect correlation between different metrics, which is nearly impossible. Both the automated and the different human raters can sometimes “overestimate” or “underestimate” a given region, but no consistent bias on over- or underestimation was detected for any of the methods.
MRI Studio is a powerful coregistration tool, with templates based on different types of contrast, including T1-weighted, T2-weighted, DTI, and now QSM images, which allows various possibilities for inter-subject coregistration. QSM contrast is particularly useful for delineating gray matter regions like the substantia nigra, red nucleus, and dentate nucleus, which are typically difficult to segment in the T1-weighted templates used in software like FreeSurfer and the previous T1-weighted template for MRI Studio. Addition of the QSM contrast to either of these will enhance the capabilities to segment these nuclei.
By segmenting many regions of interest in an automated and timely fashion, data analysis on large datasets may be performed. In this first paper, the brains of five subjects were delineated in an automated process within 24 hours, allowing us to compare these susceptibility values from multi-orientation QSM images to known age-matched iron values in the literature. Determination of the concentration of iron within the brain from these susceptibilities is not straightforward to measure, largely due to the fact that iron concentration changes with age. Many of the papers that assess iron concentration have averaged the iron per brain structure over a small number of subjects that span a large age range. Nonetheless, as Table 7 shows, interpolation of iron concentration for various gray matter structures based on the automated segmentation of multi-orientation quantitative susceptibility values seems to match the appropriate range of iron for these structures, as compared to the literature. A more thorough analysis across a wider range of ages involving more subjects would allow the creation of a baseline susceptibility across various ages, possibly leading to correlating iron concentration in the brain throughout development and aging.
5. Conclusion
We have created a single-subject template that may be used to conduct group analyses of both multi-orientation and single-orientation quantitative susceptibility maps, improving analysis efficiency by automating region of interest delineation of the left and right structures for over 60 brain areas. We have also provided an estimate of brain iron in several deep gray matter regions as correlated with quantitative susceptibility measurements from multi-orientation QSM images. The atlas and MRI Studio software utilized here can be downloaded from the MRI Studio website (https://www.mristudio.org), with further instructions available in the software section of the website for the National Research Resource for Functional MRI (http://www.mriresource.kennedykrieger.org).
Highlights.
We added a Quantitative Susceptibility Mapping (QSM) template to the Eve atlas.
We utilized MRI Studio software to coregister QSM images to the Eve atlas.
Automated segmentation took less than 24 hours for over sixty brain regions.
We derived a susceptibility-iron calibration curve based on known iron values.
This curve was used to determine iron concentration in other gray matter regions.
6. Acknowledgements
The authors thank Mr. Carlos Renjifo, Mr. Joseph S. Gillen, Ms. Terri Brawner, Ms. Kathleen Kahl, Ms. Ivana Kusevic, Dr. Craig Jones, Dr. Kenichi Oishi, Dr. James Pekar, Dr. Carolyn Lauzon, Dr. Brian Caffo, Dr. Peter Barker, and Dr. Doris Lin for assistance with data acquisition and processing. This research was supported by NIH resource grant P41 EB051909 (formerly P41 RR015241), with training funded in part by the NeuroEngineering Training Initiative (NETI), the NeuroEngineering Training Grant, NIH T32EB003383, and the NIH grant for Interdisciplinary Training in Psychiatry and Neuroscience, 5 T32 MH015330. The contents of this publication are solely the responsibility of the authors and do not necessarily represent the official view of NCRR, NIBIB, or NIH. Dr. Peter van Zijl is partly supported by a grant from Philips Healthcare. Dr. Peter van Zijl is a paid lecturer for Philips Healthcare and is the inventor of technology that is licensed to Philips. Dr. Susumu Mori is a partial owner and CEO of AnatomyWorks. These arrangements have been approved by The Johns Hopkins University in accordance with its Conflict of Interest policies.
Abbreviations
- AIR
Automated Image Registration
- CC
Corpus Callosum
- CCb
Body of the Corpus Callosum
- CCg
Genu of the Corpus Callosum
- CCs
Splenium of the Corpus Callosum
- CN
Caudate Nucleus
- CSF
Cerebrospinal Fluid
- COSMOS
Calculation of Susceptibility through Multiple Orientation Sampling
- CX
Cortex
- DGMPM
Deep Gray Matter Parcellation Map (derived from QSM calculations)
- DN
Dentate Nucleus
- ETAAS
Electro-thermal Atomic Absorption Spectroscopy
- EvePM
“Everything” Parcellation Map with gray and white matter ROIs
- EC
External Capsule
- GM
Gray Matter
- GP
Globus Pallidus
- GRE
Gradient Recalled Echo
- IC
Internal Capsule
- INAA
Instrumental Neutron Activation Analysis
- LDDMM
Large Deformation Diffeomorphic Metric Mapping
- LSQR
Algorithm for sparse linear equations and sparse least squares
- LVL
Lateral Ventricle
- MEDI
Morphology Enabled Dipole Inversion
- MRI
Magnetic Resonance Imaging
- PT
Putamen
- QSM
Quantitative Susceptibility Mapping
- RN
Red Nucleus
- ROI
Region of Interest
- RSO
Regularized Single Orientation
- SHARP
Sophisticated Harmonic Artifact Reduction for Phase data
- SN
Substantia Nigra
- SS
Sagittal Stratum
- TH
Thalamus
- TKD
Thresholded K-space Division
- TR
Thalamic Radiations
- WKD
Weighted K-space partial Derivatives
- WM
White Matter
- WMPM
White Matter Parcellation Map (derived from previous T1-weighted and DTI measurements)
7. Appendix 1. Calculating accuracy of segmentation
7.1 Definitions of Variables
Truth: Regions of interest drawn by expert rater (e.g., Rater A)
Results: Intra-rater: regions of interest drawn by expert rater (Rater A) one week later Inter-rater: regions of interest drawn by other raters (e.g., Rater B, Rater C) Automated: regions of interest drawn with MRI Studio software
(coregistered with AIR and LDDMM, with transforms applied to atlas) True Positive: overlapping regions defined within regions for T and R
| A.1 |
True Negative: overlapping regions defined as not T and not R
| A.2 |
False Positive: regions not part of T but part of R
| A.3 |
False Negative: regions part of T but not part of R
| A.4 |
These values are illustrated in Table A.1.
Table A1.
Definitions of variables for gauging rater accuracy
| Truth: Included in ROI |
Truth: Excluded from ROI |
Total | |
|---|---|---|---|
| Result: Included in ROI |
True Positive (TP) | False Positive (FP) | All Result Positives: TP + FP |
| Result: Excluded from ROI |
False Negative (FN) | True Negative (TN) | All Result Negatives: FN + TN |
| Total | TP + FN | FP + TN | # Total Voxels Analyzed = TP + TN + FN + FP |
Only regions within the brain were considered for the true negative calculation, so the number of total voxels equals the region within the brain mask. The diagonal elements of this table indicate the number of voxels that are in the same class for both the truth and the results; that is, they agreed on the TP and TN, and disagreed on the FP and FN.
7.2 Calculations
Success and Error Rates (Shattuck et al., 2009)
The sensitivity, specificity, false positive rate (FPR), and false negative rate (FNR) are calculated based on the total elements in a particular set (i.e., ∣A∣ is the size of set A). The positive predictive value (PPV) is based on the number of all positives and the negative predictive value (NPV) is based on the number of all negatives.
| A.5 |
| A.6 |
| A.7 |
| A.8 |
| A.9 |
| A.10 |
Boundary-Based Metric (Zhang et al., 2010)
This metric is the scalar product of the normal vector at each voxel of the ROI contour by the magnitude of the LDDMM deformation field that transforms a set of ROIs (e.g., the automated method) to another (e.g., Rater A, the “gold-standard”) on that voxel. The value is inversely proportional to the agreement between delineations.
7.2.1 Similarity between Datasets
Kappa Analysis (Bartko and Carpenter, 1976; Zijdenbos et al., 1994)
The Kappa Coefficient compares the difference between the percentage of agreement in positives and negatives between raters that is observed (pobserved) versus the percentage of agreement due to chance (pchance):
| A.11 |
where the observed agreement is the quotient between the number of true positives and true negatives over the total number of voxels:
| A.12 |
and the chance agreement is calculated from the independent assignation of each rater to voxels of the same class:
| A.13 |
Therefore, the Kappa Coefficient is equal to:
| A.14 |
Jaccard Similarity Coefficient (Jaccard, 1912; Shattuck et al., 2009)
The Jaccard Similarity Coefficient, also known as the Jaccard Index, is equal to the positive agreement between two datasets divided by all of the positives within the datasets:
| A.15 |
Dice Coefficient (Dice, 1945; Shattuck et al., 2009; Zou et al., 2004)
The Dice Coefficient is equal to the positive agreement between the two datasets divided by their average size:
| A.16 |
8. Appendix 2. Referencing susceptibility values to a region of interest
Due to the arbitrary setting of the scanner resonance frequency, magnetic susceptibility values are relative, and must be referenced to a particular region in order to obtain reproducible quantitative values. Often, the cerebrospinal fluid is used as a reference region, with the average susceptibility set to 0.00pm. However, the CSF is spread throughout the brain in the large, somewhat inhomogeneous ventricles, and is especially prone to artifacts like flow effects, proximity to iron-containing gray matter regions, etc. Segmentation with the EvePM allows efficient comparison between various CSF-containing regions, enabling us to compare the histograms of susceptibility values per region. For example, as Figure A1 shows, the average susceptibility in one structure, the lateral ventricle, exhibits substantial differences between various areas of the ventricle, e.g., the body of the lateral ventricle (Fig. A1b) versus the frontal portion of the lateral ventricle (Fig. A1c). Differences are found both within and between volunteers, showing that CSF may be an erratic referencing tool.
Figure A1.
Histograms showing the susceptibility values calculated from multi-orientation QSM images in the (a) bundled white matter region of interest used to reference the susceptibility values, (b) body of the lateral ventricle, and (c) frontal portion of the lateral ventricle. Comparing the regions containing CSF show substantial differences within and between volunteers. Abbreviations: Vol = Volunteer, LVL = Lateral Ventricle.
For this project, we created a large reference region by combining several large white matter bundles: cerebral peduncles, internal capsule, posterior thalamic radiations (including the optic radiations), corona radiata, centrum semiovale, superior longitudinal fasciculi, fronto-occipital fasciculi (including inferior longitudinal fasciculi), and corpus callosum. This large region showed consistent average and standard deviation in susceptibility values across all volunteers. Granted, the choice of white matter as a reference ROI may not be appropriate for all subject populations; for example, multiple sclerosis patients may have lesions in the white matter. However, a large ROI in the white matter has also been shown to be a consistent choice for normal control populations (Deistung et al., 2013; Li et al., 2012b; Wharton and Bowtell, 2010).
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
Author Contributions: IAL, AVF, XL, PCMvZ designed the research; IAL performed the research; IAL, AVF, XL contributed new analytical tools; IAL, AVF, XL, JTH, RDA analyzed data; and IAL, AVF, XL, SM, PCMvZ wrote the paper. All authors edited the paper.
10. References
- Bartko JJ, Carpenter WT. On the Methods and Theory of Reliability. The Journal of Nervous and Mental Disease. 1976;163:307–317. doi: 10.1097/00005053-197611000-00003. [DOI] [PubMed] [Google Scholar]
- Beg MF, Miller MI, Trouve A, Younes L. Computing Large Deformation Metric Mapping via Geodesic Flows of Diffeomorphisms. International Journal of Computer Vision. 2005;61:139–157. [Google Scholar]
- Bilgic B, Pfefferbaum A, Rohlfing T, Sullivan EV, Adalsteinsson E. MRI estimates of brain iron concentration in normal aging using quantitative susceptibility mapping. Neuroimage. 2011;59:2625–2635. doi: 10.1016/j.neuroimage.2011.08.077. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brass SD, Chen N-K, Mulkern RV, Bakshi R. Magnetic resonance imaging of iron deposition in neurological disorders. Topics in Magnetic Resonance Imaging. 2006;17:31–40. doi: 10.1097/01.rmr.0000245459.82782.e4. [DOI] [PubMed] [Google Scholar]
- Cao Y, Miller MI, Winslow RL, Younes L. Large Deformation Diffeomorphic Metric Mapping of Vector Fields. IEEE Trans Med Imaging. 2005;24:1216–1230. doi: 10.1109/tmi.2005.853923. [DOI] [PubMed] [Google Scholar]
- de Rochefort L, Liu T, Kressler B, Liu J, Spincemaille P, Lebon V, Wu J, Wang Y. Quantitative susceptibility map reconstruction from MR phase data using bayesian regularization: validation and application to brain imaging. Magnetic Resonance in Medicine. 2010;63:194–206. doi: 10.1002/mrm.22187. [DOI] [PubMed] [Google Scholar]
- Deibel MA, Ehmann WD, markesbery WR. Copper, iron, and zinc imbalances in severely degenerated brain regions in Alzheimer’s disease: possible relation to oxidative stress. Journal of Neurological Sciece. 1996;143:137–142. doi: 10.1016/s0022-510x(96)00203-1. [DOI] [PubMed] [Google Scholar]
- Deistung A, Rauscher A, Sedlacik J, Stadler J, Witoszynskyj S, Reichenbach JR. Susceptibility weighted imaging at ultra high magnetic field strengths: theoretical considerations and experimental results. Magnetic Resonance in Medicine. 2008;60:1155–1168. doi: 10.1002/mrm.21754. [DOI] [PubMed] [Google Scholar]
- Deistung A, Schaefer A, Schweser F, Biedermann U, Turner R, Reichenbach JR. Toward in vivo histology: a comparison of quantitative susceptibility mapping (QSM) with magnitude-, phase-, and R2*-imaging at ultra-high magnetic field strength. Neuroimage. 2013;65:299–314. doi: 10.1016/j.neuroimage.2012.09.055. [DOI] [PubMed] [Google Scholar]
- Dice LR. Measures of the Amount of Ecologic Association Between Species. Ecology. 1945;26:297–302. [Google Scholar]
- Drayer B, Burger P, Darwin R, Riederer S, Herfkens R, Johnson GA. MRI of Brain Iron. American Journal of Roentgenology. 1986;147:103–110. doi: 10.2214/ajr.147.1.103. [DOI] [PubMed] [Google Scholar]
- Duyn JH, van Gelderen P, Li T-Q, de Zwart JA, Koretsky AP, Fukunaga M. High-field MRI of brain cortical substructure based on signal phase. Proceedings of the National Academy of Sciences. 2007;104:11796–11801. doi: 10.1073/pnas.0610821104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Faria AV, Hoon A, Stashinko E, Li X, Jiang H, Mashayekh A, Akhter K, Hsu J, Oishi K, Zhang J, Miller MI, van Zijl PCM, Mori S. Quantitative analysis of brain pathology based on MRI and brain atlases--applications for cerebral palsy. Neuroimage. 2011;54:1854–1861. doi: 10.1016/j.neuroimage.2010.09.061. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Faria AV, Joel SE, Zhang Y, Oishi K, van Zijl PC, Miller MI, Pekar JJ, Mori S. Atlas-based analysis of resting-state functional connectivity: Evaluation for reproducibility and multi-modal anatomy-function correlation studies. Neuroimage. 2012;61:613–621. doi: 10.1016/j.neuroimage.2012.03.078. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Faria AV, Zhang J, Oishi K, Li X, Jiang H, Akhter K, Hermoye L, Lee S.-k., Hoon A, Stashinko E, Miller MI, Zijl PCMV, Mori S. Atlas-based analysis of neurodevelopment from infancy to adulthood using diffusion tensor imaging and applications for automated abnormality detection. Neuroimage. 2010;52:415–428. doi: 10.1016/j.neuroimage.2010.04.238. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fukunaga M, Li T-Q, van Gelderen P, de Zwart JA, Shmueli K, Yao B, Lee J, Maric D, Aronova MA, Zhang G, Leapman RD, Schenck JF, Merkle H, Duyn JH. Layer-specific variation of iron content in cerebral cortex as a source of MRI contrast. Proceedings of the National Academy of Sciences. 2010;107:3834–3839. doi: 10.1073/pnas.0911177107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Haacke EM, Cheng NYC, House MJ, Liu Q, Neelavalli J, Ogg RJ, Khan A, Ayaz M, Kirsch W, Obenaus A. Imaging iron stores in the brain using magnetic resonance imaging. Magn Reson Imaging. 2005;23:1–25. doi: 10.1016/j.mri.2004.10.001. [DOI] [PubMed] [Google Scholar]
- Haacke EM, Tang J, Neelavalli J, Cheng YCN. Susceptibility mapping as a means to visualize veins and quantify oxygen saturation. Journal of Magnetic Resonance Imaging. 2010;32:663–676. doi: 10.1002/jmri.22276. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hallgren B, Sourander P. The effect of age on the non-haemin iron in the human brain. J Neurochem. 1958;3:41–51. doi: 10.1111/j.1471-4159.1958.tb12607.x. [DOI] [PubMed] [Google Scholar]
- Jaccard P. The Distribution of Flora in the Alpine Zone. New Phytologist. 1912;XI:37–50. [Google Scholar]
- Jenkinson M, Bannister PR, Brady M, Smith S. Improved Optimiation for the Robust and Accurate Linear Registration and Motion Correction of Brain Images. Neuroimage. 2002;17:825–841. doi: 10.1016/s1053-8119(02)91132-8. [DOI] [PubMed] [Google Scholar]
- Jenkinson M, Smith S. A global optimisation method for robust affine registration of brain images. Med Image Anal. 2001;5:143–156. doi: 10.1016/s1361-8415(01)00036-6. [DOI] [PubMed] [Google Scholar]
- Jiang H, van Zijl PCM, Kim J, Pearlson GD, Mori S. DtiStudio: resource program for diffusion tensor computation and fiber bundle tracking. Computer methods and programs in biomedicine. 2006;81:106–116. doi: 10.1016/j.cmpb.2005.08.004. [DOI] [PubMed] [Google Scholar]
- Kuchel PW, Chapman BE, Bubb WA, Hansen PE, Durrant CJ, Hertzberg MP. Magnetic Susceptibility: Solutions, Emulsions, and Cells. Concepts In Magnetic Resonance. 2003;18A:56–71. [Google Scholar]
- Landis JR, Koch GG. The Measurement of Observer Agreement for Categorical Data. Biometrics. 1977;33:159–174. [PubMed] [Google Scholar]
- Langkammer C, Krebs N, Goessler W, Scheurer E, Ebner F, Yen K, Fazekaa F, Ropele S. Quantitative MR Imaging of Brain Iron: A Postmortem Validation Study. Radiology. 2010;257:455–462. doi: 10.1148/radiol.10100495. [DOI] [PubMed] [Google Scholar]
- Lee J, Hirano Y, Fukunaga M, Silva AC, Duyn JH. On the contribution of deoxy-hemoglobin to MRI gray-white matter phase contrast at high field. Neuroimage. 2009;49:193–198. doi: 10.1016/j.neuroimage.2009.07.017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee J, Shmueli K, Fukunaga M, van Gelderen P, Merkle H, Silva AC, Duyn JH. Sensitivity of MRI resonance frequency to the orientation of brain tissue microstructure. Proceedings of the National Academy of Sciences. 2010;107:5130–5135. doi: 10.1073/pnas.0910222107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li W, Wu B, Avram AV, Liu C. Magnetic susceptibility anisotropy of human brain in vivo and its molecular underpinnings. Neuroimage. 2012a;59:2088–2097. doi: 10.1016/j.neuroimage.2011.10.038. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li W, Wu B, Liu C. Quantitative susceptibility mapping of human brain reflects spatial variation in tissue composition. Neuroimage. 2011;55:1645–1656. doi: 10.1016/j.neuroimage.2010.11.088. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li X, Vikram DS, Lim IAL, Jones CK, Farrell JAD, van Zijl PCM. Mapping magnetic susceptibility anisotropies of white matter in vivo in the human brain at 7T. Neuroimage. 2012b;62:314–330. doi: 10.1016/j.neuroimage.2012.04.042. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu C. Susceptibility tensor imaging. Magnetic Resonance in Medicine. 2010;63:1471–1477. doi: 10.1002/mrm.22482. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu C, Li W, Wu B, Jiang Y, Johnson GA. 3D fiber tractography with susceptibility tensor imaging. Neuroimage. 2012;59:1290–1298. doi: 10.1016/j.neuroimage.2011.07.096. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu T, Liu J, de Rochefort L, Spincemaille P, Khalidov I, Ledoux JR, Wang Y. Morphology enabled dipole inversion (MEDI) from a single-angle acquisition: Comparison with COSMOS in human brain imaging. Magnetic Resonance in Medicine. 2011;66:777–783. doi: 10.1002/mrm.22816. [DOI] [PubMed] [Google Scholar]
- Liu T, Spincemaille P, de Rochefort L, Kressler B, Wang Y. Calculation of susceptibility through multiple orientation sampling (COSMOS): a method for conditioning the inverse problem from measured magnetic field map to susceptibility source image in MRI. Magnetic Resonance in Medicine. 2009;61:196–204. doi: 10.1002/mrm.21828. [DOI] [PubMed] [Google Scholar]
- Mazziotta J, Toga A, Evans A, Fox P, Lancaster J, Zilles K, Woods R, Paus T, Simpson G, Pike B, Holmes C, Collins L, Thompson P, MacDonald D, Iacoboni M, Schormann T, Amunts K, Palomero-Gallagher N, Geyer S, Parsons L, Narr KL, Kabani N, Le Goualher G, Boomsma D, Cannon T, Kawashima R, Mazoyer B. A probabilistic atlas and reference system for the human brain: International Consortium for Brain Mapping (ICBM) Philosophical Transactions of The Royal Society. 2001;356:1293–1322. doi: 10.1098/rstb.2001.0915. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mazziotta JC, Toga AW, Evans A, Fox P, Lancaster J. A Probabilistic Atlas of the Human Brain: Theory and Rationale for Its Development: The International Consortium for Brain Mapping (ICBM) Neuroimage. 1995;2:89–101. doi: 10.1006/nimg.1995.1012. [DOI] [PubMed] [Google Scholar]
- Miller MI, Trouve A, Younes L. On the Metrics and Euler-Lagrange Equations of Computational Anatomy. Annual review of biomedical engineering. 2002;4:375–405. doi: 10.1146/annurev.bioeng.4.092101.125733. [DOI] [PubMed] [Google Scholar]
- Mori S, Oishi K, Faria AV. White matter atlases based on diffusion tensor imaging. Current opinion in neurology. 2009;22:362–369. doi: 10.1097/WCO.0b013e32832d954b. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mori S, Oishi K, Jiang H, Jiang L, Li X, Akhter K, Hua K, Faria AV, Mahmood A, Woods R, Toga AW, Pike GB, Neto R, Evans A, Zhang J, Huang H, Miller MI, Zijl PV, Mazziotta J. Stereotaxic white matter atlas based on diffusion tensor imaging in an ICBM template. Brain. 2008;40:570–582. doi: 10.1016/j.neuroimage.2007.12.035. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mugler JP, III, Brookeman JR. Three-Dimensional Magnetization-Prepared Rapid Gradient-Echo Imaging (3D MP RAGE) Magnetic Resonance in Medicine. 1990;15:152–157. doi: 10.1002/mrm.1910150117. [DOI] [PubMed] [Google Scholar]
- Oishi K, Faria A, Jiang H, Li X, Akhter K, Zhang J, Hsu JT, Miller MI, van Zijl PCM, Albert M, Lyketsos CG, Woods R, Toga AW, Pike GB, Rosa-Neto P, Evans A, Mazziotta J, Mori S. Atlas-based whole brain white matter analysis using large deformation diffeomorphic metric mapping: Application to normal elderly and Alzheimer’s disease participants. Neuroimage. 2009;46:486–499. doi: 10.1016/j.neuroimage.2009.01.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pruessmann KP, Weiger M, Scheidegger MB, Boesiger P. SENSE: sensitivity encoding for fast MRI. Magnetic Resonance in Medicine. 1999;42:952–962. [PubMed] [Google Scholar]
- Schenck JF. The role of magnetic susceptibility in magnetic resonance imaging: MRI magnetic compatibility of the first and second kinds. Med Phys. 1996;23:815–850. doi: 10.1118/1.597854. [DOI] [PubMed] [Google Scholar]
- Schenck JF, Zimmerman EA. High-field magnetic resonance imaging of brain iron: birth of a biomarker? NMR Biomed. 2004;17:433–445. doi: 10.1002/nbm.922. [DOI] [PubMed] [Google Scholar]
- Schofield MA, Zhu Y. Fast phase unwrapping algorithm for interferometric applications. Optics Letters. 2003;28:1194–1196. doi: 10.1364/ol.28.001194. [DOI] [PubMed] [Google Scholar]
- Schweser F, Deistung A, Lehr BW, Reichenbach JR. Quantitative imaging of intrinsic magnetic tissue properties using MRI signal phase: an approach to in vivo brain iron metabolism? Neuroimage. 2011;54:2789–2807. doi: 10.1016/j.neuroimage.2010.10.070. [DOI] [PubMed] [Google Scholar]
- Shattuck DW, Prasad G, Mirza M, Narr KL, Toga AW. Online resource for validation of brain segmentation methods. Neuroimage. 2009;45:431–439. doi: 10.1016/j.neuroimage.2008.10.066. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shmueli K, de Zwart JA, van Gelderen P, Li T-Q, Dodd SJ, Duyn JH. Magnetic susceptibility mapping of brain tissue in vivo using MRI phase data. Magnetic Resonance in Medicine. 2009;62:1510–1522. doi: 10.1002/mrm.22135. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smith SM. Fast robust automated brain extraction. Hum Brain Mapp. 2002;17:143–155. doi: 10.1002/hbm.10062. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smith SM, Jenkinson M, Woolrich MW, Beckmann CF, Behrens TEJ, Johansen-Berg H, Bannister PR, De Luca M, Drobnjak I, Flitney DE, Niazy RK, Saunders J, Vickers J, Zhang Y, De Stefano N, Brady JM, Matthews PM. Advances in functional and structural MR image analysis and implementation as FSL. Neuroimage. 2004;23:S208–S219. doi: 10.1016/j.neuroimage.2004.07.051. [DOI] [PubMed] [Google Scholar]
- Talairach J, Tournoux P. Co-Planar Stereotaxis Atlas of the Human Brain, 3-Dimensional Proportional System: An Approach to Cerebral Imaging. Thieme Medical; New York, NY: 1988. [Google Scholar]
- Wharton S, Bowtell R. Whole-brain susceptibility mapping at high field: a comparison of multiple-and single-orientation methods. Neuroimage. 2010;53:515–525. doi: 10.1016/j.neuroimage.2010.06.070. [DOI] [PubMed] [Google Scholar]
- Woods RP, Grafton ST, Holmes CJ, Cherry SR, Mazziotta JC. Automated Image Registration: I. General Methods and Intrasubject, Intramodality Validation. J Comput Assist Tomogr. 1998a;22:139–152. doi: 10.1097/00004728-199801000-00027. [DOI] [PubMed] [Google Scholar]
- Woods RP, Grafton ST, Watson JDG, Sicotte NL, Mazziotta JC. Automated Image Registration: II. Intersubject Validation of Linear and Nonlinear Models. J Comput Assist Tomogr. 1998b;22:153–165. doi: 10.1097/00004728-199801000-00028. [DOI] [PubMed] [Google Scholar]
- Woolrich MW, Jbabdi S, Patenaude B, Chappell M, Makni S, Behrens T, Beckmann C, Jenkinson M, Smith SM. Bayesian analysis of neuroimaging data in FSL. Neuroimage. 2009;45:S173–S186. doi: 10.1016/j.neuroimage.2008.10.055. [DOI] [PubMed] [Google Scholar]
- Yablonskiy DA. Quantitation of intrinsic magnetic susceptibility-related effects in a tissue matrix. Phantom study. Magnetic Resonance in Medicine. 1998;39:417–428. doi: 10.1002/mrm.1910390312. [DOI] [PubMed] [Google Scholar]
- Yao B, Li T-Q, van Gelderen P, Shmueli K, de Zwart JA, Duyn JH. Susceptibility contrast in high field MRI of human brain as a function of tissue iron content. Neuroimage. 2009;44:1259–1266. doi: 10.1016/j.neuroimage.2008.10.029. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zecca L, Zucca FA, Toscani M, Adorni F, Giaveri G, Rizzio E, Gallorini M. Iron, copper and their proteins in substantia nigra of human brain during aging. Journal of Radioanalytical and Nuclear Chemistry. 2005;263:733–737. [Google Scholar]
- Zhang J, Peng Q, Li Q, Jahanshad N, Hou Z, Jiang M, Masuda N, Langbehn DR, Miller MI, Mori S, Ross CA, Duan W. Longitudinal characterization of brain atrophy of a Huntington’s disease mouse model by automated morphological analyses of magnetic resonance images. Neuroimage. 2010;49:2340–2351. doi: 10.1016/j.neuroimage.2009.10.027. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zijdenbos AP, Dawant BM, Margolin RA, Palmer AC. Morphometric Analysis of White Matter Lesions in MR Images: Method and Validation. IEEE Trans Med Imaging. 1994;13:716–724. doi: 10.1109/42.363096. [DOI] [PubMed] [Google Scholar]
- Zou KH, Warfield SK, Bharatha A, Tempany CMC, Kaus MR, Haker SJ, Wells WM, III, Jolesz F, Kikinis R. Statistical validation of image segmentation quality based on a spatial overlap index: scientific reports. Acad Radiol. 2004;11:178–189. doi: 10.1016/S1076-6332(03)00671-8. [DOI] [PMC free article] [PubMed] [Google Scholar]