In silico investigation of pH-dependence of prolactin and human growth hormone binding to human prolactin receptor

Abstract

Experimental data shows that the binding of human prolactin (hPRL) to human prolactin receptor (hPRLr-ECD) is strongly pH-dependent, while the binding of the same receptor to human growth hormone (hGH) is pH-independent. Here we carry in silico analysis of the molecular effects causing such a difference and reveal the role of individual amino acids. It is shown that the computational modeling correctly predicts experimentally determined pKa’s of histidine residues in an unbound state in the majority of the cases and the pH-dependence of the binding free energy. Structural analysis carried in conjunction with calculated pH-dependence of the binding revealed that the main reason for pH-dependence of the binding of hPRL-hPRLr-ECD is a number of salt- bridges across the interface of the complex, while no salt-bridges are formed in the hGH-hPRlr-ECD. Specifically, most of the salt-bridges involve histidine residues and this is the reason for the pH-dependence across a physiological range of pH. The analysis not only revealed the molecular mechanism of the pH-dependence of the hPRL-hPRLr-ECD, but also provided critical insight into the underlying physic-chemical mechanism.

Introduction

Most biomolecules, including proteins, perform their function by interacting with large or small ligands and ultimately, during this process, undergo conformational and/or ionization changes [1–5]. Virtually every association event is pH-dependent and thus involves proton uptake/release at a particular pH [6–8]. The ionization changes are strongly coupled to the energetics of binding and thus contribute to its specificity [3]. Understanding the details of molecular recognition, which form the foundation of protein-protein interaction networks, requires better understanding of protonation events induced by protein-ligand association and their relation to the characteristic pH of the subcellular compartment where the unliganded proteins exist [3, 6, 9] and binding occurs [7, 8]

The importance of proton uptake/release in receptor-ligand interactions is demonstrated by the experimental observation that practically all known receptor-ligand interactions are pH-dependent [10–14]. Frequently, the variation of several pHs results in binding free energy changes of several kcal/mol [14, 15] or can even change the ligand binding preferences [16]. Moreover, different binding interactions can occur at different pHs; for example, as found in the case of beta-lactoglobulin, which is a dimer at low pH but forms a tetramer at high pH [17]. A similar phenomena was found in the case of calmodulin, whose domains adopt a compact arrangement at low pH while at high pH form a “dumbbell” shaped structure [18–20]. From a practical perspective, the ability to re-engineer enzymatic pH-activity profiles is important for the industrial application of enzymes [21]. This possibility has been theoretically and experimentally explored to re-engineer enzymatic pH-activity profiles and pH-dependence of kinetic parameters by changing active site pKa values using point mutations [22–26]

Frequently, experiments on measuring binding constants are done at a particular pH, which may not correspond to the physiological in vivo pH of the corresponding protein-protein complex. Not correcting the experimental value for the difference in pH may lead to serious error of assessing the physiological binding constant. However, if the pH-dependence of proton uptake/release is available, then this correction can easily be made [27]. Even more, one can use the 3D structure of the corresponding protein complex to predict the proton uptake/release [3, 7]

The overall proton uptake/release induced by protein-ligand association originates from individual pKa shifts of titratable groups induced by the complex formation [28–30]. Therefore successful pKa calculations on the pKa’s of the titratable groups before and after the binding would be sufficient to determine the proton uptake/release as a function of the pH of the solution and to obtain the pH-dependence of the binding free energy [27, 31]. These pKa’s can be either experimentally measured or predicted in silico and thus the contributions of the individual amino acids to the pH-dependence can be revealed. In reverse, one can find the pH-dependence of the binding, but will not be able to pin-point the residues contributing to it or predict effects of mutations. In the last case, the experiments on the pH-dependence of the affinity should be complemented with either pKa measurements or with pKa calculations, as it is done in this work

In this study, we investigate two binding processes: the binding of human prolactin (hPRL) to the extracellular domain (ECD) of its receptor (hPRLr) and binding of human growth hormone (hGH) to the same hPRLr-ECD, for which experimental data is available [32, 33]. Experimentally, the former binding is strongly pH-dependent and the latter binding is pH-independent and requires a Zn⁺² ion [33]. The intermolecular interface between hPRL and hPRLr-ECD contains many polar and charged interactions, including four closely packed histidine imidazoles. Three of them are located in hPRL (His27, His30 and His180) and another within hPRLr-ECD (His188). Comparison with the intermolecular interface of hGH and hPRLr-ECD, three out of four of these histidines are “conserved”: H27 and H30 from hPRL are homologous to H18 and H21 in hGH. Obviously, the H188 from hPRLr-ECD is present in both complexes. In contrast, H180 in hPRL is replaced with Asp in hGH [32]. Another important difference is the Zn⁺² ion located on the interface of the hGH-hPRLr-ECD complex which was shown to be crucial for the binding [33]. Here we carry an in silico analysis to reveal the molecular mechanism resulting in different pH-(in)dependence for these two complexes.

Methods

Structures used

The 3D structures of both complexes are (a) the extracellular domain (ECD) of hPRL receptor (hPRLr-ECD) and human prolactin (hPRL), PDB ID 3MZG [32] and, (b) the same extracellular domain (ECD) of hPRL receptor (hPRLr-ECD) complexed with the human growth hormone (hGH), PDB ID 1BP3 [34]. For the purpose of the calculations, the water molecules were removed, while the Zn²⁺ ion was kept since it is known to be crucial for binding [33]. The structures of unbound molecules are not available and were modeled using the 3D structures on the monomers in their bound state.

The structure of the human prolactin has several missing atoms and residues. These structural defects were fixed with the profix module from Jackal package [35] (http://wiki.c2b2.columbia.edu/honiglab_public/index.php/Software:Jackal). Default parameters were used with Amber force field and heavy atoms option.

pKa calculations

The calculations of pKa’s of ionizable groups were performed with the Multi-Conformation-Continuum-Electrostatics (MCCE) program [36–38], which can be downloaded from (http://www.sci.ccny.cuny.edu/~mcce/contact.php). The MCCE program calculates the equilibrium of protein conformations and the charge state of ionizable residues taking into account side chain motions and the presence of ions and ligands. It treats the conformational and ionization changes in the same Monte Carlo procedure and thus couples the protonation events with conformational changes. This is particularly important for polar hydrogen positions and histidine tautameric states. The predictions were done as a function of pH. Default parameters were used, but internal dielectric constant of protein was varied from 4 to 8. In addition, in the calculations including Zn²⁺ ion, the reference energy of the Zn²⁺ ion (zn.tpl file) was varied as well to better match the experimental data (see below for details). Thus, the bound complex structures and unbound monomers were subjected to MCCE calculations and the net charges as a function of pH, Q_complex(pH), Q_A(pH), and Q_B(pH) were predicted. Here “complex” stands for either hPRLr-ECD: hPRL or hPRLr-ECD: hGH, “A” refers to hPRLr-ECD and “B” means either hPRL or hGH. The proton changes evoked by the binding were calculated as the difference between the net charge of the complex and monomers, which is written as:

$$Q_{\mathit{binding}}(\text{pH})=Q_{\mathit{complex}}(\text{pH})-Q_A(\text{pH})-Q_B(\text{pH})$$ (1)

where pH ranges from pH=0.0 to pH=14.0.

MCCE also outputs the pKa’s of individual groups within the complex and separated monomers. Then, the individual pKa shifts induced by the binding were calculated as:

$$\mathrm{\Delta }{\mathit{pKa}}^i=\mathrm{\Delta }{\mathit{pKa}}_{\mathit{complex}}^i-\mathrm{\Delta }{\mathit{pKa}}_{\mathit{monomers}}^i$$ (2)

where i is residue number.

pH dependence of binding affinity

The pH dependence of the binding affinity was calculated by using the formula (see for example [3, 27]):

$$\mathrm{\Delta }\text{G}(\text{pH})=2.3\text{RT}{\int }_{{pH}_{\text{o}}}^{pH}\mathrm{\Delta }Q(pH)d(pH)$$ (3)

where ΔG(pH) is the pH-dependent component of binding energy, ΔQ(pH) is the difference between the net charge of the complex and monomers (Q_binging(pH)), R is the universal gas constant, and T is the temperature (in K). The above formula is substituted with a sum, if the analytical expression for ΔQ(pH) is not available. In this work this is done by choosing ΔpH=1 and ΔQ is taken at the midpoint of the corresponding pH interval.

From eq.(3) it can be seen that the binding free energy will be pH-independent in a given pH interval if the proton uptake/release (Q_binding(pH)) is zero in this pH interval.

Global and interfacial properties

Global and interfacial properties of protein-protein complexes are important features that may be linked to the pH-dependency of the hPRL/hGH-hPRLr-ECD complexes. In this work we will investigate the possibility that the difference in these properties within hPRL and hGH may be associated with the difference of the pH-dependence of the binding. Two global properties were investigated: sequence similarity and structural similarity. The corresponding analyses were performed with GRASP2 [39] and Chimera [40]. Structural properties were analyzed using the 3D structures available in PDB and in parallel, using fixed structures with missing residues added with “profix” (see above).

Interfacial residues were identified based on their solvent accessible surface area (SASA). The SASA of the residues in the complex and in unbound monomers was calculated with the program SURFV: (http://wiki.c2b2.columbia.edu/honiglab_public/index.php/Software:SURFace_Algorithms), developed in Barry Honig’s lab at Columbia University. For each residue, ΔSASA is

$$\mathrm{\Delta }{\mathit{SASA}}^i={\mathit{SASA}}_{\mathit{unbound}}^i-{\mathit{SASA}}_{\mathit{bound}}^i$$ (4)

where i indicates the residue number.

We define an interfacial residue as one with ΔSASA different from zero. Once the interfacial residues are identified, we calculate the number of polar/hydrophobic residues at the interface of the complex and for each monomer.

The interfacial area is calculated as

$$S_{\mathit{interfacial}}=\frac{1}{2}(S_A+S_B-S_{\mathit{complex}})$$ (5)

where S_A and S_B is SASA of two monomers and S_complex is the gross SASA of the bond complex.

Results

Determining the optimal value of the internal dielectric constant

The outcome of pKa calculations and the corresponding ΔG(pH) and ΔQ(binding) depends on the values of the parameters used in MCCE. Typically the effect of the value of the internal dielectric constant on the overall pKas is relatively small [41], however, not negligible, especially in terms of the pH-dependence of the net charge. To investigate the effect and to determine which value of the dielectric constant is optimal for our analysis, we performed calculations with an internal dielectric constant of 4 and 8. These are the most commonly used values in pKa calculations utilizing MCCE. Our criterion for optimization was the experimental pH-dependence of the binding energy, which is known to be pH-independent in the pH range 5 to 8 for hGH, while pH-dependent for hPRL [32]. The numerical simulations with a dielectric constant of 4 resulted in proton uptake/release ΔQ(binding) which was opposite to the experimental data, indicating that hPLRr-hPRL binding is pH-independent. However, when we repeated the calculations with a dielectric constant of 8, the binding of hPRL to hPRLr-ECD was predicted to be pH-dependent and the trend is the same as experimentally measured (Fig. 1). This observation was used to select the optimal dielectric constant to be 8 and this value will be used for the rest of modeling. Note that the results obtained at very low pH (< 5.0) and very high pH (>8.0) may overestimate the proton uptake/release due to plausible structural changes not taken into account in our calculations.

Figure 1.

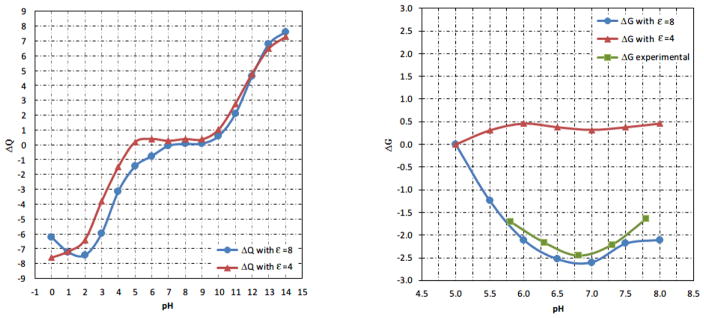
Calculated pH-dependence of proton uptake/release (ΔQ(binding)) with dielectric constant 4 and 8 (left panel, in the range pH=0 to 14). The corresponding binding energies for hPRL-hPRLr-ECD and experimental energy (right panel, in the range pH=5 to 8). The energies are adjusted to be zero at pH=5.

The role of the Zn²⁺ ion

The binding of hGH to hPRLr-ECD requires Zn²⁺ ion which is located on the binding interface of the bound state and surrounded by H18, H21, D171 in hGH and H188 in hPRLr-ECD [34]. We investigated the effect of Zn²⁺ ion on the binding of hGH to hPRLr-ECD by artificially removing the Zn²⁺ from the complex and using the optimal dielectric constant of protein obtained above. However, the binding was predicted to be pH-dependent in contrast to experimental data, confirming that Zn²⁺ is needed for correct modeling of the binding. The next step was to take the Zn²⁺ ion explicitly in the MCCE calculations. As it was mentioned above, MCCE allows for fractional occupancy of ion binding sites. Using the default values for Zn²⁺ reference energies and parameters, we obtained a very low occupancy of the Zn²⁺ at low pH and practically no occupancy at physiological pH. To correct for this discrepancy with experimental data, we reduced the reference energy of Zn²⁺ ion from its default value of −53.79 (Kcal/mol) to smaller values, taking a percentage of the original value. This resulted in an increase of the occupancy of the Zn²⁺ site and reduction of the pH-dependence of the binding. At 65% of the default reference energy (reference energy = −38.65 Kcal/mol), the occupancy of the Zn²⁺ site was essentially 100% in a pH interval of 5 to 8 and the corresponding ΔQ(pH) was calculated to be practically zero, resulting in pH-independent ΔG(pH), in accordance with experimental results (Fig. 2). Note that ΔG(pH) is not entire flat (Fig. 2, right panel), but the changes are within 1kcal/mol, which is within the accuracy of the numerical protocol.

Figure 2.

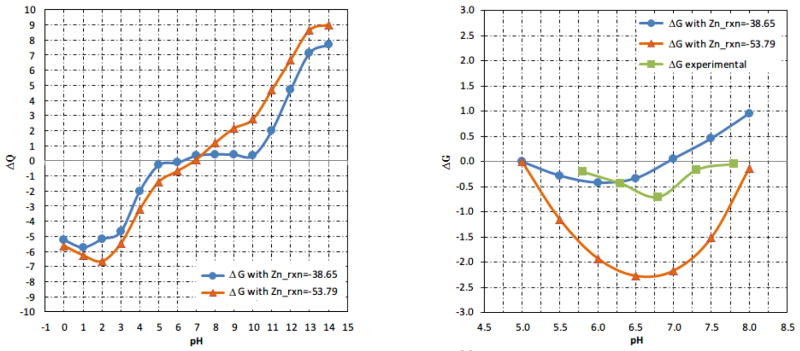
Proton uptake/release ΔQ (binding) as a function of pH for hGH-hPRLr-ECD complex with different reference energy for Zn²⁺ ion (left panel, in pH range from 0 to 14). The corresponding pH-dependent component of the binding free energy and experimental energy (right panel, in the pH range from 5 to 8). The energies are adjusted to be zero at pH=5. The “rxn” stands for “reference energy” in Kcal/mol units.

The above investigations were done to find the optimal value of an internal dielectric constant and reference energy for the Zn²⁺ such that the numerical calculations reproduce experimental data of pH-dependence of the binding. However, the pH-dependence of the binding and the corresponding proton uptake/release result from contributions of individual amino acids. These individual contributions, however, cannot be directly obtained from such data, instead they have to be either predicted or independently measured. Below we provide in silico analysis of the role of individual amino acid on the pH-dependence of the binding.

Role of Individual Residues

1. Residues predicted to contribute to the proton uptake/release: To identify titratable residues that may contribute to the proton uptake/release, pKa calculations were done using the structure of the corresponding complex and separated monomers. Residues found to have different pKas in bound and unbound states, were considered to be a plausible candidate affecting pH-dependence of the binding. Results are summarized in Table 1, where chain “A” refers to the ligand (either hPRL or hGH) and chain “B” indicates the receptor (hPRLr-ECD). Since the structures of bound and unbound molecules are identical, the change in the pKas originates from the binding interface and new interactions within the complex. Despite the long list of potential candidates, it can be noticed that most of the pKa shifts are predicted to be outside the experimental pH range from 5 to 8 and because of that were not further analyzed. The reason for this is that if the corresponding pKa’s (in bound and unbound states) are lower than pH=5 or higher than pH=8, the residue will remain either fully ionized or neutral in pH=5 to pH=8 in both states (bound and unbound) and will not contribute to the proton uptake/release (ΔQ). Only histidines were predicted to undergo pKa shifts relevant to the purposes of our investigation (Table 1).

   In the case of hPRL-hPRLr-ECD complex, four closely packed histidine imidazoles are found on the interface. Three of these are from hPRL (H27, H30, and H180) and one is from hPRLr-ECD (H188). In comparison to the intermolecular interface between hGH and hPRLr-ECD, three out of four of these histidines are conserved. H27 and H30 from hPRL are homologous to H18 and H21 in hGH, while H180 from hPRL is replaced with Asp171 in hGH. H188 from hPRLr-ECD is present in both complexes.

   The hPRL-hPRLr-ECD binding is pH-dependent according to experimental data and reproduced by our numerical simulations. Table 1 suggests that this is due to three histidines, two on the ligand (H30 and H180) and one on the receptor (H188). They all are predicted to have lower pKas in the complex (bound state) compared with the pKas in the free monomers. While the predicted change for H188 is almost negligible, it is predicted to be dramatic for the rest of histidines, resulting in a loss of a proton during the binding. This is the predicted reason for the decrease of the affinity at low pH.

   The hGH-hPRLr-ECD association is pH-independent and does not involve proton uptake/release in the pH range of 5 to 8. Analysis of the calculated pKa’s (Table 1) reveals an interesting effect: although there are two histidines, His 21 of the ligand side and His 188 on the receptor side, that are predicted to change their pKa’s in physiological pH, their effect cancels out. The pKa of His 21 is calculated to increase from free to bound state, while the pKa of His 188 is expected to experience an opposite change, to be fully deprotonated in the complex. Such a change results in a zero net effect and the proton uptake/release is zero.

2. Comparison with experimental pKa’s: The pKa’s of histidines at the interface of the hPRLr-ECD and hPRL complex were experimentally determined in free state by the lab of Dr. Hodsdon [32, 42]. This provides the opportunity to compare our predictions with experimental data. Table 2 shows the calculated and experimental pKa for unbound state. It can be seen that the calculated and experimentally measured pKa’s are in very good agreement, except for His 27. Our protocol predicts that His 27 is fully deprotonated in the free state at physiological pH and does not participate in the pH-dependence. The structural reason for such prediction will be discussed later in the manuscript.

3. Effect of single point mutations: To further investigate the effects of histidines pKa’s on pH-dependent affinity of binding and to take advantage of available experimental data [32], the above mentioned histidines were mutated in silico to Ala in both hPRLr-ECD and hPRL. It was done with scap program [43] using default parameters with Amber force field and heavy atoms option. Then, the mutant structures, the complex, and the separated monomers were subjected to the same procedures described above for the wild type proteins and the corresponding pKa’s were predicted with MCCE. The results are presented in Table 3 along with the corresponding experimental pKa’s taken from Ref. [32]. It can be seen (Table 3) that our predictions generally agree with experimental data, especially for His 180 and His 188. The predictions are not so impressive for the His 27 and His 30, but are still quite reasonable, keeping in mind that the 3D structures of unbound monomers are not available and that the mutations were done in silico. Particularly, one can speculate that structural reorganization may occur in unbound state which will provide favorable interactions (neighboring Lys residue) to these histidines and to reduce their desolvation penalties, leading to increased pKa values.

Table 1.

Calculated pKa’s of titratable residues within the corresponding complex (bound state) and separated monomers (free state). Left half of the table refers to hPRL-hPRLr-ECD and the right half to hGH-hPRLr-ECD.

Residue Number	bound state	free state	Residue Number	bound state	free state
HIS27.A	<0	1.472	HIS18.A	<0	<0
HIS30.A	2.4	5.772	HIS21.A	6.1	3.6
HIS180.A	<0	6.06	ASP171.A	<0	2.1
ASP183.A	<0	<0	LYS172.A	>14	12.9
LYS187.A	>14	12.968	ARG178.A	11.319	11.732
LYS17.B	>14	12.282	LYS17.B	9.411	10.296
GLU18.B	0.59	2.634	GLU18.B	4.14	4.19
GLU43.B	<0	4.077	GLU43.B	3.266	2.7
ASP96.B	<0	2.902	ASP96.B	<0	3.23
LYS136.B	12.393	12.605	LYS136.B	11.338	11.6
ASP187.B	<0	2.771	ASP187.B	3.264	2.768
HIS188.B	6.44	6.81	HIS188.B	<0	6.97

Table 2.

pKa’s of interfacial histidines in unbound state for hPRLr-hPRL.

Residue	Experiment	Predicted
His 27 (hPRL)	6.7	1.5
His 30 (hPRL)	6.3	5.8
His 180 (hPRL)	6.1	6.1
His 188 (hPRLr-ECD)	7.7	6.8

Table 3.

Histidine pKa values for mutants H27A, H30A, H180A in hPRL and H188A in hPRLr-ECD for unbound state. The predicted pKa’s were calculated using the corresponding bound structure taken from the corresponding X-ray structure of the complex. This is the reason why predicted pKa’s of the ligand are affected by mutations introduced at the receptor and vice versa.

	H27A		H30A		H180A		H188A
	Calc.	Exp.	Calc.	Exp.	Calc.	Exp.	Calc.	Exp.
HIS27.A			4.22	6.9	3.6	6.8	5.4	6.7
HIS30.A	4.7	6.5			6.2	6.7	3.6	6.3
HIS180.A	6.3	6.2	6.4	6.3			6.2	6.1
HIS188.B	6.8	7.7	6.8	7.7	6.8	7.7

Amino Acid Composition analysis

Although the 3D structures of hPRL and hGH are very similar (see supplementary material), the corresponding sequences are not (here we focus on the ligand only because the receptor is the same in both complexes). In this section we analyze two types of sequence characteristics: global characteristics over the entire structure and interfacial characteristics associated with residues at the interface only. Figure 3 shows the distribution of all twenty amino acids within hPRL and hGH.

Figure 3.

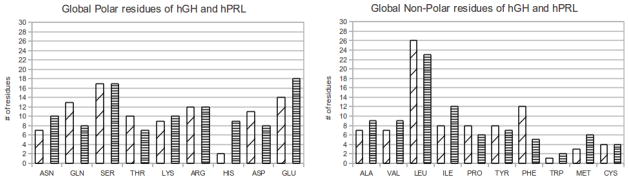
Global amino acid count of hGH and hPRL for polar and non-polar residues. The wide slanted hatches represent hGH while horizontal hatches represent hPRL.

Figure 3 shows that the major differences when comparing the global residue count of hGH and hPRL reside in histidine and glutamine (polar residues), with hGH having 13 glutamines and 3 histidines and hPRL having only 8 glutamines but 9 histidines. As for global, non-polar residues, the largest difference is within the amount of isoleucine and phenylalanine with hGH having 8 isoleucines and 12 phenylalanines and hPRL having 12 isoleucines and only 5 phenylalanines. The pH-dependent case, hPRL-hPRLr-ECD complex, shows an increase in histidines which may serve as a proton buffer at physiological pH.

A similar trend can be seen for interfacial amino acids (Fig. 4). Histidines are more abundant at the hPRL interface compared with hGH, while the number of acidic (Asp and Glu) and basic (Arg and Lys) residues is practically the same in both interfaces. Such a bias toward a particular amino acid type combined with different a pH-dependence of the binding, may indicate the crucial role of interfacial histidines to the observed proton uptake/release.

Figure 4.

Interfacial amino acid count of hGH and hPRL for polar and non-polar residues. The wide slanted hatches represent hGH while horizontal hatches represent hPRL.

Structural analysis

In this section, we analyze structural properties of both the receptor and the ligands with respect to salt bridges. Breaking or forming a salt bridge typically results in large change of the pKa’s of the participating residues and thus could be relevant to proton uptake/release of the binding. This is due to the balance between favorable interactions within the salt bridge and the desolvation penalty which each of the residues should pay being within the salt bridge. If the salt bridge breaks, the favorable component vanishes and the corresponding residues are left with the desolvation penalty only, which in turn results in large pKa shifts. If the pKa’s within the bridge or after the bridge being broken are within the pH range of interest, then such an event will contribute to proton uptake/release, and thus will result in pH dependence of the binding free energy. Figure 5 and Table 4 summarize the results.

Figure 5.

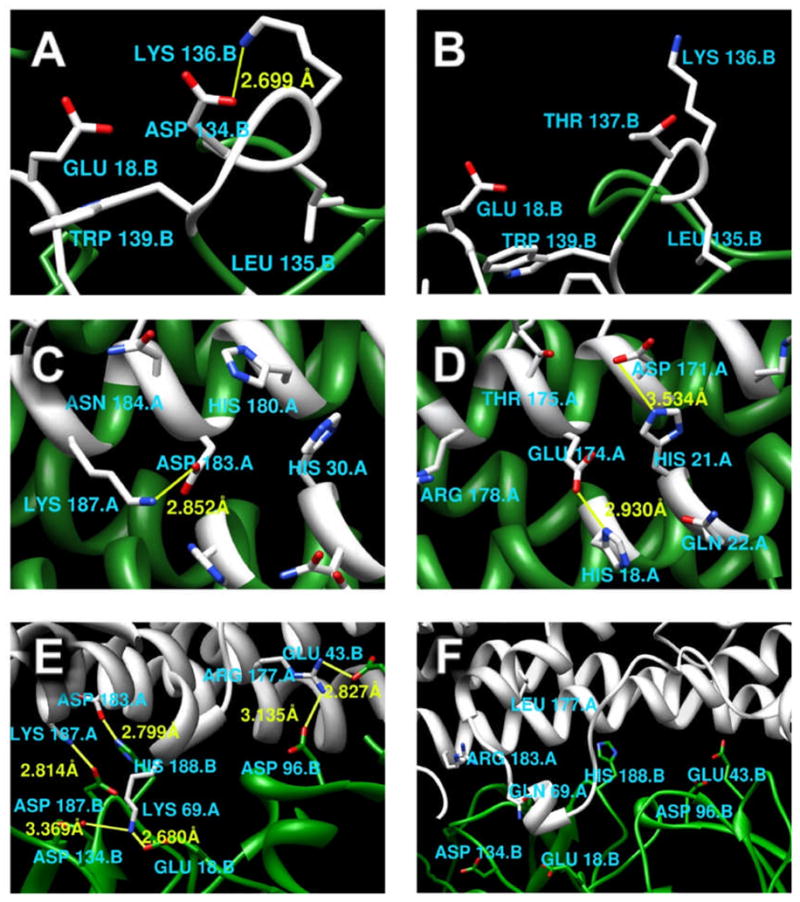
Salt bridge analysis: (A) The interface of hPRLr-ECD taken from the complex with hPRL. (B) The interface of hPRLr-ECD taken from the complex with hGH. (C) The interface of hPRL taken from the complex with hPRLr-ECD. (D) The interface of hGH taken from the complex with hPRLr-ECD. (E) Interfacial salt-bridges within hPRLr-ECD and hPRL complex. (F) Interfacial salt bridges within hPRLr-ECD and hGH complex. Yellow bonds between atoms represent salt bridges; In figure A, B, C, D, interface residues are white, non-interface residues are green; In figure E, F, hPRL receptors are green, ligands are white.

Table 4.

Salt bridge analysis.

Structure	Residue	Residue	Distance
Salt bridge at the interface of hPRLr when it is associated with hPRL	ASP134	LYS136	2.699
Salt bridge at the interface of hPRL when it is associated with hPRLr-ECD	ASP183	LYS187	2.852
	hGH	hPRLr-ECD
Salt bridges at the interface of hGH when it is associated with hPRLr-ECD	HIS18	GLU174	2.930
	HIS21	ASP171	3.534
Salt bridges across the interface of hPRL-hPRLr- ECD	hPRL	hPRLr-ECD
	LYS69	GLU18	2.680
	LYS69	ASP134	3.369
	ARG177	GLU43	2.827
	ARG177	ASP96.	3.135
	LYS187	ASP187	2.814
	HIS188	ASP183	2.799

On the receptor side, the bound structures of hPRLr-ECD to the corresponding ligand, either hPRL or hGH, are structurally quite similar. There is a salt bridge at the interface of hPRLr-ECD in the complex hPRL-hPRLr-ECD, but not in hGH-hPRLr-ECD (Fig. 5A,B, and Table 4). Specific interest is His188 which is involved in weak interaction with the neighboring Asp187. It is quite possible that H188 and Asp187 may form a salt bridge in unbound state by relaxing the bound structure.

In the case of the ligand, the analysis shows that there is only one salt bridge in hPRL while there are two in case of hGH (Fig. 5C,D and Table 4). However, the distance between NZ and OD polar atoms is shorter in hPRL bound to hPRLr-ECD as compared with the case of complex with hGH bound to hPRLr-ECD, which results in a slightly increased strength of interactions (Table 4).

The main difference is revealed by analyzing interfacial salt bridges. Dramatic differences between hPRL and hGH interfaces are found (Fig. 5E,F). The hGH-hPRLr-ECD interface has no salt bridges. In contrast, six salt bridges were identified within the hPRL-hPRLr-ECD interface. Some of them are very strong, resulting in hydrogen bonds of about 1.6A. Forming such strong salt bridges, results in a dramatic change of the corresponding pKa’s.

Conclusions

An analysis of pH-dependence of the binding of two complexes, hPR-hPRLr-ECD and hGH-hPRLr-ECD, were carried out with the goal to reveal the molecular mechanism of the difference of their pH-(in)dependent association. It was shown that the difference in physiological pH stems from several histidine residues located at the interface of the complexes. These histidine residues serve as proton buffer and change their pKa’s upon the binding.

The completely different pH sensitivity of the binding cannot be attributed to the global structural difference, since the 3D structures of the interacting pairs are very similar as shown in the supplementary material. At the same time, it was shown that sequence composition, both within the entire structures and within the interface, is quite different between hPRL and hGH. The main difference being that of the number of histidines, both globally and interfacially.

Different amino acid composition on the ligand side was found to result in dramatic differences of electrostatic interactions across the interface of the complex. The hPRL-hPRLr-ECD interface is rich of salt bridges while the hGH-hPRLr-ECD interface has none. These differences not only affect the amino acids involved in specific interactions but also affect the distribution of the electrostatic potential across the interface as well.