Concerted or Stepwise: How Much Do Free-Energy Landscapes Tell Us about the Mechanisms of Elimination Reactions?

Abstract

The base-catalyzed dehydration of benzene cis-1,2-dihydrodiols is driven by formation of an aromatic product as well as intermediates potentially stabilized by hyperaromaticity. Experiments exhibit surprising shifts in isotope effects, indicating an unusual mechanistic balance on the E2-E1cB continuum. In this study, both 1- and 2-dimensional free energy surfaces are generated for these compounds with various substituents, using density functional theory and a mixed implicit/explicit solvation model. The computational data help unravel hidden intermediates along the reaction coordinate and provide a novel conceptual framework for distinguishing between competing pathways in this and any other system with borderline reaction mechanisms.

Introduction

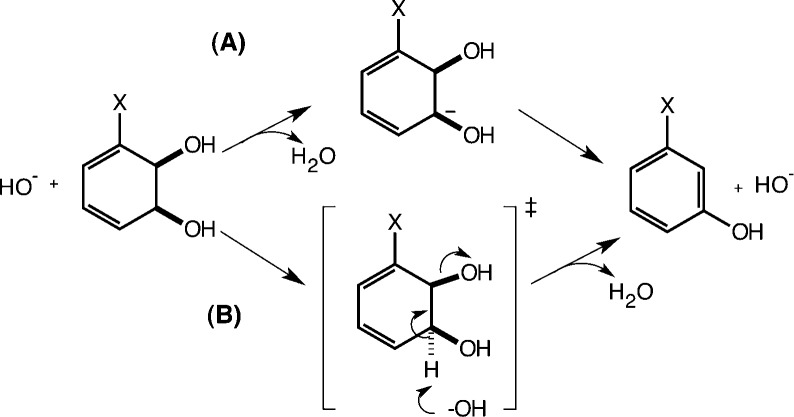
The acid-catalyzed dehydration of arene dihydrodiols¹⁻³ and arene hydrates⁴ has been extensively studied experimentally and is generally thought to proceed through a carbocation intermediate. Recently, More-O’Ferrall provided the first evidence that, for benzene cis-1,2-dihydrodiols, this reaction also occurs under base catalysis at room temperature with aqueous sodium hydroxide.⁵ Conceptually, this is a very interesting system because the generation of an aromatic system provides a potent thermodynamic driving force that can overcome the disadvantages of a very poor leaving group. Moreover, the experiments suggest an unusual shift in mechanism and kinetic isotope effects with the addition of electron-withdrawing groups. That is, in principle, this process could occur either through a stepwise mechanism involving a carbanion intermediate or, alternately, through a concerted E2 pathway in which proton abstraction and bond cleavage to the leaving group occur in a single transition state (Figure 1). To date, no evidence has been shown for such a concerted dehydration mechanism; however, as discussed previously,⁵ there are a number of factors that would make it tempting to assign such a mechanism here. The first of these is that the reaction is very exothermic (by almost 40 kcal/mol⁵) due to the formation of a fully aromatic product. This suggests that the loss of hydroxide from the carbanion is not limited by the energetics of the system and may be controlled only by the time scale of solvent relaxation to and from the solvation shell of the ion, which could enforce concertedness on the reaction. Additionally, in the case of benzene cis-1,2-dihydrodiols, the β-hydrogen and the OH leaving group are able to achieve a nearly ideal antiperiplanar conformation, which would be favorable for a concerted reaction (although this does not in and of itself exclude an E1cB pathway⁶).

Figure 1.

Base-catalyzed dehydration of 3-substituted benzene cis-1,2-dihydrodiols. This process can occur either through a stepwise mechanism involving a carbanion intermediate (A) or, alternately, through a concerted E2 pathway (B) in which proton abstraction and bond cleavage to the leaving group occur in a single transition state.

Interestingly, kinetic isotope effects (KIE) have been measured⁵ for a series of substituted benzene cis-1,2-dihydrodiols, and in the case of the cyano-substituted system, an extremely large KIE of 16.7 was obtained. Such measurements have historically played a significant role in discerning organic reaction mechanisms.^7,8 The large KIE of 16.7 could, in itself, correspond to either an E2 mechanism or an irreversible E1cB mechanism in which proton abstraction to form the carbanion is the rate-limiting step (potentially with a tunneling component). However, this KIE drops dramatically as the substituent is changed, going from 16.7 for X = CN to ∼6.3 for X = Cl and 1.2 for the unsubstituted benzene cis-1,2-dihydrodiol (X = H). Such a trend strongly suggests either a change in mechanism or a change in rate-limiting step, from initial proton transfer to subsequent leaving group expulsion, within the framework of an E1cB mechanism. Additionally, no isotope exchange is seen in the X = H system experimentally, so a standard E1cB path with leaving group expulsion as the rate-limiting step is not consistent with the data. The current study uses computational tools to probe the details of this mechanistic landscape.

Distinguishing between E1cB and E2 mechanisms has historically been a subject of substantial debate,^9,10 where the most challenging case would be that of reactions such as those of the present system, which lie on the boundary between the two mechanisms. In this context, Jencks has argued that an E1cB mechanism would turn into an enforced E2 mechanism in a situation where the intermediate is no longer stable enough to exist¹⁰ and that this can be quite a sharp transformation.¹¹ However, other more recent work has suggested a much smoother transition between the two mechanisms.¹²⁻¹⁵ Additionally, a recent, detailed computational study of the elimination reactions of a range of esters and thioesters has suggested that while most of the systems appear to proceed through clear E1cB_I mechanisms, substrates with better leaving groups and less acidic β-hydrogens can transition to a concerted E2 mechanism but with an E1cB-like transition state.¹⁶ This latter paper, in particular, highlights the importance of utilizing free energy surfaces in order to be able to distinguish between E1cB and E2 mechanisms, particularly at the border between the two. As such, this paper¹⁶ is arguably one of the most detailed computational studies of the fine mechanistic details of elimination reactions in solution to date; however, this work presents only 1-D free energy landscapes. Therefore, by necessity, this work only explores one out of a multitude of potential pathways for each system, rather than providing information about the nature of the surface in the vicinity of the minimum energy pathway. Additionally, the main driving force for the reactions studied by these authors was the presence of good leaving groups, whereas in our systems an unfavorable reaction is made favorable by harnessing aromaticity.

Herein, we have performed a detailed investigation of the base-catalyzed dehydration of these benzene diols using both 1- and 2-D free energy landscapes in implicit solvent and also by optimizing key stationary points. We reproduce the observed substituent effects and show explicit atomic details of a delicate structural and energetic balance on the E1cB to E2 continuum for these reactions.

Methodology

Our starting point for this study was a 2-dimensional free energy landscape for the dehydration of the unsubstituted benzenediol (X = H, Figure 1), in the space defined by the C–OH distance between the α-carbon and the departing hydroxide (x-axis), as well as the oxygen of the hydroxide ion and the β-hydrogen (y-axis). At each point on this surface, the two relevant distances were kept fixed, and all other degrees of freedom were allowed to freely optimize. As the surface is only a two-dimensional projection of the full multidimensional energy landscape, it was obtained by careful reaction coordinate pushing using a grid spacing of 0.1 Å increments in order to follow the minimum energy path along two dimensions. Such gradual reaction coordinate pushing is critical to prevent unwanted crossings into different parts of the hypersurface, due to changes in unconstrained degrees of freedom along the projected reaction coordinate. Initial geometry optimizations were performed using the 6-31+G* basis set, the M06-2X density functional,¹⁷ and the SMD solvation model,¹⁸ followed by single point frequency calculations on the obtained structures with a larger (6-311+G**) basis set, to correct for the inclusion of zero point energies and entropies and obtain the final free energy for each point (relative to the reactant complex). Once all points for the parent, unsubstituted compound had been optimized, we also used this surface as a starting point to generate the corresponding free energy surface for the 4-cyano-substituted compound (which shows the most extreme difference in experimentally measured KIE⁵) by perturbing each point for the unsubstituted compound with the new substituent and reoptimizing accordingly. Note, however, that direct geometry optimization was not possible for all of the points on the surface, in which case the nearest neighbor on the grid was used as a starting point for subsequent geometry optimization.

In addition to providing information about the overall topology of the relevant chemical landscapes, the original free energy surface (X = H) was also used in order to identify an approximate transition state, which was then subjected to a full, unconstrained geometry optimization, directly using a larger triple-ζ basis set, and with an ultrafine numerical integration grid. The resulting structure was characterized both by frequency calculations and by following the intrinsic reaction coordinate (IRC)^19,20 in both directions and was found to correspond to the transfer of a proton from the β-carbon to the hydroxide ion, leading to a carbanion intermediate. Specifically, relevant stationary points for this process were obtained by following the IRC to minima in both directions, followed by unconstrained geometry optimizations. As outlined in the main text, the subsequent transition state for leaving group elimination was trivial to obtain from the intermediate simply by elongating the C–O bond and performing a transition state optimization on the resulting structure. Once all stationary points had been obtained, zero point energies and entropies for each state were estimated by calculating the vibrational frequencies and adding them as a correction to the overall energetics (using a scaling factor of 0.970, by analogy to suggestions presented in ref (21) for other related basis sets). As the surface is very flat, this can potentially affect the reliability of the calculated zero point energies and entropies; however, these corrections at least provide insight into the relative magnitude of these effects for the different species examined in this work.

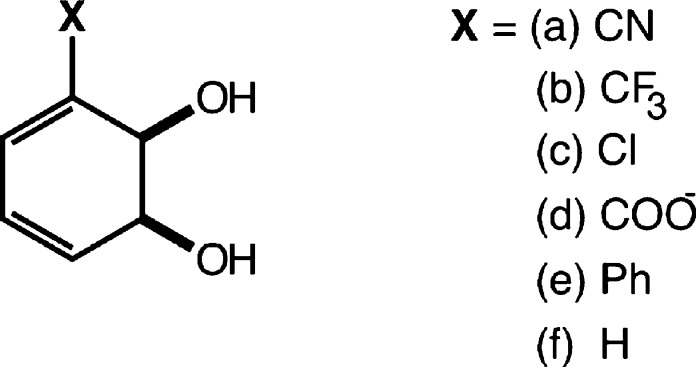
Once the one-dimensional free energy profile had been fully obtained and characterized for the unsubstituted benzene cis-1,2-dihydrodiol, we perturbed the initial transition state by adding the relevant substituents at the 3-position (Figure 2) and repeated the procedure outlined above for each compound to explore the effect of substituents on the reaction mechanism. Finally, for comparison, we also obtained a 1-D free energy profile for the dehydration of the parent compound in the presence of four explicit water molecules. The main purpose of this was to explore the effect of microsolvating the two hydroxide ions involved in the reaction (i.e., the base and the leaving group) on the obtained energetics and transition state structures due to the potential of inadequate charge shielding by the implicit solvent model. All quantum chemical calculations were performed using the Gaussian 09 simulation package.²²

Figure 2.

Benzene cis-1,2-dihydrodiols examined in this work.

Finally, the semiclassical kinetic isotope effects (KIE), without any tunneling correction, were obtained by using the program package Quiver.²³ This program allows one to calculate the partition functions of different isotopomers from the vibrational frequency calculations of the corresponding optimized ground and transition-state structures. The KIE is calculated using the Biegeleisen–Mayer formalism,^24,25 as follows:

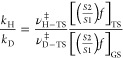where v_H-TS^⧧ is the imaginary frequency in the nondeuterated transition state, v_D-TS is the corresponding value for the deuterated isotopomer, [((S2)/(S1))f]_TS is the Biegeleisen–Mayer function for the transition state (the ratio of partition functions between the deuterated and normal transition state), and [((S2)/(S1))f]_GS is the corresponding value for the ground state.

Results and Discussion

Computationally generating multidimensional free energy landscapes for reactions such as these base-catalyzed dehydrations, even in implicit solvent, are made particularly challenging by the fact that the high basicity of the nucleophile can lead to spurious proton transfers and create substantial convergence issues. This makes such surfaces extremely demanding to generate, a problem that would only be compounded if modeling such reactions in explicit solvent using for instance ab initio molecular dynamics or metadynamics calculations. Multidimensional surfaces are important, however, because they offer the possibility to examine (a reduced representation of) the full free energy landscape and possibly obtain a very different mechanistic picture than by examining isolated stationary points alone. Conversely, as the overall free energy landscape is very flat and dominated by the extreme exothermicity of the reaction, examining the surface alone would result in the loss of the fine mechanistic details provided by the isolated stationary points. To illustrate this point, we have generated 2-dimensional free energy landscapes for the reaction of hydroxide ion with benzene-cis-1,2-dihydrodiol (X = H, Figure 1), as well as the cyano-substituted analogue. In the present work, we have only taken into account the pathway leading to the meta-phenol (which can be stabilized by both negative hyperconjugation and aromaticity) rather than the mechanism proceeding through the less thermodynamically favorable ortho-anion (which can only be stabilized by aromaticitiy), as experiment also suggests this is the dominant outcome of the reaction.⁵ As noted in the Introduction, the reactivity of these compounds appears to be on the E2-E1cB borderline, with intermediates and transition states that are potentially stabilized by hyperaromaticity. Our calculated free energy landscapes for the dehydration of these two diols are shown in Figure 3A and B, respectively, where the x-axis of the leaving group corresponds to the distance between the β-carbon and the oxygen atom of the departing leaving group, and the y-axis corresponds to the distance between the oxygen of the hydroxide ion and the β-hydrogen.

Figure 3.

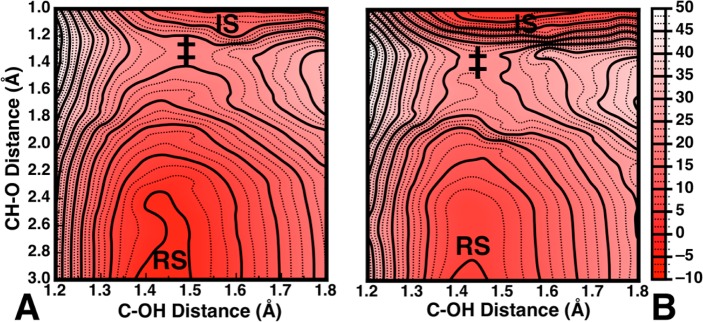
Free energy landscapes for the dehydration of (A) benzene cis-1,2-dihydrodiol and (B) the 3-cyano-substituted analogue, as a function of C–O distance to the leaving group (x-axis) and O–H distance to the base (y-axis). RS and IS denote reactant and intermediate states, respectively, and the approximate position of the transition state is marked by ‡. The product state can start to be seen at the upper right corner of the surface; however, extending the plot beyond 1.8 Å on the x-axis is complicated by the (expected) competing proton transfer from the OH groups of the benzene diol to the basic hydroxide ion.

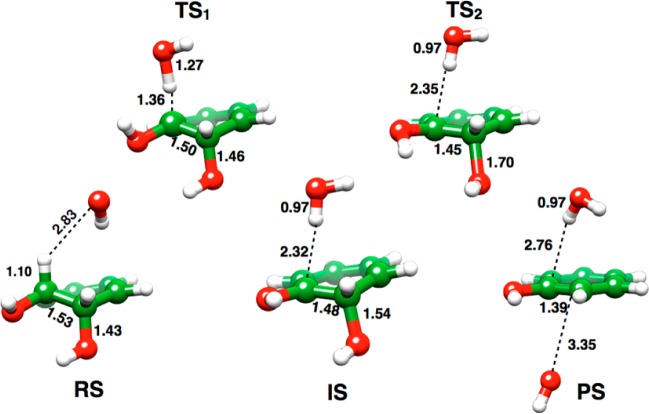
In the case of the unsubstituted compound (X = H, Figure 3A), the lowest energy path in the resulting landscape involves a highly asynchronous but concerted process with proton abstraction much more advanced than leaving group expulsion. However, as the surface is very flat, this would allow for many low-energy concerted pathways to products. Therefore, to further characterize this system, an unconstrained transition state optimization was performed on the approximate transition state on the surface (Figure 3A, C–O = 1.45 Å and O–H = 1.30 Å), and the resulting structure was characterized by both frequency and IRC calculations. The resulting optimized transition state possesses a large imaginary frequency (1568.5 cm^–1), which is in the range that would be expected for a transition state that is dominated by proton abstraction, with little contribution from cleavage of the C_α–OH bond. This was further corroborated by following the intrinsic reaction coordinate (IRC) from this transition state to the reactant and a carbanion intermediate. Full geometry optimization on these structures yielded the actual reactant complex and intermediate shown in Figure 4.

Figure 4.

Key stationary points for the dehydration of benzene cis-1,2,dihydrodiol. Shown here are the reactant complex (RS), the transition state for proton abstraction (TS₁), the carbanion intermediate (IS), the transition state for leaving group expulsion (TS₂), and the product complex (PS), obtained in a pure implicit solvent model.

Once this intermediate had been obtained, it was possible to obtain the transition state for leaving group elimination simply by elongating the C_α–OH bond. IRC and frequency calculations verified that this transition state led backward to the carbanion intermediate and forward to product. Therefore, in contrast to the free-energy surface, examining the stationary points alone suggests an E1cB-like mechanism. However, the overall energetics of this process is able to reconcile the outcomes of the two approaches (Figure 5 and Tables 1 and S1). Supplementary Table S1 provides the energy decomposition for the relative energies of each stationary point involved in the dehydration of the unsubstituted system, and the total energies are shown in Table 1. From these tables, it can be seen that while the reaction is stepwise in bonding pattern, leaving group expulsion occurs essentially spontaneously because once corrections have been added for the zero-point energy and entropy, this transition state essentially vanishes, leaving a process that is once again energetically concerted.

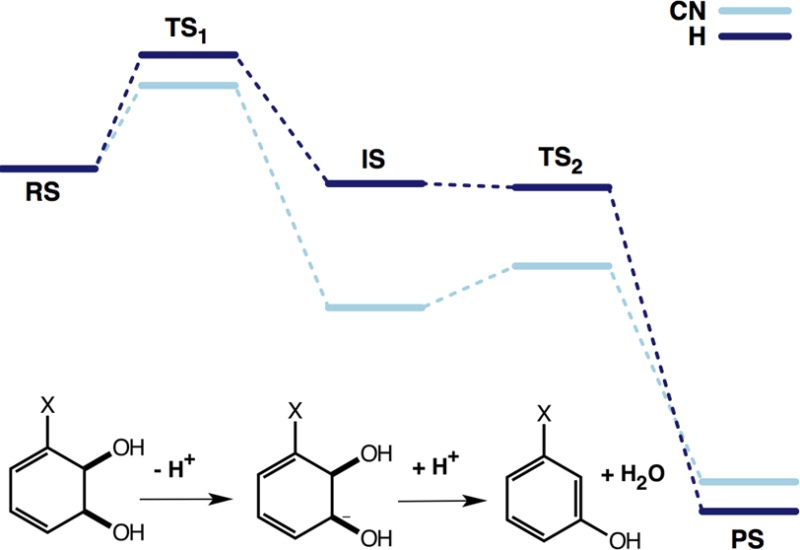
Figure 5.

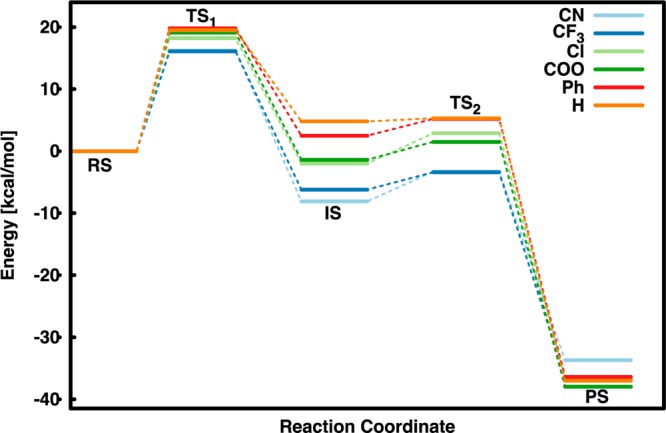
Calculated free energy profiles for the hydrolysis of the 3-substituted benzene cis-1,2-dihydrodiols examined in this work. These profiles were obtained using an implicit solvent model with no extra explicit water molecules. All energies are in kcal/mol, relative to the relevant reactant complex.

Table 1. Comparison of Calculated and Experimental Energetics for All Species Examined in This Work^a.

Xb	RSc	TS1c	ISc	TS2c	PSc	Δgexp⧧d
CN	0.0	16.2	–8.1	–3.3	–33.7	17.8
CF3	0.0	16.1	–6.2	–3.4	–36.5	19.9
Cl	0.0	18.2	2.0	2.9	–36.8	21.1
COO–	0.0	19.1	–1.4	1.5	–38.0	21.3
Ph	0.0	19.8	2.5	5.2	–36.4	21.9
H	0.0	19.5	4.8	5.2	–37.0	22.3

^aAll energies are in kcal/mol, relative to the reactant complex, and including corrections for zero point energies and entropies, as well as a −7.2 kcal/mol correction applied to the solvation free energies of the reactant and product states to account for undersolvation of the hydroxide ion by the implicit solvent model (see discussion in ref (26) and the main text). The corresponding uncorrected energy decompositions are shown in Supplementary Table S1.

^bSubstituent at 3-position, cf. Figure 1. All calculations presented in this Table were performed in implicit solvent with no extra explicit water molecules.

^cRS, TS₁, IS, TS₂, and PS denote the reactant complex, the transition state for proton abstraction, the carbanion intermediate, the transition state for leaving group expulsion, and the product complex, respectively.

^dExperimental activation barrier, based on kinetic data presented in ref (5). Since the calculated energetics are being considered relative to a reactant complex that has already been formed, for completeness, we have corrected the experimental value by 0.017 M^–1 to take into account the entropic cost of bringing the reacting fragments into the encounter complex, following ref (27).

Interestingly, a superficial examination of the 2-D free energy surface for the dehydration of the cyano-substituted analog (Figure 3B) would suggest that this process proceeds through a similar mechanism and transition states to the parent benzene diol, with once again a very flat free energy landscape and no discernible intermediate. However, in this case, following the 1-D free energy profile yields a very different mechanistic picture. That is, while the “intermediate” found in the case of the parent compound has no apparent lifetime, in the case of the cyano-substituted compound (Figure 5 and Tables 1 and S1), the 1-D profile now shows a transition toward an E1cB mechanism proceeding via a carbanion intermediate, with a subsequent barrier of ∼5 kcal/mol for leaving group expulsion. This can be easily rationalized by the presence of the highly electron-withdrawing substituent, which appears to provide a very large amount of stabilization to the carbanion. This intermediate is masked on the 2-D surface, however, by the extreme exothermicity of the product state, once again highlighting the importance of examining both multidimensional free energy landscapes and the relevant minimum free energy path across the surface.

One potential concern about our calculations in a pure implicit solvent model is the poor quantitative agreement with experiment (Table 1). That is, while we can reproduce the relative effect of the substituents reasonably well, our calculated absolute activation barriers for both the unsubstituted and cyano-substituted diols are ∼10 kcal/mol lower than the corresponding experimental value (Supplementary Table S1). This is in part due to the well-known problems of implicit solvation models dealing with the hydroxide ion, which would be expected to underestimate the stability of the ground state and give an artificially low activation barrier; for instance, in the case of the SMD solvation model, we obtain a solvation free energy of −97 kcal/mol for the hydroxide ion, whereas the actual solvation free energy is −105 ± 1 kcal/mol.²⁸⁻³⁰ Such underestimation of the activation barrier when modeling anionic nucleophiles in implicit solvent is not unique to the present system and has been observed when modeling a range of other reactions,^31,32 including, most recently, the alkaline hydrolysis of aryl benzenesulfonates.²⁶ In this latter work, we have discussed possible causes for this underestimate of the activation barriers and proposed a correction of −7.2 kcal/mol to the calculated solvation free energies of species containing free hydroxide ion (i.e., the reactant and product complexes in the present work) to account for the undersolvation of the hydroxide ion by the continuum model. Note that other authors have also suggested similar corrections (see, e.g., ref (33)). Indeed, it can be seen that adding this correction to these states (Table 1) gives much better agreement with experience and provides a consistent correction across the series. As a note of caution, when one is dealing with shifting transition states as in the case of the recently studied benzenesulfonates,²⁶ there is a risk that this correction is not consistent for each compound studied, and even here it may not necessarily be the same for different mechanisms. Therefore, to validate whether incomplete solvation is playing a role in the underestimation of the calculated activation barriers, we have also calculated the 1-D free energy profile for the dehydration of the parent (unsubstituted) compound including four extra explicit water molecules to complete the solvation shell of the hydroxide ion (cf. ref (16)). The purpose of this was to assess whether the lack of explicit hydrogen-bonding interactions in the implicit solvent model affects the relative energies and geometries of the key transition state(s) and putative intermediate along the reaction pathway and, therefore, whether such a model is at least qualitatively if not quantitatively accurate. A challenge here is the need to sample all possible positions of the water molecules during the reaction, which could hypothetically affect the calculated energetics. Since this is not computationally feasible, even with such comparatively small systems, we have limited our calculations to including two water molecules symmetrically so as to optimally stabilize the base and the leaving group in the first transition state (corresponding to proton abstraction) and then obtained the 1-D free energy profile in the same way as for the calculations in pure implicit solvent (see Supplementary Figure S1 for a comparison of the two free energy profiles for the unsubstituted compound).

As can be seen from Supplementary Table S1, which shows the uncorrected energetics for all compounds, adding the extra water molecules improves the match with experiment by providing better solvation of the hydroxide ion in the ground state but still does not bring full quantitative agreement with experiment. However, this deficiency should primarily affect the reactant and product states, as these are the states in which the hydroxide ion is present as a discrete entity. In both transition states and the intermediate, the hydroxide ion is at least partially bonded, and one may assume that this solvation error is small and similar in all cases and therefore that the relative energies of these key stationary points remain unaffected. By the same merit, as the error is expected to be similar in reactant and product states, adding the extra explicit water molecules changes the absolute energies but has a much smaller effect on the overall exothermicity. Therefore, the relative values for these species should still provide valuable information about the nature of the individual free energy profiles. Additionally, a comparison of the key distances highlighted in Table 2 and Figure 6 show that the inclusion of explicit microsolvation does not significantly change any of the geometries of the isolated stationary points compared to the pure continuum model, nor does it change our qualitative finding of a reaction that is stepwise in bonding pattern but energetically concerted, and therefore we believe that the simplified model in implicit solvent can nevertheless provide a fairly reliable mechanistic picture for the base-catalyzed dehydration of these compounds.

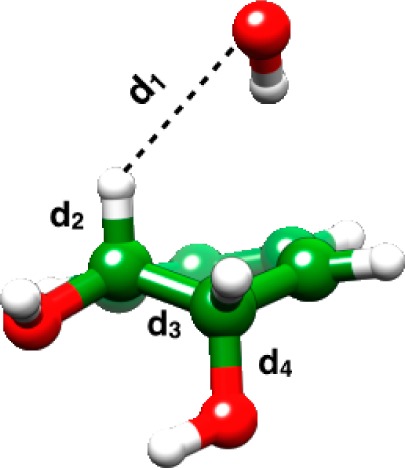
Table 2. Key Distances (Å) at Relevant Stationary Points with Different Substituents^a.

distanceb		H(4)	H	Ph	COO–	Cl	CF3	CN
RS	d1	2.62	2.83	2.90	2.96	2.78	2.95	2.88
	d2	1.10	1.10	1.10	1.10	1.10	1.10	1.10
	d3	1.53	1.53	1.53	1.53	1.54	1.53	1.53
	d4	1.44	1.43	1.43	1.43	1.42	1.42	1.42
TS1	d1	1.25	1.27	1.28	1.29	1.28	1.33	1.35
	d2	1.39	1.36	1.35	1.34	1.35	1.31	1.30
	d3	1.50	1.50	1.50	1.50	1.51	1.51	1.51
	d4	1.48	1.46	1.46	1.46	1.45	1.45	1.45
IS	d1	0.98	0.97	0.96	0.97	0.97	0.96	0.97
	d2	3.17	2.31	3.17	2.91	2.81	2.95	2.90
	d3	1.48	1.48	1.49	1.49	1.48	1.49	1.49
	d4	1.55	1.54	1.50	1.50	1.52	1.50	1.48
TS2	d1	0.98	0.97	0.96	0.97	0.97	0.96	0.97
	d2	3.05	2.35	3.17	2.93	2.81	3.05	2.94
	d3	1.46	1.45	1.45	1.44	1.48	1.44	1.44
	d4	1.66	1.70	1.76	1.80	1.74	1.83	1.89
PS	d1	0.97	0.97	0.97	0.97	0.97	0.97	0.97
	d2	2.92	2.76	2.88	3.24	3.17	2.99	3.00
	d3	1.39	1.39	1.39	1.39	1.39	1.39	1.39
	d4	3.29	3.35	3.52	3.44	3.54	3.56	3.61

^aFor each substituent, all stationary points were obtained in a pure continuum model. The only exception is the H(4) case, which was obtained in the presence of four explicit water molecules (two each on the basic and leaving group hydroxide ions).

^bRS, TS₁, IS, TS₂, and PS denote the reactant complex, transition state for proton abstraction, intermediate state, transition state for leaving group expulsion, and product state, respectively. d₁ denotes the distance between the oxygen of the base and the β-hydrogen, d₂ denotes the distance between the β-carbon and the β-hydrogen, d₃ denotes the distance between the α- and β-carbon atoms, and d₄ denotes the distance between the α-carbon and the oxygen of the departing leaving group.

Figure 6.

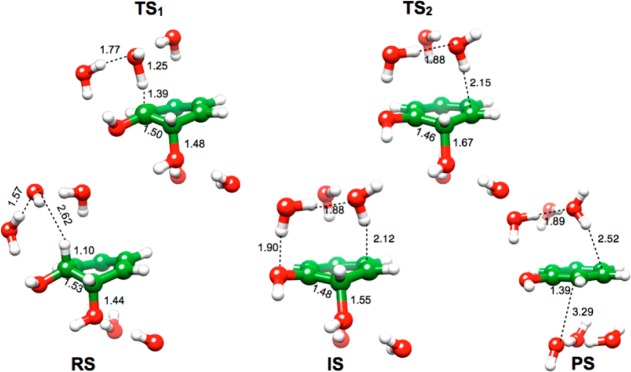
Key stationary points for the dehydration of benzene cis-1,2,dihydrodiol. Shown here are the reactant complex (RS), the transition state for proton abstraction (TS₁), the carbanion intermediate (IS), the transition state for leaving group expulsion (TS₂), and the product complex (PS), obtained in a mixed implicit/explicit solvent model, with microsolvation from four added water molecules.

In our previous work,⁵ we also examined the effect of adding a range of substituents to the diol. Here, in addition to examining the 3-cyano substitution, we have also considered the 1-D free energy profiles for the dehydration of benzene diols with a further set of substituents at the 3-position that span a range of electron-donating/withdrawing capabilities while remaining computationally tractable. The set we have selected (X = H, CN, CF₃, Cl, COO^–, and Ph) includes variations not only in electron-withdrawing ability but also in electrostatic and steric effects by including a charged (COO^–) and bulky (Ph) substituent. A comparison of the resulting free energy profiles across the series of substituents is shown in Figure 5, with the full energy profiles shown in Table 1 (corrected for the undersolvation of the hydroxide ion) and Supplementary Table S1 (uncorrected energy decomposition).

These data show that moving across the series results in progressive stabilization of the carbanion intermediate, with a gradual and subtle transition from an E1cB to an E2 pathway. Additionally, examining key distances at each stationary point (Table 2) shows that while the first transition state in both extremes of the series is asymmetrical, this asymmetry flips across the series such that proton abstraction is earlier in the 3-cyano compound than in the parent compound. As would be expected from a reaction that is driven by aromaticity, the C_α–C_β bond gradually contracts moving along the reaction pathway to a fully aromatic product, and leaving group expulsion becomes increasingly advanced in the second transition state. Note also that even though we do not provide absolute qualitative fidelity with experiment, the calculations are doing a very good job of reproducing the experimentally observed trends in energetics upon substitution, despite the general similarities of the first transition states for this process (proton abstraction, cf. Table 2). The fact that the structure of the first transition state is nearly identical regardless of the substituent or the exothermicity of the first step is particularly surprising, considering the shifting profiles shown in Figure 5 and Table 1. When this is combined with an analysis of the partial charges on these atoms at each state (Tables 3 and S3), one can see that the substituents also have little impact on the charge distributions of the first transition state and intermediate and likely stabilize/destabilize them via inductive/polar effects rather than resonance effects. It can also be seen that already at the intermediate the charge of the carbanion has become delocalized onto the ring, with C_β starting to take on sp² character. Following from this, the strongest trend seen in the series is in the structure of the second transition states, with the C–O distance to the leaving group becoming elongated by 0.24 Å upon moving across the series, resulting in a slight loss of bond order from 0.65 to 0.52 moving across the series, assuming an equilibrium C–O bond length of 1.43 Å. The later transition state for hydroxide expulsion is consistent with the increased barrier to leaving group elimination upon adding electron-withdrawing substituents.

Table 3. Key Charges at the Reactant Complex, Transition State for Proton Abstraction, and Intermediate Complex for All Compounds Studied in This Work^a.

Xb	Cβ	Cα	Olg	CX
X = CN
reactant	0.058	0.104	–0.793	–0.206
TS1	–0.057	0.102	–0.819	–0.262
intermediate	0.272	0.045	–0.845	–0.459
X = CF3
reactant	0.061	0.079	–0.779	–0.169
TS1	–0.061	0.073	–0.810	–0.215
intermediate	0.249	0.018	–0.854	–0.438
X = Cl
reactant	0.064	0.063	–0.795	–0.044
TS1	–0.066	0.052	–0.829	–0.078
intermediate	0.208	–0.020	–0.883	–0.253
X = COO–
reactant	0.061	0.080	–0.805	–0.149
TS1	–0.066	0.074	–0.838	–0.204
intermediate	0.250	0.028	0.868	–0.424
X = Ph
reactant	0.064	0.087	–0.801	–0.043
TS1	–0.065	0.078	–0.835	–0.094
intermediate	0.248	0.022	–0.863	–0.302
X = H
reactant	0.059	0.069	–0.802	–0.213
TS1	–0.072	0.058	–0.841	–0.268
intermediate	0.166	–0.013	–0.904	–0.429

^aAtomic charges were obtained using natural population analysis (NPA)³⁴ at the same level of theory as the geometry optimizations (see Methodology). All calculations presented in this table were performed using a pure continuum model with no extra explicit water molecules.

^bSubstituent at 3-position, cf. Figure 1. C_β, C_α, O_lg, and C_X denote the β-carbon, the α-carbon, the oxygen atom of the leaving group, and the substituted carbon atom at the 3-position, respectively.

The similarity of the first transition states is particularly striking due to the very large difference in the measured isotope effects in the hydroxide-catalyzed elimination of the unsubstituted versus cyano-substituted diol.⁵ In the experimental study, the observed isotope effects and isotope exchange behavior put severe limitations on the mechanistic possibilities. In the unsubstituted system, there was no evidence of isotopic exchange at the β-carbon during the elimination process, which would suggest either a concerted E2 or an irreversible E1cB mechanism. A very large primary deuterium isotope effect was observed for the cyano system (k_H/k_D > 16), which could be consistent with either the E2 or E1cB mechanism. However in moving to weaker electron-withdrawing groups, the isotope effect dropped and for the unsubstituted system approached unity, an outcome that would be unexpected for either an E2 or an irreversible E1cb mechanism. The data was rationalized by assuming that the unsubstituted system underwent extensive internal return in the deprotonation process of an E1cB mechanism, which mitigated the kinetic isotope effect and prevented isotopic exchange before the elimination (see also refs (35) and (36)). With electron-withdrawing groups, it was assumed that the proton transfer would be irreversible and produce a significant kinetic isotope effect. The mechanistic picture from the experiments is that in the activated systems an E2 or an irreversible E1cB mechanism is at play, but in the unsubstituted system, an E1cB path dominated by internal return is operative.

The computed free energy surfaces and transition states are not fully consistent with this mechanistic picture. The calculations do point to a situation on the borderline between an E2 and an irreversible E1cB mechanism but do not indicate that internal return would be an important process. The energy of the second transition state (leaving group expulsion) is well below that of the first transition state (proton transfer) so when the carbanion intermediate is formed, it is unlikely to recross the proton transfer barrier in an internal return process. All indications are that aromatization makes leaving group expulsion extremely facile from a carbanion intermediate and this process wold out-compete the internal return of the proton. Given the computed surfaces and transition sates, internal return could be active only if solvent rearrangement or a dynamical effect created a barrier in the leaving group expulsion process, thereby making internal return competitive with leaving group expulsion. Although unusual, this situation is possible. However, given the complexity of the system and the long timeframes of the reaction processes, it would not be possible to computationally explore this aspect of the reaction in a realistic manner. Additionally, although unlikely, one of course cannot completely rule out the simpler possibility that there exist some error in the experiments of ref (5) such that what is being measured in the experiment is not actually the isotope effect for the elimination process.

Alternatively the isotopic behavior could be explained by variations in the proton transfer transition state. A very early or late transition state would lead to a small isotope effect in the proton transfer. Given that the small kinetic isotope effect is seen in the least favorable proton transfer, the logical assumption in this line of thinking would be a late transition state in the unsubstituted system. As electron-withdrawing groups are added to ring, the deprotonation would become more favorable and an earlier, more central transition state, with a larger isotope effect would be expected. This general trend is observed in the calculated proton transfer transition states but is not sufficient to explain the large variation in kinetic isotope effects. In fact, the substituted system appears to have the more central transition state (see below). For example, the C–H and H–O distances to the transferring proton vary from 1.36 and 1.27 Å for X = H to 1.30 and 1.35 Å for X = CN, respectively (Table 2). The proton transfer transition states also are not very sensitive to the solvation model or the level of theory. The addition for 4 explicit water molecules to the system only shifts the C–H and H–O distances to 1.40 and 1.25 Å in X = H (Table 2). Moving to optimizations at the MP2/6-31+G* level in a PCM solvent model gives C–H and H–O distances of 1.36 and 1.28 Å for X = H and 1.32 and 1.33 Å for X = CN (all MP2 data are in the Supporting Information). In an extreme perturbation, the gas-phase transition states at the MP2/6-31+G* level give C–H and H–O distances of 1.36 and 1.28 Å, respectively, for X = H and 1.33 and 1.28 Å in X = CN. In each case, a relatively central proton transfer is observed, which should produce a significant isotope effect. This is illustrated in Table 4 where it can be seen that substituents have little effect on the computed isotope effects (all in the range of ∼3–4) and the unsubstituted system is predicted to give the largest isotope effect by a small margin. In short, the computational examination of the proton transfer transition states indicates that there is little malleability in these systems. At this point, the available computational tools cannot reconcile the differences between the potential surfaces presented here and the observed isotopic behavior. As noted above, solvation effects not accounted for in this work or dynamics effects could be at play, or conversely, there may be a disconnect between the phenomena that produced the experimental isotopic behavior and the processes that are being modeled here.

Table 4. Calculated Kinetic Isotope Effects (KIE) for All Substituted Benzene cis-1,2-Dihydrodiols Presented in This Work,^a Using Stationary Points Obtained in a Pure Continuum Model without the Presence of Extra Explicit Water Molecules.

substituent	KIEcalc
CN	3.70
CF3	3.76
Cl	3.85
COO–	3.73
Ph	3.80
H	3.86

^aAll KIE calculated from the vibrational frequencies using the Biegeleisen–Meyer equation as implemented in Quiver (see Methodology for details).

Conclusions

In the present work, we have presented calculated free energy landscapes for a range of 3-substituted benzene cis-1,2-dihydrodiols, obtained using DFT calculations in both implicit and mixed implicit/explicit solvent models. These compounds are interesting because their reaction mechanisms appear to lie on the elusive border between E2 and E1cB pathways, as well as the fact that these elimination reactions are unique in harnessing aromaticity to make an unfavorable reaction favorable.⁵ In this work, the 2-dimensional surfaces provide a clear picture of the subtle balance between mechanisms, and the 1-dimensional surfaces allow for a careful analysis of the transition states and barriers. There are two important aspects to the data presented here. First, the calculations appear to be doing a very good job of matching the relative barriers across this series of compounds, despite underestimating the calculated activation barriers, presumably due to the underestimation of the hydroxide solvation energy by the continuum model. Second, as we move across the series to stronger electron-withdrawing groups, the stability of the carbanion intermediate increases relative to the other stationary points such that there is a gradual transition from an E1cB-like but energetically concerted pathway to an unquestionably E1cB pathway, as leaving group elimination becomes increasingly unfavorable (although never by more than ∼5 kcal/mol). Again, we would like to emphasize that given the extreme exothermicity of the reaction, such subtlety may have been lost by examining just the free energy surface, which would likely suggest an E2 pathway, whereas just examining the stationary points hides how flat the surface is around the transition state for leaving group expulsion; both of these issues are critical in understanding the reaction system. An additional encouraging point to emerge from these calculations is the fact that despite the underestimation of the activation barriers, the calculations do a very good job of reproducing experimental trends, and explicit microsolvation using even four water molecules is sufficient to substantially improve agreement with experiment without qualitatively affecting our results. Therefore, in principle, one could obtain much better quantitative fidelity to experiment using ab initio molecular dynamics (MD) or hybrid quantum mechanical/molecular mechanical calculations in explicit solvent that fully solvate the hydroxide charges in the reactant and product states. However, this is unlikely to provide a qualitatively different picture to that presented here, while substantially increasing computational cost, particularly in light of the potential of generating an extremely large number of unproductive trajectories due to spurious proton transfers. In conclusion, the combination of 2-dimensional free energy surfaces and stationary point calculations provides a framework for understanding complex reactions that lie on the borderline between concerted and stepwise processes. Moreover, as in this case, they can point to potential dynamical issues (i.e., the isotope effect behavior) that could not be discerned without a comprehensive understanding of the reaction profile.

Supporting Information Available

Energy breakdown for the systems examined and coordinates of all stationary points. This material is available free of charge via the Internet at http://pubs.acs.org.

The authors declare no competing financial interest.