Efficient Parameter Estimation of Generalizable Coarse-Grained Protein Force Fields Using Contrastive Divergence: A Maximum Likelihood Approach

Abstract

Maximum Likelihood (ML) optimization schemes are widely used for parameter inference. They maximize the likelihood of some experimentally observed data, with respect to the model parameters iteratively, following the gradient of the logarithm of the likelihood. Here, we employ a ML inference scheme to infer a generalizable, physics-based coarse-grained protein model (which includes Go̅-like biasing terms to stabilize secondary structure elements in room-temperature simulations), using native conformations of a training set of proteins as the observed data. Contrastive divergence, a novel statistical machine learning technique, is used to efficiently approximate the direction of the gradient ascent, which enables the use of a large training set of proteins. Unlike previous work, the generalizability of the protein model allows the folding of peptides and a protein (protein G) which are not part of the training set. We compare the same force field with different van der Waals (vdW) potential forms: a hard cutoff model, and a Lennard-Jones (LJ) potential with vdW parameters inferred or adopted from the CHARMM or AMBER force fields. Simulations of peptides and protein G show that the LJ model with inferred parameters outperforms the hard cutoff potential, which is consistent with previous observations. Simulations using the LJ potential with inferred vdW parameters also outperforms the protein models with adopted vdW parameter values, demonstrating that model parameters generally cannot be used with force fields with different energy functions. The software is available at https://sites.google.com/site/crankite/.

1. Introduction

The aim of predicting unknown protein structures from only their primary sequences¹ or to elucidate the folding process or function of proteins with known structures is one of the central aims of computational biology. The increase in the number of protein sequences and structures deposited in the protein databases^2,3 highlights the need for efficient modeling of proteins. Although all-atom molecular force fields have been successfully applied to model fast folding mini-proteins,⁴ they are too expensive for modeling larger proteins without the use of specialist hardware. Coarse-grained (CG) protein models, which are simpler than all-atom models, but still capture the physics of interest, have shown an increasing popularity in their use in computer simulations of proteins.⁵

In general, CG force fields are usually classified into two main categories:^5,6 structure-based or native-centric models, such as elastic network^7,8 and Go̅ models,⁹ where only the native interactions are modeled as attractive interactions; and structure-independent force fields⁶ that are modeling physicochemical interactions that are often used in simulations of aggregates,¹⁰⁻¹² protein structure prediction,¹³ or protein folding studies.^11,14−18 Here, we optimize a Go̅-like CG force field, CRANKITE,¹⁹ which was developed to efficiently model peptides and proteins at room temperature by exploiting a fast conformational sampling algorithm,²⁰ and to stabilize secondary structure elements at room temperature,²¹ which would allow it to be used for protein structure prediction²² using predicted secondary structure and β–β contact maps.²³ It is an extended Go̅-type model, where, although some of the secondary structure interactions are constrained using a harmonic bias potential, non-native attractive interactions are also modeled. In this paper, the bias potential acting on the backbone conformation of residues with known α-helical and β-strand secondary structure and the β-carbon distances of known β-sheet contacts will be referred to as secondary structure bias. Hence, this model allows the exploration of a more realistic folding funnel, compared to the “perfect” funnel of standard Go̅ models. Thus, CRANKITE represents an intermediate between the two main classes of CG protein models. CRANKITE also uses a full atom representation of the protein backbone, together with explicit side chain β and γ atoms, to include entropic contributions coming from the torsional flexibility of side chains.²⁴ This is important, because it has been shown that although polyalanine models (including only β atoms) are excellent for modeling secondary structure elements, they form more compact structures than real proteins.²⁵

When optimizing force field parameters, protein models should be parametrized to stabilize the native conformation of the protein compared to unfolded and misfolded conformations; that is, the native conformation lies at the global minimum of the free-energy landscape.²⁶ Traditionally, statistical-knowledge-based potentials have been used to estimate model parameters of the energy function to reproduce certain features of a model dataset,²⁷ such as dihedral angles and distance distributions, assuming that the selected features are statistically independent and that their distribution in the dataset of native conformations comply with the Boltzmann distribution. This assumption is called the Boltzmann hypothesis. Although the Boltzmann hypothesis is supported by numerous empirical studies (see the Discussion section in refs (27) or (28)), the assumption of statistical independence is often poor. Moreover, a reference state is usually introduced in the potential of mean force formulation without a rigorous definition, and the decoy sets used to describe the reference state will affect the optimized potential parameters, as demonstrated by Hamelryck et al.,²⁹⁻³¹ who give a rigorous statistical definition of a reference state.

Alternatively, native structure discriminant methods use a set of decoy conformations to optimize the parameter values, such that the folding characteristics of the protein are reproduced, with the lowest energy assigned to the native state, using various optimization techniques.³²⁻⁴⁰ However, these methods do not incorporate temperature into the model, and so they do not take into account the thermodynamic stability of proteins, only the relative strength of intermolecular interactions to a set of decoys.

An alternative way of estimating the potential parameters is by using maximum likelihood (ML) methods, which infer the potential parameters by maximizing the likelihood of the experimentally observed (or computationally generated) protein conformations, with respect to the model parameters iteratively (or analytically,⁴¹ for very simple models), following the gradient of the logarithm of likelihood.^{12,20,41−44} The model with the parameters giving the highest likelihood would generate a distribution of conformations (model distribution) closest to the experimentally observed distribution of conformations (data distribution, also referred to as the target distribution of the parameter estimation). The free-energy landscape of the inferred model potential is closest to the free energy landscape corresponding to the data distribution, which was demonstrated using a simple model of water,⁴⁴ for which the free energies could be calculated analytically. Winther and Krogh,⁴² followed by Podtelezhnikov et al.^20,21 used a ML approach to train a protein model (i.e., a model applicable to globular proteins), while Shell et al.¹² used a ML approach to train a protein model specific to a 15-residue polyalanine, a prototype molecule used to model amyloid formation. The relation of this ML approach (also referred to as the relative entropy method⁴⁴) to the force matching method⁴⁵ was analyzed by Chaimovich and Shell⁴⁶ and Rudzinski and Noid,⁴⁷ in the context of fitting CG potentials to all-atom models.

As we show below, the difficulty of the ML approach lies in the calculation of ensemble averages over the model distribution at every iteration. Winther and Krogh⁴² conducted extensive simulations using replica exchange molecular dynamics to calculate the ensemble averages, restricting their training set to a small set of short peptides (24 different 11–14-residue-long protein fragments), which resulted in poor transferability to model peptides not in the training set. To efficiently estimate the gradient of the log likelihood, instead of re-evaluating the ensemble averages at each ML iteration, Podtelezhnikov et al.^20,21 used a statistical machine learning technique, known as contrastive divergence (CD),⁴⁸ which was developed in the neural network literature to efficiently estimate the parameters of Boltzmann machines.^49,50 This enabled the use of a larger data set of proteins and resulted in a transferable protein model, which was subsequently used in folding simulations of proteins not in the training set. Shell et al.¹² presented another solution to reduce computational costs, using reweighted ensemble averages between successive iterations. To accelerate the convergence of the ML optimization, Hinton⁵¹ suggested an adaptive learning rate with an associated momentum, while Bilionis and Zabaras⁵² have proposed an optimization algorithm that makes use of the second derivative of the energy, with respect to the parameters of the energy function.

In our earlier work, we have used the CD algorithm to efficiently estimate potential parameters (hydrogen-bond strength in proteins²⁰ and the secondary structure bias parameters²¹) of a CG protein model, CRANKITE. The aim of this work is to improve the CRANKITE protein model, as an exemplar for a CG force field, by inferring, or learning, the van der Waals (vdW) parameters of the CG protein model using this statistical machine learning approach. Two potential forms are considered in this paper: a computationally efficient hard cutoff model, employed by the original CRANKITE force field that models short-range repulsion due to the Pauli exclusion between overlapping electron densities, and the Lennard-Jones (LJ) potential form⁵³ that also models long-range attraction due to fluctuating charge densities of induced dipoles. Following the explanation of the method, the parameter inference and the effect of the simulation parameters on the inference are discussed. Subsequently, the improvement of the force field is investigated by a comparison of the performance of the hard cutoff and LJ type potential forms through the investigation of structural and thermodynamic properties, calculated from Monte Carlo (MC) and folding simulations of 16-residue peptides and protein G (Protein Databank (PDB) code: 1PGA). Transferability between different protein models is tested by comparisons of LJ type potentials with learnt vdW parameters (LJ_learnt) and parameters adopted from the widely used AMBER⁵⁴ and CHARMM⁵⁵ all-atom force fields (LJ_AMBER and LJ_CHARMM, respectively). The assumptions of the method are also discussed.

2. Methods

2.1. Maximum Likelihood Inference for Parameter Estimation of Generalizable Protein Models

We assume that we have n₀ independent observations of the conformation Ω₀ of a protein with amino acid sequence S₀, {Ω₀|S₀} = {Ω₀^j|S₀: j = 1, ..., n₀}, distributed according to the Boltzmann distribution at inverse temperature β (e.g., the outcomes of an experiment or a computer simulation). The interaction parameters, θ, of a protein model, such as force constants, distance cutoffs, dielectric permittivity or atomic charges, specific to the protein with amino acid sequence S₀, can be estimated by maximizing the likelihood, L = P(θ|{Ω₀},S₀), by a gradient ascent using an iterative scheme. At iteration k+1,

1

where η is the learning rate, and ∇_θ ln L is the gradient of the logarithm of likelihood, with respect to parameter θ. Assuming that the observations {Ω₀} are independent and come from the Boltzmann distribution at inverse temperature β for a given parameter set θ,

2

Using Bayes’ equality with a uniform prior P(θ|S₀), the gradient of the likelihood, with respect to the model parameters, can be written as

3

where ⟨A(Ω)⟩_θ,S0 = ∫A(Ω)P(Ω|θ,S₀)dΩ is the ensemble average of A(Ω) in the model distribution. The first term in the parentheses of eq 3 is an average over the data, approximating an ensemble average over the data distribution. Maximizing the likelihood is equivalent to minimizing the Kullback–Leibler divergence (or relative entropy) of the data distribution and the model distribution:

4

since the entropy of the data distribution, H(P(Ω₀)) = −∑_j=1^n₀P(Ω₀|S₀)lnP(Ω₀^j|S₀), does not depend on the parameters θ, and the observations are drawn from the data distribution.

Such a protein model will be specific to the protein with sequence S₀ it was trained on, and is unlikely to be transferable to proteins with arbitrary amino acid sequences. A generalizable protein model, that is, one that is transferable to proteins not in the dataset, must be trained on a set of proteins that are representative of all the proteins we aim to model, and which are independent of each other. Hence, let us take observations of the conformations of N proteins with amino acid sequences {S₀} = {S₀ⁱ: i = 1, ..., N}. Let us allow that, for some proteins with sequence S₀, more than one independent observation of the conformation is available, {Ω₀ⁱ} = {Ω₀|S₀ⁱ: j = 1, ..., n_i}, and that all observations come from the Boltzmann distribution corresponding to the same inverse temperature β. The parameters of the generalizable protein model (we use the same parameter set θ to describe all proteins) maximize the likelihood of the parameters, given the observed conformations. The probability of finding the dataset, given the sequences and the parameters, is

5

as a conformation is only dependent on its own protein sequence and the general θ parameters. Following a similar derivation to that for eq 3, the gradient of the logarithm of likelihood, with respect to the model parameters θ, can be written as

6

This is equivalent to minimizing the average of KL divergences between the data and model distributions for all sequences,

7

Note that neither the length of the proteins, nor other properties of the protein sequences explicitly affect the parameter estimation; the direction of the gradient ascent is given by the unbiased average of the KL divergences of the model and data distributions for all sequences S₀ⁱ. Also note that if there is only one observation available for any protein sequence, the first term of the inner sum of eq 6, the average over the data distribution for S₀, is approximated by one data point. Even in this case, the ML estimate is still correct, as long as all protein conformations are described by the Boltzmann distribution at the same inverse temperature β, and they are representative of the proteins we aim to model.

2.2. Contrastive Divergence

In contrastive divergence,⁴⁸ to avoid the cumbersome calculation of the ensemble average in the model distribution at every step of the ML iteration (eq 6), the Kullback–Leibler divergence of the data distribution and a perturbed data distribution is minimized, instead of the KL divergence of the model and data distributions. Samples from the perturbed distribution are generated by performing K MC steps starting from the observed conformations representing the data distribution, using the model parameters θ^k at iteration k. For a protein with amino acid sequence S₀, we use P⁰(Ω|S₀) = P(Ω₀|S₀) to denote the data distribution, P_θ^∞(Ω|S₀) = P(Ω|θ,S₀) to denote the equilibrium distribution of the model with parameters θ, and P_θ(Ω|S₀) to denote the perturbed data distribution, which is generated by performing K MC steps starting from the data distribution using the model parameters θ at every iteration. The direction of gradient ascent is given by

8

where ⟨A(Ω|S₀)⟩₀ = (1/n₀) × ∑_j=1^n₀A(Ω₀|S₀) is the ensemble average in the data distribution, and ⟨A(Ω|θ, S₀)⟩_K = (1/n₀) × ∑ _j=1^n₀A(Ω_K|θ, S₀) is the corresponding average in the perturbed data distribution, with Ω_K^j being a conformation in the perturbed data distribution. In the original work by Hinton,⁴⁸ simulation results of restricted Boltzmann machines with a small number of visible and hidden units demonstrate that the third term may be safely ignored, and so the CD parameter estimation algorithm becomes

9

For the problem at hand, we additionally provide the following argument. As K → ∞, eq 1 is recovered. However, even for a small number of steps, unless the model distribution reproduces the data distribution, P_θ^K(Ω|S₀) drifts away from the data distribution, toward the model distribution KL(P⁰(Ω|S₀) ∥ P_θ(Ω|S₀)) > KL(P_θ^K(Ω|S₀) ∥ P_θ(Ω|S₀)), and the drift in the energy gradient observed during the MC simulation can be used as the estimate of ∇_θ ln L. Changing the parameters according to eq 9 reduces the tendency of the model distribution to drift away from the data distribution. To support this argument for the convergence of the algorithm using the approximate gradient, we calculated the distribution of the approximate ∇_θ ln L for different model parameter values, and plotted the distributions at the initial and converged values of one of the model parameters (Figure S1 in the Supporting Information). The expected value of the distribution at the initial parameter values is nonzero (and has the correct sign), while at the converged parameter values, it is zero.

When the observed conformations belong to proteins with different amino acid sequences (i.e., when inferring a generalizable protein model with n_i = 1 for all sequences S₀ⁱ), the ML algorithm takes the form

10

when using the CD estimation of the KL divergences for all proteins with amino acid sequence S₀ⁱ. This equation is used throughout this work in the ML inference of the protein model parameters. As a constant during the ML inference, β can be incorporated into the learning rate.

2.3. The Protein Model

We use a protein model with an all-atom backbone and coarse-grained side chains represented up to the gamma atoms, as described by Podtelezhnikov et al.²⁰ and Burkoff et al.²² Bond lengths and bond angles are rigid, with values taken from Srinivasan et al.⁵⁶ and Burkoff et al.,²² except for the C_α valence angle τ (the angle determined by the amide N, C_α and carbonyl C atoms of a residue), which is allowed to change. Peptide bond geometries are kept fixed, resulting in fixed C_α–C_α distances. The conformational flexibility of the backbone comes from free rotation around the φ and ψ dihedral angles and the C_α valence angle. The side-chain (N–C_α–C_β–C_γ) dihedral angles can take values of ±60° or 180°. During MC simulations, the move set consists of crankshaft rotations around any axes connecting up to 4 C_α atoms, and rotations at the termini around any axis passing through the C_α atom, as implemented in the CRANKITE software.^19,57 At every fourth MC step, the side-chain dihedral angles were reassigned by drawing from the frequency distribution of side chain dihedral angles in the dataset.

The energy function of the protein model depends on the conformation Ω containing all coordinates of its N residues, and the parameter set θ. It consists of six terms,²²

11

E^B is the backbone stress term due to deviations of the C_α valence angle τ_i of residue i from the equilibrium value τ₀ = 69°,⁵⁸ and k_τ is the force constant of the quadratic potential. E^vdW is the van der Waals interaction term described below, employed to prevent atomic clashes, and to model long-range weak attractive interactions. E^HB is the hydrogen bonding term with hydrogen-bond strength H. n_l→m^HB is a number between 0 and 1 representing the strength of hydrogen bonding between the amide H atom of residue l (H_l) and the carbonyl O atom of residue m (O_m), determined using a distance cutoff δ and two angle cutoffs (Θ_COH and Ψ_OHN). (For the exact function form, see the Supporting Information.) E^hyd is a hydrophobic interaction term with interaction strength k_h, a hydrophobic match factor M_lm, and the cutoff function f_cut. The hydrophobic match takes a value of 2 if both amino acids are hydrophobic, 1 if one is hydrophobic and the other one is amphipathic, and 0 otherwise. The cutoff function changes linearly from 1 to 0 as the distance of the C_β atoms of residues l and m goes from the sum of vdW radii (from the hard cutoff model) across 2.8 Å. E^SC is the side-chain–side-chain interaction term representing a secondary structure bias on the dihedral angles of the residues as well as β-sheet contacts. The γ_l,l+1 dihedral angle, N_l–C_α,l–C_α,l+1–C_l+1, is restrained to an equilibrium value γ_0,ss typical for the corresponding secondary structure element ss (γ_0,α = 82° for α-helical conformation, and γ_0,β = 180° for β strand conformation) using the force constant η_ss (η_α for residues in an α-helical, and η_β for residues in β-strand conformation, and 0 otherwise, defined by a predetermined secondary structure). The C_β,l–C_β,m distances of residues l and m (r_lm) that are in β-sheet contact, defined by a predetermined binary contact map C_lm are restrained by a quadratic potential to an equilibrium value r_0,β using a force constant κ_β. E^P is a proline term, specific due to deviations of the C_l–1–N_l–C_α,l–C_l dihedral angle, ϕ_l, of the proline residue l from the equilibrium value of ϕ₀ = −60°,⁵⁹ and k_P = 30RT is the force constant of the quadratic potential.²⁰

In this paper, we consider the following forms of the vdW interactions acting between atoms:

• A hard cutoff potential, often used by CG models, because of its simplicity and computational efficiency,^56,57,60 with a distance-dependent excess energy for clashing atoms:^22,57

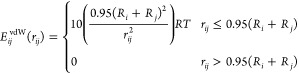12

where R_i and R_j are the vdW radii of atoms i and j taken from the original CRANKITE model,²⁰ and r_ij is their distance.

•A Lennard-Jones potential form, also used in more sophisticated CG models.^32,61,62 Here, the vdW energy is

13

between atoms i and j at a distance r_ij, where ε_ij is the vdW energy contribution at the minimum energy separation, R_min,ij (see Figure S2 in the Supporting Information). The energies are shifted to obtain zero vdW energy at the cutoff, 2R_min,ij. For simplicity, the ε parameters of the LJ model are kept the same for all atom types.

More-sophisticated approximations of the vdW potential (for example, the Buckingham potential⁶³ or many-body Axilrod–Teller–Muto contributions⁶⁴) would be computationally too expensive to include in our CG simulations, where the aim is to develop the simplest protein model that captures the physics of the systems of interest.

2.4. The Optimization Procedure

In this work, the following parameters of the energy function (eq 11) were inferred for all models considered: the backbone stress force constant (k_τ), the hydrogen-bond strength (H), the hydrogen-bond distance cutoff (δ) and angle cutoffs (Θ_COH and Ψ_OHN), the hydrophobic interaction strength (k_h), the secondary structure biasing dihedral angle force constants (η_α and η_β), and the C_β–C_β contact equilibrium distance (r_0,β) and force constant (κ_β). For the hard cutoff model, no further parameters were inferred. For the LJ model (eq 13), a mutual vdW energy contribution ε_i parameter for all atom types and the minimum energy separation parameters R_min,i for every atom type (CA, CB, C, N, O and S) were also inferred (LJ_learnt model), or adapted from the CHARMM and AMBER force fields (LJ_CHARMM and LJ_AMBER; see Table 1). Note that, in the LJ_learnt model, the CRANKITE atom types have the same ε_i parameter, while in the LJ_CHARMM and LJ_AMBER models they have individual ones.

Table 1. The CHARMM and AMBER Atom Types Whose LJ Parameters Were Adopted for the CRANKITE Atom Types in the LJ_CHARMM and LJ_AMBER Models.

CRANKITE	CA	CB	C	N	O	S
CHARMM	CT1	CT2	C	NH2	O	S
AMBER	CT	CT	C	N	O	S

During the ML inference, the parameters were inferred in two stages, following a multigrid approach.⁶⁵ The potential parameters that govern the local and global configurations are separated in the inference, starting with local parameters, and then moving to more global parameters. The local parameters were chosen as those affecting the local configuration of atoms and short atomic distances near atomic clashes, namely, the hydrogen bonding (H, δ, Θ_COH, and Ψ_OHN), C_α valence angle stress (k_τ), and vdW potential parameters (R_min,i and ε, only for the LJ model), and were inferred together in the first stage. The other parameters acting over larger distances, namely, the secondary structure bias (η_α, η_β, κ_β, and r_0,β), and hydrophobicity (k_h), were learnt subsequently, with the former ones being fixed. Note that the LJ potential also acts at long distances, and hence, the length scale separation is not perfect. In fact, it is an effective way to decouple the effects of potentially competing long-range parameters, such as the hydrophobic interaction potential or the C_β–C_β contact potential, from the short-range part of the LJ parameters, which cannot be decoupled from the long-range part of the LJ parameters.

As the data set of known protein structures representing thermodynamic equilibrium, we use a subset of the protein structures in the ASTRAL 1.75 database.⁶⁶ To avoid proteins with high sequence similarity, proteins with less than 40% sequence identity were included. The ASTRAL 1.75 database contains three-dimensional (3D) structures of protein domains, classified into folding classes. For each structure, a Summary PDB ASTRAL Check Index (SPACI)⁶⁷ score is assigned, indicating the reliability of crystallographically determined structures. All PDB structures from the α, β, α+β, and α/β classes of the ASTRAL 1.75 database with SPACI scores above 0.8 were included in the dataset, excluding the ones with missing residues, disulfide bonds, or unusual residues.

Following the inference, the hydrophobic interaction strength k_h needed modification. k_h was increased by 0.1 RT, which was necessary for the protein folding simulations to stabilize the conformation with the hydrophobic residues in the interior of the protein. Although the hydrophobic interaction strength was sufficient to preserve the folded structure of the proteins in the database, it was not sufficiently strong for folding proteins from an unfolded state. A possible reason for the learnt value of k_h being too small could be that the ASTRAL 1.75 database used contains individual domains of multidomain proteins, thus including numerous hydrophobic residues on the surfaces of proteins in the dataset, although these would be in the interior of the native multidomain proteins. Moreover, increasing the hydrophobic interaction strength in effect incorporates a penalty term for hydrophobic–hydrophilic interactions of hydrophobic side chains with water molecules. All other potential parameters were used unmodified.

The convergence was monitored by calculating the mean and the standard deviation of parameter values for consecutive 1000-step intervals. When the mean changed by less than the standard deviation and it fluctuated over three consecutive steps, convergence was achieved. The simulations were further run for another 5000 steps, and from these steps, the mean and standard deviation of the distributions of the parameter values were calculated.

2.5. Simulation Parameters

For the parameter estimation, structures in the protein database were mapped onto the protein model. In the mapping process, in which constraints of the CG model are enforced, a few atomic clashes are introduced. In order to eliminate high-energy configurations due to clashing atoms, the following modifications were made to the PDB library. The C_β–C_γ distances of amino acids with long and flexible side chains (lysine, methionine, glutamine, and arginine) were set to their real C_β–C_γ bond lengths: 1.52 Å for lysine, methionine, and arginine, and 1.53 Å for glutamine. Furthermore, any γ atoms that caused atomic clashes (for instance, due to nonstandard side-chain dihedral angles), 765 atoms in total, were removed from the PDB structures used. Subsequently, PDB structures whose backbone atoms were involved in further atomic clashes after the mapping onto the protein model, 6 proteins in total, were also removed from the library. The list of the proteins used with their SPACI scores, ASTRAL class information, and the α-carbon root-mean-square distance (RMSD) of the mapped and the original structures are included in Table S1 of the Supporting Information. The maximum C_α RMSD between a mapped and an original structure was 0.045 Å, while the mean C_α RMSD between the mapped and the original structures was 0.025 Å.

In the CD learning simulations, we use 4096 MC moves per CD learning iteration, and a temperature of 298 K was used in calculating the Metropolis–Hastings acceptance criterion. The learning rate of the CD learning simulations for each parameter was determined by a trial-and-error method and set to be sufficiently large to speed up the convergence, but small enough to avoid instabilities in the convergence. The effect of the maximum amplitude of the crankshaft rotations during the CD learning was also investigated (see the Results section).

To validate the model parameters against the data, the model distributions of some geometric observables using the optimized parameters were compared to the data distribution of the training set. The model distributions were generated by 10⁶ step MC simulations using the protein models with optimized parameters, starting from the training set, or from an independent PDB set consisting of structures of the ASTRAL 1.75 database with SPACI scores between 0.7 and 0.8.

The inferred vdW potentials were further tested using 16-residue peptides and a 56-residue protein, Protein G (1PGA). First, a 10⁸ step MC simulation was performed on a 16-residue polyalanine peptide, using only the stress, vdW, and hydrogen-bond contributions of the energy function, to determine the accessible areas on the Ramachandran map, and the stable secondary structure forms without using any secondary structure bias. Subsequently, nested sampling (NS)^22,68 simulations of β-hairpin folding were performed on a 16-residue polyalanine and its glycine mutants, introducing a β-hairpin secondary structure bias, to examine the behavior of the unbiased loop. In the mutants, a glycine residue was introduced at amino acid positions 8, 9, or 10, corresponding to the i+1, i+2, and i+3 positions in the turn. Nested sampling is a Bayesian sampling technique,⁶⁸ which has been shown to be superior to parallel tempering with regard to finding the native basin of Protein G using the CRANKITE protein model in our previous work.²² Further NS simulations were performed on the 16-residue polyalanine peptide using α-helix and β-hairpin secondary structure bias, respectively, to determine melting heat capacity curves of the secondary structure. The NS simulations were performed until the partition function converged to T = −100 °C, which implies that the thermodynamically accessible states have been sampled for all temperatures above T, and hence, the heat capacity values have been converged for any temperature above −100 °C. In the NS simulations of the 16-residue peptides, 10 000 active points were used, and 10 000 MC steps were used to generate new points in the NS iterations. In the NS simulations of Protein G, 20 000 MC steps and 20 000 active points were used, and the partition function was converged down to 25 °C.

3. Results

3.1. Effect of the Simulation Parameters on the Inference

In a contrastive divergence iteration, a short MC simulation is performed to estimate the gradient of the energy, with respect to the simulation parameters. The number of MC steps, K, during each CD iteration affects the quality of the gradient estimation, that is, the smaller the K value, the more stochastic the gradient estimate becomes; however, K does not affect the overall maximum likelihood.⁴⁸ A more-stochastic estimate of the gradient slows the convergence of the CD simulations; however, it will not prevent convergence. Following an argument by Hinton,⁴⁸ even for K as small as 1, on average, over the training set, the perturbed data distributions are closer than the data distribution to the equilibrium distribution of the current model parameters (unless the data and model distributions are equal), even if individual MC simulations might result in an opposing gradient at any iteration. Throughout this work, we use K = 4096, which was found to be effective for the parameter inference.

During the MC evolution of each CD iteration, the maximum allowed amplitude of the crankshaft rotations affects the local exploration, thus influencing the converged potential parameter values (Figure 1), and this can cause significant variations in the converged parameter values. Our aim is to infer a protein model that can be used in protein folding simulations; hence, the exploration must be local for the quadratic functions to describe the local basin, but it should also be able to describe the energy surface nonlocally, and not only the energy restrained to the crystal structure. In this work, we approximate many terms of the energy function using quadratic functions. On rugged energy landscapes where this harmonic approximation of the curvature of the landscape is a very crude approximation, larger MC moves facilitate the crossing (effectively tunnelling) of energy barriers that smaller MC moves could not climb over, and this makes the potential energy surface appear to be different, often flatter (e.g., increasing the MC step size from 0.01 to 0.2 in Figures 1a, 1b, 1c, and 1f). Since the parameter estimates do not change by more than 5% for amplitudes of 0.001–0.01 radians for H and k_τ and 0.002–0.02 radians for η_α, in the following, we chose to use a maximum crankshaft rotation of 0.01 radians in the CD estimations of the parameters for all models, and we will be comparing results using this maximum rotation amplitude. For the other parameters, we accept that the harmonic approximation is probably far from perfect.

Figure 1.

Dependence of the converged potential parameter values, as a function of the Monte Carlo (MC) step size, inferred using the ASTRAL PDB structures after removing overlapping atoms (solid lines), thus using a dataset that better represents the Boltzmann distribution. The plots correspond to (a) hydrogen-bond strength (H), (b) α-helix backbone dihedral angle bias potential strength (η_α), (c) β-strand backbone dihedral angle bias potential strength (η_β), (d) β–β contact bias potential strength (κ_β), (e) β–β contact equilibrium distance (r_0,β), and (f) C_α valence angle stress potential strength (k_τ). For the hydrogen-bond strength plot (panel a) only, parameter values inferred using the ASTRAL PDB structures without removing overlapping atoms are also shown (represented by a dotted line). Vertical dashed lines mark a crankshaft MC step size of 0.01. The error bars correspond to one standard deviation of the distribution of the converged parameter value.

We also note that, although the convergence of parameters for the individual maximum amplitude sizes is not prohibited, the speed of convergence also depends on the MC step size. Decreasing the MC step size increases the acceptance rate, although from an MC step size of 0.02, the acceptance rate is over 80% (see Figure S3 in the Supporting Information), and it does not give much advantage in the exploration of the energy surface during the short MC simulations used to estimate the gradient in the CD iterations. On the other hand, when the allowed MC step size is set to be small (for a given number of MC steps), the exploration of the energy surface becomes poorer, and the poorer gradient estimate slows the convergence of the CD simulations.

3.2. Estimation of the Protein Model Parameters

When inferring several potential parameters together, learning correlated potential parameters is crucial for the convergence of the ML estimation. This can be done by considering the functional form of the energy function. When using the LJ-type potential that is designed to have a nonspecific long-range attractive energy contribution, we find problems with the convergence of the CD learning of the parameters. The reason for this is that the attractive interactions of the LJ potential compete with the short-range attractive interactions. For example, the vdW interaction between a N atom and an O atom of a hydrogen bond would compete with the hydrogen-bond interaction between them, both trying to describe an attractive interaction between the two atoms at the same time. Similarly, distances that occur frequently in secondary structure elements (and are therefore enforced by the secondary structure bias interactions), e.g., the C_β–C_β distance of interacting amino acid residues in a β-sheet, would introduce an artificial bias to the LJ potential parameters. To avoid these problems, we only evaluate the hard cutoff part of the LJ potential between atoms of amino acid residues that are connected via a hydrogen bond, or whose neighbors are connected via a hydrogen bond. This way, only nonspecific nonbonded interactions are taken into account in the parameter estimation of the LJ potential, and the correlation of the potential parameters are suppressed for the inference. Other ways to address this problem include fixing a parameter value, or the ratio of the competing parameters together (e.g., merging the hydrogen bond with a hydrophobicity into one function). However, introducing such constraints on the potential parameters could introduce an artificial bias on the parameter values.

The inferred values of the vdW potentials, hydrogen bond, secondary structure bias, and hydrophobicity potential parameters are summarized in Table 2, together with corresponding values taken from the CHARMM and AMBER force fields. While there is no noticeable difference between the hydrogen-bond potential parameters for the two vdW models, the force constant k_τ of the backbone stress interaction is higher for the protein model using the LJ potential than for the one using the hard cutoff potential. This indicates that when using the LJ functional form, as opposed to the hard cutoff functional form, to represent the atoms, a larger conformation space might be available by applying the vdW potential, and a higher backbone stress force constant compensates for this, to obtain the equilibrium distribution of C_α valence angles in the dataset. This is supported by the comparison of vdW interaction functions between various atom types using the model parameters. Also, the β-strand backbone bias potential parameter, η_β, is noticeably higher for the protein model using the hard cutoff vdW potential, which shows that the LJ models favor the extended conformation more than the hard sphere model. On the other hand, the β–β contact potential is slightly stronger in the protein model using the LJ-type vdW potential, with shorter equilibrium distance, r_0,β, for the interacting C_β atoms, and a slightly higher force constant. The α-helices might also be slightly more stable without a bias potential, suggested by the lower α-helix backbone bias force constant, η_α.

Table 2. Inferred Potential Parameters Using Contrastive Divergence, for the Protein Models Using the Hard Cutoff and the Lennard-Jones (LJ)-Type van der Waals (vdW) Potentials^a.

vdW and Backbone Stress Potential Parameters
vdW potential	RminCA	RminCB	RminC	RminN	RminO	RminS	ε(RT)	kτ(RT)
hard cutoff	1.57	1.57	1.42	1.29	1.29	2.00		90
LJlearnt	2.43	1.97	1.82	1.74	1.98	3.10	0.018	98
LJCHARMM	2.275	2.175	2.00	1.85	1.70	2.00	b	103
LJAMBER	1.908	1.908	1.908	1.824	1.6612	2.00	c	114

Hydrogen-Bond Potential Parameters
vdW potential	H (RT)	δ (Å)	cos ΘCOH	cos ψOHN
hard cutoff	4.95	2.01	0.770	0.930
LJlearnt	4.98	2.01	0.772	0.928
LJCHARMM	4.80	2.01	0.772	0.925
LJAMBER	4.91	2.01	0.771	0.921

Secondary Structure Bias Potential Parameters
vdW potential	ηβ (RT)	ηα (RT)	Kβ (RT/Å2)	Rβ (Å)
hard cutoff	4.5	18.0	0.80	5.65
LJlearnt	3.7	15.3	0.85	5.39
LJCHARMM	4.5	18.6	1.00	5.62
LJAMBER	2.6	19.7	1.18	5.15

Hydrophobic Interaction Potential Parameters
vdW potential	kh (RT)
hard cutoff	0.030
LJlearnt	0.022
LJCHARMM	0.051
LJAMBER	0.057

^aThe vdW potential parameters of the hard cutoff model were taken from ref (20), while those of the LJ_CHARMM and LJ_AMBER models were taken from the CHARMM⁵⁵ and AMBER⁵⁴ force fields, respectively.

^bε/RT values from the CHARMM force field (0.0338, 0.0929, 0.186, 0.338, 0.203, and 0.760 for the CA, CB, C, N, O, and S atom types respectively).

^cε/RT values from the AMBER force field (0.185, 0.185, 0.145, 0.287, 0.355, and 0.422 for the CA, CB, C, N, O, and S atom types respectively). The potential parameters are described in section 2.3; wherever a unit of length is not indicated, the unit of length is Å.

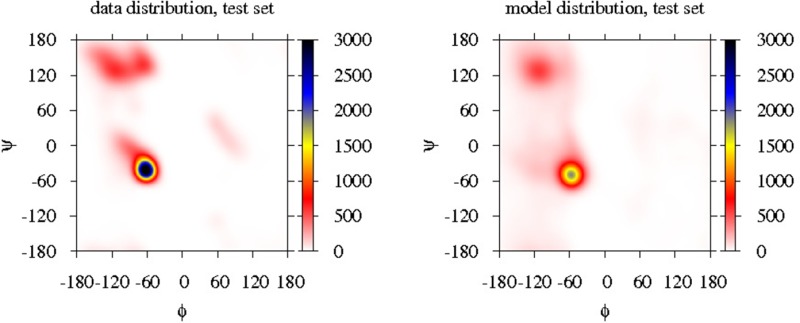
During the ML inference, the KL divergence of the model and data distributions is minimized. However, for an unrealistic energy function, the model distribution might still be far from the data distribution. To validate our protein models for describing the training set of proteins, we calculate various structural observables in the model and data distributions, such as the backbone dihedral angles (see Figures S4 (left) and S5 in the Supporting Information), the α-carbon valence angle (see Figure S7 (left) in the Supporting Information) and the distribution of the distance between β-carbon atoms of interacting amino acid residues in β-sheets (see Figure S7 (left) in the Supporting Information). Although the above distributions are 1-dimensional (1D) or two-dimensional (2D) marginalizations of the joint distributions, they would provide a good indication if the model distribution were different from the data distribution. In our current work, all model distributions of the α carbon valence angle are identical to the data distribution. The model distribution of the β-carbon atoms of interacting amino acid residues in β-sheets in the LJ_AMBER model is shifted to smaller values by 0.3 Å (potentially indicating a slightly too strong bias on β sheets), while all other model distributions are identical to the data distribution. All model distributions of the backbone dihedral angles show the same features as their distribution in the training set with high occurrences in the α-helical, extended, and left-handed helical regions, although the model distributions tend to be more diffuse, spanning a larger area of the Ramachandran map than in the distribution of the training set. These differences reflect the residual KL divergence between the optimized model distribution and the data distribution, arising from the mapping entropy (i.e., that several configurations in the atomistic model translate to the same CG configuration), which is the same for all models, and from the differences in the potential energy functions, which are unable to perfectly describe the native data distribution. For example, the CG protein model employed here allows for slightly more flexibility of the backbone by its side-chain beads filling less space than the full side chains in an atomistic representation, and this manifests in the more diffuse Ramachandran plots of the backbone dihedral angles.

The transferability of the protein models was investigated using a test set of proteins independent of the training set, consisting of all 78 proteins in the ASTRAL database with a SPACI score between 0.7 and 0.8. The data and model distributions of the above-mentioned structural observables were calculated for this test set (see Figures S4 (right), S6, S7 (right), and S8 (right) in the Supporting Information). These model distributions were practically identical to the data distributions of the test set, indicating the transferability of the protein models to proteins not in the training set. This is an improvement over the nontransferable protein model of Winther et al.,⁴² who were limited to a small set of short peptides as their training set by the cumbersome calculation of the ensemble averages in the model distributions at every iteration. Here (and in our previous work^20,21), it is the efficient estimation of the gradient of the logarithm of likelihood by the CD approximation that allows for the employment of a more-realistic training set. We note that other efficient methods also exist to avoid the re-evaluation of ensemble averages (for example, Shell et al. used a reweighting of ensemble averages¹²).

3.3. Accessible Regions of the Ramachandran Plot from MC Simulations of an Ala₁₆ Peptide

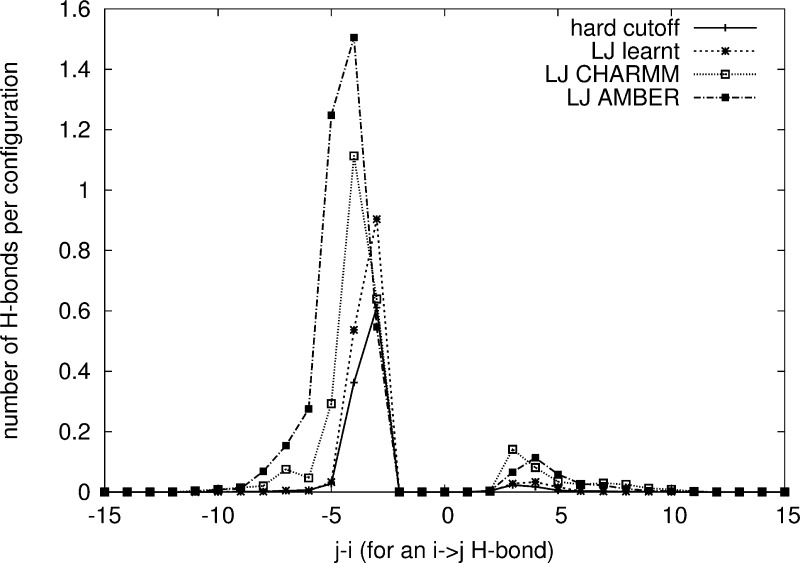
To test the available regions of the Ramachandran plot using the two vdW models described in the Methods section, MC simulations of a 16-residue peptide, Ala₁₆, were carried out at room temperature, using the vdW and hydrogen-bond energy contributions, together with the C_α valence backbone stress, without the secondary structure bias. For all models investigated, the accessible regions of the Ramachandran maps in the MC simulations at room temperature cover the allowed regions calculated from the ASTRAL 1.75 database (see Figure S9 in the Supporting Information). On the individual residue level, for all models, helical backbone dihedral angles occur most frequently, with the extended and left helical conformations also being significant. The distributions for the LJ_learnt and hard cutoff models are more diffuse and more connected between the positive and negative ϕ values, indicating a smaller energy barrier for the conformational changes of the peptide backbone within these regions of the probability map. During the simulations, there is approximately one hydrogen bond per configuration at any time, indicating that random coil is the main conformation. The hydrogen-bond distribution is plotted in Figure 2. For the hard cutoff model and the LJ model with learnt vdW parameters (LJ_learnt), the most commonly observed hydrogen bonds correspond to 3,10- (i→(i–3) hydrogen bonds) and α-helices (i→(i–4) hydrogen bonds). This is consistent with experimental studies of polypeptides with high alanine content.⁶⁹ However, when using the LJ potential with vdW parameters adopted from CHARMM (LJ_CHARMM) or AMBER (LJ_AMBER), π-helices (i→(i–5) hydrogen bonds) are also found to be common, which are not seen experimentally. This problem was also seen in previous molecular dynamics simulations of short peptides⁷⁰ using the CHARMM force field. The difference between the hydrogen-bond distribution using the various LJ potential parameters implies that it is possible to change the relative stability of the different helix types by tuning the LJ potential parameters, and this is confirmed by simulations using the hydrogen-bond and the C_α valence angle stress parameters of the LJ_learnt model with the LJ parameters of the three LJ models investigated (see Figure S10 in the Supporting Information). For all models, left handed helices (i→i+3,4) are also present, in agreement with the allowed regions of the Ramachandran map, indicating that turn formation in unbiased loop regions of proteins is conformationally accessible.

Figure 2.

Hydrogen-bond pattern from MC simulations of an Ala₁₆ peptide, using the protein models employing the hard cutoff vdW potential (solid line), the LJ_learnt model (dashed line), the LJ_CHARMM model (dotted line), and the LJ_AMBER model (dash-dotted line). Potential parameters are listed in Table 2. On the horizontal axis, −4 represents a hydrogen-bond between amino acid residues i→j = i–4, typical of α-helices, while −3 is typical of (3,10)-helices, and −5 of π-helices. The small peak between +3 and +5 corresponds to left-handed helices.

3.4. Studying Steric Effects in Turn Conformations on 16-Residue Peptides with a Hairpin Bias

The protein model employed here is designed to be used with a known (or predicted) secondary structure and β–β residue contact bias. To further test how the hard cutoff and LJ type vdW models perform in unbiased regions of proteins, in particular in turn regions of β-hairpins, nested sampling simulations of 16-residue peptides were performed employing a hairpin bias, where the turn is located at the center of the peptide (residues 8 and 9). The peptides used in this test were an Ala₁₆ peptide, and its mutated forms, where one of the turn residues is replaced by Gly. These will be referred to as A-G-A-A, A-A-G-A and A-A-A-G, corresponding to the glycine being at the i+1, i+2, or i+3 position of the turn, respectively. The secondary structure bias of the energy function keeps the backbone of residues 1–7 and 10–16 extended, as well as restraining the C_β–C_β distances of the interacting amino acid residue pairs of the two strands. The inner two residues of the turn are unbiased, thus allowing the investigation of whether or not the protein models described in the Methods section reproduce observed correlations between the position of glycine in a β-turn and the observed turn conformation.⁷¹ The turn types found in the NS simulations are listed in Table 3, with their relative probabilities at 298 K, where we used the turn definitions of Venkatachalam⁷² (see Figure S11 in the Supporting Information). The relative probability of a turn type at 298 K is calculated by summing the posterior weights of all NS configurations that fall into the definition of the turn type, and then normalizing it by the sum of the posterior weights of all turn types. [The posterior weights of NS configurations are proportional to the available phase space volume at a given temperature; hence, they provide the probability of finding the system in that configuration.] Turn type IV, that is, when no particular turn type can be assigned to the dihedral angles of residues 8 and 9, is omitted from this analysis.

Table 3. Relative Probabilities of the Turn Types Identified from Nested Sampling Simulations of 16-Residue Peptides Applying a β-Hairpin Bias, at 298 K^a.

turn residues	vdW model	turn II′	turn I′	turn I	turn II
AAAA	hard cutoff	0.968	0.000	0.000	0.032
AAAA	LJlearnt	0.983	0.000	0.003	0.014
AAAA	LJCHARMM	0.965	0.000	0.028	0.000
AAAA	LJAMBER	0.997	0.000	0.002	0.001
AGAA	hard cutoff	0.980	0.000	0.001	0.020
AGAA	LJlearnt	0.993	0.000	0.001	0.006
AGAA	LJCHARMM	0.997	0.000	0.003	0.000
AGAA	LJAMBER	1.000	0.000	0.000	0.000
AAGA	hard cutoff	0.864	0.022	0.001	0.113
AAGA	LJlearnt	0.873	0.023	0.001	0.102
AAGA	LJCHARMM	0.619	0.091	0.029	0.182
AAGA	LJAMBER	0.588	0.383	0.001	0.025
AAAG	hard cutoff	0.944	0.000	0.009	0.046
AAAG	LJlearnt	0.980	0.000	0.007	0.012
AAAG	LJCHARMM	0.931	0.000	0.066	0.000
AAAG	LJAMBER	0.969	0.000	0.030	0.000

^aTurn type IV was excluded from the analysis. Substituting the i+1, i+2, or i+3 residue of the turn by glycine (AGAA, AAGA, and AAAG, respectively) increases the relative probability of the type II′, the types I′ and II, and the type I turn, respectively.

All models investigated show the same trend of the turn types adopted in the corresponding simulations, although significant differences between the models used can be observed for simulations of peptides with the i+2 residue of the turn substituted with a glycine (A-A-G-A). In all the simulations of the peptides, the type II′ turn is the dominant turn type. When substituting the i+1 residue of the turn of the polyalanine peptide with a glycine (A-G-A-A), the posterior weight of type II′ turn increases further, and becomes almost the exclusive turn type. This is consistent with the findings of Sibanda et al.⁷¹ that, among the protein structures investigated, type II′ turns mostly occurred with X-G-[ST]-X turn residues (with X being an unspecified amino acid). Substituting the i+3 residue of the turn with a glycine (A-A-A-G) increases the probability of adopting a type I turn (by more than a factor of 2). This is consistent with type I turns typically having glycine residues at the i+3 position of the turn (X-X-X-G).⁷¹ When substituting the i + 2 residue of the turn with a glycine (A-A-G-A), the type I′ and type II turns become much more significant compared to simulations of other glycine-substituted peptides. The increase in the probability of type I′ turns is consistent with type I′ turns most often consisting of X-[NDG]-G-X residues.⁷¹ Simulations using the LJ_AMBER model appear to demonstrate this best. However, this discrepancy might also be attributable to the LJ_AMBER model being best at artificially compensating for the lack of explicit side-chain–main-chain hydrogen bonds in our model. If this were the case, including side-chain-main-chain interactions in our model would further increase the probability of the type I′ turn for an A-[ND]-G-A peptide for the other models investigated, and the apparent advantage of the LJ_AMBER model would be lost; however, this is beyond the scope of the present paper.

When comparing the fully learnt (LJ_learnt) model with the hard cutoff model, the two models perform very similarly, and consistently with findings in the literature. We find no apparent superiority of the more-elaborate LJ function of the vdW potential in this test. However, note that this does not imply that, generally, vdW interactions would be unimportant in modeling small peptides; for example, they have been found to have a stabilizing effect in quantum mechanical studies of short polyalanine helices.⁷³ In our CG model, secondary structure bias contributions are optimized to stabilize the secondary structure, and, for this particular model, no superiority of any one of the investigated vdW models is indicated.

3.5. Heat Capacity Curves of an Ala₁₆ Peptide with Varying Secondary Structure Bias

Since purely structural properties of polyalanine peptides are not sufficient to rank the protein models, we also investigated the energetics of the models. However, analyzing the energetics of solely the vdW contributions would be misleading, since all other model parameters might depend on the values of the vdW parameters. Instead, we investigated relative stabilities and heat-capacity curves from polyalanine simulations. One of the major advantages of nested sampling is that, by post-processing the results of the simulation, thermodynamic properties such as heat capacity curves may be calculated for any temperature. Here, we calculate heat capacity curves for a 16-residue polyalanine peptide under the assumption of either an α-helix or β-hairpin secondary structure by using an α-helical or β-hairpin secondary structure bias.

The critical temperatures of the heat-capacity curves (T_c) (i.e., the peak position) and the heat capacities C_v,c at these temperatures are listed in Table 4, with the heat capacity curves given in Figure S12 in the Supporting Information. Also shown in Table 4 are some indicative experimental values taken from calorimetric measurements of a variety of peptides 20–30 amino acid residues in length,⁷⁴ although the secondary structures of these peptides were not reported. Specific β-hairpin peptides (see, e.g., ref (75)) involve a significant amount of stabilizing side-chain interactions which are not modeled by the polyalanine peptides, so they were omitted from this comparison. The heat capacities for all four models correlate better with the experimental values under the assumption of a α-helix rather than a β-hairpin. This is consistent with experimental NMR studies of polyalanine peptides, which find a helical form at room temperature,⁶⁹ and strongly suggests that the α-helix form is indeed the more stable.

Table 4. Critical Temperatures (T_c) of Heat-Capacity Curves and the Heat-Capacity Value at T_c (C_v,c) in Units of R for the Ala₁₆ Nested Simulations with α-Helix and β-Hairpin Secondary Structure Bias, Using the Hard Cutoff (Hard) and Lennard-Jones Type vdW Models^a.

Critical Temperature Data (°C)
	Tchard	TcLJlearnt	TcLJCHARMM	TcLJAMBER	Tcexp
α-helix	130	70	0	150	0–30
β-hairpin	10	40	20	30

Heat-Capacity Data (R)
	Cv,chard	Cv,cLJlearnt	Cv,cLJCHARMM	Cv,cLJAMBER	Cv,cexp
α-helix	170	130	90	80	100–200
β-hairpin	67	63	43	47

^aApproximate experimental values (exp) are taken from ref (74).

Of the four models, the LJ_CHARMM model initially appears to give the best prediction for the critical temperature. However, this is the only simulation that predicts the β-hairpin to be more stable than the α-helix (i.e., to have a higher T_c values). In contrast, the very high critical temperatures predicted for the hard cutoff potential and LJ_AMBER model show that these models cause the α-helix secondary structure to be overly stable, which is consistent with the critical temperature (∼400 K, or 127 °C) found by Peng et al.,⁷⁶ using the AMBER force field for a 15-residue polyalanine peptide. The critical temperatures calculated using the LJ_learnt model correlate best with the experimentally observed range while still predicting the correct relative secondary structure stability. Comparing the hard cutoff model and the LJ_learnt model (for which all parameters including the LJ parameters were inferred), the heat capacity results and the relative stabilities suggest that the LJ potential may be more suitable than the hard cutoff vdW potential for calculating the thermodynamic properties of peptides. We also note that there is sufficient flexibility in the LJ parameters to change the relative stabilities of helical and strand conformations. The LJ parameter values of the LJ_CHARMM model overstabilizes the β-hairpin form, while the LJ_AMBER model overstabilizes the α-helical form, when used with the CRANKITE force field.

3.6. Folding Simulations of Protein G

In the previous sections, simulations of small peptides with fixed secondary structure were described, where the form of the vdW interactions was found to have no significance using our CG force field including a secondary structure bias. The effects of the long-range vdW interaction contributions of our force field on side-chain packing between interacting secondary structure units (α-helices and β-sheets) can be investigated by protein folding simulations, because this tertiary level of structure formation is not modeled by other interaction parameters in our force field. We present folding simulations of protein G, including secondary structure bias and hydrophobic interaction contributions in the models used. Protein G is a 56-residue protein consisting of an antiparallel four-stranded β-sheet and an α-helix, with a β-Grasp (ubiquitin-like) fold (see Figure S13 (right) in the Supporting Information). Conformations found in simulations using the different vdW models were assessed visually (which side of the β-sheet the helix was on, whether the hydrophobic residues are in the interior of the protein or exposed), as well as quantitatively, by calculating the C_α root-mean-square distance (RMSD) from the crystal structure present in the PDB database, and the angle of the helix orientation with respect to the axis of the β-sheet. The helix orientation angle is calculated as the directional angle between the axis of the N-terminal β-strand (the vector pointing from the C_α atom of residue 7 to the C_α atom of residue 3) and the axis of the α-helix (the vector pointing from the center of mass of the C_α atoms of residues 24–27 to the center of mass of the C_α atoms of residues 31–34), around the surface normal of the β-sheet (the cross product of the vector pointing from the C_α atom of residue 7 to the C_α atom of residue 3, and the vector pointing from the C_α atom of residue 7 to the C_α atom of residue 54).

For all vdW models investigated here, the main conformation at room temperature is topologically correct. The helix was on the correct side of the β-sheet at room temperature in all simulations, as opposed to earlier simulations using the CRANKITE protein model without including the γ atoms (and without hydrophobic interactions), which allowed the helix to be equally on either side of the sheet.²¹ Since there is no information coded in the secondary structure bias about which side of the sheet the helix may pack against, this indicates that having the γ atoms and the hydrophobic interactions in the model makes a clear distinction between the two basins. Previous simulations including γ atoms but no hydrophobic interactions (data not shown) showed a preference for the helix to be on the correct side of the sheet, probably due to the steric clashes of large residues in the loops that prohibit the folding of the helix onto the wrong side of the sheet at room temperature. The inclusion of hydrophobic interactions enables a qualitative shaping of the energy landscape, representing a driving force for the correct collapse of the protein in the folding simulations, in agreement with previous studies arguing for the importance of the hydrophobic interactions in protein folding.⁷⁷

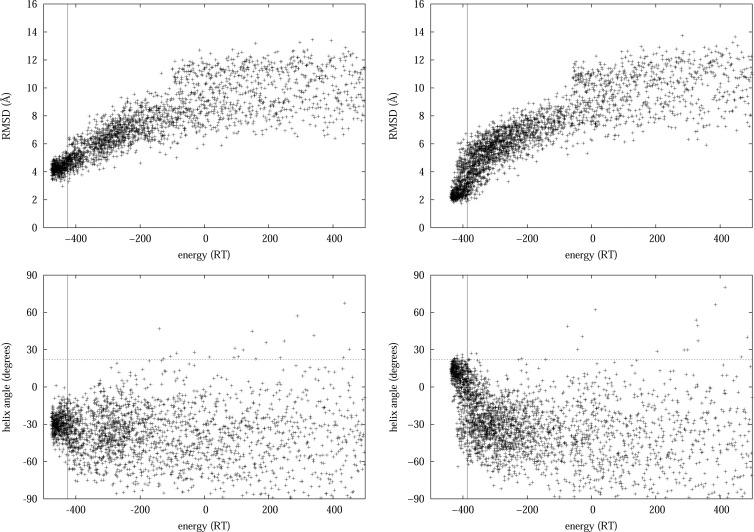
When comparing the RMSD of the conformations in the main basin from the native conformation in the PDB database, the LJ_learnt model outperforms the hard cutoff potential. Conformations in the main basin of the energy landscape, explored by NS simulations using the LJ_learnt model, have an RMSD from the native conformation as small as 2 Å, while the model employing the hard cutoff potential cannot find conformers that have an RMSD distance of less than 3 Å (see Figure 3, top). The reason for this is that the packing of the helix with respect to the β sheet can be better described by the LJ model. Indeed, the orientation of the α-helix, with respect to the β-sheet, is closer to the native orientation when using the LJ_learnt model (see Figure 3 (bottom), as well as Figure S13 in the Supporting Information). The native helix orientation angle, with respect to the sheet, only appears using the LJ potential, and a wide range of orientation angles are accessible at room temperature, showing that a twisting motion of the helix is allowed. This is consistent with rigidity analysis of Protein G,²² where the lowest-frequency nontrivial mode of the normal-mode analysis of Protein G was found to correspond to a rotation of the helix about an axis perpendicular to the β-sheet, allowing a deviation of more than 30° in the helix orientation angle from the crystal structure while maintaining the network of hydrophobic bonds present in the crystal structure.

Figure 3.

The backbone RMSD from the native state (top), and the angle of the helix with respect to the axis of the β-strands (bottom), as a function of the potential energy for the conformations in the main basin of the energy landscape, explored by nested sampling simulations using the protein model with (left) hard cutoff vdW potential and (right) Lennard-Jones type vdW potential with inferred vdW parameters. The estimated energy at room temperature is marked by solid vertical lines. Conformations obtained by using the LJ potential show a wide range of allowed helix orientation angle at room temperature, including the native angle in the crystal structure, 21.8° (dashed horizontal line), while simulations using the hard cutoff potential fail to find the native helix orientation.

The reasons why the LJ potential form could be better than the hard cutoff at modeling the packing of Protein G could be 2-fold. First, as discussed in section 3.2, the LJ potential is softer than the hard cutoff potential, allowing for more flexibility of the loop regions at the two ends of the helix; and second, the weak long-range attractive interactions might favor the packing of the helix in the native orientation, which would appear as a zero-energy contribution using a hard cutoff. However, we have found that the hard cutoff and the LJ potentials behaved similarly in modeling small loop regions of peptides with simple tertiary structure, suggesting that it is more likely that the long-range attractive interactions make the Lennard-Jones potential a more-realistic model for proteins. Our results confirm previous observations about the importance of the long-range attractive interactions of the vdW interactions in the modeling of the packing of protein interior⁷⁸ and small clusters.⁷⁹ We find that, in the CRANKITE model, while the hydrophobic interactions are responsible for stabilizing the correct tertiary assembly of the secondary structure elements enabling the qualitatively correct collapse of the protein during the folding process, the vdW interactions are important for the fine-tuning of the energy landscape within its main basin. This agrees with previous experimental and simulation results (see citations given in ref (80)), which found that both the hydrophobic interactions and the packing are important in protein folding.

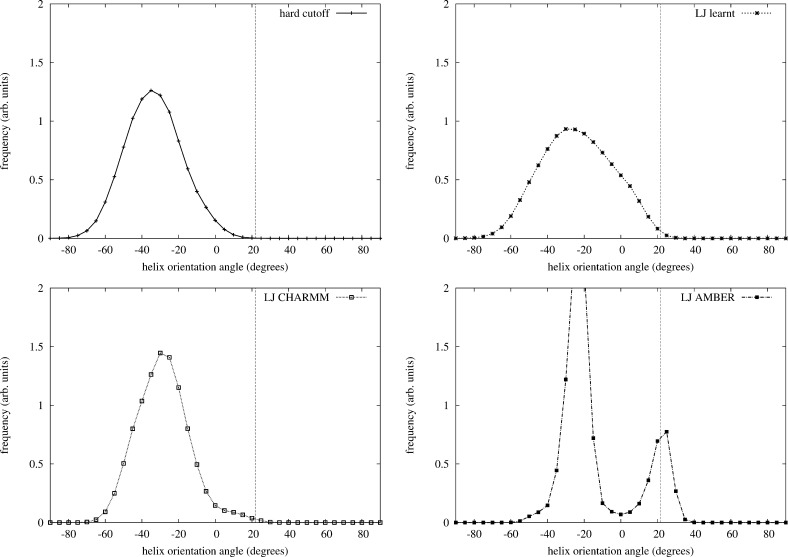
When comparing simulations using the LJ potential with learnt or adopted vdW parameters, we find that, although low RMSD structures with the native orientation are observed in all LJ simulations (see Figure S14 in the Supporting Information), the distributions of the helix orientation angle exhibit significant differences: while the helix distribution angle follows a broad unimodal distribution for the LJ_learnt model, it follows a bimodal distribution using the LJ_CHARMM and LJ_AMBER models, implying a two-state model with a high energy barrier. This is shown by the distribution (Figure 4), the trace plots (Figure S15 in the Supporting Information), and the autocorrelation functions (Figure S16 in the Supporting Information) of the helix orientation angle, calculated in room temperature MC simulations of 10¹⁰ steps, starting from the crystal structure. The energy barrier of twisting the helix is so high using the LJ_AMBER model that the helix orientation angle only switched once between the two main basins. The trace plots and the long autocorrelation time of the helix orientation angle of the LJ_CHARMM model suggest the presence of an energy barrier for this model. The rigidity analysis of Protein G²² suggests a broad unimodal distribution without the implication of an energy barrier, supporting the distribution generated by the LJ_learnt model. We note that the helix angle distribution is far from perfect, being shifted toward negative values, which indicates that there are other effects not considered in the model that play a role in the helix packing, for example, electrostatic interactions.

Figure 4.

Distribution of the helix angle at room temperature from a MC simulation for the different models: (top left) hard cutoff model, (top right) LJ_learnt , (bottom left) LJ_CHARMM, and (bottom right) LJ_AMBER. Simulation length: 10¹⁰ MC steps, starting from the crystal structure. Vertical dashed lines show the helix orientation angle in the crystal structure.

4. Discussion

When inferring a generalizable protein force field using a training set of proteins with varying sequences (see section 2.1), our ML approach with the CD approximation relies on the following assumptions. First, the protein conformations of the various sequences S₀ⁱ come from their respective Boltzmann distributions corresponding to the same inverse temperature, and second, the training set of protein conformations represents independent and representative samples from a set of proteins that is intended to be modeled by the protein force field.

The training set of protein conformations may be experimentally observed,^20,21,42 or computer-generated.^12,28 When conformations are generated from computer simulations at a given temperature, although the assumption of Boltzmann distribution of each sequence holds a priori, the fitted CG model will have the limitations of the all-atom model at best. The same holds for fitting to NMR structures optimized by all-atom force fields. Hence, we used only crystal structures in the training set of our protein model. The assumption that the individual conformations in the training set, all of which are crystal structures, are representative of the native structure in thermodynamic equilibrium in solution, is based on previous studies.^81,82 When the atomic coordinates of proteins are mapped onto the CG model, high energy states, nonrepresentative of the Boltzmann distribution were eliminated by removing the clashing gamma atoms. This causes the converged parameter values (hydrogen bond strength, bias potential strength) to be consistently up to 5% lower than when the ensemble including high energy conformations is used (Figure 1a). A possible explanation of this is that stronger attractive interactions (hydrogen bonds and side-chain–side-chain interaction) are necessary to compensate the high energy atomic clashes, in order to be able to preserve the structure of the proteins in an MC simulation. This demonstrates the importance of the data set of known proteins being drawn from an ensemble representing thermodynamic equilibrium at room temperature. One might argue that it could be better to keep all atoms, and relax the structure by minimization or perturbation of the structures. However, at this stage, we do not know the parameters of the energy function, and the energy function used would bias the equilibrium state, and the inferred potential parameter values. We also note that, in PDB structures, there are missing atoms, and none of the potential parameters of our CG model are dependent on whether all atoms in a residue are present. In the parameter inference, the dataset with the clashing atoms removed was used.

According to the Boltzmann hypothesis, the statistics of structural features such as hydrogen-bond distances in the native state of proteins comply with the Boltzmann distribution.⁸³⁻⁸⁵ It has been argued that the Boltzmann hypothesis represents an evolutionary equilibrium where these structural features are maintained around a narrow set of values,⁸³ for example it has been proposed that protein sequences have evolved maintaining an optimal mean hydrophobicity profile.⁸⁴ According to the maximum entropy principle, these may be considered as evolutionary constraints on the evolution of protein sequences (see the Discussion section in the work of Podtelezhnikov et al.²⁷). This argument suggests the existence of a generalizable protein force field that captures these evolutionary constraints, which we infer using a training set of protein conformations that is representative of the proteins to be modeled (that is, proteins with a globular structure). In another study, to recover a very simple underlying CG force field, a training set of 5 proteins have been found to be sufficient,²⁸ where the training set is called an extended canonical ensemble, referring to the collection of equilibrium systems that are governed by the same underlying general force field.

To test that our training set is representative of this distribution, we considered parameter estimation using different subsets of the ASTRAL library, marked by a minimum SPACI score, representing the quality of the crystallographic structures. The higher the SPACI score the better the crystallographic structures are, although the variability of folds may be lower, due to the smaller number of structures. The parameter estimation using the different subsets reveals a trend for the hydrogen bond strength (a 10% increase for SPACI score 0.8 as opposed to 0.4), corresponding to more perfectly formed hydrogen bonds in the dataset, but no dependence of the bias potential parameters on the quality of protein structures. The weak dependence of the protein model parameters on the quality of the crystal structures indicate that the ASTRAL data set is sufficiently diverse to estimate parameters of a generalizable protein model, and as such, in the parameter inference, we used the subset of the database with a minimum SPACI score of 0.8, comprising 73 proteins of varying length from 43 to 690. In comparison, Winther and Krogh⁴² used a dataset of 24, 11–14-residue-long peptides as the training set of their ML inference. Although the training set was successfully folded with their optimized potential, the inferred protein model was not found to be transferable to peptides not included in the training set. One of the reasons for this was that the training set was not representative of the native distribution of protein sequences.

The CD approximation allows a significant acceleration of the ML inference. Assuming 10⁶ MC steps for the convergence of the ensemble average, which might be a reasonable estimate for the peptide size used by Winter and Krogh,⁴² the acceleration of the ML inference coming from the use of the CD approximation is over 200-fold for the same dataset of peptide conformations. Moreover, larger proteins included in the dataset will have longer equilibration and decorrelation times (for example, in the MC simulations of Protein G using the LJ_AMBER model, even 10¹⁰ MC steps are not sufficient to calculate the equilibrated distributions), further increasing the acceleration of the current algorithm over a naïve ML algorithm.

5. Conclusion

In this work, the potential parameters of a generalizable coarse-grained (CG) force field for modeling proteins were inferred, or learnt, from a data set of known protein structures, using a maximum likelihood (ML) approach. We show how our method of inferring a generalizable protein model relates to inferring protein models specific to an amino acid sequence. This ML inference of a specific force field relies on the assumption that the training set contains independent observations of conformations of not only one, but a set of proteins, which are independent and representative of the proteins to be modeled by the force field. While the training set used here is a subset of crystal structures from the Protein Database (PDB) database (the only available experimental data on protein structures), it could also be generated by computer simulations.^12,28

To avoid the necessity of equilibrating each protein of the training set in the model distribution at each iteration of the ML optimization, we employ contrastive divergence for a computationally efficient approximation of the gradient of the energy with respect to the potential parameters, reducing the computational requirements by several orders of magnitude. The contrastive divergence approximation relies on the assumption that the conformations of any protein in the training set represent samples from a thermal equilibrium. We show that if this assumption does not hold (due to including several high energy conformations), a systematic error in the parameter estimation is introduced. The algorithm is very simple, increasing the number of the parameters of the ML inference by only two; the number and the maximum amplitude of Monte Carlo (MC) steps to generate the perturbed data distribution. While the number of MC steps only affects the noise on the gradient estimate, we find that, because of the ruggedness of the energy landscape, selection of the maximum allowed MC step size affects the local exploration of the energy landscape. Preliminary tests show that the ML optimization can be further accelerated by employing an adaptive learning rate with an associated momentum, as suggested by Hinton.⁵¹

We infer parameters for protein models employing two different van der Waals (vdW) interaction potentials: a hard cutoff potential and a Lennard-Jones (LJ) potential using inferred parameters (LJ_learnt) and parameters adopted from the CHARMM and AMBER force fields (LJ_CHARMM and LJ_AMBER, respectively). We find that the LJ_learnt model better models heat capacities of small peptides, as well as the helix orientation distribution of Protein G at room temperature, when used within the CRANKITE force field, which is an improvement over the original version of the force field employing the hard cutoff potential form. In the improved force field, the hydrophobic interactions determine the main basin of the energy landscape into which the protein collapses during the folding simulations, while the vdW interactions serve to fine-tune the potential energy landscape within the main basin. The simulation results suggest that the CRANKITE force field can be further improved by incorporating electrostatic interactions or side-chain–main-chain hydrogen-bond interactions. Our simulations demonstrate that model parameters generally are not transferable between different models. When comparing the all-atom CHARMM or AMBER force fields using our CG force field, both the atomistic resolution and the energy function differ significantly. Adopting vdW parameters without further optimization was found to cause a significant change in the secondary structure bias potential parameters (not present in the CHARMM or AMBER force fields), and the relative stability of the secondary structure elements was also found to be altered. However, the maximum likelihood inference using the contrastive divergence approximation employed here provides an efficient general inference scheme to achieve a model distribution closest to the data distribution in the training set, as long as the assumptions of the model discussed above hold.

Supporting Information Available

The Supporting Information contains details of the function form of the hydrogen-bond interaction, the convergence plot of the hydrogen-bond strength parameter and the distribution of the ∇_θ log L estimate, the LJ potential form (as implemented in this work), the acceptance rate (as a function of the MC step size), distribution plots of backbone dihedral angles, α carbon valence angles and β carbon distances in β-sheet interactions for both the training set of proteins and the independent test set of proteins, the distribution plots of backbone dihedral angles and H-bond interactions for the Ala₁₆ peptides, the turn type definitions, heat capacity curves of Ala₁₆ peptides, the conformational ensembles at room temperature from NS simulations of Protein G for the hard cutoff and LJ_learnt potential, trace plots and autocorrelation functions of MC simulations of Protein G, and a list of the training set of proteins. This material is available free of charge via the Internet at http://pubs.acs.org/.

The authors declare no competing financial interest.