Hip and knee joint loading during vertical jumping and push jerking

Abstract

Background

The internal joint contact forces experienced at the lower limb have been frequently studied in activities of daily living and rehabilitation activities. In contrast, the forces experienced during more dynamic activities are not well understood, and those studies that do exist suggest very high degrees of joint loading.

Methods

In this study a biomechanical model of the right lower limb was used to calculate the internal joint forces experienced by the lower limb during vertical jumping, landing and push jerking (an explosive exercise derived from the sport of Olympic weightlifting), with a particular emphasis on the forces experienced by the knee.

Findings

The knee experienced mean peak loadings of 2.4-4.6 × body weight at the patellofemoral joint, 6.9-9.0 × body weight at the tibiofemoral joint, 0.3-1.4 × body weight anterior tibial shear and 1.0-3.1 × body weight posterior tibial shear. The hip experienced a mean peak loading of 5.5-8.4 × body weight and the ankle 8.9-10.0 × body weight.

Interpretation

The magnitudes of the total (resultant) joint contact forces at the patellofemoral joint, tibiofemoral joint and hip are greater than those reported in activities of daily living and less dynamic rehabilitation exercises. The information in this study is of importance for medical professionals, coaches and biomedical researchers in improving the understanding of acute and chronic injuries, understanding the performance of prosthetic implants and materials, evaluating the appropriateness of jumping and weightlifting for patient populations and informing the training programmes of healthy populations.

Introduction

The quantification of the forces experienced by the hip and knee during movement has been of great interest to the biomedical research community and there have been a large number of studies that have sought to quantify this loading through both musculoskeletal modelling techniques and direct measurement. The majority of these studies have focussed on activities of daily living (ADLs; movements like “sit to stand”, “stand to sit”, gait, stair ascent/descent), or rehabilitation exercises characterized by relatively slow execution speeds (exercises like the squat or lunge). The breadth of this literature, allows a typical, albeit quite wide, range for the loading during these types of activities to be suggested. For instance, at least 15 different groups have calculated internal knee forces during squatting using musculoskeletal modelling techniques (Collins, 1994; Dahlkvist et al., 1982; Escamilla et al., 1998; Nagura et al., 2006; Nisell, 1985; Reilly and Martens, 1972; Salem and Powers, 2001; Sharma et al., 2008; Shelburne and Pandy, 1998; Shelburne and Pandy, 2002; Smith et al., 2008; Thambyah, 2008; Toutoungi et al., 2000; Wallace et al., 2002; Wilk et al., 1996) and the internal forces suggested during body weight squatting include a patellofemoral joint force (PFJF) range of 2.5-7.6 × BW and a tibiofemoral joint force (TFJF) range of 2.5-7.3 × BW.

In contrast, there are fewer musculoskeletal modelling studies that have sought to understand the loading of the hip and knee joints during more dynamic movements with faster execution speeds. Those studies that do exist are often based on simple biomechanical models with inherently limiting assumptions and which thus may not accurately capture the nature of the joint loading (Nisell and Mizrahi, 1988; Simpson and Kanter, 1997; Simpson and Pettit, 1997; Smith, 1975). In particular, there is a tendency for these studies to report joint loadings that seem very high in comparison to those found in ADLs, even when accounting for a premium attributable to the more demanding nature of these activities. For example, Simpson and colleagues (Simpson et al., 1996; Simpson and Kanter, 1997; Simpson and Pettit, 1997) found that during a landing from a travelling jump (a horizontal jump to a single leg landing) the PFJF was 10.4 × BW and the TFJF 16.8 × BW. Similarly, in a pioneering study, Smith (1975) suggested that the TFJF experienced during a jump landing was in the range of 17.0-24.4 × BW. These high values may be a result of the lack of detail in the biomechanical models employed (Cleather and Bull, 2010b; Cleather and Bull, 2012b) or even inaccurate model assumptions. In recent years, the prevalence of sporting injuries to the anterior cruciate ligament (ACL) of the knee (Majewski et al., 2006) has prompted an interest in quantifying the loading of this structure during movement, also by employing musculoskeletal modelling techniques (Kernozek and Ragan, 2008; Pflum et al., 2004). A common approach is to calculate the anterior shear force (that is the force that tends to displace the tibia anteriorly on femur) and to use this as a proxy for the ACL loading (as the ACL is the primary restraint to anterior drawer of the knee). However, these studies also tend to be based upon inappropriately simple biomechanical models (Sell et al., 2007; Yu et al., 2006), and thus even a clear idea as to the shear forces experienced by the knee is largely unknown.

The development of instrumented prostheses has permitted the in vivo measurement of forces in the hip and knee, and provided new insights. For instance, D’Lima and colleagues have shown that during ADLs the magnitude of the TFJF is in the range of 2.0-3.0 × BW, but that during sporting activities (including jogging, tennis and golf) this rises to 3.0-4.5 × BW (D’Lima et al., 2005b; D’Lima et al., 2005a; D’Lima et al., 2006; D’Lima et al., 2007; D’Lima et al., 2008). These values also seem to suggest that the higher internal forces predicted during more dynamic activities by earlier biomechanical models could be questionable. The highly invasive nature of this research restricts these studies to patient populations (of often advanced ages) however, and it does seem likely that young, healthy populations might experience a greater loading.

It is clear that the magnitude of the forces experienced by the hip and knee joints during dynamic activities characterized by rapid movement speeds is not well understood. In particular, a typical upper range for the loading of the hip and knee joints in sporting movements in young healthy populations is generally unknown. The purpose of this study was therefore to use a previously developed model of the musculoskeletal model of the lower limb (Cleather et al., 2011a; Cleather et al., 2011b; Cleather and Bull, 2010b) to quantify the nature and magnitude of the forces experienced at the joints of the lower extremity by a young athletic male population during vertical jumping and push jerking (two lower extremity activities characterized by high movement speeds and force loading and that are similar in kinematic character) with a particular focus on the forces experienced by the knee.

Methods

In this study a previously described biomechanical model (Cleather, 2010; Cleather et al., 2011a; Cleather et al., 2011b; Cleather and Bull, 2010a; Cleather and Bull, 2010b) of the right lower limb was employed to calculate the internal joint forces produced during vertical jumping and push jerking. The validation and verification of the model has been described in previous work (Cleather, 2010; Cleather et al., 2011a; Cleather et al., 2011b; Cleather and Bull, 2010b) as has the sensitivity of the model to some key parameters (Cleather, 2010; Cleather and Bull, 2010a; Cleather and Bull, 2010b; Cleather and Bull, 2011). The study was approved by the local research ethics committee and all participants provided informed consent. Twelve athletic males (mean age 27.1 SD 4.3 years; mean mass 83.7 SD 9.9 kg) were recruited to take part in this study. After performing a standardized warm up consisting of lower extremity body weight exercises (such as squats, lunges and vertical jumps) each subject performed 5 maximal countermovement jumps with their hands on their hips and the highest jump (mean height 0.38 SD 0.05 m) was chosen for analysis. Nine of the subjects (mean age 27.3 SD 4.1 years; mean mass 84.1 SD 10.7 kg) who where familiar with the push jerk exercise (more than six months experience in Olympic weightlifting) also performed 3 repetitions of a push jerk with 40 kg – a movement derived from the competitive sport of Olympic weightlifting where a barbell is thrust overhead primarily by forces produced by extension of the lower limb joints. The data set comprised the position of reflective markers placed on key anatomical landmarks (Van Sint Jan, 2005; Van Sint Jan and Croce, 2005) determined using the Vicon motion capture system (Vicon MX System, Vicon Motion Systems Ltd, Oxford, UK) and the ground reaction force recorded by a portable force plate (Kistler Type 9286AA, Kistler Instrumente AG, Winterthur, Switzerland). The marker set employed in this study is described in detail elsewhere (Cleather, 2010), and comprises markers on the pelvis (4 markers on the anterior and posterior supra-iliac spines), thigh (5 markers – including markers on the medial and lateral epicondyles), calf (5 markers – including markers on the medial and lateral epicdonyles) and foot (4 markers – including markers on the rear of calcaneus and the head of the second metatarsal). As the musculoskeletal model is of the right limb alone, each subject performed each trial with only their right foot on the force plate, thus the ground reaction force was that impressed by the right limb alone. All data was collected at 200 Hz. The raw data was filtered using generalized cross validatory spline filtering (Woltring, 1986; otherwise known as a Woltring filter) using a 5^th order spline and a cut-off frequency of 10 Hz. Following the recommendation of Bisseling and Hof (2006), the force data was filtered using the same cut-off frequency as the kinematic data.

The musculoskeletal model consists of a linked series of four segments representing the foot, calf, thigh and pelvis articulated by ball and socket joints at the ankle, knee and hip. After filtering these segments were constructed from the positions of the markers using the method of Horn (1987) to establish the position and orientation of each segment. The anthropometry used in the model was taken from the work of de Leva (1996).

The data of Klein Horsman and colleagues (2007) was used to create a subject-specific musculoskeletal geometry of the lower limb. This consisted of 163 different line elements representing 38 different muscles of the lower limb. The position of the patella relative to the femur was calculated using the Klein Horsman data to determine the position of the patellar origin relative to the femur as a function of the knee flexion angle. The orientation of the patella relative to the femur (i.e. its sagittal plane rotation) for a given knee flexion angle was calculated using the data of Nha and colleagues (2008) using spline interpolation (using “Numerical Recipes in C++”; Press et al., 2002). The patellofemoral joint model also included the addition of via points to model the wrapping of the quadriceps around the femoral condyles in deep knee flexion. This was achieved by simply defining a via point for each quadriceps muscle element through which the element was constrained to pass once the quadriceps had begun to wrap around the femoral condyles. Finally, the changing ratio between quadriceps and patellar tendon forces (Mason et al., 2008) with increased knee flexion angle was calculated based upon the geometrical relationship between patella, patellar tendon and quadriceps tendons assuming the maintenance of force and moment equilibrium at the patella.

Muscle forces were determined using an optimization based approach to inverse dynamics (Cleather, 2010; Cleather et al., 2011a; Cleather et al., 2011b). The inverse dynamics method of Dumas and colleagues (2004) was used to formulate the equations of motion of each segment as a function of the unknown muscle forces:

$$\left[\begin{array}{c}\hfill {\widehat{S}}_i\hfill \\ \hfill \sum _{j=1}^K{F}_j\cdot {\widehat{r}}_{ji}\times {\widehat{n}}_{ji}-\sum _{j=1}^K{F}_j\cdot {\widehat{r}}_{j(i-1)}\times {\widehat{n}}_{j(i-1)}+\sum _{j=1}^K{b}_{ji}{F}_j\cdot {\widehat{d}}_i\times {\widehat{n}}_{j(i-1)}\hfill \end{array}\right]=\left[\begin{array}{cc}\hfill m_i{E}_{3\times 3}\hfill & \hfill 0_{3\times 3}\hfill \\ \hfill m_i{\tilde{c}}_i\hfill & \hfill I_i\hfill \end{array}\right]\left[\begin{array}{c}\hfill {\widehat{a}}_i-\widehat{g}\hfill \\ \hfill {\ddot{\widehat{\theta }}}_i\hfill \end{array}\right]+\left[\begin{array}{c}\hfill 0_{3\times 1}\hfill \\ \hfill {\dot{\widehat{\theta }}}_i\times I_i{\dot{\widehat{\theta }}}_i\hfill \end{array}\right]+\left[\begin{array}{cc}\hfill E_{3\times 3}\hfill & \hfill 0_{3\times 3}\hfill \\ \hfill {\tilde{d}}_i\hfill & \hfill E_{3\times 3}\hfill \end{array}\right]\left[\begin{array}{c}\hfill {\widehat{S}}_{i-1}\hfill \\ \hfill {\widehat{M}}_{i-1}\hfill \end{array}\right]$$ (1)

b_ji = 1 for biarticular muscles that cross but do not attach to segment i;

b_ji = 0 for all other muscles

Where ${\widehat{M}}_{i-1}$ was set to zero for i>1 and:

i	– segment number or joint number (1 represents the most distal segment or joint)
Ŝ i	– proximal joint reaction forces
Ŝ i−1	– distal joint reaction forces
${\widehat{M}}_{i-1}$	– distal joint moments
Ii	– inertia tensor
${\dot{\widehat{\theta }}}_i$	– angular velocity about COM
${\ddot{\widehat{\theta }}}_i$	– angular acceleration about COM
mi	– segment mass
E3×3	– identity matrix
â i	– linear acceleration of segment COM
ĉ i	– vector from the proximal joint to the segment COM
${\widehat{d}}_i$	– vector from the proximal to the distal joint
ĝ	– acceleration due to gravity
K	– number of muscles
Fj	– individual muscle force
F maxj	– maximum possible muscle force
${\widehat{n}}_{ji}$	– line of action of muscle j about joint i
r̂ji	– moment arm of muscle j about joint i

and c̃ and d̃ represent the skew symmetric matrix of a 3D vector:

$$\tilde{c}=\left(\begin{array}{ccc}\hfill 0\hfill & \hfill -c_3\hfill & \hfill c_2\hfill \\ \hfill c_3\hfill & \hfill 0\hfill & \hfill -c_1\hfill \\ \hfill -c_2\hfill & \hfill c_1\hfill & \hfill 0\hfill \end{array}\right)$$ (2)

Equation 1 represents a system of 9 equations of inter-segmental force equilibrium that are determinate and 9 equations of moment equilibrium that are indeterminate (the equations of motion are posed by considering the foot, calf and thigh segments). The indeterminate problem is solved with an optimization approach by seeking to minimize the cost function of Crowninshield and Brand (1981). This cost function is based upon minimizing the sum of the muscle stress raised to the power n. It has previously been shown that this solution tends towards a limit with increasing n (Rasmussen et al., 2001), and in this model a value of n = 30 produces physiologically realistic results (Cleather et al., 2011a):

$$\underset{F_j}{\min }f=\sum _{i=j}^{163}{\left(\frac{F_j}{F_{{\max }_j}}\right)}^{30}$$ (3)

Subject to the constraints that:

$$0\le F_j\le F_{{\max }_j}$$ (4)

The maximum muscle force was calculated by multiplying the physiological cross-sectional area of each muscle given in the Klein Horsman data set (2007) by an assumed maximum muscle stress (3.139 × 10⁵ N/m²; Yamaguchi, 2001).

Finally, the calculated muscle forces were combined with the inter-segmental forces to calculate internal joint forces. The magnitude of the total joint reaction force was calculated for the ankle (AF), patellofemoral joint (PFJF), tibiofemoral joint (TFJF) and the hip (HF). In addition, the anterior and posterior shear at the tibiofemoral joint (AS and PS; presented in the tibial coordinate frame) was also computed in an effort to understand the loading experienced by the cruciate ligaments of the knee. A repeated measures ANOVA with post hoc Bonferroni corrected pair wise comparisons was used to evaluate whether the joint forces experienced in each activity were different. A significance level of p<0.05 was set a priori.

Results

The optimization found a solution for over 99% of the frames of interest. Where a solution could not be found the frame was omitted from the results. Table 1 presents the mean peak forces in the lower limb during jump takeoff, landing, the push jerk drive and the push jerk catch. There were significant differences in the forces experienced at the PFJ (jumping significantly greater than jerk catching and jerk drive significantly greater than jerk catching – p < 0.05) and in posterior shear at the TFJ (again, both jumping and jerking significantly greater than jerk catching – p < 0.05). The ankle joint experienced the greatest loading whereas the PFJ was loaded the least during all activities.

Table 1. Mean (SD) peak normalized forces (× BW) calculated during the four activities.

(* = p<0.05, when compared to jumping; ‡ = p<0.05, when compared to jerking; # = p<0.05, when compared to catching)

	Ankle	Knee				Hip	GRF
		PFJ	TFJ	AS	PS
Jump n=12	8.9 (1.8)	4.2 (1.2) #	6.9 (1.0)	0.6 (0.4)	2.4 (1.1) #	5.5 (1.1)	1.3 (0.1) ‡
Land n=12	9.7 (4.1)	3.6 (0.9)	7.6 (2.1)	0.7 (0.5)	2.0 (1.2)	6.0 (3.0)	1.6 (0.3)
Jerk n=9	10.0 (1.4)	4.6 (1.2) #	9.0 (1.3)	0.3 (0.2)	3.1 (1.6) #	7.8 (4.2)	1.6 (0.2) *#
Catch n=9	9.9 (5.6)	2.4 (0.9) *‡	7.8 (4.0)	1.4 (1.4)	1.0 (0.9) *‡	8.4 (7.8)	1.1 (0.2) ‡

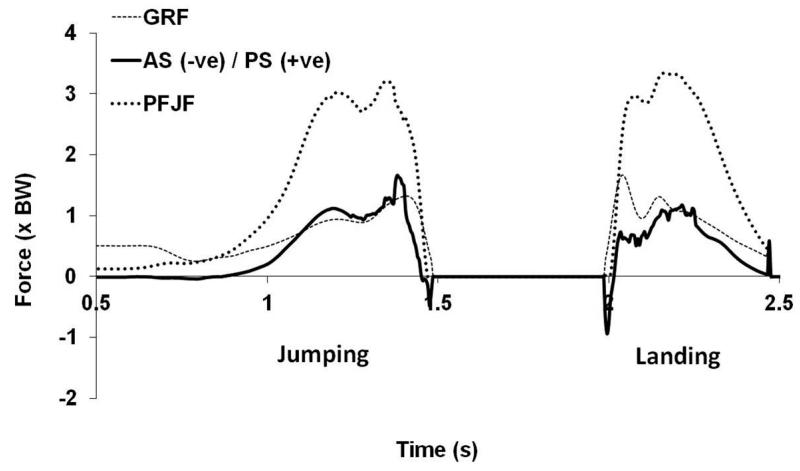
Figures 1 and 2 present the forces experienced at the knee by a typical subject during vertical jumping and landing. In particular, Figure 2 illustrates the shear loading of the knee where positive shear represents posterior tibial shear (i.e. the posterior cruciate ligament (PCL) is loaded), whereas anterior tibial shear (loading of the ACL) is negative. The majority of subjects experienced a consistent pattern in the shear loading of the knee during takeoff. Early in the takeoff there was a small degree of anterior shear, which was followed by a sustained posterior shear for the bulk of the jump. Finally, immediately prior to takeoff the shear force oscillated between anterior and posterior. There was more variation in the pattern of shear loading during landing, although there were some weak trends. Initial impact was generally associated with at least one spike directed anteriorly (in many trials there was a period of variability, which sometimes resulted in the direction of shear loading switching multiple times between anterior and posterior) before a more sustained period of posterior shearing.

Figure 1. Ankle, TFJF and hip loading experienced by a typical subject during vertical jumping and landing.

(AF = ankle joint reaction force; TFJF = tibiofemoral joint reaction force; HF = hip joint reaction force; GRF = ground reaction force)

Figure 2. PFJF and tibial shear experienced by a typical subject during vertical jumping and landing.

(PFJF = patellofemoral joint reaction force; AS = anterior shear; PS = posterior shear; GRF = ground reaction force)

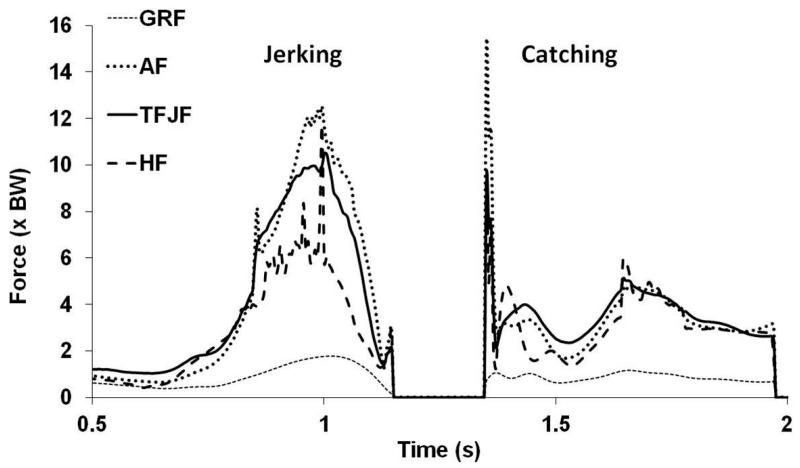
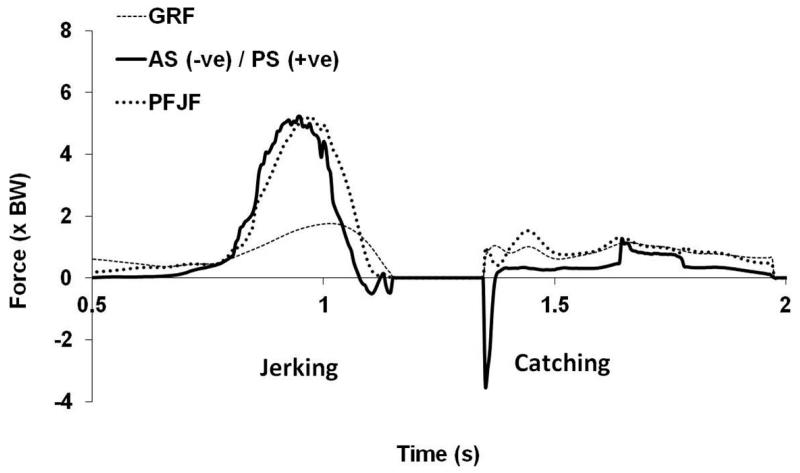
Figures 3 and 4 present the forces experienced at the knee by a typical subject during push jerking. During the push jerk drive for the majority of subjects the pattern of tibial shear was similar to that experienced during jumping with principally posterior shearing followed by brief anterior shearing. In contrast to the jump landing, no clear pattern in the direction or loading of tibial shear during push jerk catching emerged (although there was a weak trend towards early brief anterior shear followed by sustained posterior shearing).

Figure 3. Ankle, TFJF and hip loading experienced by a typical subject during the jerking and catching.

(AF = ankle joint reaction force; TFJF = tibiofemoral joint reaction force; HF = hip joint reaction force; GRF = ground reaction force)

Figure 4. PFJF and tibial shear experienced by a typical subject during jerking and catching.

(PFJF = patellofemoral joint reaction force; AS = anterior shear; PS = posterior shear; GRF = ground reaction force)

Discussion

In this study a previously described musculoskeletal model of the right lower limb was used to calculate the internal joint forces experienced during vertical jumping, landing and jerking with a focus on the knee. In general, the forces experienced at each joint were of similar magnitude in all four activities, although there were some statistically significant differences. When the data is taken as a whole, the TFJ appeared to experience a peak loading in the range of 6.9-9.0 × BW, the ankle joint a loading of 8.9-10.0 × BW and the hip joint a loading of 5.5-8.4 × BW. The peak PFJF was in the range of 2.4-4.6 × BW and the AS at the tibia were in the range 0.3-1.4 × BW whereas the PS was of the order of 1.0-3.1 × BW.

The magnitude of the total internal hip (HF) and knee (PFJF and TFJF) forces found in this work are greater than those that have been suggested to occur during ADLs and rehabilitation exercises characterized by slow movement speeds, or than have been measured in patient populations (Bergmann et al., 2001; D’Lima et al., 2005a; D’Lima et al., 2006; D’Lima et al., 2007; D’Lima et al., 2008; Escamilla et al., 2008a; Escamilla et al., 2008b; Escamilla et al., 2009a; Escamilla et al., 2009b). For instance, D’Lima and colleagues (2008) have reported that the highest tibial loadings recorded by a telemeterized knee implant in a patient population were between 3.0 and 4.5 × BW during jogging, golf and tennis. This is a finding that might be expected given that the activities considered in this study are typified by faster segmental accelerations and higher ground reaction forces, and supported by the fact that previous research has suggested that activities like vertical jumping and weightlifting yield greater joint reaction forces (Collins, 1994; Simpson et al., 1996; Simpson and Kanter, 1997; Simpson and Pettit, 1997). Despite this, the total knee joint contact forces (PFJF and TFJF only) suggested by this study are less than half as great as those suggested by previous analyses of vertical jumping (Simpson et al., 1996; Simpson and Kanter, 1997; Simpson and Pettit, 1997; Smith, 1975).

Previous research that has evaluated the tensile strength of the cruciate ligaments suggests a failure limit of around 2 kN for the ACL of young healthy males (Chandrashekar et al., 2006; Noyes and Grood, 1976; Woo et al., 1991) and 4.5 kN for the PCL (Amis et al., 2003). This study suggests a mean peak anterior shear during jumping, landing and jerking in the range of 240-1150 N and a mean peak posterior shear of 820-2550 N. The cruciate ligaments provide the primary restraint to anterior-posterior shear at the knee joint and these values are well within the ranges that could potentially be borne by the cruciate ligaments.

There is a growing body of evidence that asserts the importance of modelling the musculoskeletal system with appropriate detail as to provide physiologically realistic results (Cleather and Bull, 2012a; Cleather and Bull, 2012b). Previous studies as to the internal knee forces experienced during vertical jumping have been limited by the simplifying assumptions employed in order to permit a solution. These have included a lack of detail (in terms of the number and variability of force actuators; Cleather and Bull, 2010b; Valente et al., 2012) or the employment of only 2D models. The strength of the current work is that it is based upon a well posed model that is 3D and incorporates more detail than previous studies of these activities. Despite this the model lacked an adequate number of force actuators to easily find a solution for a limited number of frames immediately before take-off or after landing for some subjects (a higher force upper bound for the muscles was required to find a solution). This may suggest that when considering these types of activities an even greater degree of subject-specific detail may be necessary. An interesting question is whether the difficulty in finding a solution is representative of a physiological imperative (in which case the relatively higher joint forces found in these cases may be representative of the true loading) or whether it is an artefact of a less well posed approximation of the geometry (in which case the calculated force is likely to be an upper bound for the loading). It should also be noted that if the musculoskeletal model has a more favourable geometry than the actual subject then the model may underestimate the joint loading (Southgate et al., 2012), which further illustrates the importance of future work to understand the effect of changes in subject-specific detail on this type of model.

Other potential limitations of the model include the use of a cost function that is predicated upon the imperative to maximize muscular endurance (and thus may not represent the motor control strategy employed during maximal vertical jumping). Equally, the model has a lack of detail describing the tibiofemoral joint (which does not separate the loading experienced by the lateral and medial compartments).

An understanding as to the forces experienced by the hip and knee is of critical importance for a variety of medical professionals, coaches and biomedical researchers. The importance of the current study is therefore in defining a range for the joint contact forces that may be experienced by athletic subjects during routine sporting activities. This study suggests that the total joint contact forces experienced at the knee and hip during vertical jumping and push jerking are larger than in ADLs or slower rehabilitation exercises, but that forces at the knee are smaller than had been indicated in previous studies.