Skip to main content
PMC home page
PLOS ONE logoLink to PLOS ONE
. 2014 Mar 26;9(3):e92337. doi: 10.1371/journal.pone.0092337

Pan-Tropical Analysis of Climate Effects on Seasonal Tree Growth

Fabien Wagner 1,2,*, Vivien Rossi 3,4, Mélaine Aubry-Kientz 5, Damien Bonal 6, Helmut Dalitz 7, Robert Gliniars 7, Clément Stahl 2,8, Antonio Trabucco 9,10, Bruno Hérault 2
Editor: Morag Mcdonald11
PMCID: PMC3966775  PMID: 24670981

Abstract

Climate models predict a range of changes in tropical forest regions, including increased average temperatures, decreased total precipitation, reduced soil moisture and alterations in seasonal climate variations. These changes are directly related to the increase in anthropogenic greenhouse gas concentrations, primarily CO2. Assessing seasonal forest growth responses to climate is of utmost importance because woody tissues, produced by photosynthesis from atmospheric CO2, water and light, constitute the main component of carbon sequestration in the forest ecosystem. In this paper, we combine intra-annual tree growth measurements from published tree growth data and the corresponding monthly climate data for 25 pan-tropical forest sites. This meta-analysis is designed to find the shared climate drivers of tree growth and their relative importance across pan-tropical forests in order to improve carbon uptake models in a global change context. Tree growth reveals significant intra-annual seasonality at seasonally dry sites or in wet tropical forests. Of the overall variation in tree growth, 28.7% was explained by the site effect, i.e. the tree growth average per site. The best predictive model included four climate variables: precipitation, solar radiation (estimated with extrasolar radiation reaching the atmosphere), temperature amplitude and relative soil water content. This model explained more than 50% of the tree growth variations across tropical forests. Precipitation and solar radiation are the main seasonal drivers of tree growth, causing 19.8% and 16.3% of the tree growth variations. Both have a significant positive association with tree growth. These findings suggest that forest productivity due to tropical tree growth will be reduced in the future if climate extremes, such as droughts, become more frequent.

Introduction

Tropical forests are being threatened on an unprecedented scale by global changes. Temperatures across tropical forest regions are currently increasing [1] and are expected to continue to increase with a concomitant decrease in precipitation over the next decades [2]–[4]. Climate models predict a range of changes in tropical forest regions, including increased frequency of extreme climatic events, increased average temperatures, increased atmospheric CO2 and changes in seasonal distribution and interannual variability of rainfall [5]–[9]. Tropical forests play an important role in the mitigation of anthropogenic atmospheric CO2 emissions by constituting a major reservoir of terrestrial carbon and a large and persistent carbon sink [10]–[12]. Feedback between tropical forests and the local and regional climate has also been demonstrated [4], [13].

Tree growth is linked with atmospheric CO2 through photosynthesis. The last 20 years have seen a substantial increase in the number of publications focusing on the effects of climate on tropical tree growth. A search performed on Web of Science in March 2013 using the keywords 'climate', 'tropical forest', 'growth' and 'trees' returned fewer than 15 articles per year before 2000 and more than 60 articles in 2012, for a total of 541 articles focusing on the effect of climate on tropical tree growth. Long-term variations in tree growth have been reported on long-term forest plots, but the determinants of these variations are still being discussed [14]–[19]. Due to the annual or multi-annual census frequency of long-term forest plots, most studies focus on the annual or multi-annual variation in tree growth even though most tropical forests undergo an intrannual seasonality in climate [1], [6], [20]–[22]. In single-site-based studies, seasonal rhythms of tree growth have been linked to seasonal variations in water availability, rainfall, temperature and solar radiation (Table 1).

Table 1. Expected tropical tree growth response to climate variables.

variable predicted effecta references processb
REW + [28], [62] photosynthesis, xylem tension, stomatal closure, leaf flush
rainfall + [19, 23, 24, 35, 58, 59, 61, 97–90] photosynthesis, xylem tension, stomatal closure, leaf flush
− [89], [91]
T mean − [31]–[33], [92], [93] photosynthesis kinetic, stomatal closure
T min − [14], [17], [35], [66] photosynthesis kinetic, stomatal closure
no [94], [95]
T max − [19], [31], [33] photosynthesis kinetic, stomatal closure
+ [96]
no [94], [95]
VPD no [97], [98] stomatal closure, transpiration
irradiance + [17], [21], [29], [30], [64], [70], [74] photosynthesis, phenology
− [21]
no [17], [63], [70]
U* + [99] photosynthesis, transpiration
Open in a new tab
a

: expected growth response to the climate variable: (+) trees are expected to grow faster with high values of the climate variable, (−) trees are expected to grow slower with high values of the climate variable. b: biological processes involve in the tree growth response to a given climate variation. VPD is vapour pressure deficit, and Friction velocity (U*) is a climate variable provided by eddy flux data, which is correlated with wind speed. Relative extractable water (REW), is a daily value between 0 and 1; when 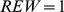Inline graphic, the amount of extractable water by the tree is at its maximum and when 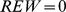Inline graphic, no water is available for the trees [28].

Rain or lack of rain is often implicitly viewed as the main drivers of forest dynamics [23], as annual net primary production (NPP) positively correlates with the annual sum of precipitation at large scales [24] and rainfall seasonality plays a key role in the forest's response to climate variability [25]. The relation between the amount of rainfall and water availability for trees is not straightforward and is determined by various soil and plant characteristics (i.e. permanent wilting point, field capacity, root distribution). Consequently, water stresses are increasingly estimated using soil water balance models [26], [27], including some that are explicitly designed for tropical forests [28]. Irradiance is directly linked to plant photosynthetic capacity, which in turn drives carbon uptake and plant growth [29]. The occurrence of dry periods linked to cloud-cover reduction was found to enhance canopy photosynthetic capacity by 25% throughout Amazonia [30]. The effects of rising temperatures on the physiology of tropical trees are currently debated within the scientific community [21], [32]. Some studies suggest that reductions in photosynthetic rates at temperatures above 30°C are driven by reductions in stomatal conductance in response to higher leaf-to-air vapour pressure deficits [31] or by a direct down-regulation of biochemical processes during CO2 fixation [33,33]. Recent studies, however, suggest that tropical tree mortality may increase significantly with increasing night-time temperatures, while tree growth appears surprisingly sensitive to variations in mean annual night-time temperatures of 1–2°C [35].

A pantropical analysis of the effects of climate seasonality on tropical tree growth is still missing in the literature. Most of our knowledge comes from single-site-based studies that often suffer from collinearity problems between climate drivers. In this paper, we ran a meta-analysis of monthly tropical tree growth at the pan-tropical scale in which multiple gradients of climate variables allowed us to disentangle the effect of each climate driver on tropical tree growth. We focused on the seasonal effect of climate on tree growth in tropical forests by using data from papers reporting tree growth measurements with a high periodicity (from daily to monthly censuses) and global climate datasets. We gathered 30 datasets in which growth measurements have been recorded for 3412 individual trees from 25 pantropical forest sites. This paper has three specific objectives: (i) to find the climate drivers of tree growth across tropical forests; (ii) to quantify tree growth variations in response to climate among tropical forests; and (iii) to give a modeling framework to improve the model predictions of seasonal carbon uptake by tropical tree growth in a global change context.

Materials and Methods

Climate datasets

We used climate datasets from two sources (Table 2): the Climate Research Unit (CRU) at the University of East Anglia [36] and the Consortium for Spatial Information website (CGIAR-CSI, http://www.cgiar-csi.org). From the CRU, we used variables from the CRU-TS3.1 and CRU-TS3.10.01 monthly climate global datasets available at 0.5° resolution from 1901–2009: cloud cover (cld, unit:%); precipitation (pre, mm); daily mean, minimal and maximal temperatures (respectively tmp, tmn and tmx, °C); temperature amplitude (dtr, °C); vapour pressure (vap, hPa); and potential evapotranspiration (pet, mm). pet was calculated using the grass reference evapotranspiration equation [37], [38], which is a variant of the Penman-Monteith method using the gridded tmp, tmn, tmx, vap and cld. pre was square-root transformed prior to data modeling to address heteroscedasticity. From the CGIAR-CSI, we used the monthly average of extraterrestrial solar radiation as well as the Global Soil-Water Balance [27]. The first dataset defines the solar radiation reaching the top of the Earth's atmosphere (sol) and is a function of Earth-sun geometry and time of year. sol per day (mm/day equivalent) is calculated using the methodology presented in [39] specifically for the 15th day of each month to describe averages per month. Total sol per month (mm/month equivalent) is calculated by multiplying the value of sol for the 15th day of the month by the number of days in the month, 1 mm.day−1 equivalent of evaporation  =  2.45 MJ.m−2.day−1. The latter dataset provides hydrological raster data (ESRI Grid format) describing actual evapo-transpiration and soil water content for a monthly time-series from period 1901–2009 using CRU-TS3.1 as the primary climate data input. The monthly time-series of relative soil water content swc (unitless, 0–1) is calculated as the ratio of the soil water content from the soil water balance over the maximum available soil moisture (in mm water per 1 m soil depth, from the Digital Soil Map of the World and Derived Soil Properties [40], [41]) along the ecosystem rooting depth [42].

Table 2. Climate datasets used to model seasonal tropical tree growth at a pantropical scale.

climate variable full name unit origin
pre precipitation mm CRU-TS3.10.01
sol a Extraterrestrial solar radiation mm/month as equivalent of evaporation CGIAR-CSI
cld cloud cover % CRU-TS3.1
Pre Potential Evapotranspiration mm CRU-TS3.1
swc relative soil water content unit less CGIAR-CSI
tmp mean temperature °C CRU-TS3.1
tmn minimal temperature °C CRU-TS3.1
tmx maximal temperature °C CRU-TS3.1
vap vapour pressure hPa CRU-TS3.1
dtr temperature amplitude °C CRU-TS3.1
Open in a new tab
a

: sol per day (mm/day equivalent) is calculated using the methodology presented in [39] specifically for the 15th day of each month to describe averages per month. Total sol per month (mm/month equivalent) is calculated by multiplying the value of sol for the 15th day of the month by the number of days in the month, 1 mm.day−1 equivalent of evaporation  =  2.45 MJ.m−2.day−1.

Tree growth data

A search performed on Web of Science in March 2013 using the keywords 'climate', 'tropical forest', 'growth' and 'trees' returned 541 articles focusing on effect of climate on tropical tree growth. Among these publications, our analysis used only the publications with seasonal tree growth data (from daily to monthly censuses) available in the article graphics, available in an online repository or provided by the authors. The tree growth data were extracted from the article graphics using WebPlotDigitizer 2.5 (http://arohatgi.info/WebPlotDigitizer/, Table 3). Three types of data were found: (i) single observations by tree and time step at a given site (see [43]); (ii) mean and standard deviation (SD) by species at a given site for each time step (see [44]); and (iii) only the mean and SD of all trees at a site for each time step [35]. In addition, these data may come from measurements with dendrometer bands, electronic point surveys, tree ring analyses or graduated tapes. The minimum diameter at breast height (DBH) used in the articles is 10 cm. Among sites, Selangor and Muara Bungo are forest plantations. Finally, they have different time step between measurements: monthly, weekly or daily. We converted these primary datasets by making a linear approximation of the growing trajectory in order to obtain a mean and a standard deviation by month and dataset for each available calendar year. Datasets from the same site were assumed to be samples from the same population and were not analyzed separately. This could affect the value of the whole population mean growth, but here we are only interested in the monthly variations of tree growth (site effect is considered as a random effect). The final dataset is comprised of 30 datasets of 25 pantropical forest sites, for a total of 3412 individual trees (Figure 1, Table 3). The data, monthly tree growth mean and SD, are freely available upon request to the corresponding author. No specific permits were required for the described field studies and this study did not involve endangered or protected species.

Table 3. Description of the tree growth data.

reference country site Long. Lat. method time scale No. of trees Typeb duration (mm/yyyy) dbh growth mean±SD (mm/month)
[78] Ghana Tinte Bepo −2.10 7.07 dendrometer band monthly 42 2 11/1997–3/1999 0.32 ± 0.28
[43] Costa Rica Guanacaste −85.50 10.75 dendrometer band daily 19 3 2/1978–1/1979 0.27 ± 0.33
[100] Ecuador RBSF −79.07 −3.97 electronic point dendrometer daily 5 3 4/2006–2/2009 0.27 ± 0.38
[101] Brazil Rio Cachoiera −49.71 −25.25 dendrometer band weekly 120 2 11/2007–9/2008 1.11 ± 0.97
[35] Costa Rica La Selva −84.00 10.43 dendrometer band monthly 28 1 6/2006–11/2008 0.3 ± 0.09
[44] DRC Luki forest 13.18 −5.58 graduated tape monthly 30 2 5/2006–7/2007 0.19 ± 0.59
[102] Brazil ZF-2 −60.12 −2.59 dendrometer band Monthly 272 1 1/2000–12/2000 0.15 ± 0.05
[103] Costa Rica Guanacaste −85.50 10.75 dendrometer band weekly 40 3 8/1969–7/1970 0.39 ± 0.37
[104] French Guiana Paracou −52.91 5.28 dendrometer band weekly 9 3 10/1979–6/1982 0.64 ± 0.23
[105] Ivory Coast Lamto −5.03 6.22 dendrometer band daily 6 3 2/1973–7/1981 0.28 ± 0.2
[106] Brazil Tapajos −54.97 −2.85 dendrometer band monthly 734 3 12/2001–12/2005 0.31 ± 0.14
[107] Uganda Budongo 31.54 1.73 dendrometer band monthly 318 3 7/2003–12/2009 0.1 ± 0.05
[19] Kenya Kakamega 34.86 0.35 dendrometer band monthly 770 3 7/2003–12/2009 0.19 ± 0.03
[90] Brazil Marajoara −50.27 −7.83 dendrometer band monthly 67 2 2/1997–11/2001 0.5 ± 0.55
[90] Brazil Marajoara −50.27 −7.83 dendrometer band monthly 40 3 1/1997–10/2001 0.51 ± 0.55
[80] Ethiopia Munessa-Shashamene Forest 38.87 7.43 electronic point dendrometer daily 4 3 4/2008–8/2009 0.45 ± 0.39
[108] Ghana Pinkwae −0.13 5.75 dendrometer band weekly 79 2 2/1978–4/1979 −0.2 ± 0.78
[108] Ghana Pinkwae −0.13 5.75 dendrometer band weekly 2 3 3/1978–4/1979 −0.24 ± 0.79
[109] Brazil Ibicatu −47.72 −22.78 dendrometer band monthly 5 3 3/1999–4/2006 0.34 ± 0.47
[110] Mexico El Palmar −104.47 19.13 dendrometer band monthly 23 2 9/2002–8/2003 0.24 ± 0.36
[110] Mexico La Barcinera −104.42 19.15 dendrometer band monthly 14 2 9/2002–8/2003 0.09 ± 0.29
[61] Brazil Tapajos −54.97 −2.85 dendrometer band monthly 450 2 11/1999–5/2001 0.21 ± 0.06
[111] Malaysia Selangor plantation 101.52 3.51 dendrometer band weekly 6 3 1/1993–12/1995 0.55 ± 0.32
[112] Thailand SERS 101.93 14.50 dendrometer band weekly 6 3 4/2004–2/2006 0.04 ± 0.04
[113] Brazil CPM −50.50 −29.00 tree ring analysis monthly 12 1 5/2005–5/2006 0.08 ± 0.08
[114] India Attapadi 76.45 11.08 dendrometer band monthly 101 3 3/1980–10/1983 0.19 ± 0.12
[79] French Guiana Paracou −52.91 5.28 dendrometer bands weekly 161 3 6/2007–1/2009 0.14 ± 0.06
[115] Indonesia Muara Bungo 102.21 −1.49 meter monthly 40 3 4/2004–4/2006 0.84 ± 0.23
[116] Ecuador RBSF −79.07 −3.97 electronic point dendrometer daily 1 3 4/2006–8/2009 0.23 ± 0.38
[117] Venezuela RFC −70.75 7.50 dendrometer band monthly 6 3 4/1978–4/1982 0.75 ± 0.52
[118] Brazil FLONA SFP −50.42 −29.42 dendrometer band monthly 2 3 9/2003–7/2006 0.23 ± 0.19
Open in a new tab

Description of the data used in this analysis, references, site location, site name, latitude and longitude in °, method of measurement, number of trees, follow-up type (b: Type 1: only mean and sd for the N trees of a site per month, Type 2: mean and sd by species for a site per month and Type 3: one observation by tree for a site per month.), follow-up duration and mean ± standard deviation of monthly diameter at breast height (dbh) growth.

Figure 1. Locations of the 25 study sites and their countries (grey areas).

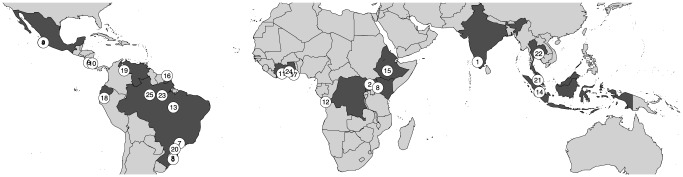
Figure 1

Open in a new tab

1: Attapadi; 2: Budongo; 3: CPM; 4: El Palmar; 5: FLONA SFP; 6: Guanacaste; 7: Ibicatu; 8: Kakamega; 9: La Barcinera; 10: La Selva; 11: Lamto; 12: Luki forest; 13: Marajoara; 14: Muara Bungo; 15: Munessa-Shashamene Forest; 16: Paracou; 17: Pinkwae; 18: RBSF; 19: RFC; 20: Rio Cachoiera; 21: Selangor plantation; 22: SERS; 23: Tapajos; 24: Tinte Bepo; 25: ZF-2.

Preliminary analysis

First, we investigated the association between climate variables on a monthly time scale through a principal component analysis (PCA) on the normalized climate dataset, i.e. climate variables were centred and scaled, to describe how the variance of the climate dataset was structured. Next, to measure spatial autocorrelation in tree growth observations between sites, we computed the Moran's Index statistics of the mean monthly growth by sites [45]. This index range from -1, strong negative spatial autocorrelation, to +1, strong positive spatial autocorrelation. The significance of Moran's I is evaluated by using a Z score and p-value generated by random permutation [46]. The null hypothesis states that there is no spatial autocorrelation for the variable within the geographic area. The interannual and intra-annual variability climate variable was described by computing the coefficient of variation (CV) for each variable (i.e. standard deviation × 100 divided by the mean) of the annual mean and monthly values of the climate time series over the period of the CRU data (1901–2009). To detect, estimate and test seasonal patterns in the tree growth time series, we used temporal regression models from the R package season [47]. The model was fitted using a sine and cosine term that together described the sinusoid. These parameters were added to a generalized linear model to explain tree growth data and test the existence of a seasonal pattern. The existence of a seasonal pattern was determined by the zero-test based on Snedecor's F statistic. This method is known as the cosinor test.

Modeling seasonal tree growth

We modeled the link between tree growth, site and climate variables in a mixed linear model framework at a monthly time step. Here, we assumed that each growth measurement was independent and that our multiple-site design enabled us to deal with the collinearity of climate variable present in each site. We set the climate variables as fixed effects and the site as a random effect. We set the site effect as a random effect in order to avoid any statistical bias in our results. This site effect was not further analyzed as the main objective of the study was to understand seasonal variations of tree growth. In order to rank the climate effects, we considered various growth models:

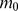• Inline graphic, the reference model:

graphic file with name pone.0092337.e004.jpg (1)

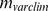•Inline graphic, for each climate variable 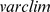Inline graphic, an univariate model:

graphic file with name pone.0092337.e007.jpg (2)

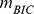•Inline graphic, the model with the best combination of climate variables, CombBIC, according to the Bayesian Information Criterion (BIC):

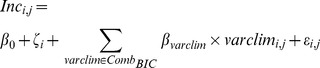graphic file with name pone.0092337.e009.jpg (3)

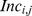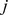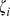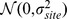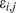Where Inline graphic is the average tree diameter growth for the site Inline graphic for the month Inline graphic, Inline graphic is the random site effect assumed to follow a normal distribution Inline graphic and Inline graphic is the residual error assumed to follow a normal distribution 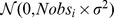Inline graphic weighted by 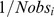Inline graphic, which is the inverse of the number of observation periods by site. The mixed model parameters were estimated with the algorithms of the R package lme4 [48]. To estimate the parameter confidence intervals with a probability of 95%, we generated 10000 parameter samples from the posterior distribution of the fitted model parameters using the Markov Chain Monte Carlo methods [48]. Then, the confidence intervals for the parameters (Highest Posterior Density [HPD] intervals) were constructed from the empirical posterior distribution of the 10000 samples as the intervals containing the parameters with the nominal probability [48]. Evaluation of the model performance was made by computing goodness-of-fit-measures with the R package lmmfit [49]–[52]. To find the best variable linear combination that contains the maximum of information to link growth and climate variables (the model mBIC), we ran an exhaustive screening of the candidate models using a stepwise procedure based on the Bayesian information criterion, BIC [53]. We used BIC, instead of the classically used AIC, to avoid over-parameterization and multicollinearity problems, as this criterion is consistent and parsimonious for model selection with respect to large datasets [54]. We made a residual analysis to verify if the error of the model mBIC had a bias for any of the selected variables in this model. That is, we computed the Pearson's product-moment correlation coeffiecient (ρ) between the residual of the model mBIC and the variables of this model and tested if this coefficient was statistically or different not from zero.

The predictive quality of the fitted models was assessed by computing the root mean square errors of predictions, RMSEP.

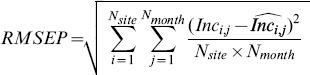graphic file with name pone.0092337.e018.jpg (4)

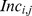where Inline graphic is the observed values of tree growth for the site i and for the month j, and 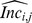Inline graphic are the model predictions of growth.

All analyses were performed using the R-project software (http://www.r-project.org/).

Results

Climate gradients

The 25 sites represent a large sample of tropical forests under different tropical climates corresponding to five global ecological tropical zones [55](Table 4). The gradient of the annual mean of precipitation ranges from 973.9 mm (RBSF, Ecuador) per year to 3948.1 mm (La Selva, Costa Rica). The coefficient of variation (CV) of interannual precipitation ranges from 12.5% (SERS, Thailand) to 35.2% (RBSF, Ecuador). Intra-annual CV of monthly precipitation distribution precipitation ranges from 13% (CPM,Brazil) to 116.9% (El Palmar and La Barcinera, Mexico). The sites undergo a large variability in the distribution of precipitations throughout the year, from zero months (La Selva) to 8–9 months with less than 100 mm of rain (Lamto, Tinte Bepo, Pinkwae, RBSF). The relative soil water content exhibits the same intra-annual pattern, ranging from sites without seasonality, intra-annual CVswc < 3.5% (Cpm, La Selva, Muara Bungo, Rio Cachoiera and Selangor), to sites with an intra-annual CVswc > 37.8% (El Palmar, la Barcinera, RBSF). The annual average of relative soil water content is above 60% for 24 of the 25 sites. The annual cloud cover mean ranges from 42.9% (Munessa-Shashamene, Ethiopia) to 87.2% (Luki Forest, DRC) and its intra-annual variation is similar to the intra-annual variation of precipitation.

Table 4. Descriptive statistics of climate variables.

site GESa pre pet tmn tmp tmx dtr swc vap cld sol
Attapadi TAr 2158 (18.1/100.5) 1498.3 (1.9/19.9) 21.4 (2.1/5.8) 25.7 (1.8/5.2) 30.2 (1.7/6.2) 8.8 (3.8/19.6) 0.8 (3.4/30.6) 24.7 (2.5/9.3) 50.5 (2.5/38.2) 5214.7 (0/7.7)
Budongo TAr 1322.1 (15.4/41.6) 1363.8 (2.8/10) 17.5 (4/3.1) 23.4 (2.9/3.5) 29.3 (2.4/4.4) 11.9 (3/9) 0.8 (8/20.2) 20.5 (4.2/5.5) 59.9 (3.5/9.3) 5313.8 (0/3.3)
CPM SCf 1741.4 (16.9/13) 935.1 (2.4/34.2) 12.1 (4/27.4) 16.5 (2.6/20.6) 21 (1.9/16.8) 9 (2.4/5.1) 1 (2.3/1.5) 15.3 (3.3/21.4) 65.8 (2.7/5.9) 4745 (0/28.4)
El Palmar TAwa 1076.3 (26.8/116.9) 1414.3 (2.4/12.9) 17.7 (2.6/16.7) 24.6 (1.6/7.1) 31.6 (1.4/4) 13.9 (3.3/20.5) 0.6 (9.1/42.1) 21 (1.8/15) 55.5 (4.7/22.9) 5028.8 (0/14.5)
FLONA SFP SCf 1643.1 (16.2/13.6) 888.7 (2.6/32.7) 11.6 (4.1/28.2) 15.9 (2.7/20.7) 20.2 (1.9/16.4) 8.6 (2.3/3.4) 0.9 (4.1/4.7) 15 (3.4/21.5) 66.8 (2.5/6.5) 4729.1 (0/28.8)
Guanacaste TAwb 1749.7 (24/86.8) 1606.9 (2.8/19) 21.1 (2.7/3.3) 26.8 (2.1/3.4) 32.5 (1.7/4.1) 11.4 (0.6/9.8) 0.9 (5.1/20.2) 28.2 (2.7/6.5) 49.9 (2/20.1) 5220.8 (0/7.4)
Ibicatu TAwa 1518.2 (22/59.8) 1097.7 (2.5/18.9) 16.1 (5/17.3) 21.3 (3.4/11) 26.6 (2.6/7.4) 10.5 (3.8/8.8) 0.9 (10.1/14.3) 18.2 (3.9/18.1) 73.7 (0.9/10.1) 4966.1 (0/22.3)
Kakamega TM 1770.9 (14.4/37) 1501.1 (2.7/13.3) 14 (4.3/3.9) 21.4 (2.7/3.2) 28.8 (2.2/4.1) 14.9 (2.8/8.1) 0.9 (7/15.7) 15.5 (3.5/6.5) 62.9 (3.6/6.3) 5317.5 (0/3.8)
La Barcinera TAwa 1076.3 (26.8/116.9) 1414.3 (2.4/12.9) 17.7 (2.6/16.7) 24.6 (1.6/7.1) 31.6 (1.4/4) 13.9 (3.3/20.5) 0.6 (11.5/40.2) 21 (1.8/15) 55.5 (4.7/22.9) 5028.8 (0/14.5)
La Selva TAr 3948.1 (19.4/44.7) 1358.2 (3.7/13.5) 17.9 (3.9/3.4) 23.1 (3/2.6) 28.3 (2.4/3.4) 10.4 (0.6/10.3) 1 (1.7/2.9) 23.5 (3.4/5) 52.9 (2.9/13.1) 5225.8 (0/7.2)
Lamto TAr 1381.5 (21.3/60.9) 1122.5 (1.5/15.4) 21.8 (1.5/3.7) 26.5 (1.2/3.7) 31.2 (1.1/5.3) 9.4 (2.5/18.1) 0.9 (5.7/16.5) 27.3 (2/4.8) 77.2 (1.1/15.8) 5282.3 (0/4.3)
Luki forest TAr 1069.1 (18.4/83.7) 947.8 (1.3/12.8) 20.8 (1.3/8.9) 24.6 (1.1/8.5) 28.6 (1/8.2) 7.8 (0/7.8) 0.8 (6.3/17.1) 24.8 (1.7/11.6) 87.2 (0.8/5.9) 5301.4 (0/7.6)
Marajoara TAr 1873.6 (12.8/74.2) 1068.4 (2.6/14.9) 19.5 (3.5/4.8) 25.6 (2.6/1.7) 31.8 (2.1/4.3) 12.3 (0/17.5) 0.8 (4.5/21.6) 28.5 (3/4.1) 77.2 (0.2/20.6) 5281.7 (0/9.4)
Muara Bungo TAr 2686.8 (14.6/34.2) 1260.5 (2.9/4.7) 22.9 (2/1.6) 27.2 (1.7/1.3) 31.6 (1.6/1.8) 8.7 (3.5/7.3) 1 (4.8/3.5) 29.9 (2.4/1.9) 68.4 (3.1/7) 5318.1 (0/4.8)
Munessa-Shashamene Forest TM 1192 (15.3/56.6) 1203.5 (3.8/12.9) 10.1 (5.4/17.5) 17 (3.2/5.2) 23.8 (2.7/6.9) 13.7 (3.8/21.3) 0.8 (10/25.5) 13.1 (4.2/13.5) 42.9 (10.7/37.1) 5268.6 (0/5)
Paracou TAr 3025.2 (17.3/64.6) 1246.2 (1.9/16.7) 22.5 (2.2/0.9) 26.3 (1.9/2.2) 30.1 (1.6/3.9) 7.6 (0/16.3) 0.9 (4.2/20.2) 29.5 (1.6/1.9) 58.7 (1.7/24.3) 5291.3 (0/3.8)
Pinkwae TAwb 998.1 (22.2/64.7) 1255 (2.1/11.7) 24.1 (2/2.2) 27.5 (1.7/3.7) 30.9 (1.4/5.2) 6.8 (2.9/18.7) 0.7 (12.3/26.3) 27.7 (2.2/3.2) 73.6 (1.9/14.5) 5287.1 (0/4)
RBSF TM 973.9 (35.2/65.6) 1439.9 (4.8/12) 4.7 (10.8/19.4) 13.1 (3.8/3) 21.7 (2.3/2.6) 17 (0.8/7.8) 0.5 (17/50) 11.4 (5.3/6.1) 75 (1.9/10) 5311 (0/6.4)
RFC TAwa 1696.7 (13.7/70.8) 1184.6 (7.4/15.4) 22.3 (3.3/2.5) 27.3 (1.6/2.8) 32.4 (1.9/4.8) 10.1 (10.2/17.7) 0.9 (4/19.6) 27.6 (3.1/6.9) 82 (7.8/10) 5268 (0/5.1)
Rio Cachoiera SCf 1526.6 (18.4/27) 913.4 (3/24.7) 12.6 (5.8/26.9) 18.1 (3.6/16.1) 23.7 (2.5/10.5) 11.1 (3/7.8) 1 (3.6/1.7) 16.5 (4.2/18.1) 78.1 (2.1/6.8) 4884.2 (0/24.7)
Selangor plantation TAr 2840.3 (16.7/29.7) 1065.9 (3/8.4) 20.3 (3/1.7) 24.7 (2.1/1.5) 29.1 (1.5/2.1) 8.7 (3.7/8) 1 (1.8/1.5) 27.4 (2.6/2.6) 72.7 (2.6/10.6) 5304.8 (0/3.2)
SERS TAwb 1558.7 (12.6/81) 1284.1 (2.7/14.7) 21.6 (2.5/10.9) 26.7 (1.7/6.5) 31.9 (1.4/5.5) 10.2 (4/21.7) 0.7 (5.7/37.8) 26.9 (2.1/14.8) 59.5 (4.4/34.2) 5147.3 (0/10.5)
Tapajos TAr 1958.8 (19.9/63.6) 1126.8 (1.4/18.1) 21.8 (1.6/2.1) 26.5 (1.4/2.3) 31.2 (1.2/3.4) 9.4 (1.4/11.4) 0.9 (6.4/17.8) 29.7 (2/1.4) 75.5 (0.3/18.4) 5315.2 (0/5.7)
Tinte Bepo TAr 1246.7 (15.5/61) 1123 (1.6/15.9) 21.8 (1.8/5.8) 26.5 (1.4/5.4) 31.3 (1.4/6.7) 9.5 (2.9/20.4) 0.8 (5.3/20.4) 25.1 (2.6/10) 75.7 (1.6/16.4) 5273.1 (0/4.8)
ZF-2 TAr 2232 (12.5/46.6) 1161.1 (1.9/16) 23.2 (1.7/1.1) 27.4 (1.3/1.8) 31.6 (1.3/2.7) 8.4 (4.5/9.7) 0.9 (5.5/11.2) 30.3 (2/2.3) 82.2 (1/13.6) 5316 (0/5.5)
Open in a new tab

Descriptive statistics of climate variables: Annual mean; coefficient of variation of annual means (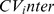Inline graphic) and coefficient of variation of monthly values (Inline graphic) of precipitation (pre); potential evapotranspiration (pet); minimal, mean and maximal temperatures (respectively tmn, tmp and tmx); daily temperature amplitude (dtr); soil water content (swc); vapour pressure (vap); cloud cover (cld); and extraterrestrial solar radiation (sol). Coefficients of variations (standard deviation divided by the mean of the variable) of monthly climate time series are computed over the period of the CRU data (1901–2009). a Globale Ecological Zone defined by FAO [55]; TAr: Tropical rainforest; TAwa: Tropical moist deciduous forest; TAwb: Tropical dry forest; TM: Tropical mountain system; and SCf: Subtropical humid forest.

Three major climate gradients are represented in the Principal component analysis (PCA)(Figure 2). The first axis (x-axis in Figure 2a) represents a gradient of increasing temperature, that is highly correlated with vapour pressure. Sites close to the equator that are located at high altitudes are on the left of this axis, with sites far from the equator experiencing a cold season (Figure 2e). The second axis (y-axis in Figure 2a) has a strong contribution from variables that reflect water availability. The third axis (y-axis in Figure 2b) appears to be related to solar radiation. Ordination of the continental location of the studied sites on the PCA axis (Figure 2d) revealed that sites in Asia were slightly warmer and had higher vapour pressures than those in America and Africa. Ordination of the studied countries on the PCA axis (Figure 2c) reveals that some countries are separated from others because of climate: from cold (Ecuador) to warm (Indonesia) and from dry tropical (Mexico) to wet tropical (Malaysia)(Figure 2e). In the following analysis, we kept all the climate variables as we have a strong physiological assumption of their effect on tree growth (Table 1).

Figure 2. Principal component analysis of the climate variables.

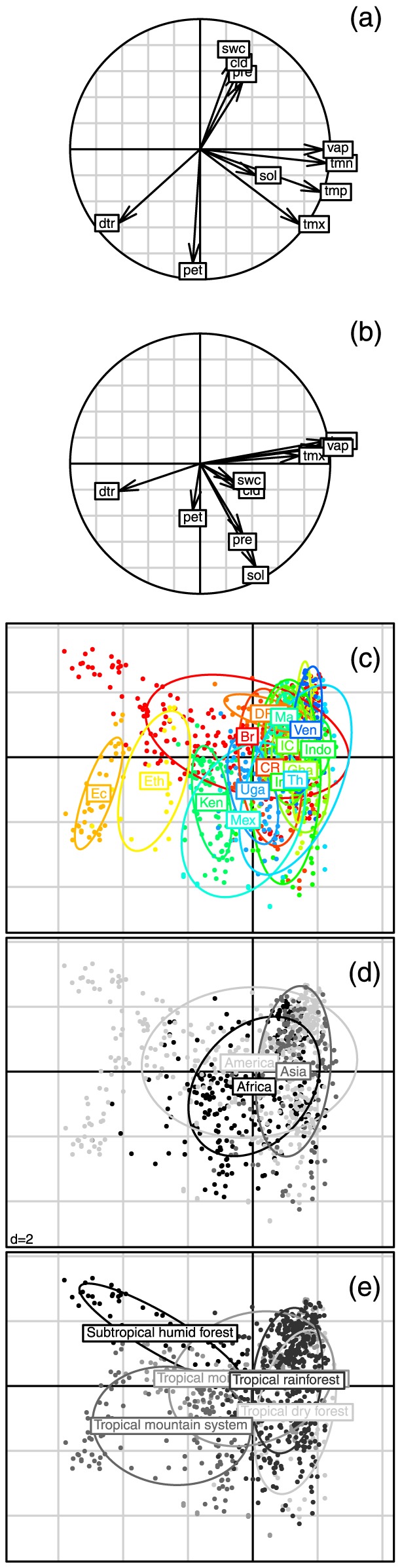
Figure 2

Open in a new tab

cld: cloud cover; pre: precipitation; sol: extraterrestrial solar radiation; tmp, tmn and tmx are respectively the daily mean, minimal and maximal temperatures; dtr: temperature amplitude; vap: vapour pressure; pet: potential evapotranspiration; and swc: relative soil water content. (a) correlation circle of axis 1 and 2; (b) correlation circle of axis 1 and 3; (c) projection of the country classes on the pca axis, India (Indi), Uganda (Uga), Brazil (Bra), Mexico (Mex), Costa Rica (CR), Kenya (Ken), Ivory Coast (IC), DRC (DRC), Indonesia (Indo), Ethiopia (Eth), French Guiana (FG), Ghana (Gha), Ecuador (Ec), Venezuela (Ven), Malaysia (Ma), Thailand (Th); (d) projection of the continental classes on the pca axis; and (e) projection of the global ecological zones on the pca axis (i.e. Tropical rainforest, Tropical moist deciduous forest, Tropical dry forest, Tropical mountain system and Subtropical humid forest). Note that axis 1 and 2 explain 41.70% and 28.12% of the total variation respectively, (a). The third axis explained 11.30% of the variance and was linked negatively to sol and pre, (b).

Tree growth descriptive analysis

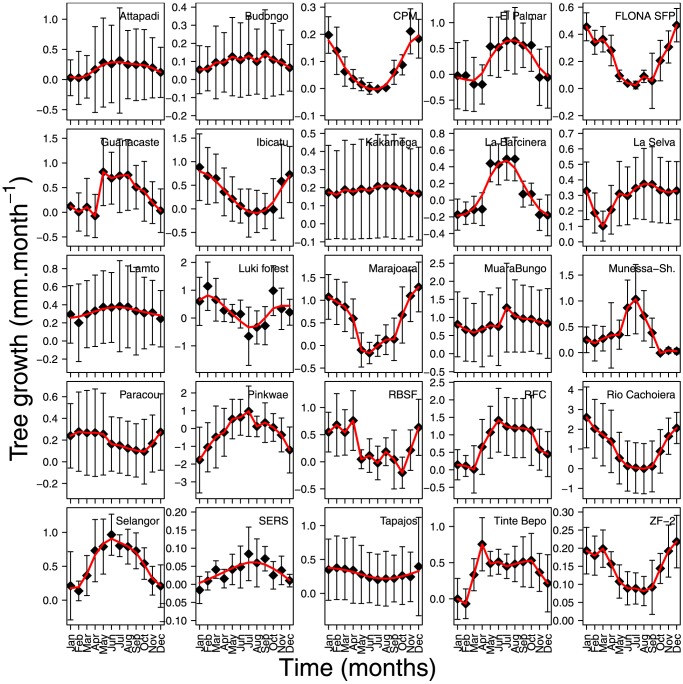
We cannot reject the null hypothesis that there is no spatial autocorrelation present in mean tree growth observations between sites at alpha  =  0.05 (Moran's I observed = 0.0102, expected =  −0.042, SD 0.123, p.value  =  0.672). Tree diameter growth shows a significant intra-annual seasonality at all the studied sites, even sites with mean annual precipitation rates close to 4000 mm (La Selva, Costa Rica)(Table 5 and Figure 3).

Table 5. Seasonality of mean monthly tree growth with cosinor analysis for the studied sites.

Site Amplitude Phase Low phase p value
Attapadi 0.129 Month  =  7.6 Month  =  1.6 <0.05
Budongo 0.031 Month  =  7.3 Month  =  1.3 <0.05
CPM 0.104 Month  =  12.2 Month  =  6.2 <0.05
El Palmar 0.437 Month  =  7.7 Month  =  1.7 <0.05
FLONA SFP 0.213 Month  =  1.1 Month  =  7.1 <0.05
Guanacaste 0.396 Month  =  7.3 Month  =  1.3 <0.05
Ibicatu 0.470 Month  =  1.5 Month  =  7.5 <0.05
Kakamega 0.019 Month  =  7.5 Month  =  1.5 <0.05
La Barcinera 0.361 Month  =  6.8 Month  =  12.8 <0.05
La Selva 0.092 Month  =  9 Month  =  3 <0.05
Lamto 0.067 Month  =  6.9 Month  =  12.9 <0.05
Luki forest 0.535 Month  =  1.4 Month  =  7.4 <0.05
Marajoara 0.684 Month  =  12.6 Month  =  6.6 <0.05
Muara Bungo 0.211 Month  =  8.6 Month  =  2.6 <0.05
Munessa-Shashamene Forest 0.380 Month  =  6.4 Month  =  12.4 <0.05
Paracou 0.091 Month  =  2.6 Month  =  8.6 <0.05
Pinkwae 1.033 Month  =  7 Month  =  13 <0.05
RBSF 0.361 Month  =  2.2 Month  =  8.2 <0.05
RFC 0.645 Month  =  7.6 Month  =  1.6 <0.05
Rio Cachoiera 1.235 Month  =  1.3 Month  =  7.3 <0.05
Selangor plantation 0.380 Month  =  6.7 Month  =  12.7 <0.05
SERS 0.033 Month  =  7.4 Month  =  1.4 <0.05
Tapajos 0.089 Month  =  1.9 Month  =  7.9 <0.05
Tinte Bepo 0.223 Month  =  6.9 Month  =  12.9 <0.05
ZF-2 0.066 Month  =  1.1 Month  =  7.1 <0.05
Open in a new tab

Month  =  1 corresponds to January. The amplitude is the difference between the higher and lower points in mm.month−1 of the sinusoid fitted in the cosinor analysis. The phase and the low phase are, respectively, the month with the highest/lowest tree growth value according to the sinusoid fitted in the cosinor analysis. A 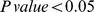Inline graphic indicates that the statistically significant existence of a seasonal pattern cannot be rejected.

Figure 3. Evolution of mean monthly tree growth values and standard deviation for the studied forest sites.

Figure 3

Open in a new tab

The red line represents a cubic smoothing spline.

Climate effects on tree growth

More than 28.69% of the observed seasonal variation in tree growth may be imputable to the site effect (reference model m0, Table 6), while climate variables alone explain a maximum of 19.82% (squared root monthly precipitation). The variables sol, cld, vap, dtr, tmn and swc explained between 9.65 and 16.30% of the climate effect, while tmp, pet and tmx explained less than 2.13%. The selection procedure, which used the BIC criterion, kept four climatic variables (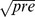Inline graphic, sol, dtr, swc) in the final multivariate model mBIC (Table 6). These four climate variables together explained 29.79% of the total observed monthly tree growth variation. The parameter values for the fixed effect in the univariate analysis indicate the direction of the relation between the climate variables and tree growth (Table 6). Among the four selected variables, pre (0.03), swc (0.58) and sol (0.09) have a positive link with tree growth and dtr (−0.08) has a negative link (Table 6). The obtained root mean squared error of prediction (RMSEP) was slightly below the mean value of observed monthly growth in diameter (mean growth  =  0.325 mm.month−1, RMSEP = 0.279 mm.month−1). In general, the model underestimated growth when it was above 1 mm.month−1 (Figure 4). 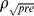There was no significant correlation between the selected variable and the residuals of the model mBIC (Inline graphic  =  4.6×10−6, pvalue > 0.99; ρsol  =  1.8×10−5, pvalue > 0.99; ρdtr  =  1.9×10−4, pvalue > 0.99; ρswc  =  6.1×10−6, pvalue > 0.99). Tree growth values increase linearly with extrasolar radiations (Figure 5), and a strong increase in tree growth occurred between 0 and 200 mm.month −1 of precipitation; above these values, the increase in tree growth was less pronounced and had a linear shape.

Table 6. Model parameters, standard errors, t values and posterior densities of the univariate (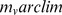Inline graphic) and complete (mBIC) analyses.

Model Parameter Effect Estimates Std. Error t value Variance Std. Dev. MCMC median MCMC mean HPD95 lower HPD95 upper pMCMC Pr(>|t|) RMSEP BIC R2 fixed R2
mBIC site.names random 0.0355 0.1885 0.1577 0.1596 0.1184 0.2038 0.2787 412.4698 29.79 50.25
Residual random 0.0800 0.2829 0.2845 0.2846 0.2713 0.2975
(Intercept) fixed −0.7247 0.1635 −4.4336 −0.7492 −1.0585 −0.4339 0.0001 0.0000
I(pre∧0.5) fixed 0.0118 0.0027 4.4017 0.0120 0.0067 0.0171 0.0001 0.0000
sol_m fixed 0.0024 0.0002 10.3592 0.0024 0.0019 0.0028 0.0001 0.0000
dtr fixed −0.0300 0.0078 −3.8291 −0.0283 −0.0430 −0.0139 0.0002 0.0001
swc fixed 0.2426 0.0674 3.5999 0.2492 0.1196 0.3817 0.0002 0.0003
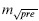
Inline graphic site.names random 0.0346 0.1861 0.1588 0.1608 0.1192 0.2057 0.2983 515.5249 19.82 42.99
Residual random 0.0914 0.3023 0.3038 0.3040 0.2901 0.3184
(Intercept) fixed −0.0158 0.0394 −0.4006 −0.0157 −0.0860 0.0562 0.6666 0.6888
I(pre∧0.5) fixed 0.0303 0.0020 15.1909 0.0303 0.0264 0.0343 0.0001 0.0000
msol site.names random 0.0414 0.2034 0.1695 0.1715 0.1296 0.2177 0.3043 556.2737 16.30 40.67
Residual random 0.0951 0.3084 0.3103 0.3104 0.2956 0.3245
(Intercept) fixed −1.0027 0.1042 −9.6261 −0.9997 −1.1959 −0.7884 0.0001 0.0000
sol_m fixed 0.0030 0.0002 13.4849 0.0030 0.0026 0.0035 0.0001 0.0000
mcld site.names random 0.0333 0.1825 0.1576 0.1594 0.1183 0.2040 0.3065 563.8953 15.56 39.81
Residual random 0.0965 0.3106 0.3120 0.3122 0.2975 0.3264
(Intercept) fixed −0.4837 0.0691 −6.9952 −0.4766 −0.6100 −0.3444 0.0001 0.0000
cld fixed 0.0115 0.0009 13.1090 0.0114 0.0097 0.0132 0.0001 0.0000
Mpre site.names random 0.0345 0.1856 0.1601 0.1621 0.1193 0.2073 0.3078 571.9796 14.82 39.34
Residual random 0.0972 0.3118 0.3133 0.3135 0.2992 0.3284
(Intercept) fixed 0.1542 0.0352 4.3855 0.1542 0.0933 0.2184 0.0001 0.0000
pre fixed 0.0011 0.0001 12.7430 0.0011 0.0009 0.0013 0.0001 0.0000
mdtr site.names random 0.0705 0.2655 0.1957 0.1982 0.1523 0.2514 0.3060 579.4892 14.60 40.01
Residual random 0.0962 0.3102 0.3134 0.3136 0.2998 0.3290
(Intercept) fixed 1.2160 0.0842 14.4368 1.1559 0.9919 1.3130 0.0001 0.0000
dtr fixed −0.0840 0.0066 −12.655 −0.0783 −0.0925 −0.0650 0.0001 0.0000
mvap site.names random 0.1335 0.3653 0.2128 0.2152 0.1607 0.2740 0.3063 596.8096 13.87 39.89
Residual random 0.0964 0.3105 0.3167 0.3169 0.3017 0.3314
(Intercept) fixed −1.1021 0.1306 −8.4356 −0.8118 −1.0723 −0.5445 0.0001 0.0000
vap fixed 0.0593 0.0048 12.3119 0.0472 0.0368 0.0579 0.0001 0.0000
mswc site.names random 0.0319 0.1785 0.1564 0.1582 0.1146 0.2039 0.3174 625.9566 9.77 35.49
Residual random 0.1034 0.3215 0.3229 0.3230 0.3082 0.3382
(Intercept) fixed −0.1696 0.0580 −2.9216 −0.1715 −0.2826 −0.0609 0.0038 0.0036
swc fixed 0.5807 0.0578 10.0435 0.5837 0.4723 0.7025 0.0001 0.0000
mtmn site.names random 0.0944 0.3072 0.2038 0.2063 0.1523 0.2625 0.3143 635.0120 9.65 36.71
Residual random 0.1015 0.3186 0.3231 0.3233 0.3085 0.3387
(Intercept) fixed −0.8685 0.1291 −6.7262 −0.6662 −0.9239 −0.4010 0.0001 0.0000
tmn fixed 0.0623 0.0062 10.0385 0.0517 0.0393 0.0656 0.0001 0.0000
mtmp site.names random 0.0396 0.1989 0.1693 0.1716 0.1238 0.2187 0.3299 701.8122 2.13 30.27
Residual random 0.1117 0.3343 0.3359 0.3361 0.3210 0.3522
(Intercept) fixed −0.3704 0.1566 −2.3648 −0.3351 −0.6345 −0.0317 0.0266 0.0182
tmp fixed 0.0283 0.0063 4.5113 0.0269 0.0146 0.0388 0.0001 0.0000
mpet site.names random 0.0329 0.1814 0.1600 0.1620 0.1178 0.2075 0.3320 709.0369 1.40 29.38
Residual random 0.1132 0.3364 0.3377 0.3379 0.3219 0.3532
(Intercept) fixed 0.5525 0.0724 7.6338 0.5589 0.4147 0.6951 0.0001 0.0000
pet fixed −0.0023 0.0006 −3.6135 −0.0023 −0.0036 −0.0011 0.0002 0.0003
mtmx site.names random 0.0400 0.2000 0.1717 0.1738 0.1278 0.2217 0.3334 721.5133 0.05 28.78
Residual random 0.1141 0.3378 0.3395 0.3396 0.3234 0.3550
(Intercept) fixed 0.4356 0.1755 2.4825 0.4047 0.0543 0.7394 0.0190 0.0132
tmx fixed −0.0039 0.0058 −0.6821 −0.0029 −0.0141 0.0086 0.6180 0.4954
m0 site.names random 0.0385 0.1962 0.1696 0.1717 0.1270 0.2214 0.3337 715.0984 0.00 28.69
Residual random 0.1142 0.3379 0.3395 0.3396 0.3240 0.3551
(Intercept) fixed 0.3184 0.0347 9.1815 0.3187 0.2571 0.3784 0.0001 0.0000
Open in a new tab

Model parameters, standard errors and t-values. The parameter values of posterior parameters densities (MCMC median and MCMC mean) and their 95% confidence intervals (Highest posterior density at 95% [HPD95] lower and upper) and associated p-value are estimated from a distribution of 10000 parameter samples computed with Monte Carlo Markov Chains from the model parameters. Goodness-of-fit criterion of the growth models are root mean square error of prediction (RMSEP), Bayesian Information Criterion (BIC), R2 of the fixed part of the model (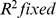Inline graphic) and R2 of the complete model (fixed plus random part).

Figure 4. Observed versus predicted diameter at breast height (dbh) growth under the model mBIC.

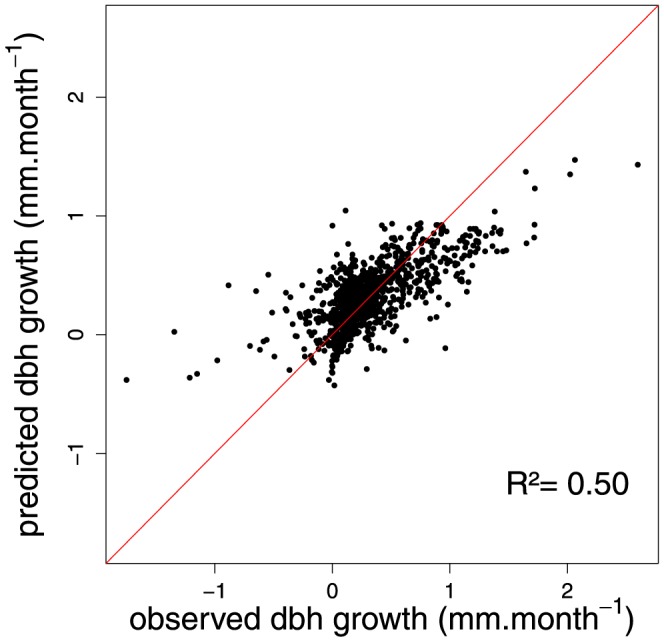
Figure 4

Open in a new tab

The red line is the identity line y  =  x. Note that the model underestimated the diameter growth above 1 mm.month−1.

Figure 5. Predicted diameter at breast height (dbh) growth under the model mBIC and relationship with precipitation and extra solar radiation.

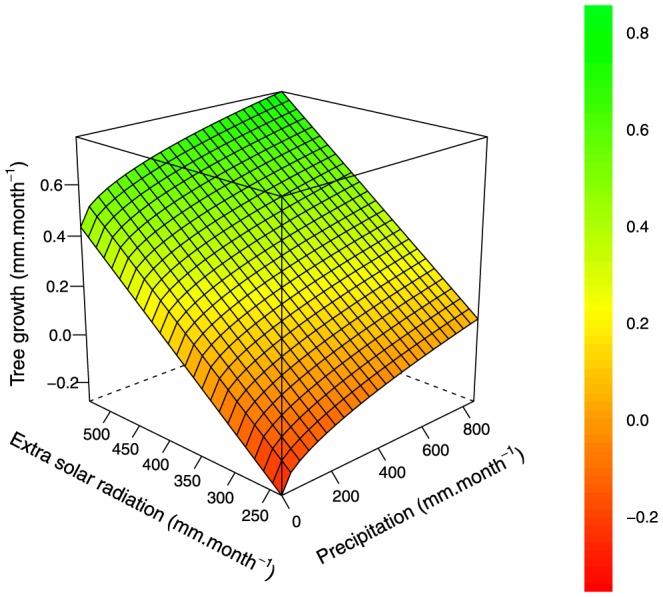
Figure 5

Open in a new tab

Predictions were computed using pre, sol, mean dtr, mean swc and mean of the random effect. The extra solar radiation unit is equivalent of evaporation in mm.month−1, 1 mm.month−1 equivalent of evaporation  =  2.45 MJ.m−2.month−1.

Discussion

Our meta-analysis provides the first overview of climate effects on tree growth variations at a seasonal time scale for tropical forest areas. Tree growth reveals a strong intra-annual seasonality at all sites (Table 5), including seasonally dry sites and wet tropical forests. We found a common climatic signal explaining 29.79% of the observed seasonality in forest growth (Table 6). Precipitation (19.82%) and extraterrestrial solar radiation (16.30%) were the major climate drivers. The tree growth average per site (i.e. the random site effect) explained 28.69% of overall growth variation, and a substantial fraction of variation (50%) in growth remained unexplained with our modeling framework. We have to acknowledge than our sample of 3412 trees could not be used to fully reproduce the complete behavior of all the tropical forests, however our analysis demonstrated that a common signal in the climate determinism of tree growth seasonality is observed at the pan-tropical scale.

Climate effect on tree growth

In this study, precipitation was found to be the major seasonal driver of tree growth. Precipitation strongly impacts tree growth, as directly observed in seasonal and unseasonal tropical climates [19], [35], [56]–[59] and as deduced from experimental forest droughts [60], [61]. The prominence of precipitation as a predictor of forest growth is slightly different from previous studies [62]; in French Guiana, we found that soil water availability was the main determinant of diameter growth, i.e. better than rainfall. Of course, both variables are strongly correlated (Figure 2), but this difference could be explained by some sites where relative soil water availability swc was at its maximum throughout the year despite marked precipitation seasonality (e.g. La Selva, CPM, Muara Bungo, Rio Cachoiera and Selangor). At the same time, the importance of solar radiation, sol, in the complete model (mBIC) reflects the obvious role of light in shaping tree growth (Figure 5). Solar radiation is directly linked to PPFD (Photosynthetic Photon Flux Density), which in turn drives carbon uptake and plant growth [29]. Some authors support the hypothesis that increasing surface solar radiation contributes to the increasing forest growth rate over the Amazon [63], [64]. It must be noted that the extraterrestrial solar radiation we used has a value above the real solar radiation value reaching the forest surface. Indeed, sol was computed as a monthly mean over 50 years and does not account for local cloud cover or aerosol radiation absorption.

Investigating the effects of temperature on the physiology of tropical forest trees [31], [65] is of primary importance today given the temperature increases expected over the next century [5], [7]. Some authors suggest that tropical trees are more sensitive to temperatures than other trees because (i) they live at or close to the highest annual average temperatures on Earth, and (ii) tropical species naturally encounter limited variation in temperatures (<4°C over 20° of latitude) [32]. Our results suggest that temperature variations are of secondary importance in shaping tropical tree seasonal growth; nevertheless, they do play a role. Minimal temperature was slightly positively correlated with tree growth, whereas maximal temperature had no effect. This positive relation between tree growth and temperature is not consistent with previous observations in Costa Rica [35], [66], where an increase in night-time temperatures had a negative effect on tree growth, and in East Africa [19], where maximum temperatures had a negative effect on tree growth. Such patterns were not found at our global working scale.

Tree growth variability in time and space

Our results suggest that most tropical trees experience seasonal cycling growth even in extremely wet environments, as already reported at la Selva [35]. On a pantropical scale, we showed that secondary growth was higher during the wet season; tree growth increased with precipitation and relative soil water content (Table 6). This result is not consistent with other studies that have shown that tropical forests are able to maintain or even to increase their productivity during the dry season [67]–[70]. This suggests different uses of carbohydrates. Some studies have reported that evergreen species in seasonally dry environments accumulate carbohydrates during the dry season because photosynthesis continues while wood production ceases [71] and that deciduous species accumulate carbohydrates at the onset of the dry season to support respiration costs when they are leafless [72], [73]. Some studies relied on the Enhanced Vegetation Index (EVI, an index of canopy photosynthetic capacity [30]) to highlight changes in forest phenology driven by the solar cycle [74], [75]. In the same way, a variation in the EVI has been observed for the entire Amazon region [30], and the link between phenology and the solar cycle has also been reported for Terra Firme forests [76]. The variability in tree growth at a seasonal scale is likely driven by climate seasonality and dependent on the seasonal allocation of carbohydrates to processes other than tree diameter growth, such as leaf and root production or respiration.

Stem shrinkage during dry periods may be an important limitation of this work [77]–[79], e.g. the negative value of mean annual tree growth at Pinkwae. Other negative monthly growth values exist at almost all the study sites. In a tropical forest in Ethiopia experiencing a strong seasonality, high-resolution electronic dendrometers have been combined with wood anatomy investigation to describe cambial growth dynamics [80]. These authors concluded that water scarcity during the long dry season induced cambial dormancy. Furthermore, after the onset of the rainy season, (i) bark swelling started quite synchronously among trees; (ii) bark swelling was maximum after few rainy days; and (iii) evergreen trees were able to quickly initiate wood formation. Recently at the Paracou forest site, some authors have showed that biomass increments were highly correlated between the first and the last quantile of trunk bark thickness and between the first and the last quantile of trunk bark density, suggesting that secondary growth is driven by cambial activity [75].

In this study, we focused on seasonal variation of tree growth, but the inter-site variance must be studied to build a full predictive model. At our pantropical working scale, there was no evident spatial auto-correlation. The site effect, i.e. the average growth of trees at a given site, is likely shaped by several additional environmental variables, such as soil fertility, forest floristic composition and competition for light and nutrients [81]–[83]. These effects were included in the model through the random site effect Inline graphic, and we assumed that these effects were constant over the study period. We also did not consider the different ontogenetic stages of trees and the ontogenetic growth trajectory that depends on complex environmental changes that may have occurred during the census period [84]. Recently, a study using LiDAR and a four-year diameter growth census demonstrated that variation in canopy metrics appeared to be essential to predict biomass growth [85]. Clearly, remote sensing methods, whether radar, LiDAR or optical [86], can help us to derive stand variables, especially canopy height, and therefore can be used as valuable additional predictors to monitor forest growth over large tropical areas.

Tropical tree growth under climate change

Globally, current IPCC scenarios predict an intensification of the dry season in tropical areas during the 21st century [7]. Amongst climate variables, our results highlighted the predominant role of precipitation in shaping seasonal forest growth. If a global rainfall reduction is confirmed in the future, it can be expected that tree growth will be affected (Figure 5). Climate change is not the only possible cause for reductions in precipitation; deforestation could lead to reductions in precipitation as the air passages over forests increase tropical rainfall intensity [4]. Solar radiation appeared almost as important as rainfall. Cloud reduction due to drier dry seasons, may subsequently improve tree growth. Our results suggest that, with the global changes observed, forest productivity due to tropical tree growth will encounter modifications due to change in climate seasonality.

Acknowledgments

We thank James Grogan and Mark Schulze; the French Institute of Pondichry and Raphael Pelissier; and Vincent Grgoire for provided the tree growth data of Marajoara, Attapadi and Muara Bungo respectively. We thank Morag Mcdonald, Adrian Newton and two anonymous referees for useful comments on previous drafts of the manuscript.

Funding Statement

Funding came from the project Climfor (Fondation pour la Recherche sur la Biodiversité, www.fondationbiodiversite.fr/), from the project Guyasim (European structural fundings, PO-Feder, http://www.europe-guyane.eu/index.php?option=com_content&task=view&id=14&Itemid=206), and from the Fapesp (Fundação de Amparo à Pesquisa do Estado de São Paulo, processo 13/14520-6, http://www.bv.fapesp.br/pt/bolsas/146751/quantificacao-e-modelagem-da-sazonalidade-da-producao-primaria-liquida-florestal-pantropical-usando-/). This work has also benefited from an “Investissement d'Avenir” grant managed by Agence Nationale de la Recherche (CEBA, ref. ANR-10-LABX-0025). The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.

References

  • 1. Malhi Y, Wright J (2004) Spatial patterns and recent trends in the climate of tropical rainforest regions. Philosophical Transactions of the Royal Society of London Series B-Biological Sciences 359: 311–329. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 2. Solomon S, Plattner GK, Knutti R, Friedlingstein P (2009) Irreversible climate change due to carbon dioxide emissions. Proceedings of the National Academy of Sciences of the United States of America 106: 1704–1709. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 3. Harris NL, Hall CAS, Lugo AE (2008) Estimates of species- and ecosystem-level respiration of woody stems along an elevational gradient in the Luquillo Mountains, Puerto Rico. Ecological Modelling 216: 253–264. [Google Scholar]
  • 4. Spracklen D, Arnold S, Taylor C (2012) Observations of increased tropical rainfall preceded by air passage over forests. Nature 489: 282–285. [DOI] [PubMed] [Google Scholar]
  • 5. Malhi Y, Aragao LEOC, Galbraith D, Huntingford C, Fisher R, et al. (2009) Exploring the likelihood and mechanism of a climate-change-induced dieback of the Amazon rainforest. Proceedings of the National Academy of Sciences of the United States of America 106: 20610–20615. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 6. Feng X, Porporato A, Rodriguez-Iturbe I (2013) Changes in rainfall seasonality in the tropics. Nature Climate Change 3: 811–815. [Google Scholar]
  • 7.Solomon S, Qin D, Manning M, Marquis M, Averyt K, et al., editors (2007) Climate Change 2007, the Fourth Assessment Report (AR4). Intergovernmental Panel on Climate Change, 103 pp. 14
  • 8. Orlowsky B, Seneviratne SI (2012) Global changes in extreme events: regional and seasonal dimension. Climatic Change 110: 669–696. [Google Scholar]
  • 9.Field C, Barros V, Stocker T, Qin D, Dokken D, et al. (2012) IPCC, 2012: Managing the risks of extreme events and disasters to advance climate change adaptation. A special report of Working Groups I and II of the Intergovernmental Panel on Climate Change. B M J Publishing Group. doi: 10.1136/jech-2012-201045. [DOI]
  • 10. Pan Y, Birdsey RA, Fang J, Houghton R, Kauppi PE, et al. (2011) A large and persistent carbon sink in the world's forests. Science 333: 988–993. [DOI] [PubMed] [Google Scholar]
  • 11. Houghton R (2005) Aboveground forest biomass and the global carbon balance. Global Change Biology 11: 945–958. [Google Scholar]
  • 12. Saatchi SS, Houghton RA, Alvala RCDS, Soares JV, Yu Y (2007) Distribution of aboveground live biomass in the Amazon basin. Global Change Biology 13: 816–837. [Google Scholar]
  • 13. Bonan GB (2008) Forests and climate change: forcings, feedbacks, and the climate benefits of forests. Science 320: 1444–1449. [DOI] [PubMed] [Google Scholar]
  • 14. Clark DA, Piper SC, Keeling CD, Clark DB (2003) Tropical rain forest tree growth and atmospheric carbon dynamics linked to interannual temperature variation during 1984–2000. Proceedings of the National Academy of Sciences of the United States of America 100: 5852–5857. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 15. Chave J, Condit R, Lao S, Caspersen JP, Foster RB, et al. (2003) Spatial and temporal variation of biomass in a tropical forest: results from a large census plot in Panama. Journal of Ecology 91: 240–252. [Google Scholar]
  • 16. Lewis SL, Lloyd J, Sitch S, Mitchard ETA, Laurance WF (2009) Changing ecology of tropical forests: evidence and drivers. Annual Review of Ecology Evolution and Systematics 40: 529–549. [Google Scholar]
  • 17. Feeley KJ, Davies SJ, Ashton PS, Bunyavejchewin S, Supardi MNN, et al. (2007) The role of gap phase processes in the biomass dynamics of tropical forests. Proceedings of the Royal Society B-Biological Sciences 274: 2857–2864. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 18. Metcalf CJE, Clark JS, Clark DA (2009) Tree growth inference and prediction when the point of measurement changes: modelling around buttresses in tropical forests. Journal of Tropical Ecology 25: 1–12. [Google Scholar]
  • 19. Gliniars R, Becker GS, Braun D, Dalitz H (2013) Monthly stem increment in relation to climatic variables during 7 years in an east african rainforest. Trees 27: 1129–1138. [Google Scholar]
  • 20. Sombroek W (2001) Spatial and temporal patterns of Amazon rainfall - Consequences for the planning of agricultural occupation and the protection of primary forests. Ambio 30: 388–396. [DOI] [PubMed] [Google Scholar]
  • 21. Xiao X, Hagen S, Zhang Q, Keller M, Moore B III (2006) Detecting leaf phenology of seasonally moist tropical forests in South America with multi-temporal MODIS images. Remote Sensing of Environment 103: 465–473. [Google Scholar]
  • 22. Marengo J (1992) Interannual variability of surface climate in the Amazon basin. International Journal of Climatology 12: 853–863. [Google Scholar]
  • 23. Phillips OL, Aragao LEOC, Lewis SL, Fisher JB, Lloyd J, et al. (2009) Drought sensitivity of the Amazon rainforest. Science 323: 1344–1347. [DOI] [PubMed] [Google Scholar]
  • 24. Tian HQ, Melillo JM, Kicklighter DW, McGuire AD, Helfrich JVK, et al. (1998) Effect of interannual climate variability on carbon storage in Amazonian ecosystems. Nature 396: 664–667. [Google Scholar]
  • 25. Borchert R (1998) Responses of tropical trees to rainfall seasonality and its long-term changes. Climatic Change 39: 381–393. [Google Scholar]
  • 26. Granier A, Breda N, Biron P, Villette S (1999) A lumped water balance model to evaluate duration and intensity of drought constraints in forest stands. Ecological Modelling 116: 269–283. [Google Scholar]
  • 27. Zomer RJ, Trabucco A, Bossio DA, Verchot LV (2008) Climate change mitigation: A spatial analysis of global land suitability for clean development mechanism afforestation and reforestation. Agriculture Ecosystems and Environment 126: 67–80. [Google Scholar]
  • 28. Wagner F, Herault B, Stahl C, Bonal D, Rossi V (2011) Modeling water availability for trees in tropical forests. Agricultural and Forest Meteorology 151: 1202–1213. [Google Scholar]
  • 29. Graham EA, Mulkey SS, Kitajima K, Phillips NG, Wright SJ (2003) Cloud cover limits net CO2 uptake and growth of a rainforest tree during tropical rainy seasons. Proceedings of the National Academy of Sciences of the United States of America 100: 572–576. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 30.Huete AR, Didan K, Shimabukuro YE, Ratana P, Saleska SR, et al. (2006) Amazon rainforests green-up with sunlight in dry season. Geophysical Research Letters 33.
  • 31. Lloyd J, Farquhar GD (2008) Effects of rising temperatures and [CO2] on the physiology of tropical forest trees. Philosophical Transactions of the Royal Society B-Biological Sciences 363: 1811–1817. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 32. Wright SJ (2010) The future of tropical forests. Year in Ecology and Conservation Biology 2010 1195: 1–27. [DOI] [PubMed] [Google Scholar]
  • 33.Doughty CE, Goulden ML (2008) Are tropical forests near a high temperature threshold? Journal of Geophysical Research-Biogeosciences 113.
  • 34. Doughty CE (2011) An in situ leaf and branch warming experiment in the Amazon. Biotropica 43: 658–665. [Google Scholar]
  • 35. Clark DB, Clark DA, Oberbauer SF (2010) Annual wood production in a tropical rain forest in NE Costa Rica linked to climatic variation but not to increasing CO(2). Global Change Biology 16: 747–759. [Google Scholar]
  • 36. Mitchell T, Jones P (2005) An improved method of constructing a database of monthly climate observations and associated high-resolution grids. International Journal of Climatology 25: 693–712. [Google Scholar]
  • 37. Ekstrom M, Jones PD, Fowler HJ, Lenderink G, Buishand TA, et al. (2007) Regional climate model data used within the SWURVE project 1: projected changes in seasonal patterns and estimation of PET. Hydrology and Earth System Sciences 11: 1069–1083. [Google Scholar]
  • 38. Allen R, Smith M, Pereira LS, Perrier A (1994) An update for the calculation of reference evapotranspiration. Journal of the ICID 43: 35–92. [Google Scholar]
  • 39.Allen R, Pereira L, Raes D, Smith M (1998) Crop evapotranspiration: Guidelines for computing crop requirements. irrigation and drainage paper no. 56. Rome, ItalyTechnical report, FAO
  • 40. Batjes N (1997) A world dataset of derived soil properties by FAO-UNESCO soil unit for global modelling. Soil Use and Management 13: 9–16. [Google Scholar]
  • 41.Batjes NH (2012) Isric-wise derived soil properties on a 5 by 5 arc-minutes global grid (version 1.2). Technical report, ISRIC - World Soil Information.
  • 42.Schenk H, Jackson R (2009) Islscp ii ecosystem rooting depths. In: Hall, Forrest G., G. Collatz, B. Meeson, S. Los, E. Brown de Colstoun, and D. Landis (eds.). ISLSCP Initiative II Collection. Data set. Available: http://daac.ornl.gov/, from Oak Ridge National Laboratory Distributed Active Archive Center, Oak Ridge, Tennessee, U.S.A. doi: 10.3334/ORNLDAAC/929. [DOI]
  • 43. Borchert R (1999) Climatic periodicity, phenology, and cambium activity in tropical dry forest trees. Iawa Journal 20: 239–247. [Google Scholar]
  • 44. Couralet C, Sterck FJ, Sass-Klaassen U, Van Acker J, Beeckman H (2010) Species-specific growth responses to climate variations in understory trees of a central african rain forest. Biotropica 42: 503–511. [Google Scholar]
  • 45. Moran PAP (1950) Notes on continuous stochastic phenomena. Biometrika 37: 17–23. [PubMed] [Google Scholar]
  • 46. Paradis E, Claude J, Strimme K (2004) APE: analyses of phylogenetics and evolution in R language. Bioinformatics 20: 289–290. [DOI] [PubMed] [Google Scholar]
  • 47.Barnett A, Dobson A (2010) Analysing seasonal health data. Springer.
  • 48.Bates D, Maechler M, Bolker B (2013) lme4: Linear mixed-effects models using S4 classes. Available: http://CRAN.R-project.org/package=lme4. R package version 0.999999-2.
  • 49. Gurka M (2006) Selecting the best linear mixed model under REML. American Statistician 60: 19–26. [Google Scholar]
  • 50. Magee L (1990) R2 Measures based on Wald and likelihood ratio joint significance tests. American Statistician 44: 250–253. [Google Scholar]
  • 51. Vonesh E, Chinchilli V, Pu K (1996) Goodness-of-fit in generalized nonlinear mixed-effects models. Biometrics 52: 572–587. [PubMed] [Google Scholar]
  • 52. Orelien JG, Edwards LJ (2008) Fixed-effect variable selection in linear mixed models using statistics. Computational Statistics & Data Analysis 52: 1896–1907. [Google Scholar]
  • 53. Schwarz G (1978) Estimating the dimension of a model. Annals of Statistics 6 (2): 461–464. [Google Scholar]
  • 54. Burnham K, Anderson D (2004) Multimodel inference - understanding AIC and BIC in model selection. Sociological Methods & Research 33: 261–304. [Google Scholar]
  • 55.FAO (2012) Forest resources assessment working paper 179, global ecological zones for forest reporting: 2010 update. Technical report, Food and Agriculture Organization of the United Nations.
  • 56. Nath CD, Dattaraja HS, Suresh HS, Joshi NV, Sukumar R (2006) Patterns of tree growth in relation to environmental variability in the tropical dry deciduous forest at mudumalai, southern india. Journal of Biosciences 31: 651–669. [DOI] [PubMed] [Google Scholar]
  • 57. Baker TR, Swaine MD, Burslem DFRP (2003) Variation in tropical forest growth rates: combined effects of functional group composition and resource availability. Perspectives in Plant Ecology Evolution and Systematics 6: 21–36. [Google Scholar]
  • 58. Toledo M, Poorter L, Pena-Claros M, Alarcon A, Balcazar J, et al. (2011) Climate is a stronger driver of tree and forest growth rates than soil and disturbance. Journal of Ecology 99: 254–264. [Google Scholar]
  • 59. Vieira S, de Camargo PB, Selhorst D, da Silva R, Hutyra L, et al. (2004) Forest structure and carbon dynamics in Amazonian tropical rain forests. Oecologia 140: 468–479. [DOI] [PubMed] [Google Scholar]
  • 60. Lola da Costa AC, Galbraith D, Almeida S, Tanaka Portela BT, da Costa M, et al. (2010) Effect of 7 yr of experimental drought on vegetation dynamics and biomass storage of an eastern Amazonian rainforest. New Phytologist 187: 579–591. [DOI] [PubMed] [Google Scholar]
  • 61.Nepstad DC, Moutinho P, Dias MB, Davidson E, Cardinot G, et al. (2002) The effects of partial throughfall exclusion on canopy processes, aboveground production, and biogeochemistry of an amazon forest. Journal of Geophysical Research-Atmospheres 107.
  • 62.Wagner F, Rossi V, Stahl C, Bonal D, Herault B (2012) Water availability is the main climate driver of neotropical tree growth. Plos One 7. [DOI] [PMC free article] [PubMed]
  • 63. Nemani R, Keeling C, Hashimoto H, Jolly W, Piper S, et al. (2003) Climate-driven increases in global terrestrial net primary production from 1982 to 1999. Science 300: 1560–1563. [DOI] [PubMed] [Google Scholar]
  • 64. Arias PA, Fu R, Hoyos CD, Li W, Zhou L (2011) Changes in cloudiness over the Amazon rainforests during the last two decades: diagnostic and potential causes. Climate Dynamics 37: 1151–1164. [Google Scholar]
  • 65. Chambers JQ, Higuchi N, Teixeira LM, dos Santos J, Laurance SG, et al. (2004) Response of tree biomass and wood litter to disturbance in a Central Amazon forest. Oecologia 141: 596–611. [DOI] [PubMed] [Google Scholar]
  • 66. Clark DA, Clark DB, Oberbauer SF (2013) Field-quantified responses of tropical rainforest aboveground productivity to increasing co2 and climatic stress, 1997–2009. Journal of Geophysical Research: Biogeosciences 118 (2): 783–794. [Google Scholar]
  • 67. Saleska SR, Miller SD, Matross DM, Goulden ML, Wofsy SC, et al. (2003) Carbon in Amazon forests: Unexpected seasonal fluxes and disturbance-induced losses. Science 302: 1554–1557. [DOI] [PubMed] [Google Scholar]
  • 68.Hutyra LR, Munger JW, Saleska SR, Gottlieb E, Daube BC, et al. (2007) Seasonal controls on the exchange of carbon and water in an Amazonian rain forest. Journal of Geophysical Research-Biogeosciences 112.
  • 69. Baker PJ, Palmer JG, D'Arrigo R (2008) The dendrochronology of Callitris intratropica in northern Australia: annual ring structure, chronology development and climate correlations. Australian Journal of Botany 56: 311–320. [Google Scholar]
  • 70. Bonal D, Bosc A, Ponton S, Goret JY, Burban B, et al. (2008) Impact of severe dry season on net ecosystem exchange in the Neotropical rainforest of French Guiana. Global Change Biology 14: 1917–1933. [Google Scholar]
  • 71. Wurth MKR, Pelaez-Riedl S, Wright SJ, Korner C (2005) Non-structural carbohydrate pools in a tropical forest. Oecologia 143: 11–24. [DOI] [PubMed] [Google Scholar]
  • 72. Poorter L, Kitajima K (2007) Carbohydrate storage and light requirements of tropical moist and dry forest tree species. Ecology 88: 1000–1011. [DOI] [PubMed] [Google Scholar]
  • 73. Janzen D, Wilson D (1974) The cost of being dormant in the tropics. Biotropica 6: 260–262. [Google Scholar]
  • 74. Pennec A, Gond V, Sabatier D (2011) Tropical forest phenology in French Guiana from MODIS time series. Remote Sensing Letters 2 4: 337–345. [Google Scholar]
  • 75. Wagner F, Rossi V, Stahl C, Bonal D, Hérault B (2013) Asynchronism in leaf and wood production in tropical forests: a study combining satellite and ground–based measurements. Biogeosciences Discussion 10: 8247–8281. [Google Scholar]
  • 76. Bradley AV, Gerard FF, Barbier N, Weedon GP, Anderson LO, et al. (2011) Relationships between phenology, radiation and precipitation in the Amazon region. Global Change Biology 17: 2245–2260. [Google Scholar]
  • 77. Sheil D (2003) Growth assessment in tropical trees: large daily diameter fluctuations and their concealment by dendrometer bands. Canadian Journal of Forest Research-Revue Canadienne De Recherche Forestiere 33: 2027–2035. [Google Scholar]
  • 78. Baker T, Affum-Baffoe K, Burslem D, Swaine M (2002) Phenological differences in tree water use and the timing of tropical forest inventories: conclusions from patterns of dry season diameter change. Forest Ecology and Management 171: 261–274. [Google Scholar]
  • 79. Stahl C, Burban B, Bompy F, Jolin ZB, Sermage J, et al. (2010) Seasonal variation in atmospheric relative humidity contributes to explaining seasonal variation in trunk circumference of tropical rain-forest trees in French Guiana. Journal of Tropical Ecology 26: 393–405. [Google Scholar]
  • 80. Krepkowski J, Brauning A, Gebrekirstos A, Strobl S (2011) Cambial growth dynamics and climatic control of different tree life forms in tropical mountain forest in Ethiopia. Trees-Structure and Function 25: 59–70. [Google Scholar]
  • 81. Herault B, Ouallet J, Blanc L, Wagner F, Baraloto C (2010) Growth responses of neotropical trees to logging gaps. Journal of Applied Ecology 47: 821–831. [Google Scholar]
  • 82. Uriarte M, Canham C, Thompson J, Zimmerman J (2004) A neighborhood analysis of tree growth and survival in a hurricane-driven tropical forest. Ecological Monographs 74: 591–614. [Google Scholar]
  • 83.Rueger N, Berger U, Hubbell SP, Vieilledent G, Condit R (2011) Growth strategies of tropical tree species: disentangling light and size effects. Plos One 6. [DOI] [PMC free article] [PubMed]
  • 84. Herault B, Bachelot B, Poorter L, Rossi V, Bongers F, et al. (2011) Functional traits shape ontogenetic growth trajectories of rain forest tree species. Journal of Ecology 99: 1431–1440. [Google Scholar]
  • 85. Stark SC, Leitold V, Wu JL, Hunter MO, de Castilho CV, et al. (2012) Amazon forest carbon dynamics predicted by profiles of canopy leaf area and light environment. Ecology Letters 15: 1406–1414. [DOI] [PubMed] [Google Scholar]
  • 86. Goetz S, Dubayah R (2011) Advances in remote sensing technology and implications for measuring and monitoring forest carbon stocks and change. Carbon Management 2(3): 231–244. [Google Scholar]
  • 87. Brando PM, Nepstad DC, Davidson EA, Trumbore SE, Ray D, et al. (2008) Drought effects on litterfall, wood production and belowground carbon cycling in an Amazon forest: results of a throughfall reduction experiment. Philosophical Transactions of the Royal Society of London Series B-Biological Sciences 363: 1839–1848. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 88. Nepstad DC, Tohver IM, Ray D, Moutinho P, Cardinot G (2007) Mortality of large trees and lianas following experimental drought in an Amazon forest. Ecology 88: 2259–2269. [DOI] [PubMed] [Google Scholar]
  • 89. Rozendaal DMA, Zuidema PA (2011) Dendroecology in the tropics: a review. Trees-Structure and Function 25: 3–16. [Google Scholar]
  • 90. Grogan J, Schulze M (2012) The Impact of Annual and Seasonal Rainfall Patterns on Growth and Phenology of Emergent Tree Species in Southeastern Amazonia, Brazil. Biotropica 44: 331–340. [Google Scholar]
  • 91. Condit R, Aguilar S, Hernandez A, Perez R, Lao S, et al. (2004) Tropical forest dynamics across a rainfall gradient and the impact of an El Nino dry season. Journal of Tropical Ecology 20: 51–72. [Google Scholar]
  • 92. Way DA, Oren R (2010) Differential responses to changes in growth temperature between trees from different functional groups and biomes: a review and synthesis of data. Tree Physiology 30: 669–688. [DOI] [PubMed] [Google Scholar]
  • 93. Braswell BH, Schimel DS, Linder E, Moore B (1997) The response of global terrestrial ecosystems to interannual temperature variability. Science 278: 870–872. [Google Scholar]
  • 94. Brienen RJW, Wanek W, Hietz P (2011) Stable carbon isotopes in tree rings indicate improved water use efficiency and drought responses of a tropical dry forest tree species. Trees-Structure and Function 25: 103–113. [Google Scholar]
  • 95. Enquist BJ, Leffler AJ (2001) Long-term tree ring chronologies from sympatric tropical dry-forest trees: individualistic responses to climatic variation. Journal of Tropical Ecology 17: 41–60. [Google Scholar]
  • 96. Laurance SGW, Laurance WF, Nascimento HEM, Andrade A, Fearnside PM, et al. (2009) Longterm variation in Amazon forest dynamics. Journal of Vegetation Science 20: 323–333. [Google Scholar]
  • 97. Brando PM, Goetz SJ, Baccini A, Nepstad DC, Beck PSA, et al. (2010) Seasonal and interannual variability of climate and vegetation indices across the Amazon. Proceedings of the National Academy of Sciences of the United States of America 107: 14685–14690. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 98. Franks PJ, Farquhar GD (1999) A relationship between humidity response, growth form and photosynthetic operating point in C-3 plants. Plant Cell and Environment 22: 1337–1349. [Google Scholar]
  • 99. Reichstein M, Tenhunen J, Roupsard O, Ourcival J, Rambal S, et al. (2002) Ecosystem respiration in two Mediterranean evergreen Holm Oak forests: drought effects and decomposition dynamics. Functional Ecology 16: 27–39. [Google Scholar]
  • 100. Brauning A, Volland-Voigt F, Burchardt I, Ganzhi O, Nauss T, et al. (2009) Climatic control of radial growth of Cedrela montana in a humid mountain rainforest in southern Ecuador. Erdkunde 63: 337–345. [Google Scholar]
  • 101. Cardoso FCG, Marques R, Botosso PC, Marques MCM (2012) Stem growth and phenology of two tropical trees in contrasting soil conditions. Plant and Soil 354: 269–281. [Google Scholar]
  • 102. da Silva R, dos Santos J, Tribuzy E, Chambers J, Nakamura S, et al. (2002) Diameter increment and growth patterns for individual tree growing in Central Amazon, Brazil. Forest Ecology and Management 166: 295–301. [Google Scholar]
  • 103. Daubenmire R (1972) Phenology and other characteristics of tropical semi-deciduous forest in north-western Costa Rica. Journal of Ecology 60: 147–170. [Google Scholar]
  • 104.Detienne P, Barbier C (1988) Rythmes de croissance de quelques essences de guyane française. Revue Bois et Forets des Tropiques 3eme Trimestre.
  • 105. Devineau JL (1991) The variability of girth increment of trees in the semi-deciduous tropical forests of Lamto, Ivory-Coast. Revue d'Ecologie-La Terre Et La Vie 46: 95–124. [Google Scholar]
  • 106.Figueira A, Miller S, de Sousa C, Menton M, Maia A, et al. (2011) Lba-eco cd-04 dendrometry, km 83 tower site, tapajos national forest, brazil. data set. Available: http://daac.ornl.gov, from oak ridge national laboratory distributed active archive center, oak ridge, tennessee, u.s.a. doi: 10.3334/ornldaac/989. [DOI]
  • 107.Gliniars R, Dalitz H (2012) data from BIOTA East Africa.
  • 108. Lieberman D (1982) Seasonality and phenology in a dry tropical forest in Ghana. Journal of Ecology 70: 791–806. [Google Scholar]
  • 109. Lisi CS, Tomazello M, Botoss PC, Roig FA, Maria VRB, et al. (2008) Tree-ring formation, radial increment periodicity, and phenology of tree species from a seasonal semi-deciduous forest in southeast Brazil. Iawa Journal 29: 189–207. [Google Scholar]
  • 110. Lopez-Ayala J, Valdez-Hernandez J, Terrazas T, Valdez-Lazalde J (2006) Diameter growth of tree species in a semideciduous tropical forest at Colima, Mexico. Agrociencia 40: 139–147. [Google Scholar]
  • 111. Ohashi Y, Sahri M, Yoshizawa N, Itoh T (2001) Annual rhythm of xylem growth in rubberwood (Hevea brasiliensis) trees grown in Malaysia. Holzforschung 55: 151–154. [Google Scholar]
  • 112. Ohashi S, Okada N, Nobuchi T, Siripatanadilok S, Veenin T (2009) Detecting invisible growth rings of trees in seasonally dry forests in Thailand: isotopic and wood anatomical approaches. Trees-Structure and Function 23: 813–822. [Google Scholar]
  • 113. Oliveira JM, Santarosa E, Pillar VD, Roig FA (2009) Seasonal cambium activity in the subtropical rain forest tree Araucaria angustifolia. Trees-Structure and Function 23: 107–115. [Google Scholar]
  • 114. Pelissier R, Pascal JP (2000) Two-year tree growth patterns investigated from monthly girth records using dendrometer bands in a wet evergreen forest in India. Journal of Tropical Ecology 16: 429–446. [Google Scholar]
  • 115.Vincent G (2012) data from IRD-World Agroforestry Center.
  • 116. Volland-Voigt F, Brauning A, Ganzhi O, Peters T, Maza H (2011) Radial stem variations of Tabebuia chrysantha (Bignoniaceae) in different tropical forest ecosystems of southern Ecuador. Trees-Structure and Function 25: 39–48. [Google Scholar]
  • 117. Worbes M (1999) Annual growth rings, rainfall-dependent growth and long-term growth patterns of tropical trees from the Caparo Forest Reserve in Venezuela. Journal of Ecology 87: 391–403. [Google Scholar]
  • 118. Zanon MLB, Finger CAG (2010) Relationship of meteorological variables with the growth of Araucaria angustifolia (Bertol.) Kuntze trees in implanted stands. Ciencia Florestal 20: 467–476. [Google Scholar]

Articles from PLoS ONE are provided here courtesy of PLOS

RESOURCES