Skip to main content
PMC home page
NIHPA Author Manuscripts logoLink to NIHPA Author Manuscripts
. Author manuscript; available in PMC: 2014 Mar 26.
Published in final edited form as: Phys Med Biol. 2014 Feb 7;59(4):961–973. doi: 10.1088/0031-9155/59/4/961

Global point signature for shape analysis of carpal bones

Abhijit J Chaudhari 1, Richard M Leahy 2, Barton L Wise 3, Nancy E Lane 3, Ramsey D Badawi 1,4, Anand A Joshi 2
PMCID: PMC3966902  NIHMSID: NIHMS564423  PMID: 24503490

Abstract

We present a method based on spectral theory for the shape analysis of carpal bones of the human wrist. We represent the cortical surface of the carpal bone in a coordinate system based on the eigensystem of the two-dimensional Helmholtz equation. We employ a metric—global point signature (GPS)—that exploits the scale and isometric invariance of eigenfunctions to quantify overall bone shape. We use a fast finite-element-method to compute the GPS metric. We capitalize upon the properties of GPS representation—such as stability, a standard Euclidean (ℓ2) metric definition, and invariance to scaling, translation and rotation—to perform shape analysis of the carpal bones of ten women and ten men from a publicly-available database. We demonstrate the utility of the proposed GPS representation to provide a means for comparing shapes of the carpal bones across populations.

Keywords: carpal bone, shape comparison, global point signature, morphometry, eigenfunctions, wrist

1. Introduction

The human wrist consists of eight carpal bones, each possessing a unique shape. The morphometric features of carpal bones such as curvature and shape are intimately linked to the resulting mechanics of the corresponding joint (Kauer 1980, Nakamura et al 2000, Crisco et al 2005, Burgess 1990, van de Giessen et al 2012). Abnormal joint mechanics related to bone shape may produce high levels of focal stress across the joint (Felson 2013, van de Giessen et al 2012), and hence have been associated with the risk of wrist instability (Taleisnik 1988) and osteoarthritis (Brandt et al 2008, Lane et al 2011). Detailed quantitative shape analysis of carpal bones therefore presents the potential to allow for the investigation of biomechanical properties of the wrist joints, and enables the detection of abnormal wrist pathologies. Further, bone shape information may find utility in the development of patient-specific prostheses (Modgil et al 2002), determining skeletal growth and maturity patterns (Gilsanz and Ratib 2005, Pietka et al 2001), in reconstructive surgery (Craigen and Stanley 1995), and studying carpal bone shape across species (Tocheri et al 2007).

Quantitative analysis of bone shape may allow the identification of unique phenotypes across populations (Crisco et al 1999). Such studies are possible with the availability of databases of normal and abnormal pathologies. A digital database of the wrist bones of healthy individuals was created by Moore et al (2007) and is publicly available from that article's website. The database consists of cortical surfaces of the eight carpal bones, the proximal cortical surfaces of the five metacarpal bones and the distal cortical surfaces of the radius and ulna (figure 1) for both hands in the neutral position for healthy women and men. The same group of researchers measured the size of the bounding box placed around the individual carpal bones whose sides were parallel to the principal axes of inertia (Crisco et al 2005). They found that although the size of the carpal bone, based on the bounding box dimensions, in women was significantly smaller than those in men, individual carpal bone size, again based on the bounding box dimensions, as a percentage of the entire carpus did not differ based on sex indicating no systematic, sex-specific variations in bone size. A limitation, also noted by the authors of that article, was that their analysis measured only the linear dimension of the bones and did not incorporate the detailed analyses of shape differences. In a separate cohort, van der Giessen et al (2010) used statistical shape modeling (Cootes et al 1995) to show shape variation for the scaphoid and lunate in the population. The same research group further employed the method for 4D motion modeling of the carpal bones (van de Giessen et al 2012). The proposed method however required a large (>50), robust, well-characterized training data set that governed method accuracy. The bone shapes also needed to be co-registered before analysis and the study did not explicitly compare across populations.

Figure 1.

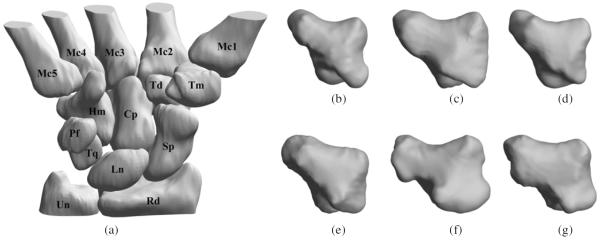
Figure 1

Open in a new tab

The digital carpal bone database and morphometric diversity. (a) A 3D rendering of the bones of the right wrist in a healthy female. The scaphoid (Sp), lunate (Ln), and triquetrum (Tq) are located proximal to the body and articulate with the radius (Rd). The trapezium (Tm), trapezoid (Td), capitate (Cp), and hamate (Hm) adjoin the five metacarpals (Mc1–5) of the wrist. The pisiform (Pf) is generally considered an accessory ossicle and articulates only with the triquetrum (Belsole et al 1988, Kauer 1980). The styloid process of the ulna (Un) projects from the medial and back part of the bone, while the hook of the hamate protrudes on the palmar aspect. 3D renderings of the surfaces of the trapezium for three women ((b), (c), and (d)) and three men ((e), (f), and (g)) from the database.

In this paper we use a representation that characterizes the shape of the cortical surface of a carpal bone in terms of a coordinate system based on the eigensystem of the 2D Helmholtz equation. The representation exploits the isometric invariance of the eigenfunctions and introduces a metric, global point signature (GPS) (Rustamov 2007, Reuter 2010), that quantifies overall bone shape. We present a fast finite-element-method (FEM) for computing the GPS coordinates. We demonstrate the utility of this representation for two applications using data from the publicly-available database (Moore et al 2007): (1) analysis of the differences in carpal bone shapes between women and men, and (2) analysis of carpal bone shape differences between the right and left hand across the population.

2. Methods

2.1. Global Point Signature (GPS)-based bone shape representation

Quantitative comparison of shapes is a fundamental problem in computer vision and medical imaging. The conventional representation of surfaces is by embedding manifolds in R3. This is not ideal for shape comparisons since identical shapes can have significantly different representations in 3D space due to isometric transformations generated by Euclidean motion. For our analysis we model the bone surface S as a homogeneous vibrating membrane based on spectral theory (Rustamov 2007, Reuter 2010). Its harmonic behavior is therefore governed by the 2D Helmholtz equation (Riley et al 2006, Rosenberg 1997). The eigenspectrum of the Laplacian (or the Laplace–Beltrami operator) generates a representation of the shape that is invariant to Euclidean motion and provides a new way to quantitatively measure surface differences and perform detailed shape analysis. This invariant spectral geometric representation of surfaces is termed the GPS. Under this representation, since surfaces are modeled as vibrating membranes, the Laplace–Beltrami eigenspectrum corresponds to the modes of vibrations of this membrane. Thus the GPS representation encodes information about the modes of vibration of membranes (surface patches) as the basis for shape modeling. The Helmholtz equation for 2D surfaces with the Neumann boundary condition, written to compute the spectral components of the Laplace–Beltrami operator, is given by:

{ΔΦ(s)=λΦ(s)∂Φ(s)∂n→∣∂s=0,∀s∈S.} (1)

where Δ denotes the Laplacian operator defined over the geometry of S, Φ(s) represents an eigenfunction with eigenvalue λ, ∂S is the boundary of the surface patch, and n→ is the normal to the surface patch. The eigenfunctions Φ0, Φ1, Φ2, … are sorted according to the ascending order of the eigenvalues λ0, λ1, λ2, …. We note that the zeroth eigenvalue is λ0 = 0 and the corresponding eigenvector is constant-valued over the whole surface. Since it does not contain shape information, we ignore it for this analysis. We then use the remaining eigenfunctions and eigenvalues to define the GPS embedding of the surface S in the spectral domain by the map:

GPS(S(s))=(1λ1Φ1(s),1λ2Φ2(s),1λ3Φ3(s),…),s∈S (2)

where Φ1, Φ2, … are eigenfunctions with corresponding eigenvalues λ1, λ2, … arranged in an ascending order. The individual elements of the GPS embedding are called GPS coordinates. Each surface point of the manifold is therefore embedded into an infinite-dimensional space in the GPS representation. For practical purposes, we truncate the shape signature using an order that is able to capture sufficient information regarding shape but is not sensitive to segmentation or tessellation noise. Our focus in this paper is on providing an overall shape difference measure between two surfaces rather than a point-wise measure. Therefore, we only use the set of eigenvalues as a representation of shape:

GPS(S)=(1λ1,1λ2,1λ3,…). (3)

It has been shown that this representation contains all the shape information for surfaces with spherical topology (closed surfaces with no holes or handles) (Rosenberg 1997), as is the case with the bone surfaces.

The GPS embedding presented in (3) has several favorable properties for shape analysis of carpal bones.

  • Its coordinates are isometrically invariant as they depend only on the derivative operators that are computed with respect to the intrinsic geometry of the bone surface, which in turn are dependent only on shape and not on position or rotation. Thus, as opposed to methods such as statistical shape modeling (Cootes et al 1995, van de Giessen et al 2010), the bone surfaces to be compared need not be co-registered before performing the quantitative shape analysis—making the analysis simpler and free from registration errors.

  • Scaling the manifold by a factor α results in the scaling of the GPS coordinates by 1/α2. The same scaling transform also results in a change in surface area A to α2A. Scale-invariance for the GPS coordinates can therefore be obtained by normalizing the eigenvalues by surface area A. This property of the GPS embedding is desirable in the comparison of bone shapes because the analysis can explicitly focus on examination of shape as opposed to just size.

  • Continuous changes of the manifold's shape result in continuous changes in the spectrum

  • In the embedding space, the inner product is given by the Green's function due to the identity: G(s1,s2)=ΣkΦk(s1)Φk(s2)λk, s1, s2 ∈ S (Rosenberg 1997). As a result, the GPS representation encodes diffusion distances (Lipman et al 2010) on the surface. The GPS embedding therefore represents both local and global shape information (Rosenberg 1997, Bronstein and Bronstein 2011). Local perturbations in shape lead to local changes in curvature which are captured in higher-order GPS coordinates. Global shape changes, on the other hand, lead to curvature changes everywhere in the shape which are captured by lower-order GPS coordinates. Due to this association between the GPS coordinates and the spatial extent of shape changes, the GPS based comparisons provide a natural description of changes in shape at different scales.

  • Since the space of the representation has a Euclidean metric, the shape space is the ℓ2 space of square summable series at each point s ∈ S. A full description of shape difference at different scales can be conducted by analyzing coordinate-wise GPS differences, as was done in this paper. Shape differences between the GPS coordinates of cortical surface S1 and S2 may also be defined by the standard ℓ2 norm: d(S1, S2) = ∥GPS(S1)–GPS(S2)∥2. The GPS representation provided here assumes that the eigenfunctions computed for the two surfaces are in exactly the same order. For bone surfaces, this is true because the surfaces lack symmetry (Rosenberg 1997). If however the surfaces have symmetries, there could be repeated eigenvalues and the eigenfunctions may not correspond. This ambiguity can be resolved using a sorting technique (Jain and Zhang 2006). Although not an issue for bone shape comparison because we do not employ eigenfunctions as part of the metric, there may be a sign ambiguity in the eigenfunctions that must be resolved using techniques listed in (Jain and Zhang 2006).

2.2. Numerical implementation of the GPS solver

In order to solve (1), we used a FEM to discretize the Helmholtz equation. We discretize the derivative operators using FEM directly in the geometry of the triangulated surface mesh, and therefore we did not need to explicitly compute the Riemannian metric coefficients as is often done if the surfaces are mapped to a plane or sphere (Thompson et al 2000). We chose linear FEMs for functions and Galerkin's formulation (Smith 1985) for robustness to tessellation errors. Let Φ(s) = Σi ϕiei(s) be an eigenfunction and N(s) = Σi ηiei(s) be a test function, each represented as weighted sums of linear elements ei(s). The eigenvalue problem from (1) then becomes:

ΔΦ(s)=λΦ(s) (4)
⇒∫S(ΔΦ(s))N(s)ds=λ∫SΦ(s)N(s)ds (5)
⇒−∫S∇Φ(s)∇ηN(s)ds=λ∫SΦ(s)N(s)ds (6)

where the latter follows using integration by parts and the Neumann boundary condition specified in (1). Substituting the FEM into this equation, we obtain:

−∑i∑jϕiηj∫∇ei(s)∇ej(s)ds=λ∑i∑jϕiηj∫ei(s)ej(s)ds⇒SΦ=−λMΦ (7)

where Φ is a column vector with the ith entry given by ϕi. For a triangulated surface mesh with linear elements, the element-wise matrix is given by

Mel=Ael12[211121112] (8)

and the element-wise stiffness matrix is given by Sel = DxDx + DyDy where Dx and Dy are discretizations of derivatives in the x and y directions respectively, and Ael denotes the area of the element. The mass and stiffness matrices M and S are obtained from the corresponding element-wise matrices Mel and Sel respectively by using finite-element matrix assembly procedures as described in (Smith 1985).

The matrix equation (7) is a generalized eigenvalue problem. This equation was solved using an implementation of the QZ factorization algorithm for generalized eigenvalues in MATLAB® (the eigs function)(Moler and Stewart 1973). The first 30 coordinates of the otherwise infinite-dimensional GPS were used for analysis based on the spread of the eigenvalue spectrum. The MATLAB implementation took 13 s for the computation of the 30 GPS coordinates for a typical surface mesh (~33 000 faces, ~15 000 vertices), on a computer with an AMD FX®-8150 eight-core processor with 32 GB of RAM. The computed eigenvalues were multiplied by the square of the surface area to make the resulting GPS representation scale-invariant.

2.3. Carpal bone surfaces used for analysis

The bone surfaces used for analysis were obtained for the right and left wrist for healthy women (n = 10, average age: 24.4 years, range: 21–28 years) and healthy men (n = 10, average age: 25 years, range: 22–28 years) from the publicly-available database (Moore et al 2007)(figure 1). The surfaces of the eight carpal bones, namely, capitate, hamate, lunate, pisiform, scaphoid, trapezium, trapezoid, and triquetrum, and the first metacarpal for both wrists were used for analysis. We added the first metacarpal bone to this analysis since the trapeziometacarpal joint of the thumb is a common site of osteoarthritis, with disproportional prevalence in women (Zhang et al 2002). The data for each bone was in the form of the mesh connectivity list and vertex locations for the surface tessellation elements, with triangles as prototiles. The surfaces of the bones of the left wrist have already been mirrored in the database to allow for an easier comparison with those of the right wrist (Moore et al 2007).

2.4. Bone shape comparisons using GPS

We illustrate the potential of the proposed GPS representation for shape analysis and comparison using carpal bones from the database described in subsection 2.3. We conducted the following analyzes.

2.4.1. GPS representation and invariance with respect to bone size and orientation

The trapezium and hamate bones of the right wrist of two randomly chosen women and two randomly chosen men were used for this analysis. The X, Y, and Z coordinates of the surface nodes were scaled by factors of 0.1, 1 and 100. The GPS coordinates corresponding to the first 30 eigenvalues/eigenfunctions were computed for the original and the scaled surfaces. Each surface was also rotated in the range 0°–180° in steps of 30°, and translated by −50, −20, 20 and 50 mm. The normalized mean-squared-error (NMSE) between the GPS coordinates of the original bone surface, denoted by So, and the scaled/rotated/translated surfaces, denoted by Sw, was computed using ‖GPS(So)−GPS(Sw)‖22∕‖GPS(So)‖22.

2.4.2. Comparison of the shapes of the carpal bones in women versus men

The GPS coordinates corresponding to the first 30 eigenvalues/eigenfunctions for each carpal bone (eight total) and the first metacarpal bone were generated for each subject for both the right and left wrists. For comparison of bone shape based on sex, we compared the GPS coordinates for each bone of the right and left wrist separately for the two groups (ten women versus ten men) using one-way multivariate analysis of variance (MANOVA). Given the small sample size we used non-parametric permutation tests as the resampling procedure to further confirm our findings. We chose differences of multivariate means as the test statistic. In conventional MANOVA where the samples represent a multivariate Gaussian distribution this statistic has a χ2 distribution. For permutation testing, we randomly shuffled the male/female labels of the samples for 1000 times, and computed the test statistics to generate the null distribution. We then generated the same statistic without shuffling and computed the percentile of that score, which is the p-value of the non-parametric permutation test. We report both the p-values obtained from MANOVA and those after permutation testing. We also report on the minimum number of GPS coordinates that were required for achieving a statistically significant difference between the two groups based on a p < 0.05, based on the outcomes of the permutation tests.

2.4.3. Comparison of the carpal bones of the left and right wrist for each subject

We computed the GPS coordinates corresponding to the first 30 eigenvalues/eigenfunctions for each bone in the right and left wrist in women and men. We used the non-parametric Wilcoxon rank-sum test to compare the GPS coordinates for each bone of the right versus left wrist for each subject.

3. Results

3.1. Eigenfunctions and implications to shape analysis

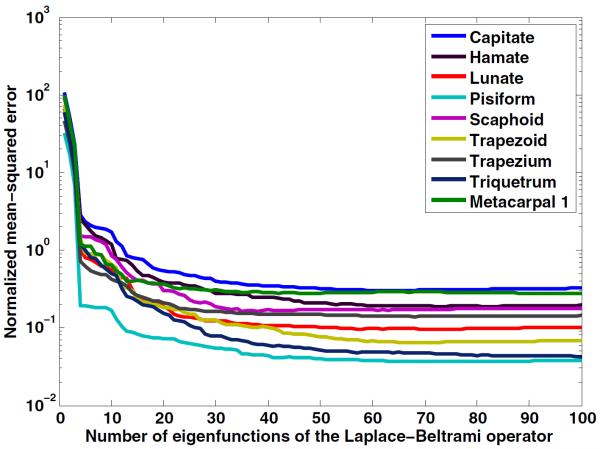
We demonstrate the ability of the eigenfunctions of the Laplace–Beltrami operator to represent shape-based features using the hamate bone of a healthy female (figure 2). We chose the hamate for illustration because it has a hook-like process projecting from its palmar surface that could be visualized for the different eigenfunctions. The lower-order eigenfunctions appear to capture global shape, while with increasing order, more details of the curvature of the bone are captured. Figure 2 also shows the spatial distribution of the first four eigenfunctions of the Laplace–Beltrami operator rendered on the surface of the hamate. Figure 3 shows the NMSE between the original bone surface and that reconstructed from an increasing number of eigenfunctions of the Laplace–Beltrami operator. Although the space of the Laplace–Beltrami eigenfunctions is infinite-dimensional, our analysis in the subsequent sections shows that a small number (<20) of eigenfunctions captured adequate features on the bone surface to analyze shape differences in the population studied. A lower-dimensional representation of the surface has the advantage of not being susceptible to image segmentation or tessellation noise.

Figure 2.

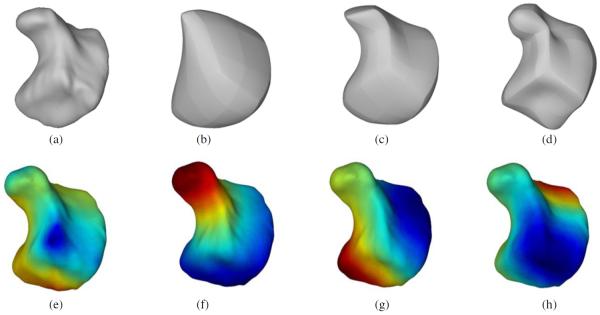
Figure 2

Open in a new tab

Eigenfunctions of the Laplace–Beltrami operator and their contribution to shape. (a) A 3D rendering of the hamate bone in a healthy woman, and contribution of first (b) five, (c) twenty, and (d) fifty eigenfunctions to the shape of the bone. These renderings were obtained by truncating the eigen spectrum to keep only the aforementioned number of eigenfunctions and re-projection. The lines, also present on the surface tessellation of the original bone, are a by-product of the segmentation method used in the creation of the digital database. A 3D surface rendering of the same hamate bone showing the distribution of the (e) first, (f) second, (g) third, and (h) fourth eigenfunction of the Laplace–Beltrami operator mapped to the bone surface. The eigenfunctions have been normalized to the [−1,1] scale for better visualization and comparison.

Figure 3.

Figure 3

Open in a new tab

The NMSE between the original bone surface and the bone surface reconstructed using the first 100 eigenfunctions of the Laplace–Beltrami operator. Data are shown for all nine bones. The knobbly, pea-shaped, pisiform bone requires the least number of eigenfunctions to capture its shape.

3.2. Validation of scaling and isometric invariance

In the study of scaling, rotating and translating the trapezium and hamate bones, the NMSE was calculated between the GPS coordinates computed from the first 30 eigenfunctions. The NMSE was found to be an average of 5 × 10−5 across all experiments. These results imply that the GPS coordinates are indeed insensitive to scaling, rotation, and translation, hence providing a validation of the representation's scaling and isometric invariance property.

3.3. Comparison of shapes of the carpal bones of between women and men

We compared the shapes of each of the eight carpal bones and that of the first metacarpal bone of the left and right wrists separately between women and men based on the GPS representation and permutation tests. Results employing the first 17 GPS coordinates are shown in table 1. Figure 4 indicates the minimum number of consecutive eigenfunctions starting from λ1 that were required to obtain a statistically significant difference between the sexes for the carpal bone shapes based on a p < 0.05. This analysis showed that <20 GPS coordinates were sufficient for showing statistically significant differences in the shapes of the carpal bones of both right and left wrists between the sexes. These results indicate that the shape differences between the sexes are contained in the relatively smooth curvatures of the bone surface (see figure 2(c) constructed with only 20 eigenfunctions for comparison and figure 3). We also evaluated the minimum number of eigenfunctions that were required to obtain a statistically significant difference in carpal bone shape in the same population based on sex when the size-invariance constraint in the GPS formulation is dropped. In this case, just the first one or two GPS coordinates were enough to separate the populations. This latter analysis demonstrated that the GPS representation is indeed capable of also capturing size changes in addition to shape differences, and that the scale (size) difference is a dominant contributor to the differences of carpal bone shape between women and men, in agreement with previous work (Crisco et al 2005). The GPS representation without the size-invariance constraint may therefore provide a metric associated with overall carpal bone size and may allow for bone size comparisons across populations.

Table 1.

p-values from MANOVA and those obtained from permutation tests comparing the eight carpal and the first metacarpal bones in men versus women employing the first 17 GPS coordinates. For the lunate and triquetrum, where the corresponding p-values exceeded 0.05, more than 17 GPS coordinates were required to attain a p < 0.05, as further indicated in figure 4.

Right wrist
 Left wrist
Bone MANOVA Permutation test MANOVA Permutation test
Capitate 0.0226 0.0493 0.0148 0.0416
Hamate 0.0065 0.0097 0.0048 0.0089
Lunate 0.0379 0.0210 0.0532 0.0766
Pisiform 0.0428 0.0365 0.0102 0.0201
Scaphoid 0.0135 0.0255 0.0012 0.0120
Trapezoid 0.0004 0.0087 0.0022 0.0136
Trapezium 0.0007 0.0101 0.0023 0.0140
Triquetrum 0.0015 0.0124 0.0449 0.0836
Metacarpal 1 0.0137 0.0245 0.0015 0.0129
Open in a new tab

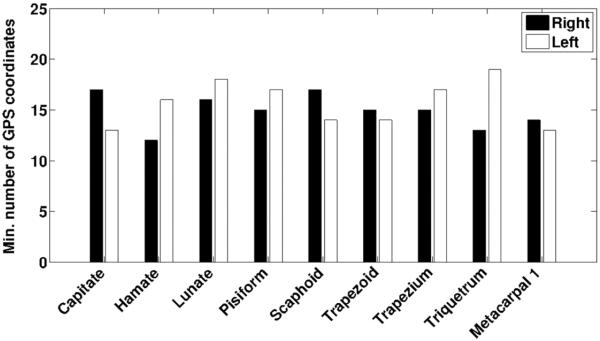
Figure 4.

Figure 4

Open in a new tab

Minimum number of GPS coordinates (eigenfunctions) required to evaluate sex-based differences in bone shape. The plot shows the minimum number of GPS coordinates required to obtain a statistically significant difference (p < 0.05) in the shape of the eight carpal and first metacarpal bones of women and men. The solid bars indicate results for the right wrist while the unfilled bars indicate results of the left wrist.

3.4. Comparison of shapes of the carpal bones of the right versus left wrist

Shape comparisons were conducted for each of the eight carpal bones of the right and left wrist for all 20 subjects. We found statistically insignificant shape differences for all eight carpal bones of the right versus the left wrist in women (p > 0.11) and men (p > 0.1). These findings agree with those reported by Crisco et al (2005) for the carpal bones of the right and left hand for healthy men and women. There are also reports of insignificant shape differences of the left and right bones of other joints such as those of the knee (Murshed et al 2005, Young et al 2013).

4. Discussion

We demonstrated the utility of the GPS representation for the comparison of carpal bones in healthy women and men. Our analysis, albeit in a small population, was able to show statistically significant shape differences for carpal bones between the sexes, but not between the carpal bones of the right versus the left wrist in individuals of both sexes. Our results indicate that there is value in the analysis of shape in addition to size for improving our understanding of bone morphology across populations. The sample size used in this work was small and further studies are planned in larger sample sizes. The database used for the study consisted of subjects who were young, healthy individuals and who lacked significant pathological findings. It is therefore unknown if the shape differences of the carpal bones may predispose one group to specific pathologies such as wrist instability or osteoarthritis. Further, the database did not contain information regarding the dominant hand of the subjects and therefore its probable association with shape differences could not be established. The two groups (women and men) were in the same age range therefore age-related factors were not accounted for in our analysis. Other factors that may influence bone shape such as body size, or metabolic, genetic and environmental factors were not controlled for in our analysis as these data were not available in the database.

We note that the GPS representation encodes knowledge about the intrinsic geometry of the bones. This representation therefore carries information about the Gaussian curvature but not the mean curvature. We know that for surfaces with spherical topology, the GPS representation encodes all the shape information (Rosenberg 1997). We have therefore chosen to use the usual Laplace–Beltrami operator for this work. We however also note that in order to have full information about the surface in the GPS representation, we need to have infinitely many eigenvalues and eigenfunctions. It would be interesting to use mean curvature as an anisotropy term in the GPS representation (Joshi et al 2012) to see if it reduces the number eigenfunctions required or improves performance for this application. Based on these results, we plan to explore this aspect in the future. Our current study provided a metric for overall shape differences, but did not localize these differences to specific anatomical locations of interest on the bone surface, such as articulating surfaces. Our future work will focus on addressing this aspect.

The proposed GPS representation induces a Euclidean metric on the shape space, therefore it is possible to perform shape averaging in shape space. From a population of bones, an average bone shape could be computed by performing shape averaging and be used as an atlas for shape comparisons. Shape variability of a certain bone can then be found by estimating the population variance of the GPS coordinates by:

σ2=1N∑n=1N‖GPS(Sn)−1N∑m=1NGPS(Sm)‖22. (9)

Such an atlas of carpal bones can be used for computation of the shape variance across populations but also for detecting abnormalities in the bone shapes in a quantitative manner.

Detailed information related to bone shape derived from the proposed method may be useful for the development of subject-specific prostheses or implants (Crisco et al 2005) and in reconstructive surgical training (Craigen and Stanley 1995). Sex-based differences in growth and development (Stinson 1985) can be investigated to better guide intervention. Further, there are reported differences in populations based on age-related, genetic, nutritional, lifestyle related, demographic, racial and other environmental factors and how these factors may interact with the skeletal development and maturity, and hence the shape of carpal bones (Gilsanz et al 1998, Zhang et al 2009). A detailed study using the proposed method is planned to better understand the corresponding morphological diversity in populations and eventually enable the incorporation of the knowledge gained in the reconstructive surgery algorithm. With the current advances in re-materialization studies and rapid prototyping, replicas of the bones based on shape analysis may be produced by 3D printers and may provide a powerful tool for surgical training (Potamianos et al 1998), for a more adequate selection and placement of surgical implants and eventually for actual production of replacement bone implants.

The proposed method also has the potential for providing an objective way of analyzing the evolutionary basis of carpal bone shape or phylogeny across species. The carpus is considered a morphologically diversified region of the vertebrate body (Lewis 1985, Tocheri et al 2007), and has been studied as a developmental system in the past (Oster et al 1988, Greulich and Pyle 1959, Lewis 1970, Michejda 1987). There is also a rich fossil record documenting the evolution of the carpus (Hinchliffe 1991) that could be analyzed using the proposed method.

The focus of our study was on analysis of overall bone shape, however, a potential area of investigation is the combination of the shape information initially with the static spatial orientation of the carpal bones (Kauer 1980, Tagare et al 1993, Canovas et al 2004), and eventually with carpal bone motion (Crisco et al 1999, van de Giessen et al 2012). This type of analysis will require the definition of a robust and elegant coordinate system such as that developed by Coburn et al (Coburn et al 2007) and the ability to perform dynamic imaging of the hand during active motion (Crisco et al 1999, Shores et al 2013, Boutin et al 2013).

5. Conclusion

We have demonstrated a method for analyzing the shapes of the carpal bones of the wrist. This method is independent of position, rotation and scaling and these attributes may improve the assessment of carpal bone shape. Additional studies are now required in a larger population to better characterize the performance of the method for delineating the influence of sex on carpal bone shape from potential confounding factors including age, body size, and metabolic, genetic and environmental factors.

Acknowledgments

AJC was supported by the Building Interdisciplinary Research Careers in Women's Health award (K12 HD051958) funded by the National Institute of Child Health and Human Development (NICHD), Office of Research on Women's Health (ORWH), Office of Dietary Supplements (ODS), and the National Institute of Aging (NIA). The authors further acknowledge funding from the National Institutes of Health (NIH) grants R03EB015099 to AJC, P41 EB015992 and R01 NS074980 to RML and AAJ and K24 AR04884, AR043052, P50 AR060752 and P50 AR063043 to NEL. The content is solely the responsibility of the authors and does not necessarily represent the official views of the National Institutes of Health. The authors would like to thank Dr Joseph Crisco for this input regarding the content of the manuscript.

List of abbreviations

GPS

Global point signature

FEM

Finite element method

NMSE

Normalized mean-squared error

MANOVA

Multivariate analysis of variance

References

  1. Belsole RJ, Hilbelink DR, Llewellyn JA, Stenzler S, Greene TL, Dale M. Mathematical analysis of computed carpal models. J. Orthop. Res. 1988;6:116–22. doi: 10.1002/jor.1100060115. [DOI] [PubMed] [Google Scholar]
  2. Boutin RD, Buonocore MH, Immerman I, Ashwell Z, Sonico GJ, Szabo RM, Chaudhari AJ. Real-time magnetic resonance imaging (MRI) during active wrist motion—initial observations. PloS One. 2013;8:e84004. doi: 10.1371/journal.pone.0084004. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Brandt KD, Dieppe P, Radin EL. Etiopathogenesis of osteoarthritis. Rheum. Dis. Clin. North Am. 2008;34:531–59. doi: 10.1016/j.rdc.2008.05.011. [DOI] [PubMed] [Google Scholar]
  4. Bronstein MM, Bronstein AM. Shape recognition with spectral distances. IEEE Trans. Pattern Anal. Mach. Intell. 2011;33:1065–71. doi: 10.1109/TPAMI.2010.210. [DOI] [PubMed] [Google Scholar]
  5. Burgess R. Anatomic variations of the midcarpal joint. J. Hand Surg. 1990;15:129. doi: 10.1016/s0363-5023(09)91119-4. [DOI] [PubMed] [Google Scholar]
  6. Canovas F, Roussanne Y, Captier G, Bonnel F. Study of carpal bone morphology and position in three dimensions by image analysis from computed tomography scans of the wrist. Surg. Radiol. Anat. 2004;26:186–90. doi: 10.1007/s00276-003-0207-x. [DOI] [PubMed] [Google Scholar]
  7. Coburn JC, Upal MA, Crisco JJ. Coordinate systems for the carpal bones of the wrist. J. Biomech. 2007;40:203–9. doi: 10.1016/j.jbiomech.2005.11.015. [DOI] [PubMed] [Google Scholar]
  8. Cootes TF, et al. Active shape models-their training and application. Comput. Vis. Image Underst. 1995;61:38–59. [Google Scholar]
  9. Craigen M, Stanley J. Wrist kinematics: row, column or both? J. Hand Surg. [Br.] 1995;20:165–70. doi: 10.1016/s0266-7681(05)80044-0. [DOI] [PubMed] [Google Scholar]
  10. Crisco JJ, Coburn JC, Moore DC, Upal MA. Carpal bone size and scaling in men versus in women. J. Hand Surg. 2005;30:35–42. doi: 10.1016/j.jhsa.2004.08.012. [DOI] [PubMed] [Google Scholar]
  11. Crisco JJ, McGovern RD, Wolfe SW. Noninvasive technique for measuring in vivo three-dimensional carpal bone kinematics. J. Orthop. Res. 1999;17:96–100. doi: 10.1002/jor.1100170115. [DOI] [PubMed] [Google Scholar]
  12. Felson D. Osteoarthritis as a disease of mechanics. Osteoarthritis Cartilage. 2013;21:10–5. doi: 10.1016/j.joca.2012.09.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Gilsanz V, Ratib O. Hand Bone Age: A Digital Atlas of Skeletal Maturity. Springer; Berlin: 2005. [Google Scholar]
  14. Gilsanz V, Skaggs DL, Kovanlikaya A, Sayre J, Loro ML, Kaufman F, Korenman SG. Differential effect of race on the axial and appendicular skeletons of children. J. Clin. Endocrinol. Metab. 1998;83:1420–7. doi: 10.1210/jcem.83.5.4765. [DOI] [PubMed] [Google Scholar]
  15. Greulich WW, Pyle SI. Radiographic atlas of skeletal development of the hand and wrist. Am. J. Med. Sci. 1959;238:393. [Google Scholar]
  16. Hinchliffe R. Developmental Patterning of the Vertebrate Limb. Springer; Berlin: 1991. pp. 313–23. [Google Scholar]
  17. Jain V, Zhang H. Robust 3D shape correspondence in the spectral domain. SMI'06: IEEE Int. Conf. on Shape Modeling and Applications; Matsushima, Japan. 2006. p. 19. [Google Scholar]
  18. Joshi AA, Ashrafulla S, Shattuck DW, Damasio H, Leahy RM. An invariant shape representation using the anisotropic Helmholtz equation. Proc. Conf. on Medical Image Computing and Computer Assisted Intervention; 2012. pp. 607–14. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Kauer JM. Functional anatomy of the wrist. Clin. Orthop. Relat. Res. 1980;149:9–20. [PubMed] [Google Scholar]
  20. Lane N, Brandt K, Hawker G, Peeva E, Schreyer E, Tsuji W, Hochberg M. OARSI-FDA initiative: defining the disease state of osteoarthritis. Osteoarthritis Cartilage. 2011;19:478–82. doi: 10.1016/j.joca.2010.09.013. [DOI] [PubMed] [Google Scholar]
  21. Lewis O. The development of the human wrist joint during the fetal period. Anat. Rec. 1970;166:499–515. doi: 10.1002/ar.1091660308. [DOI] [PubMed] [Google Scholar]
  22. Lewis O. Derived morphology of the wrist articulations and theories of hominoid evolution: part I. The lorisine joints. J. Anat. 1985;140:447. [PMC free article] [PubMed] [Google Scholar]
  23. Lipman Y, Rustamov R, Funkhouser T. Biharmonic distance. ACM Trans. Graph. 2010;29:27. [Google Scholar]
  24. Michejda M. Skeletal Development of the Wrist and Hand in Macaca Mulatta and Man. Karger; Basel: 1987. [Google Scholar]
  25. Modgil S, Hutton T, Hammond P, Davenport J. Combining biometric and symbolic models for customised, automated prosthesis design. Artif. Intell. Med. 2002;25:227–45. doi: 10.1016/s0933-3657(02)00026-x. [DOI] [PubMed] [Google Scholar]
  26. Moler CB, Stewart GW. An algorithm for generalized matrix eigenvalue problems. SIAM J. Numer. Anal. 1973;10:241–56. [Google Scholar]
  27. Moore DC, Crisco JJ, Trafton TG, Leventhal EL. A digital database of wrist bone anatomy and carpal kinematics. J. Biomech. 2007;40:2537–42. doi: 10.1016/j.jbiomech.2006.10.041. [DOI] [PubMed] [Google Scholar]
  28. Murshed KA, Ç içekcibaş AE, Karabacakoğlu A, ŞSeker M, Ziylan T. Distal femur morphometry: a gender and bilateral comparative study using magnetic resonance imaging. Surg. Radiol. Anat. 2005;27:108–12. doi: 10.1007/s00276-004-0295-2. [DOI] [PubMed] [Google Scholar]
  29. Nakamura K, Beppu M, Patterson RM, Hanson CA, Hume PJ, Viegas SF. Motion analysis in two dimensions of radial-ulnar deviation of type I versus type II lunates. J. Hand Surg. 2000;25:877–88. doi: 10.1053/jhsu.2000.9411. [DOI] [PubMed] [Google Scholar]
  30. Oster GF, Shubin N, Murray JD, Alberch P. Evolution and morphogenetic rules: the shape of the vertebrate limb in ontogeny and phylogeny. Evolution. 1988;862:84. doi: 10.1111/j.1558-5646.1988.tb02508.x. [DOI] [PubMed] [Google Scholar]
  31. Pietka E, Gertych A, Pospiech S, Cao F, Huang H, Gilsanz V. Computer-assisted bone age assessment: image preprocessing and epiphyseal/metaphyseal ROI extraction. IEEE Trans. Med. Imaging. 2001;20:715–29. doi: 10.1109/42.938240. [DOI] [PubMed] [Google Scholar]
  32. Potamianos P, Amis A, Forester A, McGurk M, Bircher M. Rapid prototyping for orthopaedic surgery. Proc. Inst. Mech. Eng. H. 1998;212:383–93. doi: 10.1243/0954411981534150. [DOI] [PubMed] [Google Scholar]
  33. Reuter M. Hierarchical shape segmentation and registration via topological features of Laplace–Beltrami eigenfunctions. IJCV. 2010;89:287–308. [Google Scholar]
  34. Riley KKF, Hobson MMP, Bence SSJ. Mathematical Methods for Physics and Engineering. Cambridge University Press; Cambridge: 2006. [Google Scholar]
  35. Rosenberg S. The Laplacian on a Riemannian Manifold. Cambridge University Press; Cambridge: 1997. [Google Scholar]
  36. Rustamov R. Laplace–Beltrami eigenfunctions for deformation invariant shape representation. Proc. 5th Eurographics Symp. on Geometry Processing. 2007:225–33. [Google Scholar]
  37. Shores JT, Demehri S, Chhabra A. Kinematic `4 dimensional' CT imaging in the assessment of wrist biomechanics before and after surgical repair. Eplasty. 2013;13:e9. [PMC free article] [PubMed] [Google Scholar]
  38. Smith GD. Numerical Solution of Partial Differential Equations: Finite Difference Methods. Clarendon; Oxford: 1985. [Google Scholar]
  39. Stinson S. Sex differences in environmental sensitivity during growth and development. Am. J. Phys. Anthropol. 1985;28:123–47. [Google Scholar]
  40. Tagare H, Elder K, Stoner D, Patterson R, Nicodemus C, Viegas S, Hillman G. Location and geometric description of carpal bones in CT images. Ann. Biomed. Eng. 1993;21:715–26. doi: 10.1007/BF02368650. [DOI] [PubMed] [Google Scholar]
  41. Taleisnik J. Current concepts review. Carpal instability. J. Bone Joint Sur. Am. 1988;70:1262. [PubMed] [Google Scholar]
  42. Thompson P, Woods R, Mega M, Toga A. Mathematical/computational challenges in creating deformable and probabilistic atlases of the human brain. Hum. Brain Mapp. 2000;9:81–92. doi: 10.1002/(SICI)1097-0193(200002)9:2&#x0003c;81::AID-HBM3&#x0003e;3.0.CO;2-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
  43. Tocheri MW, et al. The primitive wrist of homo floresiensis and its implications for hominin evolution. Science. 2007;317:1743–5. doi: 10.1126/science.1147143. [DOI] [PubMed] [Google Scholar]
  44. van de Giessen M, Foumani M, Streekstra GJ, Strackee SD, Maas M, van Vliet LJ, Grimbergen KA, Vos FM. Statistical descriptions of scaphoid and lunate bone shapes. J. Biomech. 2010;43:1463–9. doi: 10.1016/j.jbiomech.2010.02.006. [DOI] [PubMed] [Google Scholar]
  45. van de Giessen M, Foumani M, Vos F, Strackee S, Maas M, Van Vliet L, Grimbergen C, Streekstra G. A 4d statistical model of wrist bone motion patterns. IEEE Trans. Med. Imaging. 2012;31:613. doi: 10.1109/TMI.2011.2174159. [DOI] [PubMed] [Google Scholar]
  46. Young EY, Gebhart J, Cooperman D, Ahn NU. Are the left and right proximal femurs symmetric? Clin. Orthop. 2013:1–9. doi: 10.1007/s11999-012-2704-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
  47. Zhang A, Sayre JW, Vachon L, Liu BJ, Huang H. Racial differences in growth patterns of children assessed on the basis of bone age. Radiology. 2009;250:228–35. doi: 10.1148/radiol.2493080468. [DOI] [PMC free article] [PubMed] [Google Scholar]
  48. Zhang Y, Niu J, Kelly-Hayes M, Chaisson CE, Aliabadi P, Felson DT. Prevalence of symptomatic hand osteoarthritis and its impact on functional status among the elderly the Framingham study. Am. J. Epidemiol. 2002;156:1021–7. doi: 10.1093/aje/kwf141. [DOI] [PubMed] [Google Scholar]

RESOURCES