PSAR-Align: improving multiple sequence alignment using probabilistic sampling

Abstract

Summary: We developed PSAR-Align, a multiple sequence realignment tool that can refine a given multiple sequence alignment based on suboptimal alignments generated by probabilistic sampling. Our evaluation demonstrated that PSAR-Align is able to improve the results from various multiple sequence alignment tools.

Availability and implementation: The PSAR-Align source code (implemented mainly in C++) is freely available for download at http://bioen-compbio.bioen.illinois.edu/PSAR-Align.

Contact: jbkim@konkuk.ac.kr or jianma@illinois.edu

1 INTRODUCTION

Multiple sequence alignment (MSA) is one of the most important foundations for cross-species comparative genomic analysis (Kumar and Filipski, 2007; Notredame, 2007). Although many algorithms for MSA have been developed (Kemena and Notredame, 2009), MSA is still error-prone. For example, it was estimated that at least 10% of the human-mouse whole-genome alignment is misaligned at the UCSC Genome Browser and the number increases for other species (Prakash and Tompa, 2007).

We previously developed a novel measure, called PSAR (Kim and Ma, 2011), which can assess the reliability of an MSA based on its agreement with probabilistically sampled suboptimal alignments (SAs). SAs provide additional information that cannot be obtained by the optimal alignment alone, especially when the optimal alignment is not far superior to the SAs.

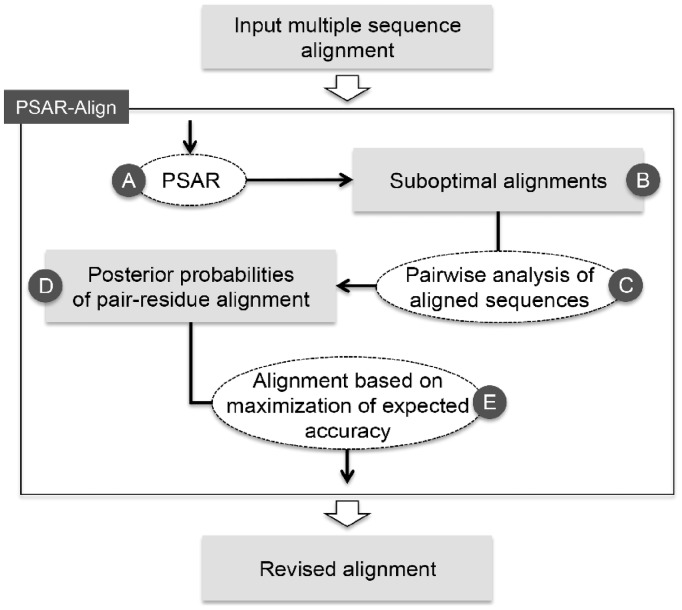
In this article, we introduce a new realignment method, PSAR-Align, which refines a given MSA based on a probabilistic framework that takes advantage of the SAs of the given MSA. Briefly, PSAR-Align (i) samples SAs from the given MSA, (ii) estimates posterior probabilities of aligning two residues from two different sequences and (iii) generates a revised MSA using an expected accuracy-based alignment algorithm (Bradley et al., 2009; Do et al., 2005; Paten et al., 2009; Roshan and Livesay, 2006).

2 METHODS

1.1 PSAR-Align algorithm

Given an input MSA, PSAR-Align first generates SAs by probabilistic sampling (Fig. 1A and B). Specifically, for each pair of one sequence and a remaining sub-alignment, PSAR-Align compares them based on a special pair hidden Markov model (pair-HMM) that emits columns of an MSA, which can be represented by dynamic programming matrix. To generate the SAs, PSAR-Align traces back through the dynamic programming matrix based on a probabilistic choice at each step that can take into account the relative score of a current path in comparison with neighboring paths (Kim and Ma, 2011). Then, for each pair of two residues x_i and y_j from two different sequences X and Y in the input MSA, their alignment in the sampled SAs are counted and converted to the posterior probability P(x_i∼ y_j|X,Y) (Fig. 1C and D), which is defined as follows:

(1)

where S is the set of the SAs, |S| is the total number of alignments in S and 1{x_i ∼ y_j∈S_k} is an indicator function that returns 1 only when x_i and y_j are aligned in an SA S_k.

Fig. 1.

Overview of the PSAR-Align algorithm. Given input MSA, PSAR-Align first samples SAs (A and B). These SAs are analyzed by a pair of sequences at a time (C), and posterior probabilities of aligning two residues from two different sequences are computed (D). By using these probabilities, PSAR-Align finds the revised alignment based on the maximization technique of expected accuracy (E)

PSAR-Align uses these probabilities to generate the revised alignment by maximizing an expected accuracy of an MSA A [acc(A)] against the (unknown) true alignment. The expected accuracy is the sum of the posterior probabilities of aligned pairs of residues and unaligned (aligned with a gap) residues in a given MSA (Bradley et al., 2009), which is defined as follows:

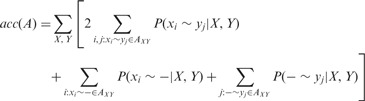(2)

where A_XY is a pairwise alignment between two sequences X and Y, P(x_i ∼ y_j|X,Y) is the posterior probability of pairwise alignment mentioned earlier in the text and P(x_i ∼ − |X,Y) and P(− ∼ y_j|X,Y) are the posterior probabilities of aligning each residue with a gap that can be computed as follows:

(3)

(4)

For the maximization of the expected accuracy, we used the sequence annealing algorithm in the FSA program (Bradley et al., 2009).

The current version of PSAR-Align was implemented mainly in C++ with additional Perl scripts, and the expected accuracy maximization step was implemented on top of the source code of FSA (Bradley et al., 2009).

2.2 Evaluation

We assessed the performance of PSAR-Align by using a simulated benchmark generated by Dawg (Cartwright, 2005). The benchmark mimics non-coding DNA sequences of five mammalian species (human, mouse, rat, dog and cow), whose phylogenetic tree was obtained from the UCSC Genome Browser (Meyer et al., 2013). The benchmark consists of 1000 replicates of ∼1 kb-long sequences, and ClustalW (Thompson et al., 2002), MAFFT (Katoh et al., 2005), MAVID (Bray and Pachter, 2004), MUSCLE (Edgar, 2004) and Pecan (Paten et al., 2008) were used to generate the input MSA. Two evaluation measures were used: (i) alignment sensitivity, which is the fraction of aligned and unaligned (aligned with a gap) residues in the true alignment that agree with the predicted alignment and (ii) alignment specificity, which is the fraction of aligned and unaligned (aligned with a gap) residues in the predicted alignment that agree with the true alignment.

2.3 Computational complexity

The time and memory complexites of alignment sampling are O(L²NS) and O(LN), respectively, where L is the alignment length, N is the number of sequences and S is the number of sampling trials (Kim and Ma, 2011). The pairwise posterior probability computation requires O(N²L) time and memory complexity, and the maximization of the expected accuracy was done efficiently by FSA (Bradley et al., 2009). In the evaluation, a single run of PSAR-Align for each input MSA took ∼3 min in an Intel (R) Xeon 2.67 GHz machine with 64 GB memory.

3 RESULTS

We evaluated PSAR-Align by using simulated sequences of five mammalian species (see Section 2). By using ClustalW, MAFFT, MAVID, MUSCLE and Pecan, input MSAs were generated and fed into PSAR-Align, which resulted in a refined MSA. The original (by the aforementioned five programs) and revised (by PSAR-Align) MSAs were compared with true MSAs, which were known from the simulation. We used two evaluation measures: alignment sensitivity and specificity (see Section 2). As shown in Table 1, the alignment specificity of the original MSA by all five programs increased in the PSAR-Align MSA. The amount of increases ranges from 0.662 (Pecan) to 2.591 (ClustalW). Similar differences were also observed for alignment sensitivity, which showed an increase ranging from 0.554 (MAVID) to 2.602 (ClustalW). In the case of Pecan, alignment specificity of the revised alignment by PSAR-Align was slightly higher than the original, but the opposite pattern was observed from alignment sensitivity. Our evaluation results indicate that (i) PSAR-Align can be used to improve MSAs from different types of MSA programs and (ii) Pecan is a high-quality MSA program based on our evaluation datasets.

Table 1.

Benchmark results of PSAR-Align

Input MSA	Sensitivityc		Specificityc
	Originala	PSAR-Alignb	Originala	PSAR-Alignb
ClustalW	28.844	31.446	20.920	23.511
	(28.51–29.18)	(31.08–31.81)	(20.66–21.19)	(23.19–23.83)
MAFFT	58.751	59.820	48.595	50.605
	(58.54–58.96)	(59.61–60.03)	(48.36–48.82)	(50.36–50.85)
MAVID	61.185	61.739	52.782	53.913
	(61.00–61.37)	(61.56–61.92)	(52.57–53.00)	(53.70–54.13)
MUSCLE	55.054	56.352	44.200	46.305
	(54.82–55.29)	(56.12–56.58)	(43.96–44.44)	(46.05–46.56)
Pecan	70.948	70.273	64.952	65.614
	(70.78–71.11)	(70.10–70.44)	(64.71–65.19)	(65.38–65.85)

Note: Better scores between original and PSAR-Align are shown in bold.

^aInput MSA to PSAR-Align.

^bRevised MSA of the original by PSAR-Align.

^cAverage across 1000 replicates with 95% confidence interval in parentheses.

4 CONCLUSION

We have developed a new alignment refinement tool, PSAR-Align, which is a realignment algorithm based on probabilistically sampled SAs. The performance of PSAR-Align was evaluated by simulation-based benchmarks. This tool will be useful for comparative genomics studies using MSA.

Funding: National Research Foundation of Korea Grant (2012R1A1A1015186 to J.K.) and National Institutes of Health grant (HG006464 to J.M.).

Conflict of Interest: none declared.