Efficient clustering of identity-by-descent between multiple individuals

Abstract

Motivation: Most existing identity-by-descent (IBD) detection methods only consider haplotype pairs; less attention has been paid to considering multiple haplotypes simultaneously, even though IBD is an equivalence relation on haplotypes that partitions a set of haplotypes into IBD clusters. Multiple-haplotype IBD clusters may have advantages over pairwise IBD in some applications, such as IBD mapping. Existing methods for detecting multiple-haplotype IBD clusters are often computationally expensive and unable to handle large samples with thousands of haplotypes.

Results: We present a clustering method, efficient multiple-IBD, which uses pairwise IBD segments to infer multiple-haplotype IBD clusters. It expands clusters from seed haplotypes by adding qualified neighbors and extends clusters across sliding windows in the genome. Our method is an order of magnitude faster than existing methods and has comparable performance with respect to the quality of clusters it uncovers. We further investigate the potential application of multiple-haplotype IBD clusters in association studies by testing for association between multiple-haplotype IBD clusters and low-density lipoprotein cholesterol in the Northern Finland Birth Cohort. Using our multiple-haplotype IBD cluster approach, we found an association with a genomic interval covering the PCSK9 gene in these data that is missed by standard single-marker association tests. Previously published studies confirm association of PCSK9 with low-density lipoprotein.

Availability and implementation: Source code is available under the GNU Public License http://cs.au.dk/~qianyuxx/EMI/.

Contact: qianyuxx@gmail.com

Supplementary information: Supplementary data are available at Bioinformatics online.

1 INTRODUCTION

In a finite population, haplotypes are identity-by-descent (IBD) if they are identical and inherited from a common ancestor. Tracts of IBD are broken up by recombination during meiosis. To be detectable, a pairwise IBD segment must be sufficiently long and contain a sufficient number of genotyped markers (Browning and Browning, 2013a; Gusev et al., 2009). Detected IBD segments have several important applications, for example, detecting signals of natural selection (Albrechtsen et al., 2010), inference of population structure (Ralph and Coop, 2013) and IBD mapping in association studies (Browning and Browning, 2012).

The current resolution of IBD detection in single-nucleotide polymorphism (SNP) array data is ∼1–2 cM, corresponding to a common ancestor within the past 25–50 generations; therefore, many short segments will be missed in pairwise IBD detection (Browning and Browning, 2012). The missing information can be partly retrieved by multiple-haplotype analysis that identifies clusters of haplotypes that are all identical by descent, which we refer to as multiple-IBD clusters later in the text. Because IBD is an equivalence relation on haplotypes, if haplotypes A and B are IBD and haplotypes A and C are IBD, then haplotypes B and C are also IBD by definition, even though their shared segment may be too short to be detected in pairwise IBD detection. Within a certain region, if we only observe pairwise IBD segments of (A, B) and (A, C), but not (B, C), we say that there is inconsistency in the pairwise IBD segments. Such inconsistency can be resolved by grouping A, B and C into a multiple-IBD cluster, where each member in the cluster is IBD to all the other members.

There have been several previous attempts to detect multiple-IBD. MCMC IBD finder (Moltke et al., 2011) is a Markov Chain Monte Carlo approach that considers multiple individuals simultaneously; however, it is not computationally tractable for genome-wide analysis with large sample sizes. The DASH method (Gusev et al., 2011) builds on pairwise IBD segments and applies an iterative minimum cut algorithm to identify densely connected haplotypes as IBD clusters. The method scans the genome through sliding windows and output subgraphs of desired density. The performance of the DASH method in terms of speed and accuracy has not been investigated previously. IBD-Groupon (He, 2013) is a recently developed method that also detects group-wise IBD tracts based on pairwise IBD segments. Unlike DASH, which takes the length of windows and density threshold of subgraphs as input parameters, IBD-Groupon is almost parameter-free and it uses a hidden Markov model (HMM) to determine the cliques and the length of group-wise IBD tracts automatically. The performance of IBD-Groupon was evaluated on simulation data of chromosome 22 with 6159 SNPs, based on a real pedigree in HapMap, and it shows high power in detecting short IBD tracts (He, 2013). In comparison with DASH, IBD-Groupon has a similar execution time with higher accuracy for a sample size of 90 related individuals; however, the relative performance of DASH and IBD-Groupon was not evaluated using population data, larger samples sizes or multiple parameter settings. In this study, we evaluate DASH using population samples with thousands of individuals in a range of different parameters settings. We do not evaluate IBD-Groupon v1.1 because it required too much memory (>12 Gb) when analyzing the simulated datasets in this study.

In this work, we present the efficient multiple-IBD (EMI) algorithm to search for multiple-IBD clusters along sliding windows in the genome. In contrast to DASH, which builds clusters from a largest connected component and iteratively divides it into smaller clusters by a minimum cut algorithm, EMI takes an agglomerative approach. It builds each cluster from initial seed haplotypes and recursively adds qualifying haplotypes to expand the cluster. High computational efficiency is ensured by the use of priority queues. We evaluate our results based on coalescence simulations. Coalescence simulations allow the investigation of realistic scenarios while enabling determination of the true multiple-IBD status. We compare the performance of EMI and DASH with thousands of samples.

Although DASH, IBD-Groupon and EMI all use graph-based clustering methods, there is an important difference in how clusters are identified. IBD-Groupon uses an HMM to find the most likely maximal cliques within each chunk of genome so as to resolve inconsistencies. Such a procedure only involves pruning edges (an edge is a pairwise IBD segment), even though sometimes adding a few edges can not only resolve inconsistencies but also recover missing pairwise IBD segments in the input. Both EMI and DASH build clusters that are highly connected and therefore can prune incorrect edges as well as add missing edges. Missing edges should not be ignored, especially for short segments, as the state-of-the-art pairwise IBD detection methods only achieve high power (e.g. 0.8) for IBD tracts longer than 2 cM in SNP data (Browning and Browning, 2013a).

Detected IBD segments have many applications, one of which is IBD mapping in association studies (Browning and Thompson, 2012; Francks et al., 2010; Gusev et al., 2011; Lin et al., 2013; Purcell et al., 2007). One can code the multiple-IBD clusters as genetic markers and use them for association testing in genome-wide association studies (GWAS).

GWAS have identified many common variants associated with diseases, yet they have explained relatively little of the heritability of complex diseases. Rare genetic variants, often defined as variants with minor allele frequency (MAF) <1% ∼ 5%, can play important roles in complex diseases and traits (Schork et al., 2009). It has been suggested that rare variants may contribute to disease and thus partly explain the missing heritability (Eichler et al., 2010). IBD mapping falls into the category of focusing mainly on signals from rare variants because IBD detection methods detect long shared segments that correspond to a relatively short time to the common ancestor. Variants arising shortly before the most recent common ancestor of a group of IBD haplotypes will be correlated with the IBD group membership; these variants, being recent, are rare. Studies have shown that IBD mapping may have higher power than association analysis of SNP data when multiple rare causal variants are clustered within a gene (Browning and Thompson, 2012).

A multiple-IBD cluster-based association test is essentially a rare-variant association test. The frequency of each cluster is determined by the number of haplotypes in that cluster, which is often small because large IBD groups are rare, especially for outbred populations. Standard methods used in GWAS evaluate each variant individually with univariate statistics, such as the Cochran–Armitage test for trend, and are underpowered for rare variants unless sample sizes or effect sizes are large (Li and Leal, 2009). Over the past few years, many group-wise association tests have emerged as to overcome this limitation, including burden tests (Madsen and Browning, 2009) and variance-component tests (Wu et al., 2011). Burden tests are typically based on collapsing or summarizing the rare variants within a region by a single value, which is then tested for association with the trait. However, a limitation for such methods is that they implicitly assume that all rare variants influence the phenotype in the same direction, which might not be true in real applications. Alternatively, we can cast the problem in the framework of linear mixed models with random effects and apply a global score test for the null hypothesis that all the variance components are 0. This can be conveniently tested with a variance-component score test in the corresponding mixed model, which is known to be a locally powerful test (Lin, 1997). Because most of our IBD clusters to be tested are rare, we chose to use mixed models and test for random effects of all the variants in a region. We chose to use the sequence kernel association test (SKAT) (Wu et al., 2011) for our analysis, as it provides a supervised flexible regression model to test for association between genetic variants (common and rare) in a region. SKAT allows for adjustment for covariates and has been shown to be powerful for most underlying hypotheses concerning the relationship of variants and complex traits (Ladouceur et al., 2012).

2 MATERIALS AND METHODS

In this section, we first describe the algorithm framework of EMI, and then we describe the simulation framework for comparing and evaluating the multiple-IBD clusters found by EMI and DASH. Finally, we describe the real data to which we will apply IBD mapping.

2.1 Algorithm outline

EMI clusters pairwise IBD segments into multiple-IBD clusters with an algorithm that is similar to one used in the systems biology domain for fast clustering of biological networks such as protein–protein interaction networks (Jiang and Singh, 2010). The predicted clusters can be used to predict missing links in the network and to search for protein complexes and functional modules.

Extending the algorithm to a genome-wide scale, EMI builds a graph with nodes representing individual haplotypes and edges representing IBD in the local region. The algorithm moves to the next region through sliding windows. The term multiple-IBD cluster means a highly connected subgraph where each haplotype in the graph is estimated to be IBD to all the other haplotypes in the same subgraph.

Consider a genomic region that is divided into K consecutive windows of length H. For each window win_k, its left and right window boundary is denoted as win_k(L) and win_k(R), and we have win_k(R) = win_k(L) + H. Given N haploid copies of genome, the construction of multiple-IBD clusters is fundamentally dependent on the presence of pairwise IBD segments, which can be efficiently detected by existing tools such as Beagle Refined IBD (Browning and Browning, 2013a) and GERMLINE (Gusev et al., 2009).

Assume a set S of pairwise IBD segments in this dataset, where each element s ∈ S has the form s = (i, j, l, r), i, j ∈ 1, … , N and represents a shared IBD segment between haplotypes i and j in the genomic interval [l,r]. Note that the order of i and j does not matter, and s can also be written as s = (j, i, l, r). Within window win_k, the corresponding pairwise IBD collection S_k is the subset of S, containing member s of S that cover the entire window, that is satisfying l ≤ win_k(L) and r ≥ wink(R).

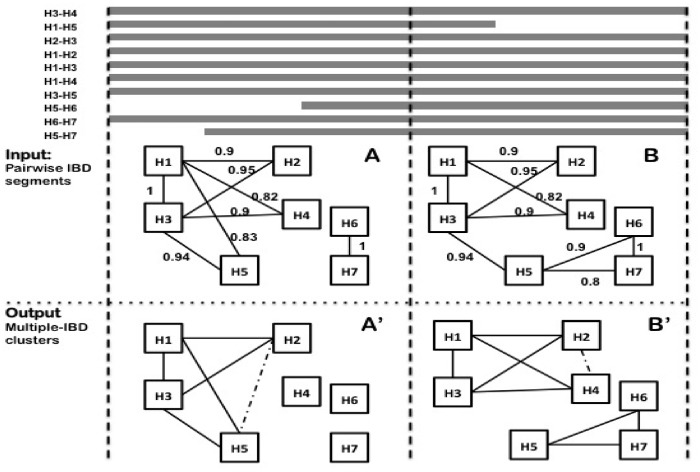
A running example is shown in Figure 1, and the details of the algorithm are described below. User-defined parameters include the minimum density of a cluster den_min and the sliding window size H.

Fig. 1.

A running example of EMI in two adjacent sliding windows, with density cutoff den_min = 0.8. (A) An edge denotes a pairwise IBD segment that spans the entire window. Numbers denote the weights of the edges, which are determined from the total length of IBD sharing (as described in Section 2). H3 is selected as the first node because it has the highest weighted degree of 3.79. H1 has the largest edge weight among all the outgoing edges of H3 and is selected as the second seed node. The cluster expansion starts with {H3, H1}, then H2 is added, as it has the largest support for the existing cluster, which is 1.85 (0.9 + 0.95). The cluster continues to expand and we get {H3, H1, H2, H5, H4}. However, density is below the cutoff after adding H4, so we remove H4 and output the clusters (of minimum size 3) to (A’). (B) When we move the next window, an edge is removed from the current cluster {H3, H1, H2, H5}, The new density is below the cutoff, so we remove the edge and check whether H5 should be removed. After removing H5, we start with the remaining nodes. {H3, H1, H2} stays and is considered as a single node. We then start the expansion again. We end up with two clusters {H3, H1, H2, H4} and {H5, H6, H7}, shown in (B’)

2.1.1 Single-locus clustering

Readers are encouraged to read the paper by Jiang and Singh (2010) wherein they explain the similar technical details. Here we only briefly outline the algorithm framework and its implementation.

Definitions: Within window win_k along the genome, we define a weighted undirected graph G^k = (V,E^k,W^k), V = 1 … N, with vertices V representing N haploid individuals, and edges E^k corresponding to IBD segments in S_k. An edge e_a,b ∈ E^k, a,b ∈ V exists if there is an IBD segment s = (a,b,l,r) in S_k; otherwise, there is no edge between node a and b. An edge e_a,b has a weight w_a,b ∈ [W_min, 1] with W_min > 0, which represents a confidence score for IBD segment sharing between a and b. The weight can be determined by various methods such as the length of IBD segment or a likelihood ratio for an IBD versus a non-IBD model in the output of Beagle Refined IBD (Browning and Browning, 2013a). In our analyses, we first applied 90% winsorization on all the IBD segment length (i.e. segment lengths below the 5th percentile were set to the 5th percentile, and segment lengths above the 95th percentile were set to the 95th percentile), and we then linearly transformed the resulting length into a weight between [W_min, 1], where W_min = 0.8. However, the winsorization might not be necessary, as results without winsorization are similar.

If previously detected pairwise IBD collections S are error-free, a fully connected subgraph of G^k would indicate a multiple-IBD cluster. In the presence of error in pairwise IBD segments, we would see false or missing edges in the graph; thus, multiple-IBD clusters can be identified by dense subgraphs that are nearly complete.

We define the following terms that are specific to our implementation:

• d_w(a) = 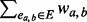, the weighted degree for node a.

• C, a cluster of nodes (haplotypes). Each cluster of nodes determines a subgraph of G^l

• density (C) =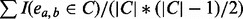, the density of cluster C. I is an indicator function and takes the value of 1 if edge e_a,b exists in cluster C, and 0 otherwise.

• C a, a 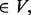a temporary new cluster constructed by adding node a to cluster C.

• support (a, C) = 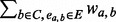, the support of node a to cluster C.

Expanding clusters: Given a weighted network, the algorithm outputs a set of disjoint dense subgraphs, which are the multiple-IBD clusters in our application.

• (i) Seed selection

• The vertex a with highest weighted degree in the current network is selected as the first seed node. Then we divide the neighboring nodes of a into five bins based on the edge weight, for example, if W_min = 0.8, then the corresponding five bins are [0.8, 0.84], [0.84, 0.88], [0.88, 0.92], [0.92, 0.96], and [0.96, 1]. We search from highest weight bin [0.96, 1] to lowest. If the current bin is not empty, node argmax_b d_w(b) in this bin is chosen as the second seed node.

• (ii) Cluster expansion

• The current cluster C starts with the two seed nodes and the edge between them. Then we search for a node b with a maximum value of support (b, C) in the remaining unclustered nodes. If density (C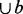) is above a threshold den_min, node b is added to cluster C; otherwise, output cluster C.

• (iii) Repeating

• The above procedure of seed selection and cluster expanding is repeated for the remaining unclustered nodes until all nodes are clustered or there is no edge left among the un-clustered nodes.

• (iv)Implementation

• The implementation uses priority queues. The first priority queue is used to pick the seed haplotype with the highest weighted degree. Once a haplotype has been used in a cluster, it is removed from the queue and the weighted degrees of all its neighbors are decreased accordingly. The second priority queue is used for expanding clusters. Each haplotype b adjacent to one of the haplotypes in cluster C being built is included in the queue and is prioritized based on support (b, C). It is implemented in the Fibonacci heap and supports insertion and key decrease, with a theoretical complexity of O (|V| log(|V|) + |E|) (Fredman and Tarjan, 1987)

2.1.2 Multilocus clustering

In application to genome-wide data, EMI slides the local window along the genome and extends the single-locus clustering to multilocus clustering.

The first window win₀ is analyzed with the single-locus algorithm, and we get an initial set of multiple-IBD clusters π₀. When we move to a new window win_k+1 from the previous window win_k, we use a modified version of single-locus clustering that includes three steps.

• (i) Dissolving of old clusters

• For each pairwise IBD segment s = (i, j, l, r) that belongs to IBD collection S_k but not S_k+1, if its edge e_{i, j} connects two nodes in a cluster C, remove this edge and check the density of the updated cluster C. Dissolve cluster C if the density is below a threshold.

• (ii) Expanding and merging existing clusters.

• For each unclustered node a, add it to an existing cluster C 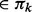if support (a, C) using IBD segments in S_k+1 is above a threshold. If an IBD segment that belongs to S_k+1 but not S_k, connects two existing clusters C_m and C_n (C_m, C_n π_k), merge these two clusters if the density of combined cluster is above the threshold.

• (iii) Single-locus clustering

• For the remaining nodes that are not included in any cluster, create new clusters in window win_k+1 with the single-locus clustering.

2.1.3 Software implementation

The above algorithm is implemented in C++ and is freely available at http://cs.au.dk/∼qianyuxx/EMI/

2.2 Evaluation of clusters

2.2.1 Data simulation

The coalescent model with recombination describes genealogies of underlying chromosomes from unrelated individuals (McVean and Cardin, 2005). We used the program MaCS (version 0.4f) (Chen et al., 2009) to simulate sequence data under the coalescent model with recombination. Ten datasets were simulated; each consists of 4000 haplotypes spanning a 10 Mb region. The simulated recent effective population size is 3000 individuals, whereas the ancient (before 5000 generations ago) population size is 24 000 individuals. The mutation rate is 1.38 × 10⁻⁸, and the recombination rates follow the HapMap recombination map for chromosome 20 (Frazer et al., 2007). The parameters for MaCS were ‘4000 10000000 T -t 0.0001656 -r 0.00012 -h 1000 -R chr20map -G 0.0 -eN 0.4167 8.0’. The simulation is designed to mimic an isolated population such as that for the Northern Finland Birth Cohort (NFBC) data, on which we conducted IBD mapping.

We then generated simulated SNP array data by thinning the sequence data. All variants with MAF <2% were removed; ∼3000 markers were selected among the remaining variants in each 10 Mb region, with MAF uniformly distributed between 2 and 50%. The number of variants corresponds to a SNP density of 1 million SNPs genome wide.

The multiple-IBD clustering requires pairwise IBD as input, which we generated using two different approaches. The first one uses the thinned SNP array data and applies to the standard GWAS settings, where SNP data are often available. We use Beagle version 4 Refined IBD (r1058) for haplotype phasing and pairwise IBD detection. All the parameters were left at their default values, i.e. ibdcm = 1.0 (the minimum length in centiMorgans of reported IBD) and ibdlod = 3 (the minimum LOD score for reported IBD).

The second approach uses sequencing data and evaluates the optimal performance of multiple-IBD clustering when we have nearly perfect power for pairwise IBD detection, even for IBD tracts as short as 0.2 cM. Two haplotypes are identical-by-state (IBS) if they are identical within a region, and we treat all the pairwise IBS segments longer than 0.2 cM as pairwise IBD segments after removing variants with MAF <0.25%. This frequency filtering removes variants that arise from mutation events since the most recent common ancestor. Using IBS to approximate IBD tracts is, however, not applicable in real data due to sequencing error and haplotype phasing error.

2.2.2 True IBD clusters

The coalescent tree traces the ancestry of sample chromosomes back in time until there is a single common ancestor. When recombination is involved, the ancestral relationship among chromosomes is complicated. At any single position along the genome, there is still a tree, but the trees at nearby positions may differ.

Multiple-IBD essentially means multiple haplotypes share a common ancestor. In our simulated data, we define the true multiple-IBD cluster as a cluster of haplotypes that share the same common ancestor across a region of length H_true. We choose to use H_true = 200 kb (approximately equivalent to 0.2 cM) in the evaluation framework, which is also the window size we used for IBD mapping. More specifically, within a region T of size H_true, a multiple-IBD cluster C_Ti is defined as any sub-tree of the true coalescent trees, which contains all descendants of the root of the sub-tree and spans this region without topology changes. Shorter H_true results in decreased performance for EMI and DASH, due to the limitations of pairwise IBD resolution, while longer H_true leads to too few true multiple-IBD clusters, as recombination breaks down the IBD signals.

2.2.3 Performance metrics

The power and accuracy of resulting clusters are measured by how well different methods recover the true underlying genealogy. The number of true IBD clusters C_Ti in region T depends on the local recombination rate as well as on the length of region T. As any sub-tree (a true IBD cluster) of the coalescent tree also forms a true IBD cluster, there is a hierarchy structure in the true multiple-IBD clusters, and therefore evaluating how well the clustering algorithm works is challenging.

2.2.4 Overlap measure

Two overlap measurements, the Jaccard measure (Jaccard) and the Precision-Recall (PR) measure, are widely used in systems biology (Kelley and Ideker, 2005; Song and Singh, 2009) when there is a hierarchy structure in functional modules.

Jaccard: given two sets, the Jaccard similarity coefficient is defined as the size of the intersection over the size of the union. For each output cluster C, its Jaccard value with a true IBD cluster C_Ti is defined as 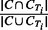. The Jaccard measure for cluster C is the maximum Jaccard value over all true IBD clusters in region T.

PR: Similarly, for each cluster C and true IBD cluster C_Ti, the PR score is defined as 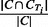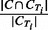. The PR measure for cluster C is the maximum of PR scores over all true IBD clusters C_Ti in region T.

2.2.5 Coverage measure

Recall Rate (RR) is used to quantify how many individuals are assigned to a correct cluster, with the following definitions: (i) True Positive (TP) node: a node is called TP node if it belongs to a cluster C, and there exists a true IBD cluster C_Ti in region T, such that 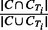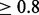. (ii) True node: any node in a true IBD cluster C_Ti is called a true node. The RR is defined as the number of TP nodes divided by number of true nodes. Note that the number of true nodes is the union of nodes in all C_Ti, and this can be less than the number of haplotypes.

2.3 IBD mapping

2.3.1 Data set

We ran EMI for multiple-IBD clustering in the NFBC 1966 GWAS data, downloaded from dbGaP (accession number phs000276.v1.p1), and subsequently tested for association with low-density lipoprotein (LDL) cholesterol, which has shown a high level of heritability in previous studies (Browning and Browning, 2013b). The 5402 individuals included in NFBC are drawn from genetically isolated Finnish regions and thus have relatively more IBD than other populations. A standard GWAS analysis has been published, and multiple genome-wide significant common variants were found (Sabatti et al., 2009).

Pairwise IBD detection was done as reported previously (Browning and Browning, 2013b). On chromosome 1, IBD detection took 83 h with a minimum IBD length parameter of 1.0 cM. Close relatives and outlying individuals based on the value of the first 20 eigenvectors were removed. For LDL, we also excluded individuals who were pregnant, had diabetes or were not fasting at the time of measurement. After data filtering, we were left with 4406 individuals.

2.3.2 Linear mixed model

We ran EMI in this dataset with the best parameters tuned in our simulation, including the cluster density cutoff den_min and the sliding window size H. Each multiple-IBD cluster is considered as a variant, and the cluster frequency is therefore defined as the cluster size (number of haplotypes in this cluster) divided by the total number of haplotypes, which is 8812 for 4406 individuals.

Because most of the multiple-IBD clusters are rare (with frequency < 0.01) and may have small effects on the trait, the standard single variant test will be underpowered.

In contrast to the concept behind the single SNP test, we fit the effects of all clusters as a random effect in a linear mixed model. Consider the linear model

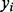denotes the phenotype for the ith subject, is a vector of fixed effects and 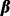is a vector of random effects with mean 0. 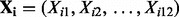denotes the 15 covariates of sex, oral contraceptive use and the first 10 eigenvectors. 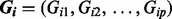, with G_ij = 0, 1, 2 represents the number of haplotypes in cluster j for the ith subject for the p clusters within the region. 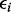is an error term with mean 0 and variance of 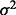. Testing association of p clusters with the trait corresponds to testing the null hypothesis H₀: 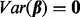, which can be tested with a variance-component score test. Such a test of non-zero variance in a linear mixed model is implemented using the software SKAT (version 0.82) (Wu et al., 2011) and was used in our analysis.

3 RESULTS

3.1 Performance of clustering in simulated data

In this section, we evaluate the performance of clustering with different parameters, and we compare EMI and DASH, with respect to the running time and accuracy of multiple-IBD clusters. All the computation times in this study are from runs on a single processor of a 2.4 GHz computer. The clusters are evaluated in terms of RR and PR (or Jaccard measure). RR measures the proportion of haplotypes that are assigned to a correct cluster, and it is similar to the definition of power in a hypothesis test. PR or the Jaccard measure measures the accuracy of clusters, which is an analog to 1 minus the type 1 error rate. Often a higher power is preferred while keeping the type 1 error rate under control in association tests. Similarly, in our application, we prefer a higher RR while keeping the PR or Jaccard measure above a certain level.

3.1.1 Grid search of parameters

DASH has two versions according to the documentation on the Web site (http://www.cs.columbia.edu/∼gusev/dash/). One version is DASH_cc, which is parameter-free and does not apply dense-subgraph searching. DASH_cc iteratively searches for all clusters without enforcing a minimum density, e.g. den_min = 0, and thus it generates a few large clusters that do not accurately approximate the true multiple-IBD clusters. The other version is DASH_adv, for which the goal of finding dense subgraphs is similar and comparable with EMI. In our experiments, DASH_adv also runs faster than DASH_cc, so we used DASH_adv in the analysis. For simplicity, we drop the subscript adv and refer to it as DASH in the following.

Both DASH and EMI take two input parameters, den_min (minimum density) and H (window length), but no previous studies have shown which parameters should be recommended. Using simulation data, we performed a grid search in the 2D parameter space with den_min taking values of [0.4, 0.5, 0.6, 0.7, 0.8] and H taking values of [100, 200 and 400 kb]. We generated 10 datasets as described in Section 2.2.1. From each dataset, 10 windows,200 kb in length, were chosen at random. Within each window, we evaluated the quality of clusters by comparing them with the true multiple clusters. The average results from all 100 windows are shown in Table 1. One can see that with different combinations of den_min and H, both DASH and EMI have similar performance. However, a lower density cutoff, such as 0.5, gives better results for both EMI and DASH. We decided to use den_min = 0.5 and H = 200 kb for further analysis, where EMI reaches the highest RR and a high PR that is not different from the highest average PR.

Table 1.

The average performance for grid search in the parameter space

Method	denmin	0.5			0.6			0.7			0.8
	H (kb)	100	200	400	100	200	400	100	200	400	100	200	400
EMI	RR	0.830	0.834	0.832	0.823	0.826	0.825	0.809	0.811	0.811	0.797	0.801	0.799
	J	0.744	0.753	0.767	0.731	0.742	0.756	0.735	0.744	0.760	0.726	0.734	0.750
DASH	RR	0.729	0.736	0.743	0.734	0.742	0.748	0.730	0.736	0.740	0.738	0.746	0.745
	J	0.776	0.776	0.779	0.752	0.759	0.766	0.742	0.747	0.752	0.710	0.717	0.727

Note: Each cell shows the mean value of the performance metrics in 100 random windows, with Htrue = 200 kb as the benchmark for calculation. J denotes Jaccard measure and RR denotes Recall Rate.

3.1.2 Comparison with DASH

Two types of pairwise IBD segments are generated as input for EMI and DASH, as described in Section 2.2.1, which we refer to as SNP data and IBS data, respectively.

SNP data: Given thinned SNP data, we used Beagle Refined IBD to generate pairwise IBD segments, which are used as input for multiple-IBD clustering afterward. The time and performance in 10 simulated datasets are shown in Table 2. Compared with DASH, EMI has slightly lower accuracy in terms of the Jaccard measure and PR, and slightly higher power in terms of how many haplotypes are assigned to the correct cluster.

Table 2.

Average performance of the clustering in simulation

Data	Method	J	PR	RR	Time (seconds)
SNP	DASH	0.775 (0.003)	0.767 (0.003)	0.736 (0.007)	6.016
	EMI	0.753 (0.003)	0.744 (0.003)	0.835 (0.008)	0.712
IBS	DASH	0.884 (0.001)	0.882 (0.001)	0.910 (0.002)	252.267
	EMI	0.864 (0.001)	0.863 (0.001)	0.938 (0.002)	13.542

Note: In each of the 10 datasets, 10 random windows of size H_true = 200 kb are chosen to calculate the performance metrics. The columns of J (Jaccard measure), PR (PR measure) and RR (Recall Rate) show the mean (standard error) values in overall 100 windows. The Time column shows mean over 10 datasets. Parameters for DASH and EMI are H = 200 kb and den_min = 0.5. The corresponding short terms are J (Jaccard measure), PR (Precision-Recall measure) and RR (Recall Rate) as defined in the main text.

IBS data: It has been shown that most existing pairwise IBD detection methods have lower power for short IBD segments (e.g. shorter than 2 cM) given SNP data. Therefore, the performance of multiple-IBD clustering might be limited by the input of pairwise IBD segments. To explore the optimal performance a clustering method can achieve, we also generated pairwise IBS segments from the sequencing data and used them as input for the clustering. The results are shown in Table 2. As expected, the performance increased significantly compared with the results with thinned SNP data. However, neither EMI nor DASH achieved 100% power or accuracy because both methods use heuristics, and the input IBS segments differ somewhat from true IBD segments.

The IBS data have more pairwise IBD segments than the thinned SNP data, and the number of edges (|E|) increases within each window; hence the running time also increases significantly. Within each window, the average value of |E| is 45 325 for SNP data and 158 951 for IBS data. We can see that the computing time for EMI scales better than DASH as |E| increases.

3.2 IBD mapping in NFBC data

3.2.1 Multiple-IBD clustering

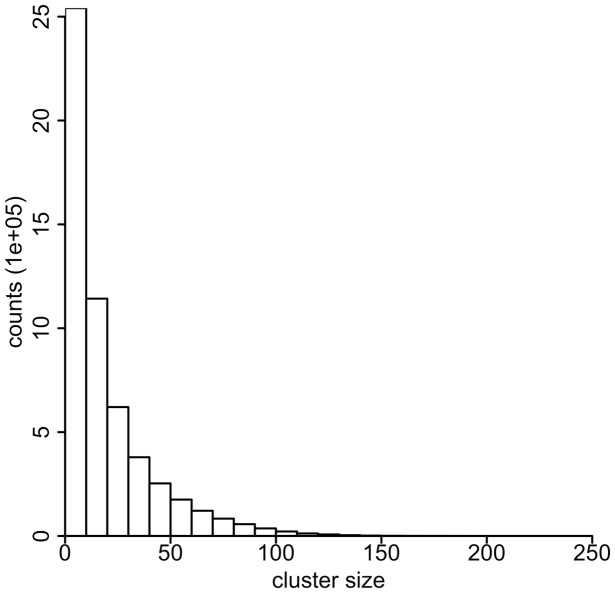
We use cluster density cutoff den_min = 0.5 and sliding window size H = 0.2 cM as input parameters for EMI, which is close to the optimal parameters in our simulation. Runs with slightly different parameters do not change the results significantly (data not shown). Running on a single processor, EMI takes ∼50 min to analyze the 22 autosomes in the NFBC data with 5402 individuals. EMI outputs all the clusters with a minimum size 3. The cluster frequency distribution is shown in Figure 2. As we expected, most of the clusters have small sizes. Approximately 98% of them have a frequency < 0.01.

Fig. 2.

The distribution of sizes of multiple-IBD clusters in NFBC data

3.2.2 Association mapping with linear mixed models

After removing close relatives and individuals with missing covariates, we were left with 4406 individuals in the NFBC data for the association test with LDL. We ran SKAT on sliding windows of size 0.2 cM, which is also the window size we used for EMI. Across the 22 autosomes, there were 22 630 sliding windows wherein multiple-IBD clusters were found.

For each window, all the clusters spanning the entire window are considered and contribute to the random effects in the mixed model, and a P-value is calculated against the null hypothesis of 0 variance of random effects. The P-values along the sliding windows are shown in Supplementary Figure S1 and the Quantile–Quantile (QQ) plot is shown in Supplementary Figure S2.

To correct for multiple testing, we performed 1000 permutations of the trait values, keeping the covariates unchanged, and ran SKAT for each permutation. We obtained the experiment-wide distribution of minimal P-values over all loci from the permutation replicates. The empirical P is defined as the proportion of minimal P values from permutations that are smaller than the P-value on the original data in this region. The QQ plot shows that the variance-component score test is anti-conservative. By using empirical P-values, we not only adjust for multiple testing but also correct for the anti-conservative nature of the original P-values.

The empirical experiment-wide P-value 0.05 corresponds to a SKAT P-value of 1.13 × 10⁻⁵ in this analysis. As shown in Table 3, we found two loci, the APO cluster and the PCSK9 gene, that have an empirical P-value <0.05.

Table 3.

Loci reaching the significance threshold in the analysis of LDL

Chromosome	Window start	Window end	SKAT P	Empirical P	Gene
1	55230403	55258652	7.44 × 10−6	0.013
1	55258652	55293452	9.37 × 10−6	0.015	PCSK9
19	50016356	50069307	1.51 × 10−6	0.002
19	50069307	50140305	4.52 × 10−7	0.001	APO cluster

Note: Window start and window end are the boundaries of sliding windows. SKAT P is the P-value reported by SKAT, showing the significance of random effects in the mixed model. Empirical P is obtained based on minimal P values from 1000 permutations, as detailed in the text, to adjust for multiple testing across the autosomes.

Sabatti et al. (2009) conducted standard GWAS analysis on this dataset and reported six loci associated with LDL traits. The APO cluster (MIM107730) was found with both standard GWAS analysis (P-value 4.96e-8) and with our multiple-IBD approach (P-value 4.52e-7). The signals around the APO cluster span several windows.

The second strongest signal found in our study is located near the PCSK9 (MIM 607786) gene, which is known to be involved in regulation of LDL cholesterol. Previous studies suggested that mutations in PCSK9 have a strong effect on LDL cholesterol (Cohen et al., 2006). This association was first reported in a GWAS-based analysis for a variant of MAF 1% in a sample of 8816 individuals (Kathiresan et al., 2008). In the NFBC dataset, there are no SNPs in strong LD with the reported SNP, and therefore the standard methods failed to report it. The association with PCSK9 was also reported later by one of the largest lipid meta-analyses to date with a sample size of >100 000 individuals of European descent (Teslovich et al., 2010) and a recent GWAS of African Americans and Hispanic Americans (Coram et al., 2013), which indicates that the signal we found is real.

It is worth mentioning that the third strongest signal we found is chromosome 19 [11145302, 11225495 bp] (hg18), ∼40 kb downstream of the LDLR gene (MIM 606945). Although this signal (P-value 8.22e⁻⁵) failed to show significance after the multiple-testing correction, it was one of the loci reported by Sabatti et al. (2009) and has been validated by many other GWAS with larger sample sizes (Coram et al., 2013; Teslovich et al., 2010).

4 DISCUSSION

IBD haplotype sharing is useful for many applications, such as imputation, improved accuracy in haplotype phasing, IBD mapping and population genetic inference. Most existing methods for IBD detection only consider pairwise IBD, yet the implementation and applications of multiple-IBD have not been fully explored.

In this study, we developed EMI to detect IBD segments that are shared by multiple individuals. Unlike the existing method DASH, which searches for a highly connected graph by dividing the big graph iteratively with a minimum cut algorithm, EMI is implemented in an agglomerative manner and uses a heuristic approach to greedily build clusters. Using efficient data structures, EMI runs faster than DASH in application to genome-wide data, with comparable performance. The theoretical time complexity is hard to obtain because both DASH and EMI use methods to reduce computational effort when moving across sliding windows along the genome. However, our simulations show that the difference in running time between EMI and DASH becomes larger in a region with increased pairwise IBD sharing, such as data from isolated populations.

The accuracy of inferred multiple-IBD clusters has not previously been evaluated. We used coalescent simulations to evaluate the accuracy of resulting multiple-IBD clusters and found the optimal parameters for subsequent analysis. Although multiple-IBD clusters are supposed to be highly connected, a density cutoff as low as 0.5 has a fairly good performance. The best density cutoff may depend on the pairwise IBD detection program, which has to make a trade-off between power and type 1 error. For example, we used Beagle Refined IBD for pairwise IBD detection, which has a low type 1 error rate but also low power for short IBD segments. Therefore, with Beagle Refined IBD, we use a low-density cutoff so that we favor adding missing edges over cutting existing edges from the pairwise IBD input. If we use GERMLINE, which has weaker control of type 1 error to detect pairwise IBD segments, a higher density cutoff may work better.

The speedup EMI achieves might seem to be insignificant in the context of GWAS, where a lot more time is spent on the upstream analysis. We have shown in our study that the simple heuristic performs fairly well, but the results are not optimal and can be further improved. For example, one can combine the information of clusters of all windows into a global probabilistic framework, similar to the idea behind IBD-Groupon. When it requires many iterations to train an HMM, computational speed matters. Therefore, our method is suitable for use in more complicated models.

The concept of IBD mapping is not new, yet the approach used here is different from the approaches used previously. Previous IBD analyses have either used pairwise IBD and looked for differences in IBD frequency between pairs of cases and pairs of controls (Browning and Thompson, 2012; Purcell et al., 2007) or have tested each multiple-IBD cluster individually (Gusev et al., 2011). Here we use a variance components approach to jointly test the multiple-IBD clusters in a region. The multiple-IBD cluster approach is expected to be more powerful when multiple low-frequency causal variants contribute to a trait.

Funding: Research grants (HG004960, HG005701, GM099568 and GM075091) from the National Institutes of Health, USA, and the Danish Council for Independent Research (DFF) Natural Sciences grant (09-065923). The NFBC1966 Study is conducted and supported by the National Heart, Lung and Blood Institute (NHLBI) in collaboration with the Broad Institute, UCLA, University of Oulu, and the National Institute for Health and Welfare in Finland. This article does not necessarily reflect the opinions or views of the NFBC1966 Study Investigators, Broad Institute, UCLA, University of Oulu, National Institute for Health and Welfare in Finland and the NHLBI.

Conflict of Interest: none declared.