A Quantitative Process for Enhancing End of Phase 2 Decisions

Abstract

The objectives of the phase 2 stage in a drug development program are to evaluate the safety and tolerability of different doses, select a promising dose range, and look for early signs of activity. At the end of phase 2, a decision to initiate phase 3 studies is made that involves the commitment of considerable resources. This multifactorial decision, generally made by balancing the current condition of a development organization's portfolio, the future cost of development, the competitive landscape, and the expected safety and efficacy benefits of a new therapy, needs to be a good one. In this article, we present a practical quantitative process that has been implemented for drugs entering phase 2 at Amgen Ltd. to ensure a consistent and explicit evidence-based approach is used to contribute to decisions for new drug candidates. Broadly following this process will also help statisticians increase their strategic influence in drug development programs. The process is illustrated using an example from the pancreatic cancer indication. Embedded within the process is a predominantly Bayesian approach to predicting the probability of efficacy success in a future (frequentist) phase 3 program.

1. Introduction

The aim of clinical drug development decision making is to stop the development of nonviable treatments as soon as possible. This avoids administering patients unsafe or ineffective medicines, mitigates the drug development costs, and makes both resources and patients available for the development of other potentially more promising treatments. There are a number of decision points within the clinical drug development process, the key ones being the decision to go into humans for the first time, the transition to phase 2 after gaining evidence of biological activity, the decision to initiate phase 3 (herein referred to as the end of phase 2 (EOP2) decision) after completion of dose ranging and finding, the commitment to file with regulatory bodies and commitment to launch into the market. It is well documented that considerable attrition of potential drug candidates occurs in late phase development (Kola and Landis 2004; Arrowsmith 2011a; DiMasi et al. 2012), with lack of efficacy being the main reason for failing phase 3 (Paul et al 2010; Arrowsmith 2011a,b). This is not good for patients or drug development companies. It results in companies incurring the majority of the drug development costs, which in turn translates to a higher cost of medicines. The oncology therapeutic area is a particularly noteworthy example, where success rates for transitioning from phase to phase have been lower than other therapeutic areas, with success rate in phase 3 arguably unacceptably low (Kola and Landis 2004; Arrowsmith 2011a). This is due to several factors, including but not limited to, the use of outcome measures in phase 2 with poor predictive value for the outcome measure used in phase 3 for drug registration purposes and possible differences between the patient populations used for the corresponding phase 2 and 3 studies.

The EOP2 decision is influenced by a number of factors, including the current condition of a development organizations portfolio, the future cost of development, the competitive landscape, and the expected safety and efficacy benefit of a new therapy. There is a pressing need to develop and implement methodologies and processes to enhance the EOP2 decision-making capabilities within the industry. The EOP2 decision should involve a quantitative assessment of the available evidence, and statisticians with experience in systematic data reviews, quantitative modeling and experimental design have a fundamental role to play in this. In this article, we present a quantitative process for enhancing EOP2 decisions that has been implemented for drugs entering phase 2 at Amgen Ltd. which if followed could ensure a more consistent and explicit evidence-based approach is used to make decisions for new drug candidates. While many of the individual components of this process are not new from a statistical sense, the process formulation will be a useful guide to pharmaceutical statisticians. The process is divided into two stages as follows.

Stage 1: Systematic Literature Review and Data Abstraction

For any disease area under investigation, ideally prior to starting phase 2, the process begins with a literature review focused on addressing the following core set of questions:

• 1.Has the definition of disease changed over time?
• 2.What are the important prognostic markers for the targeted indication?
• 3.What is the expected absolute treatment effect of the current standard of care, and other drugs either marketed or in development, for both the phase 2 and primary phase 3 outcome measures?
• 4.What are the observed treatment effects of other drugs relative to the standard of care for both the phase 2 and primary phase 3 outcome measures?
• 5.What is the impact of the important prognostic factors on the ability to detect a treatment effect relative to the standard of care in both the phase 2 and primary phase 3 outcome measures (i.e., is there a prognostic factor by relative treatment effect interaction)?
• 6.Have the absolute and relative treatment effects changed over time?
• 7.What are the most common side effects and their expected incidence rate?
• 8.What are the relationships between the phase 2 and primary phase 3 outcome measures for individual treatment groups and also for differences between treatment groups?
• 9.Are these relationships likely to hold for drugs with different modes of action?
• 10.What is the impact of previous treatments on the relationships between the phase 2 and 3 outcome measures?

The relevant data are then systematically abstracted and meta-analytical techniques applied to answer these questions. These results enhance the EOP2 decision by facilitating an appropriate choice of phase 2 and 3 study design and trial populations, the selection of phase 2 outcome measures, a comparison of the new treatment over currently available and potential future competitor therapies, and providing prior information on the relationship between the phase 2 and phase 3 outcome measures for use in Stage 2. It is very important to follow good practice guidelines when conducting systematic literature reviews to ensure that appropriate historical trials are selected to support the decision making process (Moher et al. 2009; Higgins and Green 2011). The inappropriate inclusion or exclusion of trials will have a direct effect on the quality of decisions made.

Stage 2: A Statistical Model for Predicting the Probability of Success in Phase 3

One of the most important factors in the EOP2 decision is the expected efficacy. In this stage, a Bayesian model is implemented to evaluate the probability of achieving the required statistical criteria for efficacy success in a future phase 3 study. The model synthesizes the relationships between phase 2 and phase 3 study outcome measures (on the relative treatment difference scale), the influence of prognostic factors on the relationship, the treatment difference observed for the phase 2 outcome measure in the phase 2 study, the prior opinion of key decision makers for the treatment difference in the phase 2 outcome measure, and knowledge of the proposed phase 3 study design to predict the probability of success (PoS) in a future phase 3 study analyzed using frequentist statistical methods. Additionally, reasonable bounds of belief for the PoS are generated by running the model prediction incorporating a range of subjective prior opinions representing different attitudes of key decision makers for the treatment difference in the phase 2 outcome measure.

The entire data package generated provides direct evidence on the unmet need and expected clinical value of the new treatment, and can also be used as inputs to determine the cost of development (e.g., through sample size calculations), the benefit-risk and economic value of a new treatment. Also, by implementing the process for all new drugs entering phase 2, we aim to ensure all projects competing for funding are assessed in a similar way and on an equal footing.

Broadly following the concepts highlighted in this article will enable statisticians to contribute greatly to many aspects of the decision-making process, and therefore ensure that good development plans, decision points, and criteria are in place, as well as enhancing their strategic influence. We expect that clinical development leaders will highly value statisticians who are able to make these types of contributions.

Some theoretical work has already been published in this area. O'Hagan, Stevens, and Campbell (2005) introduced the concept of assurance; an unconditional probability that a trial will achieve a specific outcome based on prior knowledge for the unknown true treatment effect. Stallard, Whitehead, and Cleall (2005) proposed an approach in which the posterior probability that a future frequentist phase 3 study will be successful is calculated and used to inform the decision to initiate phase 3 at the interim and final analyses of a phase 2 trial. Nixon et al. (2009a) described a model to predict the six-month American College of Rheumatology (ACR) response rate based upon the ACR response rate collected at earlier time points, for trials in rheumatoid arthritis. In this article, the modeling is performed within a treatment arm on the absolute scale. Nixon et al. (2009b) presented a rheumatoid arthritis drug development model (RADDM), which simulates proposed phase 2b and 3 trials based upon efficacy evidence on the ACR response rate at the end of phase 2a, evidence of efficacy from existing treatments and expert opinion on three key safety markers. Bayesian clinical trial simulation is then used to determine the assurances of licensing approval at the end of phase 3. Hong and Shi (2012) presented a method that uses predictive power to predict the probability of success in a phase 3 outcome measure (i.e., the overall survival (OS) log hazard ratio) based on a different phase 2 outcome measure (the progression-free survival (PFS) log hazard ratio). This approach requires specification of a prior for the correlation between the treatment difference for the phase 2 outcome measure and the treatment difference for the phase 3 outcome measure.

In the following sections, we present the process to enhance EOP2 decisions implemented in practice for all disease areas at Amgen Ltd., provide a case study using the pancreatic cancer indication to highlight the modeling performed to predict the PoS in phase 3, draw some conclusions, and indicate some areas for future methodological development. The modeling approach adopted in the example differs from the Hong and Shi (2012) publication by its use of meta-regression techniques to estimate the relationship between the primary phase 2 outcome measure (PFS log hazard ratio) and the different primary phase 3 outcome measure (OS log hazard ratio).

2. A Quantitative Process for Enhancing End of Phase 2 Decisions

Stage 1: Systematic Literature Review and Data Abstraction

For any disease area under investigation, the process begins (ideally prior to starting phase 2) with a literature review focused on identifying published trials relevant to addressing the 10 core questions highlighted in Section 1. The relevant data are then systematically abstracted from the published literature and synthesized using standard meta-analytical techniques. The data abstraction process can be repeated prior to the EOP2 meeting to ensure that any new information is incorporated into the EOP2 decision. Given a large part of the EOP2 decision revolves around predicting the treatment difference in the phase 3 study from the treatment difference observed in the phase 2, for the remainder of this section we focus on core questions 8–10, and the development of a statistical (usually meta-regression) model to relate the treatment differences seen with the phase 2 outcome measure to treatment differences seen with the phase 3 outcome measure. This relationship forms part of the prior knowledge required for the statistical model for predicting the probability of success in phase 3 described in stage 2.

In many situations where the phase 2 and phase 3 outcome measures are different, for example, phase 2 studies may use short-term intermediate outcome measures, rather than the longer-term outcome measures needed for regulatory approval, using meta-regression to investigate their relationship provides an understanding of how good the outcome measure selected for phase 2 may be at predicting the phase 3 outcome measure. Determining this relationship, from completed studies where both the phase 2 and phase 3 outcome measures have been collected, on the relative treatment effect scale is particularly valuable. This enables the development of a model for estimating phase 3 outcome measure differences from any given fixed value for the phase 2 outcome measure difference. For example, assuming the relationship is linear and passes through the origin, the model to be fitted is

where μ_i is the true phase 3 outcome measure treatment difference in the ith study, z_i is the phase 2 outcome measure treatment difference, considered as a fixed effect at this stage, in the ith study, and β is the slope of the regression line. It should also be noted that the functional form of the model does not have to be linear or forced through the origin. As with any model it is simply a matter of choosing a functional form that makes sense. If the treatment differences are believed to be dependent upon certain important prognostic characteristics of the studies included in the meta-analysis, the above model may be further expanded to include the prognostic characteristics as trial level covariates.

The meta-data consist of study estimates of phase 3 outcome measure treatment differences, 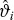, with variance ∊_i². To use a random effects model we assume 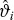is normally distributed with mean μ_i, such that

and that μ_i is itself a realization of a normally distributed random variable such that

In our application of this method, we take a Bayesian approach where β and τ are considered as hyperparameters with independent prior distributions. A noninformative prior N(0,10⁴) is given to β. Lambert et al. (2005) and Spiegelhalter, Abrams, and Myles (2004) highlighted the importance of carefully selecting the prior for τ. The choice of prior for τ should be made following a review of the data, and sensitivity analyses conducted using a range of realistic vague prior distributions. For the pancreatic cancer example described later, we selected a uniform (0,2) prior. The posterior distributions for β and τ can be approximated using Markov chain Monte Carlo (MCMC) methods.

Here, we also assume that the relationship between the phase 2 and phase 3 outcome measures, determined from the systematic review, will apply to the new drug being tested. We recommend that sensitivity analyses are performed to assess how robust predictions are for departures from this relationship. This may be particularly important when the new drug has a different mode of action to many of the previous treatments. Alternatively, if data permit, the relationship may be determined from studies on treatments with similar modes of action.

Stage 2: A Statistical Model for Predicting the PoS in Phase 3

A general overview of the statistical model used to estimate the PoS of the compound is provided in Figure 1. The model synthesizes the relationships between phase 2 and phase 3 study outcome measures (on the relative treatment difference scale), the influence of prognostic factors on the relationship, the treatment difference observed for the phase 2 outcome measure in the phase 2 study (prior to starting phase 2, simulated results may be used to optimize the phase 2 design), a range of prior opinions of key decision makers for the treatment difference in the phase 2 outcome measure, and knowledge of the proposed phase 3 study design to predict the probability of success in a future phase 3 study analyzed using frequentist statistical methods. The definition of success may differ depending upon the objectives of the phase 3 study. In general, this is likely to be the probability of achieving a favorable statistically significant efficacy result from an appropriate statistical test designed to reject, or not the null-hypothesis of no difference between treatments, on the primary Phase 3 outcome measure at the conventional 5% two-sided level of significance.

Figure 1.

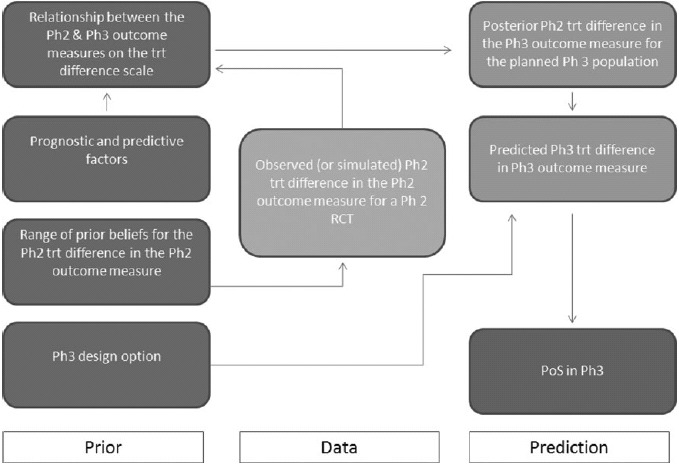
Statistical model for predicting the probability of success in phase 3. Ph: Phase; trt: treatment; RCT: Randomized Controlled Trial; PoS: probability of success.

The model uses a predominantly Bayesian approach to what is a prediction problem, which we divide into four steps.

• Step 1.

  Ideally the first step would begin prior to starting phase 2 where a range of plausible treatment differences for the phase 2 outcome measure in the planned phase 2 study is simulated. Each of these simulations may in turn be used to evaluate the PoS for the planned phase 3 study. Repeating this process using different options for the phase 2 and 3 designs can help optimize the development strategy for a specific indication. It may be more usual that the process begins after the phase 2 has already started or even completed. In either case, we assume the observed (or simulated) treatment difference in the phase 2 outcome measure may be expressed as

  
• Step 2.

  A range of prior statistical distributions for the phase 2 outcome measure treatment difference reflecting differing opinions of key decision makers is elicited. These priors enable us to develop reasonable bounds of evidence in Step 3 for the PoS in phase 3. These are chosen to represent a noninformative prior distribution δ ∼ N(δ_n, σ_n²) an optimistic opinion for the phase 2 treatment difference δ ∼ N(δ₀, σ₀²), and a skeptical opinion δ ∼ N(δ_s, σ_s²) (Spiegelhalter, Freedman, and Palmer 1993). Taking the prior belief of key decision makers into account was an important component in the successful implementation of this framework. In addition to using the observed evidence, the ability to make statements at the end of phase 2 meeting that the PoS in phase 3 is still above a certain value taking the point of view of the most skeptical decision maker, or that the PoS is still below a certain value taking into account the view of the optimist decision maker brings valuable perspective to the go/no-go discussions. These priors are combined with the results from Equation (2) to obtain a range of posterior statistical distributions for the treatment difference in terms of the phase 2 outcome measure

  

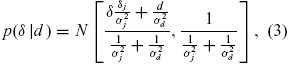
  where j = n, o, s.

• Step 3.

  We now use the distribution of our expected phase 2 outcome measure treatment differences (Equation (3)), and the relationship between the treatment differences for phase 2 and phase 3 outcome measures determined using meta- regression from the systematic review (Equation (1)) to form distributions for the phase 3 outcome measure treatment difference. In our Bayesian approach, we use the three different prior distributions for the phase 2 treatment difference (representing skeptical, optimistic, and noninformative opinions of key decision makers) to form three different predictive distributions for the phase 3 outcome measure treatment difference. If the relative treatment differences are believed to be dependent upon certain important prognostic characteristics of the studies included in the meta-analysis, the model for the relationship should include the prognostic characteristics as trial level covariates. The predictive distributions of the phase 3 outcome measure treatment difference may then be estimated from the relationship by predicting the response for the planned characteristics of the phase 3 study.

  Recall that the model for the relationship (Equation (1)) assumed Z_i represents a fixed value of the phase 2 outcome measure treatment difference. During this step, the model is extended to ensure the uncertainty in the phase 2 outcome measure treatment difference in incorporated into the estimation of the posterior distributions of the phase 3 outcome measure. This is done within the MCMC simulation by assuming the phase 2 outcome measure treatment difference (Equation (3)) is a normally distributed random variable.

• Step 4.

  The range of predictive distributions for the phase 3 outcome measure treatment differences is used to simulate the results of the proposed phase 3 study design and estimate the PoS for the future frequentist phase 3 study. The earlier inclusion of skeptical and optimistic priors leads to the development of reasonable bounds of belief for the PoS.

The phase 3 study design parameters considered include the required level of statistical significance, the desired size of the treatment difference, variance, and the trial sample size. The PoS may be determined by again using MCMC simulation. Assuming the predictive distributions for the phase 3 outcome measure treatment differences found in Step 3 are normally distributed d₃ ∼ N(μ, σ₂²), and the future phase 3 data are normally distributed X₃ ∼ N(d₃, σ₃²):

• 1.Sample a value for the phase 3 treatment difference, d₃⁽ⁿ⁾ from the posterior distribution in Step 4.
• 2.Sample a value x₃⁽ⁿ⁾ given x₃⁽ⁿ⁾.
• 3.Calculate the confidence interval for x₃⁽ⁿ⁾ and determine whether this represents a favorable statistically significant result.
• 4.Repeat n times and determine the proportion of statistically significant outcomes.

Alternatively the PoS may be approximated as described in Spiegelhalter, Abrams, and Myles (2004). Rewriting 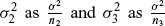, the PoS for the hypothesis x < 0 may be approximated by

where ϕ denotes the cumulative standard normal distribution. In addition to simulating the PoS, this approach can be extended to simulate the probability of observing a particular outcome in the phase 3 trial, that is, the probability P(x₃ > y) that the phase 3 treatment difference is greater than a selected value of interest y.

3. Worked Example: Predicting the PoS in Pancreatic Cancer

We present a worked example of predicting the probability of success in pancreatic cancer. The example implicitly shows where a project statistician was instrumental in working with their project team and other key decision makers in the organization to understand the phase 2 results in the light of the EOP2 decision about to be made. Gemcitabine is indicated for use in the first-line treatment of advanced pancreatic cancer and is the most commonly used treatment in this setting. Here, we assume that it is being used as the control group for a randomized phase 2 study and is planned to be used for a future phase 3 study. The primary outcome measure being used in the phase 2 study is PFS, a short-term outcome measure for the phase 3 regulatory outcome measure, OS. The EOP2 decision is based upon treatment differences expressed in terms of hazard ratios. We focus on predicting the distribution for the OS hazard ratio in a planned phase 3 study from the distribution of the PFS hazard ratio observed in phase 2. The modeling is performed on the log hazard ratio scale to allow the use of the normal distribution and is transposed back onto the hazard ratio scale for presentation purposes. The presence of metastases and ECOG performance status are both considered to be prognostic factors for OS. The phase 2 study is being conducted in a 100% metastatic patient population with an ECOG performance status of 0 or 1 at randomization. In this example, the PoS in a future phase 3 study reflects the probability of rejecting the null hypothesis that the log OS hazard ratio (HR) = 0 (in favor of the experimental treatment) at a two-sided 5% level of significance.

A thorough systematic literature review was conducted to identify all published randomized trials over the period from 2000 to 2012 in which gemcitabine was used alone or in combination with other therapies. Details of the selection criteria and chosen publications can be found in the supplementary materials. In total, 43 studies were selected for detailed analysis. The methods in Tierney et al. (2007) were used to estimate the median survival, hazard ratio, and their associated standard errors for the PFS and OS outcome measures. Data that were relevant to predicting the gemcitabine control group PFS and OS, the relationship between median PFS and median OS, the relationship between the PFS hazard ratio and the OS hazard ratio, and the pattern of treatment differences seen with important study level covariates were synthesized. Key learnings from this step pertinent to predicting the PoS included:

• There is a strong association between the PFS hazard ratio and the OS hazard ratio (Figure 2).

• Plots of the PFS hazard ratio and OS hazard ratio against the study level characteristics percentage of metastatic subjects, and percentage of ECOG 0/1 subjects showed there to be a wide range of values for the percentage of metastatic subjects, and percentage of subjects with ECOG = 0/1, where positive treatment effects have been shown. Moreover, there is no range of values where a treatment effect has not been shown, and no evidence of association between these study-level covariates and outcome.

Figure 2.

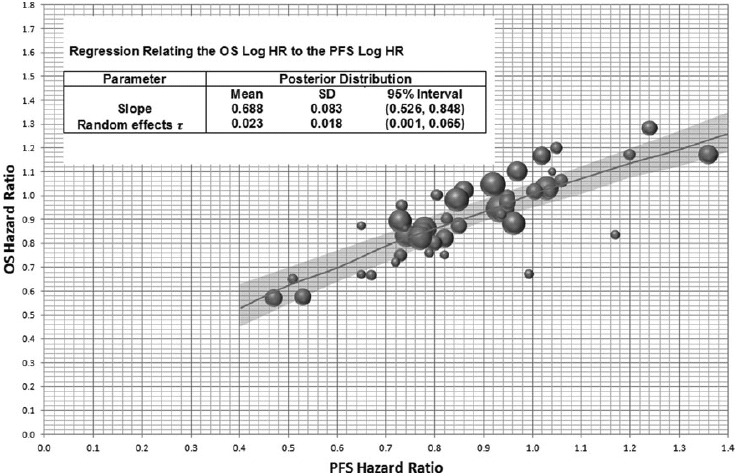
Random effects meta-regression for OS hazard ratio from PFS hazard ratio. Axes are back transposed from a linear regression between OS log(HR) and PFS log(HR), The diameter of the circles is inversely proportional to the SE of the OS log(HR) for each published study. Plot shows the predicted mean and 95% CI of a new study for fixed PFS hazard ratios.

• Step 1.

  Table 1 presents an example assuming that the PFS HR observed in phase 2 is 0.8 (log PFS HR = −0.223, with variance 0.05). This represents a phase 2 study comparing a new treatment with gemcitabine analyzed after 80 subjects have experienced a PFS event.

• Step 2.

  Three prior distributions for the log PFS hazard ratio were elicited from key decision makers to represent noninformative N(0, 10²), skeptical N(0, 0.2168²), and optimistic N(−0.357, 0.3441²) prior opinions. The skeptical distribution reflects the opinion that the new treatment shows on average no benefit in PFS time relative to gemcitabine, but there is a 5% chance that the new treatment is better than gemcitabine with a hazard ratio ≤0.70. The optimistic distribution represents an average a hazard ratio of 0.70, with a 15% chance that the new treatment is no better than control, that is, a hazard ratio ≥ 1. Each of these distributions is then combined with the observed phase 2 results to obtain a range of posterior estimates for the PFS log HR (Table 1).

• Step 3.

  The relationship between the PFS hazard ratio and OS hazard ratio using the systematically abstracted data was investigated using Bayesian meta-regression (Figure 2). Each point in Figure 2 represents the results of one completed study, from which both the PFS hazard ratio and corresponding OS hazard ratio were abstracted. In this example, we apply a no-intercept model forcing the regression through the origin. The potential for publication bias was minimized by including all randomized phase 2 and 3 studies in the model. Sensitivity analysis excluding the small earlier phase studies from the analysis was conducted and showed the small studies to have little impact on the parameter estimates. Also, given no evidence of association between the percentage of metastatic patients or percentage of ECOG 0/1 patients, and the PFS log HR or OS log HR was observed, the selected model did not include these factors as study-level covariates. Each of the posterior distributions for the phase 2 outcome measure (PFS log HR) is synthesized with the meta-regression to estimate the predictive distribution for the phase 3 outcome measure treatment difference, that is, the OS log HR (Table 1). Within this step, the meta-regression shown in Figure 2 is extended to ensure the uncertainty in the phase 2 outcome measure, PFS log HR, is incorporated. An example including the noninformative prior is shown in Figure 3, which shows the posterior predicted OS HR, assuming the PFS HR from a phase 2 study to be analyzed after 80 PFS events are observed is at this stage unknown.

• Step 4.

  In this example, we assume the sample size for the frequentist phase 3 study requires 380 deaths to enable 80% power to detect an OS hazard of 0.75 or less with a statistical significance level of 0.05 (5%). In this step, the predictive distributions for the log OS HR calculated in Step 3 are used to simulate the results of the proposed phase 3 study design, which in turn can be used to determine the probability of different patterns of study results, including the PoS. Table 1 completes the example determining the PoS for the planned phase 3 study assuming an observed phase 2 PFS hazard ratio of 0.8. The skeptical and optimistic priors can be viewed as providing reasonable bounds of belief for the estimated PoS. Assuming we observe a PFS HR = 0.8 in our phase 2 study we can conclude a PoS in phase 3 ranging from 19% to 46% depending on the prior belief. Figure 4 expands on the example to show the estimated PoS across a range of potentially observed phase 2 PFS hazard ratios and prior distributions. It can be seen that a PoS of at least 60% in phase 3 would require the phase 2 PFS hazard ratio to be 0.7 or lower, with a noninformative or optimistic prior belief. Note, the lines for optimistic and uninformative prior will naturally cross at the point where the observed phase 2 results become more favorable than the optimistic prior.

Table 1.

Estimating the probability of success with a phase 2 PFS result (HR = 0.8)

	Skeptical		Noninformative		Optimistic
	Mean	SE	Mean	SE	Mean	SE
Prior PFS log HR	0	0.217	0	10	−0.357	0.344
Observed Ph 2 PFS log HR	−0.223	0.224	−0.223	0.224	−0.223	0.224
Posterior PFS log HR	−0.108	0.155	−0.224	0.223	−0.264	0.189
Predicted Ph 2 OS log HR	−0.072	0.109	−0.151	0.155	−0.183	0.135
Probability of Ph 3 success	0.19		0.39		0.46

Figure 3.

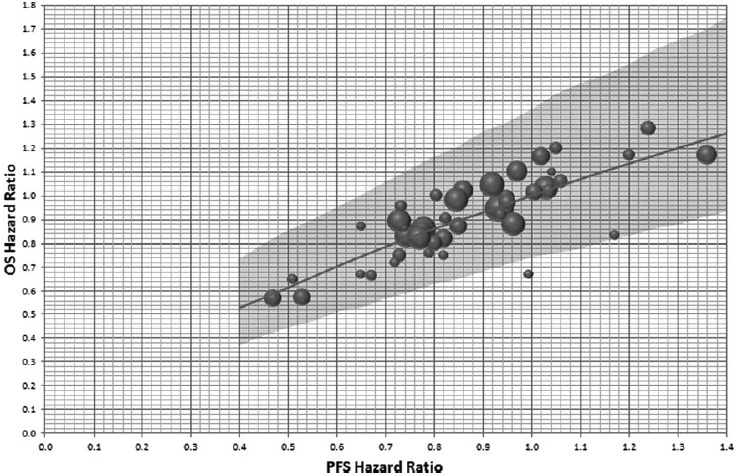
Posterior predicted OS hazard ratio with a noninformative prior. Axes are back transposed from a linear regression between OS log(HR) and PFS log(HR). The diameter of the circles is inversely proportional to the SE of the OS log(HR). Plot shows the OS HR posterior predicted mean and 95% CrI assuming a phase 2 study with 80 observed PFS events and a noninformative prior for the PFS log HR.

Figure 4.

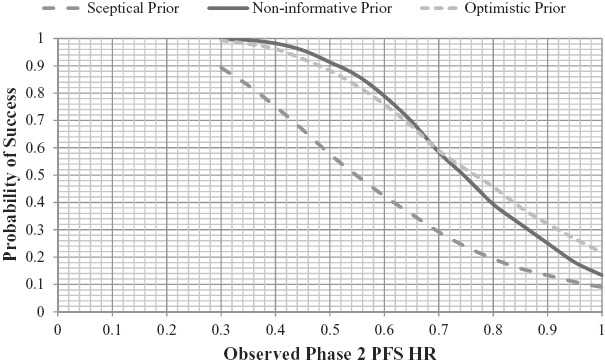
Probability of success in a phase 3 study Analyzed after 380 deaths.

4. Discussion

The quantitative process for enhancing EOP2 decisions presented in this article is designed to ensure a consistent and explicit evidence-based approach is used to inform decisions for new drug candidates. This requires the systematic abstraction of data to support the choice of phase 2 and 3 study design and population, the appropriate selection of phase 2 outcome measures, a comparison of the new treatment over currently available and potential future competitor therapies, and evaluation of the probability of achieving the required statistical criteria for efficacy success in a future phase 3 study. The process results in a data package that provides direct evidence on the unmet need and expected clinical value of the new treatment, and can also be used as inputs to determine the cost of development, risk-benefit, and economic value of a new treatment. It therefore contributes widely to the value assessment undertaken at the EOP2. Evaluating the probability of efficacy success in phase 3 using the methodology outlined in this article requires the relationship between treatment differences seen using the phase 2 study outcome measure and treatment differences seen using the phase 3 outcome measure to be developed from prior studies. It also requires knowledge of how prognostic factors could influence the treatment difference. The process emphasizes the need to target a treatment difference in phase 3 that is clinically worthwhile, realistic, and cost effective. The probability of success implicitly assumes that this has been done.

By broadly following the concepts highlighted in this article, statisticians can contribute greatly to project strategy and the decision making process. In many ways, the structure and process presented herein are just making explicit many of the implicit assumptions and decisions that are made when deciding whether to move on from a phase 2 result to a phase 3 trial. Additionally, as highlighted in the publication by Sargent et al. (2005), if convincing evidence of a strong relationship between a short-term outcome measure and the currently used phase 3 outcome measure is found, there is potential to validate the use of the phase 2 outcome measure as a surrogate for the phase 3 outcome measure, and therefore influence current practice. This may subsequently translate into reduced drug development times.

Operationally, following such an approach is getting easier over time. With study results now registered on www.clinicaltrials.gov, more complete data are available for meta-analyses which should translate to more robust analyses. Additionally, access to the necessary software is improving. Pharmaceutical statisticians may wish to take note that the introduction of PROC MCMC means that all of the MCMC-based analyses shown in this article can now be easily conducted in SAS®.

5. Future Work

In this article, we have presented a statistical model for enhancing decisions based on predictions of treatment differences for phase 3 outcome measures and using these to simulate specific trial designs to assess the probability of phase 3 success. We have intentionally not specified a probability of phase 3 success that should be achieved to make a “go-to-phase 3” decision. The selection of a benchmark for this PoS will be specific to a funder/sponsor and their current portfolio, or could be chosen relative to the reported industry averages for being successful in phase 3. For example, in oncology the percentage of successful phase 3 studies for new treatments has been reported to be as low as 40% (Kola and Landis 2004) so predicted PoS lower than 40% would be aiming at a “lower than industry average” chance of being successful.

Our approach could also help to decide among different development strategies for a specific indication. For example, strategy A could be to conduct a small phase 2 study and begin a phase 3 study but with an early futility analysis. Strategy B could be to conduct an interim analysis within a phase 2 study with a possible decision to begin the phase 3 study immediately, or wait until completion of the phase 2 study to decide on beginning a phase 3 study. Using the process in this article to produce phase 3 predictions and EOP2 decisions in simulations for therapies that have a range of efficacy could be used to decide the best strategy. This would entail finding the operating characteristics of the decision rule including the false positive and false negative rates. In some instances, it may be that only minimal phase 2 evidence will be enough to make an adequate decision, whereas other instances may require much larger phase 2 studies. In our approach, we have considered the size of the phase 3 study to be fixed at the size required to show a frequentist success (e.g., for a superiority study with α = 0.05) and look at the PoS for this study for a range of results for a fixed size phase 2 study. Another approach could be to fix the PoS for the phase 3 study (at say 65%) and determine the size of the phase 2 study required to achieve this for a range of phase 2 results. This could indicate how reliant a good EOP2 decision could be on the size of the phase 2 study.

Following regulatory approval of a new treatment, it is important to gain agreement for reimbursement in many different geographical regions. This may require a form of Health Technology Appraisal to take place which usually necessitates the use of indirect treatment comparisons between treatments not already compared in head-to-head trials. It would be valuable to extend the methods outlined in this article to produce an early prediction of the outcomes of these indirect comparison analyses using the predictions of phase 3 outcomes at the end of phase 2. As well as likely phase 3 efficacy outcomes, the competitor situation is also an element of EOP2 decision making and these types of analyses could be used to quantify not only the magnitude of the indirect treatment comparisons, but also their levels of uncertainty at the phase 2 stage of the development. This is likely to include analyses of outcome measures other than phase 3 outcome measures that are important to assessing the comparative value of treatments.

Additional work exploring approaches to synthesize a prior for the control group response with the control arm in the phase 2 study may be useful. The approach used in the pancreatic cancer example takes the view that the observed treatment difference is the best unbiased estimate available and uses the control prior simply as an external assessment of the trials robustness. An alternative could be to assume that the control arms from the studies selected in the systematic review are compatible with the new phase 2 study control group data. Then assuming the phase 2 study is comparative, a posterior expected treatment difference in the phase 2 outcome measure calculated after initially combining the prior and phase 2 study control results together. If the phase 2 is randomized, such an approach would however break the randomization and potentially introduce bias. However, this approach may help to discount early optimistic phase 2 results (Kirby et al. 2012). Additionally, our pancreatic model assumes that the baseline hazard survivor function is consistent across studies. While this may be a reasonable assumption for a model that uses the relative treatment effects from randomized trials, incorporating methods to adjust for differences in the baseline hazard would be an important attribute to develop for an approach that combines the absolute treatment effects of trial arms across different studies.

The pancreatic model assumes proportional hazards within each study. While we do not have reason to doubt this assumption in this indication, a potentially beneficial alternative but more resource intensive approach would be to use methods of data abstraction that reproduce the individual patient data (Guyot et al. 2012). This would facilitate selection of an appropriate model from a wide set of parametric survival distributions. It would also allow for estimates of the difference in mean survival between treatments to be generated for use in cost effectiveness analysis without the need for the proportional hazard assumption.

The model has focused on the methods for enhancing decision-making at the EOP2 with respect to the likely efficacy of a new treatment. With some adjustment, the general approach used in this article could be applied to the evaluation of comparative safety data. This would require investigating the relationships between phase 2 and phase 3 safety outcome measures to predict phase 3 safety outcomes given the results of phase 2 safety assessment. If prediction of the likely efficacy and safety outcomes for a phase 3 study can be achieved, then it may also be possible to investigate the benefit-risk of a new drug by employing one of the Benefit-Risk methods that are currently being identified (EMA Benefit-Risk Methodology Project, 2011).

In conclusion, this article has outlined the process that has been implemented for drugs entering phase 2 at Amgen Ltd. designed to ensure a consistent and explicit evidence-based approach is used to contribute to EOP2 decisions for new drug candidates. It also provides a structured approach for collecting and synthesizing prior data with the phase 2 data for a new treatment to predict outcomes in future phase 3 studies. In this way, the statistician can enhance the subsequent EOP2 decision making for the funder/sponsor.

Supplementary Materials

Web appendix detailing the pancreatic cancer literature search and review.