Abstract
Using highly precise and accurate Monte Carlo simulations of 20,000,000 replications and 102 independent simulation experiments with extremely low simulation errors and total uncertainties, we evaluated the performance of four single outlier discordancy tests (Grubbs test N2, Dixon test N8, skewness test N14, and kurtosis test N15) for normal samples of sizes 5 to 20. Statistical contaminations of a single observation resulting from parameters called δ from ±0.1 up to ±20 for modeling the slippage of central tendency or ε from ±1.1 up to ±200 for slippage of dispersion, as well as no contamination (δ = 0 and ε = ±1), were simulated. Because of the use of precise and accurate random and normally distributed simulated data, very large replications, and a large number of independent experiments, this paper presents a novel approach for precise and accurate estimations of power functions of four popular discordancy tests and, therefore, should not be considered as a simple simulation exercise unrelated to probability and statistics. From both criteria of the Power of Test proposed by Hayes and Kinsella and the Test Performance Criterion of Barnett and Lewis, Dixon test N8 performs less well than the other three tests. The overall performance of these four tests could be summarized as N2≅N15 > N14 > N8.
1. Introduction
As summarized by Barnett and Lewis [1], a large number of discordancy tests are available for determining an outlier as an extreme (i.e., legitimate) or a discordant (i.e., contaminant) observation in normal samples at a given confidence or significance level. These discordancy tests are likely to be characterized by different power or performance. Numerous researchers [1–6] have commented on the properties of these tests under the slippage of location or central tendency and slippage of scale or dispersion by one or more observations, but very few studies have been reported on the use of Monte Carlo simulation for precise and accurate performance measures of these tests. Relatively more recently using Monte Carlo simulation of M = 100,000 replications or runs, Hayes and Kinsella [7] evaluated the performance criteria of two discordancy tests (Grubbs single outlier test N2 and Grubbs multiple outlier test N4k2; the nomenclature is after Barnett and Lewis [1]) and discussed their spurious and nonspurious components of type II error and power function. However, four single extreme outlier type discordancy tests, also called two-sided discordancy tests by Barnett and Lewis [1], are available, which are Grubbs type N2, Dixon type N8, skewness N14, and kurtosis N15. Their relative performance measures should be useful for choosing among the different tests for specific applications.
Monte Carlo simulation methods have been extensively used in numerous simulation studies [8–18]. Some of the relatively recent papers are by Efstathiou [12], Gottardo et al. [13], Khedhiri and Montasser [14], P. A. Patel and J. S. Patel [15], Noughabi and Arghami [16], Krishnamoorthy and Lian [17], and Verma [18]. For example, Noughabi and Arghami [16] compared seven normality tests (Kolmogorov-Smirnov, Anderson-Darling, Kuiper, Jarque-Bera, Cramer von Mises, Shapiro-Wilk, and Vasicek) for sample sizes of 10, 20, 30, and 50 and under different circumstances recommended the use of Jarque-Bera, Anderson-Darling, Shapiro-Wilk, and Vasicek tests.
We used Monte Carlo simulations to evaluate comparative efficiency of four extreme outlier type discordancy tests (N2, N8, N14, and N15, the nomenclature after Barnett and Lewis [1]) for sample sizes of 5 to 20. Our approach to the statistical problem of test performance is novel because, instead of using commercial or freely available software, we programmed and generated extremely precise and accurate random numbers and normally distributed data, used very large replications of 20,000,000, performed 102 independent experiments, and reduced the simulation errors to such an extent that the differences in test performance are far greater than the total uncertainties expressed as 99% confidence intervals of the mean. This is an approach hitherto practiced by none (see, e.g., [8–18]) except by our group [19–23]. This work, therefore, supersedes the approximate simulation results of test performance reported by the statisticians Hayes and Kinsella [7].
2. Discordancy Tests
For a data array x 1, x 2, x 3,…, x n−2, x n−1, x n or an ordered array x (1), x (2), x (3),…, x (n−2), x (n−1), x (n) of n observations, with mean and standard deviation s, four test statistics were objectively evaluated in this work. For a statistically contaminated sample of size of 5 to 20, n − 1 observations of this data array were obtained from a normal distribution N(0,1) and the remaining observation was taken from a central tendency shifted distribution N(0 + δ, 1) or dispersion shifted distribution N(0,1 × ε), where the contaminant parameters δ for modeling slippage of central tendency and ε for slippage of dispersion can be either positive or negative. For an uncontaminated sample, the simulations were done for δ = 0 and ε = ±1. In order to achieve an unbiased comparison, the application of the tests was always forced to the upper outlier x (n) for positive values of δ or ε and to the lower outlier x (1) for negative values of δ or ε.
Thus, the first test was the Grubbs test N2 [24] for an extreme outlier x (n) or x (1), for which the test statistic is as follows:
| (1) |
The second test was the Dixon test N8 [2] as follows:
| (2) |
The third test was sample skewness N14 as (note that the absolute value is used for evaluation):
| (3) |
Finally, the fourth test was the sample kurtosis N15 as follows:
| (4) |
All tests were applied at a strict 99% confidence level using the new precise and accurate critical values (CV99) simulated using Monte Carlo procedure by Verma et al. [19] for N2, N8, and N15 and Verma and Quiroz-Ruiz [20] for N14, which permitted an objective comparison of their performance.
3. Monte Carlo Simulations
Random numbers U(0,1) uniformly distributed in the interval (0,1) and normal random variates N(0,1) were generated from the method summarized by Verma and Quiroz-Ruiz [21]. However, instead of only 10 series or streams of N(0,1) as done by Verma and Quiroz-Ruiz [21], a total of 102 different streams of N(0,1) were simulated. Similarly, the replications were much more than those used by Verma and Quiroz-Ruiz [21] for generating precise and accurate critical values.
For a data array of size n, (n − 1) observations x 1, x 2, x 3,…, x n−2, x n−1 were drawn from one stream of N(0,1) and the contaminant observation (x c) was added from a different central tendency shifted stream of N(0 + δ, 1) where δ was varied from +0.1 − +20 and −0.1 − −20 or a dispersion shifted distribution N(0,1 × ε) where ε was varied from +1.1 − +200 and −1.1 − −200. The simulation experiments were also carried out for uncontaminated distributions, in which (n − 1) observations were taken from one stream of normal random variates N(0,1) and an additional observation was incorporated from a different stream with no contamination; that is, δ = 0 and ε = ±1.
Now, if we were to arrange the complete array from the lowest to the highest observations, the ordered array could be called x (1), x (2), x (3),…, x (n−2), x (n−1), x (n) after Barnett and Lewis [1]. All four tests under evaluation could then be applied to the resulting data array.
If δ > 0, δ < 0, ε > 1, or ε < −1 (the contaminant x c present), two possibilities would arise for the ordered array x (1), x (2), x (3),…, x (n−2), x (n−1), x (n) as follows (Table 1): (i) the contaminant x c occupies an inner position in the ordered array; that is, x c < x (n) if δ > 0 or ε > 1 or x c > x (1) if δ < 0, or ε < −1; this array is called a type event and the contaminant x c was not used in the test statistic; and (ii) the contaminant x c occupies the extreme position; that is, x c = x (n) if δ > 0 or ε > 1, or x c = x (1) if δ < 0, or ε < −1; this array was called a C type event and the contaminant x c was used in the test statistic.
Table 1.
Sample simulation and test outcome (modified after Hayes and Kinsella [7]).
| Discordancy test result | Contaminant x c (M replications) | ||
|---|---|---|---|
| Present (δ> 0, δ< 0, ε > 1, or ε< −1) | Absent (δ = 0 or ε = 1) |
||
| Contaminant x
c not used in a discordancy test ( type event) |
Contaminant x
c used in a discordancy test (C type event) |
||
| Not significant (TN ≤ CV99) |
Spurious type II error probability () (Figure 3) |
Nonspurious type II error probability () (Figures 5 and 7) |
True negative probability () (Figures 3, 5, and 7) |
|
| |||
| Significant (TN > CV99) |
Spurious power probability () (Figure 4) |
Nonspurious power probability (πDC) (Figures 6 and 8) |
Type I error probability (πD) (Figures 4, 6, and 8) |
TN: calculated test statistic for a sample (TN2, TN8, TN14, or TN15); CV99: critical value for a given discordancy test at 99% confidence level.
To an event of type when any of these four tests (N2, N8, N14, or N15) was applied, the outcome was called either a spurious type II error probability () if the test was not significant or a spurious power () if it was significant (Table 1). For this decision, the calculated test statistic TN (TN2, TN8, TN14, or TN15) for a sample was compared with the respective CV99 [19, 20]. If TN ≤ CV99, the outcome of the test was considered as not significant; else when TN > CV99, the outcome of the test was considered as significant (Table 1).
Similarly, to an event of C type, when a discordancy test was applied, the outcome was either a nonspurious type II error probability () if the test was not significant or a nonspurious power (π DC) if the test was significant (Table 1).
If δ = 0 or ε = ±1 (the contaminant x c absent) and a discordancy test was applied to the ordered array x (1), x (2), x (3),…, x (n−2), x (n−1), x (n) to evaluate the extreme observation x (n) or x (1), the outcome would either be a true negative (the respective probability ) if the test was not significant, that is, if it failed to detect x (n) or x (1) as discordant, or a type I error (probability π D) if the test was significant; that is, it succeeded in detecting x (n) or x (1) as discordant (Table 1).
4. Test Performance Criteria
Hayes and Kinsella [7] documented that a good discordancy test would be characterized by a high nonspurious power probability (high π DC), a low spurious power probability (low ), and a low nonspurious type II error probability (low ).
Hayes and Kinsella [7] defined the Power of Test (Ω) as
| (5) |
Similarly, they also defined the Test Performance Criterion π D∣C (which is equivalent to the probability P5 of Barnett and Lewis [1]) or the Conditional Power as
| (6) |
5. Optimum Replications
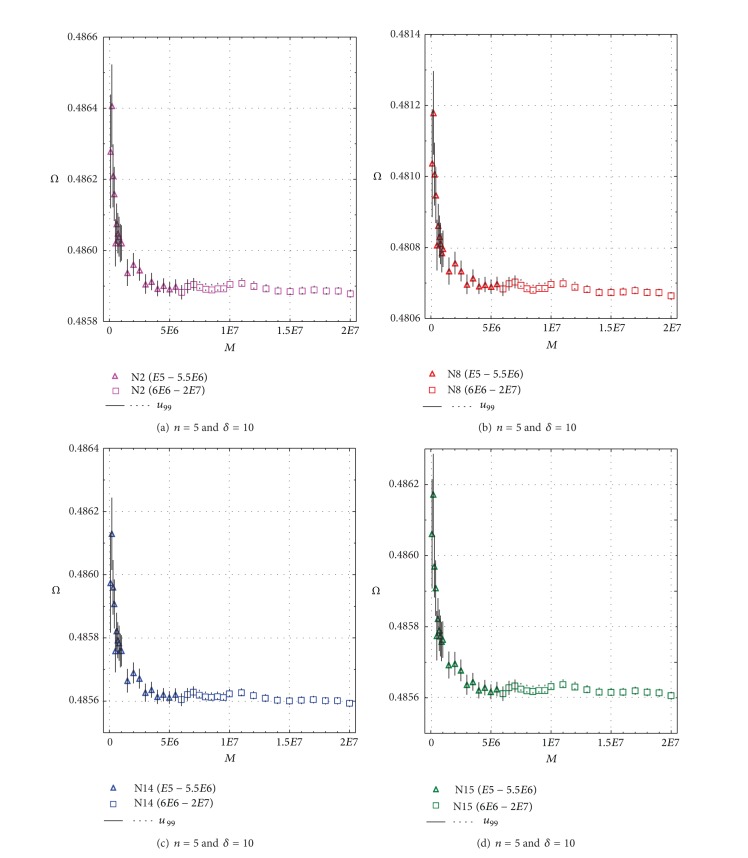
The optimum replications (M) required for minimizing the errors of Monte Carlo simulations were decided from representative results summarized in Figures 1 and 2, in which the vertical error bar represents total uncertainty at 99% confidence level (u 99, equivalent to 99% confidence interval of the mean) for 102 simulation experiments. For example, for n = 5 and δ = 10, Power of Test Ω is plotted in Figures 1(a)–1(d) as a function of the replications (M = 100,000 to 20,000,000) for N2, N8, N14, and N15. Although Ω mean values remain practically constant (within the confidence limits of the mean) for replications of about 8,000,000, still higher replications of 20,000,000 (Figures 1 and 2) were used in all simulation experiments.
Figure 1.
Determination of optimum simulation replication (M) for Power of Test (Ω) as a function of replications for sample size n = 5 and contaminant parameter δ = 10; symbols are explained in each figure; the vertical error bars represent uncertainty (u 99) at 99% confidence level from 102 simulations. (a) test N2; (b) test N8; (c) test N14; and (d) test N15.
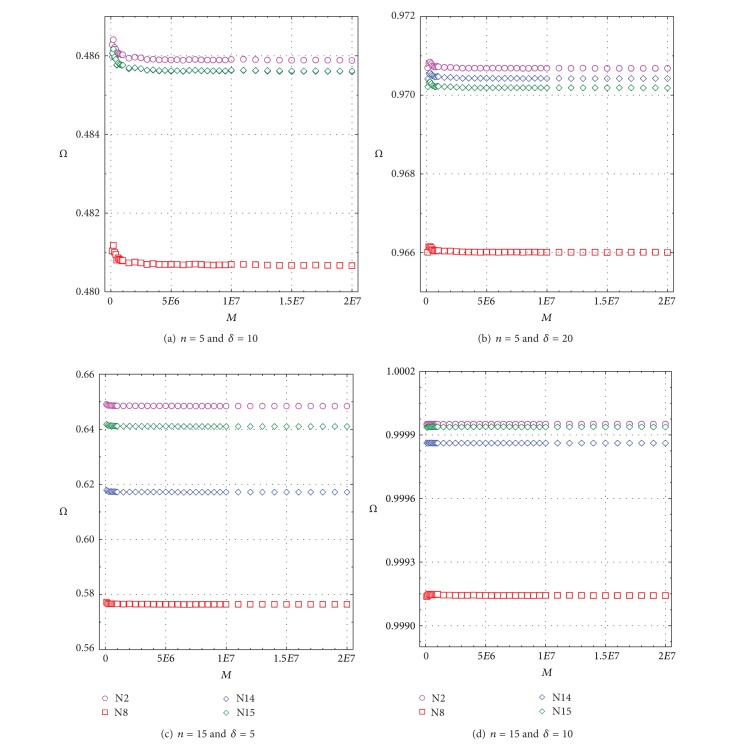
Figure 2.
Determination of optimum simulation replication (M) for Power of Test (Ω) as a function of replications for all tests N2, N8, N14, and N15; symbols are explained in each figure. (a) Sample size n = 5 and contaminant parameter δ = 10; (b) n = 5 and δ = 20; (c) n = 15 and δ = 5; and (d) n = 15 and δ = 10.
Similarly, Ω for all four tests as a function of replications is also shown in Figures 2(a)–2(d), which allows a visual comparison of this performance parameter for different sample sizes and δ values. Error bars (u 99) for the 102 simulation experiments are not shown for simplicity, but, for replications larger than 10,000,000, they were certainly within the size of the symbols. The replications of 20,000,000 routinely used for comparing the performance of discordancy tests clearly show that the differences among Ω values (Figures 2(a)–2(d)) are statistically significant at a high confidence level; that is, these differences are much greater than the simulation errors.
Alternatively, following Krishnamoorthy and Lian [17] the simulation error for the replications of 20,000,000 used routinely in our work can be estimated approximately as .
Because we carried out 102 independent simulation experiments, each with 20,000,000 replications, our simulation errors were even less than the above value. Thus, the Monte Carlo simulations can be considered highly precise. They can also be said to be highly accurate, because our procedure was modified after the highly precise and accurate method of Verma and Quiroz-Ruiz [21]. These authors had shown high precision and accuracy of each U(0,1) and N(0,1) experiments and had also applied all kinds of simulated data quality tests suggested by Law and Kelton [25]. Besides, in the present work a large number of such experiments (204 streams of U(0,1) and 102 streams of N(0,1)) have been carried out. Therefore, as an innovation in Monte Carlo simulations we present the mean values as well as the total uncertainty (u 99) of 102 independent experiments in terms of the confidence interval of the mean at the strict 99% confidence level.
Finally, in order to evaluate the test performance, test N2 was used as a reference and differences in mean () values of the other three tests were calculated as
| (7) |
where the subscript Nj stands for N8, N14, or N15.
6. Results and Discussion
6.1. Type and Contaminant-Absent Events
According to Barnett and Lewis [1] this type of events is of no major concern, because the contaminant x c occupies an inner position in the ordered array and the extreme observation x (n) or x (1) under evaluation from discordancy tests is a legitimate observation. An inner position of the contaminant would affect much less the sample mean and standard deviation [1]. For small values of δ or ε close to 0 or ±1, respectively, most events generated from the Monte Carlo simulation are of type. The and values for n = 5 to n = 20 as a function of δ are presented in Figures 3(a)–3(d) and Figures 4(a)–4(d), respectively. For ε, these parameters behave very similarly and, therefore, the corresponding diagrams are not presented.
Figure 3.
Spurious type II error probability () as a function of δ from −2.5 to +2.5 for all tests N2, N8, N14, and N15. values for uncontaminated samples (δ = 0) are shown by open circles. (a) n = 5; (b) n = 10; (c) n = 15; and (d) n = 20.
Figure 4.
Spurious power probability () as a function of δ from −2.5 to +2.5 for all tests N2, N8, N14, and N15. values for uncontaminated samples (δ = 0) are shown by open circles. (a) n = 5; (b) n = 10; (c) n = 15; and (d) n = 20.
When the contaminant is absent (δ = 0 or ε = ±1), the and values are close to the expected values of 0.99 and 0.01, respectively, because the discordancy tests were applied at the 99% confidence level (open circles in Figures 3(a)–3(d) and Figures 4(a)–4(d)). As δ changes from 0 to about ±2.5, the values slightly increase from 0.99 to about 0.996 for n = 5 (Figure 3(a)), 0.996 for n = 10 (Figure 3(b)), 0.994-0.995 for n = 15 (Figure 3(c)), and 0.993-0.994 for n = 20 (Figure 3(d)). The values show the complementary behavior (Figures 4(a)–4(d)). Because in this type of events , a legitimate extreme observation is being tested, our best desire is that the and values remain close to the theoretical values of 0.99 and 0.01, respectively, for contaminant-absent events. This is actually observed in Figures 3 and 4.
6.2. C Type and Contaminant-Absent Events
The C type events are of major consequence for sample statistical parameters. In such events, because the contaminant x c occupies an extreme outlying position (x (n) or x (1)) in an ordered data array, it is desirable that the discordancy tests detect this contaminant observation as discordant. The and π DC values for n = 5 to n = 20 as a function of δ are presented in Figures 5(a)–5(d) and Figures 6(a)–6(d), respectively. Similarly, these values as a function of ε are shown in Figures 7(a)–7(d) and Figures 8(a)–8(d), respectively.
Figure 5.
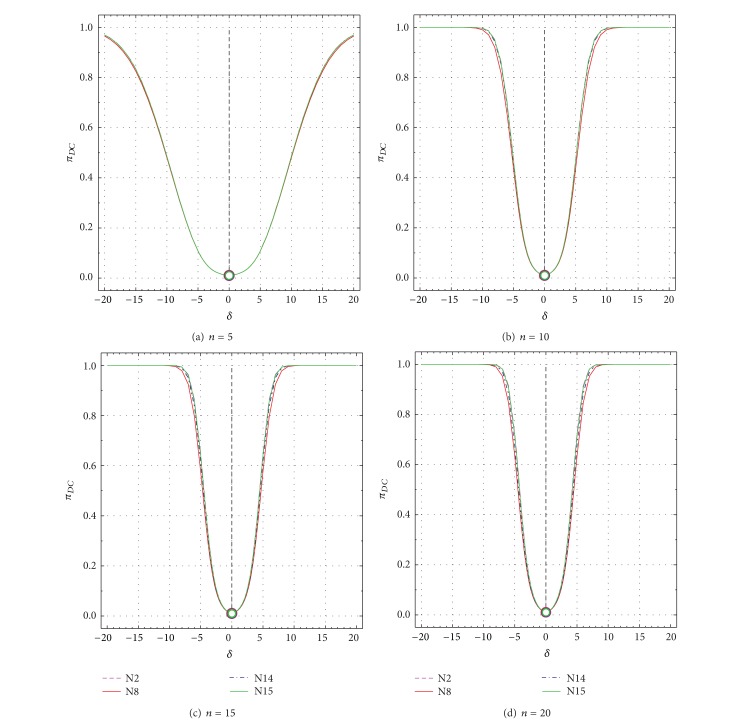
Nonspurious type II error probability () as a function of δ from −20 to +20 for all tests N2, N8, N14, and N15. values for uncontaminated samples (δ = 0) are shown by open circles. (a) n = 5; (b) n = 10; (c) n = 15; and (d) n = 20.
Figure 6.
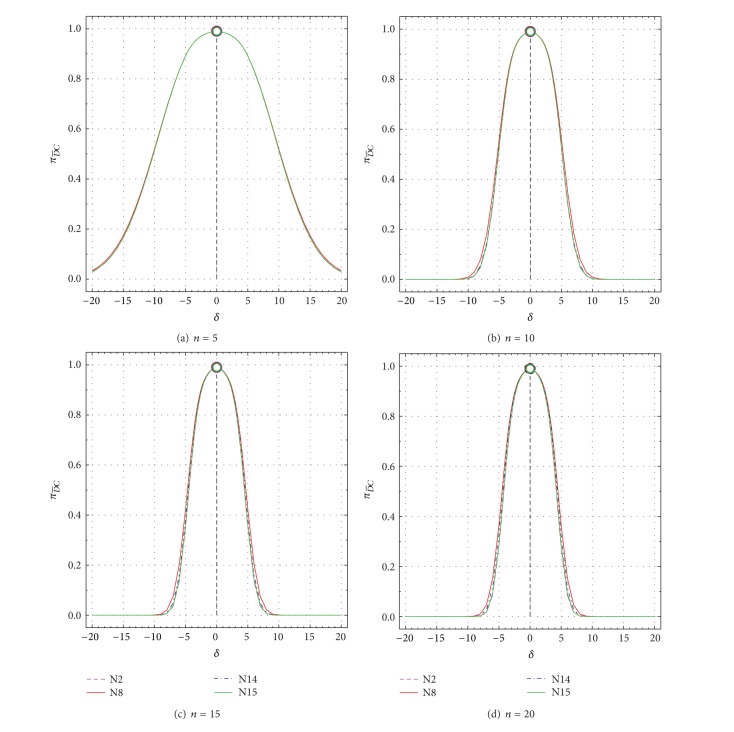
Nonspurious power probability (π DC) as a function of δ from −20 to +20 for all tests N2, N8, N14, and N15. π DC values for uncontaminated samples (δ = 0) are shown by open circles. (a) n = 5; (b) n = 10; (c) n = 15; and (d) n = 20.
Figure 7.
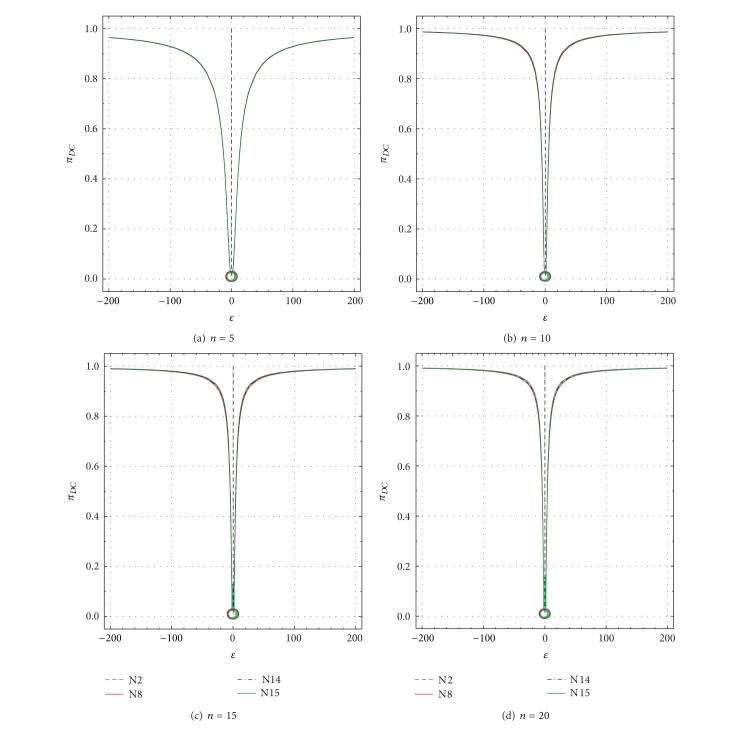
Nonspurious type II error probability () as a function of ε from −1 to −200 and +1 to +200 for all tests N2, N8, N14, and N15. values for uncontaminated samples (ε = ±1) are shown by open circles. (a) n = 5; (b) n = 10; (c) n = 15; and (d) n = 20.
Figure 8.
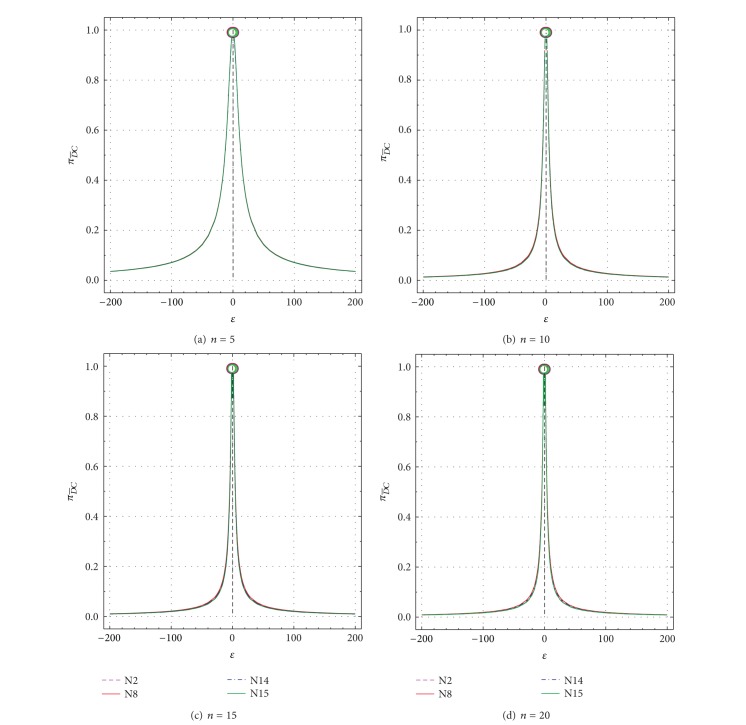
Nonspurious power probability (π DC) as a function of ε from −1 to −200 and +1 to +200 for all tests N2, N8, N14, and N15. π DC values for uncontaminated samples (ε = ±1) are shown by open circles. (a) n = 5; (b) n = 10; (c) n = 15; and (d) n = 20.
For uncontaminated samples (δ = 0 in Figures 5(a)–5(d) and Table 2, or ε = ±1 in Figures 7(a)–7(d)) the probability values were close to the theoretical value of 0.99 (which corresponds to the confidence level used for each test). Similarly, for such samples, π DC values for all sample sizes were close to the theoretical value of 0.01 (complement of 0.99 is 0.01; Figures 6 and 8).
Table 2.
NonSpurious type II error probability () parameter for four single extreme outlier discordancy tests.
| n | δ | Discordancy tests | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| N2 | N8 | N14 | N15 | |||||||||
| (u 99)N2 | (u 99)N8 | (u 99)N14 | (u 99)N15 | |||||||||
| 5 | 0 | 0.990003 | 0.0000057 | 0.990026 | 0.0000058 | 0.0023 | 0.990005 | 0.0000057 | 0.0002 | 0.989994 | 0.0000058 | −0.0009 |
| 5 | ±0.1 | 0.989948 | 0.0000139 | 0.989975 | 0.0000140 | 0.0027 | 0.989950 | 0.0000140 | 0.0002 | 0.989940 | 0.0000144 | −0.0009 |
| 5 | ±2 | 0.977285 | 0.0000113 | 0.977358 | 0.0000125 | 0.0075 | 0.977290 | 0.0000111 | 0.0005 | 0.977267 | 0.0000116 | −0.0018 |
| 5 | ±3 | 0.961486 | 0.0000148 | 0.961632 | 0.0000142 | 0.0152 | 0.961497 | 0.0000146 | 0.0012 | 0.961459 | 0.0000146 | −0.0028 |
| 5 | ±5 | 0.891864 | 0.0000205 | 0.892491 | 0.0000194 | 0.070 | 0.891901 | 0.0000200 | 0.0043 | 0.891823 | 0.0000208 | −0.0046 |
| 5 | ±6 | 0.834635 | 0.0000222 | 0.835779 | 0.0000231 | 0.137 | 0.834704 | 0.0000226 | 0.0084 | 0.834602 | 0.0000225 | −0.0038 |
| 5 | ±7 | 0.764660 | 0.0000240 | 0.766559 | 0.0000257 | 0.248 | 0.764766 | 0.0000250 | 0.0139 | 0.764661 | 0.0000237 | 0.0002 |
| 5 | ±8 | 0.685336 | 0.0000253 | 0.688202 | 0.0000255 | 0.418 | 0.685496 | 0.0000249 | 0.0234 | 0.685401 | 0.0000247 | 0.0095 |
| 5 | ±10 | 0.514122 | 0.0000280 | 0.519336 | 0.0000282 | 1.01 | 0.514407 | 0.0000292 | 0.056 | 0.514394 | 0.0000287 | 0.053 |
| 5 | ±12 | 0.351103 | 0.0000258 | 0.358468 | 0.0000275 | 2.10 | 0.351500 | 0.0000257 | 0.113 | 0.351629 | 0.0000258 | 0.150 |
| 5 | ±15 | 0.165615 | 0.0000194 | 0.174053 | 0.0000215 | 5.1 | 0.166070 | 0.0000196 | 0.275 | 0.166367 | 0.0000196 | 0.45 |
| 5 | ±18 | 0.062959 | 0.0000126 | 0.069566 | 0.0000148 | 10.5 | 0.063321 | 0.0000127 | 0.58 | 0.063618 | 0.0000134 | 1.05 |
| 5 | ±20 | 0.029322 | 0.0000082 | 0.033997 | 0.0000089 | 15.9 | 0.029577 | 0.0000084 | 0.87 | 0.029815 | 0.0000081 | 1.68 |
| 10 | 0 | 0.990008 | 0.0000057 | 0.990041 | 0.0000057 | 0.0034 | 0.990003 | 0.0000054 | −0.0006 | 0.990025 | 0.0000059 | 0.0017 |
| 10 | ±0.1 | 0.989851 | 0.0000197 | 0.989888 | 0.0000173 | 0.0037 | 0.989844 | 0.0000207 | −0.0006 | 0.989869 | 0.0000195 | 0.0019 |
| 10 | ±1 | 0.978810 | 0.0000183 | 0.979321 | 0.0000174 | 0.052 | 0.978911 | 0.0000179 | 0.0103 | 0.978879 | 0.0000188 | 0.0070 |
| 10 | ±2 | 0.949169 | 0.0000168 | 0.951501 | 0.0000163 | 0.246 | 0.949704 | 0.0000165 | 0.056 | 0.949433 | 0.0000175 | 0.0279 |
| 10 | ±3 | 0.878974 | 0.0000199 | 0.886717 | 0.0000192 | 0.88 | 0.880804 | 0.0000197 | 0.208 | 0.879762 | 0.0000202 | 0.090 |
| 10 | ±4 | 0.736953 | 0.0000241 | 0.756911 | 0.0000242 | 2.71 | 0.741679 | 0.0000266 | 0.64 | 0.738849 | 0.0000253 | 0.257 |
| 10 | ±5 | 0.523889 | 0.0000273 | 0.561084 | 0.0000257 | 7.1 | 0.532523 | 0.0000263 | 1.65 | 0.527197 | 0.0000266 | 0.63 |
| 10 | ±6 | 0.300940 | 0.0000248 | 0.349468 | 0.0000258 | 16.1 | 0.311799 | 0.0000260 | 3.61 | 0.304921 | 0.0000249 | 1.32 |
| 10 | ±7 | 0.136560 | 0.0000182 | 0.181585 | 0.0000226 | 33.0 | 0.146058 | 0.0000174 | 7.0 | 0.139899 | 0.0000185 | 2.44 |
| 10 | ±8 | 0.048488 | 0.0000122 | 0.079155 | 0.0000144 | 63 | 0.054422 | 0.0000118 | 12.2 | 0.050495 | 0.0000130 | 4.14 |
| 10 | ±9 | 0.013431 | 0.0000074 | 0.029234 | 0.0000092 | 118 | 0.016139 | 0.0000075 | 20.2 | 0.014300 | 0.0000074 | 6.5 |
| 10 | ±10 | 0.002900 | 0.0000031 | 0.009248 | 0.0000056 | 219 | 0.003821 | 0.0000036 | 31.8 | 0.003180 | 0.0000030 | 9.6 |
| 10 | ±11 | 0.000489 | 0.0000013 | 0.002529 | 0.0000029 | 418 | 0.000726 | 0.0000016 | 49 | 0.000556 | 0.0000014 | 13.8 |
| 15 | 0 | 0.989998 | 0.000006 | 0.990015 | 0.0000062 | 0.0017 | 0.98998 | 0.0000061 | −0.0018 | 0.989989 | 0.000006 | −0.0010 |
| 15 | ±0.1 | 0.989768 | 0.0000204 | 0.989811 | 0.0000210 | 0.0044 | 0.989766 | 0.0000209 | −0.0002 | 0.989759 | 0.0000200 | −0.0009 |
| 15 | ±0.5 | 0.985307 | 0.0000236 | 0.985665 | 0.0000202 | 0.0364 | 0.985507 | 0.0000249 | 0.0204 | 0.985345 | 0.0000240 | 0.0039 |
| 15 | ±2 | 0.974943 | 0.0000225 | 0.976229 | 0.0000186 | 0.132 | 0.975702 | 0.0000241 | 0.078 | 0.975113 | 0.0000236 | 0.0174 |
| 15 | ±5 | 0.932551 | 0.0000202 | 0.938851 | 0.0000184 | 0.68 | 0.936096 | 0.0000207 | 0.380 | 0.933417 | 0.0000206 | 0.093 |
| 15 | ±4 | 0.827672 | 0.0000245 | 0.848433 | 0.0000236 | 2.51 | 0.838586 | 0.0000251 | 1.32 | 0.830350 | 0.0000236 | 0.324 |
| 15 | ±4.5 | 0.621647 | 0.0000288 | 0.669717 | 0.0000270 | 7.7 | 0.644852 | 0.0000332 | 3.73 | 0.627283 | 0.0000285 | 0.91 |
| 15 | ±5 | 0.487591 | 0.0000276 | 0.550018 | 0.0000319 | 12.8 | 0.516243 | 0.0000322 | 5.9 | 0.494476 | 0.0000290 | 1.41 |
| 15 | ±5 | 0.351577 | 0.0000269 | 0.423601 | 0.0000266 | 20.5 | 0.382834 | 0.0000290 | 8.9 | 0.358972 | 0.0000287 | 2.10 |
| 15 | ±6 | 0.137443 | 0.0000198 | 0.204194 | 0.0000211 | 49 | 0.162735 | 0.0000196 | 18.4 | 0.143150 | 0.0000201 | 4.15 |
| 15 | ±7 | 0.035757 | 0.0000093 | 0.074779 | 0.0000144 | 109 | 0.048090 | 0.0000112 | 34.5 | 0.038352 | 0.0000098 | 7.3 |
| 15 | ±8 | 0.006107 | 0.0000043 | 0.021184 | 0.0000094 | 249 | 0.009822 | 0.0000054 | 61 | 0.006819 | 0.0000042 | 11.7 |
| 15 | ±9 | 0.000682 | 0.0000015 | 0.004748 | 0.0000039 | 600 | 0.001393 | 0.0000019 | 104 | 0.000802 | 0.0000017 | 17.6 |
| 15 | ±10 | 0.000049 | 0.0000004 | 0.000858 | 0.0000017 | 1640 | 0.000138 | 0.0000007 | 180 | 0.000062 | 0.0000005 | 25.7 |
| 20 | 0 | 0.990017 | 0.0000057 | 0.990004 | 0.000006 | −0.0014 | 0.990026 | 0.000006 | 0.0009 | 0.990004 | 0.0000059 | −0.0014 |
| 20 | ±0.1 | 0.989743 | 0.0000259 | 0.989771 | 0.0000248 | 0.0028 | 0.989786 | 0.0000243 | 0.0043 | 0.989734 | 0.0000277 | −0.0009 |
| 20 | ±0.5 | 0.984600 | 0.0000243 | 0.985127 | 0.0000258 | 0.054 | 0.985093 | 0.0000265 | 0.050 | 0.984682 | 0.0000246 | 0.0083 |
| 20 | ±1 | 0.972754 | 0.0000237 | 0.974729 | 0.0000256 | 0.203 | 0.974439 | 0.0000213 | 0.173 | 0.973084 | 0.0000225 | 0.0339 |
| 20 | ±2 | 0.922859 | 0.0000259 | 0.932611 | 0.0000219 | 1.06 | 0.930457 | 0.0000234 | 0.82 | 0.924463 | 0.0000266 | 0.174 |
| 20 | ±3 | 0.798422 | 0.0000265 | 0.829677 | 0.0000230 | 3.91 | 0.820494 | 0.0000248 | 2.76 | 0.803167 | 0.0000283 | 0.59 |
| 20 | ±4 | 0.561409 | 0.0000283 | 0.628839 | 0.0000267 | 12.0 | 0.604043 | 0.0000273 | 7.6 | 0.570474 | 0.0000288 | 1.61 |
| 20 | ±4.5 | 0.415514 | 0.0000280 | 0.498225 | 0.0000261 | 19.9 | 0.464616 | 0.0000262 | 11.8 | 0.425784 | 0.0000285 | 2.47 |
| 20 | ±5 | 0.276626 | 0.0000244 | 0.365289 | 0.0000265 | 32.1 | 0.325675 | 0.0000297 | 17.7 | 0.286659 | 0.0000245 | 3.63 |
| 20 | ±6 | 0.085535 | 0.0000163 | 0.152881 | 0.0000198 | 79 | 0.116833 | 0.0000185 | 36.6 | 0.091506 | 0.0000175 | 7.0 |
| 20 | ±7 | 0.015809 | 0.0000070 | 0.046048 | 0.0000127 | 191 | 0.026842 | 0.0000087 | 70 | 0.017699 | 0.0000079 | 12.0 |
| 20 | ±8 | 0.001716 | 0.0000021 | 0.010242 | 0.0000053 | 500 | 0.003921 | 0.0000036 | 128 | 0.002041 | 0.0000025 | 18.9 |
| 20 | ±9 | 0.000109 | 0.0000006 | 0.001733 | 0.0000024 | 1500 | 0.000366 | 0.0000011 | 237 | 0.000139 | 0.0000007 | 28.5 |
| 20 | ±10 | 0.000004 | 0.0000001 | 0.000229 | 0.0000010 | 5600 | 0.000022 | 0.0000002 | 450 | 0.000006 | 0.0000001 | 41.3 |
A complementary behavior of and π DC exists for all other δ or ε values as well (Figures 5 and 7 or Figures 6 and 8). Thus, for all tests decreases sharply from 0.99 for δ = 0 to very small values of about 0.03 for δ = ±20 and n = 5, to about 0.01–0.03 for δ = ±9 and n = 10, to about 0.006–0.02 for δ = ±8 and n = 15, and to about 0.001–0.01 for δ = ±8 and n = 20 (Table 2; Figures 5(a)–5(d)). On the contrary, π DC increases very rapidly from very small values of 0.01 to close to the maximum theoretical value of 0.99 (see the complementary behavior π DC in Figures 6(a)–6(d) and Figures 5(a)–5(d)). These probability ( and π DC) values show a similar behavior for larger values of ε than for δ (compare Figures 7 and 8 with Figures 5 and 6, resp.). There are some differences in these probability values among the different tests (Table 2; Figures 5–8), but they will be better discussed for the test performance criteria.
6.3. Test Performance Criteria (Ω and π D∣C)
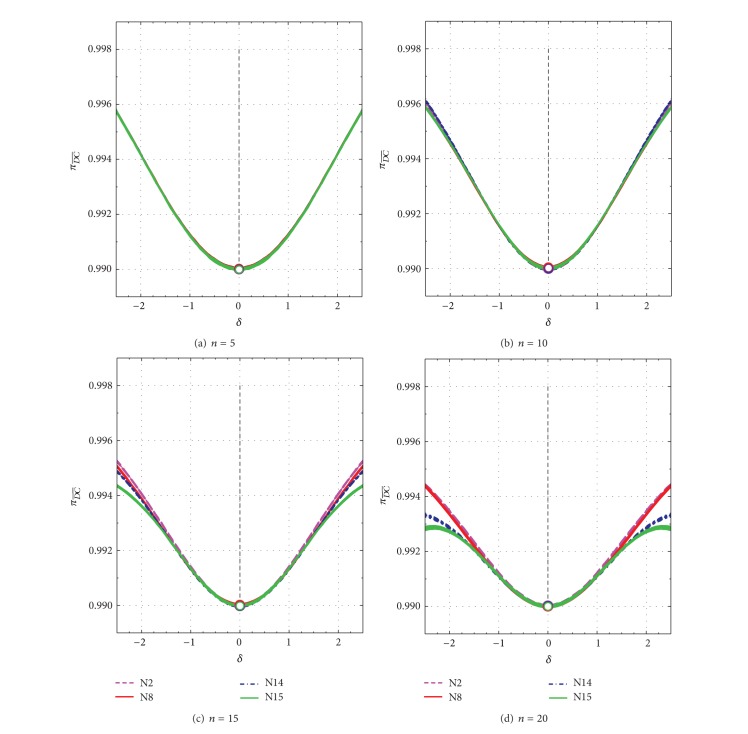
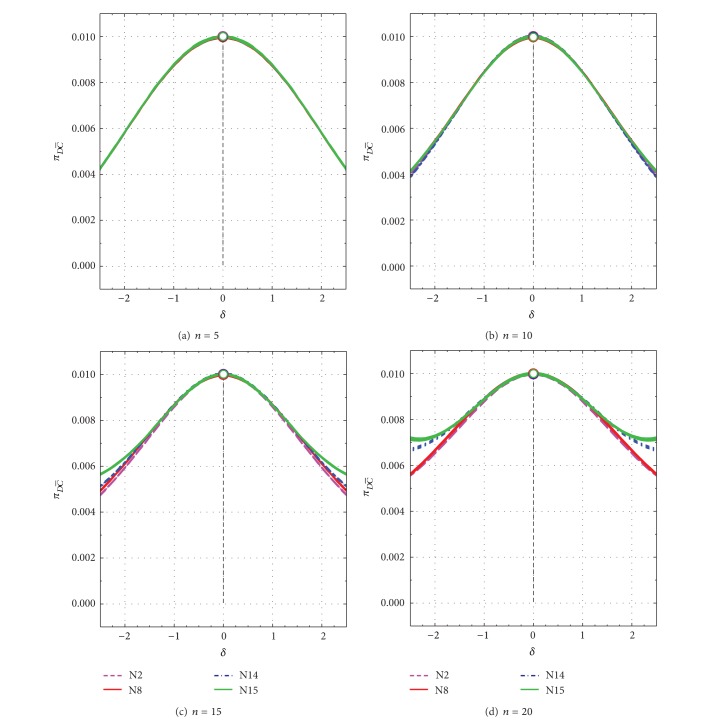
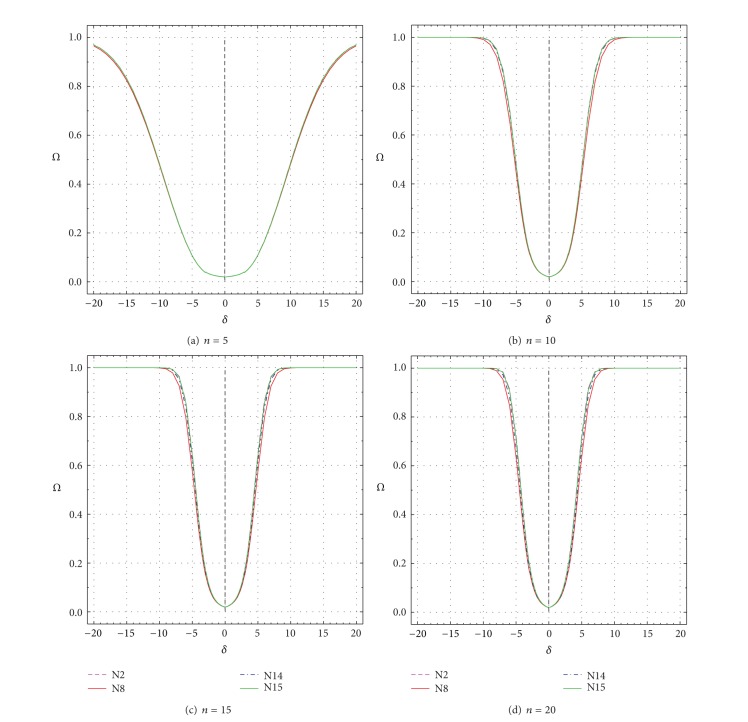
These two parameters are plotted as a function of δ and ε in Figures 9, 10, 11, and 12 and the most important results are summarized in Tables 3–6. For a good test, both Ω (; (5)) and π D∣C (6) should be large [1, 7]. Values of both performance criteria (Ω and π D∣C) increase as δ or ε values depart from the uncontaminated values of δ = 0 or ε = ±1 (Figures 9–12; Tables 3–6). However, Ω and π D∣C increase less rapidly for smaller n than for larger n. For n = 5, even for δ = ±20 or ε = ±200, none of the two parameters truly reaches the maximum theoretical value of 0.99 (Figure 9(a) to Figure 12(a)). For larger n (10–20), however, both Ω and π D∣C get close to this value for all tests and for much smaller values of δ or ε than the maximum values of 20 and 200, respectively (Figures 9(b)–9(d) to Figures 12(b)–12(d); Tables 3–6).
Figure 9.
Power of Test (Ω) as a function of δ from −20 to +20 for all tests N2, N8, N14, and N15. (a) n = 5; (b) n = 10; (c) n = 15; and (d) n = 20.
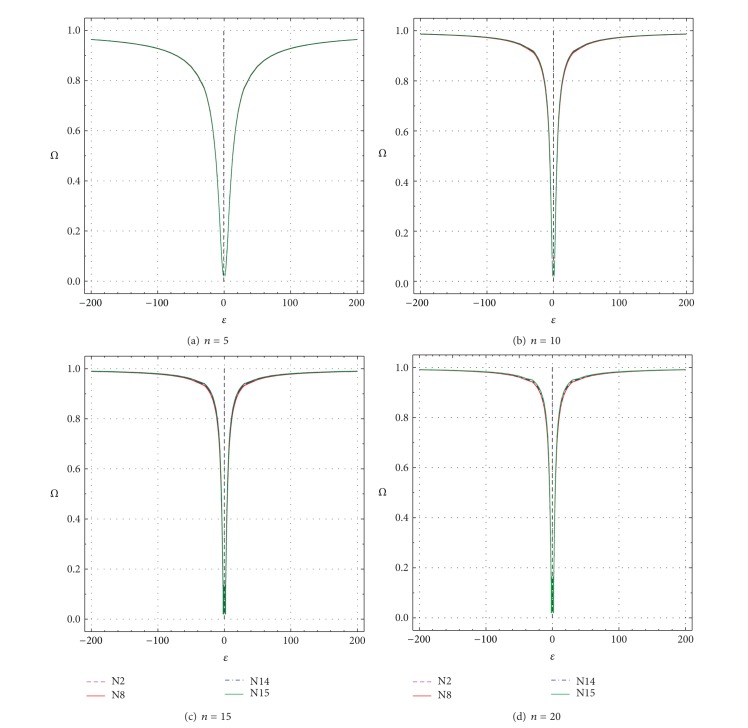
Figure 10.
Power of Test (Ω) as a function of ε from −1 to −200 and +1 to +200 for all tests N2, N8, N14, and N15. (a) n = 5; (b) n = 10; (c) n = 15; and (d) n = 20.
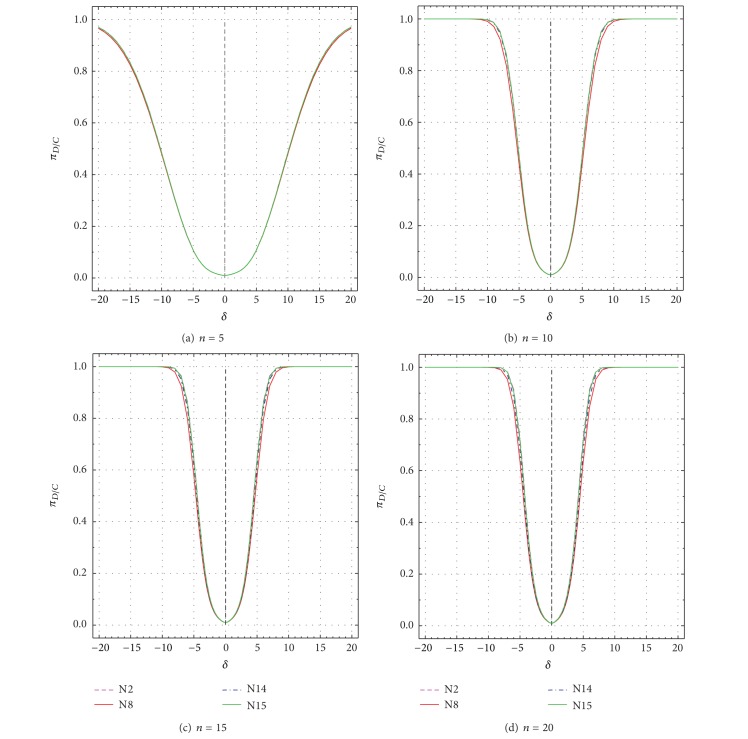
Figure 11.
Test Performance Criterion (π D∣C, or Conditional Power P5) as a function of δ from −20 to +20 for all tests N2, N8, N14, and N15. (a) n = 5; (b) n = 10; (c) n = 15; and (d) n = 20.
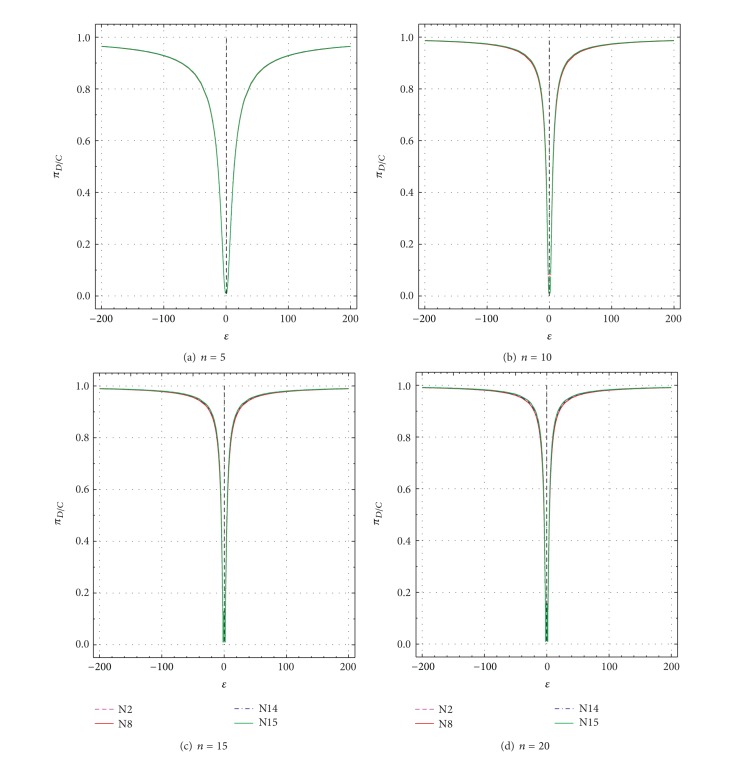
Figure 12.
Test Performance Criterion (π D∣C, or Conditional Power P5) as a function of ε from −1 to −200 and +1 to +200 for all tests N2, N8, N14, and N15. (a) n = 5; (b) n = 10; (c) n = 15; and (d) n = 20.
Table 3.
Power of Test (Ω) values for four single extreme outlier discordancy tests as a function of δ.
| n | δ | Discordancy tests | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| N2 | N8 | N14 | N15 | |||||||||
| (u 99)N2 | (u 99)N8 | (u 99)N14 | (u 99)N15 | |||||||||
| 5 | ±0.1 | 0.020034 | 0.0000163 | 0.019986 | 0.0000163 | −0.243 | 0.020031 | 0.0000165 | −0.0191 | 0.020053 | 0.0000167 | 0.092 |
| 5 | ±2 | 0.028537 | 0.0000125 | 0.028456 | 0.0000128 | −0.283 | 0.028531 | 0.0000124 | −0.0224 | 0.028563 | 0.0000127 | 0.089 |
| 5 | ±3 | 0.038514 | 0.0000148 | 0.038368 | 0.0000142 | −0.380 | 0.038503 | 0.0000146 | −0.0291 | 0.038541 | 0.0000146 | 0.070 |
| 5 | ±4 | 0.065920 | 0.0000155 | 0.065606 | 0.0000154 | −0.48 | 0.065900 | 0.0000155 | −0.0309 | 0.065955 | 0.0000157 | 0.054 |
| 5 | ±5 | 0.108136 | 0.0000205 | 0.107509 | 0.0000194 | −0.58 | 0.108099 | 0.0000200 | −0.0351 | 0.108177 | 0.0000208 | 0.0379 |
| 5 | ±6 | 0.165365 | 0.0000222 | 0.164221 | 0.0000231 | −0.69 | 0.165296 | 0.0000226 | −0.0422 | 0.165398 | 0.0000225 | 0.0194 |
| 5 | ±7 | 0.235340 | 0.0000240 | 0.233441 | 0.0000257 | −0.81 | 0.235234 | 0.0000250 | −0.045 | 0.235339 | 0.0000237 | −0.0007 |
| 5 | ±8 | 0.314664 | 0.0000253 | 0.311798 | 0.0000255 | −0.91 | 0.314504 | 0.0000249 | −0.051 | 0.314599 | 0.0000247 | −0.0206 |
| 5 | ±10 | 0.485878 | 0.0000280 | 0.480664 | 0.0000282 | −1.07 | 0.485593 | 0.0000292 | −0.059 | 0.485606 | 0.0000287 | −0.056 |
| 5 | ±10.17 | 0.50044 | 0.0000279 | 0.49503 | 0.0000287 | −1.08 | 0.50014 | 0.0000280 | −0.059 | 0.50015 | 0.0000280 | −0.058 |
| 5 | ±12 | 0.648897 | 0.0000258 | 0.641532 | 0.0000275 | −1.14 | 0.648500 | 0.0000257 | −0.061 | 0.648371 | 0.0000258 | −0.081 |
| 5 | ±15 | 0.834385 | 0.0000194 | 0.825947 | 0.0000215 | −1.01 | 0.833930 | 0.0000196 | −0.055 | 0.833633 | 0.0000196 | −0.090 |
| 5 | ±18 | 0.937041 | 0.0000126 | 0.930434 | 0.0000148 | −0.71 | 0.936679 | 0.0000127 | −0.0387 | 0.936382 | 0.0000134 | −0.070 |
| 5 | ±20 | 0.970678 | 0.0000082 | 0.966003 | 0.0000089 | −0.48 | 0.970423 | 0.0000084 | −0.0263 | 0.970185 | 0.0000081 | −0.051 |
| 10 | ±0.1 | 0.020121 | 0.0000216 | 0.020050 | 0.0000181 | −0.352 | 0.020131 | 0.0000218 | 0.052 | 0.020087 | 0.0000211 | −0.169 |
| 10 | ±1 | 0.029615 | 0.0000189 | 0.029124 | 0.0000180 | −1.66 | 0.029522 | 0.0000185 | −0.316 | 0.029546 | 0.0000193 | −0.233 |
| 10 | ±2 | 0.056182 | 0.0000169 | 0.053967 | 0.0000177 | −3.94 | 0.055608 | 0.0000161 | −1.02 | 0.056005 | 0.0000176 | −0.314 |
| 10 | ±3 | 0.121026 | 0.0000199 | 0.113283 | 0.0000192 | −6.4 | 0.119196 | 0.0000197 | −1.51 | 0.120238 | 0.0000202 | −0.65 |
| 10 | ±4 | 0.263047 | 0.0000241 | 0.243089 | 0.0000242 | −7.6 | 0.258321 | 0.0000266 | −1.80 | 0.261151 | 0.0000253 | −0.72 |
| 10 | ±5 | 0.476111 | 0.0000273 | 0.438916 | 0.0000257 | −7.8 | 0.467477 | 0.0000263 | −1.81 | 0.472803 | 0.0000266 | −0.69 |
| 10 | ±5.105 | 0.500474 | 0.0000285 | 0.461588 | 0.0000261 | −7.8 | 0.491473 | 0.0000273 | −1.80 | 0.497048 | 0.0000272 | −0.68 |
| 10 | ±6 | 0.699060 | 0.0000248 | 0.650532 | 0.0000258 | −6.9 | 0.688201 | 0.0000260 | −1.55 | 0.695079 | 0.0000249 | −0.57 |
| 10 | ±7 | 0.863440 | 0.0000182 | 0.818415 | 0.0000226 | −5.2 | 0.853942 | 0.0000174 | −1.10 | 0.860101 | 0.0000185 | −0.387 |
| 10 | ±8 | 0.951512 | 0.0000122 | 0.920845 | 0.0000144 | −3.22 | 0.945578 | 0.0000118 | −0.62 | 0.949505 | 0.0000130 | −0.211 |
| 10 | ±9 | 0.986569 | 0.0000074 | 0.970766 | 0.0000092 | −1.60 | 0.983861 | 0.0000075 | −0.274 | 0.985700 | 0.0000074 | −0.088 |
| 10 | ±10 | 0.997100 | 0.0000031 | 0.990752 | 0.0000056 | −0.64 | 0.996179 | 0.0000036 | −0.092 | 0.996820 | 0.0000030 | −0.0280 |
| 10 | ±11 | 0.999511 | 0.0000013 | 0.997471 | 0.0000029 | −0.204 | 0.999274 | 0.0000016 | −0.0237 | 0.999444 | 0.0000014 | −0.0067 |
| 15 | ±0.1 | 0.020212 | 0.0000214 | 0.020157 | 0.0000214 | −0.272 | 0.020236 | 0.0000217 | 0.117 | 0.020233 | 0.0000212 | 0.106 |
| 15 | ±0.5 | 0.024306 | 0.0000241 | 0.023963 | 0.0000203 | −1.41 | 0.024143 | 0.0000259 | −0.67 | 0.024284 | 0.0000250 | −0.091 |
| 15 | ±1 | 0.033660 | 0.0000236 | 0.032450 | 0.0000192 | −3.60 | 0.032982 | 0.0000251 | −2.01 | 0.033545 | 0.0000245 | −0.341 |
| 15 | 2.5 | 0.113807 | 0.0000218 | 0.102067 | 0.0000195 | −10.3 | 0.107680 | 0.0000210 | −5.4 | 0.113112 | 0.0000226 | −0.61 |
| 15 | ±3 | 0.172328 | 0.0000245 | 0.151567 | 0.0000236 | −12.0 | 0.161414 | 0.0000251 | −6.3 | 0.169650 | 0.0000236 | −1.55 |
| 15 | ±4 | 0.378353 | 0.0000288 | 0.330283 | 0.0000270 | −12.7 | 0.355148 | 0.0000332 | −6.1 | 0.372717 | 0.0000285 | −1.49 |
| 15 | ±4.46 | 0.501373 | 0.0000279 | 0.439974 | 0.0000313 | −12.2 | 0.473072 | 0.0000321 | −5.6 | 0.494564 | 0.0000297 | −1.36 |
| 15 | ±5 | 0.648423 | 0.0000269 | 0.576399 | 0.0000266 | −11.1 | 0.617166 | 0.0000290 | −4.8 | 0.641028 | 0.0000287 | −1.14 |
| 15 | ±6 | 0.862557 | 0.0000198 | 0.795806 | 0.0000211 | −7.74 | 0.837265 | 0.0000196 | −2.93 | 0.856850 | 0.0000201 | −0.66 |
| 15 | ±7 | 0.964243 | 0.0000093 | 0.925221 | 0.0000144 | −4.05 | 0.951910 | 0.0000112 | −1.28 | 0.961648 | 0.0000098 | −0.269 |
| 15 | ±8 | 0.993893 | 0.0000043 | 0.978816 | 0.0000094 | −1.52 | 0.990178 | 0.0000054 | −0.374 | 0.993181 | 0.0000042 | −0.072 |
| 15 | ±9 | 0.999318 | 0.0000015 | 0.995252 | 0.0000039 | −0.407 | 0.998607 | 0.0000019 | −0.071 | 0.999198 | 0.0000017 | −0.0120 |
| 15 | ±10 | 0.999951 | 0.0000004 | 0.999142 | 0.0000017 | −0.081 | 0.999862 | 0.0000007 | −0.0089 | 0.999938 | 0.0000005 | −0.00127 |
| 20 | ±0.1 | 0.020222 | 0.0000253 | 0.020213 | 0.0000242 | −0.046 | 0.020175 | 0.0000238 | −0.237 | 0.020248 | 0.0000270 | 0.126 |
| 20 | ±0.5 | 0.025049 | 0.0000251 | 0.024566 | 0.0000260 | −1.93 | 0.024578 | 0.0000267 | −1.88 | 0.024992 | 0.0000255 | −0.227 |
| 20 | ±1 | 0.036024 | 0.0000249 | 0.034154 | 0.0000266 | −5.2 | 0.034454 | 0.0000228 | −4.36 | 0.035781 | 0.0000235 | −0.67 |
| 20 | 2.5 | 0.132180 | 0.0000257 | 0.113955 | 0.0000238 | −13.8 | 0.119739 | 0.0000238 | −9.4 | 0.130861 | 0.0000269 | −1.00 |
| 20 | ±3 | 0.201578 | 0.0000265 | 0.170323 | 0.0000230 | −15.5 | 0.179506 | 0.0000248 | −10.9 | 0.196833 | 0.0000283 | −2.35 |
| 20 | 4 | 0.438591 | 0.0000283 | 0.374722 | 0.0000286 | −14.6 | 0.395957 | 0.0000273 | −9.7 | 0.429526 | 0.0000288 | −2.07 |
| 20 | ±4.21 | 0.499301 | 0.0000272 | 0.424653 | 0.0000266 | −15.0 | 0.453296 | 0.0000268 | −9.2 | 0.489576 | 0.0000279 | −1.95 |
| 20 | ±5 | 0.723374 | 0.0000244 | 0.634711 | 0.0000265 | −12.3 | 0.674325 | 0.0000297 | −6.8 | 0.713341 | 0.0000245 | −1.39 |
| 20 | ±6 | 0.914465 | 0.0000163 | 0.847119 | 0.0000198 | −7.4 | 0.883167 | 0.0000185 | −3.42 | 0.908494 | 0.0000175 | −0.65 |
| 20 | ±7 | 0.984191 | 0.0000070 | 0.953952 | 0.0000127 | −3.07 | 0.973158 | 0.0000087 | −1.12 | 0.982301 | 0.0000079 | −0.192 |
| 20 | ±8 | 0.998284 | 0.0000021 | 0.989758 | 0.0000053 | −0.85 | 0.996079 | 0.0000036 | −0.221 | 0.997959 | 0.0000025 | −0.0325 |
| 20 | ±9 | 0.999891 | 0.0000006 | 0.998267 | 0.0000024 | −0.162 | 0.999634 | 0.0000011 | −0.0258 | 0.999861 | 0.0000007 | −0.00309 |
| 20 | ±10 | 0.999996 | 0.0000001 | 0.999771 | 0.0000010 | −0.0225 | 0.999978 | 0.0000002 | −0.00180 | 0.999994 | 0.0000001 | −0.00017 |
Table 6.
Test Performance Criterion P5 (πD∣C) values for four single extreme outlier discordancy tests as a function of ε.
| n | ε | Discordancy tests | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| N2 | N8 | N14 | N15 | |||||||||
| (u 99)N2 | (u 99)N8 | (u 99)N14 | (u 99)N15 | |||||||||
| 5 | ±1.1 | 0.011106 | 0.0000274 | 0.011080 | 0.0000273 | −0.237 | 0.011101 | 0.0000274 | −0.0425 | 0.011115 | 0.0000280 | 0.076 |
| 5 | ±3 | 0.056787 | 0.0000393 | 0.056474 | 0.0000387 | −0.55 | 0.056768 | 0.0000397 | −0.0321 | 0.056810 | 0.0000382 | 0.0408 |
| 5 | ±5 | 0.146913 | 0.0000462 | 0.145680 | 0.0000452 | −0.84 | 0.146842 | 0.0000447 | −0.048 | 0.146893 | 0.0000452 | −0.0131 |
| 5 | ±7 | 0.250890 | 0.0000523 | 0.248598 | 0.0000537 | −0.91 | 0.250762 | 0.0000512 | −0.051 | 0.250790 | 0.0000524 | −0.0397 |
| 5 | ±10 | 0.390462 | 0.0000624 | 0.387183 | 0.0000608 | −0.84 | 0.390280 | 0.0000627 | −0.047 | 0.390249 | 0.0000624 | −0.055 |
| 5 | ±13.1 | 0.50043 | 0.0000544 | 0.49686 | 0.0000559 | −0.71 | 0.50023 | 0.0000544 | −0.0406 | 0.50018 | 0.0000553 | −0.050 |
| 5 | ±15 | 0.552883 | 0.0000554 | 0.549351 | 0.0000535 | −0.64 | 0.552692 | 0.0000547 | −0.0346 | 0.552630 | 0.0000551 | −0.046 |
| 5 | ±20 | 0.653179 | 0.0000491 | 0.649982 | 0.0000501 | −0.49 | 0.653009 | 0.0000491 | −0.0262 | 0.652941 | 0.0000480 | −0.0365 |
| 5 | ±30 | 0.764071 | 0.0000476 | 0.761610 | 0.0000464 | −0.322 | 0.763935 | 0.0000480 | −0.0178 | 0.763882 | 0.0000487 | −0.0248 |
| 5 | ±40 | 0.822288 | 0.0000430 | 0.820357 | 0.0000442 | −0.235 | 0.822181 | 0.0000431 | −0.0130 | 0.822138 | 0.0000428 | −0.0182 |
| 5 | ±60 | 0.881517 | 0.0000389 | 0.880180 | 0.0000385 | −0.152 | 0.881443 | 0.0000392 | −0.0084 | 0.881408 | 0.0000394 | −0.0124 |
| 5 | ±80 | 0.911274 | 0.0000321 | 0.910263 | 0.0000327 | −0.111 | 0.911218 | 0.0000324 | −0.0061 | 0.911195 | 0.0000311 | −0.0087 |
| 5 | ±120 | 0.941005 | 0.0000307 | 0.940328 | 0.0000307 | −0.072 | 0.940970 | 0.0000306 | −0.00371 | 0.940951 | 0.0000306 | −0.0058 |
| 5 | ±160 | 0.955830 | 0.0000281 | 0.955330 | 0.0000269 | −0.052 | 0.955801 | 0.0000285 | −0.00302 | 0.955792 | 0.0000281 | −0.00395 |
| 5 | ±200 | 0.964715 | 0.0000244 | 0.964312 | 0.0000248 | −0.0417 | 0.964693 | 0.0000241 | −0.00226 | 0.964681 | 0.0000242 | −0.00345 |
| 10 | ±1.1 | 0.013593 | 0.0000385 | 0.013418 | 0.0000340 | −1.29 | 0.013562 | 0.0000384 | −0.227 | 0.013564 | 0.0000378 | −0.209 |
| 10 | ±3 | 0.222304 | 0.0000659 | 0.207623 | 0.0000591 | −6.6 | 0.218930 | 0.0000661 | −1.52 | 0.220981 | 0.0000656 | −0.60 |
| 10 | ±5 | 0.458753 | 0.0000661 | 0.437008 | 0.0000668 | −4.7 | 0.453946 | 0.0000689 | −1.05 | 0.456939 | 0.0000667 | −0.395 |
| 10 | ±5.41 | 0.499554 | 0.0000668 | 0.477805 | 0.0000682 | −4.35 | 0.494764 | 0.0000629 | −0.96 | 0.49776 | 0.0000674 | −0.359 |
| 10 | ±7 | 0.602388 | 0.0000651 | 0.582111 | 0.0000625 | −3.37 | 0.597979 | 0.0000649 | −0.73 | 0.600766 | 0.0000684 | −0.269 |
| 10 | ±10 | 0.721760 | 0.0000501 | 0.705530 | 0.0000527 | −2.25 | 0.718290 | 0.0000492 | −0.48 | 0.720482 | 0.0000517 | −0.177 |
| 10 | ±15 | 0.817312 | 0.0000418 | 0.805848 | 0.0000426 | −1.40 | 0.814868 | 0.0000429 | −0.299 | 0.816420 | 0.0000412 | −0.109 |
| 10 | ±20 | 0.864739 | 0.0000433 | 0.856024 | 0.0000408 | −1.01 | 0.862890 | 0.0000426 | −0.214 | 0.864058 | 0.0000439 | −0.079 |
| 10 | ±30 | 0.911335 | 0.0000299 | 0.905514 | 0.0000319 | −0.64 | 0.910096 | 0.0000294 | −0.136 | 0.910883 | 0.0000309 | −0.050 |
| 10 | ±40 | 0.934126 | 0.0000272 | 0.929776 | 0.0000294 | −0.47 | 0.933203 | 0.0000279 | −0.099 | 0.933789 | 0.0000276 | −0.0360 |
| 10 | ±50 | 0.947611 | 0.0000234 | 0.944143 | 0.0000241 | −0.366 | 0.946875 | 0.0000242 | −0.078 | 0.947342 | 0.0000238 | −0.0284 |
| 10 | ±100 | 0.974142 | 0.0000183 | 0.972421 | 0.0000184 | −0.177 | 0.973777 | 0.0000185 | −0.0374 | 0.974010 | 0.0000184 | −0.0136 |
| 10 | ±150 | 0.982843 | 0.0000161 | 0.981700 | 0.0000168 | −0.116 | 0.982600 | 0.0000166 | −0.0247 | 0.982756 | 0.0000161 | −0.0089 |
| 10 | ±200 | 0.987171 | 0.0000142 | 0.986318 | 0.0000144 | −0.086 | 0.986991 | 0.0000138 | −0.0183 | 0.987105 | 0.0000143 | −0.0067 |
| 15 | ±1.1 | 0.015232 | 0.0000509 | 0.014804 | 0.0000414 | −2.81 | 0.014971 | 0.0000442 | −1.71 | 0.015180 | 0.0000518 | −0.340 |
| 15 | ±3 | 0.307670 | 0.0000774 | 0.277454 | 0.0000694 | −9.8 | 0.293796 | 0.0000758 | −4.5 | 0.304363 | 0.0000734 | −1.08 |
| 15 | ±4.5 | 0.508306 | 0.0000693 | 0.473352 | 0.0000627 | −6.9 | 0.493247 | 0.0000686 | −2.96 | 0.504762 | 0.0000674 | −0.70 |
| 15 | ±5 | 0.555712 | 0.0000644 | 0.521524 | 0.0000708 | −6.2 | 0.541147 | 0.0000721 | −2.62 | 0.552297 | 0.0000664 | −0.61 |
| 15 | ±7 | 0.684663 | 0.0000590 | 0.655963 | 0.0000589 | −4.19 | 0.672765 | 0.0000603 | −1.74 | 0.681886 | 0.0000602 | −0.406 |
| 15 | ±10 | 0.784156 | 0.0000518 | 0.762607 | 0.0000574 | −2.75 | 0.775363 | 0.0000548 | −1.12 | 0.782114 | 0.0000522 | −0.260 |
| 15 | ±15 | 0.860198 | 0.0000416 | 0.845545 | 0.0000444 | −1.70 | 0.854249 | 0.0000423 | −0.69 | 0.858831 | 0.0000422 | −0.159 |
| 15 | ±20 | 0.897091 | 0.0000348 | 0.886105 | 0.0000350 | −1.22 | 0.892656 | 0.0000352 | −0.49 | 0.896063 | 0.0000350 | −0.115 |
| 15 | ±30 | 0.932834 | 0.0000271 | 0.925572 | 0.0000285 | −0.78 | 0.929908 | 0.0000291 | −0.314 | 0.932159 | 0.0000271 | −0.072 |
| 15 | ±40 | 0.950189 | 0.0000256 | 0.944782 | 0.0000263 | −0.57 | 0.948017 | 0.0000256 | −0.228 | 0.949688 | 0.0000258 | −0.053 |
| 15 | ±60 | 0.967191 | 0.0000212 | 0.963613 | 0.0000224 | −0.370 | 0.965751 | 0.0000218 | −0.149 | 0.966859 | 0.0000207 | −0.0343 |
| 15 | ±80 | 0.975546 | 0.0000199 | 0.972878 | 0.0000213 | −0.274 | 0.974475 | 0.0000198 | −0.110 | 0.975299 | 0.0000200 | −0.0253 |
| 15 | ±140 | 0.986132 | 0.0000140 | 0.984621 | 0.0000148 | −0.153 | 0.985524 | 0.0000143 | −0.062 | 0.985992 | 0.0000137 | −0.0142 |
| 15 | ±200 | 0.990334 | 0.0000113 | 0.989278 | 0.0000127 | −0.107 | 0.989908 | 0.0000116 | −0.0429 | 0.990235 | 0.0000116 | −0.0099 |
| 20 | ±1.1 | 0.016228 | 0.0000577 | 0.015531 | 0.0000546 | −4.29 | 0.015647 | 0.0000516 | −3.58 | 0.016119 | 0.0000580 | −0.67 |
| 20 | ±3 | 0.354224 | 0.0000726 | 0.313612 | 0.0000769 | −11.5 | 0.329474 | 0.0000698 | −7.0 | 0.349056 | 0.0000732 | −1.46 |
| 20 | ±4 | 0.500954 | 0.0000639 | 0.457154 | 0.0000653 | −8.7 | 0.475548 | 0.0000651 | −5.1 | 0.495727 | 0.0000620 | −1.04 |
| 20 | ±5 | 0.601015 | 0.0000617 | 0.559904 | 0.0000661 | −6.8 | 0.577809 | 0.0000665 | −3.86 | 0.596262 | 0.0000581 | −0.79 |
| 20 | ±7 | 0.721004 | 0.0000628 | 0.687842 | 0.0000622 | −4.6 | 0.702741 | 0.0000577 | −2.53 | 0.717289 | 0.0000637 | −0.52 |
| 20 | ±10 | 0.810844 | 0.0000448 | 0.786525 | 0.0000468 | −3.0 | 0.797652 | 0.0000469 | −1.63 | 0.808171 | 0.0000433 | −0.330 |
| 20 | ±15 | 0.878244 | 0.0000370 | 0.861918 | 0.0000398 | −1.86 | 0.869456 | 0.0000419 | −1.00 | 0.876461 | 0.0000382 | −0.203 |
| 20 | ±20 | 0.910617 | 0.0000332 | 0.898443 | 0.0000353 | −1.34 | 0.904086 | 0.0000333 | −0.72 | 0.909299 | 0.0000325 | −0.145 |
| 20 | ±30 | 0.941779 | 0.0000246 | 0.933781 | 0.0000270 | −0.85 | 0.937486 | 0.0000248 | −0.46 | 0.940911 | 0.0000255 | −0.092 |
| 20 | ±40 | 0.956868 | 0.0000229 | 0.950924 | 0.0000258 | −0.62 | 0.953687 | 0.0000219 | −0.332 | 0.956225 | 0.0000226 | −0.067 |
| 20 | ±60 | 0.971612 | 0.0000209 | 0.967685 | 0.0000218 | −0.404 | 0.969514 | 0.0000209 | −0.216 | 0.971191 | 0.0000210 | −0.0434 |
| 20 | ±80 | 0.978856 | 0.0000170 | 0.975928 | 0.0000185 | −0.299 | 0.977289 | 0.0000179 | −0.160 | 0.978541 | 0.0000170 | −0.0322 |
| 20 | ±140 | 0.988015 | 0.0000127 | 0.986356 | 0.0000127 | −0.168 | 0.987127 | 0.0000139 | −0.090 | 0.987837 | 0.0000128 | −0.0181 |
| 20 | ±200 | 0.991646 | 0.0000107 | 0.990487 | 0.0000113 | −0.117 | 0.991025 | 0.0000109 | −0.063 | 0.991520 | 0.0000113 | −0.0126 |
The performance differences of the four tests are now briefly discussed in terms of both δ and ε as well as n. The total uncertainty u 99 values of the simulations are extremely small (the error is at the fifth or even sixth decimal place; Tables 3–6). Therefore, most differences among the tests ( for test N8, for test N14, and for test N15; all percent differences are with respect to test N2; see (7)) are statistically significant (Tables 3–6). A negative value of (where Nj stands for N8, N14, or N15) means that Ω or π D∣C value for a given test (N8, N14, or N15) is less than that of test N2, implying a worse performance of the given test as compared to test N2, whereas a positive value of signifies just the opposite. Note that test N2 is chosen as a reference test, because it shows generally the best performance (values of are mostly negative in Tables 3–6). Additional fine-scale simulations were also carried out for which both Ω and π D∣C become about 0.5 for the reference test N2 (0.5 is about the half of the maximum value of one for Ω or π D∣C). Hence, the values of Ω and π D∣C can be visually compared in Tables 3–6 (see the rows in italic font).
For n = 5, all tests show rather similar performance, because the maximum difference () is only about −1.1% for N8 (as compared to N2) and <−0.1% for N14 and N15 (see the first set of rows corresponding to n = 5 in Tables 3–6). Test N2 shows Ω = 0.50044 for δ = ±10.17, whereas tests N8, N14, and N15 have Ω values of 0.49503, 0.50014, and 0.50015, respectively, (Table 3). The respective values are about −1.1%, −0.06%, and −0.06% (Table 3). Practically the same results are valid for π D∣C as well (see the row in italic font in Table 4). Similar results were documented for Ω and π D∣C as a function of ε (rows for ε = ±12.9 or ±13.1 in Tables 5 and 6, resp.).
Table 4.
Test Performance Criterion P5 (πD∣C) values for four single extreme outlier discordancy tests as a function of δ.
| n | δ | Discordancy tests | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| N2 | N8 | N14 | N15 | |||||||||
| (u 99)N2 | (u 99)N8 | (u 99)N14 | (u 99)N15 | |||||||||
| 5 | ±0.1 | 0.010052 | 0.0000139 | 0.010025 | 0.0000140 | −0.262 | 0.010050 | 0.0000140 | −0.0153 | 0.010060 | 0.0000144 | 0.085 |
| 5 | ±2 | 0.022715 | 0.0000113 | 0.022642 | 0.0000125 | −0.322 | 0.022710 | 0.0000111 | −0.0212 | 0.022733 | 0.0000116 | 0.079 |
| 5 | ±3 | 0.038514 | 0.0000148 | 0.038368 | 0.0000142 | −0.380 | 0.038503 | 0.0000146 | −0.0291 | 0.038541 | 0.0000146 | 0.070 |
| 5 | ±4 | 0.065920 | 0.0000155 | 0.065606 | 0.0000154 | −0.48 | 0.065900 | 0.0000155 | −0.0309 | 0.065955 | 0.0000157 | 0.054 |
| 5 | ±5 | 0.108136 | 0.0000205 | 0.107509 | 0.0000194 | −0.58 | 0.108099 | 0.0000200 | −0.0351 | 0.108177 | 0.0000208 | 0.0379 |
| 5 | ±6 | 0.165365 | 0.0000222 | 0.164221 | 0.0000231 | −0.69 | 0.165296 | 0.0000226 | −0.0422 | 0.165398 | 0.0000225 | 0.0194 |
| 5 | ±7 | 0.235340 | 0.0000240 | 0.233441 | 0.0000257 | −0.81 | 0.235234 | 0.0000250 | −0.045 | 0.235339 | 0.0000237 | −0.00066 |
| 5 | ±8 | 0.314664 | 0.0000253 | 0.311798 | 0.0000255 | −0.91 | 0.314504 | 0.0000249 | −0.051 | 0.314599 | 0.0000247 | −0.0206 |
| 5 | ±10 | 0.485878 | 0.0000280 | 0.480664 | 0.0000282 | −1.07 | 0.485593 | 0.0000292 | −0.059 | 0.485606 | 0.0000287 | −0.056 |
| 5 | ±10.17 | 0.50044 | 0.0000279 | 0.49503 | 0.0000287 | −1.08 | 0.50014 | 0.0000280 | −0.059 | 0.50015 | 0.0000280 | −0.058 |
| 5 | ±12 | 0.648897 | 0.0000258 | 0.641532 | 0.0000275 | −1.14 | 0.648500 | 0.0000257 | −0.061 | 0.648371 | 0.0000258 | −0.081 |
| 5 | ±15 | 0.834385 | 0.0000194 | 0.825947 | 0.0000215 | −1.01 | 0.833930 | 0.0000196 | −0.055 | 0.833633 | 0.0000196 | −0.090 |
| 5 | ±18 | 0.937041 | 0.0000126 | 0.930434 | 0.0000148 | −0.71 | 0.936679 | 0.0000127 | −0.0387 | 0.936382 | 0.0000134 | −0.070 |
| 5 | ±20 | 0.970678 | 0.0000082 | 0.966003 | 0.0000089 | −0.48 | 0.970423 | 0.0000084 | −0.0263 | 0.970185 | 0.0000081 | −0.051 |
| 10 | ±0.1 | 0.010149 | 0.0000197 | 0.010112 | 0.0000173 | −0.364 | 0.010156 | 0.0000207 | 0.061 | 0.010131 | 0.0000195 | −0.181 |
| 10 | ±1 | 0.021190 | 0.0000183 | 0.020679 | 0.0000174 | −2.41 | 0.021089 | 0.0000179 | −0.48 | 0.021121 | 0.0000188 | −0.323 |
| 10 | ±2 | 0.050831 | 0.0000168 | 0.048499 | 0.0000163 | −4.6 | 0.050296 | 0.0000165 | −1.05 | 0.050567 | 0.0000175 | −0.52 |
| 10 | ±3 | 0.121026 | 0.0000199 | 0.113283 | 0.0000192 | −6.4 | 0.119196 | 0.0000197 | −1.51 | 0.120238 | 0.0000202 | −0.65 |
| 10 | ±4 | 0.263047 | 0.0000241 | 0.243089 | 0.0000242 | −7.6 | 0.258321 | 0.0000266 | −1.80 | 0.261151 | 0.0000253 | −0.72 |
| 10 | ±5 | 0.476111 | 0.0000273 | 0.438916 | 0.0000257 | −7.8 | 0.467477 | 0.0000263 | −1.81 | 0.472803 | 0.0000266 | −0.69 |
| 10 | ±5.105 | 0.500474 | 0.0000285 | 0.461588 | 0.0000261 | −7.8 | 0.491473 | 0.0000273 | −1.80 | 0.497048 | 0.0000272 | −0.68 |
| 10 | ±6 | 0.699060 | 0.0000248 | 0.650532 | 0.0000258 | −6.9 | 0.688201 | 0.0000260 | −1.55 | 0.695079 | 0.0000249 | −0.57 |
| 10 | ±7 | 0.863440 | 0.0000182 | 0.818415 | 0.0000226 | −5.2 | 0.853942 | 0.0000174 | −1.10 | 0.860101 | 0.0000185 | −0.387 |
| 10 | ±8 | 0.951512 | 0.0000122 | 0.920845 | 0.0000144 | −3.22 | 0.945578 | 0.0000118 | −0.62 | 0.949505 | 0.0000130 | −0.211 |
| 10 | ±9 | 0.986569 | 0.0000074 | 0.970766 | 0.0000092 | −1.60 | 0.983861 | 0.0000075 | −0.274 | 0.985700 | 0.0000074 | −0.088 |
| 10 | ±10 | 0.997100 | 0.0000031 | 0.990752 | 0.0000056 | −0.64 | 0.996179 | 0.0000036 | −0.092 | 0.996820 | 0.0000030 | −0.0280 |
| 10 | ±11 | 0.999511 | 0.0000013 | 0.997471 | 0.0000029 | −0.204 | 0.999274 | 0.0000016 | −0.0237 | 0.999444 | 0.0000014 | −0.0067 |
| 15 | ±0.1 | 0.010232 | 0.0000204 | 0.010189 | 0.0000210 | −0.425 | 0.010234 | 0.0000209 | 0.0204 | 0.010241 | 0.0000200 | 0.089 |
| 15 | ±0.5 | 0.014693 | 0.0000236 | 0.014335 | 0.0000202 | −2.44 | 0.014493 | 0.0000249 | −1.37 | 0.014655 | 0.0000240 | −0.260 |
| 15 | ±1 | 0.025057 | 0.0000225 | 0.023771 | 0.0000186 | −5.1 | 0.024298 | 0.0000241 | −3.03 | 0.024887 | 0.0000236 | −0.68 |
| 15 | ±2.5 | 0.109047 | 0.0000212 | 0.097138 | 0.0000185 | −10.9 | 0.102549 | 0.0000212 | −6.0 | 0.107459 | 0.0000213 | −1.46 |
| 15 | ±3 | 0.172328 | 0.0000245 | 0.151567 | 0.0000236 | −12.0 | 0.161414 | 0.0000251 | −6.3 | 0.169650 | 0.0000236 | −1.55 |
| 15 | ±4 | 0.378353 | 0.0000288 | 0.330283 | 0.0000270 | −12.7 | 0.355148 | 0.0000332 | −6.1 | 0.372717 | 0.0000285 | −1.49 |
| 15 | ±4.46 | 0.501373 | 0.0000279 | 0.439974 | 0.0000313 | −12.2 | 0.473072 | 0.0000321 | −5.6 | 0.494564 | 0.0000297 | −1.36 |
| 15 | ±5 | 0.648423 | 0.0000269 | 0.576399 | 0.0000266 | −11.1 | 0.617166 | 0.0000290 | −4.82 | 0.641028 | 0.0000287 | −1.14 |
| 15 | ±6 | 0.862557 | 0.0000198 | 0.795806 | 0.0000211 | −7.7 | 0.837265 | 0.0000196 | −2.93 | 0.856850 | 0.0000201 | −0.66 |
| 15 | ±7 | 0.964243 | 0.0000093 | 0.925221 | 0.0000144 | −4.05 | 0.951910 | 0.0000112 | −1.28 | 0.961648 | 0.0000098 | −0.269 |
| 15 | ±8 | 0.993893 | 0.0000043 | 0.978816 | 0.0000094 | −1.52 | 0.990178 | 0.0000054 | −0.374 | 0.993181 | 0.0000042 | −0.072 |
| 15 | ±9 | 0.999318 | 0.0000015 | 0.995252 | 0.0000039 | −0.407 | 0.998607 | 0.0000019 | −0.071 | 0.999198 | 0.0000017 | −0.0120 |
| 15 | ±10 | 0.999951 | 0.0000004 | 0.999142 | 0.0000017 | −0.081 | 0.999862 | 0.0000007 | −0.0089 | 0.999938 | 0.0000005 | −0.00127 |
| 20 | ±0.1 | 0.010257 | 0.0000259 | 0.010229 | 0.0000248 | −0.271 | 0.010214 | 0.0000243 | −0.414 | 0.010266 | 0.0000277 | 0.086 |
| 20 | ±0.5 | 0.015400 | 0.0000243 | 0.014873 | 0.0000258 | −3.42 | 0.014907 | 0.0000265 | −3.20 | 0.015318 | 0.0000246 | −0.53 |
| 20 | ±1 | 0.027246 | 0.0000237 | 0.025271 | 0.0000256 | −7.2 | 0.025561 | 0.0000213 | −6.2 | 0.026916 | 0.0000225 | −1.21 |
| 20 | ±2.5 | 0.126609 | 0.0000249 | 0.108344 | 0.0000227 | −14.4 | 0.113053 | 0.0000241 | −10.7 | 0.123707 | 0.0000263 | −2.29 |
| 20 | ±3 | 0.201578 | 0.0000265 | 0.170323 | 0.0000230 | −15.5 | 0.179506 | 0.0000248 | −10.9 | 0.196833 | 0.0000283 | −2.35 |
| 20 | ±4 | 0.438591 | 0.0000283 | 0.371161 | 0.0000267 | −15.4 | 0.395957 | 0.0000273 | −9.7 | 0.429526 | 0.0000288 | −2.07 |
| 20 | ±4.21 | 0.499301 | 0.0000272 | 0.424653 | 0.0000266 | −15.0 | 0.453296 | 0.0000268 | −9.2 | 0.489576 | 0.0000279 | −1.95 |
| 20 | ±5 | 0.723374 | 0.0000244 | 0.634711 | 0.0000265 | −12.3 | 0.674325 | 0.0000297 | −6.8 | 0.713341 | 0.0000245 | −1.39 |
| 20 | ±6 | 0.914465 | 0.0000163 | 0.847119 | 0.0000198 | −7.4 | 0.883167 | 0.0000185 | −3.42 | 0.908494 | 0.0000175 | −0.65 |
| 20 | ±7 | 0.984191 | 0.0000070 | 0.953952 | 0.0000127 | −3.07 | 0.973158 | 0.0000087 | −1.12 | 0.982301 | 0.0000079 | −0.192 |
| 20 | ±8 | 0.998284 | 0.0000021 | 0.989758 | 0.0000053 | −0.85 | 0.996079 | 0.0000036 | −0.221 | 0.997959 | 0.0000025 | −0.0325 |
| 20 | ±9 | 0.999891 | 0.0000006 | 0.998267 | 0.0000024 | −0.162 | 0.999634 | 0.0000011 | −0.0258 | 0.999861 | 0.0000007 | −0.00309 |
| 20 | ±10 | 0.999996 | 0.0000001 | 0.999771 | 0.0000010 | −0.0225 | 0.999978 | 0.0000002 | −0.00180 | 0.999994 | 0.0000001 | −0.00017 |
Table 5.
Power of Test (Ω) values for four single extreme outlier discordancy tests as a function of ε.
| n | ε | Discordancy tests | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| N2 | N8 | N14 | N15 | |||||||||
| (u 99)N2 | (u 99)N8 | (u 99)N14 | (u 99)N15 | |||||||||
| 5 | ±1.1 | 0.020850 | 0.0000310 | 0.020803 | 0.0000314 | −0.227 | 0.020844 | 0.0000307 | −0.0313 | 0.020869 | 0.0000314 | 0.087 |
| 5 | ±3 | 0.064711 | 0.0000419 | 0.064385 | 0.0000419 | −0.50 | 0.064691 | 0.0000425 | −0.0304 | 0.064743 | 0.0000412 | 0.050 |
| 5 | ±5 | 0.154521 | 0.0000496 | 0.153274 | 0.0000481 | −0.81 | 0.154449 | 0.0000483 | −0.046 | 0.154511 | 0.0000480 | −0.0066 |
| 5 | ±7 | 0.258413 | 0.0000570 | 0.256108 | 0.0000574 | −0.89 | 0.258284 | 0.0000555 | −0.050 | 0.258324 | 0.0000568 | −0.0344 |
| 5 | ±10 | 0.397926 | 0.0000695 | 0.394635 | 0.0000687 | −0.83 | 0.397744 | 0.0000695 | −0.046 | 0.397724 | 0.0000691 | −0.051 |
| 5 | ±12.9 | 0.50175 | 0.0000610 | 0.49817 | 0.0000609 | −0.71 | 0.50155 | 0.0000594 | −0.0389 | 0.50151 | 0.0000620 | −0.047 |
| 5 | ±15 | 0.560321 | 0.0000690 | 0.556782 | 0.0000652 | −0.63 | 0.560129 | 0.0000682 | −0.0341 | 0.560080 | 0.0000690 | −0.0429 |
| 5 | ±20 | 0.660616 | 0.0000600 | 0.657405 | 0.0000600 | −0.49 | 0.660442 | 0.0000600 | −0.0264 | 0.660386 | 0.0000588 | −0.0347 |
| 5 | ±30 | 0.771476 | 0.0000629 | 0.769007 | 0.0000655 | −0.320 | 0.771337 | 0.0000637 | −0.0181 | 0.771296 | 0.0000644 | −0.0233 |
| 5 | ±40 | 0.822288 | 0.0000430 | 0.820357 | 0.0000442 | −0.235 | 0.822181 | 0.0000431 | −0.0130 | 0.822138 | 0.0000428 | −0.0182 |
| 5 | ±60 | 0.881517 | 0.0000389 | 0.880180 | 0.0000385 | −0.152 | 0.881443 | 0.0000392 | −0.0084 | 0.881408 | 0.0000394 | −0.0124 |
| 5 | ±80 | 0.911274 | 0.0000321 | 0.910263 | 0.0000327 | −0.111 | 0.911218 | 0.0000324 | −0.0061 | 0.911195 | 0.0000311 | −0.0087 |
| 5 | ±120 | 0.941005 | 0.0000307 | 0.940328 | 0.0000307 | −0.072 | 0.940970 | 0.0000306 | −0.00371 | 0.940951 | 0.0000306 | −0.0058 |
| 5 | ±160 | 0.955830 | 0.0000281 | 0.955330 | 0.0000269 | −0.052 | 0.955801 | 0.0000285 | −0.00302 | 0.955792 | 0.0000281 | −0.00395 |
| 5 | ±200 | 0.964715 | 0.0000244 | 0.964312 | 0.0000248 | −0.0417 | 0.964693 | 0.0000241 | −0.00226 | 0.964681 | 0.0000242 | −0.00345 |
| 10 | ±1.1 | 0.023252 | 0.0000400 | 0.023052 | 0.0000335 | −0.86 | 0.023228 | 0.0000400 | −0.106 | 0.023210 | 0.0000386 | −0.181 |
| 10 | ±3 | 0.230007 | 0.0000688 | 0.215369 | 0.0000615 | −6.4 | 0.226613 | 0.0000671 | −1.48 | 0.228723 | 0.0000691 | −0.56 |
| 10 | ±5 | 0.466178 | 0.0000675 | 0.444482 | 0.0000696 | −4.7 | 0.461346 | 0.0000693 | −1.037 | 0.464412 | 0.0000674 | −0.379 |
| 10 | ±5.4 | 0.501202 | 0.0000668 | 0.479497 | 0.0000682 | −4.33 | 0.496385 | 0.0000629 | −0.96 | 0.499458 | 0.0000674 | −0.348 |
| 10 | ±10 | 0.609736 | 0.0000680 | 0.589504 | 0.0000642 | −3.32 | 0.605299 | 0.0000668 | −0.73 | 0.608161 | 0.0000726 | −0.258 |
| 10 | ±10 | 0.729058 | 0.0000551 | 0.712878 | 0.0000551 | −2.22 | 0.725561 | 0.0000548 | −0.48 | 0.727835 | 0.0000575 | −0.168 |
| 10 | ±15 | 0.824592 | 0.0000517 | 0.813173 | 0.0000531 | −1.38 | 0.822123 | 0.0000498 | −0.299 | 0.823755 | 0.0000530 | −0.101 |
| 10 | ±20 | 0.872018 | 0.0000545 | 0.863336 | 0.0000533 | −1.00 | 0.870142 | 0.0000543 | −0.215 | 0.871397 | 0.0000552 | −0.071 |
| 10 | ±30 | 0.918594 | 0.0000550 | 0.912810 | 0.0000579 | −0.63 | 0.917335 | 0.0000538 | −0.137 | 0.918194 | 0.0000540 | −0.0435 |
| 10 | ±40 | 0.934126 | 0.0000272 | 0.929776 | 0.0000294 | −0.47 | 0.933203 | 0.0000279 | −0.099 | 0.933789 | 0.0000276 | −0.0360 |
| 10 | ±50 | 0.947611 | 0.0000234 | 0.944143 | 0.0000241 | −0.366 | 0.946875 | 0.0000242 | −0.078 | 0.947342 | 0.0000238 | −0.0284 |
| 10 | ±100 | 0.974142 | 0.0000183 | 0.972421 | 0.0000184 | −0.177 | 0.973777 | 0.0000185 | −0.0374 | 0.974010 | 0.0000184 | −0.0136 |
| 10 | ±150 | 0.982843 | 0.0000161 | 0.981700 | 0.0000168 | −0.116 | 0.982600 | 0.0000166 | −0.0247 | 0.982756 | 0.0000161 | −0.0089 |
| 10 | ±200 | 0.987171 | 0.0000142 | 0.986318 | 0.0000144 | −0.086 | 0.986991 | 0.0000138 | −0.0183 | 0.987105 | 0.0000143 | −0.0067 |
| 15 | ±1.1 | 0.024941 | 0.0000507 | 0.024516 | 0.0000434 | −1.70 | 0.024714 | 0.0000454 | −0.91 | 0.024907 | 0.0000523 | −0.137 |
| 15 | ±3 | 0.315624 | 0.0000816 | 0.285482 | 0.0000707 | −9.6 | 0.301908 | 0.0000791 | −4.35 | 0.312616 | 0.0000768 | −0.95 |
| 15 | ±4.4 | 0.505574 | 0.0000745 | 0.470626 | 0.0000677 | −6.9 | 0.490624 | 0.0000697 | −2.96 | 0.502393 | 0.0000705 | −0.63 |
| 15 | ±5 | 0.563420 | 0.0000689 | 0.529313 | 0.0000721 | −6.1 | 0.549047 | 0.0000748 | −2.55 | 0.560407 | 0.0000698 | −0.53 |
| 15 | ±7 | 0.692305 | 0.0000627 | 0.663682 | 0.0000610 | −4.13 | 0.680599 | 0.0000638 | −1.69 | 0.689963 | 0.0000629 | −0.338 |
| 15 | ±10 | 0.791754 | 0.0000591 | 0.770289 | 0.0000590 | −2.71 | 0.783169 | 0.0000580 | −1.08 | 0.790166 | 0.0000564 | −0.201 |
| 15 | ±15 | 0.867777 | 0.0000506 | 0.853207 | 0.0000541 | −1.68 | 0.862030 | 0.0000516 | −0.66 | 0.866870 | 0.0000525 | −0.105 |
| 15 | ±20 | 0.904654 | 0.0000486 | 0.893754 | 0.0000511 | −1.20 | 0.900431 | 0.0000428 | −0.47 | 0.904100 | 0.0000549 | −0.061 |
| 15 | ±30 | 0.940391 | 0.0000448 | 0.933225 | 0.0000533 | −0.76 | 0.937686 | 0.0000478 | −0.288 | 0.940194 | 0.0000497 | −0.0209 |
| 15 | ±40 | 0.950189 | 0.0000256 | 0.944782 | 0.0000263 | −0.57 | 0.948017 | 0.0000256 | −0.229 | 0.949688 | 0.0000258 | −0.053 |
| 15 | ±60 | 0.967191 | 0.0000212 | 0.963613 | 0.0000224 | −0.370 | 0.965751 | 0.0000218 | −0.149 | 0.966859 | 0.0000207 | −0.0343 |
| 15 | ±80 | 0.975546 | 0.0000199 | 0.972878 | 0.0000213 | −0.274 | 0.974475 | 0.0000198 | −0.110 | 0.975299 | 0.0000200 | −0.0253 |
| 15 | ±140 | 0.986132 | 0.0000140 | 0.984621 | 0.0000148 | −0.153 | 0.985524 | 0.0000143 | −0.062 | 0.985992 | 0.0000137 | −0.0142 |
| 15 | ±200 | 0.990334 | 0.0000113 | 0.989278 | 0.0000127 | −0.107 | 0.989908 | 0.0000116 | −0.0429 | 0.990235 | 0.0000116 | −0.0099 |
| 20 | ±1.1 | 0.025959 | 0.0000600 | 0.025296 | 0.0000570 | −2.551 | 0.025396 | 0.0000534 | −2.17 | 0.025877 | 0.0000610 | −0.313 |
| 20 | ±3 | 0.362436 | 0.0000753 | 0.321879 | 0.0000782 | −11.2 | 0.338086 | 0.0000708 | −6.7 | 0.357843 | 0.0000754 | −1.27 |
| 20 | ±4 | 0.509029 | 0.0000677 | 0.465277 | 0.0000661 | −8.6 | 0.484093 | 0.0000691 | −4.9 | 0.504506 | 0.0000649 | −0.89 |
| 20 | ±5 | 0.609022 | 0.0000669 | 0.567957 | 0.0000706 | −6.7 | 0.586331 | 0.0000707 | −3.73 | 0.605042 | 0.0000639 | −0.65 |
| 20 | ±7 | 0.728947 | 0.0000692 | 0.695836 | 0.0000693 | −4.5 | 0.711240 | 0.0000640 | −2.43 | 0.726084 | 0.0000696 | −0.393 |
| 20 | ±10 | 0.818758 | 0.0000462 | 0.794479 | 0.0000533 | −2.97 | 0.806135 | 0.0000486 | −1.54 | 0.816978 | 0.0000476 | −0.217 |
| 20 | ±15 | 0.886139 | 0.0000424 | 0.869861 | 0.0000430 | −1.84 | 0.877932 | 0.0000468 | −0.93 | 0.885261 | 0.0000465 | −0.099 |
| 20 | ±20 | 0.918508 | 0.0000399 | 0.906382 | 0.0000446 | −1.32 | 0.912559 | 0.0000407 | −0.65 | 0.918085 | 0.0000427 | −0.046 |
| 20 | ±30 | 0.949667 | 0.0000432 | 0.941715 | 0.0000507 | −0.84 | 0.945966 | 0.0000481 | −0.390 | 0.949717 | 0.0000506 | 0.0053 |
| 20 | ±40 | 0.956868 | 0.0000229 | 0.950924 | 0.0000258 | −0.62 | 0.953687 | 0.0000219 | −0.332 | 0.956225 | 0.0000226 | −0.067 |
| 20 | ±60 | 0.971612 | 0.0000209 | 0.967685 | 0.0000218 | −0.404 | 0.969514 | 0.0000209 | −0.216 | 0.971191 | 0.0000210 | −0.0434 |
| 20 | ±80 | 0.978856 | 0.0000170 | 0.975928 | 0.0000185 | −0.299 | 0.977289 | 0.0000179 | −0.160 | 0.978541 | 0.0000170 | −0.0322 |
| 20 | ±140 | 0.988015 | 0.0000127 | 0.986356 | 0.0000127 | −0.168 | 0.987127 | 0.0000139 | −0.090 | 0.987837 | 0.0000128 | −0.0181 |
| 20 | ±200 | 0.991646 | 0.0000107 | 0.990487 | 0.0000113 | −0.117 | 0.991025 | 0.0000109 | −0.063 | 0.991520 | 0.0000113 | −0.0126 |
For n = 10, Dixon test N8 becomes considerably less efficient than Grubbs test N2, because the values become as low as −7.8% for δ = ±5 or −6.4% for ε = ±3 (Tables 3–6). Skewness test N14 also shows slightly lower Ω and π D∣C than N2 (% for δ = ±4- ± 5, or % for ε = ±3; Tables 3–6). Kurtosis test N15 shows a similar performance as test N2; the maximum difference is about 0.7 (Tables 3–6). For n = 10 test N2 shows Ω = 0.5 (or π D∣C = 0.5) for δ = ±5.105; for this case, the other three tests (N8, N14, and N15) show values of about −7.8%, −1.8%, and −0.7% (Tables 3 and 4). Similarly, for such cases, Ω and π D∣C show , , and values of about −4.3%, −1.0%, and −0.4%, respectively.
For n = 15 and n = 20, test N8 shows the worst performance and the values become as large as −12.2% to −15.5% for δ (Tables 3 and 4) or −9.8% to −11.5% for ε (Tables 5 and 6). For these sample sizes, test N14 also shows a worse performance as compared to N2, because the maximum differences represented by values are about −6.3% to −10.9% for δ (Tables 3 and 4) or −4.5% to −7.0% for ε (Tables 5 and 6). Test N15 shows a comparable performance, because the maximum differences ( values) are about −1.5% to −2.4% for δ (Tables 3 and 4) or −1.1% to −1.5% for ε (Tables 5 and 6). For n = 15 and n = 20, when test N2 shows Ω = 0.5 or π D∣C = 0.5, the , , and values range from about −6.9% to −15.0%, −3.0% to −9.2%, and −0.6% to −1.9%, respectively.
The significantly lower Ω and π D∣C values of the Dixon test N8 as compared to the Grubbs test N2, skewness test N14, and kurtosis test N15 may be related to the masking effect of the penultimate observation x (n−1) on x (n) or of x (2) on x (1) as documented by Barnett and Lewis [1]. The masking effect may also be responsible for a somewhat worse performance of N14 as compared to N2.
6.4. Final Remarks
The two performance criteria (Ω and π D∣C) [1, 7] used in this work provide similar estimates (Tables 3–6) and, more importantly, similar conclusions. Therefore, any of them can be used to evaluate numerous other discordancy tests for single or multiple outliers [1, 26–28]. The main result of Monte Carlo simulations concerning the performance of the single extreme outlier discordancy tests could be stated as follows: N2≅N15 > N14 > N8.
Additional simulation work is required to evaluate other discordancy tests, such as the single upper or lower outlier tests, as well as more complex statistical contamination involving two or more discordant outliers and the comparison of consecutive application of single outlier discordancy tests with multiple outlier tests [1, 7, 26–28]. Then, the multiple test method, initially proposed by Verma [29] and used by many researchers [30–35], would be substantially improved for subsequent applications. These performance results could then be incorporated in new versions of the computer programs DODESSYS [36], TecD [37], and UDASYS [38].
7. Conclusions
Our simulation study clearly shows that Dixon test N8 performs less well than the other three extreme single outlier tests (Grubbs N2, skewness N14, and kurtosis N15). Both performance parameters (the Power of Test Ω and Test Performance Criterion π D∣C) have up to about 16% less values for N8 than test N2. Test N8, therefore, shows the worst performance for outlier detection. For certain values of δ or ε test N14 also shows lesser values of Ω and π D∣C than N2, which means that N14 is also somewhat worse than N2. The other two tests (N2 and N15) could be considered comparable in their performance.
Acknowledgments
The computing facilities for this work were partly from the DGAPA-PAPIIT project IN104813. The second author (Lorena Díaz-González) acknowledges PROMEP support to the project “Estadística computacional para el tratamiento de datos experimentales” (PROMEP/103-5/10/7332). The third author (Mauricio Rosales-Rivera) thanks the Sistema Nacional de Investigadores (Mexico) for a scholarship that enabled him to participate in this research as Ayudantes de Investigador Nacional Nivel III of the first author (Surendra P. Verma).
Conflict of Interests
The authors declare that there is no conflict of interests regarding the publication of this paper.
References
- 1.Barnett V, Lewis T. Outliers in Statistical Data. 3rd edition. Chichester, UK: John Wiley & Sons; 1994. [Google Scholar]
- 2.Dixon WJ. Analysis of extreme values. Annals of Mathematical Statistics. 1950;21(4):488–506. [Google Scholar]
- 3.Ferguson TS. Rules for rejection of outliers. Revue de l'Institut International de Statistique. 1961;29(3):29–43. [Google Scholar]
- 4.Shapiro SS, Wilk MB, Chen HJ. A comparative study of various tests for normality. Journal of American Statistical Association. 1968;63(324):1343–1371. [Google Scholar]
- 5.Hawkins DM. Analysis of three tests for one or two outliers. Statistica Nederlandica. 1978;32(3):137–148. [Google Scholar]
- 6.Prescott P. Examination of the behavior of tests for outliers when more than one outlier is present. Applied Statistics. 1978;27(1):10–25. [Google Scholar]
- 7.Hayes K, Kinsella T. Spurious and non-spurious power in performance criteria for tests of discordancy. Journal of the Royal Statistical Society Series D. 2003;52(1):69–82. [Google Scholar]
- 8.Tietjen GL, Moore RH. Some Grubbs-type statistics for the detection of several outliers. Technometrics. 1972;14(3):583–597. [Google Scholar]
- 9.Rosner B. On the detection of many outliers. Technometrics. 1975;17(2):221–227. [Google Scholar]
- 10.Royston JP. The W test for normality. Journal of the Royal Statistical Society C. 1982;31(2):176–180. [Google Scholar]
- 11.Simonoff JS. The breakdown and influence properties of outlier rejection-plus-mean procedures. Communications in Statistics. 1987;16(6):1749–1760. [Google Scholar]
- 12.Efstathiou CE. Estimation of type I error probability from experimental Dixon’s “Q” parameter on testing for outliers within small size data sets. Talanta. 2006;69(5):1068–1071. doi: 10.1016/j.talanta.2005.12.031. [DOI] [PubMed] [Google Scholar]
- 13.Gottardo R, Raftery AE, Yeung KY, Bumgarner RE. Quality control and robust estimation for cDNA microarrays with replicates. Journal of the American Statistical Association. 2006;101(473):30–40. [Google Scholar]
- 14.Khedhiri S, Montasser GE. The effects of additive outliers on the seasonal KPSS test: a Monte Carlo analysis. Journal of Statistical Computation and Simulation. 2010;80(6):643–651. [Google Scholar]
- 15.Patel PA, Patel JS. A monte carlo comparison of some variance estimators of the Horvitz-Thompson estimator. Journal of Statistical Computation and Simulation. 2010;80(5):489–502. [Google Scholar]
- 16.Noughabi HA, Arghami NR. Monte carlo comparison of seven normality tests. Journal of Statistical Computation and Simulation. 2011;81(8):965–972. [Google Scholar]
- 17.Krishnamoorthy K, Lian X. Closed-form approximate tolerance intervals for some general linear models and comparison studies. Journal of Statistical Computation and Simulation. 2012;82(4):547–563. [Google Scholar]
- 18.Verma SP. Geochemometrics. Revista Mexicana de Ciencias Geológicas. 2012;29(1):276–298. [Google Scholar]
- 19.Verma SP, Quiroz-Ruiz A, Díaz-González L. Critical values for 33 discordancy test variants for outliers in normal samples up to sizes 1000, and applications in quality control in Earth Sciences. Revista Mexicana de Ciencias Geologicas. 2008;25(1):82–96. [Google Scholar]
- 20.Verma SP, Quiroz-Ruiz A. Corrigendum to Critical values for 22 discordancy test variants for outliers in normal samples up to sizes 100, and applications in science and engineering [Revista Mexicana de Ciencias Geologicas, vol. 23, pp. 302–319, 2006] Revista Mexicana de Ciencias Geologicas. 2011;28(1):p. 202. [Google Scholar]
- 21.Verma SP, Quiroz-Ruiz A. Critical values for six Dixon tests for outliers in normal samples up to sizes 100, and applications in science and engineering. Revista Mexicana de Ciencias Geologicas. 2006;23(2):133–161. [Google Scholar]
- 22.Cruz-Huicochea R, Verma SP. New critical values for F and their use in the ANOVA and Fisher’s F tests for evaluating geochemical reference material granite G-2 (U.S.A.) and igneous rocks from the Eastern Alkaline Province (Mexico) Journal of Iberian Geology. 2013;39(1):13–30. [Google Scholar]
- 23.Verma SP, Cruz-Huicochea R. Alternative approach for precise and accurate Student's t critical values in geosciences and application in geosciences. Journal of Iberian Geology. 2013;39(1):31–56. [Google Scholar]
- 24.Grubbs FE. Procedures for detecting outlying observations in samples. Technometrics. 1969;11(1):1–21. [Google Scholar]
- 25.Law AM, Kelton WD. Simulation Modeling and Analysis. 3rd edition. Boston, Mass, USA: McGraw Hill; 2000. [Google Scholar]
- 26.Verma SP, Díaz-González L, González-Ramírez R. Relative efficiency of single-outlier discordancy tests for processing geochemical data on reference materials and application to instrumental calibrations by a weighted least-squares linear regression model. Geostandards and Geoanalytical Research. 2009;33(1):29–49. [Google Scholar]
- 27.Verma SP. Estadística Básica para el Manejo de Datos Experimentales: Aplicación en la Geoquímica (Geoquimiometría) México, DF: UNAM; 2005. [Google Scholar]
- 28.González-Ramírez R, Díaz-González L, Verma SP. Eficiencia relativa de 15 pruebas de discordancia con 33 variantes aplicadas al procesamiento de datos geoquímicos. Revista Mexicana de Ciencias Geologicas. 2009;26(2):501–515. [Google Scholar]
- 29.Verma SP. Sixteen statistical tests for outlier detection and rejection in evaluation of international geochemical reference materials: example of microgabbro PM-S. Geostandards Newsletter. 1997;21(1):59–75. [Google Scholar]
- 30.Gómez-Arias E, Andaverde J, Santoyo E, Urquiza G. Determinación de la viscosidad y su incertidumbre en fluidos de perforación usados en la construcción de pozos geotérmicos: aplicación en el campo de Los Humeros, Puebla, México. Revista Mexicana de Ciencias Geológicas. 2009;26(2):516–529. [Google Scholar]
- 31.Marroquín-Guerra SG, Velasco-Tapia F, Díaz-González L. Evaluación estadística de materiales de referencia geoquímica del Centre de Recherches Pétrographiques et Géochimiques (Francia) aplicando un esquema de detección y eliminación de valores desviados. Revista Mexicana de Ciencias Geológicas. 2009;26(2):530–542. [Google Scholar]
- 32.Pandarinath K. Evaluation of geochemical sedimentary reference materials of the Geological Survey of Japan (GSJ) by an objective outlier rejection statistical method. Revista Mexicana de Ciencias Geologicas. 2009;26(3):638–646. [Google Scholar]
- 33.Pandarinath K. Clay minerals in SW Indian continental shelf sediment cores as indicators of provenance and palaeomonsoonal conditions: a statistical approach. International Geology Review. 2009;51(2):145–165. [Google Scholar]
- 34.Pandarinath K, Verma SK. Application of four sets of tectonomagmatic discriminant function based diagrams to basic rocks from northwest Mexico. Journal of Iberian Geology. 2013;39(1):181–195. [Google Scholar]
- 35.Verma MP. IAEA inter-laboratory comparisons of geothermal water chemistry: critiques on analytical uncertainty, accuracy, and geothermal reservoir modelling of Los Azufres, Mexico. Journal of Iberian Geology. 2013;39(1):57–72. [Google Scholar]
- 36.Verma SP, Díaz-González L. Application of the discordant outlier detection and separation system in the geosciences. International Geology Review. 2012;54(5):593–614. [Google Scholar]
- 37.Verma SP, Rivera-Gómez MA. New computer program TecD for tectonomagmatic discrimination from discriminant function diagrams for basic and ultrabasic magmas and its application to ancient rocks. Journal of Iberian Geology. 2013;39(1):167–179. [Google Scholar]
- 38.Verma SP, Cruz-Huicochea R, Díaz-González L. Univariate data analysis system: deciphering mean compositions of island and continental arc magmas, and influence of underlying crust. International Geology Review. 2013;55(15):1922–1940. [Google Scholar]