Skip to main content
PMC home page
Scientific Reports logoLink to Scientific Reports
. 2014 Mar 28;4:4496. doi: 10.1038/srep04496

A transparent broadband ultrasonic detector based on an optical micro-ring resonator for photoacoustic microscopy

Hao Li 1,4, Biqin Dong 1,2,4, Zhen Zhang 2, Hao F Zhang 1,3,b, Cheng Sun 2,a
PMCID: PMC3968454  PMID: 24675547

Abstract

Photoacoustic microscopy (PAM) does not rely on contrast agent to image the optical absorption contrast in biological tissue. It is uniquely suited for measuring several tissue physiological parameters, such as hemoglobin oxygen saturation, that would otherwise remain challenging. Researchers are designing new clinical diagnostic tools and multimodal microscopic systems around PAM to fully unleash its potential. However, the sizeable and opaque piezoelectric ultrasonic detectors commonly used in PAM impose a serious constraint. Our solution is a coverslip-style optically transparent ultrasound detector based on a polymeric optical micro-ring resonator (MRR) with a total thickness of 250 μm. It enables highly-sensitive ultrasound detection over a wide receiving angle with a bandwidth of 140 MHz, which corresponds to a photoacoustic saturation limit of 287 cm−1, at an estimated noise-equivalent pressure (NEP) of 6.8 Pa. We also established a theoretical framework for designing and optimizing the MRR for PAM.

Despite the rapid progress in developing a wide range of optical microscopic imaging technologies, photoacoustic microscopy (PAM) remains the only choice for directly imaging optical absorption contrast in biomedicine without the need of contrast agents1. Compared with other existing high-resolution optical imaging modalities, including confocal microscopy2, two-photon microscopy3,4, and optical coherence tomography5, PAM can extract three-dimensional physiologically specific optical absorption properties in biological tissue at a lateral resolution that is subject only to the optical diffraction limit6. In PAM, a short-pulsed laser beam is focused onto biological tissues. The absorbed laser energy leads to a transient thermo-elastic expansion and, subsequently, launches ultrasonic waves containing a wide-range of frequency components, which can be detected to construct optical absorption contrast-based images. The amplitude of the induced ultrasonic wave is proportional to the product of the local optical fluence and optical absorption coefficient. The traveling time of the induced ultrasonic wave is proportional to the distance between its origin and the ultrasonic detector7. PAM can image either endogenous sources, such as hemoglobin and melanin, or exogenous contrast agents, such as chemical dyes, nanoparticles, and reporter gene products1. The broad range of available contrast sources allows PAM to reveal abundant anatomical and functional information, such as intracellular thermal transmission8, energy difference in molecular vibrational bands9, tumor angiogenesis10, melanoma10, brain cortex functions11, water and lipid concentration12,13, and metabolic rate of oxygen14,15.

Although unique and versatile, PAM is not capable of imaging samples that exhibit poor optical absorption. To investigate more sophisticated physiological processes, integrating PAM with other well-established optical microscopic imaging modalities becomes necessary for providing a comprehensive tool that can simultaneously capture multiple optical contrasts in tissue; however, previous efforts to integrate PAM with confocal microscopy16,17 and optical coherence tomography18,19,20 were found to have rather limited lateral and axial resolutions. The lateral resolution was fundamentally limited by the small numerical aperture (NA) being used due to the long working distance required to accommodate sizeable piezoelectric detectors. The axial resolution was constrained by the finite detection bandwidth of commonly used piezoelectric detectors. Due to the limitations of these piezoelectric detectors, it becomes technically difficult to integrate PAM with a conventional high-resolution optical microscopic system in which the working distance of an objective lens is normally less than 1 mm. Although a piezoelectric detector with openings at the center was created to reduce the obstruction to the optical imaging path21,22, it often reduced axial resolution due to the decreased bandwidth and detection angle23,24. To this end, optical-based ultrasonic detection techniques may offer a more desirable solution. The rapid progress in integrated photonic circuits permits an opportunity for creating miniaturized and transparent ultrasonic detectors, which are the necessary features for integrating PAM with optical microscopic systems. In addition, because light oscillates more than five orders of magnitude faster than ultrasonic waves, optical-based detection methods further allow more sensitive ultrasonic detection over a much wider frequency band.

A variety of optical-based ultrasound detection methods have been developed in the past25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42, and the implementations generally fall into three categories: 1) free-space approaches that use a Michelson interferometer25, Fabry-Perot optic-film26, or confocal Fabry-Perot interferometer27,28; 2) prism-based approaches that rely on surface-bonded photonic modes, such as total internal reflection29, surface plasmon resonance30,31,32,33, photonic crystal surface wave34, and metamaterial35; and 3) integrated photonics approaches, such as intrinsic optical fiber interferometer36, waveguide Mach-Zehnder interferometer37, Fabry-Perot cavity38, and MRR39,40,41,42.

Among all these methods, MRR exhibits its unique advantages. First, the highly sensitive ultrasound detection can be achieved using a sub-millimeter-size MRR with the effective optical path length magnified more than one thousand-fold through strong optical resonance; thereby helping to minimize the interference to the optical path of the optical microscope system. Second, MRR offers a much broader ultrasonic detection bandwidth that subsequently improves the saturation limit43 and axial resolution in functional photoacoustic (PA) imaging7. Optical frequency is much higher than ultrasonic frequency, so even at reduced temporal response due to resonance, MRR is still capable of offering a remarkably broader detection bandwidth compared with traditional piezoelectric detectors42. Finally, the miniaturized MRR detector permits sensitive ultrasound detection within a larger detection angle44, which is favorable for increasing the field-of-view (FOV) in laser-scanning PAM systems45. Although MRRs fabricated on silicon substrate have been studied extensively, these MRRs are optically opaque39,40,41,42; therefore, the resulting PAM system can only be implemented in a transmission configuration, which is not practical for imaging thick biological samples40 and shows only marginal improvement over existing PAMs. Hence, an optically transparent MRR ultrasonic detector has yet to be developed.

In this paper, we designed and fabricated a miniaturized, optically-transparent ultrasonic detector consisting of a polymeric MRR on a 250 μm-thick microscope coverslip. We systematically analyzed the principle of MRR ultrasonic detection and formulated a general designing guideline. We fabricated the MRR detector using well-established nanofabrication methods and characterized its performances experimentally. After employing the MRR ultrasonic detector in a PAM system, we demonstrated that: 1) the MRR ultrasonic detector is fully compatible with microscopic imaging systems and can be used with high-NA objective lenses; 2) an axial resolution of 5.3 μm has been obtained experimentally as a result of the MRR's ultra-wide frequency response; and 3) there can be a nearly two-fold improvement in the PA saturation limit compared with piezoelectric detectors. The convenience in integrating the MRR detector with commercially available optical microscopic systems may open up a new gateway for both biomedical research and clinical diagnoses.

Results

The working principle of the MRR ultrasonic detector is illustrated in Fig. 1. The MRR detector consists of a bus waveguide and a ring-shaped waveguide separated by a low-dielectric gap (Fig. 1a). The bus waveguide serves as the input and output ports, and the coupling to the ring waveguide is accomplished by evanescently tunneling across the low-dielectric gap. The light wave circulating inside the ring waveguide leads to a strong optical resonance supported by the whisper gallery mode (WGM) with an extremely high-quality factor (Q-factor) exceeding 1010 being experimentally demonstrated46. The resulting optical resonance can be characterized by the narrow dip in the light transmitted through the bus waveguide due to deconstructive interference associated with optical resonance. Theoretically, zero transmission can be achieved when the intrinsic loss of the ring resonator matches with the coupling loss, which is normally referred to as critical coupling condition46.

Figure 1. Geometry and working principle of the MRR ultrasonic detector.

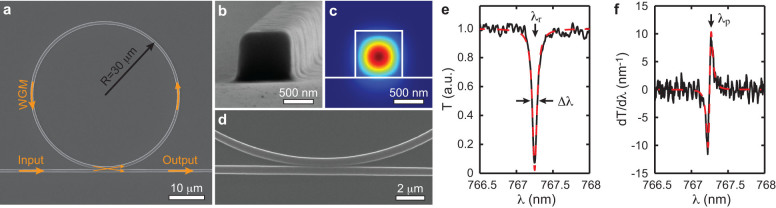
Figure 1

Open in a new tab

(a) Scanning electron micrograph of the MRR. (b) High-magnification view shows the square-shaped cross-section of the waveguide with a side length of 800 nm. (c) Calculated electric field distribution of the TM mode when the waveguide is immersed in water. (d) Close-up view of the gap between the ring and bus waveguides. (e) Transmission spectrum shows the dip caused by the strong WGM-induced optical resonance. Black line: experimental data; red dashed-line: fitted curve based on Lorenzian model. λr is 767.27 nm, Δλ is 73.8 pm, Q factor is λr/Δλ = 10400. (f) The normalized transmission change with respect to the resonance shift derived by the first derivative of the transmission spectrum. Black line: experimental data; red dashed-line: calculated curve from the fitted result in the panel (e). The probing wavelength λp indicated by arrow is set to the maximum sensitivity point of PA detection at 767.31 nm.

Built upon such a strong optical resonance, an MRR made from soft polymeric materials can be used as an ultra-sensitive detector that converts ultrasonic pressure wave-induced deformation of MRR into a measurable quantity in the shift of its optical resonance modes. The deformation causes changes in both the geometry and refractive index (RI) of the polymer MRR and subsequently alters the corresponding effective refractive index (neff) of the guided mode. The resulting changes in the optical path length of the MRR are accumulated while the lightwave is circulating inside. The amplified optical path length changes can then be quantified by measuring the wavelength shift of the resonance modes. Using a narrow-band laser source, such a resonance shift can be measured as the modulation of the transmitted optical intensity at given wavelength39.

The sensitivity of detecting pressure variation using MRR can be defined as39,47,48:

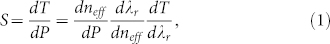graphic file with name srep04496-m1.jpg

where T is the transmission through the bus waveguide; P is the ultrasonic pressure; λr is the resonance wavelength. The first term dneff/dP defines the pressure-induced effective refractive index change in the polymer waveguide that takes into account the Young's modulus and the elasto-optic coefficient of the polymer as well as the cross-sectional shape of the waveguide (see Supplementary Information for simulation details). The second term dλr/dneff is the resulting shift of the resonance wavelength due to changes of neff. The resonance wavelength can be derived from the standing wave condition of the WGM:

graphic file with name srep04496-m2.jpg

where m is the order of the resonance mode and R is the radius of the ring resonator. Considering a small perturbation in neff, we have

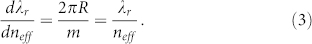graphic file with name srep04496-m3.jpg

The optimal sensitivity can be obtained at the rising or falling edge of the resonance dip; therefore, dT/dλr can be defined as the slope of its linear region, which can be approximated as linearly proportional to the Q-factor. The maximum detectable PA pressure is also constrained by the wavelength range of the linear region, which is inversely proportional to the Q-factor. Overall, the detection sensitivity can be simplified as

graphic file with name srep04496-m4.jpg

where A is a design-specific parameter that is collectively determined by the materials properties and the guided mode profile of the polymeric waveguide. It can be treated as a constant for a given polymer material and the cross-sectional shape of the waveguide. Therefore, an MRR with a higher Q-factor and a longer wavelength will favorably increase its ultrasonic detection sensitivity.

Theoretically, the detection bandwidth is determined by the temporal response of two concurrent processes: the optical resonance due to the WGM and the propagation of ultrasonic wave in the surrounding media. From the perspective of optical resonance, when ultrasonic pressure induces resonance mode change, it takes time for the WGM to gradually accumulate energy to reach a steady state again. The corresponding time constant for reestablishing a steady state is comparable to the effective photon life time in resonator τ = Q/ω, where ω is the angular frequency of the light wave. When MRR is used for ultrasonic detection, the resulting resonance-limited cutoff ultrasonic frequency (f0) is inversely proportional to the time constant f0 = 1/τ = ω/Q39,49,50. On the other hand, from the perspective of acoustic wave propagation, in order to avoid deconstructive interference between an incoming acoustic wave and the subsequent reflection from the surface of the rigid substrate, the thickness of the waveguide is constrained by the quasi-static limit39. Since acoustic scattering by the MRR itself can be negligible, the resulting geometry-limited cutoff frequency (ft) can be approximated as ft = v/2h, where v is the ultrasound speed in water and h is the waveguide thickness27.

A planar ultrasonic detector with finite dimension often exhibits angular-dependent sensitivity to a point PA source42. For a ring-shaped detector, the angular-dependent sensitivity follows44

graphic file with name srep04496-m5.jpg

where θ is the incident angle of the ultrasound wave; J0 is the 0th order Bessel function of the first kind; and k = 2πf/v is the ultrasonic wave vector at a given ultrasound frequency f. The full-width-half-max (FWHM) of the angular-dependent sensitivity is inversely proportional to the radius of the ring resonator R; thus, a smaller MRR permits sensitive ultrasound detection over a wider incident angle, which, in turn, allows a larger FOV in laser-scanning PAM systems45.

We fabricated the polymeric MRR and the matching bus waveguide on a fused quartz microscope coverslip (GE124, Ted Pella) using the E-beam lithography process (Fig. 1a, detailed procedure is available in Methods). The optical waveguide has a square-shaped cross-section with a side length of 800 nm. The corresponding scanning electron microscope (SEM) image and the calculated mode profile at 765 nm (Comsol Multiphysics) are shown in Fig. 1b and Fig. 1c, respectively. Our MRR is designed to support a fundamental mode over the tunable wavelength range between 765–780 nm of the narrow-band laser (TLB-6712, New Focus). This wavelength range was selected to minimize optical absorption by polymer and water. The gap between the ring and the bus waveguides was experimentally optimized to 150 nm to achieve critical coupling, as shown in Fig. 1d. The measured transmission spectrum of the MRR, shown in Fig. 1e, indicates a Q-factor of 10400 (calculated by λr/Δλ ). The corresponding maximum sensitivity of transmission change to resonance shift (dT/dλr) is 11.6 nm−1 at 767.31 nm, as shown in Fig. 1f. During ultrasonic detection, the MRR probing laser was tuned at this wavelength to provide the optimal sensitivity. The linear region of the resonance dip determines the maximum PA pressure-detection range to be 2 MPa, which is calculated by dividing its wavelength range (Δλ) by pressure-induced resonance shift (dλr/dP) in Eq. 1. The pressure in biological PA imaging is usually a few hundreds Pascal, which leads to a wavelength shift less than 0.1 pm; therefore, the wavelength shift can be seen as a minute perturbation and the MRR pressure sensitivity can be considered linear. The time for optical resonance to reach a steady state is estimated to be τ = Q/ω = 4.15 ps, which corresponds to a cut-off frequency of f0 = 241 GHz. On the other hand, by considering sound velocity in water, the phase retardation of acoustic wave traveling along the thickness of the MRR further yields a much lower cutoff frequency ft of 0.938 GHz; therefore, ft determines the operational bandwidth of this MRR-based ultrasound detector. Using such a detector in a PAM system, one should expect an axial resolution better than 5 μm45.

To prepare the MRR ultrasound detector for PAM, we experimentally quantified its key characteristics, including NEP, detection bandwidth, angular sensitivity, and the corresponding PA saturation limit. The packaged MRR ultrasound detector is illustrated in Fig. 2a. We used two tapered fiber tips to couple light in and out of the bus waveguide by closely matching the mode-profile51. The bus waveguide features a 90-degree bend to minimize cross-talk between the input and output ports. In contrast to the previously reported butt-coupling method, which brings a cleaved fiber facet to the open end of the polymer waveguide39,40,41,42, our method requires placing the tapered fiber probes only to the ends of the waveguide. This simplifies the packaging procedure by eliminating the intricate process of dicing the non-crystallized-fused quartz substrate, and it could potentially yield better coupling efficiency due to better mode matching between the taper fiber tip and the polymer waveguide51.

Figure 2. Schematic illustrations of (a) the packaged MRR ultrasonic detector coupled to two tapered optical fibers, and (b) an experimental PAM setup used to characterize the performance of the MRR ultrasonic detector.

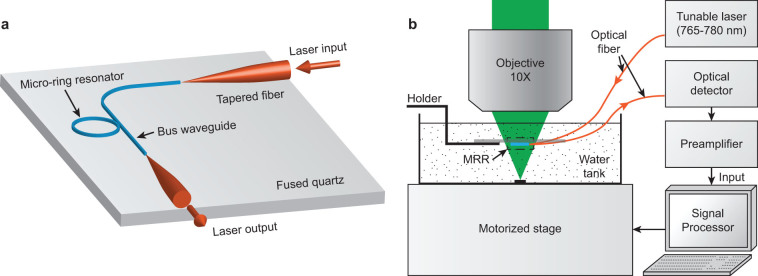
Figure 2

Open in a new tab

Fig. 2b shows an experimental PAM setup. Testing samples were placed at the bottom of a water tank mounted on a two-dimensional translational stage. The MRR ultrasonic detector was attached to an adjustable holder and was immersed in water. A pulsed laser (output wavelength: 532 nm; pulse duration: 1 ns; Elforlight Ltd.) was focused onto the samples by a 10× objective lens (NA 0.25, Mitutoyo) through the transparent MRR ultrasonic detector. A narrow band tunable laser (TLB-6712, New Focus) with an output wavelength range of 765 nm–780 nm was coupled into the bus waveguide through a tapered fiber. The transmitted light was collected by another tapered fiber and measured by an avalanche photodetector (APD, bandwidth: 5 MHz–1 GHz, APD210, Menlo Systems). The detected signal was amplified by 28 dB (ZFL500NL+, Mini-circuits; bandwidth: 10 MHz–500 MHz) and digitized by a PC-based data acquisition system (CobraMax high-speed PCI digitizer, GaGe). As previously described, we detected PA signals by capturing changes in the transmission intensity of MRR caused by ultrasound-induced deformation. The optical axis of the PA illumination was carefully aligned with the center of the MRR. PA imaging was obtained by raster-scanning the samples, and the MRR ultrasonic detector was kept stationary.

We characterized the frequency-dependent sensitivity of the MRR ultrasound detector using a PA point source. The PA point source was created by focusing the excitation light onto a 1.5-μm-thick carbon black thin film spin-coated on a glass substrate. Fig. 3a shows the detected time-resolved PA impulse response. The corresponding Fourier-transformed frequency spectrum shows a 3-dB bandwidth of 140 MHz (Fig. 3b), which is considered sufficient for imaging biological samples using PAM due to significant ultrasonic attenuation in the tissue at frequencies higher than 100 MHz52. The frequency linearity was verified to be uniform up to 75 MHz by comparing the ultrasound signals detected by MRR and piezoelectric transducers. The long-term stability was tested by maintaining the PA excitation light intensity and monitoring the detected PA signal for 15 min. The root-mean-square amplitude fluctuation was 1.6%, indicating a good PA measurement stability (See Supplementary Information for details).

Figure 3. Impulse response of the MRR-based PAM system.

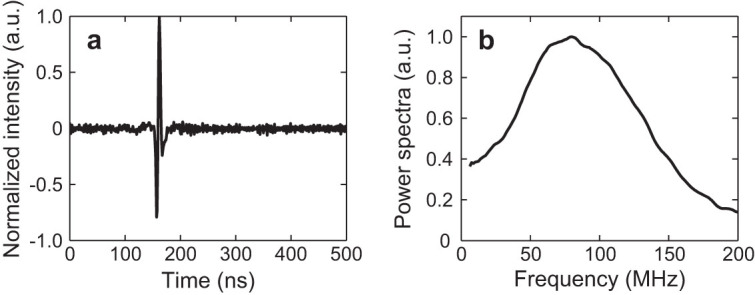
Figure 3

Open in a new tab

(a) Temporal profile of the impulse response. (b) Spectral profile of the impulse response after a 10-point moving averaging.

The ultrasonic sensitivity of MRR is calculated to be 75.0 mV/MPa using the APD210 and 47.3 V/MPa after being amplified by 28 dB based on the measured transmission power, geometry, and the Q-factor of the MRR. The noise level directly measured from Fig. 3a is 0.32 mV, which corresponds to an NEP of 6.8 Pa. The NEP obtained from this study is several orders of magnitude better than conventional piezoelectric transducers with comparable size53, and it is comparable with the best optical detectors reported in the literature42.

In order to achieve functional PAM imaging of, for example, hemoglobin oxygen saturation (sO2) in tissue, PA saturation should be avoided so that spectroscopic PA measurements can be used for inverse calculation43. When a sample exhibits strong optical absorption, the optical penetration depth decreases and, therefore, leads to a temporal compression of the PA signal. PA saturation occurs when the detector's bandwidth cannot match the induced PA signal bandwidth, which leads to a reduced amplitude in the measured PA signal43.

In a semi-infinite optical absorbing medium, the amplitude of a PA signal APA can be approximated as43,54

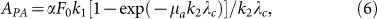graphic file with name srep04496-m6.jpg

where α is the detection sensitivity; F0 is the optical fluence on the surface of the medium; k1 is the converting efficiency from absorbed energy to PA signal; μa is the optical absorption coefficient; k2 is a dimensionless coefficient (0.8 ~ 0.92); and λc is the cutoff wavelength of the ultrasound detector. In the low-absorption limit (μa → 0), PA amplitude (APA ≈ αF0k1μa) is linearly proportional to the optical absorption coefficient. With an elevated μa, the increases of APA will gradually approach an asymptotic limit, αF0k1/k2λc; thus, the PA saturation limit is defined as the value of the optical absorption coefficient when the reduction of APA reaches 1/e of the asymptotic limit. Such a saturation condition is fulfilled when μa = 1/k2λc, which is linearly proportional to the cutoff frequency of the ultrasound detector. Therefore, detectors with larger bandwidth can better quantify samples with high-absorption coefficients.

To quantify the PA saturation limit of our MRR ultrasonic detector, a plastic tube filled with black ink was used to mimic a blood vessel for PA measurements43. Black ink with gradually increased concentrations created a variation in μa. Besides the MRR detector, four piezoelectric transducers with different center frequencies (10 MHz, 15 MHz, 20 MHz, and 40 MHz) were also used for comparison. Fig. 4 shows that the experimentally measured saturation curves are in good agreement with the theoretical model for the five different ultrasonic detectors. As expected, the broadband MRR detector exhibits a higher saturation limit and enables functional PAM imaging with wider linear response range for quantitative analysis of optical absorption properties.

Figure 4. Comparison of PA saturation limits of the MRR ultrasonic detector (black star) and four commercial piezoelectric transducers.

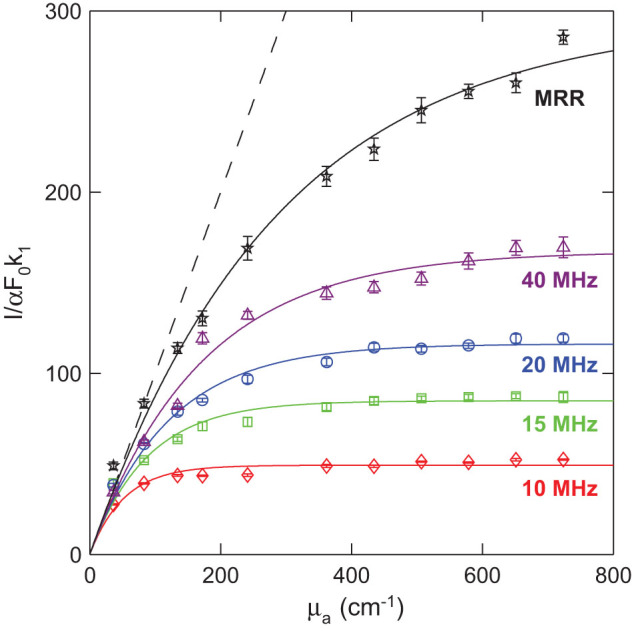
Figure 4

Open in a new tab

The center frequencies of the piezoelectric transducers are 10 MHz (red diamond), 15 MHz (green square), 20 MHz (blue circle), and 40 MHz (purple triangle). The solid lines are respectively fitted curves from their corresponding experimental data. The black dash line is the ideal linear PA response from the theoretical model with no frequency cutoff. The saturation limits for 10-MHz, 15- MHz, 20- MHz and 40-MHz transducers are 58 cm−1, 91 cm−1, 125 cm−1, and 173 cm−1, respectively. The saturation limit of MRR is higher than 287 cm−1, which is about two-fold improved from the 40-MHz piezoelectric detector.

We characterized the MRR detector's angular-dependent frequency response by linearly translating the MRR detector horizontally for 1.5 mm with respect to a stationary PA point source. A carbon black thin film was placed 1.9 mm underneath the MRR ultrasonic detector to create a PA point source when illuminated by focused laser pulses. The time-resolved PA signals are mapped in Fig. 5a according to their corresponding lateral displacements with respect to the PA point source. The angular-dependent frequency response from 10 MHz to 120 MHz is illustrated in Fig. 5b by taking the Fourier transform of the waveforms shown in Fig. 5a. The intensity was normalized to its peak value for every frequency for clarity. The black lines are the 3-dB cut-off line calculated from Eq. 6. The experimental data fits well with the theoretical estimation.

Figure 5. Angular dependence of the frequency response of the MRR ultrasonic detector.

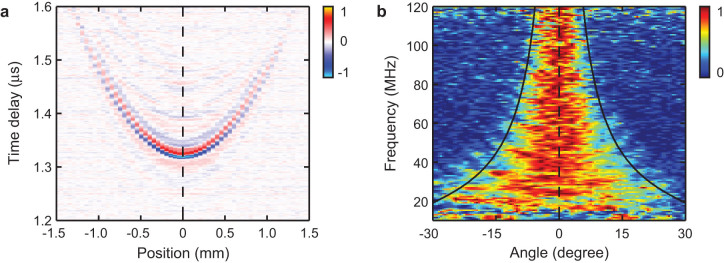
Figure 5

Open in a new tab

(a) Time-resolved PA signals with respective to the positions of the PA point source. (b) Normalized angular dependence of frequency response obtained by Fourier transfer of the PA signals in panel (a). The black lines are the FWHM angular-dependent sensitivity calculated from the theoretical model.

High-frequency components in the PA signal are essential in achieving a high-axial resolution in PAM. In laser-scanning PAM, the detected PA signal amplitude and the imaging FOV highly depend on the angular detection range45. One should notice the angular detection range is inversely proportional to the detection bandwidth. In this particular case, an MRR detector with a ring diameter of 60 μm exhibits a ±4.9 degree angular-detection range at a detection bandwidth from DC to 140 MHz. If an MRR detector is placed 1.6 mm away from the sample, the corresponding FOV will have the diameter of 0.27 mm, which is sufficiently large for a high-magnification, long working distance objective lens. For example, a 100× objective lens with an NA of 0.8 and a working distance of 2 mm provides an FOV of 0.26 mm in diameter.

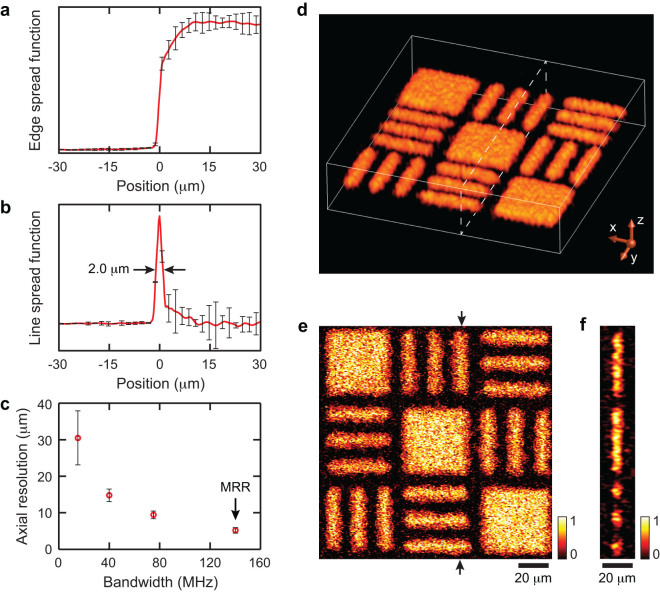
Taking advantage of the broadband MRR detector, we further achieved high-axial resolution volumetric PAM imaging and quantified its voxel size by imaging a fabricated carbon black thin film target (see Methods and Supplementary Information for fabrication details and SEM images). To quantify the lateral resolution, we obtained the edge-spread-function (ESF, Fig. 6a) by imaging an edge of the target (as highlighted in Fig. S2b). We then calculated the corresponding line-spread-function (LSF, Fig. 6b) by taking the first derivative of the ESF. The LSF suggests a lateral resolution of 2.0 μm, which agrees with the theoretical diffraction-limited resolution at NA = 0.25. The axial resolution was estimated from the time-resolved PA A-line signal using a “shift and sum” method45,55. The axial resolutions of three commercial piezoelectric transducers with different bandwidths and the MRR detector are plotted in Fig. 6c for comparison. Using the MRR detector, we reached an axial resolution of 5.3 μm, which shows a nearly two-fold improvement over the piezoelectric transducer with a center frequency of 75 MHz. Fig. 6d shows the 3D visualization of the PA image from the target. Its maximum amplitude projection (MAP) image in the x-y plane and a cross-sectional image along the highlighted plane are shown in Fig. 6e and 6f, respectively. In the MAP image, the 8-micron-wide feature in the target can be clearly resolved. The cross-sectional image shows that the mean imaged full-width-half-maximum (FWHM) thickness of the thin film is 7.6 μm, which is reasonable when accounting for the actual 1.5-μm thickness of the carbon black film and the 5.3-μm axial resolution.

Figure 6. The lateral and axial resolutions of the MRR-based PAM system and volumetric imaging of a carbon-black thin-film target.

Figure 6

Open in a new tab

(a) Experimentally obtained ESF. (b) Calculated LSF from the ESF to quantify lateral resolution. Error-bars were calculated from 128 data sets. The lateral resolution is estimated to be 2.0 μm. (c) Axial resolutions of three commercial piezoelectric transducers with different center frequencies: 15 MHz (P15), 40 MHz (P40), and 75 MHz (P75), and the MRR ultrasonic detector. Error-bars were calculated from 20 measurements. (d) Volumetric visualization of the imaged target. (e) The MAP image of the target along the x-y plane. (f) A cross-sectional image of the target at the position highlighted by the dashed box in the panel (d) and the arrows in the panel (e).

The transparent “coverslip” MRR detector demonstrated here offers significant improvement in both lateral and axial resolutions. The lateral resolution is determined by the focal spot size of the laser excitation and can be improved by using high-NA objective lenses or reducing the optical excitation wavelength; however, high-NA objective lenses have a very limited working distance, which imposes challenges to PAM using piezoelectric transducers unless a transmission scheme is used. The thin transparent detector can easily fit into the tight working distance between the samples and objective lenses and, thus, permits the use of high-NA objective lenses to dramatically improve PAM's lateral resolution. On the other hand, the MRR detector can be optimized to provide sufficiently large detection bandwidth to improve PAM's axial resolution. Ultimately, using the MRR, PAM will be able to provide isometric voxels in volumetric imaging, which greatly simplifies the spatial image registrations with other imaging modalities such as confocal microscopy and two-photon microscopy. One should note, however, that the imaging depth will be sacrificed due to the strong frequency-dependent ultrasonic attenuation when the ultrasonic frequency is too high (such as ~100 MHz); as a result, the high-axial resolution needed for producing isometric voxel can only be maintained within a limited depth comparable to one optical transport mean free path. Although this depth constraint does not prohibit the application of MRR to high-resolution isometric PAM, the clinical applications are limited to optically thin tissues such as ophthalmic imaging of the retina and endoscopic imaging of endothelium layers. In addition, the angular sensitivity distribution of MRR is frequency-dependent. High axial resolution can be better maintained within the central zone of the FOV and gradually reduce towards the peripheral of the FOV, as shown in the Figure 5b. Although, isometric voxel cannot be achieved within a large FOV when high-NA objective lenses are used, it is nevertheless possible for a lower-NA imaging system such as retinal imaging18,56. Finally, the sub-millimeter-sized MRR offers opportunities to miniaturize the PAM system to fit, for example, into small catheters for endoscopic applications.

Conclusion

In summary, a miniaturized, optically transparent, “coverslip”-type ultrasonic detector based on polymeric MRR was fabricated and systematically characterized. We demonstrated that the device has a high sensitivity, a low NEP, a larger sensitivity angle, and an ultra-broad linear frequency bandwidth from DC to 140 MHz. Such a performance led to a great improvement in axial resolution and a much higher PA saturation limit for functional PAM. To further enhance imaging performance, better sensitivity of the MRR detector can be obtained by using relatively softer materials to increase the pressure-induced effective RI change of the waveguide and increase the Q-factor of the MRR. The latter can be improved by using materials with a lower optical absorption coefficient to reduce the propagation loss, or by introducing onsite reflow technology to smooth the waveguide surface and hence suppress the scattering loss41.

The potential to conveniently employ this transparent MRR detector with a broad range of well-established imaging modalities, such as confocal fluorescence microscopy, optical coherence tomography, and miniaturized fiber optic endoscopy, may lead to increased applications for PAM for cancer research, neuroscience, and ophthalmology. MRR also can be mass-manufactured and potentially fabricated on various substrates, including flexible plastic film. MRR offers a promise for flexible and disposable ultrasonic detectors, which is highly desired in endoscopy and ophthalmoscopy56.

Methods

Fabrication of a cover-slip-type MRR ultrasound detector

The optically transparent MRR ultrasonic detector, which consists of a circular and a matching bus waveguide, was fabricated on a fused quartz coverslip (Ted Pella). The coverslip was pre-cleaned in piranha solution. Then, an 800 nm-thick SU-8 (MicroChem) layer was spin-coated (Laurell WS-650-23) on the coverslip at 800 rpm for 30 seconds. It was further soft-baked on a hot plate at 65°C for 1 min and 95°C for 1 min to evaporate extra solvent. After patterning with an electron beam lithography system (FEI Quanta 600F), the sample was followed by a post-exposure bake process at 65°C for 1 min and 95°C for 1 min, and then immersed in SU-8 developer (MicroChem) for 1 min to dissolve the unexposed region. Finally, the sample was cleaned with isopropyl alcohol and air-dried.

Patterning absorption targets on carbon black thin film

Carbon black (CB) particles with a nominal radius of 50 nm were mixed with photoresist SU-8 in cyclopentanone solvent. The volume fraction of CB is 3%. The mixture was spin-coated on a glass substrate and soft-baked to achieve a thin layer 1.5 μm-thick. The pattern consists of three rows of elements alternately arranged by two sets of bars at right angles and a solid square. Each set of bars consists of three bars separated by an interval equivalent to its width. Each bar has a width of 8 μm and a length of 40 μm. After pattering the targets with electron beam lithography, the sample was further coated with a 1.5 μm SU-8 thin layer for reinforcing the mounting of CB targets.

Author Contributions

C.S. and H.F.Z. initiated and supervised the project. H.L. and B.D. performed the experimental characterizations and theoretical analysis. Z.Z. fabricated the polymeric micro-ring resonators. All authors discussed the results and contributed to the manuscript.

Supplementary Material

Supplementary Information

Supplementary Information

srep04496-s1.doc (539KB, doc)

Acknowledgments

We sincerely acknowledge the generous financial support from the National Institutes of Health grants 1RC4EY021357, 1R01EY019951, and 1R24EY022883 to HFZ, and the National Science Foundation grants CBET-1055379 and CBET-1066776 to HFZ, and CMMI-0955195 and CMMI-0751621 to CS.

References

  1. Wang L. V. & Hu S. Photoacoustic tomography: In vivo imaging from organelles to organs. Science 335, 1458–1462 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Wilson T. & Sheppard C. Theory and Practice of Scanning Optical Microscopy (Academic Press, London, 1984). [Google Scholar]
  3. Denk W., Strickler J. H. & Webb W. W. Two-photon laser scanning fluorescence microscopy. Science 248, 73–76 (1990). [DOI] [PubMed] [Google Scholar]
  4. So P. T. C., Dong C. Y., Masters B. R. & Berland K. M. Two-photon excitation fluorescence microscopy. Annu. Rev. Biomed. Eng. 2, 399–429 (2000). [DOI] [PubMed] [Google Scholar]
  5. Huang D. et al. Optical coherence tomography. Science 254, 1178–1181 (1991). [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Hu S., Maslov K. & Wang L. V. Three-dimensional optical-resolution photoacoustic microscopy. J. Vis. Exp. 3, 2729 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Zhang H. F., Maslov K. & Wang L. V. In vivo imaging of subcutaneous structures using functional photoacoustic microscopy. Nat. Protoc. 2, 797–804 (2007). [DOI] [PubMed] [Google Scholar]
  8. Gao L., Zhang C., Li C. & Wang L. V. Intracellular temperature mapping with fluorescence-assisted photoacoustic-thermometry. Appl. Phys. Lett. 102, 193705 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Yakovlev V. V. et al. Stimulated Raman photoacoustic imaging. Proc. Natl. Acad. Sci. USA 107, 20335–20339 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Zhang H. F., Maslov K., Stoica G. & Wang L. V. Functional photoacoustic microscopy for high-resolution and noninvasive in vivo imaging. Nat. Biotech. 24, 848–851 (2006). [DOI] [PubMed] [Google Scholar]
  11. Jo J., Zhang H., Cheney P. D. & Yang X. Photoacoustic detection of functional responses in the motor cortex of awake behaving monkey during forelimb movement. J. Biomed. Opt. 17, 110503 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Wang H.-W. et al. Lable-free bond-selective imaging by listening to vibrationally excited molecules. Phys. Rev. Lett. 106, 238106 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Xu Z., Zhu Q. & Wang L. V. In vivo photoacoustic tomography of mouse cerebral edema induced by cold injury. J. Biomed. Opt. 16, 066020 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Wang Y. et al. In vivo integrated photoacoustic and confocal microscopy of hemoglobin oxygen saturation and oxygen partial pressure. Opt. Lett. 36, 1029–1031 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Yao J., Maslov K., Zhang Y., Xia Y. & Wang L. V. Label-free oxygen-metabolic photoacoustic microscopy in vivo. J. Biomed. Opt. 16, 076003 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Zhang H. F. et al. Collecting back-reflected photons in photoacoustic microscopy. Opt. Express 18, 1278–1282 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Wang Y. et al. In vivo integrated photoacoustic and confocal microscopy of hemoglobin oxygen saturation and oxygen partial pressure. Opt. Lett. 36, 1029–1031 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Song W. et al. integrating photoacoustic ophthalmoscopy with scanning laser ophthalmoscopy, optical coherence tomography, fluorescein angiography for multimodal retinal imaging platform. J. Biomed. Opt. 17, 061206 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Cai X. et al. Investigation of neovascularization in three-dimensional porous scaffolds in vivo by a combination of multiscale photoacoustic microscopy and optical coherence tomography. Tissue Eng. Part C-Methods 19, 196–204 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Zhang E. Z. et al. Multimodal photoacoustic and optical coherence tomography scanner using an all optical detection scheme for 3D morphological skin imaging. Biomed. Opt. Express 2, 2202–2215 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Yuan Y., Yang S. & Xing D. Preclinical photoacoustic imaging endoscope based on acousto-optic coaxial system using ring transducer array. Opt. Lett. 35, 2266–2268 (2010). [DOI] [PubMed] [Google Scholar]
  22. Kong F. et al. High-resolution photoacoustic imaging with focused laser and ultrasonic beams. Appl. Phys. Lett. 94, 033902–033903 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Janas V. F. & Safari A. Overview of fine scale piezoelectric ceramic/polymer composite processing. J. Am. Ceram. Soc. 78, 2945–2955 (1995). [Google Scholar]
  24. Shung K. K., Cannata J. M. & Zhou Q. F. Piezoelectric materials for high frequency medical imaging applications: A review. J. Electroceram. 19, 141–147 (2007). [Google Scholar]
  25. Rousseau G., Gauthier B., Blouin A. & Monchalin J. P. Non-contact biomedical photoacoustic and ultrasound imaging. J. Biomed. Opt. 12, 061217 (2012). [DOI] [PubMed] [Google Scholar]
  26. Beard P. C., Pérennès F. & Mills T. N. Transduction mechanisms of the Fabry-Perot polymer film sensing concept for wideband ultrasound detection. IEEE Trans. Ultrason., Ferroelectr., Freq. Control 46, 1575–1582 (1999). [DOI] [PubMed] [Google Scholar]
  27. Monchalin J. P., Heon R., Bouchard P. & Padioleau C. Broadband optical detection of ultrasound by optical sideband stripping with a confocal Fabry-Perot. Appl. Phys. Lett. 55, 1612–1614 (1989). [Google Scholar]
  28. Hamilton J. D. & O'Donnell M. High frequency ultrasound imaging with optical arrays. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 45, 216–235 (1998). [DOI] [PubMed] [Google Scholar]
  29. Paltauf G., Schmidt-Kloiber H., Kostli K. P. & Frenz M. Optical method for two-dimensional ultrasonic detection. Appl. Phys. Lett. 75, 1048–1050 (1999). [Google Scholar]
  30. Boneberg J., Briaudeau S., Demirplak Z., Dobler V. & Leiderer P. Two-dimensional pressure measurements with nanosecond time resolution. Appl. Phys. A 69, S557–S560 (1999). [Google Scholar]
  31. Nuster R., Paltauf G. & Burgholzer P. Comparison of surface plasmon resonance devices for acoustic wave detection in liquid. Opt. Express 15, 6087–6095 (2007). [DOI] [PubMed] [Google Scholar]
  32. Schilling A., Yavas O., Bischof J., Boneberg J. & Leiderer P. Absolute pressure measurements on a nanosecond time scale using surface plasmons. Appl. Phys. Lett. 69, 4159–4161 (1996). [Google Scholar]
  33. Wong C.-l., Ho H., Chan K.-S., Wu S.-Y. & Lin C. Application of spectral surface plasmon resonance to gas pressure sensing. Opt. Eng. 44, 124403–124403 (2005). [Google Scholar]
  34. Chow C. M. et al. Broadband optical ultrasound sensor with a unique open-cavity structure. J. Biomed. Opt. 16, 017001 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Yakovlev V. V. et al. ultrasensitive non-resonant detection of ultrasound with plasmonic metamaterials. Adv. Mater. 25, 2351–2356 (2013). [DOI] [PubMed] [Google Scholar]
  36. Wild G. & Hinckley S. Acousto-ultrasonic optical fiber sensors: overview and state-of-the-art. IEEE Sens. J. 8, 1184–1193 (2008). [Google Scholar]
  37. Gallego D., Wang M., Hiltunen J., Myllylä R. & Lamela H. Polymer inverted-rib optical waveguide interferometric sensor for optoacoustic imaging. Proc. SPIE 8223, 822343 (2012). [Google Scholar]
  38. Song Y. J. & Peters K. J. Self-repairing, interferometric waveguide sensor with a large strain range. Appl. Opt. 51, 6886–6895 (2012). [DOI] [PubMed] [Google Scholar]
  39. Chao C. Y., Ashkenazi S., Huang S. W., O'Donnell M. & Guo L. J. High-frequency ultrasound sensors using polymer microring resonators. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 54, 957–965 (2007). [DOI] [PubMed] [Google Scholar]
  40. Xie Z., Chen S.-L., Ling T., Guo L. J., Carson P. L. & Wang X. Pure optical photoacoustic microscopy. Opt. Express 19, 9027–9034 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
  41. Ling T., Chen S.-L. & Guo L. J. Fabrication and characterization of high Q polymer micro-ring resonator and its application as a sensitive ultrasonic detector. Opt. Express 19, 861–869 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
  42. Ling T., Chen S.-L. & Guo L. J. High sensitivity and wide-directivity ultrasound detection using high Q polymer microring resonators. Appl. Phys. Lett. 98, 204103 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
  43. Wang J. et al. Saturation effect in functional photoacoustic imaging. J. Biomed. Opt. 15, 5 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
  44. Blackstock D. T. Fundamentals of Physical Acoustics (Wiley, NewYork, 2000). [Google Scholar]
  45. Xie Z. X., Jiao S. L., Zhang H. F. & Puliafito C. A. Laser-scanning optical-resolution photoacoustic microscopy. Opt. Lett. 34, 1771–1773 (2009). [DOI] [PubMed] [Google Scholar]
  46. Grudinin I. S., Ilchenko V. S. & Maleki L. Ultrahigh optical Q factors of crystalline resonators in the linear regime. Phys. Rev. A 74, 063806 (2006). [Google Scholar]
  47. Govindan V. & Ashkenazi S. Bragg waveguide ultrasound detectors. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 59, 2304–2311 (2012). [DOI] [PubMed] [Google Scholar]
  48. Westerveld W. J. et al. Characterization of a photonic strain sensor in silicon-on-insulator technology. Opt. Lett. 37, 479–481 (2012). [DOI] [PubMed] [Google Scholar]
  49. Sacher W. D. & Poon J. K. S. Dynamics of microring resonator modulators. Opt. Express 16, 15741–15753 (2008). [DOI] [PubMed] [Google Scholar]
  50. Kalli K. & Jackson D. A. Analysis of the dynamic response of a ring resonator to a time-varying input signal. Opt. Lett. 18, 465–467 (1993). [DOI] [PubMed] [Google Scholar]
  51. Alder T., Stöhr A., Heinzelmann R. & Jäger D. High-efficiency fiber-to-chip coupling using low-loss tapered single-mode fiber. IEEE Photonics Technol. Lett. 12, 1016–1018 (2000). [Google Scholar]
  52. Xu M. & Wang L. V. Photoacoustic imaging in biomedicine. Rev. Sci. Instrum. 77, 041101 (2006). [Google Scholar]
  53. http://www.acoustics.co.uk/
  54. Wang L. V. & Wu H.-I. Photoacoustic tomography in Biomedical Optics: Principles and Imaging. (Wiley, 2007).
  55. Zhang C., Maslov K., Yao J. & Wang L. V. In vivo photoacoustic microscopy with 7.6-μm axial resolution using a commercial 125-MHz ultrasonic transducer. J. Biomed. Opt. 17, 116016 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
  56. Jiao S. et al. Photoacoustic ophthalmoscopy for in vivo retinal imaging. Opt. Express 18, 3967–3972 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Information

Supplementary Information

srep04496-s1.doc (539KB, doc)

Articles from Scientific Reports are provided here courtesy of Nature Publishing Group

RESOURCES