Linear and angular control of circular walking in healthy older adults and subjects with cerebellar ataxia

Abstract

Linear and angular control of trunk and leg motion during curvilinear navigation was investigated in subjects with cerebellar ataxia and age-matched control subjects. Subjects walked with eyes open around a 1.2-m circle. The relationship of linear to angular motion was quantified by determining the ratios of trunk linear velocity to trunk angular velocity and foot linear position to foot angular position. Errors in walking radius (the ratio of linear to angular motion) also were quantified continuously during the circular walk. Relative variability of linear and angular measures was compared using coefficients of variation (CoV). Patterns of variability were compared using power spectral analysis for the trunk and auto-covariance analysis for the feet. Errors in radius were significantly increased in patients with cerebellar damage as compared to controls. Cerebellar subjects had significantly larger CoV of feet and trunk in angular, but not linear, motion. Control subjects also showed larger CoV in angular compared to linear motion of the feet and trunk. Angular and linear components of stepping differed in that angular, but not linear, foot placement had a negative correlation from one stride to the next. Thus, walking in a circle was associated with more, and a different type of, variability in angular compared to linear motion. Results are consistent with increased difficulty of, and role of the cerebellum in, control of angular trunk and foot motion for curvilinear locomotion.

Introduction

Understanding the neural control of turning during locomotion is important. Turning is associated with a greater risk of injury when falls occur (Nevitt et al. 1991; Cumming and Klineberg 1994) and measurements of turning discriminate elderly fallers from nonfallers (Dite and Temple 2002). In Parkinson’s Disease, turning is associated with freezing and falling (Stack et al. 2006), and slow turning may occur even when linear gait speed is normal (Zampieri et al. 2010). Why curvilinear locomotion is more challenging is unclear, but may be related to the increased biomechanical challenges of angular than linear locomotion and/or a heightened neural load associated with coordinating linear and angular degrees of freedom.

A valuable framework for understanding the neural control of turning may be obtained by comparing kinematics of circular walking in humans to kinematics of circular motion. In circular motion, the radius of trajectory must equal the ratio of the change in linear position to the corresponding change in angular position and the ratio of linear velocity to angular velocity (Fig. 1a). In comparison, humans navigate a circle using a bi-pedal system that generates pulsatile foot control to continuously move the body. Linear and angular motion must be coordinated within each body segment and across body segments (Duysens et al. 2008; Earhart et al. 2001; Gordon et al. 1995; Courtine and Schieppati 2003).

Fig. 1.

a Circular motion requires a constant radius independent of variability in linear and angular motion. To what extent does variability in linear and angular body segments influence the way humans walk a circle? b Trunk measurements include forward linear velocity, angular trunk velocity, and trunk radius; and c foot measurements include stride length, change in foot angle between strides, and foot radius

Previous studies have shown that measures of radius are valuable in quantifying performance of turns in several populations, including normal subjects and patients with vestibular, cerebellar and Parkinson’s disease (Takei et al. 1996; Takei et al. 1997; Paquette et al. 2011). However, no previous study has described how walking radius is controlled continuously, which is required to produce a desired trajectory. The current study characterizes how radius of the trunk and feet vary continuously throughout a circular walk.

The results of previous studies also showed that rotation of the foot can be adaptively modified independent of stride length by stepping in place on a rotating disk (Weber et al. 1998; Earhart et al. 2001). Similarly, during split-belt treadmill walking, adaptive changes in stride length occur without changes in foot rotation (Reisman et al. 2005). We therefore hypothesized that the nervous system exerts different type of control of linear and angular motion during curvilinear locomotion. The current study compares the extent and pattern of linear and angular variability of the feet and trunk during circular walking.

We also determined the extent to which the cerebellum contributes to the coordination and control of linear and angular motion during locomotion. To examine this, we characterized the control of radius and variability of linear and angular motion in patients with cerebellar ataxia and compared them to age-matched healthy control subjects. Preliminary results of these studies have been reported in abstract form (Melvill Jones et al. 2006; Paquette et al. 2007).

Experimental procedures

Subjects

Nine subjects with a clinical diagnosis of cerebellar ataxia and a control group participated in this experiment. The cerebellar group was on average 61 (10 SD) years in age, 170 (10.1 SD) cm in height, 76 (13 SD) kg in mass, and contained 3 males. The average SARA score (Scale for the Assessment and Rating of Ataxia) for cerebellar subjects was 14.2 (3.2 SD), with an average score of 5.8 (2.1 SD) for stance and gait. These scores indicate that cerebellar subjects had mild-to-moderate ataxia. The pathologies were primarily midline with anterior lobe cerebellar involvement, consistent with balance and gait affected more than limb movements. No abnormal dizziness was present in the cerebellar group. Controls were of similar age, mass, and height to their respective patients. All subjects gave their informed consent prior to being tested using a protocol approved by the Institutional Review Board at Oregon Health & Science University.

Protocol

The protocol was described previously in detail (Paquette et al. 2011). Briefly, subjects walked with arms folded around a circle of approximately 1.2 m radius. After walking in a complete circle in one direction, subjects turned around and walked in a complete circle in the opposite direction. This sequence was repeated five times for each subject, first with eyes open and then with eyes closed. For each subject, all gait variables were averaged across circular walks. A circle with radius of 1.2 m was taped on the floor for guidance. After subjects examined the tape on the floor, they were instructed to look forward and not to focus attention on the tape. Control subjects first completed one set of tests walking at a self-selected velocity where walking speed and cadence were measured with a stopwatch. Because many gait parameters are related to gait speed, control subjects completed a second set of tests in which they were instructed to slow down their walking speed and cadence by a specific amount to approximate their matched cerebellar subject counterpart; see Table 1 for comparison between groups. Subjects were coached orally to ‘slow down’ or ‘speed up’ their stepping after each circle was completed. Data in this study were taken from the matched walking speed (to highlight the influence of cerebellar ataxia), eyes-open, waking in a clockwise direction (left foot outside).

Table 1.

Summary kinematics of mean subject (SD)

Group	Velocity (m/s)	Cadence stride/s	Outside ΔLFOOT (cm)	Inside ΔLFOOT (cm)	(Outside ΔLFOOT)/(Inside ΔLFOOT)	Outside ΔθFOOT (deg)	Inside ΔθFOOT (deg)	(Outside ΔθFOOT)/(Inside ΔθFOOT)	RTRUNK (cm)	Outside RFOOT (cm)	Inside RFOOT (cm)
Control	0.69 (0.11)	0.78 (0.12)	91* (15)	81* (12)	1.1 (0.027)	40* (6.0)	40* (6.1)	1.0 (0.024)	122 (6.0)	134* (5.1)	119 (3.8)
Cerebellar	0.64 (0.07)	0.87 (0.06)	79* (8.2)	68* (8.8)	1.2 (0.058)	34* (4.3)	34* (4.5)	1.0 (0.022)	126 (8.9)	142* (9.5)	125 (14)

^*Denotes significant difference in measurement between cerebellar and control group

Data collection and analysis

Kinematic measures of each foot were obtained from reflectors placed over the second metatarsal heads, calcanei, and acromio-clavicular joints. Reflector locations were measured with an eight-camera Motion Analysis system (Santa Rosa, CA, USA) with data sampling at 60 Hz. Results are presented only for “steady-state” steps. Steady-state steps did not include the first and last step of each foot because transient motor programs associated with acceleration and deceleration during gait initiation and stopping, respectively, was not a focus of this study. The beginning and end of the steady-state period was determined with foot strikes. Foot strike was defined as the first point in time when the foot velocity was zero while approaching the floor. Midpoint of the foot waveforms were obtained by averaging time series of the second metatarsal head and calcaneus.

Trunk kinematics

For trunk kinematics in the horizontal plane, the mid-point of the trunk was defined as the point halfway between the acromio-clavicular joints. V_TRUNK is the forward velocity of the mid-point of the trunk (Fig. 1b). Ω_TRUNK is the angular velocity of the mid-point of the trunk with respect to the center of the circle. R_TRUNK was defined as the ratio of V_TRUNK to Ω_TRUNK calculated at every sampled data point (Paquette et al. 2011) and represents the instantaneous trunk radius outputted by participants.

R_TRUNK is based on the components of trunk velocity because the trunk may be viewed as being under velocity control (Osaki et al. 2007) as trunk velocity is fairly constant during natural walking. R_TRUNK reflects the coordination of V_TRUNK and Ω_TRUNK. A constant R_TRUNK value at all times indicates that linear to angular trunk motion was coordinated to walk in a perfect circle, independent of variability in V_TRUNK and Ω_TRUNK. Deviations from a constant R_TRUNK were considered a measure of performance and were quantified as the percent error between R_TRUNK and the mean R_TRUNK across steady-state steps for each test condition. Because V_TRUNK and Ω_TRUNK measures had different units, coefficients of variation (CoV) were calculated to describe their relative variability.

We incorporated a frequency domain analysis of trunk kinematics to describe how spectral power was distributed across frequencies for R_TRUNK, Ω_TRUNK, and V_TRUNK. Comparing power spectra between V_TRUNK and Ω_TRUNK enabled us to quantify the pattern of variability of linear and angular trunk motion. Comparing power spectra between the cerebellar and control group was used to determine if damage to the cerebellum would influence trunk variability at specific frequencies or equally across all frequencies. Quantifying frequency-specific changes in variability gives insight into neural control of circular walking because foot motion during walking contains power at harmonics of the stride frequency (Kavanagh et al. 2005; and Fig. 4a). Thus, when regular patterns of stepping occurred, power at harmonics of the stride frequency in R_TRUNK, Ω_TRUNK, and V_TRUNK was closely related to the mechanical influences of stepping while power contained at frequencies other than the stride and stepping frequencies was related to neural processes associated with coordination and navigation of the circle.

Fig. 4.

a Sample time series of foot and zero-mean trunk velocity from one control and cerebellar subject and corresponding amplitude spectra. b Power spectra averaged across subjects were calculated at specific frequencies (F_stride and F_step) and summed across other frequencies (F_low, F_mid, F_high); and expressed as a percentage of the total power contained within the zero-mean time series. For clarity, only the upper 95 % confidence intervals are included

To obtain power spectra, discrete Fourier transforms (Bendat and Piersol 2000) were applied to the zero-meaned velocity waveforms of R_TRUNK, Ω_TRUNK, and V_TRUNK evaluated at multiples of the fundamental frequency (1/time of steady-state stepping) up to 7.5 Hz. Fundamental frequencies were on average 0.11 Hz for the cerebellar group and 0.12 Hz for the control group. Each subject had a different fundamental frequency because cadence and number of steps was not rigidly controlled in the experiments. Therefore, for each subject, power spectra were first evaluated or summed according to the criteria illustrated in Fig. 4a top right panel: below stride frequency (F_low), at stride frequency (=F_stride), between stride and stepping frequency (F_mid), at stepping frequency (=F_step), and above stepping frequency (F_high). Then, for each frequency range, the summation of power was expressed as a percent of the total power across all frequencies, and was then averaged across subjects.

Feet kinematics

Kinematic measures of the feet were also analyzed to describe coordination of foot position throughout the circular walk. For foot kinematics in the horizontal plane, variables of interest included stride length (ΔL_FOOT), change in foot rotation angle between strides (Δθ_FOOT), and foot radius (R_FOOT). ΔL_FOOT was calculated at each stride and defined as the Euclidian distance between adjacent strides measured at the mid-point of the foot (Fig. 1c). Δθ_FOOT was calculated by first constructing a line between the calcaneus and second metatarsal head, then extending the construction line each time a foot was stationary on the floor (i.e., when both reflector markers on the foot where stationary), and finally defining Δθ_FOOT as the angle inscribed by adjacent extended constructed lines. A Δθ_FOOT value of zero indicates that foot angle did not change from one step to the next. R_FOOT was calculated at each step according to the geometric equation $R_{\text{FOOT}}=\mathrm{\Delta }{\mathrm{L}}_{\text{FOOT}}/(2·sin(\mathrm{\Delta }{\theta }_{\text{FOOT}}/2))$. R_FOOT is based on foot position because swing phase can be viewed as being under position control (Osaki et al. 2007); where control of foot position is needed to maintain an adequate base of support for balance and body propulsion. Similar to trunk radius, R_FOOT reflects the coordination between angular and linear control of foot motion. Performance in foot control was quantified through deviations from a constant R_FOOT, and expressed as the percentage error between R_FOOT and the average R_FOOT across steady-state strides.

To describe relative variability, CoV was calculated for ΔL_FOOT and Δθ_FOOT. To describe the pattern of variability in R_FOOT, ΔL_FOOT, and Δθ_FOOT, an unbiased auto-covariance (scaled to be between −1 and 1) was calculated for R_FOOT, ΔL_FOOT, and Δθ_FOOT for each test. The auto-covariance indicated the extent to which each foot kinematic measure was correlated with itself from one stride to the next. Comparing auto-covariance of R_FOOT between subject groups enabled us to determine if damage to the cerebellum influenced the way the cerebellar group compensated for deviations in R_FOOT; and thus gave insight into the neural control of foot position when stepping around a circle. Comparing the auto-covariance between ΔL_FOOT and Δθ_FOOT enabled us to compare patterns of variability between linear and angular motion.

Average stance width during each circular walk was determined by fitting the equation of a circle to the midpoint of each foot in the horizontal plane. Stance width was defined as the difference between the outside and inside foot radius derived from the fit to the circular equation.

Statistics

For each gait variable, a separate statistical test was performed. Independent samples t tests were used to compare each variable between control and cerebellar subjects. Paired t tests were used to compare CoV between linear to angular variables within each subject group. Statistical tests were performed with JMP SAS software (Carey, NC, USA). 95 % confidence intervals were calculated on normalized power spectra using 1,000 bootstrap samples (Zoubir and Boashash 1998). Linear regression was used to determine the relationship (1) between clinical SARA scores and the CoV of each variable and errors in radius and (2) between stance width and the CoV of each variable and errors in radius. In all statistical measures, significance levels were set to P <0.05.

Results

Summary kinematic measures

Table 1 provides the mean values and standard deviations of kinematic measurements for each group. Cerebellar and control subjects had similar walking velocities, but cerebellar subjects had ~15 % shorter ΔL_FOOT (P = 0.019 inside and P = 0.036 outside) and Δθ_FOOT (P = 0.018 inside and P = 0.015 outside), and 1.06 times larger outside R_FOOT (P = 0.034) compared to the control group. For both groups, outside ΔL_FOOT/inside ΔL_FOOT was 1.1–1.2 and outside Δθ_FOOT/inside Δθ_FOOT was 1.0. Consequently, outside R_FOOT was on average 1.13 times larger than inside R_FOOT. Mean R_TRUNK was similar to the radius of tape on the floor (1.2 m) for both groups and was between the outside and inside R_FOOT.

Deviations in trunk and foot radius

Figure 2a shows representative records of the continuously varying R_TRUNK and R_FOOT from one control subject and one cerebellar subject. As illustrated in Fig. 2b, the cerebellar group had significantly larger errors of trunk and foot radius compared to controls. Compared to controls, the cerebellar group had 1.5 times the error in R_TRUNK (P = 0.007), 2.1 times the error in inside R_FOOT (P = 0.0003), and 1.7 times the error in outside R_FOOT (P = 0.003). For all subjects, R_TRUNK error was significantly less than R_FOOT error.

Fig. 2.

a Sample trunk and outside foot radius of one control and one cerebellar subject. Line at 120 cm represents the radius marked on floor. b Summary of radius error averaged across subjects (±1 SD). *Significant difference between subject groups

Variability in linear and angular motion

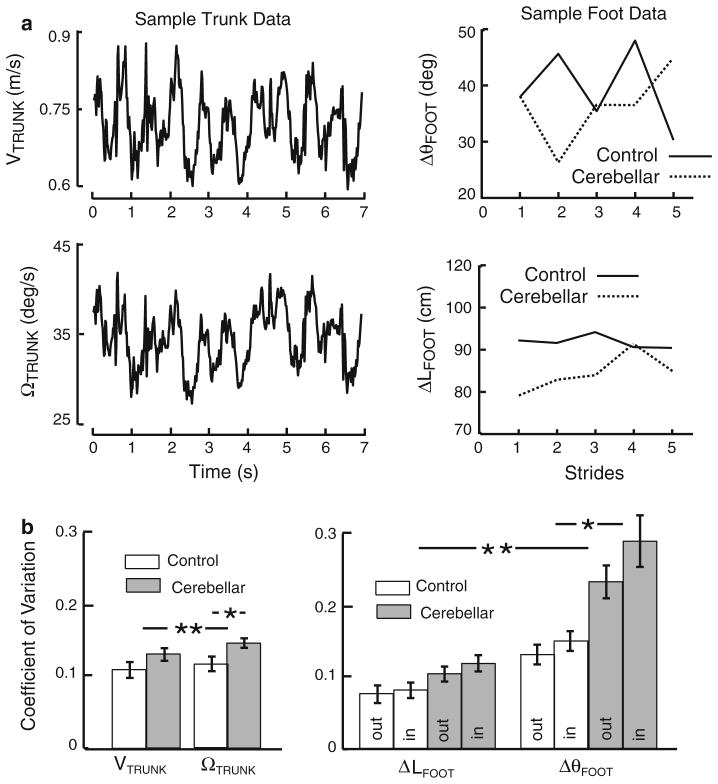
Figure 3a shows representative examples of the linear and angular trunk velocities of one control subject and the linear and angular changes in foot position per stride of one control subject and one cerebellar subject. Linear and angular velocities of the trunk fluctuated rhythmically about the mean linear and angular velocity. Mean linear and angular velocities remained fairly constant throughout the steady-state steps. The change in angular foot position per stride (Δθ_FOOT) exhibited larger variation than that of linear foot position (ΔL_FOOT). Δθ_FOOT exhibited an “up–down,” or “saw-tooth,” pattern whereas ΔL_FOOT exhibited more random variation across strides. Figure 3b shows that for both groups, CoV of the angular measurements were significantly greater than that of corresponding linear measurements. The left panel shows that averaged across both groups, CoV of Ω_TRUNK was 10 % larger than V_TRUNK (P = 0.0016 for the control group and P = 0.0024 for the cerebellar group) and right panel shows CoV of Δθ_FOOT was about twice as large as ΔL_FOOT (P <0.0001 for the control group and P <0.0001 for the cerebellar group, across inside and outside feet).

Fig. 3.

a Sample time series of linear and angular trunk velocities for one control subject and outside foot change in position of one control and one cerebellar. b Coefficient of variation (CoV) for trunk and feet measurements averaged across subjects (±1 SE). *Significant difference in CoV between the cerebellar and control groups. **Significant difference between linear and angular measures for both subject groups

The cerebellar group also showed significantly greater variation of angular, but not linear, CoV compared to those of controls. The cerebellar group’s CoV of Ω_TRUNK was 1.24 times larger (P = 0.04) and Δθ_FOOT was 1.86 times larger (P = 0.0005) compared to the control group. Thus, the significant increase in variability in cerebellar subjects’ radius errors was accompanied by increases in CoV of angular trunk and feet measurements.

Patterns of trunk kinematics

Trunk kinematics was characterized through frequency domain analyses. Figure 4a shows sample time series and amplitude spectra for the outside foot velocity and V_TRUNK from a control subject and a cerebellar subject. The foot velocity time series resulted in an amplitude spectrum that primarily contained power at the stride and stepping frequencies (F_stride and F_step). However, the cerebellar subject exhibited a greater spread in amplitude across frequencies. The control subject’s V_TRUNK sample time series showed large oscillations at the stepping frequency (F_step). Consequently, the amplitude spectrum of V_TRUNK contained most power at F_step. In contrast, the cerebellar subject showed a larger spread in V_TRUNK amplitude across frequencies.

Amplitude spectra were used to calculate the normalized power spectra shown in Fig. 4b for all subjects and continuous measures. In the control group (left panel), V_TRUNK, Ω_TRUNK, and R_TRUNK waveforms exhibited unique variation as a function of frequency. At low frequencies (F_low and F_stride), the relative power in R_TRUNK was>Ω_TRUNK >V_TRUNK. At higher frequencies (F_step and F_high), this pattern was reversed; that is, relative power in V_TRUNK was >Ω_TRUNK >R_TRUNK. Thus, the frequencies at which power was concentrated differed across linear trunk velocity, angular trunk velocity, and trunk radius.

In control group, more power of trunk linear velocity was concentrated at F_step than any other single frequency or frequency band; meaning that the changes in forward trunk velocity were primarily associated with stepping. Power in Ω_TRUNK was equally distributed across F_step and F_stride, and contained a larger percentage of power at the lowest frequency band compared to V_TRUNK. Power in R_TRUNK was concentrated at the lowest bandwidth and at F_stride (approximately 80 % of all power ≤F_stride). This result indicates that subjects coordinated their linear (V_TRUNK) and angular (Ω_TRUNK) trunk velocity such that variation in R_TRUNK was contained at and below the stride frequency.

The cerebellar group (Fig. 4b right panel) exhibited different power distribution across frequencies compared to controls. Specifically, differences across V_TRUNK, Ω_TRUNK, and R_TRUNK were much less pronounced in cerebellar compared to control subjects. The cerebellar group had most power in the lowest frequency band and approximately equal power distributed across the remaining frequency spectrum. This exaggerated power at low frequencies was accompanied by foot velocity power that was distributed across more frequencies compared to controls. About 80 % of the foot velocity power was contained at F_stride and F_step in cerebellar subjects compared to over 90 % in control subjects. Thus, the cerebellar subjects showed frequency specific changes in trunk variability accompanied by changes in stepping dynamics.

Patterns of feet kinematics

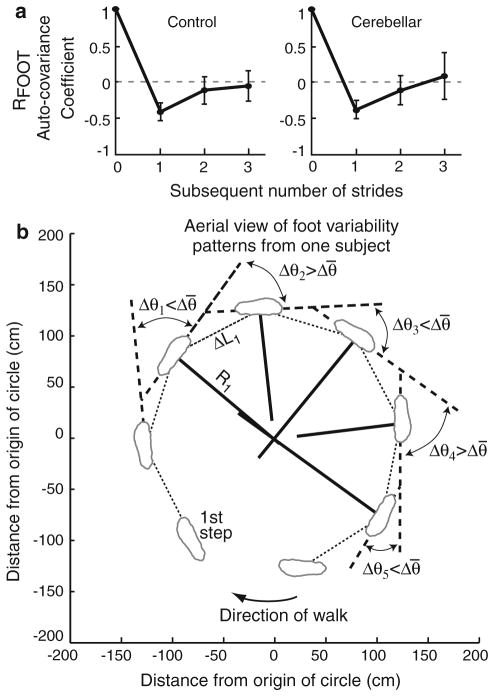
Patterns of feet kinematics were analyzed using auto-covariance of Δθ_FOOT, ΔL_FOOT, and R_FOOT. Figure 5a shows auto-covariance measures with ±1SD across subjects for the inside R_FOOT. Patterns were similar between feet. The auto-covariance of R_FOOT was equal to ~−0.35 to −0.45 at one subsequent stride, and approached zero at two and three subsequent strides. The negative auto-covariance at one subsequent stride means there was a negative correlation in foot radius from one stride to the next. In other words, subjects’ stride radius alternated between being greater than, then being less than, the mean R_FOOT; but R_FOOT was not correlated with itself beyond one stride.

Fig. 5.

a Mean subject (±1 SD across subjects) auto-covariance of inside foot radius (R_FOOT) exhibited a negative covariance at the first subsequent stride. b Aerial view of data taken from one sample subject’s outside foot. Δθ₁–Δθ₅ are the change in foot angle for five gait cycles, Δθ̄ is the mean change in foot angle, ΔL₁ is the first stride length, and R₁ is the first foot radius. The sample subject took fewer steps than most subjects

Patterns of Δθ_FOOT were similar to R_FOOT in both subject groups (data not shown). At one subsequent stride, the Δθ_FOOT auto-covariance was negative and approached zero at two and three subsequent strides (−0.35 ± 0.15 SD at one, −0.12 ± 0.24 SD at two, and −0.03 ± 0.26 SD at three strides, averaged between inside and outside feet and across all subjects).

In contrast, ΔL_FOOT exhibited a different pattern of variation. ΔL_FOOT did not exhibit a negative auto-covariance at one subsequent stride, but was approximately zero at one, two, and three subsequent strides (−0.02 ± 0.22 SD at one stride, −0.14 ± 0.21 SD at two strides, and −0.15 ± 0.24 SD at three strides, averaged between inside and outside feet and across all subjects).

Differences between linear and angular foot motion can be seen in the sample data in Fig. 3a where Δθ_FOOT exhibited an up-and-down pattern at each step while ΔL_FOOT varied in a more random fashion. The relationship across Δθ_FOOT, ΔL_FOOT, and R_FOOT can be visualized in Fig. 5b, which shows an aerial view of one representative control subject.

Clinical correlations

Correlations between clinical SARA scores and each variable in Figs. 2b and 3b (i.e., radius errors in R_TRUNK and R_FOOT and CoV of ΔL_FOOT, Δθ_FOOT, V_TRUNK, and Ω_TRUNK) were computed for the cerebellar group. No variables were significantly correlated with SARA scores. Correlations were also computed between stance width and each variable in Figs. 2b and 3b. There was a significant positive correlation with stance width and CoV of Ω_TRUNK (P = 0.029, R = 0.72) and CoV of inside ΔL_FOOT (P = 0.049, R = 0.67). When each subject’s stance width was normalized by their height (McIlroy and Maki 1997), only CoV of Ω_TRUNK was significantly correlated with stance width (P = 0.034, R = 0.71). Stance width was on average 18.8 cm (5.4 SD) in the cerebellar group and 14.7 cm (2.1 SD) in the control group.

Discussion

Role of neural structures in circular walking

The main finding of this study was that patients with cerebellar ataxia had elevated radius errors in both trunk and feet. Thus, in these experiments the cerebellum contributed to consistent foot and trunk motion during circular walking as seen in other tasks (Morton and Bastian 2006). The reduced ability of cerebellar subjects to make normal radius error corrections is consistent with the loss of effect of prior experience on the size of postural responses and the loss of curvilinear walking with eyes closed after exposure to a rotating treadmill (Horak and Diener 1994; Timmann and Horak 1997; Earhart et al. 2002).

It was also found that CoV in angular (Δθ_FOOT and Ω_TRUNK), but not linear (ΔL_FOOT and V_TRUNK), trunk and foot motion was significantly elevated in cerebellar subjects (Fig. 3b). This result is consistent with a role of the cerebellum in controlling angular motion during circular walking, but future studies are needed to determine if cerebellar gait is degraded to a greater extent as more angular motion is required.

Subjects with cerebellar gait disorders exhibited unique trunk power spectra compared to controls where the cerebellar subjects’ gait ataxia included larger trunk variability concentrated at lower frequencies with smaller variability at the stride and stepping frequencies compared to controls, Fig. 4b. The underlying cause of this frequency-dependent change in trunk variability could be linked to the frequency-dependent changes in stepping dynamics (lower power at F_stride and F_step in cerebellar subjects) or to neural processes associated with navigating the circle.

In the current study, walking speeds were matched to highlight the effects of cerebellar ataxia. It is anticipated that similar (or greater) differences between patient and control groups would be found at self-selected speeds because previous studies showed either no difference (Frenkel-Toledo et al. 2005) or decreased variability (Beauchet et al. 2009) in certain gait parameters with self-selected walking speeds in healthy populations.

The lack of correlation between SARA scores and variables in Figs. 2b and 3b (radius errors in R_TRUNK and R_FOOT and CoV of ΔL_FOOT, Δθ_FOOT, V_TRUNK, and Ω_TRUNK) suggest that these measures of linear, angular, and radius may offer different insight into neural control in cerebellar patients compared to clinical SARA scores. The significant correlation between stance width and CoV of Ω_TRUNK was also accompanied by positive correlations between stance width and CoV of R_TRUNK (R = 0.6) and between stance width and CoV of V_TRUNK (R = 0.57). Increasing stance width may permit larger trunk motion because the center of mass can travel further away from upright before reaching the base of support. Cerebellar subjects with a wider stance may have prioritized balance control over navigation accuracy. In general, balance control during curvilinear walking is different than straight-ahead and requires coordination between linear and angular motion. For example, previous studies showed that healthy subjects tilt inward during curvilinear walking, and this inward tilt increases when linear speed increases (Courtine and Schieppati 2003; Orendurff et al. 2006) and when radius of curvature decreases (Courtine and Schieppati 2003).

Control of linear and angular motion

Linear and angular trunk and feet motion exhibited different relative variability and different patterns of variability. Angular CoV was significantly larger than linear CoV in the trunk and feet (Fig. 3b), similar to straight-ahead locomotion (Stolze et al. 2000). In the current study, angular control of foot placement involved a stride-by-stride correction such that alternating strides were a bit larger or smaller than average foot radius, consistent with a stride-by-stride correction of trajectory. In contrast, linear stride trajectory did not show a systematic alteration of stride length. The different patterns of variability in foot rotation and stride length were consistent with previous studies indicating that the foot-to-trunk rotation system is adapted independently of stride length (Weber et al. 1998; Earhart et al. 2001) and that adaptive changes in step length are modified independent of foot rotation (Reisman et al. 2005).

The differences in linear and angular motion found in the current study were probably influenced by the dissimilar biomechanics between linear and angular motion, which necessitates different activation of leg and trunk muscles. For example, previous studies showed that motor commands to gastrocnemius and biceps femoris muscles in the leg and erector spinae in the trunk differ between straight-ahead and curvilinear walking (Courtine et al. 2006). Also, angular motion may require a higher level of active neural control and be subject to higher sensorimotor noise (Souman et al. 2009) compared to linear motion because linear motion is largely influenced by gravity and pendulum dynamics (Kuo and Donelan 2010).

The extent to which linear and angular control is independent is not known. However, independent linear and angular control could explain the differences in linear and angular motion observed in the current and previous (Weber et al. 1998; Earhart et al. 2001; Reisman et al. 2005) studies. In the independent control model, during straight-ahead walking, the angular control system’s output to muscles should be actively held at zero. As the radius of curvature decreases, the angular control system’s output could increase in a graded manner to change the body’s trajectory, consistent with the graded modulations previously observed in electromyography during curvilinear, compared to straight-ahead, walking (Courtine et al. 2006). Independent of the trajectory prescribed by outputs in the angular control system, the linear control system could continue to move the body in the sagittal plane (Courtine and Schieppati 2004). Thus, any walking radius could be achieved with the appropriate ratio of linear to angular motor outputs.

Limitations of the study

One study limitation is that subjects were asked to stop walking after one complete revolution to avoid any semicircular canal vestibular habituation. Thus, subjects took a relatively small number of steps for each circular walk (~14–22) and we were not able to investigate the existence of long-term correlations in step length, foot rotation, or foot radius. A second limitation of the study was that we were not able to explore the effect of vision because too many markers were obscured from the cameras in eyes-closed tests due to deviations in walking radius. Finally, only “steady-state” steps were considered. In everyday walking, however, proper initiation and termination of gait are critical to navigation and stability.

Conclusions

The main results of this study are that (1) subjects with cerebellar ataxia exhibited greater trunk and foot radius errors during circular walking in eyes open conditions and (2) linear and angular trunk and feet motion exhibited different overall variability and different patterns of variability when healthy subjects walk in a circular path. These results are consistent with (1) an important role of the cerebellum in coordinating angular locomotion and (2) different neural control of angular and linear motion during curvilinear locomotion.

Abbreviations

ΔL_FOOT

Step length

Δθ_FOOT

Change in foot angle between steps

R_FOOT

Foot radius = ΔL_FOOT/(2 sin(Δθ_FOOT/2))

V_TRUNK

Trunk linear velocity

Ω_TRUNK

Trunk angular velocity

R_TRUNK

Trunk radius = V_TRUNK/Ω_TRUNK

CoV

Coefficient of variation