Size-dependent regulation of dorsal-ventral patterning in the early Drosophila embryo

Abstract

How natural variation in embryo size affects patterning of the Drosophila embryo dorsal-ventral (DV) axis is not known. Here we examined quantitatively the relationship between nuclear distribution of the Dorsal transcription factor, boundary positions for several target genes, and DV axis length. Data were obtained from embryos of a wild-type background as well as from mutant lines inbred to size select embryos of smaller or larger sizes. Our data show that the width of the nuclear Dorsal gradient correlates with DV axis length. In turn, for some genes expressed along the DV axis, the boundary positions correlate closely with nuclear Dorsal levels and with DV axis length; while the expression pattern of others is relatively constant and independent of the width of the Dorsal gradient. In particular, the patterns of snail (sna) and ventral nervous-system defective (vnd) correlate with nuclear Dorsal levels and exhibit scaling to DV length; while the pattern of intermediate neuroblasts defective (ind) remains relatively constant with respect to changes in Dorsal and DV length. However, in mutants that exhibit an abnormal expansion of the Dorsal gradient which fails to scale to DV length, only sna follows the Dorsal distribution and exhibits overexpansion; in contrast, vnd and ind do not overexpand suggesting some additional mechanism acts to refine the dorsal boundaries of these two genes. Thus, our results argue against the idea that the Dorsal gradient works as a global system of relative coordinates along the DV axis and suggest that individual targets respond to changes in embryo size in a gene-specific manner.

INTRODUCTION

Scaling, the ability of gene expression patterns to establish relative to embryonic size, is a widespread property of animal body plans occurring at different levels of cellular organization. Scaling within an animal, for example, has been evidenced by the ability of embryos to reorganize their developmental programs and produce well-proportioned animals after being cut in half or developed under starvation conditions (rev. in De Robertis, 2006; Parker, 2011). On the other hand, scaling across different species of animals is evidenced by the evolutionary explosion of anatomically similar animals that often dramatically differ in size, while presumably employing much of the same genetic circuitry (Carroll, 2008; Prud'homme et al., 2007). For example, the relative position of anterior-posterior (AP) segments in several fruit fly species of the Drosophila genus is very similar, despite large differences in embryo sizes across species (Gregor et al., 2005; Lott et al., 2007). As the position of these segments is thought to be determined by homologous morphogen signals, it was suggested that the rates of morphogen production, transport, and/or degradation may have evolved to support similar patterning outputs across related species to encompass a range of embryo sizes (Gregor et al., 2005).

However, scaling of patterns within a population of embryos of a single species requires a mechanism to ‘estimate’ embryo size and translate positional information into a system of relative coordinates. Scaling of AP patterns that depend on the morphogen Bicoid (Bcd) in the D. melanogaster embryo has been extensively analyzed (de Lachapelle and Bergmann, 2010; Lott et al., 2007; Vakulenko et al., 2009). These studies have established the Drosophila embryo as a model system to study scaling of patterns in a population of embryos in response to natural variations in embryonic size, but little is known about scaling along the dorsal-ventral (DV) axis.

DV patterning in the Drosophila embryo is orchestrated by the maternal factor Dorsal, a Rel-containing transcription factor and NF-κB homolog (rev. in Chopra and Levine, 2009; Reeves and Stathopoulos, 2009). Maternal Dorsal is ubiquitously present in the embryo cytoplasm where it is sequestered by the IκB homolog, Cactus. However, upon activation of the Toll transmembrane receptor in ventral regions of the embryo by its ligand Spätzle, Cactus is targeted for degradation, allowing Dorsal to enter nuclei in a graded fashion (rev. in Moussian and Roth, 2005; Rushlow and Shvartsman, 2012). In the nucleus, Dorsal acts to control differential gene expression in distinct domains along the DV axis in order to define different cell types. Genes expressed along the DV axis include snail (sna) and twist (twi) within the presumptive mesoderm; single-minded (sim) in the presumptive mesectoderm; and ventral nervous system defective (vnd), intermediate neuroblasts defective (ind), and short-gastrulation (sog) within the presumptive neurogenic ectoderm (rev. in Reeves and Stathopoulos, 2009; Stathopoulos and Levine, 2002). The nuclear Dorsal distribution displays a concentration gradient that peaks at the ventral midline and decreases more dorsally, suggesting that Dorsal establishes these patterns in a concentration-dependent manner.

Recently, we investigated the temporal dynamics of the Dorsal gradient and found that the DV patterning genes examined exhibit similarly dynamic expression patterns (Reeves et al., 2012). In contrast, here we examine how DV patterning is spatially established relative to natural variations in the length of the DV axis. We conduct our analysis at late nuclear cycle (nc) 14, where we found that the Dorsal gradient and its target genes are relatively stable (Reeves et al., 2012). The generally accepted view in the field is that morphogen gradients scale to ensure conservation of pattern proportions (Ben-Zvi et al., 2011b). In this study, we show that the Dorsal gradient does correlate with embryo size along the DV axis, but our data also provide evidence that the Dorsal gradient does not work alone to establish a global system of relative coordinates in the Drosophila embryo. Genes expressed along the DV axis exhibit different scaling behaviors that do not always correlate with Dorsal concentration, suggesting that scaling is a gene-specific output that is supported by gene regulatory network interactions.

MATERIALS AND METHODS

Fly stocks

Drosophila melanogaster flies were reared under standard conditions at 25°C. All the measurements on wild-type embryo populations were conducted using embryos of yw background. We used the following inbred size-selected lines to increase the size distribution of our wild-type sample: 9.31.2 (referred to as 9.3) to examine embryos biased toward ‘small’ size, and lines 2.46.2, and 2.15.4 (referred to as 2.4 and 2.1, respectively) to examine embryos biased toward ‘large’ size (Miles et al., 2011). To reduce variability in the data due to technical manipulations, we plotted embryos from a single experiment, defined as embryos that were processed along side each other. In our plots, we only combined embryos of line 2.1 with our wild-type sample, as the other inbred lines display a small percentage of embryos with dramatically expanded Dorsal gradients a phenotype which was never observed in yw embryos and lead us to conclude that these particular inbred lines (i.e. 9.3 and 2.4) may not be normal with regard to scaling. The number of embryos in any single experiment varied as not every embryo that was manually chopped was usable for imaging/data processing; nevertheless, approximately equal numbers of yw and large 2.1 data were combined on plots.

For the mutant analysis, we use the following alleles to make wntD and rho vn mutants: wntD^K01 and rho^ve vn¹ are homozygous viable, every embryo was carrier of the mutant background (Diaz-Benjumea and Garcia-Bellido, 1990; Gordon et al., 2005). For the Decapentaplegic (Dpp) signaling deficient embryos, we used females carrying a maternally-expressed Gal4 driver (Matalpha-Gal4) (Bloomington #7062) to drive expression of a dominant negative form of the TKV receptor (UAS-DN.Tkv) (Haerry et al., 1998). For the capicua (cic) mutants we crossed cic¹/cic² virgin females to cic¹/cic² males (Jimenez et al., 2000; Roch et al., 2002).

Staining procedure and preparation of embryo cross-sections

Embryos were collected 2–4 hours after egg laying and fixed using standard protocols. The fluorescent in situ hybridization (FISH) experiments were conducted according to published methods (Kosman et al., 2004) using riboprobes to detect sna, vnd, and ind transcripts. Proteinase K treatment was omitted. Primary antibodies to Dorsal (Mouse anti-Dorsal, 1:10; Hybridoma Bank Developmental Studies) and Histone3 (H3) (Rabbit anti-H3, 1:5000; Abcam) were used.

Fixed and stained embryos were manually cross-sectioned with a razor blade to remove the anterior and posterior poles of the embryo. The remaining section was roughly a third of the embryo AP length (see Trisnadi et al., 2012). Care was taken to ensure the thickness of the embryo section was not greater than roughly 200 microns by ensuring the thickness was less or equal to the diameter of the dorsal-ventral axis of the embryo. Embryos were imaged using a Zeiss LSM 5 Pascal confocal microscope.

Image analysis

Image analysis was performed according to recently published protocols (Trisnadi et al., 2012), described briefly here. Gene expression was quantified as average values in a sliding window around the periphery of the embryo. Nuclei were detected in the following manner according to previously published methods (Trisnadi et al., 2012). First, the nuclear layer was unrolled into a strip; then a 1D representation to the unrolled nuclear layer was generated; next this 1D representation was used as a first pass to identify boundaries between nuclei using a watershed algorithm. These boundaries were used in the unrolled strip to demarcate rectangular pixel areas that contained a single nucleus. Each nucleus in each rectangular area was identified using a local best-fit threshold protocol (Otsu, 1979). The pixels identified as nuclei in the unrolled strip are then mapped back onto the original image of the nuclei. This results in both an identification of the nuclei to aid in quantifying the Dorsal nuclear gradient (see below), as well as in a count of the number of nuclei per DV slice.

Curve fitting

Gene expression profiles were quantified as described previously (Liberman et al., 2009; Trisnadi et al., 2012). Briefly, for each gene in each embryo, the measured profile of gene expression was fit to an averaged, ‘canonical’ profile (Liberman et al., 2009; Trisnadi et al., 2012). Borders of gene expression patterns were then taken as the location of half-maximal intensity of the canonical gene expression profile. Measurements of the concentration of Dorsal in each nucleus were taken to be the average intensity of the Dorsal image within a nucleus normalized by the average intensity of the nuclear image within the same nucleus (Liberman et al., 2009). Dorsal nuclear gradient profiles were then fit to Gaussian-like curves (Liberman et al., 2009; Reeves et al., 2012).

The number of nuclei in the ind domain for each embryo (Supplementary Fig. 2E,F) was calculated by multiplying the width of the ind domain (in microns) by the embryo’s linear nuclear density (# of nuclei per DV slice/DV axis length).

Statistical analysis

In comparing boundaries of gene expression (y) with respect to embryo size (L), we assumed a linear correlation:

$$y=mL+b$$

In this equation, the parameters m and b are the slope and the y-intercept, respectively, of the linear correlation. We used a simple linear least-squares method to determine the values of m and b for the best-fit line, minimizing:

$$\mathit{\text{objective function}}=\sum _{i=1}^n{(y_i-(m{L}_i+b))}^2$$

In this equation, L_i is the size of embryo i (microns) and y_i is the absolute location of the gene expression border in question for embryo i. In simple linear least squares, both m and b are distributed acccording to the t-distribution. Thus, the p-values for all statistical tests regarding these parameters were calculated accordingly. In particular, if m=0 cannot be rejected with a p-value of 0.05 or less, y was considered uncorrelated to L. Furthermore, using the t-distribution, 68% and 95% confidence intervals (roughly corresponding to ±1 and ±2 standard deviations) on m and b were also calculated to help determine the degree of scaling observed. In particular, if b=0 is contained within the 68% confidence interval of b, allow for the possibility that the correlation is strict scaling. On the other hand, if b=0 is excluded from the 95% confidence interval, we can reject strict scaling with 95% confidence. If b=0 is excluded from the 68% confidence interval, yet included in the 95% confidence interval, the case is undecided. These confidence intervals are depicted graphically as light tan corridors encompassing the plotted best-fit line.

In comparing boundaries of gene expression against the width of the Dorsal nuclear gradient, both measurements in question had a significant degree of uncertainty. Therefore, a measure of total (rather than simple) weighted least-squares was used, in which variations and uncertainties in both directions were used to determine the best-fit line (as opposed to only variations in the vertical coordinate as is the case with simple least squares). In this formulation, the square of the distance from a measured point, (σ_i, y_i) to a point (σ̃_i, ỹ_i) on the best-fit line y = mσ + b, weighted by the uncertainties in the measurements was used as the objective function:

$$\mathit{\text{objective function}}=\sum _{i=1}^n\frac{{({\sigma }_i-{\tilde{\sigma }}_i)}^2}{u_{{\sigma }_i}^2}+\frac{{(y_i-{\tilde{y}}_i)}^2}{u_{yt}^2}$$

In this equation, σ_i is the Dorsal gradient width of embryo i; y_i is the location of the gene expression border in question for embryo i; u_σi,u_yi are the uncertainties of σ_i,y_i, respectively, measured as the radius of the 68% confidence interval on our estimates of these parameters (Trisnadi et al., 2012). The algorithm for minimizing the objective function, subject to the constraints that the points (σ̃_i, ỹ_i) must lie on the best-fit line, can be found in (Krystek and Anton, 2007). In these cases, standard deviations of these parameters were obtained using the analytical solution from (Krystek and Anton, 2007) multiplied by the value of the objective function and divided by n−2. These standard deviations were used in the calculation of t-statistics for these parameters, and p-values were assigned assuming the parameters were t-distributed. Furthermore, as in the case of simple linear least squares, confidence intervals on m and b were computed and plotted as light tan corridors encompassing the best-fit line. These confidence intervals were used to help determine the degree of correlation observed as explained above.

Statistical analysis of the correlation between gene expression pattern width and σ was performed analogously. The R² values for each of the correlations are the square of the Pearson Correlation Coefficient.

RESULTS

The nuclear distribution of Dorsal scales with length of the DV axis

We first measured the variability associated with DV axis length in a laboratory population of Drosophila embryos (yw; referred hereafter as “wild-type”). Using manually cross-sectioned embryos, we defined the DV axis length as the measurement of the cross section semi-circumference at ~50% egg length (see Methods; Fig. 1A). We found that the DV axis ranges from 240 to 278 µm (the 5^th and 95^th percentile of the measured embryo size distribution), which represents a DV axis variability of about 14% [262 µm ±12 µm (mean ± standard deviation); Fig. 1B]. This variability of DV axis length is slightly larger than previous measurements along the AP axis (470.66 ± 16.33 µm) (Lott et al., 2007) where the scaling properties of the Bicoid gradient and its target genes have been investigated (de Lachapelle and Bergmann 2010). We then asked whether or not we could identify trends in the distribution of the Dorsal gradient and DV-expressed genes relative to change in size of the DV axis.

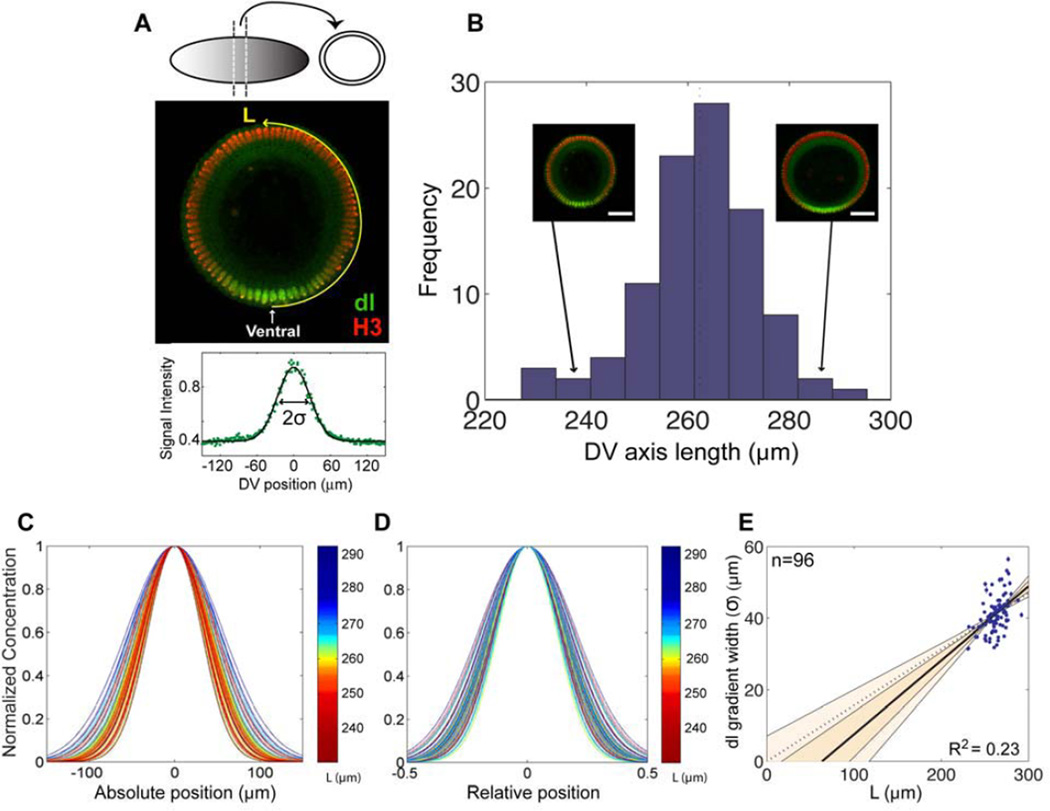
Fig. 1. The Dorsal gradient width correlates with embryo size in a wild-type population of embryos.

(A) Cross sections of yw embryos (referred simply as ‘wild-type’) carefully staged at late nuclear cycle 14 are fluorescently stained with anti-Dorsal (green) and anti-H3 (red) antibodies. The DV axis length, denoted here and throughout the study by L and measured in µm, is defined as the semi-circumference of the cross section. The profile at the bottom shows the signal intensity of nuclear Dorsal plotted in relative DV coordinates and then fitted to a Gaussian function. In all our plots, x=0 is set at the location of the ventral midline. We define the Dorsal gradient width (σ) as half of the width of the Gaussian fitted to the Dorsal profile. (B) Histogram of the distribution of DV axis length in a population of wild-type embryos. Two representative embryos from the tails of the distribution are shown to illustrate the span of the distribution (scale bar=30 µm) (C,D) Normalized Gaussian fits of Dorsal gradients plotted in absolute DV units (C) and relative DV units (D). Each curve comes from a different embryo for the wild-type population shown in B, and is color-coded according to the embryo’s DV axis length. (E) Width of the Dorsal (abbreviated as dl) gradient, a, plotted against the DV axis length, L. Each data point represents an embryo; measurement errors for each embryo are generally very small but are displayed. The solid thick line shows the line approximated by simple regression. The shaded areas delineate the 68% (dark shade) and 95% (light shade) confidence intervals for the slope of the line. The dashed line indicates strict scaling. The number of embryos in the sample, n, and the square of the Pearson coefficient, R², are displayed.

First, we investigated whether these natural variations in DV axis length correspond to relative changes in the distribution of the Dorsal gradient. Our previous studies suggest that the nuclear Dorsal gradient can be reasonably approximated using a Gaussian distribution (Liberman et al., 2009; Reeves et al., 2012). Therefore, we quantified the distribution of the Dorsal nuclear gradient in a population of wild-type embryos carefully staged at late nc 14 (Fig. 1A), and then plotted each Dorsal gradient fit to a Gaussian, color-coded according to the DV length of the respective embryo (Fig. 1C,D). We observed a clear pattern of colors when the Dorsal gradient distributions were compared in absolute units (Fig. 1C), but this pattern disappeared when we plotted the Dorsal gradient distribution in relative units (Fig. 1D). These data suggest a correlation between Dorsal gradient and DV axis length. To identify the specific properties of this correlation we compared the width (σ) of the nuclear Dorsal gradient in each embryo with our measurement of its DV length (L) (Fig. 1E). While a correlation between the Dorsal gradient and DV axis size is apparent from Fig. 1E, the variability in DV axis length was not sufficiently large with respect to the variability in Dorsal gradient width to conclusively identify a scaling trend in this population of embryos. For example, we cannot with 95% confidence exclude a strict scaling behavior, in which the y-intercept is equal to zero (Fig. 1E, dashed black line), due to the fact that the 95% confidence interval is quite wide for these data.

In order to provide more clarity into the specific correlation between the Dorsal gradient width and the DV axis length, we sought to extend the length spread of the DV axis. We chose to take advantage of size-selected Drosophila melanogaster lines derived from wild-caught females that were manually selected over several generations in a previous study to establish stocks biased for embryo size, either ‘small’ (referred as ‘small 9.3’) or ‘large’ [referred as ‘large 2.1’ and ‘large 2.4’; (Miles et al., 2011)]. Although these stocks were originally size-selected using the AP axis length as a measure, we anticipated that a similar bias in size would be apparent along the DV axis. As predicted, these ‘small’ and ‘large’ lines indeed produce embryos with smaller and larger DV axis lengths, respectively, compared to our laboratory population (Fig. 2A).

Fig. 2. Size selected ‘small’ and ‘large’ lines expand size range distribution of embryos providing a better platform for data analysis.

(A) The histogram shows the DV axis length distribution of ‘small 9.3’ (green), wild-type (red), ‘large 2.1’ (blue), and ‘large 2.4’ (pink) embryos. (B). Box-plots of the relative dl width. The orange crosses indicate outliers. Two-sample T-test show that the WT mean is statistically similar to ‘small 9.3’ (p = 0.21) and ‘large 2.1’ (0.44) and statistically different from ‘large 2.4’ (p = 9.3 × 10⁻⁶), p-value greater than 0.05 cannot reject null hypothesis that means are equal. (C) The dl gradient width for ‘small 9.3’ (green), wild-type (red) and ‘large 2.1’ (blue), plotted against DV axis length, L (µm). The dashed line represents strict scaling, the solid black line is the best-fit line to the data. The 68% and 95% confidence intervals are represented in dark and light shading respectively.. The black arrow indicates the outlier present in the small 9.3 line. Error bars for each embryo are displayed although generally small. (D) The dl gradient width for WT (red) and Large 2.1 (blue) from a single experiment, defined as embryos that were processed alongside each other, were plotted against DV axis length. For all plots n is equal to the number of embryos and the R² value is the square of the Pearson coefficient.

Next we interrogated the Dorsal gradient width normalized to DV axis size in embryos from ‘small’ and ‘large’ lines in comparison to embryos from our laboratory population (Fig. 2B). We found that the wild-type, ‘small 9.3,’ and ‘large 2.1’ lines displayed, on average, a statistically similar mean of relative Dorsal gradient widths despite their differences in DV axis range (Fig. 2B). In contrast, the ‘large 2.4’ line displayed a much wider range of Dorsal gradient widths and a statistically greater mean than wild-type (Fig. 2B). Surprisingly, we noted the presence of embryos in both the ‘small 9.3’ and ‘large 2.4’ lines that display Dorsal gradients that are nearly twice as wide as the normal range of σ, ~ 0.14 – 0.20 (Fig. 2B, orange crosses). In fact, when we plotted the width of the Dorsal gradient with respect to L, these clearly fall outside of the general trend and can be considered outliers (Fig. 2C, black arrow). While the outlier phenotype was of relatively low frequency, especially in the ‘small 9.3’ line, it was unclear how it arose and, therefore, we did not treat these lines as wild-type.

In contrast, the ‘large 2.1’ line was associated with larger embryo size while retaining a normalized Dorsal gradient width that is similar to wild-type, In addition, the scaling behavior of these embryos is very similar to the scaling behavior of our laboratory sample; therefore, we combined this particular line along with wild-type embryos to increase the size distribution and better interrogate the scaling behavior of the Dorsal gradient (Fig. 2D; see Methods). Even the yw background, which we consider wild-type, is an inbred laboratory strain that may have accumulated mutations; therefore, our rationale for combining data from wild-type (i.e. yw) and ‘large 2.1’ lines is a subjective choice, but one that we suggest is reasonable based on the scaling properties of the Dorsal gradient. Using this combination of wild-type and ‘large 2.1’ embryos that result in a broader spread of DV axis length (Fig. 2D), we strengthened the case for scaling of the width of the Dorsal gradient, given the 68% confidence interval definitively includes b = 0 and the width of the 95% confidence interval is narrower compared to the analysis of wild-type alone (Fig. 1E).

In principle, scaling of the gradient width is entirely sufficient to explain scaling of gene expression patterns. However, it is the absolute concentration of Dorsal that likely relates to gene expression. Therefore, the amplitude must be invariant to DV axis length (otherwise, this would run counter to the scaling effect of the gradient width). We then investigated whether the amplitude of the gradient correlates with the DV axis length. We found that while it appears that the amplitude decreases slightly by increasing L, we cannot exclude that the amplitude remains unaffected by variations in L (Supplementary Fig. 1). In these measurements, the variability of this parameter is too large with respect to the range of embryo sizes to conclusively determine a relationship with L. In contrast to the Dorsal gradient width that remains approximately constant throughout nuclear cycles, the Dorsal gradient amplitude never completely reaches steady state even within nuclear cycle 14 (Reeves et al., 2012), suggesting that the variability in the amplitude is likely due to gradient dynamics. Nonetheless, as we will see below, the scaling properties of the Dorsal gradient width and the border of a bona fide target gene suggest that the amplitude of the Dorsal gradient is weakly correlated at best with the length of the DV axis.

Size-dependent establishment of DV gene expression patterns

Given the evidence that Dorsal acts as a classical morphogen to establish DV patterning, we hypothesized that Dorsal-target genes would inherit the scaling behavior of the nuclear Dorsal gradient and thus that target genes, in general, would exhibit a correlation with size of the DV axis. To obtain experimental support for this prediction, we developed quantitative, semi-automated tools to measure the distance from the ventral midline to the borders associated with sna, vnd, and ind target genes within cross-sections of late nc14 embryos (Fig. 3A,B).

Fig. 3. Dorsal target genes exhibit different scaling behaviors.

(A) Cross-sections of late nuclear cycle 14 embryos in situ hybridized with sna (blue), vnd (red), and ind (green) riboprobes were imaged. “X” is the distance from the ventral midline to the boundary of sna and demonstrates how gene expression patterns were measured. “L” is the length of the DV axis. (B) An expression profile was generated by plotting the signal intensity of each gene against the relative position from the midline, 0. (C–F) The position of the sna border in absolute units, µm, was plotted against the DV axis length, L (C). The ventral border (bottom), dorsal border (top) of vnd and ind were plotted against L (D and F). The width of vnd and ind were plotted against L (E and G). Error bars for each embryo are displayed although generally small. For all plots n is equal to the number of embryos in each experiment, the R value is the square of the Pearson coefficient. (G) The p-value for the null hypothesis that the best-fit line has a slope equal to 0 is greater than 0.05 and cannot be rejected.

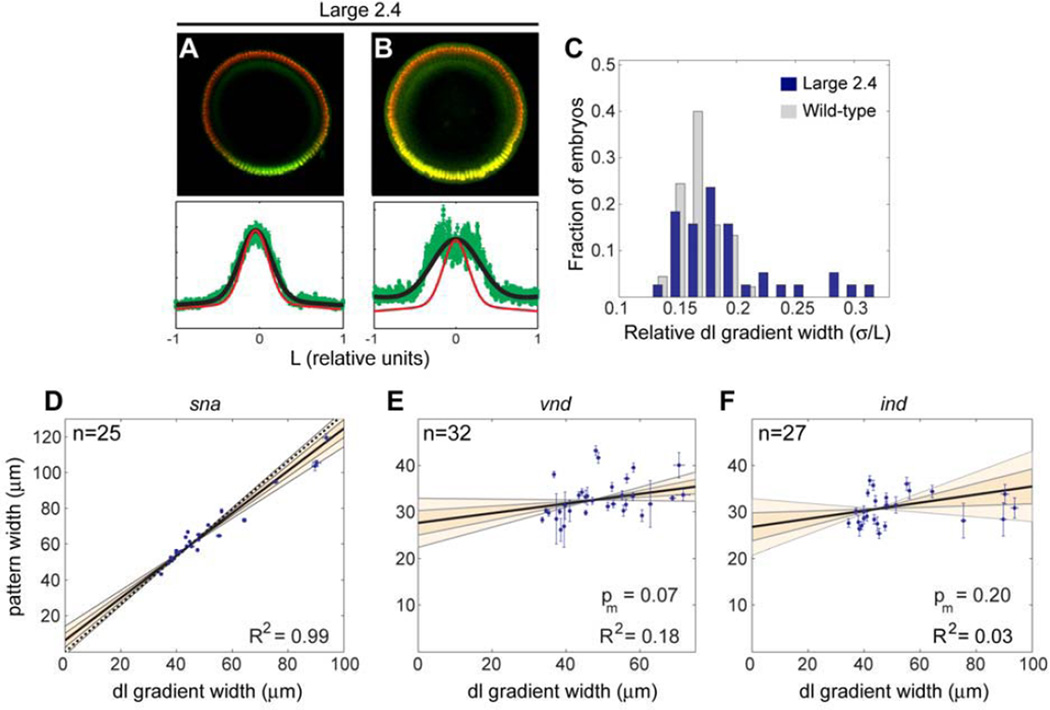
Our results show that all gene expression borders exhibit some correlation with L (Fig. 3C,D,F), but the nature of their correlation is varied. The sna domain correlates with L in a manner very similar to the Dorsal gradient, as b = 0 is definitively included in the 68% confidence interval (compare Fig. 2D with Fig. 3C). We also observed that, similar to sna, both borders of vnd scale to DV axis length (Fig. 3D), while the ventral border of ind is right on the cusp confidently declaring a scaling behavior (Fig. 3F). That the ventral borders of vnd and ind scale is expected, as Sna- and Vnd- mediated repression establish these boundaries, respectively (Cowden and Levine, 2003; Markstein et al., 2002). In contrast, the correlation of the position of the dorsal ind border with L exhibits undercompensation, meaning that this position does not shift as much as expected from a strict scaling correlation with L (b = 0 is excluded from the 95% confidence interval in Fig. 3F). We further noted the width of the ind stripe was uncorrelated to L and remained approximately constant (Fig. 3G), whereas the width of vnd appeared to be correlated with DV axis length (Fig. 3E). In summary, we found that while the location of some borders of the Dorsal target genes exhibit a correlation with L (sna and vnd borders; compare Fig. 2D with Fig. 3C,D), the dorsal border of ind undercompensates with respect to variations in L such that the width of the ind pattern is always constant, regardless of embryo size (Fig. 3F,G).

Scaling of the Dorsal gradient width and the border of sna suggest that the amplitude of the gradient is approximately constant

Our experimental data suggest that both the width of the Dorsal gradient and the border of sna display strict scaling properties (Fig. 2D and Fig. 3C). Furthermore, in a previous study we showed that sna follows closely the spatial dynamics of the Dorsal gradient suggesting that sna is positioned by an absolute Dorsal level (Reeves et al., 2012). Together, these experimental observations impose constraints on the relationship between the amplitude of the Dorsal gradient and the length of the DV axis. Since the width of the gradient, which is itself defined as the distance at which the amplitude levels drop a certain percentage, scales with the length of the DV axis (Fig. 2D), the position of the absolute threshold that determines the location of sna would be at different relative locations if the amplitude of the Dorsal gradient varies with respect to the DV axis length. However, since we observe that the relative location of the sna border is the same at the end of nc 14 for embryos that significantly vary with size (Fig. 3C), we infer that the plateau levels of the amplitude at the end of nc 14 must be approximately invariant with respect to DV axis length. This statement can be proven mathematically assuming that the shape of the Dorsal gradients is a Gaussian (see Supplementary Text). The inference that the plateau levels of the Dorsal gradient amplitude is uncorrelated to L, or only weakly correlated is also consistent with our direct measurements of the Dorsal gradient amplitude (Supplementary Fig. 1). In the rest of the study, we will assume that the amplitude of the Dorsal gradient is not significantly affected by the length of the DV axis and will rely on the Dorsal gradient width to compare the spatial properties of Dorsal levels with the distribution of DV patterns.

Dorsal target genes are not all strictly correlated to the Dorsal gradient

The differences in scaling behavior between the Dorsal gradient width and the location of target gene borders prompted us to directly measure the correlation between the Dorsal gradient and its target genes. To this end, embryos were co-stained by in situ hybridization using riboprobes to identify individual genes as well as immunostaining to detect Dorsal and Histone H3 proteins (H3) (Fig. 4A–F). All Dorsal target genes examined display an appreciable correlation with the width of the Dorsal gradient (Fig. 4G–I); however, while changes in the Dorsal gradient result in similar changes in the positions of the sna, vnd and ventral ind borders (Fig. 4G–I), the location of the dorsal ind border falls short from where it would be expected to be positioned if solely dependent on Dorsal gradient width [Fig. 4I, compare the 95% confidence intervals with dashed lines (strict correlation)]. These results were largely reproduced in replicate experiments (Supplementary Fig. 2). The data for experiments using wild-type embryos alone, which were conducted independently of those assayed with the size-selected lines, show similar scaling behaviors to experiments where wild-type and ‘large 2.1’ data were combined, with the exception that the dorsal border of vnd occasionally undercompensated with respect to the Dorsal gradient width (Supplementary Fig. 2E). This difference is indicative of a non-causal relationship between the Dorsal gradient and the dorsal border of vnd (see below).

Fig. 4. The scaling behavior of the Dorsal gradient is not reflected by all of its target genes.

(A–C) Late nuclear cycle 14 embryos were stained with Dorsal (green) and H3 (red) antibodies and in situ hybridized with riboprobes (blue) to detect sna (A), vnd (B), or ind (C). (D–F) The cross-sections were imaged and profiles were generated by plotting signal intensity vs. relative position in the embryo. The blue line represents the gene expression amplitude, while the green line is the signal intensity of the Dorsal gradient. The black line represents the Gaussian fit to the Dorsal gradient. (G–I) The positions of the respective gene borders were plotted against the Dorsal gradient width in absolute units, µm. Data for dorsal borders and ventral borders of genes is shown with dorsal on top and ventral on the bottom. The dashed line represents strict scaling, while the solid line is the best-fit line to the data. The 68% (dark shading) and 95% (light shading) confidence intervals are shown. Error bars for each embryo are displayed although generally small. For all plots n is equal to the number of embryos in each experiment, and the R² value is the square of the Pearson coefficient.

Correlations between Dorsal and target gene patterns persist even in embryos exhibiting abnormally wide Dorsal gradients

The ‘large 2.4’ inbred line that contains several embryos exhibiting abnormally wide Dorsal gradients (Fig. 2B, 5C) provided an opportunity to test how target genes respond to large changes in the Dorsal gradient in a scenario in which embryo size only changes slightly (Fig. 5A,B). If scaling of the sna and vnd patterns result from scaling of the Dorsal gradient, we predicted that these patterns would follow the Dorsal gradient in such embryos (i.e., they would expand) rather than maintain their positions relative to embryo size. In contrast, ind width, a pattern that appeared insensitive to Dorsal gradient changes associated with normal embryonic scaling, would be predicted to remain unaffected in ‘large 2.4’ embryos, which exhibit an over-expanded Dorsal gradient. As predicted, the sna pattern exhibits the expected correlation with the width of the Dorsal gradient in ‘large 2.4’ embryos (Fig. 5D). In particular, the outlier embryos in this experiment clearly show that the position of the sna border (and consequently the ventral border of vnd) expands to follow the Dorsal gradient rather than the size of the embryo (Fig. 5D; compare ventral border of vnd Supplementary Fig. 4H with 4G). Thus, these data support that scaling of the sna pattern in wild-type embryos (Fig. 3C) is a consequence of scaling of the Dorsal gradient (Fig. 2D). Also as expected, the width of ind remains approximately constant both in outliers and non-outliers (Fig. 5F), demonstrating that dramatic changes in the Dorsal gradient do not affect the size of the ind domain (Fig. 5F). These results support the view that the constancy of the ind domain is ensured by mechanisms that are largely Dorsal-independent. Surprisingly however, while the width of vnd scaled in wild-type embryos similarly to the Dorsal gradient, it remained largely constant in ‘large 2.4’ embryos and did not show a clear correlation with the width of the Dorsal gradient (Fig. 5E). This suggests that dorsal-acting factors can restrict vnd when the Dorsal gradient is abnormally expanded. We conclude that even in largely-expanded Dorsal gradients, uncovered in embryos from size-selected lines, the relationships between the width of Dorsal and sna as well as the lack of correlation between the Dorsal gradient and the width of ind are preserved. In contrast, vnd is largely uncorrelated with the Dorsal gradient in these embryos, suggesting that other factors participate in the establishment of the relative location of the dorsal border of vnd.

Fig. 5. Dorsal target genes behave differently in response to dramatic changes in the width of the Dorsal gradient.

(A, B) Cross sections from embryos of the size-selected line ‘large 2.4’ (Miles et al., 2011) immunostained with anti-Dorsal (green) and anti-H3 antibodies (red). The profile of the nuclear Dorsal staining (green curve) is plotted in relative DV coordinates at the bottom of each embryo. Most ‘large 2.4’ embryos display similar Dorsal gradient distribution in proportion to embryo size, although slightly expanded (A; compare the Gaussian fit, black curve, with an average wild-type profile, red curve). However, some embryos display dramatically-expanded gradients (B). (C) Histogram showing the distribution of relative Dorsal gradient widths (σ/L) in a sample of ‘large 2.4’ embryos (green bars), compared with a sample of wild-type embryos done at the same time and under equivalent conditions (gray bars). Note that the relative width of the Dorsal gradient in some ‘large 2.4’ embryos almost double the relative width of an average wild-type gradient. (D–F) The widths of sna (D), vnd (E), and ind (F) are plotted against the Dorsal gradient width in ‘large 2.4’ embryos co-stained with anti-Dorsal, anti-H3 antibodies and sna, ind (D,F) or vnd (E) riboprobes. The measurement errors for both, the width of the genes and the width of the Dorsal gradient, are shown for each data point. The number of embryos in the sample, n, and the square of the Pearson coefficient, R², are displayed. Note that in the cases of vnd (E) and ind (F), the null hypothesis that the data describes a horizontal line cannot be rejected (p-value that the slope of the best-fit line is 0, p_m, is greater than 0.05).

The constant domain of ind expression also relates to constant nuclei (cell) number

The observed invariance of the ind domain to DV axis length as well as to a broad range of Dorsal gradient widths suggests that an underlying mechanism might maintain a constant number of ind-expressing cells. Therefore, we investigated whether the constant width of the domain of ind expression (as measured in microns) indeed relates also to a constant number of nuclei. For example, if number of nuclei associated with the DV axis scales, then perhaps a constant ind domain of expression might correspond to an increasing number of cells in larger embryos (i.e. scaling). By measuring the number of nuclei in an embryo cross-section, we found that nuclear number increases but does not strictly scale with DV axis length (Supplementary Fig. 3A–D); similar trends were observed relative to AP axis length (Miles et al., 2011). We then estimated the average number of nuclei within the ind domain and found that the number of ind-expressing nuclei is not completely invariant of L, but does exhibit a small, yet significant, positive slope (Supplementary Fig. 3E). This means that, on average, a small and a large embryo do have a higher chance of ending up with a small difference in their number of ind-expressing cells, but this bias is rather small and cannot be explained by the width of the Dorsal gradient. In fact, the lack of correlation between the width of ind and the width of the Dorsal gradient is even more apparent when the ind domain is measured in number of nuclei than when measured in absolute length units (Supplementary Fig. 3F; compare to Fig. 5F). We conclude that the number of nuclei within the ind domain remains approximately constant in a broad range of embryo sizes and is completely uncorrelated with the relative distribution of the Dorsal gradient.

Mathematical modeling suggests that gradient scaling cannot be explained by assuming that the total levels of Dorsal are proportional to L

How does scaling of the Dorsal gradient arise? Scaling of the Dorsal gradient can be inherited by an upstream maternal signal [as in the case of the Bicoid gradient along the AP axis (Cheung et al., 2011)], or by a feedback mechanism downstream of Dorsal that modulates the distribution of Dorsal as a function of DV axis length, [as in the case of the Decapentaplegic (Dpp) gradient in the wing disc (Ben-Zvi et al., 2011a)]. In this section, we used mathematical modeling to consider the possibility that the mechanism responsible for scaling of the Dorsal gradient depends on the relationship between the maternal contribution of dorsal mRNA and egg size (e.g., larger eggs receiving larger amounts of dorsal mRNA).

In order to test whether modulating the total levels of Dorsal relative to embryo size are sufficient to explain scaling of the nuclear Dorsal gradient, we formulated a mathematical model of the Dorsal gradient in which the total levels of Dorsal are proportional to L. The model equations and assumptions are described explicitly in Fig. 6A. Briefly, we modeled the local concentrations of nuclear and cytoplasmic Dorsal (denoted by [dl_n] and [dl_c], respectively), where net Dorsal nuclear import is regulated by graded Toll signaling (Moussian and Roth, 2005). We model Toll signaling as an input function f(x) that spatially modulates the rates of nuclear import of Dorsal. In addition, we assume that cytoplasmic Dorsal is diffusible; this is a reasonable assumption as long as a concentration gradient exists and this molecule is not spatially constrained. For simplicity, we do not model nuclear divisions and assume that total levels of Dorsal remain constant (i.e., Dorsal degradation is negligible throughout the duration of Dorsal gradient formation and patterning).

Fig. 6. A mathematical model of nuclear/cytoplasmic Dorsal levels reveals a relationship between the Dorsal gradient amplitude and L.

(A) Mathematical model of nuclear and cytoplasmic concentrations of Dorsal (denoted by [dl_n] and [dl_c], respectively) in the Drosophila embryo. Nuclear internalization of Dorsal that depends on the activation of Toll signaling is modeled using an arbitrary input function f ( x). f (x) is assumed to take higher values at ventral-most locations (x_V) than at dorsal-most locations (x_D), thereby modulating the local rate of nuclear Dorsal import, k_in. k_out and D denote the rate of nuclear Dorsal export and diffusion coefficient of the Dorsal protein within the cytoplasm, respectively. The partial differential equations describing the nuclear dynamics of Dorsal under these assumptions are shown on the right. At t₀ (arbitrary initial condition), we assume that [dl_n] is zero and [dl_c] is at a constant concentration [dl₀] homogeneously. We also assume zero-flux boundary conditions at the ventral and dorsal ends of the embryo (x=0 and x=L), and that the total amount of Dorsal protein remains constant at all times (=[dl₀]L; Conservation law; see Supplementary Text for derivation). (B) The amplitude of the steady-state solution of the model [α(L) in equation (1)] is plotted as a function of L, assuming that f ( x) is a Gaussian (f(x = A₀e^−x2/2λ2), with width λ) but this choice does not affect the qualitative behavior of this plot (see Supplementary Text). Note that for the normal range of variation of the DV axis (~250–350 µm, red shaded area), the amplitude increases very slowly. (C) Steady-state nuclear distribution of Dorsal [equation (1)] plotted in absolute units for three sample values of L assuming that f(x) is independent of L. Note that the effects of the change of amplitude on the gradient are negligible.

We assume that total Dorsal levels are proportional to L (see Conservation Law in Fig. 6A) but f(x) is independent of L. Under these assumptions, as Dorsal becomes concentrated in the ventral-most nuclei, it will be depleted from the local cytoplasm, and the “excess” cytoplasmic Dorsal in dorsal regions will be expected to diffuse to ventral regions, thereby increasing the intake of Dorsal into ventral-most nuclei. The effect of this cytoplasmic diffusion process, combined with the assumption that larger embryos contain more total Dorsal, may contribute to scaling of the Dorsal gradient. In other words, we predict that two embryos of different sizes will initially form the same nuclear Dorsal gradient [because f(x) is independent of L], but as the larger embryo contains more total Dorsal, the cytoplasmic diffusion process will ventrally concentrate more Dorsal in larger embryos, resulting in a broader gradient. To test this possibility, we solved the model analytically at the steady state (see Supplementary Text) and we find the steady-state Dorsal nuclear concentration $([{\text{dl}}_{\mathrm{n}}^{\text{SS}}])$ is given by:

$$[{\text{dl}}_{\mathrm{n}}^{SS}](x)=\frac{[{\text{dl}}_0]\mathrm{L}}{\mathrm{L}\frac{k_{\mathit{\text{out}}}}{k_{\mathit{\text{in}}}}+\underset{0}{\overset{\mathrm{L}}{\int }}f(t)dt}f(x)=\alpha (\mathrm{L})f(x)$$ (1)

Note that the shape of the nuclear Dorsal gradient in this simple model is proportional to f(x), but its amplitude is modulated by a coefficient term [defined as α(L) in equation (1) that depends on L]. Equation (1) shows that as long as f(x) is a decreasing function that drops to negligible levels at some point along the DV axis [so that changes in L result in negligible changes in $\underset{0}{\overset{\mathrm{L}}{\int }}f(t)dt$] then the amplitude of the gradient increases in a non-linear manner with L. Therefore, the maternal modulation of total levels of Dorsal as a function of embryo size does affect the amplitude of the nuclear Dorsal gradient and, as a consequence of this change in the gradient, the position of Dorsal target genes will have a dependence on L. However, for the range of L comparable to DV axis size range in wild-type embryos (L=250 to 350 µm), the amplitude increases only slightly (Fig. 6B, red shaded area), such that the effect on the gradient distribution is negligible (Fig. 6C). Note that we implicitly assume that the width of the Dorsal gradient, which is determined by the input function f(x) in this model, is independent of the total maternal levels of dorsal mRNA. Since our data show that width of the Dorsal gradient scales with L and amplitude is independent of L, a volume-dependent maternal contribution of Dorsal on its own cannot explain the observed scaling properties of the system. However, scaling of Dorsal may be determined maternally by an upstream signal that scales with DV axis length; in fact, under the additional assumption that Toll signaling scales [i.e., f = f(x / L)], the amplitude of the nuclear Dorsal gradient in equation (1) no longer depends on L and strict scaling of the nuclear Dorsal gradient is ensured (see Supplementary Text).

Further investigation of Dorsal gradient scaling mechanism: mutant analyses

Next, we considered the possibility that scaling of the Dorsal gradient is dependent on other pathways that may affect DV patterning. We analyzed the scaling behavior of the Dorsal gradient in several mutant backgrounds to possibly uncover a situation where scaling of the Dorsal gradient is impaired.

We examined the distribution of Dorsal and vnd in mutant backgrounds that have been proposed to affect the shape of the Dorsal gradient or the patterns of Dorsal target genes. We focused on examination of the vnd pattern for the mutant analysis because this gene is expressed in all of the mutant backgrounds tested and it shares its ventral and dorsal borders with sna and ind, respectively. Specifically, we considered mutant embryos that affect the terminal pathway [i.e. wntD mutants], the EGFR pathway [i.e. rhomboid (rho) vein (vn) double mutants] and TGF-β signaling [using maternally-driven dominant-negative (DN) form of the Decapentaplegic (Dpp) receptor, Thickveins (Tkv)]. WntD and the EGFR signaling pathway influence the shape of the Dorsal gradient (Ganguly et al., 2005; Gordon et al., 2005; Helman et al., 2012); however, these mutants are homozygous viable and therefore we postulated these genes may play a role in scaling. We hypothesized that viable mutants such as these may exhibit a scaling phenotype that was not 100% lethal and thus their roles in the early embryo may have been overlooked in previous studies, which have focused on maternal-effect or zygotic lethal mutations. Furthermore, mutants that were homozygous viable allowed us to examine the potential role of signaling pathways or transcription factors acting either maternally (i.e. oocyte patterning as well as embryo) and/or zygotically (i.e. in the early fertilized embryo or subsequent stage). TGF-β signaling was investigated because several studies suggest this pathway may help to establish the dorsal boundaries of genes along the DV axis (Crocker and Erives, 2013; Garcia and Stathopoulos, 2011; Mizutani et al., 2006). We also looked at capicua (cic) mutants, a maternal-effect background, as cic gene encodes a transcriptional repressor necessary for proper pipe expression necessary to Toll receptor activation; this particular background, cic, was used to investigate the possibility that scaling of the DV axis is initiated in the oocyte. We were not able to uncover a distinct scaling phenotype of the Dorsal gradient width or vnd border positions, as compared to wild-type, in any of these mutant backgrounds (Fig. 7 and Supplementary Fig. 4). In particular, the data could not exclude strict scaling of the Dorsal gradient as observed in wild-type embryos (Fig. 7A–D, compare to Fig. 2D). We also did not see a significant change in the relative width of the Dorsal gradient in the mutant backgrounds analyzed (Fig. 7F).

Fig. 7. The behavior of the Dorsal gradient in several mutant backgrounds.

The Dorsal gradient width was plotted versus L for rho vn(A), wntD (B), DN-TKV (C), cic (D) and large 2.4 (E). The dashed line represents strict scaling while the solid black line is the best-fit line for the data. The 68% (dark shading) and 95% (light shading) confidence intervals are shown. Error bars for each embryo are displayed although generally small. For all plots n is equal to the number of embryos in each experiment, and the R² value is the square of the Pearson coefficient (F) Box plots of the relative Dorsal gradient width for the various mutants are shown. Two-sample T-test showed that the mean of the ‘large 2.4’ line is statistically different from WT (p = 5.9 × 10⁻⁴ ). The mean for rho vn (p = 0.90), wntD (p = 0.14), DN-IKV (p = 0.08), and cic (p = 0.05) were not statically different from WT; a p-value less than 0.05 is necessary to reject the null hypothesis, which is that the means are equal.

Despite the fact we were unable to uncover a different scaling phenotype in these mutant backgrounds, it is noteworthy that scaling in embryos obtained from the inbred ‘large 2.4’ line exhibited overcompensation of the Dorsal gradient, meaning that changes in the width of the Dorsal gradient are greater than would be expected from a strict scaling correlation with L (Fig. 7E compare to Fig. 2D). This result was not simply an influence of the outliers, since the trends prevail even when outlier embryos were excluded, and suggests that normal scaling behavior can be perturbed. The dorsal and ventral positions of vnd also exhibited overcompensation, but the 95% confidence intervals did not allow the exclusion of strict scaling (Supplementary Fig. 4G). Also, as noted above, the width of vnd remains constant in outlier embryos (Fig. 5E).

Taken together, these experimental results suggest that scaling of the Dorsal gradient requires factors other than WntD, EGFR signaling, and TGF-β signaling. The fact that we see outlier embryos with greatly expanded Dorsal gradient widths suggests that the mechanism of scaling can be challenged, either by genotypic or physiological changes. Moreover, the outlier phenotype was likely caused by a maternal-effect mutation as the expansion of the Dorsal gradient was still observed when ‘large 2.4’ females were crossed to wild-type males (data not shown).

DISCUSSION

A universal principle in animal design is the robustness of gene expression patterns to natural variability in embryonic size. During the evolution of body plans, some patterns might have been designed to be plastic to adjust to embryo size, while others are set to remain constant. Here we show that in the early Drosophila embryo the spatial extent of the Dorsal morphogen gradient scales well with embryo size. Based on our recent work that showed that sna and vnd expression could be approximately explained as Dorsal-concentration threshold outputs (Reeves et al., 2012), we expected Dorsal target genes to scale, and these one-to-one relationships between Dorsal and sna and vnd were upheld in wild-type embryos (Fig. 8A,B). However, when this hypothesis was challenged in embryos where the Dorsal gradient is abnormally wide and scaling of the Dorsal gradient is affected, sna still follows the Dorsal gradient; but the dorsal border of vnd does not (Fig. 8C). We conclude that while sna behaves as a bona fide target of Dorsal, vnd expression is constrained to a certain domain by other factors (Fig. 8C, arrow). In contrast, the pattern of the neural marker ind, expressed within the intermediate neurogenic ectoderm, appears to encompass a fixed number of cells across the range of normal DV axis length, regardless of the extent of the Dorsal gradient (Fig. 8A–C). Therefore, our data contradict the expectation that all Dorsal-target genes would follow the scaling behavior of the Dorsal gradient.

Fig. 8. Relationships between the Dorsal nuclear gradient and DV patterns in embryos of different sizes.

Cross-section images of a wild-type embryo (A, yw laboratory stock), ‘large 2.1’ embryo (B), and a ‘large 2.4’ embryo displaying an overexpanded Dorsal gradient (C). Scale bar=30µm. All three embryos were co-stained with anti-Histone H3 antibody (red) and sna and ind riboprobes (green). Diagrams illustrate the distribution of the Dorsal gradient in absolute units (microns) and the predicted location of the Dorsal target genes examined in this study. The Dorsal gradient scales with embryo size in wild-type embryos (insets in A,B), but not in ‘large 2.4’ embryos (inset in C). The behavior of the sna pattern (blue bar) is explained by a concentration-threshold of the Dorsal gradient (dotted horizontal lines). The vnd pattern (red bar) follows the behavior of the Dorsal gradient in a wild-type situation (A, B), but not when the Dorsal gradient is overexpanded (C), suggesting that an unknown factor restricts this boundary (arrow). In contrast, the width of the ind pattern (green bar) is always approximately constant regardless of the absolute range of the Dorsal gradient or DV axis length.

Thus, scaling across the entire DV axis cannot be explained by the action of the Dorsal morphogen gradient alone. We suggest that Dorsal contributes the primary positional information that must then be refined by downstream gene regulatory interactions to support size-dependent regulation of DV genes in a gene-specific manner.

Dorsal acts as a ‘pre-pattern’ and primary measure of DV axis length that is subsequently refined

Our data argue against the paradigm that the relative distribution of a morphogen gradient operates as a general system of positional coordinates throughout the DV axis. Presumably, Dorsal provides the initial DV pattern prior to nc 14, allowing other cis-regulatory factors and feedback loops to establish the final nc 14 pattern; this is most clearly exemplified by positioning of the ind gene. In the case of ind, Dorsal activation likely acts as a permissive signal rather than providing positional information; while the Vnd repressor establishes the ventral boundary, and the Capicua/‘A-box’ repressor along with Dpp signaling-mediated repression establishes the dorsal boundary (Ajuria et al., 2011; Garcia and Stathopoulos, 2011; Weiss et al., 1998).

The Dpp signaling gradient opposes the Dorsal gradient, with high levels in dorsal-most regions and low levels in dorsal-lateral regions of the embryo (Ashe and Briscoe, 2006). It is possible that Dpp signaling functions more broadly to help position the dorsal boundaries of genes expressed along the DV axis. Although we did not observe a significant effect on scaling in embryos expressing DN-TKV using a maternal driver, the fact that the width of vnd remained constant in ‘large 2.4’ outlier embryos suggests that dorsally-acting factors limit vnd expression and keep this gene from expanding to follow changes in the Dorsal gradient. Moreover, a recent study found a slight expansion in the expression pattern of a reporter gene activated by a vnd cis-regulatory module that was unable to respond to Dpp-signaling, leaving open the possibility that Dpp signaling plays a role in limiting vnd (Crocker and Erives, 2013). The effects of Dpp-signaling on vnd are difficult to measure possibly because multiple factors support a repressive role to position this boundary similar to the case of ind, in which two tiers of repression, one independent of and one dependent on Dpp-signaling, position ind’s dorsal boundary (Garcia and Stathopoulos, 2011).

Size -dependent regulation of different cell types

Different scaling behaviors associated with particular genes may reflect a need to maintain the number of certain cell-types constant, while allowing other cell-types to adjust their numbers relative to embryo size. Our results suggest that the number of mesodermal cells specified by sna and ventral neuroblast precursors specified by vnd can increase or decrease based on the size of the DV axis length (Fig. 8A,B), with the exception of greatly expanded Dorsal gradients where vnd does not follow the Dorsal gradient (Fig. 8C); while intermediate neuroblast precursors specified by ind are set to remain constant in all cases (Fig. 8A–C). In different drosophilid species, stereotypic and equivalent muscle cell patterning can be supported despite significant differences in embryo size; to keep muscle cell number constant, nuclei number within multinucleate muscle cells vary accordingly (Belu and Mizutani, 2011) and this may also be true within a species as well. Perhaps a change in neuroblast number is more difficult to accommodate, reflecting a selection pressure that retains the ind domain constant and the vnd domain also constrained.

Average embryo size, AP position, and staging should be taken into consideration when examining morphogen gradient trends

Our study uncovered that morphogen gradients and gene expression patterns are able to scale with the size of the embryo, while some patterns remain constant. This introduces a problem when conducting studies that ask if there are changes in the width of protein or gene expression patterns, especially when comparing lines that have different embryo size distributions. We observed that the rho vn line has a DV axis length that is significantly different than wild-type embryos (Supplementary Fig. 5A). If the absolute width of the Dorsal gradient is measured in rho vn embryos, it appears to be significantly larger than wild-type (Supplementary Fig. 5B). However this difference likely relates to scaling, not due to expansion of the Dorsal gradient by EGFR signaling as the relative widths normalized to DV axis length have similar means (Fig. 7F; also, Supplementary Fig. 5B compare with 5C). Our analysis shows that in cases where small changes in protein or gene expression patterns are being compared they should be normalized to the size of the embryo, in order that mutant phenotypes can be correctly interpreted.

Furthermore, several previous studies have shown that the Dorsal gradient width varies with AP position (Kanodia et al., 2011; Reeves et al., 2012) and that gene expression patterns exhibit dynamics which include shifting of expression domains in time (McHale et al., 2011; Reeves et al., 2012); because of this variability, for instance, measurements of the Dorsal gradient or gene expression patterns obtained in the trunk region should not be directly compared to measurements in more anterior or posterior regions of the embryo. However, manual sectioning certainly introduces some variability due to inadvertent change in assay position along the AP axis; while the trunk midpoint was targeted, sectioning accuracy is at best ±10%. Lastly, our previous study as well as that of McHale et al. (2011) has demonstrated that the sna boundary shifts to a more dorsal position over the course of nc 14 (McHale et al., 2011; Reeves et al., 2012), suggesting that careful staging of embryos is also necessary to support proper comparisons. For all these reasons, a careful statistical analysis of data obtained keeping AP position and staging as tightly controlled as possible, as conducted here, is necessary to support characterization of scaling trends.

Mechanism for scaling

Our mutant analysis was unable to uncover a scaling mechanism, but we were able to show that scaling can be perturbed using the ‘large 2.4’ line that displays an expanded Dorsal gradient as well as a scaling defect. When ‘large 2.4’ females were crossed to wild-type (i.e. yw) males, the expanded Dorsal gradient was retained, suggesting that this phenotype is maternal. Therefore, it is likely that scaling of the Dorsal gradient is initiated during oogenesis. However, we suggest regulation of scaling may not be as simple as adjusting the levels of maternal factors such as Pipe, an upstream signaling component required for Toll receptor activation (Moussian and Roth, 2005), as we did not see a clear effect on scaling in embryos obtained from homozygous cic mutant females (data not shown). Cic is a transcriptional repressor, which in addition to its role in establishing the ind dorsal boundary in the embryo (Ajuria et al., 2011), also plays a role in supporting proper pipe expression in ventral follicle cells that surround the oocyte (Andreu et al., 2012; Goff et al., 2001). In cic mutants, pipe expression is reduced and Dorsal targets genes, sog and sna, are still expressed but in narrower, more ventral domains (Goff et al., 2001; and data not shown). Furthermore, our modeling results suggest that while differential loading of dorsal mRNA into the embryo does not explain the observed scaling behavior, a size-dependent, modulation of Toll signaling may cause the nuclear Dorsal gradient to scale. This together with the fact that cic mutants do not show a clear scaling defect may suggest that scaling is established downstream of Pipe. Alternatively, it is possible that Pipe is also regulated by a cic-independent pathway that allows it to scale. An important area of future study will be to define the mechanism supporting scaling, and we suggest that additional study of the inbred 2.4 line and additional maternal pathway components acting upstream of Toll will be key.

Concluding remarks

Our study provides insights into the strategy used in this system to build complex patterns relative to embryo size. It appears that scaling of the nuclear Dorsal gradient with DV axis length is a primitive feature of the system that provides a “rough measure” of the size of the system while more specific properties, such as fine-tuning of this size “measurement” to ensure size-invariance of specific patterns, might have evolved through added-on gene regulatory interactions to suit specific needs of the individual animal species.

Highlights.

• DV axis size variation in wildtype embryos is ~14%, and inbred lines increase spread

• The width of the Dorsal gradient scales with respect to DV axis length

• Dorsal target genes respond to changes in DV axis length in a gene-specific manner

• snail scales and follows the Dorsal gradient, whereas ind remains relatively constant

• Scaling breaks down in one inbred line and relates to a maternal-effect mutation