Misclassification Can Explain Most Apparent Regression of Age-Related Macular Degeneration: Results From Multistate Models With Misclassification

Abstract

Purpose.

To investigate the impact of misclassification of age-related macular degeneration (AMD) on the baseline intensity and estimated effects of age, sex, and the Y402H variant in the complement factor H (CFH) gene on incidence, progression, and regression of AMD.

Methods.

The Beaver Dam Eye Study, a longitudinal population-based study of age-related eye diseases conducted in the city and township of Beaver Dam, Wisconsin, performed examinations every 5 years during a 20-year period (1988–1990 through 2008–2010). Study participants (N = 4379) aged 43 to 86 years at the baseline examination had retinal photographs taken at baseline and up to four subsequent examinations. Multistate models with misclassification in continuous time were used to model the effects of age, sex, and CFH genotype on incidence, progression, and regression of AMD and mortality.

Results.

After accounting for AMD misclassification, the occurrence of any AMD regression was rare (1%–4%), while it was relatively common (14%–21%) in models that do not account for misclassification. Failure to account for misclassification attenuated estimated age effects on incidence and progression to moderately severe early AMD and attenuated estimated CFH effects on incidence and progressions to moderately severe and severe early AMD.

Conclusions.

Apparent regression of AMD can largely, if not completely, be explained by misclassification. Estimated age effects on incidence and progression to moderately severe early AMD and estimated CFH effects on incidence and progressions to moderately severe and severe early AMD were attenuated in multistate models that did not account for misclassification.

We investigate the impact of misclassification of AMD on the baseline intensity and covariate effects on incidence, progression, and regression of AMD. Regression of AMD can largely be explained by misclassification, and effects of age and CFH were attenuated in models without misclassification.

Introduction

Information regarding the development and progression of age-related macular degeneration (AMD) has emerged from clinical and epidemiologic studies.^1–11 This has resulted in the development of severity scales with categories ranging from no or minimal AMD lesions not severe enough to categorize the earliest level of early AMD through the most severe lesions (neovascular AMD and/or geographic atrophy) that categorize the presence of late or advanced AMD.^6,12–14 Most scales use size, type and area of drusen, and pigmentary abnormalities of the retinal pigment epithelium (RPE) to define the intermediate severity levels of early AMD. Assessments of AMD lesions that characterize its severity from photographs are subject to misclassification owing to media opacity, photographic artifacts, and grader errors.

While most epidemiologic studies have investigated the incidence and progression of AMD, few studies have examined regression.^2,5,9,11 In the Chesapeake Bay Waterman Study, large soft drusen disappeared in 34% of eyes during a 5-year follow-up.² In the Melton Mowbray study, 20% of soft drusen regressed during a 7-year period.⁹ The Beaver Dam Eye Study (BDES), using side-by-side longitudinal review to minimize false-positive progression and regression of AMD severity, previously reported a cumulative disappearance of soft indistinct drusen, during a 15-year period, of 18% in the absence of the appearance of more severe lesions such as RPE depigmentation, geographic atrophy, or exudative macular degeneration.¹¹ It is unclear to what extent these high rates of apparent AMD regression reflect misclassification of AMD state rather than true regression of the disease.

Most studies that have examined relationships of the Y402H polymorphism in the complement factor H (CFH) gene on chromosome 1q have shown a relationship to incidence of early or progression to late AMD.^12–15 Few have considered progression through various stages of early AMD or regression of AMD, and none have accounted for potential misclassification of AMD state.^16–19

Multistate models (MSMs) with misclassification can be used to gain greater insight into the true course of incidence, progression, and regression of AMD. We used MSMs with misclassification to model transitions from the observed state at a study visit to the observed state at a subsequent visit.^20–24 In practice, disease states are observed with error at intermittent study visits, and exact transition times are not observed; even when the exact date of death is known, the AMD state at death is unknown.^25–28 In this article, we used MSMs with misclassification to examine the impact of misclassification on baseline intensity and the estimated effects of age, sex, and the Y402H variant in the CFH gene on incidence, progression, and regression of AMD as well as mortality in the population-based BDES.

Methods

Population

Methods used to identify the population have been described previously.^29–34 Characteristics of the population at each examination and reasons for nonparticipation appear elsewhere.^30–34

Procedures and Definitions

Similar procedures were used at all examinations.^3,5,35–39 Data were collected with institutional review board approval from the University of Wisconsin-Madison, informed consent was obtained from each participant at each examination, and the study adhered to the tenets of the Declaration of Helsinki. Pertinent parts of the examination consisted of taking stereoscopic 30° color fundus photographs centered on the disc (Diabetic Retinopathy Study standard field 1) and macula (Diabetic Retinopathy Study standard field 2) and a nonstereoscopic color fundus photograph temporal to but including the fovea of each eye.

Grading procedures have been described previously.^37–39 Information on gradability has been published elsewhere.^3,5,11,39,40 In this study, AMD status in each eye was classified by using a 5-step severity scale (Table 1).⁴¹ Subjects were classified as to severity level on the basis of the worse eye.

Table 1.

The 5-Level Beaver Dam Eye Study AMD Severity Scale

Level	Label	Description
1	No AMD	Hard drusen or small soft drusen (<125 μm in diameter) only, regardless of area of involvement, and no pigmentary abnormality (defined as presence of increased retinal pigment or RPE depigmentation) present.
2	Minimally severe early AMD	Hard drusen or small soft drusen (<125 μm in diameter), regardless of area of involvement, with any pigmentary abnormality OR soft drusen (≥125 μm in diameter) with drusen area < 196,350 μm2 (equivalent to a circle with a diameter of 500 μm) and no pigmentary abnormalities.
3	Moderately severe early AMD	Soft drusen (≥125 μm in diameter) with drusen area < 196,350 μm2 (equivalent to a circle with a diameter of 500 μm) and with any pigmentary abnormality OR soft drusen (≥125 μm in diameter) with drusen area ≥ 196,350 μm2 (equivalent to a circle with a diameter of 500 μm) with or without increased retinal pigment but no RPE depigmentation.
4	Severe early AMD	Soft drusen (≥125 μm in diameter) with drusen area ≥ 196,350 μm2 (equivalent to a circle with a diameter of 500 μm) and RPE depigmentation present, with or without increased retinal pigment.
5	Late AMD	Pure geographic atrophy in the absence of exudative macular degeneration OR exudative macular degeneration with or without geographic atrophy present.

Reprinted with permission from Gangnon RE, Lee KE, Klein BE, Iyengar SK, Sivakumaran TA, Klein R. Effect of the Y402H variant in the complement factor H gene on the incidence and progression of age-related macular degeneration: results from multistate models applied to the Beaver Dam Eye Study. Arch Ophthalmol. 2012;130:1169–1176. Copyright 2012 American Medical Association. All rights reserved.

Information on alleles for the Y402H polymorphism for CFH was available for 4479 participants. Distributions of other characteristics for these subjects did not differ from the rest of the population (data not shown).

Vital status was monitored by reading the obituaries in local newspapers and by making annual telephone contact. Persons not known to have died but who could not be contacted had their survival time entered as their last contact date.

Statistical Analysis

Incidence, progression, and regression of AMD and mortality were modeled by using MSMs in continuous time with misclassification, where the observed data are states assumed to be misclassifications of the true, underlying states. We identified mutually exclusive and exhaustive states representing the current status (current AMD severity level or death) of each subject at a given age. The observed AMD level is subject to measurement error. Replicate single gradings of AMD from fundus photographs were used to estimate the matrix of misclassification probabilities, using a latent class model for diagnostic accuracy in the absence of a known gold standard^42,43; the extension of Lo's estimator was used to ensure stochastic ordering of the misclassification probabilities.^44,45 To be specific, the likelihood of a set of k gradings of a single photograph, g₁, g₂,…, g_k, is given by Σ_s π(s) p(g₁|s) p(g₂|s)…p(g_k|s), where s is the unknown (latent) true grade for the photograph, π(s) is the prevalence of grade s in the reproducibility sample, and p(g|s) is the probability of observed grade g for a photograph with true grade s. This model assumes that (1) the gradings (g₁, g₂,…, g_k) are conditionally independent given the true AMD state (s) and (2) the (mis)classification probabilities are constant within and across subjects. With these assumptions, the unknown parameters (π(s), p(g|s)) can be estimated via maximum likelihood.

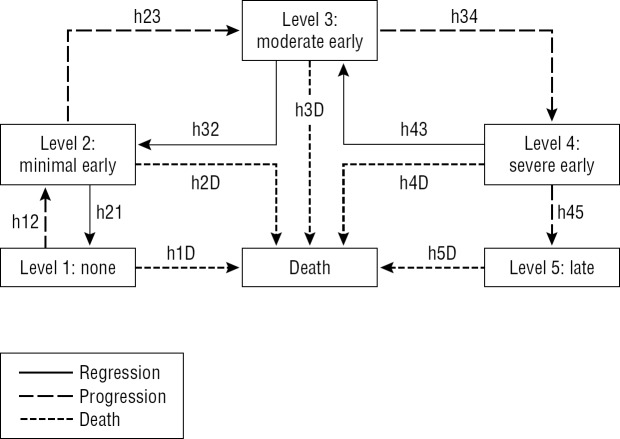
The Figure illustrates the underlying MSM; arrows indicate possible instantaneous transitions. Instantaneous transitions (the next state to which the individual moves and the time of the change) were allowed between adjacent AMD states with one exception; based on clinical observation, regression from late AMD (level 5) to severe early AMD (level 4) was not allowed. Model selection based on the Akaike information criterion (AIC)⁴⁶ was used to evaluate the need for covariate effects on other instantaneous transitions (incidence/progression, regression, or mortality).

Figure.

Transition diagram for 5-level AMD scale. Arrows indicate possible instantaneous transitions between states. hXY indicates hazard for instantaneous transition from state X (1, 2, 3, 4, or 5) to state Y (1, 2, 3, 4, 5, or D [death]). Reprinted with permission from Gangnon RE, Lee KE, Klein BE, Iyengar SK, Sivakumaran TA, Klein R. Effect of the Y402H variant in the complement factor H gene on the incidence and progression of age-related macular degeneration: results from multistate models applied to the Beaver Dam Eye Study. Arch Ophthalmol. 2012;130:1169–1176. Copyright 2012 American Medical Association. All rights reserved.

Transitions are governed by up to 12 transition intensities, one for each possible instantaneous transition between states (represented by arrows in the Fig.), which represent the hazard of moving between states. Dependence of transition intensities on age, sex, and CFH Y402H genotype was specified by using log-linear regression models. Age was entered as a linear term and updated annually. Sex and CFH Y402H genotype were entered by using indicator variables. Covariate effects on transitions within the AMD scale were unconstrained. Covariate effects on transitions to death were constrained to be equal, but intercepts were allowed to vary.

Analyses were conducted in R⁴⁷ by using the msm package.⁴⁸ Covariate effects on transition intensities are summarized as hazard ratios. We calculated estimated transition probabilities to each AMD state (and death) after 5 years and estimated cumulative incidence of each AMD state (and death) for specified subgroups. Cumulative incidence calculations used annual assessments of AMD status; subjects were assigned to the most severe AMD state observed at or before the current age.

Results

Of the 4973 subjects seen at any study visit, 134 were excluded for ungradable AMD status at all visits, and 460 were excluded for missing CFH Y402H genotype; 4379 subjects contributed data from 12,640 BDES follow-up intervals (up to four per subject). Table 2 displays characteristics of subjects at the start of each interval by observed AMD level. Subjects with more severe AMD were older and more likely to be female, to have CFH Y402H genotype CT or CC, and to be seen at later visits. Similar relationships were seen among subjects with partial AMD severity information (data not shown).

Table 2.

Characteristics of the Cohort by Current AMD Status (Worse Eye) at the Beginning of the Beaver Dam Eye Study Follow-up Intervals

	No. (%)*
Characteristic	No AMD, L1, n = 8474	Minimal Early AMD, L2, n = 1524	Moderate Early AMD, L3, n = 833	Severe Early AMD, L4, n = 250	Late AMD, L5, n = 294
Age, mean (SD), y	63 (10)	67 (10)	73 (10)	76 (9)	80 (8)
Male sex	3644 (43)	736 (48)	357 (43)	82 (33)	106 (36)
Participated in examination
BDES 1	3151 (37)	530 (35)	247 (30)	47 (19)	75 (26)
BDES 2	2185 (26)	444 (29)	239 (29)	64 (26)	67 (23)
BDES 3	1724 (20)	316 (21)	197 (24)	70 (28)	70 (24)
BDES 4	1414 (17)	234 (15)	150 (18)	69 (28)	82 (28)
CFH Y402H genotype
TT	3482 (41)	594 (39)	287 (34)	66 (26)	43 (15)
CT	3903 (46)	743 (49)	404 (48)	138 (55)	180 (61)
CC	1089 (13)	187 (12)	142 (17)	46 (18)	71 (24)

L, level. Reprinted with permission from Gangnon RE, Lee KE, Klein BE, Iyengar SK, Sivakumaran TA, Klein R. Effect of the Y402H variant in the complement factor H gene on the incidence and progression of age-related macular degeneration: results from multistate models applied to the Beaver Dam Eye Study. Arch Ophthalmol. 2012;130:1169–1176. Copyright 2012 American Medical Association. All rights reserved.

^* No. (%) of subject follow-up intervals.

Misclassification of AMD State

Replicate AMD grades were available for 89 different retinal photograph sets. The number of replicate grades for a given photograph ranged from 17 to 74 (median, 20; mean, 36). Table 3 displays the observed agreement of replicate grades for the same photographs. Observed agreement of the replicate grade for no AMD was 96% exact agreement, for level 2 it was 62%, for level 3 it was 39%, for level 4 it was 59%, and for late AMD it was 87%.

Table 3.

Observed Agreement of Replicate Gradings of Same Photographs

AMD Level (Second Grading)	AMD Level (First Grading)
	No AMD (Level 1) N = 101,159		Minimal Early AMD (Level 2) N = 11,614		Moderate Early AMD (Level 3) N = 11,333		Severe Early AMD (Level 4) N = 14,591		Late AMD (Level 5) N = 31,847
	No.*	%	No.*	%	No.*	%	No.*	%	No.*	%
1	97,158	96	1,808	16	1,379	12	768	<1	46	<1
2	1,808	2	7,202	62	2,505	22	99	<1	0	0
3	1,379	1	2,505	22	4,434	39	2,032	18	983	3
4	768	<1	99	<1	2,032	18	8,590	59	3,102	10
5	46	<1	0	0	983	9	3,102	10	27,716	87

* No., N, number of paired gradings.

Table 4 displays estimated misclassification probabilities for the underlying, unobserved true AMD states. There is an estimated probability of <1% that a participant with no AMD will be falsely graded as having AMD, but the probabilities that subjects with level 2 or level 3 will be falsely graded as having no AMD are relatively higher (16.2% and 6.5%, respectively). The probability of overgrading level 2 as level 3 was 20.9%, level 3 as level 4 was 28.4%, and level 4 as late AMD was 23.2%. The probability of undergrading level 4 as level 3 was 10.8%.

Table 4.

Estimated Misclassification Probabilities (%, 95% Confidence Interval)

True State	Observed State
	Level 1	Level 2	Level 3	Level 4	Level 5
Level 1	99.31	0.23	0.39	0.03	0.04
	(97.74–99.79)	(0.01–0.61)	(0.01–1.69)	(0.00–0.15)	(0.00–0.06)
Level 2	16.22	62.37	20.87	0.47	0.06
	(2.32–29.78)	(47.66–84.57)	(5.49–27.38)	(0.01–1.55)	(0.02–0.15)
Level 3	6.47	2.29	61.98	28.35	0.90
	(0.06–17.70)	(0.03–30.20)	(37.10–90.97)	(1.97–41.10)	(0.05–1.57)
Level 4	0.07	1.75	10.79	64.16	23.24
	(0.03–3.51)	(0.04–11.03)	(0.06–52.74)	(43.36–94.10)	(0.23–39.85)
Level 5	0.03	0.03	3.31	1.82	94.81
	(0.01–0.06)	(0.01–0.06)	(0.02–8.73)	(0.10–17.95)	(79.11–99.71)

Level 1, no AMD; level 2, minimally severe early AMD; level 3, moderately severe early AMD; level 4, severe early AMD; level 5, late AMD.

Covariate Effects on Transition Intensities

Parameter estimates are presented in Table 5 for the MSM that does not account for misclassification and in Table 6 for the MSM that accounts for misclassification. When accounting for misclassification, a reduced model with no covariate effects (age, sex, or CFH genotype) on regression (level 2 to level 1, level 3 to level 2, or level 4 to level 3) was selected by AIC.

Table 5.

Estimated Covariate Effects on Transition Intensities or Hazards Without Accounting for Misclassification

	Incidence or Progression (95% CI)				Regression (95% CI)			Mortality (95% CI)
	Level 1 to Level 2	Level 2 to Level 3	Level 3 to Level 4	Level 4 to Level 5	Level 2 to Level 1	Level 3 to Level 2	Level 4 to Level 3	Any AMD to Death
Baseline intensity,
relative to mortality	1.17	5.18	3.98	3.52	2.52	4.17	5.17
	(0.99–1.41)	(3.79–7.08)	(2.60–6.07)	(1.87–6.60)	(1.74–3.66)	(2.56–6.78)	(1.89–14.1)
Covariate HR
Age, per 5 years	1.43	1.31	1.24	1.27	1.04	0.91	0.91	1.66
	(1.37–1.49)	(1.24–1.39)	(1.14–1.34)	(1.14–1.41)	(0.95–1.13)	(0.81–1.03)	(0.68–1.21)	(1.61–1.70)
Sex, male	0.96	0.88	0.69	1.17	0.83	1.30	0.46	1.55
	(0.82–1.13)	(0.72–1.08)	(0.52–0.91)	(0.82–1.68)	(0.60–1.14)	(0.83–2.04)	(0.14–1.50)	(1.42–1.69)
CFH Y402H genotype
TT	1.00	1.00	1.00	1.00	1.00	1.00	1.00	1.00
CT	1.35	1.09	1.44	1.60	0.87	0.49	0.49	0.94
	(1.13–1.60)	(0.87–1.36)	(1.04–1.98)	(1.03–2.48)	(0.62–1.22)	(0.23–1.04)	(0.16–1.48)	(0.85–1.01)
CC	1.98	1.73	1.30	1.72	0.92	0.60	0.41	0.98
	(1.57–2.49)	(1.29–2.33)	(0.86–1.94)	(1.01–2.91)	(0.54–1.56)	(0.37–0.97)	(0.09–1.83)	(0.86–1.12)
AMD severity
Level 1								1.00
Level 2								1.04
								(0.82–1.32)
Level 3								1.01
								(0.79–1.30)
Level 4								1.05
								(0.71–1.55)
Level 5								1.37
								(1.15–1.62)

CI, confidence interval; HR, hazard ratio. Level 1, no AMD; level 2, minimally severe early AMD; level 3, moderately severe early AMD; level 4, severe early AMD; level 5, late AMD. Estimates are mutually adjusted for all other covariates listed in the table. Bold text indicates results that were significant at the 5% level. Reprinted with permission from Gangnon RE, Lee KE, Klein BE, Iyengar SK, Sivakumaran TA, Klein R. Effect of the Y402H variant in the complement factor H gene on the incidence and progression of age-related macular degeneration: results from multistate models applied to the Beaver Dam Eye Study. Arch Ophthalmol. 2012;130:1169–1176. Copyright 2012 American Medical Association. All rights reserved. Modified to add the Baseline Intensity row.

Table 6.

Estimated Covariate Effects on Transition Intensities or Hazards Accounting for Misclassification

	Incidence or Progression (95% CI)				Regression (95% CI)			Mortality (95% CI)
	Level 1 to Level 2	Level 2 to Level 3	Level 3 to Level 4	Level 4 to Level 5	Level 2 to Level 1	Level 3 to Level 2	Level 4 to Level 3	Any AMD to Death
Baseline intensity,
relative to mortality	0.88	1.54	4.73	2.49	0.44	0.10	0.20
	(0.70–1.41)	(1.07–2.21)	(1.89–11.83)	(0.80–7.70)	(0.29–0.68)	(0.01–1.70)	(0.02–2.20)
Covariate HR
Age, per 5 years	1.58	1.51	1.29	1.25				1.67
	(1.50–1.67)	(1.39–1.64)	(1.14–1.46)	(0.99–1.57)				(1.62–1.71)
Sex, male	0.90	0.63	0.85	1.25				1.55
	(0.74–1.10)	(0.47–0.85)	(0.56–1.29)	(0.99–1.57)				(1.42–1.70)
CFH Y402H genotype
TT	1.00	1.00	1.00	1.00				1.00
CT	1.46	1.61	1.72	1.58				0.94
	(1.17–1.82)	(1.18–2.20)	(1.07–2.76)	(0.63–3.99)				(0.86–1.03)
CC	2.27	2.75	1.62	1.39				1.00
	(1.71–3.01)	(1.81–4.18)	(0.92–2.83)	(0.45–4.32)				(0.87–1.14)
AMD severity
Level 1								1.00
Level 2								1.13
								(0.93–1.36)
Level 3								0.68
								(0.35–1.30)
Level 4								1.60
								(0.94–2.75)
Level 5								1.23
								(1.01–1.50)

Level 1, no AMD; level 2, minimally severe early AMD; level 3, moderately severe early AMD; level 4, severe early AMD; level 5, late AMD. Estimates are mutually adjusted for all other covariates listed in the table. Bold text indicates results that were significant at the 5% level.

Older age was associated with increased AMD incidence and progression and mortality (Tables 5, 6). Being male was associated with increased mortality, but not with AMD incidence or progression. CFH Y402H genotypes CC and CT were associated, relative to genotype TT, with increased AMD incidence and progression, but not with mortality. Late AMD was associated with increased mortality relative to no AMD, but earlier stages of AMD were not.

While misclassification did not change the qualitative findings for covariate effects, it had substantial impacts on the quantitative results. Estimated age effects on incidence and progression to moderately severe early AMD and estimated CFH effects on incidence and progressions to moderately severe and severe early AMD were attenuated in MSMs that did not account for misclassification. Estimated baseline intensities for incidence/progression and regression of AMD were exaggerated in MSMs that did not account for misclassification. The estimated effect of late AMD on mortality was similarly exaggerated in MSMs that did not account for misclassification (Tables 5, 6).

Five-Year Transition Probabilities by Age, Sex, and CFH Y402H Genotype

For individuals free of AMD at age 50 years, rates of progression to level 2 (incidence of early AMD) at age 55 years was lower in MSMs that accounted for misclassification (1.2%–2.9%) than in MSMs that did not account for misclassification (2.1%–4.2%). For those free of AMD at age 70 years, rates of progression to level 2 at age 75 years were similar between MSMs that accounted for misclassification (6.1%–12.8%) and MSMs that did not (6.7%–11.3%). At age 90 years, progression to level 2 or above at age 95 years was somewhat higher in MSMs that accounted for misclassification (10.8%–32.0%) than in MSMs that did not (10.1%–26.7%), while rates of progression to level 3 or above were similar between the two models (3.0%–22.9% with misclassification; 4.4%–18.3% without).

For individuals with AMD at level 2 at age 50 years, regression to no AMD by age 55 years was common (11.7%–16.0%) in MSMs without misclassification, but relatively infrequent (3.8%–3.9%) in MSMs with misclassification; progression to level 3 was much less common in MSMs with misclassification (1.9%–7.7% vs. 9.1%–18.9%). At age 70 years, regression remained common (8.6%–13.9%) in MSMs without misclassification and infrequent (2.8%–3.2%) in MSMs with misclassification, while progression to level 3 or above was less frequent in MSMs with misclassification (8.7%–33.4% vs. 23.5%–45.7%). At age 90 years, regression was infrequent (1.3%–4.4%) in MSMs without misclassification and rare (0.3%–0.9%) in MSMs with misclassification; progression to level 3 or above was less frequent in MSMs with misclassification (12.8%–40.4% vs. 17.7%–38.5%).

Cumulative Incidence of AMD for Individuals With No AMD at Age 45 Years

Estimated cumulative incidence of level 2 or higher was lower in MSMs with misclassification than in MSMs without misclassification. For example, cumulative incidence of level 2 by age 65 years was 16.1% (vs. 23.0%) for women with the CC genotype and 6.6% (vs. 11.7%) for men with the TT genotype; by age 80 years, it was 47.5% (vs. 61.2%) and 21.1% (vs. 34.1%), respectively; by age 100 years, it was 64.8% (vs. 67.7%) and 31.6% (vs. 38.6%), respectively. Cumulative incidence of late AMD was similarly lower in MSMs without misclassification.

Simulated Realizations of AMD History for Individuals With No AMD at Age 45 Years

We simulated realizations of AMD history for 100 subjects (for each sex and CFH genotype combination) free of AMD at age 45 years, from the MSM with misclassification and the MSM without misclassification. The occurrence of any AMD regression was rare (1%–4%) using the MSM that accounted for misclassification, while it was relatively common (14%–21%) using the MSM that did not account for misclassification.

Discussion

In a cohort followed up for 20 years, we showed that, after accounting for misclassification of observed AMD states, true regression of AMD is rare (lifetime occurrence of 1%–4%). Relatively high rates of apparent regression in AMD levels between consecutive BDES visits (10% of eyes at level 2; 9% at level 3; and 7% at level 4) likely reflect misclassification due to media opacity, photographic artifacts, and grader error. While multiple gradings for AMD, including masked side-by-side comparisons of photographs, can minimize the impact of grader error, it is difficult, if not impossible, to remove other sources of misclassification directly. The MSMs with misclassification used here provide a valuable tool for accounting for misclassification analytically.

Misclassification rates used in the MSMs were estimated from replicate single gradings of photographs by two graders rather than the full grading system, which uses a preliminary grading, a detailed grading, edits, adjudication, and longitudinal review of apparent progression. As such, the misclassification estimates used in these analyses are overestimates of the errors in the grading system. For example, after longitudinal review, rates of apparent progression by one or more steps on a 5-step scale between consecutive BDES visits decrease by up to 4% (from 17%–13%), while rates of apparent regression decrease by up to 2.4% (from 7.5%–5.1%). However, our assessment of misclassification from replicate gradings of a single photograph fails to account for other sources of misclassification, including photographic quality and day-to-day biological variation in the appearance of the eye, which are likely greater in importance than the grading error. As such, if anything, the misclassification estimates used in the MSMs may be understating the true magnitude of misclassification.

In conclusion, we provide an approach using MSMs to adjust for the effect of misclassification of the progression and regression of AMD assessed by grading of fundus photographs and categorizing AMD by using a 5-step AMD severity scale. These data strongly suggest the need for multiple gradings by multiple graders, including longitudinal review, to attempt to reduce misclassification as much as possible.