SUMMARY
There is accumulating neural evidence to support the existence of two distinct systems for guiding action-selection in the brain, a deliberative “model-based” and a reflexive “model-free” system. However, little is known about how the brain determines which of these systems controls behavior at one moment in time. We provide evidence for an arbitration mechanism that allocates the degree of control over behavior by model-based and model-free systems as a function of the reliability of their respective predictions. We show that inferior lateral prefrontal and frontopolar cortex encode both reliability signals and the output of a comparison between those signals, implicating these regions in the arbitration process. Moreover, connectivity between these regions and model-free valuation areas is negatively modulated by the degree of model-based control in the arbitrator, suggesting that arbitration may work through modulation of the model-free valuation system when the arbitrator deems that the model-based system should drive behavior.
INTRODUCTION
It has long been known that there are multiple competing systems for controlling behavior, a deliberative or “goal-directed” system, and a reflexive “habitual system”(Balleine and Dickinson, 1998). Distinct neural substrates have been identified for these systems, with regions of prefrontal and anterior striatum implicated in goal-directed control and a region of posterior lateral striatum involved in habitual control (Balleine and Dickinson, 1998; Balleine and O’Doherty, 2010; Graybiel, 2008; Tricomi et al., 2009; Valentin et al., 2007; De Wit et al., 2009; Yin and Knowlton, 2004).
However, the issue of how control passes from one system to the other has received scant empirical attention. Addressing this issue is crucial for explaining how unified behavior emerges through the interaction of these different systems, as well as for understanding why the balance between goal-directed and habitual systems might sometimes break down in diseases such as addiction or obsessive compulsive disorder. For example, persistent drug taking behavior might reflect failure to suppress inappropriate drug-related stimulus-response habits in spite of the fact that such behavior ultimately leads to highly adverse consequences (Everitt and Robbins, 2005).
To address how the arbitrator works we deployed a computational framework in which goal-directed and habitual behavior are expressed as different forms of reinforcement-learning. Goal-directed learning is described as model-based, in which the agent uses an internal model of the environment in order to compute the value of actions online (Daw et al., 2005; Doya et al., 2002), while habitual control is proposed to be model-free in that “cached” values for actions are acquired on the basis of trial and error experience without any explicit model of the decision problem being encoded (Daw et al., 2005). Empirical evidence for this computational distinction has emerged in recent years (Daw et al., 2011; Gläscher et al., 2010; Wunderlich et al., 2012). It has been hypothesized (Daw et al., 2005) but never directly tested, that an arbitrator evaluates the performance of each of these systems and sets the degree of control that each system has over behavior according to the reliability of those predictions. Here we aimed to elucidate the neural mechanisms of this arbitration process in the human brain.
RESULTS
Computational Model of Arbitration
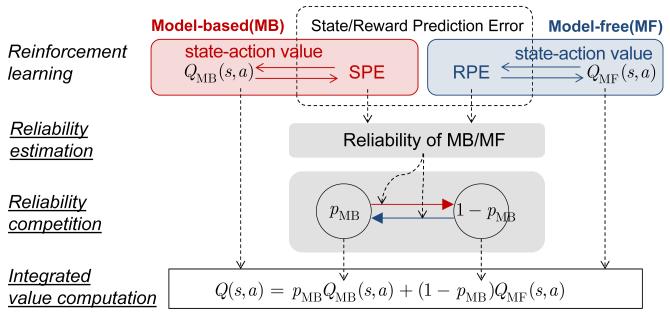
The arbitration model consists of three levels of computation – model-base/model-free learning, reliability estimation, and reliability competition. The first layer consists of model-based and model-free learning, which generates the state and reward prediction error, respectively. The second layer provides an estimation of reliability for the two learning models. Specifically, we start with a standard Bayesian framework that formally dictates prior successes and failures in predicting task contingencies in the form of prediction error. The next layer provides a competition between the two reliabilities. This bottom-up design allows us to systematically test six types of arbitration strategies (see Supplemental Methods for details).
When building the arbitrator, we leveraged the fact that learning in these two systems is suggested to be mediated by means of prediction error signals that indicate discrepancies between expected and actual outcomes. Whereas the model-free system uses a reward prediction error (RPE) that reports the difference between actual and expected rewards (Montague et al., 1996; Schultz et al., 1997), the model-based system uses a “state prediction error” (SPE) to learn and update the model of the world – in particular to acquire state-action-state transition probabilities (Gläscher et al., 2010). Our arbitrator made inferences about the degree of reliability of the model-based and the model-free systems by determining the extent to which the SPE signals and RPE signals are estimated to be high or low. If the state prediction error is close to zero, this means that the model-based system has a good and reliable estimate of the world, whereas if the state prediction error is high, this means that the model-based system has a very inaccurate and hence unreliable model of the world. Similarly, if RPEs are minimal, this means that the model-free system likely has a very accurate estimate of the expected rewards available for different actions at that moment in time, while high RPEs implies that the model-free system has inaccurate and hence unreliable predictions about future reward. To make these reliability inferences for the model-based system we formulated a bottom-up Bayesian model that estimates the probability that the SPE is set to zero at a particular moment in time. The reliability of the model-based (RelMB) is defined as the ratio of the mean prediction and the uncertainty of that prediction for SPE, a variance-to-mean ratio that is formally known as an inverse of the index of dispersion (Ma et al., 2006; Pennini and Plastino, 2010) (Figure S1A; see Supplemental Methods for definitions). For the model-free system, a similar Bayesian framework could also be used, substituting the RPE for the SPE (dualBayesArb model; see, Supplemental Methods). However, the model-free system might not use sophisticated Bayesian machinery to estimate reliability, but rather deploy a much simpler mechanism for tracking the approximate degree of reliability of the RPE (mixedArb model). A candidate mechanism would be to use the absolute value of the RPE signal to learn trial-by-trial predictions about the degree of reliability of the RPE in a model-free manner (Li et al., 2011; Preuschoff et al., 2008; Takahashi et al., 2011). Once the reliability signals are estimated for the two systems then a dynamical two-state transition rule borrowed from biophysics (see Supplemental Methods), allows these two reliability indices to compete with each other in order to set a weight (model-choice probability PMB) that governs the extent to which the model-based vs model-free systems control behavior. When PMB is high, control is dominated by the model-based system, whereas when PMB is low, control is dominated by the model-free system. Thus, control by the model-based vs model-free systems over behavior is not implemented in an all or nothing fashion, but rather the level of control each system exerts is dynamically weighted by the degree of reliability in each system (Figure S1B). Also, due to the computational demands of having to hold a model in memory, and operate on the model to dynamically compute values, model-based control is likely to be more cognitively effortful than model-free. Thus, it is reasonable to assume that at least part of the consideration should include a trade-off about cognitive complexity. The transition rule incorporates a bias term accommodating the fact that habits involve less cognitive effort than goal-directed behavior and thus should be favored, assuming all else is equal. Simulations showed that this control framework could successfully capture behavioral characteristics of goal-directed and habitual learning in the literature, such as early devaluation sensitive control of behavior by the model-based system followed by a gradual transition to devaluation insensitive model-free control with repeated training (Adams and Dickinson, 1981) (Figure S1C).
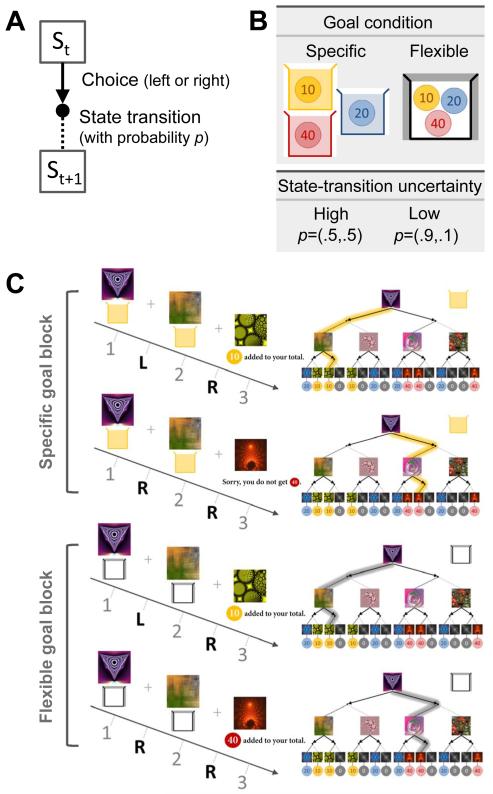
Markov Decision Task: Goal and State-transition Uncertainty
Motivated by our proposed control scheme, we designed a decision task in which on different trials, the structure of the task should optimally favor behavioral control by either the model-based or model-free systems (Figure 1 and Figure S2A). On each trial the participant makes sequential binary choices through a 2-layer Markov decision problem (MDP) in order to obtain different colored tokens that are redeemable for money (Figure 1A). The experiment consists of two main trial types – specific and flexible goal (Figure 1B). On specific goal trials, the participant is informed at the outset that only one color of token is redeemable on that trial (e.g. blue tokens can be redeemed for money, but the other color tokens have no value). The color of the tokens redeemable is switched on a trial-by-trial basis (Figure 1C). On flexible goal trials by contrast, the participant can collect any color token in order to obtain monetary reward. Specific goal trials should encourage a more model-based strategy because reward-prediction errors will be on average high due to constant changes in goal state-values, while flexible goal-trials should enable gradual transition to the model-free control scheme. In addition to this goal manipulation, we also manipulated state-action-state transition probabilities within the MDP, so that on some occasions uncertainty in state-action-state transitions is high (0.5 vs 0.5), and on other occasions uncertainty in state-action-state transitions is low (0.9 vs 0.1). Such differences in the state-action-state transition probabilities across trials are designed to elicit either high or low state-prediction errors on average, which should favor model-free vs model-based control respectively (Figure S2B). This was reflected in our reliability estimation (Figure 2 and Figure S3), which essentially leads the arbitration model to successfully adapt to the changing environment. Twenty two adult participants (six females, age between 19-40) performed the task while being scanned with fMRI.
Figure 1.
Task design. (A) Sequential two-choice Markov decision task. Participants move from one state to the other with a certain state-transition probability p following a binary choice (left or right) (B) Illustration of the specific goal condition, in which the color of the collecting box (either yellow, blue, or red) should match the color of the coin, and the flexible condition, in which participants are allowed to collect any kind of coin. The high uncertainty condition corresponds to p=(0.5,0.5) and the low uncertainty condition corresponds to p=(0.9,0.1). (C) Illustration of the task. The specific goal block requires participants to rely on a model-based strategy for guiding choices in each state, while, in the flexible goal block, an initial model-based strategy during early experience can give way to a model-free strategy after extensive experience.
See also Figure S2.
Figure 2.
Computational hypothesis to account for arbitration between model-based and model-free learning strategies. The Bayesian model computes reliability using the state-prediction error used to update state-action values of the model-based learning system and a Pearce-hall type associability model computes reliability using the reward-prediction error used for the update of the state-action value of the model-free. The computed reliability functions as a transition rate for the two-state transition model, in which each state represents the probability of choosing the model-based learning strategy (PMB) and the model-free (1-PMB), respectively. The state-action value regulating the actual choice behavior is given by the weighted average of values from the two reinforcement learning systems.
Behavioral Results
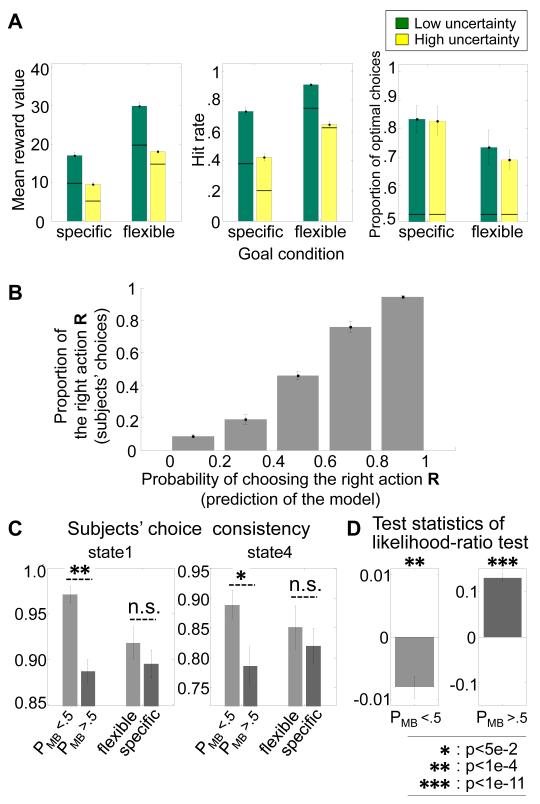
Subjects performed the task successfully in all conditions (Figure 3A). To test whether uncertainty had an influence on a subject’s outcome experience while performing the task, we ran a generalized linear model regression analysis on hit rate (Figure 3A), for which the distribution function was chosen to be the Bernoulli and the link function was the probit model. There is a main effect of the goal and the uncertainty condition (the coefficient estimate of the goal and the uncertainty condition was 0.8738 (p=1.5e-16) and -0.6355 (p=4.1e-11), respectively). The effect of state transition uncertainty is greater in the specific condition than in the flexible condition (coefficient estimate of the interaction = -0.16; p=1e-2). This suggests that the state-transition uncertainty does considerably affect subjects’ performance differently for each goal condition. It is also consistent with our prediction that the model-based system, which tends to gain control in the specific goal condition, is more sensitive to state-uncertainty than the model-free.
Figure 3.
Behavioral Results. (A) Performance of the subjects in the form of the mean total reward accrued, the reward rate, and the proportion of optimal choices. The left bar graph shows the average of reward value received in each trial, averaged over all subjects. The middle bar graph shows the reward rate, the proportion of trials the rewarding goal is reached. The right bar graph shows the optimal choices, defined by the ideal agent’s behavior in each condition (Figure S2A). The bold line in the bars refers to the baseline given by the random agent making choices. The green color code corresponds to the low state-transition uncertainty condition, and the yellow corresponds to the high uncertainty condition. Error bars = SEM across subjects. (B) Performance of the arbitrator in capturing variation in subjects’ choice behavior,to demonstrate that the model is performing well in predicting subjects’ choices. The model predicted probability of choosing the right action has been split into five equal sized bins. The proportion of subjects’ right choices increases with the model’s action probability. Error bars are SEM. (C) Performance of the arbitrator in capturing variation in model-based and model-free choice strategies on the consistency of participants’ choice behavior on a trial-by-trial basis plotted separately for situations where the arbitrator favors model based control (PMB>0.5), compared to when the arbitrator favors model-free control (PMB<0.5). The choice consistency is the proportion of changes of choices from trial to trial in each state. Choice consistency is significantly higher when the arbitrator predicts predominantly model-free control compared to when it predicts predominantly model-based control. On the other hand, simply plotting the choice consistency as a function of the experimental conditions: specific vs flexible goal is not sufficient to reveal robust differences on this behavioral measure. Results are plotted separately for two different states in the task (State 1 and 4 = the state at layer 1 and 2 of the task, respectively. States 2, 3, and 5 are rarely sampled by participants, because they lead to relatively low valued outcomes and hence are not plotted here as there are insufficient samples to enable meaningful performance plots to be extracted. Error bars are SEM. (D) Results from a log-likelihood test comparing the degree to which model-based vs model-free reinforcement-learning accounts best for participants’ choices, plotted separately for the (i) situations in which model-based control (PMB>0.5) and (ii) situations in which the arbitrator favors model-free control (PMB<0.5). The model-based and the model-free were fitted independently to prevent circularity. Test statistics of likelihood-ratio test refers to log-likelihood value of the model-based minus the model-free. The more negative the ratio, the more the model-free system accounts better for behavior, while the more positive the ratio the more the model-based system accounts better for behavior. As can be seen, in the strategic goal-condition the ratio test favors the model-free system (significant at p<1e-4), while in the flexible goal-condition the ratio test favors the model-based system (significant at p<1e-11).These findings thereby validate the task manipulations by showing that the task can successfully manipulate control to be governed predominantly by either the model-based or model-free system. Error bars are SEM.
See also Table S2.
Model Comparison of Arbitration Process
We tested six different versions of our arbitration process to establish which version of reliability computation best explains the behavioral data (see Supplemental Methods – Model-Comparison for details). We found that the versions of the arbitrator with a dynamical threshold, accommodating the fact that behavior tends to move from model-based to model-free control over time due to the increased cognitive effort associated with model-based control, performed significantly better than versions without the threshold (Table S1). We also compared a version of the arbitrator in which the model-free reliability was estimated using a full Bayesian mechanism or else via the alternate absolute RPE approximation described above. The arbitrator in which the level of control each system exerts is dynamically weighted by the degree of reliability in each system and the absolute RPE estimate is implemented on the model-free side (mixedArb-dynamic model; although the model-based arbitrator was still the full Bayesian version. Refer to Supplemental Methods for full details) performed better than the full Bayesian mechanism on the model-free side (dualBayesArb-dynamic model) in terms of the trade-off between model fit and model complexity (Wilcoxon signed rank test on BIC score data: p<0.05; Table S1) and also better than the other alternative arbitration strategies including the original arbitration scheme proposed by Daw (UncBayesArb ;Daw et al., 2005) (Wilcoxon signed rank test on BIC score data: p<0.01). We therefore feature the best version of the arbitrator (mixedArb-dynamic model; Table S2) as the primary model used in this study, although the next best model (dualBayesArb-dynamic model) and the original arbitrator form proposed by Daw (Daw et al., 2005) is used in a formal model comparison of the fMRI data below (see also Figure S4A and Figure S4B for fMRI analyses with mixedArb-dynamic model and dualBayesArb-dynamic model, respectively, and Figure S4C for the comparison of the model choice probability between the two models).
Relationship between Arbitration Model and Choice Behavior
To demonstrate that the arbitrator captures variation in subjects’ choice behaviors, we computed the proportion of times subjects took the right action (as opposed to the left action) and plotting this against the model-predicted probability of choosing the right action (binned into each size bins) (Figure 3B). As can be seen from the figure, the model does very well in predicting participant’s choice behavior.
To further examine whether our control framework predicts participants’ choice behavior, we compared the choice consistency of the subjects in chunks of trials in which model-based control is predicted by the arbitrator against other trials in which model-free control is predicted. The choice consistency quantifies the behavioral sensitivity exhibited to task structure changes. If the model-based learning strategy is preferred, then we would expect participants to exhibit a flexible profile of choice behavior due to the fact that knowledge about state-transition probabilities facilitates rapid sensitivity to the changes of the environment. If the model-free learning strategy is preferred, then we would expect otherwise. The analysis indicates that subjects’ choice consistency is well accounted for by our control framework (Figure 3C). The more the arbitrator favors the model-based learning strategy the less consistent participants’ choices become. To provide a statistical measure of the model-based influence on choice, we used a likelihood-ratio test (Figure 3D) in which we separately fit the model-based and model-free algorithms to behavior and computed the ratio between the likelihoods for the two models. This analysis revealed that choice behavior is better explained by the model-based learner when the arbitrator predicts that behavior should be under model-based control, while the choice behavior is better explained by the model-free learner when the arbitrator predicts that behavior should be predominantly under model-free control.
Neural Correlates of Arbitration
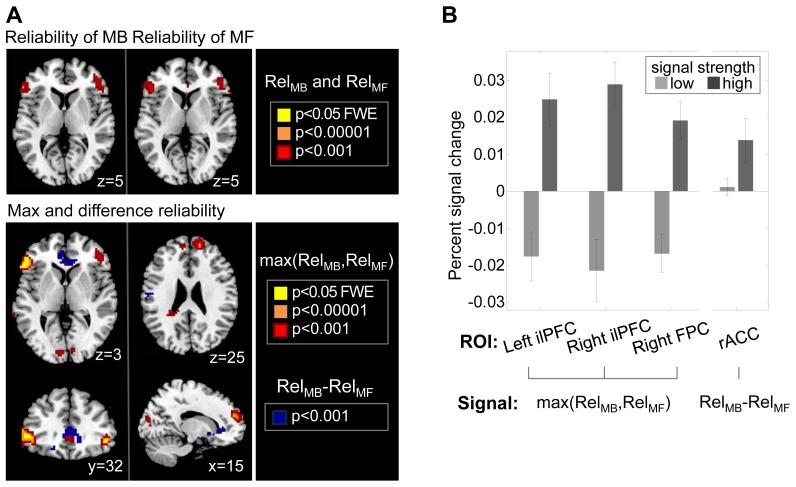
To address the neural computations underlying control between the model-based and model-free strategies, we regressed each of our computational signals against the fMRI data (Figure S4A, and see also Table S3). To validate our approach we initially attempted to replicate previous findings indicating differential neural encoding of SPE and RPE. Consistent with previous results we found SPE signals in dorsolateral prefrontal cortex and intraparietal sulcus (all p<0.05 FWE corrected), as well as in anterior insula, while RPE signals were found in the ventral striatum (p<0.05 FWE) (Gläscher et al., 2010; McClure et al., 2003; O’Doherty et al., 2003). We then tested for the computational signals needed to generate reliability estimates for the two systems. The uncertainty of zero SPE, which is used as an input for computing model-based reliability (Daw et al., 2005), was negatively correlated with activity in multiple brain areas - dorsomedial prefrontal cortex, parts of supplementary motor area, inferior parietal lobule, and thalamus (all p<0.05 FWE corrected, Table S3). The estimate of absolute RPE used by the model-free system to generate a reliability estimate was found in a region of caudate nucleus (p<0.05 cluster level corrected, Table S3).
Next, we investigated neural correlates for the reliability signals. A region of inferior lateral prefrontal cortex bilaterally was found to correlate with the reliability of both the model-based and the model-free systems (peak z-scores were 5.18, and 4.45 respectively), although activity in these areas correlated best with the reliability of whichever system had the maximum reliability (max(RelMB,RelMF; peak z-score: 5.68; p<0.05 FWE; Figure 4), alongside a region of right frontopolar cortex (FPC, p<0.05 cluster level corrected; Figure 4). The neural activities in these areas are significantly better explained by the reliability signals of our arbitration model (mixedArb-dynamic model) than the alternative hypotheses, such as the version implementing Bayesian estimation of reliability for both MB and MF (dualBayesArb-dynamic model) which showed the second best model goodness and the Bayesian value uncertainty arbitration (UncBayesArb; Daw et al., 2005) (Figure 5; see Supplemental Methods for further details). A region of ACC was also found to respond to the difference in the reliability between the two systems (RelMB-RelMF) (p<0.05 cluster level corrected; Figure 4). These findings suggest that anterior cingulate cortex may be involved in comparing reliabilities therefore forming an input into the arbitration process, while the presence in the ilPFC and FPC cortex of the “max” of the two reliabilities suggests that these regions may be involved in implementing the arbitration process itself.
Figure 4.
Neural correlates of reliability-based arbitration. (A) (Top) Bilateral Inferior lateral prefrontal cortex encodes reliability signals for the model-based (RelMB) and the model-free (RelMF) systems individually. The two reliabilities are, by and large, not highly correlated (mean:−0.26, standard deviation: 0.106), suggesting that our task successfully dissociates the model-based from the model-free. Effects significant at p<0.05 (FWE corrected) are shown in yellow. (Bottom) A region of rostral anterior cingulate cortex (rACC) was found to encode the difference in reliability between the model-based and model-free systems (RelMB-RelMF), while an area of bilateral ilPFC and right FPC was correlated with the reliability of whichever system had the highest reliability index on each trial (max(RelMB, RelMF)). (B) The mean percent signal change for a parametric modulator encoding a max and difference reliability signal in lateral prefrontal cortex (lPFC) and rostral anterior cingulate cortex (rACC). The signal has been split into two equal sized bins according to the 50th and 100th percentile. The error bars are S.E.M. across subjects.
Figure 5.
Results of a model comparison process on BOLD correlates of the arbitration process. For this we implemented a Bayesian model selection analysis, and illustrate voxels for which the exceedance probability is 0.9 in favor of a given model. UncBayesArb refers to the uncertainty-based arbitration used by Daw et al. (2005), dualBayesArb refers to the dualBayesArb-dynamic model, and mixedArb refers to the mixedArb-dynamic model. The colored blobs refer to the voxels in which exceedance proabability>0.9, indicating that the corresponding model provides a significantly better account for the neural activity in that region.
See also Figure S4.
Neural Correlates of Model-based and Model-free Value Signals
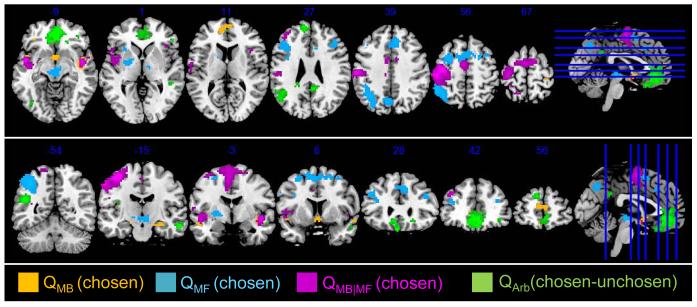
Next we tested for areas correlating with value signals computed by the two models. Shown in Figure 6 are the regions whose variance in neural activation is purely explained by QMB and QMF, respectively (Table S4). The chosen value of the model-based system (QMB), but not the model-free, is associated with activity in orbital and medial prefrontal cortex (omPFC) and parts of ACC (p<0.05, small-volume corrected, Table S4). The chosen value of the model-free (QMF), but not the model-based, is associated with activity in supplementary motor area (SMA; p<0.05 FWE corrected, Table S4), dorsomedial and dorsolateral prefrontal cortex (dmPFC and dlPFC) (p<0.05 cluster-level corrected, Table S4), significantly overlapping with value representation in right dlPFC and dmPFC (Hare et al., 2011; Rowe et al., 2010), and most notably in posterior putamen (significant at p<0.05, small volume corrected, Table S4) a region that has been implicated in habitual control and in model-free valuation in previous studies (Tricomi et al., 2009; Wunderlich et al., 2012). We also tested for regions commonly activated by either model-free and model-based value signals, revealing significant correlations in SMA and dmPFC (p<0.05 FWE and cluster-level corrected, respectively, Table S4). In order to guide behavior, the brain ultimately needs to compute an integrated value-signal in which model-based and model-free value signals are combined in a weighted manner determined by the output of the arbitrator (i.e. by PMB). We found significant correlations in ventromedial prefrontal cortex (vmPFC) with such a weighted signal corresponding to the difference in weighted values between the chosen and unchosen actions (Boorman et al., 2009; Hare et al., 2009; Rushworth et al., 2011) (p<0.05 FWE corrected, Table S4).
Figure 6.
Neural correlates of model-based and model-free value signals. QMB refers to the chosen value of the model-based system, QMF the chosen value of the model-free, the areas corresponding to QMB|MF respond to chosen values commonly for both systems. QArb refers to the encoding of the chosen minus un-chosen value signals, in which the value signals are a weighted combination of model-based and model-free values determined by the output of the arbitrator (PMB).
Neural Correlates of Value Integration
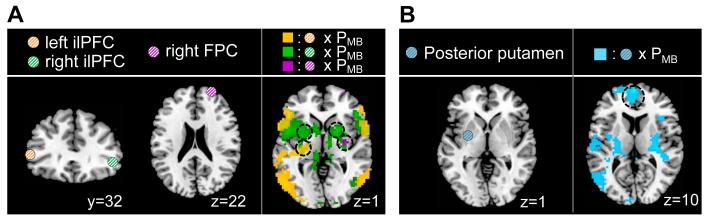
Our main novel finding is that a region of ilPFC as well as right FPC contains reliability signals that could be used to implement an arbitration between model-based and model-free control. However, in order to understand how the arbitration process might work, we next needed to characterize the nature of the interactions between the areas involved in encoding reliability and areas involved in encoding valuation within the model-free and model-based systems. To test for this we implemented PPI analyses, in which the physiological variable consisted of activity in left or right ilPFC cortex or FPC, and the psychological variable was the output of the dynamic transition model, PMB (Figure 7A; Table S5). Remarkably, we found a significant negative coupling between ilPFC and regions of the left posterior and mid-putamen, including the area of posterior putamen found to encode model-free valuation signals as well as in regions of supplementary motor cortex (p<0.05 small-volume and cluster-level corrected, respectively; see Figure S5A for a clear demonstration of the overlap between the results of the PPI and areas found to be active in model-free valuation). A negative coupling between FPC and right posterior putamen was also found (small-volume corrected; Table S5). We also looked for areas showing the opposite coupling, i.e. showing increased coupling when PMB is high, when behavior should be under model-based control. We did not find any significant effects in this case, suggesting that the arbitrator may work predominantly by acting on the model-free system, as opposed to acting directly on the model-based system. Second, we investigated modulation effects among the value areas by PMB (Figure 7B; Table S5). We found a strong negative modulation of the coupling between posterior putamen and vmPFC by PMB, (p<0.05 FWE), which strongly supports the hypothesis that model-free value signals are transmitted to vmPFC in order to be combined with model-based values as a precursor to generating choices (see Figure S5B for evidence that areas found in vmPFC in the PPI are specific to the integrated value area). Further, the strength of these connections appears to be modulated by the arbitrator.
Figure 7.
Neural correlates of value integration. (A) Connectivity analyses between reliability regions in inferior lateral prefrontal cortex and model-free value areas. The shaded circles represent seed regions from which physiological signals were extracted, and colored blobs show the psychophysiological interaction effect. Shown are significant negative correlations between activity in the left inferior lateral prefrontal cortex and a region of posterior putamen modulated by PMB (in orange), of the right inferior lateral prefrontal cortex and the bilateral anterior putamen modulated by PMB (in green), and also of the right FPC prefrontal cortex and the right posterior putamen modulated by PMB (in purple). (B) Connectivity analyses between model-value areas and vmPFC area involved in encoding integrated value signal. Shown in cyan color is the negative modulation of posterior putamen activity on ventromedial prefrontal cortex activity by PMB. All images are shown thresholded at p<0.001 for display purposes.
Effect of Reaction Time
We also tested for reaction time (RT) effects on behavior. When we compare RTs on “specific-goal trials” to those in “flexible-goal trials” there is indeed an effect of condition on RTs such that participants are slower on specific trials (where they have to select a particular goal based on which token is currently valuable) compared to when they do not (RT specific = 0.93 sec; RT flexible = 0.81 sec; paired t-test; t=5.56; p=1.61e-5).
Furthermore, when we correlate the probability that behavior is under model-based control (PMB) against RT we also find a modest albeit significant correlation in the majority of participants (median correlation coefficient=0.13; correlation coefficient test; p<1e-2 for 16 out of 22 participants). This likely reflects the possibility that model-based control is more effortful cognitively than model-free control.
On account of these RT effects in the behavioral data, an obvious concern is that RT effects could be confounded with some of the computational variables in our fMRI analysis. In order to address whether trial-by-trial changes in reaction time (RT) account for the effects reported in our fMRI data, we included reaction times as a covariate that competed for experimental variance in an additional fMRI analysis. After doing this, all of our main findings remain intact (and if anything the p-values improved marginally for our reliability signals), suggesting that reaction time per se does not explain the fMRI results.
DISCUSSION
We provide evidence for the existence in the human brain of an arbitrator mechanism that determines the extent to which model-based (goal-directed) and model-free (habitual) learning systems control behavior. Specifically, this arbitrator keeps track of the degree of reliability of the two systems and uses this information in order to proportionately allocate behavioral control.. We found evidence to indicate that computational signals corresponding to reliability for the two systems are present in a region of inferior lateral prefrontal cortex bilaterally, as well as a region of right medial frontopolar cortex. In particular, in the inferior lateral prefrontal cortex, the individual reliability signals for the two systems was present alongside the maximum reliability (whichever signal out of the two systems was the most reliable), while in the frontopolar cortex, we found evidence for the maximum reliability out of the two systems. We further found evidence for a comparison signal reflecting the difference in reliability between the model-based and model-free signals in a region of rostral cingulate cortex. In order to further test whether the areas found to encode reliability are involved in interacting with neural systems involved in encoding value signals within the two frameworks, we demonstrated that effective connectivity between the arbitrator regions and regions involved in encoding model-free values in posterior putamen and supplementary motor cortex was significantly modulated as a function of the degree to which the arbitrator allocates behavioral control to the model-based system: the more the arbitrator deems behavior should be controlled by the model-based system, the greater the negative coupling between the arbitrator regions and regions involved in model-free valuation. Furthermore, the coupling between areas involved in model-free valuation in the putamen and areas involved in encoding integrated value signals in the vmPFC was also modulated by the output of the arbitrator such that the more control is allocated to the model-free system the greater the coupling between those regions. Taken together, these findings suggest that the mechanism by which the arbitrator works is to modulate brain regions involved in model-free valuation, and to modulate the strength of connections between areas encoding model-free values and regions involved in encoding an integrated value signal for the purpose of guiding choice.
Valuation of Model-based and Model-free Learning System
Our task design also permitted us to clearly delineate brain systems involved in model-based and model-free valuation. Consistent with a number of prior reports we found evidence for model-based value signals in the ventromedial prefrontal cortex (Hampton et al., 2006; Wunderlich et al., 2012). The finding of a role for ventromedial prefrontal cortex in model-based inference is also consistent with evidence from manipulations designed to isolate brain regions involved in goal-directed control using techniques such as reinforcer devaluation and contingency manipulations imported directly from the animal literature (O’Doherty, 2011; Tanaka et al., 2008; Valentin et al., 2007; De Wit et al., 2009). The additional finding that the vmPFC also contains an integrated signal, incorporating a weighted sum of model-based and model-free value signals proportional to the degree of control allocated by the arbitrator, is consistent with the possibility that the vmPFC is responsible for integrating value signals across the two systems (Beierholm et al., 2011; Wunderlich et al., 2012). Such an integrated signal would be necessary for guiding unified choice behavior that reflects inputs from both model-based and model-free controllers.
We also found regions of posterior putamen as well as parts of supplementary motor cortex to contain model-free value signals. This finding is compatible with a previous report that value signals in this area were prominent following an over-training manipulation (Wunderlich et al., 2012), as well as a finding that activity in this area is associated with increased habitual control as manifested by insensitivity to reinforcer devaluation (Tricomi et al., 2009). Furthermore a recent DTI study found increased connectivity between the posterior putamen and premotor cortex in those individuals more susceptible to habitual control in a slip-of-action task (de Wit et al., 2012). Collectively these findings support a relatively specific role for posterior parts of the putamen in habit-learning, and further suggest that the contributions of this region in habit-learning can be well accounted for by a role for this region in encoding value-signals prescribed by a model-free reinforcement-learning algorithm.
Computations Involved in Arbitration between Two Learning Systems
The arbitration mechanism implemented in the present study used reliability measures about the two systems based on the prediction-error signals generated by each model system. State-prediction errors within the model-based system were found to be located in largely cortical systems, particularly a fronto-parietal network consistent with a previous report (Gläscher et al., 2010). To compute reliability estimates within the model-based system we used a bottom-up Bayesian approach, which generates a probability distribution over the hypothesis that state-prediction errors are zero. The ratio of the mean prediction (belief about the hypothesis) and variance of the distribution produced the reliability estimate used by the arbitrator in inferior prefrontal cortex. The notion that the model-based system uses a computationally rich Bayesian inference mechanism to generate reliability estimates is feasible given that this system appears to depend on a large extent of cortex to facilitate its implementation, including parts of parietal cortex that have previously been hypothesized to implement neural coding schemes consistent with Bayesian inference (Beck et al., 2008).
On the other hand, reward-prediction errors within the model-free system were found to be located sub-cortically in the striatum, both ventrally and dorsally, consistent with a large prior literature (McClure et al., 2003; O’Doherty et al., 2004) implicating these regions in reward-prediction error coding. Unlike the model-based system, where a Bayesian mechanism was used to estimate reliability, in the model-free system behavior was best explained using a simpler reliability estimate that essentially kept track of the average absolute value of reward-prediction errors accumulated. As in the Bayesian estimator, the more prediction errors that accumulated in the recent past, the lower the reliability estimate. The use of an absolute prediction error signal to keep track of reliability within the model-free system that can subsequently be used by the arbitrator represents a novel use of an unsigned prediction error signal, which is typically used to drive the rate of learning or degree of associability ascribed to a cue (Pearce and Hall, 1980; Roesch et al., 2010).
Arbitration Process Reflected by Functional Connectivity
It is notable that while we find evidence for effective connectivity between the inferior frontal and frontopolar arbitration regions and areas involved in model-free valuation in the putamen and supplementary motor cortex, we did not find any evidence for direct interactions between the arbitrator and regions involved in model-based valuation. These results imply an asymmetry in how the arbitrator operates: instead of modulating either model-based or model-free systems depending on which one has the most reliable estimate, the controller appears to work by selectively gating the model-free system. This could be consistent with the possibility that perhaps model-free control is in essence default behavior: unless the model-free controller has especially poor predictions, all else being equal (and due to reasons of computational efficiency), it is better for behavior to be under model-free as opposed to model-based control.
One possible interpretation of the present results is that the lateral prefrontal cortex may exert inhibitory downregulation on the value-signals in the model-free system, although other interpretations are possible given that PPI analyses cannot permit direct measurement of “inhibition”. However it is notable that many previous findings have suggested a role for inferior lateral prefrontal cortex in inhibitory control and task-switching more generally (Aron et al., 2003, 2004; Garavan et al., 1999; Tanji and Hoshi, 2008). It is likely that in many previous studies in which activity is reported in these regions during task-switching as well as pertaining to situations where inhibitory control is required, such tasks are tapping into interactions between goal-directed and habitual controllers. For instance, in reversal-learning, the switching of response-selection from a previously rewarded stimulus-response contingency to a new response likely involves the need to wrest control from a previously learned S-R habit to a new goal-directed action (Cools et al., 2002; O’Doherty et al., 2003; Xue et al., 2008). In such previous studies it was not possible to determine precisely what computations in inferior prefrontal cortex are facilitating such a switch in control (and inhibition of a pre-potent response set).
The present findings may relate to some findings in the animal literature. In the rodent brain, infralimbic cortex, a part of the rat prefrontal cortex has previously been implicated in modulating habitual control (Coutureau and Killcross, 2003; Smith et al., 2012). It is unclear to what extent the areas identified in the present study in humans relate to that infralimbic region in the rodent. We did find a region of medial frontal cortex putatively involved in the comparison of reliabilities between the two systems in the rostral cingulate cortex (which could be a candidate homologue). However, the type of arbitration found in inferior prefrontal cortex and frontopolar cortex in the present study appears not to correspond directly to the functions ascribed to the infralimbic cortex in the rodent brain. Nevertheless, there is some commonality between the findings of the present study and those rodent studies in that in both cases we find a key role for prefrontal cortex in mediating the degree of habitual control expressed over behavior. Intriguingly, a recent studies in rodents (Burguière et al., 2013) also appears to support the notion of an inhibitory mechanism involving parts of lateral prefrontal cortex in the rodent operating on the striatum, which is potentially related to what we find in our data, although that particular rodent study did not address the distinction between model-based vs model-free control.
Control Between Multiple Learning Systems in Lateral Prefrontal and Frontopolar Cortex
Our evidence additionally implicating the frontopolar cortex in the arbitration process is also compatible with previous proposals that frontopolar cortex sits at the apex of a hierarchical prefrontal organization for cognitive control (Koechlin and Hyafil, 2007). While we found that both the frontopolar cortex and inferior prefrontal cortex contained estimates about the maximum reliability out of the two systems, only the inferior prefrontal cortex contained individual reliabilities for the two controllers. It is possible that frontopolar cortex and inferior prefrontal cortex play different roles in implementing the arbitration process, and given the putative locus of frontopolar cortex at the top of the frontal hierarchy, it is tempting to speculate that this region might supervise the inhibitory control being implemented by a subservient inferior prefrontal cortex. However, further work will be needed to establish whether this is indeed the case.
Our findings implicating frontopolar cortex in reliability competition generalize previous findings about a role for this region in relative uncertainty processing in rostrolateral Prefrontal Cortex (Badre et al., 2012) and a role for this region in encoding relative unchosen action probabilities (Boorman et al., 2009). The computation of our reliability competition might accommodate both of these findings because the preferred and alternative strategy should be integrated and because it needs to be done on the basis of the estimation of the posterior uncertainty.
The inferior lateral and frontopolar areas in which we found reliability signals are also close to the region of right lateral prefrontal cortex found to process subjective confidence (De Martino et al., 2013) and the region of lateral anterior prefrontal cortex previously implicated in metacognitive processes (Baird et al., 2013), respectively. One possibility emerging from these findings is that anterior lateral and polar prefrontal cortices may serve a general role in computing estimates about the reliability of different control strategies. This interpretation might serve to unify a number of findings about the role of lateral and frontopolar cortices in meta-cognition by suggesting that the activity of this region reflects the operation of higher-level nodes in a processing hierarchy. Reliability computations about model-based and model-free control may be only one out of a number of different types of computation sub-served by these brain areas. It is important to note that it is entirely feasible that other variables apart from reliability will feed into the arbitration process, such as for example the time available to render a decision, or the amount of available cognitive resources at a given point in time. Further work will need to establish how such other considerations get incorporated into the arbitration process, as well as to determine which brain regions contribute to those aspects of the arbitration.
The arbitration framework also accounts for both competitive and co-operative effects between model-based and model-free learning in a broader sense. The arbitration mechanism undergoes competition on each choice (MB vs MF) while fostering collaboration during the transition over trials (MB[barb2right]MF or MF[barb2right]MB). The competition corresponds to the reliability computation, whereas the collaboration corresponds to the dynamics of arbitration (PMB). Moreover, the dynamics of the arbitration keeps the result of this competition as the model-choice bias (PMB), which will affect learning process in subsequent trials. The reward prediction errors that the model-free system experiences in these trials are the consequence of the choices that are based on the mixture of the model-based and the model-free value. This interpretation is supported by the recent study that model-based control can influence model-free learning (Daw et al., 2011; Staudinger and Büchel, 2013). In future work, it would be valuable to formally test the framework outlined here in a unified dynamic causal model of the arbitration process involving the brain areas implicated here on the basis of the computational fMRI and PPI analyses.
In summary, the present findings indicate how it is that the brain switches control between two very different strategies for controlling behavior. These findings open the possibility for investigating the role of impaired arbitration mechanisms in driving addictive behavior, or psychiatric disorders involving the over-dominance of habitual control such as OCD (Gillan et al., 2011), as well as opening avenues to potential novel treatments for such disorders involving pharmacological or electromagnetic modulation of neural activity in the inferior lateral or polar prefrontal cortices.
Experimental Procedures
Participants
Twenty two right-handed volunteers (six females, mean age 28; age ranging between 19-40) participated in the study. They were screened prior to the experiment to exclude those with a history of neurological or psychiatric illness. All subjects gave informed consent, and the study was approved by the Institutional Review Board of the California Institute of Technology.
Stimuli
The image set for the stimuli consisted of 126 fractal images, four kinds of collection box images (red, yellow, blue, and white), three kinds of color coins (red, yellow, and blue), and an extra four fractal images to represent outcome states. The colors of the outcome state image were accompanied by numerical amounts which indicate the amount of money that subjects could receive in that state. Before the experiment began, the stimulus computer randomly chose five fractal images that were subsequently used to represent each state, and the amount of money available in each state (40, 20, or 10 cents USD) was randomly assigned to each color coin across subjects.
Task
Participants performed a sequential two-choice Markov decision task, in which they need to make two sequential choices (by pressing “LEFT” or “RIGHT” button) to obtain a monetary outcome (coin) at the end stage. Making no choice in 4 seconds had a computer make a random choice to proceed and that trial was marked as a penalizing trial. In each trial, participants begin at the same starting state. The two choices will be followed by a coin delivery. The states were intersected by a variable temporal interval drawn from a uniform distribution between 1 to 4 seconds. The inter-trial interval was also sampled from a uniform distribution between 1 to 4 seconds. The reward was displayed for 2 seconds. At the beginning of the experiment, subjects were informed that they need to learn about the states and corresponding outcomes to collect as many coins as possible and that they will get to keep the money they cumulatively earned at the end of the experiment. Participants were not informed about the specific state-transition probabilities used in the task except they were told that the contingencies might change during the course of the experiment. In the pre-training session, they were given the opportunity to learn about the task, while they were free to make any choice. The state-transition probability was fixed at (0.5,0.5) and a white collection box was presented during this session indicating that any token color would yield monetary reward (see below). The subjects performed 100 trials in this pre-training session, which would allow them to spend enough time to learn; we learned from our previous study that 80 trials would be enough for subjects to learn about the two-choice Markov decision task (Gläscher et al., 2010). The experiment proceeded in five separate scanning sessions of 80 trials each on average.
Our experimental design incorporated two conditions: a specific-goal condition, and an outcome general condition. In the specific-goal condition participants were presented with a specific color collection box (e.g. either red, yellow, blue, or gray) which indicated the color of the specific token that was valuable on that trial. If the state associated with that token was reached then participants would gain the specific monetary amount associated with that token. If on the other hand, a different colored end-state was reached, then no money would be obtained. The specific goal-state that was valued was changed randomly from trial-to-trial. Thus participants had to continually consider which goal is currently valuable in order to make a choice. This condition was designed to favor model-based as opposed to model-free control. Conversely, in the flexible-goal condition, a white collection box was presented which indicated that any color of end state could be reached in order to yield monetary outcomes. While this condition also could involve model-based computations, simulations demonstrated that after a number of trials, control might transition to the model-free system (Figure S1C). Hence these two conditions were designed to favor model-based vs model-free control respectively (Figure S2). To further dissociate the model-based from the model-free control and to prevent participants from using multiple model-free strategies in the absence of the model-based control in the specific goal condition, in both conditions changes to the transition probabilities were implemented. Two types of state-transition probability were used – (0.9,0.1) and (0.5,0.5). They are the probabilities that the choice is followed by going into the two consecutive states. For example, if you make a left choice at state 1 when the state transition probability is (0.9,0.1), then the probability of your next state being state 2 is 0.9 and the probability for state 3 is 0.1. The order of the block conditions was randomized. Thus, the conditions are (i) specific-goal, state-transition probability (0.9,0.1), (ii) specific-goal, state-transition probability (0.5,0.5), (iii) flexible-goal, state-transition probability (0.9,0.1), and (iv) flexible-goal, state-transition probability (0.5,0.5). The blocks with the state transition probability (0.9,0.1) consists of three to five trials, whereas those with (0.5,0.5) consists of five to seven trials due to the difficulty in learning under high uncertainty. When determining the minimum length of trials and the state-transition probability values, we ensured that the estimation process of the state-transition probability of the model-based learner does not break down; also, the two transition probabilities are distinctive enough that with (0.9,0.1) participants feel that the state transition is congruent with the choice, whereas with (0.5,0.5) the state transition is random. At the beginning of each trial participants can immediately recognize the specific/flexible goal condition by seeing the color of the collection box, but they performed the task without knowing the state-transition probability.
While the changes in the transition probabilities are rapid, they are designed to induce perturbations in the predictions about state-transition probabilities, which in turn affect changes in the allocation of model-based and model-free control. We do not expect participants to fully learn these different transition probabilities in the small number of trials before a shift occurs: all that matters is that a change in the reliability of the predictions occurs following such changes. The changes occur at these rates in order to ensure that tonically varying changes in model-based vs model-free control (i.e. PMB in our model) can be detected at experimental frequencies appropriate for fMRI data. Slower-varying changes in transition probabilities might have produced changes in control at frequencies aliased with the well-known characteristics of low-frequency noise inherent in fMRI data.
Computational model of arbitration
First, in order to capture model-free learning we used a model-free SARSA learner (MF), a variant of a classical reinforcement learning model (Sutton and Barto, 1998) (the first row of Figure 2). We also implemented a model-based learner (MB), which is equipped with FORWARD learning (following our previous study (Gläscher et al., 2010) and BACKWARD planning (the first row of Figure 2). Second, we implemented a simple hierarchical empirical Bayes approach to compute the reliability of a learning strategy given the history of the prediction error (PE) (the second row of Figure 2). PE refers to SPE for the case of MB and RPE for the case of MF. Implemented was then a push-pull mechanism to govern how the reliability-based competition between MB and MF mediates value computation (the third row of Figure 2). Finally, the arbitration model selects actions stochastically according to the following softmax function (Gläscher et al., 2010; Luce, 1959) (the fourth row of Figure 2). Full details of the model description, parameter estimation, and model comparison are provided in Supplemental Methods.
fMRI data acquisition
Functional imaging was performed on a 3T Siemens (Erlangen, Germany) Trio scanner located at the Caltech Brain Imaging Center (Pasadena, CA) with a 32 channel radio frequency coil for all the MR scanning sessions. To reduce the possibility of head movement related artifact, participants’ heads were securely positioned with foam position pillows. High resolution structural images were collected using a standard MPRAGE pulse sequence, providing full brain coverage at a resolution of 1 mm × 1 mm × 1 mm. Functional images were collected at an angle of 30° from the anterior commissure-posterior commissure (AC-PC) axis, which reduced signal dropout in the orbitofrontal cortex. Forty-five slices were acquired at a resolution of 3 mm × 3 mm × 3 mm, providing whole-brain coverage. A one-shot echo-planar imaging (EPI) pulse sequence was used (TR = 2800 ms, TE = 30 ms, FOV = 100 mm, flip angle = 80°).
fMRI data analysis
The SPM8 software package was used to analyze the fMRI data (Wellcome Department of Imaging Neuroscience, Institute of Neurology, London, UK). The first four volumes of images were discarded to avoid T1 equilibrium effects. Slice-timing correction was applied to the functional images to adjust for the fact that different slices within each image were acquired at slightly different points in time. Images were corrected for participant motion, spatially transformed to match a standard echo-planar imaging template brain, and s moothed using a 3D Gaussian kernel (6 mm FWHM) to account for anatomical differences between participants. This set of data was then analyzed statistically. A high-pass filter with a cutoff at 129 seconds was used. Full details of the GLM design are provided in Supplemental Methods.
Whole brain analyses
Essentially all of the findings we report survive after the whole-brain correction for multiple comparison at the cluster level (p<0.05 corrected), except for the value signals, some of which are reported using a well-motivated SVC correction. Full details are provided in Supplemental Methods.
To avoid nonindependence bias in plotting parameter estimates of the reliability, we ran leave-one-subject-out GLM analysis (Esterman et al., 2010). Specifically, we ran 22 general linear models (GLM) with one subject left out in each, and each GLM defines the voxel cluster for the subject left out. The percent signal change (rfxplot toolbox: http://rfxplot.sourceforge.net/), illustrating how much the evoked BOLD response deviates from its voxel-wise baseline, was then computed across 22 subjects.
To formally test which version of the reliability computation provides the best account of responses in inferior lateral prefrontal cortex, we ran a Bayesian model selection(Stephan et al., 2009) on three models. We chose three models - mixedArb-dynamics and dualBayesArb-dynamics which showed the best and the second best performance in terms of the trade-off between model fit and model complexity for the behavioral data, respectively, and for comparison with an arbitration scheme proposed in prior literature we tested Daw’s version of reliability computation (UncBayesArb; (Daw et al., 2005)) in which the computation of reliability is based on the uncertainty in the state-action value.
Post hoc PPI analysis
To test whether there is a functional coupling between the areas associated with value signals and the area serving as a value comparator during choices, we performed a psychophysiological interaction (PPI) analysis (Friston et al., 1997) with the probability of choosing the model-based learning strategy (PMB) being a parametric psychological factor. We used the first eigenvariate of BOLD signals from the left and the right inferior lateral prefrontal cortex extracted from a 5mm sphere centered at (−54,38,3) and (48,35,−2), respectively, areas identified as correlating with model-based and model-free reliability. Because we found significant negatively correlating PPIs using the reliability areas as our seed regions and PMB as the psychological variable with brain regions shown to be correlated with model-free but not model-based valuation, we next performed additional PPI analyses using areas involved in encoding model-free values as our seeds: supplementary motor area (−9,8,55), and posterior putamen (−27,−4,1) (all 5mm spheres). In each of these analyses we formed an interaction term, which is the first eigenvariate of the BOLD signal multiplied by the parametric psychological variable - the model-choice probability (PMB). To avoid identifying regions in which most of the variance is accounted for by main effects, as opposed to being accounted by interaction effect, we included the psychological and physiological term from which we derived the interaction term in the GLM as covariates of no interest, followed by the interaction term as a regressor of interest.
Supplementary Material
Acknowledgements
We thank Mimi Liljeholm and Peter Bossaerts for suggestions and insightful comments and Ralph Lee for his assistance. This work was funded by NIH grant DA033077-01 to J.P.O.D., funds from the Gordon and Betty foundation to J.P.O.D., grants from JST.CREST to S.S., and by the Caltech-Tamagawa gCOE to S.S. and J.P.O.D.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Adams CD, Dickinson A. Instrumental responding following reinforcer devaluation. Quarterly Journal of Experimental Psychology. Q. J. Exp. Psychol. 1981;33:109–122. [Google Scholar]
- Aron AR, Fletcher PC, Bullmore ET, Sahakian BJ, Robbins TW. Stop-signal inhibition disrupted by damage to right inferior frontal gyrus in humans. Nat. Neurosci. 2003;6:1329. doi: 10.1038/nn1003. [DOI] [PubMed] [Google Scholar]
- Aron AR, Robbins TW, Poldrack R. a. Inhibition and the right inferior frontal cortex. Trends Cogn. Sci. 2004;8:170–177. doi: 10.1016/j.tics.2004.02.010. [DOI] [PubMed] [Google Scholar]
- Badre D, Doll BB, Long NM, Frank MJ. Rostrolateral prefrontal cortex and individual differences in uncertainty-driven exploration. Neuron. 2012;73:595–607. doi: 10.1016/j.neuron.2011.12.025. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Balleine BW, Dickinson A. Goal-directed instrumental action: contingency and incentive learning and their cortical substrates. Neuropharmacology. 1998;37:407–419. doi: 10.1016/s0028-3908(98)00033-1. [DOI] [PubMed] [Google Scholar]
- Balleine BW, O’Doherty JP. Human and rodent homologies in action control: Cortico striatal determinants of goal-directed and habitual action. Neuropsychopharmacology. 2010;35:48–69. doi: 10.1038/npp.2009.131. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Beck J, Ma WJ, Kiani R, Hanks T, Churchland AK, Roitman J, Shadlen M, Latham PE, Pouget A. Probabilistic population codes for Bayesian decision making. Neuron. 2008;60:1142–1152. doi: 10.1016/j.neuron.2008.09.021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Beierholm UR, Anen C, Quartz S, Bossaerts P. Separate encoding of model based and model free valuations in the human brain. Neuroimage. 2011;58:955–962. doi: 10.1016/j.neuroimage.2011.06.071. [DOI] [PubMed] [Google Scholar]
- Boorman ED, Behrens TE, Woolrich MW, Rushworth MFS. How Green Is the Grass on the Other Side? Frontopolar Cortex and the Evidence in Favor of Alternative Courses of Action. Neuron. 2009;62:733–743. doi: 10.1016/j.neuron.2009.05.014. [DOI] [PubMed] [Google Scholar]
- Burguière E, Monteiro P, Feng G, Graybiel AM. Optogenetic stimulation of lateral orbitofronto-striatal pathway suppresses compulsive behaviors. Science. 2013;340:1243–1246. doi: 10.1126/science.1232380. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chib VS, Rangel A, Shimojo S, O’Doherty JP. Evidence for a common representation of decision values for dissimilar goods in human ventromedial prefrontal cortex. J. Neurosci. 2009;29:12315–12320. doi: 10.1523/JNEUROSCI.2575-09.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cools R, Clark L, Owen A, Robbins TW. Defining the neural mechanisms of probabilistic reversal learning using event-related functional MRI. J. Neurosci. 2002;22:4563–4567. doi: 10.1523/JNEUROSCI.22-11-04563.2002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Coutureau E, Killcross S. Inactivation of the infralimbic prefrontal cortex reinstates goal-directed responding in overtrained rats. Behav. Brain Res. 2003;146:167–174. doi: 10.1016/j.bbr.2003.09.025. [DOI] [PubMed] [Google Scholar]
- Daw ND, Niv Y, Dayan P. Uncertainty-based competition between prefrontal and dorsolateral striatal systems for behavioral control. Nat. Neurosci. 2005;8:1704–1711. doi: 10.1038/nn1560. [DOI] [PubMed] [Google Scholar]
- Daw ND, Gershman SJ, Seymour B, Dayan P, Dolan RJ. Model-based influences on humans’ choices and striatal prediction errors. Neuron. 2011;69:1204–1215. doi: 10.1016/j.neuron.2011.02.027. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Doya K, Samejima K, Katagiri K, Kawato M. Multiple model-based reinforcement learning. Neural Comput. 2002;14:1347–1369. doi: 10.1162/089976602753712972. [DOI] [PubMed] [Google Scholar]
- Esterman M, Tamber-Rosenau B, Chiu Y, Yantis S. Avoiding nonindependence in fMRI data analysis: leave one subject out. Neuroimage. 2010;50:572–576. doi: 10.1016/j.neuroimage.2009.10.092. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Everitt BJ, Robbins TW. Neural systems of reinforcement for drug addiction: from actions to habits to compulsion. Nat. Neurosci. 2005;8:1481–1489. doi: 10.1038/nn1579. [DOI] [PubMed] [Google Scholar]
- Friston KJ, Buechel C, Fink GR, Morris J, Rolls ET, Dolan RJ. Psychophysiological and modulatory interactions in neuroimaging. Neuroimage. 1997;6:218–229. doi: 10.1006/nimg.1997.0291. [DOI] [PubMed] [Google Scholar]
- Garavan H, Ross TJ, Stein EA. Right hemispheric dominance of inhibitory control: An event-related functional MRI study. Proc. Natl. Acad. Sci. 1999;96:8301–8306. doi: 10.1073/pnas.96.14.8301. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gillan C, Papmeyer M, Morein-Zamir S, Sahakian B, Fineberg N, Robbins T, de Wit S. Disruption in the balance between goal-directed behavior and habit learning in obsessive-compulsive disorder. Am J Psychiatry. 2011;168:718–726. doi: 10.1176/appi.ajp.2011.10071062. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gläscher J, Daw ND, Dayan P, O’Doherty JP. States versus rewards: dissociable neural prediction error signals underlying model-based and model-free reinforcement learning. Neuron. 2010;66:585–595. doi: 10.1016/j.neuron.2010.04.016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Graybiel AM. Habits, rituals, and the evaluative brain. Annu Rev Neurosci. 2008;31:359–387. doi: 10.1146/annurev.neuro.29.051605.112851. [DOI] [PubMed] [Google Scholar]
- Hampton AN, Bossaerts P, O’Doherty JP. The role of the ventromedial prefrontal cortex in abstract state-based inference during decision making in humans. J. Neurosci. 2006;26:8360–8367. doi: 10.1523/JNEUROSCI.1010-06.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hare T. a, Camerer CF, Rangel A. Self-control in decision-making involves modulation of the vmPFC valuation system. Science. 2009;324:646–648. doi: 10.1126/science.1168450. (80-. ) [DOI] [PubMed] [Google Scholar]
- Hare T. a, Schultz W, Camerer CF, O’Doherty JP, Rangel A. Transformation of stimulus value signals into motor commands during simple choice. Proc. Natl. Acad. Sci. 2011;108:18120–18125. doi: 10.1073/pnas.1109322108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Koechlin E, Hyafil A. Anterior prefrontal function and the limits of human decision-making. Science. 2007;18:594–598. doi: 10.1126/science.1142995. (80-. ) [DOI] [PubMed] [Google Scholar]
- Li J, Schiller D, Schoenbaum G, Phelps EA, Daw ND. Differential roles of human striatum and amygdala in associative learning. Nat. Neurosci. 2011;14:1250–1252. doi: 10.1038/nn.2904. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Luce RD. Individual choice behavior: a theoretical analysis. Wiley; New York: 1959. [Google Scholar]
- Ma WJ, Beck JM, Latham PE, Pouget A. Bayesian inference with probabilistic population codes. Nat. Neurosci. 2006;9:1432–1438. doi: 10.1038/nn1790. [DOI] [PubMed] [Google Scholar]
- McClure SM, Berns GS, Montague PR. Temporal prediction errors in a passive learning task activate human striatum. Neuron. 2003;38:339–346. doi: 10.1016/s0896-6273(03)00154-5. [DOI] [PubMed] [Google Scholar]
- Montague PR, Dayan P, Sejnowski TJ. A Framework for Mesencephalic Dopamine Systems Based on Predictive Hebbian Learning. J. Neurosci. 1996;16:1936–1947. doi: 10.1523/JNEUROSCI.16-05-01936.1996. [DOI] [PMC free article] [PubMed] [Google Scholar]
- O’Doherty JP. Contribution of the ventromedial prefrontal cortex to goal-directed action selection. Ann. N. Y. Acad. Sci. 2011;1239:118–129. doi: 10.1111/j.1749-6632.2011.06290.x. [DOI] [PubMed] [Google Scholar]
- O’Doherty JP, Dayan P, Friston K, Critchley H, Dolan RJ. Temporal Difference Models and Reward-Related Learning in the Human Brain. Neuron. 2003;38:329–337. doi: 10.1016/s0896-6273(03)00169-7. [DOI] [PubMed] [Google Scholar]
- O’Doherty JP, Dayan P, Schultz J, Deichmann R, Friston K, Dolan RJ. Dissociable roles of ventral and dorsal striatum in instrumental conditioning. Science. 2004;304:452–454. doi: 10.1126/science.1094285. (80-. ) [DOI] [PubMed] [Google Scholar]
- Pearce JM, Hall G. A model for Pavlovian learning: Variation in the effectiveness of conditioned but not unconditioned stimuli. Psychol. Rev. 1980;87:532–552. [PubMed] [Google Scholar]
- Pennini F, Plastino A. Diverging Fano factors. J. Phys. Conf. Ser. 2010;246 [Google Scholar]
- Preuschoff K, Quartz SR, Bossaerts P. Human Insula Activation Reflects Risk Prediction Errors As Well As Risk. J. Neurosci. 2008;28:2745–2752. doi: 10.1523/JNEUROSCI.4286-07.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Roesch MR, Calu DJ, Esber GR, Schoenbaum G. Neural correlates of variations in event processing during learning in basolateral amygdala. J. Neurosci. 2010;30:2464–2471. doi: 10.1523/JNEUROSCI.5781-09.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rowe JB, Hughes L, Nimmo-Smith I. Action selection: A race model for selected and non-selected actions distinguishes the contribution of premotor and prefrontal areas. Neuroimage. 2010;51:888–896. doi: 10.1016/j.neuroimage.2010.02.045. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rushworth MFS, Noonan MP, Boorman ED, Walton ME, Behrens TE. Frontal Cortex and Reward-Guided Learning and Decision-Making. Neuron. 2011;70:1054–1069. doi: 10.1016/j.neuron.2011.05.014. [DOI] [PubMed] [Google Scholar]
- Schultz W, Dayan P, Montague PR. A neural substrate of prediction and reward. Science. 1997;275:1593–1599. doi: 10.1126/science.275.5306.1593. (8-. ) [DOI] [PubMed] [Google Scholar]
- Smith KS, Virkud A, Deisseroth K, Graybiel AM. Reversible online control of habitual behavior by optogenetic perturbation of medial prefrontal cortex. Proc. Natl. Acad. Sci. 2012;109:18932–18937. doi: 10.1073/pnas.1216264109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Staudinger MR, Büchel C. How initial confirmatory experience potentiates the detrimental influence of bad advice. Neuroimage. 2013;76:125–133. doi: 10.1016/j.neuroimage.2013.02.074. [DOI] [PubMed] [Google Scholar]
- Stephan K, Penny W, Daunizeau J, Moran R, Friston K. Bayesian Model Selection for Group Studies. Neuroimage. 2009;49:1004–1017. doi: 10.1016/j.neuroimage.2009.03.025. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sutton RS, Barto AG. Reinforcement Learning. MIT press; 1998. [Google Scholar]
- Takahashi YK, Roesch MR, Wilson RC, Toreson K, O’Donnell P, Niv Y, Schoenbaum G. Expectancy-related changes in firing of dopamine neurons depend on orbitofrontal cortex. Nat. Neurosci. 2011;14:1590–1597. doi: 10.1038/nn.2957. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tanaka S, Balleine BW, O’Doherty JP. Calculating consequences: Brain systems that encode the causal effects of actions. J. Neurosci. 2008;28:6750–6755. doi: 10.1523/JNEUROSCI.1808-08.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tanji J, Hoshi E. Role of the Lateral Prefrontal Cortex in Executive Behavioral Control. Physiol. Rev. 2008;88:37–57. doi: 10.1152/physrev.00014.2007. [DOI] [PubMed] [Google Scholar]
- Tricomi E, Balleine BW, O’Doherty JP. A specific role for posterior dorsolateral striatum in human habit learning. Eur. J. Neurosci. 2009;29:2225–2232. doi: 10.1111/j.1460-9568.2009.06796.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Valentin VV, Dickinson A, O’Doherty JP. Determining the neural substrates of goal-directed learning in the human brain. J. Neurosci. 2007;27:4019–4026. doi: 10.1523/JNEUROSCI.0564-07.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- De Wit S, Corlett PR, Aitken MR, Dickinson A, Fletcher PC. Differential engagement of the ventromedial prefrontal cortex by goal-directed and habitual behavior toward food pictures in humans. J. Neurosci. 2009:11330–11338. doi: 10.1523/JNEUROSCI.1639-09.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- De Wit S, Watson P, Harsay HA, Cohen MX, van de Vijver I, Ridderinkhof KR. Corticostriatal Connectivity Underlies Individual Differences in the Balance between Habitual and Goal-Directed Action Control. J. Neurosci. 2012;32:12066–12075. doi: 10.1523/JNEUROSCI.1088-12.2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wunderlich K, Dayan P, Dolan RJ. Mapping value based planning and extensively trained choices in the human brain. Nat. Neurosci. 2012;15:786–791. doi: 10.1038/nn.3068. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xue G, Ghahremani D, Poldrack R. Neural substrates for reversing stimulus-outcome and stimulus-response associations. J. Neurosci. 2008;28:11196–11204. doi: 10.1523/JNEUROSCI.4001-08.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yin HH, Knowlton BJ. The contributions of striatal subregions to place and response learning. Learn. Mem. 2004;11:459–463. doi: 10.1101/lm.81004. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.