Abstract
Visual attention is commonly studied by using visuo-spatial cues indicating probable locations of a target and assessing the effect of the validity of the cue on perceptual performance and its neural correlates. Here, we adapt a cueing task to measure spatial cueing effects on the decisions of honeybees and compare their behavior to that of humans and monkeys in a similarly structured two-alternative forced-choice perceptual task. Unlike the typical cueing paradigm in which the stimulus strength remains unchanged within a block of trials, for the monkey and human studies we randomized the contrast of the signal to simulate more real world conditions in which the organism is uncertain about the strength of the signal. A Bayesian ideal observer that weights sensory evidence from cued and uncued locations based on the cue validity to maximize overall performance is used as a benchmark of comparison against the three animals and other suboptimal models: probability matching, ignore the cue, always follow the cue, and an additive bias/single decision threshold model. We find that the cueing effect is pervasive across all three species but is smaller in size than that shown by the Bayesian ideal observer. Humans show a larger cueing effect than monkeys and bees show the smallest effect. The cueing effect and overall performance of the honeybees allows rejection of the models in which the bees are ignoring the cue, following the cue and disregarding stimuli to be discriminated, or adopting a probability matching strategy. Stimulus strength uncertainty also reduces the theoretically predicted variation in cueing effect with stimulus strength of an optimal Bayesian observer and diminishes the size of the cueing effect when stimulus strength is low. A more biologically plausible model that includes an additive bias to the sensory response from the cued location, although not mathematically equivalent to the optimal observer for the case stimulus strength uncertainty, can approximate the benefits of the more computationally complex optimal Bayesian model. We discuss the implications of our findings on the field’s common conceptualization of covert visual attention in the cueing task and what aspects, if any, might be unique to humans.
INTRODUCTION
Spatial cues have important effects on perceptual performance (Posner, 1980; Palmer et al., 1993; Luck et al., 1996; Carrasco, 2011) and the response of neurons in the primate brain (Cook and Maunsell, 2002; Maunsell and Cook, 2002). In the study of human visual attention, spatial cues predicting the probable location of a target are commonly used as an operational manipulation of covert visual attention. The typical result is that the response times are reduced or the accuracy is increased for trials in which the target appears at the cued location (valid cue-trials) compared to those trials in which the target appears at the uncued location (invalid cue-trials). Although there are many theories (Posner et al., 1980; Eriksen and St James, 1986; Bundesen, 1990; Eckstein et al., 2002, 2009; Shimozaki et al., 2003; Bundesen et al., 2005; Smith and Ratcliff, 2009; Vincent, 2011) proposing a variety of mechanisms to account for the typical improvement in perceptual performance when targets appear at cued locations, most of theories interpret the cue-effect as a consequence of visual attention being allocated to the cued location. The common assumption is that the spatial cueing effects are mediated by the same mechanism which mediates human ability, under verbal instruction or one’s own will, to select or attend regions of the visual field without an eye movement: covert visual attention. A common implicit notion in the study of visual attention is that it might be unique to primates, mammals, or vertebrates at the most. Exhaustively assessing whether an organism shows behavioral evidence of mechanisms akin to human visual attention is difficult because visual attention has multiple working definitions, associated tasks, and assessments (Pashler, 1999). Yet, what can be assessed is how an organism behaves in one of the most common tasks used to study visual attention: the spatial cueing task.
Studies have shown that monkeys (Cook and Maunsell, 2002; Maunsell and Cook, 2002), rats (Bushnell and Rice, 1999; Marote and Xavier, 2011) and pigeons (Shimp and Friedrich, 1993) all use predictive cues and show cueing effects. But does an organism with a small brain and no cortical structure also use predictive cues and give rise to a behavioral cueing effect? Here, we explore the effect of spatial cues on the decisions of honeybees. The goal of the current paper is to compare the effect of spatial cues on the decisions of humans, monkeys and bees in a spatial cueing task with a similar structure. Although there is a large literature on how bees can learn associations (Stach et al., 2004), discrimination between visual elements (Avarguès-Weber et al., 2010) and visual landmarks to navigate (Lehrer, 1994; Horridge, 2006), bees have not been tested in a cueing paradigm in which two visual stimuli have to be discriminated and a highly-visible cue is probabilistically predictive of the target location. Comparison across species might allow us to assess what nervous system requirements are needed to implement underlying computations associated with a cueing effect and also highlight the unique aspects of human visual attention in the context of the spatial cue paradigm. As a benchmark we compare the cueing effects present in the three animals to that of an optimal Bayesian observer which uses the cues to weight sensory evidence about the presence of the target by a prior probability determined by the cue validity to maximize the proportion correct decisions. In addition, we compare the measured cueing effects against various models: a model that ignores the cue, a model that always follows the cue, a probability matching model, and an additive bias which is equivalent to a single optimized threshold model.
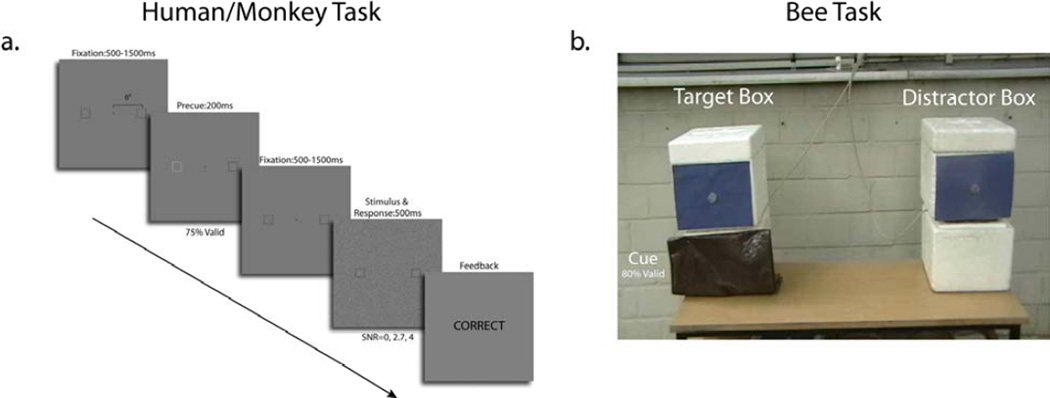
We use a simple modified two-alternative forced-choice cueing paradigm (Green and Swets, 1989) for all three species (Figure 1). The complexity of the more common cueing paradigm (yes/no task with location uncertainty) makes it too difficult for successful training of the honeybees. In the two alternative forced choice cueing paradigm, the target appears in one of two locations with equal probability and a highly visible cue which appears randomly at one of the two locations indicates with q % validity (e.g., 75 %) the likely location of the target. For the monkeys and humans, we consider a novel variation for which there is external stimulus strength uncertainty (target/distractor discriminability variation unknown to the organism).1 Models have been traditionally applied to cueing paradigms in which the signal strength is kept constant (Eckstein et al., 2002; Liston and Stone, 2008) and assumed to be known by the organism (but see Schoonveld et al., 2007; Vincent et al., 2009; Ma, 2010 for Bayesian optimal modeling for signal/distractor uncertainty in visual search). However, in the real world organisms often do not know in advance how detectable or discriminable will the target be. The question arises as to how stimulus strength uncertainty affects the optimal decision rule and its predicted cueing effect. Monkeys and humans indicated their decision by making an eye movement towards the target location (Figure 1a). Honeybees’ selection was based on the bee circling close to the box, resting or entering one of two box choices (Figure 1b).
Figure 1.
a. Sequence of presentation of images for a trial for monkeys and humans. In neutral sessions, both bounding boxes remained black during the precue period. For monkey experiments, a small volume of fruit juice was dispensed for correct responses. b. Photograph of box arrangement with target, distractor and cue for honey bee task conducted in Free University of Berlin. Photograph depicts the zero signal to noise ratio condition for which the target and distractor papers are the same (blue).
THEORY
Cueing effects have been traditionally attributed to the larger allocation of limited resources to a cued location relative to the uncued location (Posner, 1980, 1980). However, going back to work from the 1980’s, investigators have considered the behavior of models that use simple decision rules acting on sensory processing that is subject to stochastic noise (Shaw, 1980, 1984; Kinchla, 1992; Kinchla et al., 1995). In this framework, valid cues can have beneficial effects on perceptual performance by allowing the organism to better integrate or select sensory information relevant to the task and to allow to ignore or down-weight sensory information from potential noisy only locations. In these models, valid cues indicating the probable location of a target or reducing the number of physical distracters (set-size) benefits performance without postulating any limited resource mechanism. Studies have shown that there are circumstances for which cues benefit performance beyond what is predicted by these unlimited capacity models (Carrasco et al., 2000; Dosher and Lu, 2000). However, these studies do not negate the role of optimizing selection and integration of noisy sensory information as a core neural mechanism to improve perceptual performance but rather indicate that there are circumstances in which there is an additional improvement due to other processes related to limited capacity.
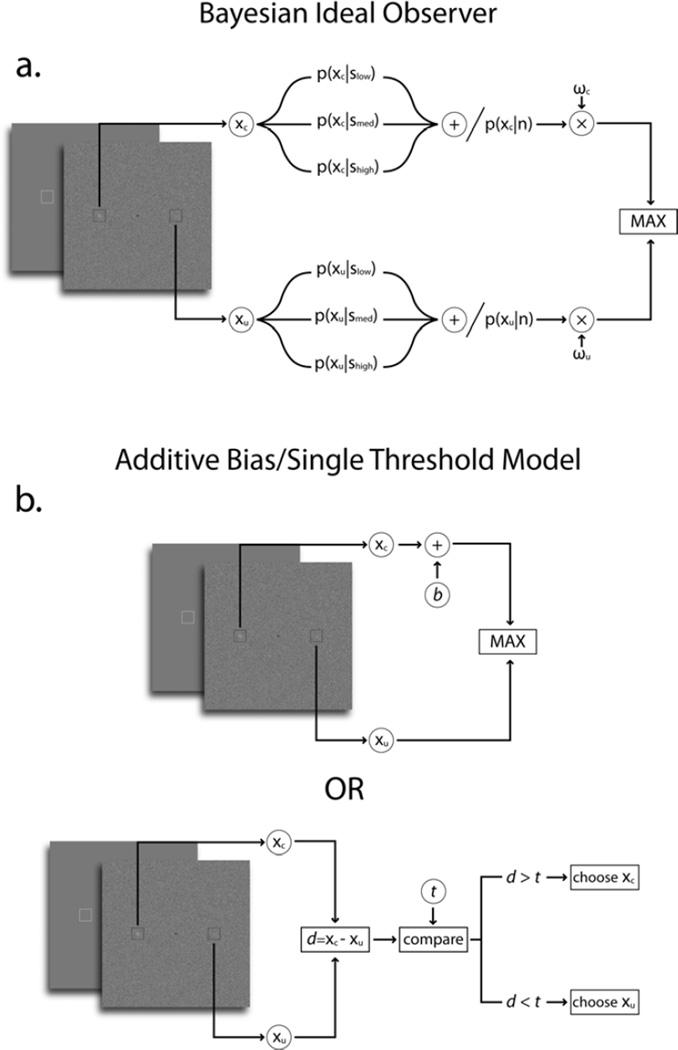
Here, we consider the possible decision rules an organism might follow when confronted with a highly visible spatial cue that is predictive of the location of the signal in a 2-alternative forced choice. We investigate various models to account for the behavioral choices for the case in which there is external signal strength uncertainty (target/distractor discriminability variation). The optimal Bayesian model2 in the cueing task has been investigated for case in which the signal strength is kept constant and assumed to be known by the model but not for the more realistic case of signal strength uncertainty (Figure 2a). For comparison, we show predictions for the more common task for which the signal strength is blocked and considered to be known to the organism. Below, we describe the task and each of the models considered.
Figure 2.
a. Bayesian ideal observer for 2 AFC cueing task for the scenario of signal strength uncertainty; b. Additive bias model in which the response from the cued location has an additive bias and compared to the response from the uncued location. The additive bias model is equivalent for a 2 AFC to a single threshold model in which the difference in response across cued and uncued locations is compared to a decision threshold t.
Two alternative forced choice tasks
In a two-alternative forced-choice task (2AFC), the organism is instructed or trained to detect a target that appears always in one of two locations and decide which location contains the target (Figure 1). Typically the target is defined to have a different contrast luminance, orientation, motion speed or direction than the distractors. We will use the term target-distractor discriminability to refer to the difference along the dimension of interest between the target and distractor. Importantly, in a spatial attention task the target co-occurs with a highly visible spatial cue q % of the trials.
General theoretical framework for the models
All models discussed below are presented within the framework of signal detection theory (Green and Swets, 1989; see Figure 2 for examples) which assumes the target and distractor elicit an internal response subject to variability (noise). The variability is commonly assumed to be of equal variance and Gaussian with the target eliciting a higher mean response. The target/distactor discriminability is then typically represented in terms of the difference between the mean response to the target and distractor divided by the standard deviation of the response. This metric is known as d’, the index of detectability.
Always select cue decision rule (ignore the sensory evidence)
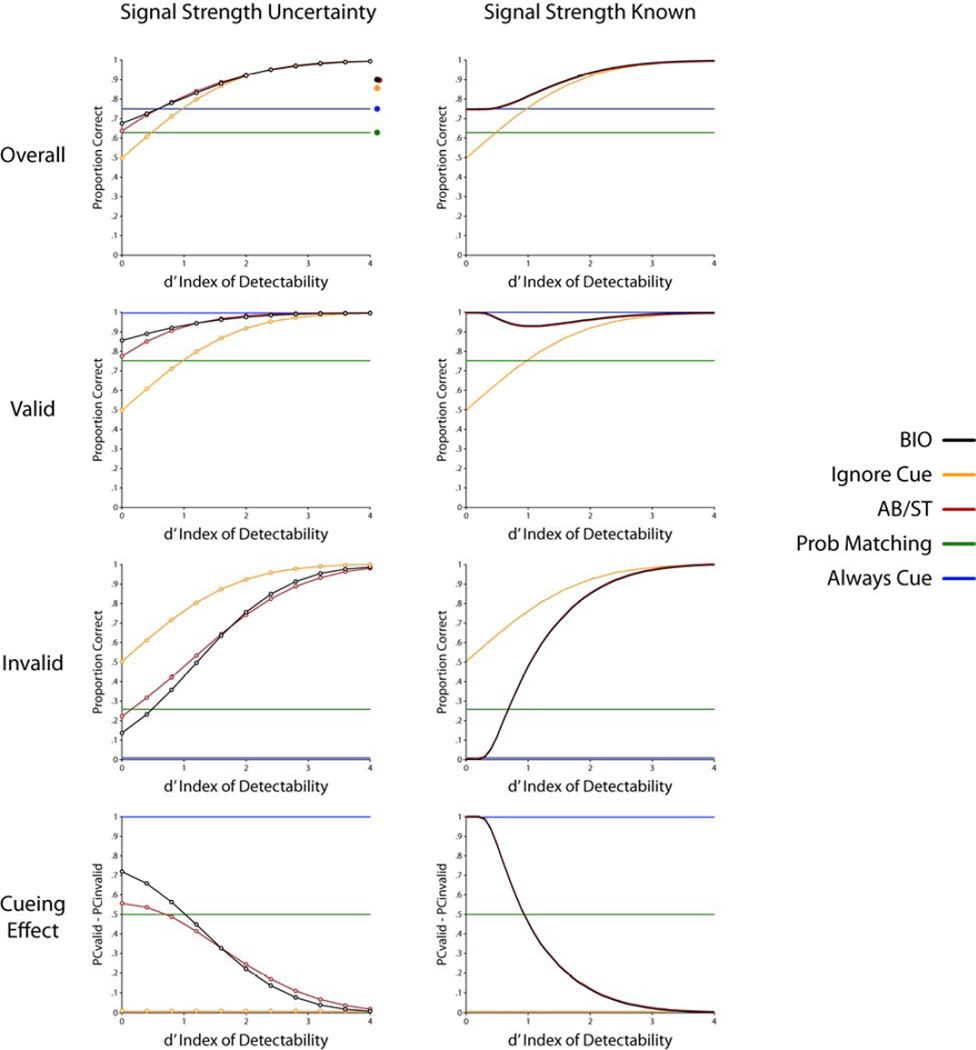
A first simple rule is to always choose the location co-occurring with the spatial cue and ignore the sensory evidence. This decision rule will maximize the cueing effect (proportion correct valid – proportion correct invalid trials = 1.0) and lead to correct trials in the q % of the trials for which the target occurs with the cue and will be incorrect in the (1- q) % of trials for which the signal appears at the uncued location. Figure 3 shows performance for a cue validity (q) of 75 % across various signal strengths parameterized in terms of (d’ on the x-axis). Note that this model’s performance does not depend on the signal strength because the decision rule ignores sensory evidence arising from the stimulus. The model is also invariant to whether the signal strength is known or not.
Figure 3.
Performance predictions (proportion correct) as a function of stimulus strength (d’) for cue-valid, cue-invalid trials and all trials (overall, top row). Bottom figure shows the cueing effect. Models include the Bayeisian ideal observer (BIO); ignore cue model; additive bias/single threshold model; probability matching and always follow the cue model. Left column corresponds to a scenario in which there is uncertainty about the strength of the signal sampled with equal probability from ten d’s at equal intervals between 0 and 4.0. The right column corresponds to a scenario in which the signal strength is blocked and known to the observers.
Probability matching
This classic model (Neimark and Shuford, 1959; Hickson, 1961; Wozny et al., 2010) posits that the organism will make selections based on the base rates. In the context of the spatial cueing task, the model chooses the cued location q % of the trials and the uncued location (1-q) % of the trials. The decision strategy’s probability of a correct choice for the 2 AFC task is given by the joint probability that the model chooses the cued location (q) and that the cued location contains the target (q) added to the joint probability that the model chooses the uncued location (1-q) and that the uncued location contains the target (1-q):
| (1) |
The probability-matching model also ignores the sensory evidence about signal presence and thus it predicts a fixed proportion correct performance as a function of signal contrast and irrespective of whether the stimulus strength is blocked or randomized (Figure 3).
Optimal Bayesian decision rule
One important decision rule within statistical decision theory is that of the Bayesian ideal observer (BIO; Geisler, 2003, 2011; Kersten et al., 2004; Maloney and Zhang, 2010) which specifies the optimal visual processing algorithm to make decisions in the presence of noise and uncertainty. For the context of visual attention in cueing (Eckstein et al., 2002, 2009; Shimozaki et al., 2003, 2012; Yu and Dayan, 2005; Liston and Stone, 2008) and search paradigms (Eckstein et al., 2009; Vincent et al., 2009; Ma et al., 2011), the model posits the optimal method to integrate sensory information across locations cued/uncued locations with varying validities and reach a decision. This approach has been applied to hypothesized internal responses within the human as well as descriptions of the responses of biologically plausible sensory units (Eckstein et al., 2009; Ma, 2010). The Bayesian ideal observer computes the probability of each of Hi hypothesis given the sensory scalar response P(Hi|x) by combining sensory evidence (likelihood of observed sensory response given the event Hi, P(x|Hi)), with prior probabilities of each hypothesis Hi occurring, (P(Hi),(Peterson et al., 1954; Green and Swets, 1989):
| (2) |
The denominator refers to the probability of the sensory data over all possible hypotheses, Hi, and is typically a normalization factor that is constant across Hi. The spatial cues provide (either through training or verbal instruction) information about the likely locations to contain a target. The Bayesian ideal observer (BIO) posits the optimal use of this prior knowledge by combining noisy sensory data in order to maximize overall accuracy across valid and invalid cue trials. In many cases the BIO is related to simpler signal detection decision rules such as the maximum response model (Palmer et al., 1993, 2000; Verghese, 2001; Baldassi and Verghese, 2002; Cameron et al., 2004; Eckstein et al., 2004; Pestilli et al., 2011). The Bayesian ideal observer can capture the behavioral benefits from the presence of informative cues and/or number of cues without positing any limited resources (Eckstein et al., 2002, 2004, 2006; Shimozaki et al., 2003; Vincent et al., 2009; Vincent, 2011).
Signal strength known (blocked condition)
For the case of a signal intensity of known constant stimulus strength (d’) it is a well-known result (Green and Swets, 1989; see Appendix A for derivation) that the ideal observer weights the likelihood ratio (LR) of the cued location by the cue validity and the likelihood ratio of the uncued location by 1-the cue validity. The model then compares the weighted likelihood ratios across the two locations and chooses the maximum:
| (3) |
otherwise, choose uncued location; where the LR is given by (see appendix for full derivation):
| (4) |
where xi is the sensory response at location i (subscripts c, cued or u, uncued) and d’ is the index of detectability. Equivalently, one can take the logarithm of the weighted likelihood ratios, divide by d’ and make a decision based on the following rule:
| (5) |
Proportion correct for valid (Pvalid) and cue invalid trials (Pinvalid) in the 2 AFC can be computed for this model using a closed form expression which calculates the probability that the decision variable from the location containing the target exceed the decision variable from the location not containing the target:
| (6) |
| (7) |
| (8) |
Overall proportion correct can be calculated as:
| (9) |
Figure 3 (right column) shows proportion correct for this model for ten different signal strengths (d’s at equal intervals from 0 to 4.0) for valid and invalid cue trials. For the optimal Bayesian observer, the cueing effect arises as a byproduct of higher weighting of the sensory evidence arising from the cued location. Figure 3 (bottom graph, cueing effect) also shows that for the 2 AFC task the cueing effect diminishes with signal strength (d’).
Signal strength uncertainty
For the case of signal strength uncertainty the model integrates for each ith hypothesis (target left vs. right) the sensory evidence across the J mutually exclusive possible indices of detectability (d’j):
| (10) |
where P(Hi) is the prior probability of the ith hypothesis and P(x|Hi,d’j) is the likelihood of the sensory data given that the signal is at the ith location with jth index of detectability. For the case of the 2 AFC spatial cueing task the decision rule of the optimal observers becomes (Peterson et al., 1954):
| (11) |
| (12) |
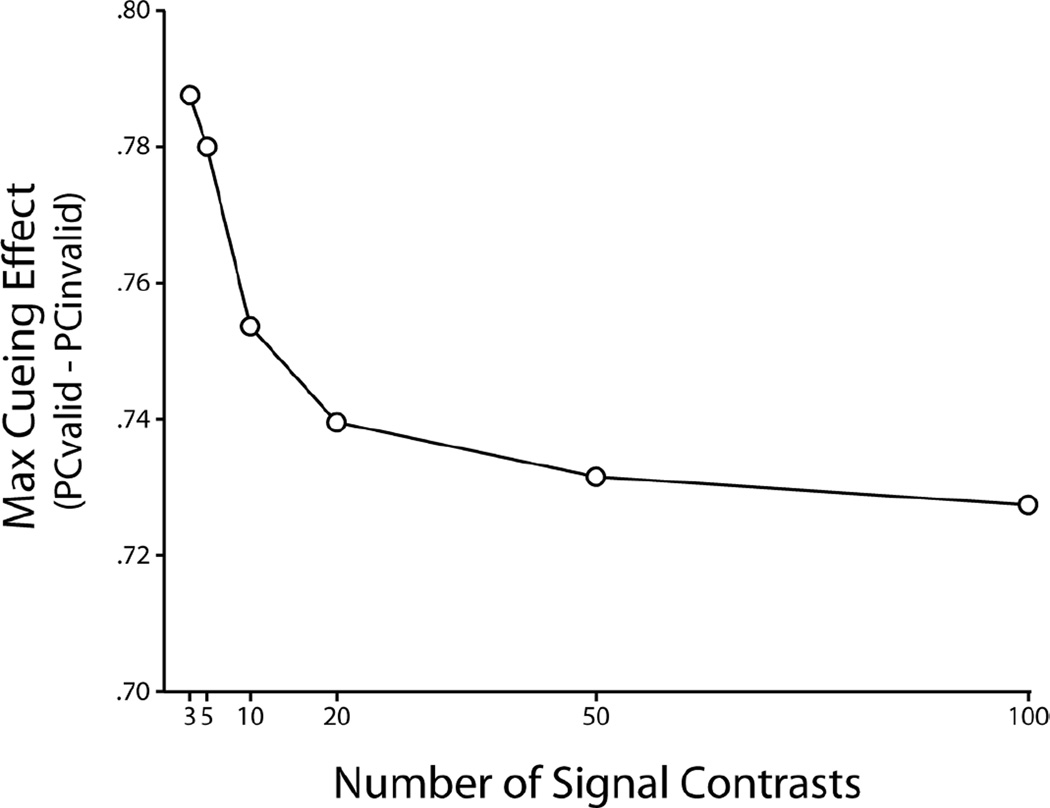
Figure 2a shows a schematic of the model for signal uncertainty case. Performance of this model was calculated using simulations. Figure 3 (left column) shows proportion correct for the ideal observer for 10 different d’s (equal intervals between d’= 0 and 4.0) that are randomly interleaved and unknown to the model. Comparisons of performance in the signal strength known vs. signal strength uncertainty condition shows that uncertainty reduces the variation of the cueing effect with d’. In particular, the cueing effect at the zero d’ trials is reduced significantly (see bottom graphs, cueing effect, in Figure 3). Figure 4 shows the maximum cueing effect (Pvalid − Pinvalid at d’=0) for an optimal Bayesian observer with increasing uncertainty about signal strength (number of d’s sampled regularly between d’=0 and d’=4.0). Results show how the maximum cueing effect of the model diminishes with signal strength uncertainty but asymptotes due to the upper limit on d’.
Figure 4.
Signal strength uncertainty reduces the cueing effect in a 2 AFC. Maximum cueing effect (proportion correct valid cue – proportion correct invalid cue) as a function of the number of signal strengths (d’) chosen in equal intervals from a range of d’= 0 to d’=4.0.
Decision based only on the sensory evidence (ignore the cue)
This strategy ignores the cue and chooses the location on each trial solely based on sensory evidence in the stimuli. The model compares the two internal responses elicited by the two locations on every trial and chooses the location that elicits the highest internal response: If xc > xu then choose cued location (H1) otherwise choose the uncued location (H2). Ignoring the cue leads to equivalent accuracy in cue-valid and invalid trials and thus no cueing effect. This model’s proportion correct would reduce to the standard 2 AFC signal detection model (Green and Swets, 1989):
| (13) |
where and ϕ is as defined before Equation 7. Figure 3 shows performance for this strategy as a function of stimulus strength with no cueing effect and inferior overall performance to the optimal Bayesian observer in particular in conditions with low stimulus strength, d’.
Additive Bias/Single decision threshold model (AB/ST)
A common model that has been proposed previously for the 2 AFC spatial cueing task is a simple model which compares the internal responses from cued and uncued locations to make a decision but simply biases its choices based on the cue validity by adjusting a decision threshold (Shaw, 1980; Sperling and Dosher, 1986; see Figure 2b):
| (14) |
For the case in which the target is equal likely at both locations, maximizing proportion correct decisions across all trial types requires setting t =0. For the case in which the signal is more likely to occur at the cued location t is set to a negative number requiring less sensory evidence to favor the cued location.
Equivalently, the single threshold model can be expressed in terms of an additive bias (b) added to the cued location followed by a comparison of responses across locations:
| (15) |
The advantage of the additive bias is that it is simple to implement biologically and is consistent with a variety of results showing biasing of neural responses by attentional manipulations (Gandhi et al., 1999). Importantly, if the bias b is equal to then this algorithm is mathematically equivalent to the optimal Bayesian decision rule for the case of signal strength known (Equation 5; (Green and Swets, 1989)). However, using the AB/ST model is not mathematically equivalent to the optimal Bayesian rule in the signal strength uncertainty condition. The optimal Bayesian algorithm makes a non-linear accelerating transformation of internal responses for cued and uncued locations assuming the various possible signal strengths (likelihoods), then sums the likelihoods and multiplies the cued and uncued location sum of likelihoods by the priors. The non-linear transformation leads to a larger influence of the priors (and larger cue effects) for low signal strength trials when compared to high signal strength trials.
The AB/ST model does not have any non-linear accelerating transformation of the internal responses. Instead, it makes decisions by operating simply on the internal responses themselves and compares the difference in responses to cued and uncued locations to a decision threshold.
Unknown is how performance of the single threshold model compares to that of an optimal Bayesian for the case of signal strength uncertainty. Figure 3 (top graph) shows that optimizing the bias, b, to achieve maximal overall accuracy for this model can attain an overall accuracy (averaged across the ten indices of detectability) that is 0.5% lower than that achieved by the optimal Bayesian decision rule. The differences between the accuracies of the models are the greatest at low d’ values (5 %). The lack of the non-linear transformation of the AB/ST model leads to lower (suboptimal) variation of the influence of the cue with signal strength but this cost in performance is not large.
METHODS
Human Studies
Participants
Observers were four undergraduates at the University of California-Santa Barbara (2 female; ages 18–21). All had normal or corrected-to-normal vision.
Stimuli
Stimulus images consisted of two Gaussian blurred disks (luminance pedestals: SNR=4.2; diameter: .6°) appearing 6° to either side of central fixation embedded in a field of Gaussian noise with a mean luminance of 25 cd/m2 and standard deviation of 4.9 cd/m2. The noise field subtended a region spanning 22.2 × 22.2°. One of the two pedestals had a contrast increment with a difference SNR of 0 (no signal), 2.7, or 4.0 where is the signal energy of the difference signal (target – pedestal) defined as: and σ is the standard deviation of the noise. Thin black bounding boxes indicated potential target locations. The luminance vs. grey level relationship of the display was linearized.
Task
Observers performed a spatial two alternative forced choice (2AFC) task in which they were to indicate which of two locations contained a brighter Gaussian-blurred disk luminance signal by making a saccade to the target location. Observers initiated each trial by fixating a central fixation point and pressing the space bar.
Predictive cue conditions
In cued sessions, following a randomized 500–1500ms delay, a 75% predictive precue appeared in the form of one of the black bounding boxes turning white for 200ms. Following another 500–1500ms fixation period, a stimulus image appeared for 500ms during which the first eye movement that deviated more than 2° to the left or right from fixation was considered the response. Binary (correct/incorrect) feedback was presented following the response. If no eye movement response was made during the stimulus interval, subjects were informed that no response was selected and the trial was considered incorrect4 (see Figure 1a for trial structure). Following a 100-trial training session to familiarize the observers with the task, observers performed twenty-four 100-trial cued sessions (except observer DB who completed twelve sessions of 100 trials). Prior to the start of the first session, observers were informed verbally and given an instruction sheet which indicated that the precue would predict the target location on 75% of the trials and on the other 25% of the trials, the target would appear at the uncued location.
Neutral cue condition
Interleaved with the predictive cue sessions were six 100 trial neutral cue sessions. In neutral sessions, no precue appeared after the initial fixation interval.
Eye position measurements
Gaze was monitored using an Eyelink 1000 infrared eye tracker (SR Research) providing a monocular left eye track at a sampling rate of 250 Hz. Changes in eye position that exceeded a velocity of 35°/sec and an acceleration of 9500°/s/s were considered to be saccades.
Monkey Studies
Two adult macaques performed a task similar to that the humans performed, with very similar images and procedures. Signal to noise ratios were matched to those in the human study (0, 2.7, and 4.0). The mean luminance of the background was 45.9 cd/ m2 and the Gaussian noise standard deviation was 9 cd/m2. Monkey K participated in forty-four sessions of 100 trials. Monkey M participated in thirty nine sessions of 100 trials. Unlike human observers, monkeys were given a small juice reward for correct decisions and eye movements were measured using the scleral search coil technique using methods described in detail previously (Hafed et al., 2008). Monkey data were collected at the Salk Institute for Biological Sciences, and all experimental protocols for the monkeys were approved by the Institute Animal Care and Use Committee and complied with Public Health Service Policy on the humane care and use of laboratory animals.
Honey Bees study
Task
Two Styrofoam boxes measuring 35 × 35 × 35 cm were placed on a table separated by a distance of 70 cm. The table was placed in front of the wall of Dr. Menzel’s lab building at the Freie University of Berlin. The front part of the box was covered with a colored paper for the various tasks (Figure 1). The center of the colored paper was perforated with a plastic tube providing an opening that led to the inside of the box where a sucrose plate was placed during training. There were four different color discrimination tasks: green target vs. green distractor (SNR =0); blue target vs. blue distractor (SNR =0); green target vs. yellow distractor (medium SNR); blue target vs. grey distractor (high SNR). The subjective color differences were calculated by applying a model of color vision of the honey bee (Vorobyev et al., 2001). The three pairs were aimed to span three different discriminabilities (low, medium and high d’). Each of the two boxes containing the colored paper was placed on top of another box. One of the two bottom boxes was covered with a black plastic bag that was the cue and co-occurred with the target color 80 % of the time (see Figure 1b). The study was conducted at the surroundings of the Department f Neurobiology at the Freie University of Berlin.
Training
The first step in the procedure was to allow for the bees to learn the location of the experimental set-up relative to the beehive. This process required that a sucrose plate was placed first close to the beehive and through a few hours progressively moved further away until it was located nearby the experimental set-up and eventually inside the boxes.
Experimental procedure
Training and testing of the bees to perform the various discrimination tasks developed over a period of 45 days. To train the bees to fly and enter the box with the target color, a small dish with sucrose was placed inside the box containing the target paper color. Training with reward consisted of periods of 10–23 minutes in which the bees entered one of the two boxes with the target box paired with the sucrose. In the predictive cue condition, the cue was also present during the training. After the training period, the sucrose plate was removed and the boxes were thoroughly cleaned. Following, the position of the target and distractor boxes were placed left and right following a pre-computed list of pseudo-random orders. The pairing with the cue box was also determined by a different pre-computed pseudo-random list. For another 10 minute period, bee behavior was then recorded without the presence of the sucrose plate. This 2nd stage was referred to as the testing section of the experiment and is the data reported in the results section. Target/distractor color pairings were blocked with the exception of the blue-blue condition that was interleaved with the green-yellow and blue-grey conditions. Thus, the signal strengths were not strictly randomized but contained some degree of uncertainty.
Data recording of bee decisions with hand coding
A single undergraduate assistant (naïve to the hypotheses of our experiment) with experience in hand coding bee behavior coded the behavior of each bee as they approached a box. If the bee circled around the box in close proximity, he would mark a C. If the bee approached a box and landed on the front of the box the research assistant would record an R (rest). If the bee entered the hole but did not enter the box, the research assistant coded this with H. Finally, if it entered the box, this would be documented using H*.
Dependent variables
We calculated, for each box (target and distractor), the number of times a bee circled or rested the color paper box (target or distractor). We then calculated for a session (training or testing) a proportion by dividing by the total number of times a bee circled or rested on the target color box (and approached the circle) divided by the total number of bee circles and rests. For simplicity we refer to this measure as the rest measure in graphs. We also calculated similar proportion correct for the proportion of times that bees entered the hole of the target-box out of all box entries. Note that these measures, unlike the human and monkey, are aggregates across many bees. The standard errors were calculated across different days with the same stimuli. The total numbers of observed choices were: for the rest measure: 310 for grey vs. blue, 296 for green vs. yellow, 168 for blue vs. blue; for the hole entry measure: 698 for blue vs. grey; 1057 for green vs. yellow; 390 for blue vs. blue. The exception is the blue vs. blue condition for which we had a single day of data due to weather conditions. For the blue vs. blue condition, jackknifing techniques were used to estimate the standard error. We calculated various measures of bee choices to attempt to isolate instances for which the bees used non-visual cues (which are detailed in the following section).
Potential confounds of non-visual cues
A fundamental potential problem in assessing visual discrimination by bees is their potential use of non-visual cues that can introduce confounds. It is well-documented that honey bees have a sophisticated pheromonal communication system with fifteen known glands (Free, 1987; Leoncini et al., 2004). Queen, drone and worker bees secrete these chemical compounds and elicit responses in other bees by direct contact For our task, this source of confound could arise if early in the session from bees entering a box and leaving a pheromonal compound (predominantly from the Nasanov gland used by bees to mark attractive locations) in the hole of the box with the reward dish5. Other bees could potentially use this pheromonal cue to decide whether to enter or not a box. For example, a bee could rest on the box with the the distractor paper, approach the hole, and, in the absence of the pheromonal cue, might not enter the distractor box and instead fly and enter the target box. To assess the use of non-visual cues, we evaluated accuracy of the bees choosing the target box in the absence of visual information (e.g., blue vs. blue paper task).
Model predictions for experimental conditions
Bayesian Ideal Observer
A one-dimensional Bayesian ideal observer (BIO) with signal strength uncertainty of the three different d’s was generated to provide a benchmark of optimal task performance (Equation 8). Because the model cueing effect depends on the indices of detectability (d’) assumed for the signal strength uncertainty, we used performance in the neutral cue condition for each individual human and monkey to independently estimate underlying d’s for the three signal contrast/color pairing conditions. We estimated three d’s (Equation 3) for each individual human and monkey as to best predict performance in the neutral condition using a weighted (inversely to the measurement error) least squares optimization procedure (chi-square χ2). For the zero signal strength condition, d’ was assumed to be zero. Therefore, estimates of underlying d’ were only free to vary for the two non-zero signal strengths. For the honeybees we estimated the indices of detectabilities for the decisions aggregated across different honey bees. Estimated observer/organism d’s were then utilized in cued simulations to generate optimal expected cueing effects for each human and monkey, and for the collective bee data. Model predictions were generated through ten iterations of 500,000 trial Monte Carlo simulations. The model predictions represented the performance and cueing effect attained by an optimal Bayesian observer with the signal strengths (d’s) of the different organisms.
Additive bias/Single threshold
The additive bias/single threshold model was fit to the behavioral data for each human, monkey and the collective decisions of the honeybees. Predictions were obtained using the estimated indices of detectability from the neural condition and fitting the single decision threshold (t in Equation 14 or equivalently, b, in Equation 15) to minimize the chi-square error (χ2) between the predicted and measured proportion correct for each stimulus strength condition. For the bee data we also fit the data estimating the indices of detectability (d’s) from the valid/invalid cue data rather than using the neutral conditions. Thus, in this fitting procedure there were four fitting parameters: three indices of detectability (one per target/distractor discriminability) and a decision threshold.
RESULTS
Cueing effect in Honey Bee choices
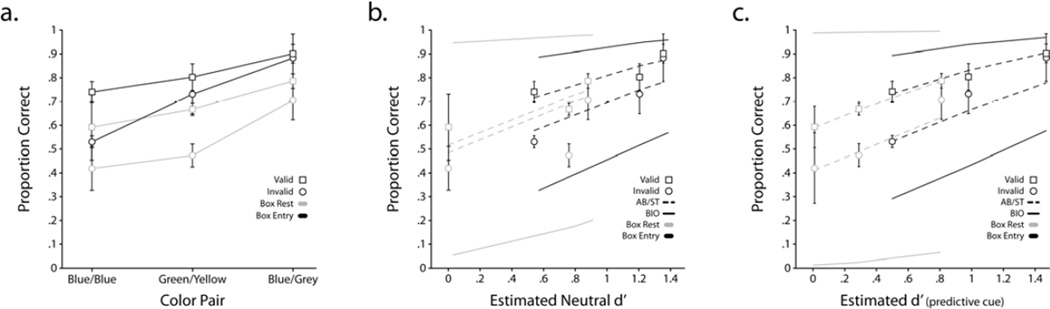
We report the proportion of correct choices by the bees using two different measures: 1. Proportion of bee circles around or rests on the target box (out of all the circling around and resting reports on any of the two boxes). For simplicity, this measure is referred to in the figures as the rest measure. 2. Proportion of entries on the target box (out of all entries on any of the two boxes). Figure 5a shows proportion correct choice for three stimulus conditions (blue vs. blue; green vs. yellow; blue vs. grey) for valid and invalid. Results show an overall statistically significant overall cueing effect for the rest on box measure (Pc valid > Pc invalid; p < 0.05). When testing for significance for individual signal strengths, the cueing effects did not reach statistical significance. For the entry measure, the cueing effect was statistically significant for the blue-blue condition but not for the green vs. yellow and blue vs. grey conditions. Figure 5b plots proportion correct against the indices of detectability (d’) estimated from the neutral condition using each of the two bee choice measures. For comparison, a Bayesian ideal observer prediction based on the estimated d’s of each measure is shown. Overall performance attained by the bees was higher for the box entries measure than the rest measure. This is likely due to the use of additional non-visual information by the bees in making their choices when entering the boxes (see next section).
Figure 5.
a. Proportion correct for valid and invalid cue trials for three target/distractor discrimination conditions: blue target vs. blue distractor; green target vs. yellow distractor; blue target vs. grey distractor. b. Proportion correct for valid and invalid cue trials as a function of signal strength (target/distractor discriminability), d’ manipulated by color differences and estimated independently using the neutral condition conditions. Solid lines are for the Bayesian ideal observer (BIO) predictions based on d’s estimated from the neutral conditions each of the two measures: box rest and box entry. The dashed lines are fits of the additive bias/single threshold model with a single fitting parameter: decision threshold. c. Data is identical to Figure 5b, but the d’ indices were fitting parameters estimated from the valid/invalid cue data rather than separately estimated from the neutral cue conditions. There are four fitting parameters for this model: 3 indices of detectability (d’) and a decision threshold.
Assessing contributions of non-visual cues by honey bees
We used the blue vs. blue visual discrimination (without a cue) to assess whether the bees’ decisions were being influenced by other than the visual information. We reasoned that if the bees’ choices were based solely on visual information, then, in the blue vs. blue discrimination, the bees’ accuracy at finding the target box should be at chance. We made a second control condition using a green vs. green discrimination task. We evaluated the two dependent variables: 1) Proportion of circles or rests on target box; 2) Proportion of entries to target box. For the proportion of entries on the target box, bee performance was significantly above chance (average across blue vs. blue and green vs. green condition = 0.575 ± 0.005; p < 0.05) even though there was no visual information to identify the target box. Quantifying bee decision by tallying the number of times bees circle around or rested on a box for the no visual information conditions resulted in accuracy of 0.465 ± 0.01 (p = 0.18) suggesting that this metric was not affected or at least less influenced by non-visual cues.
Cueing effects for humans and monkeys
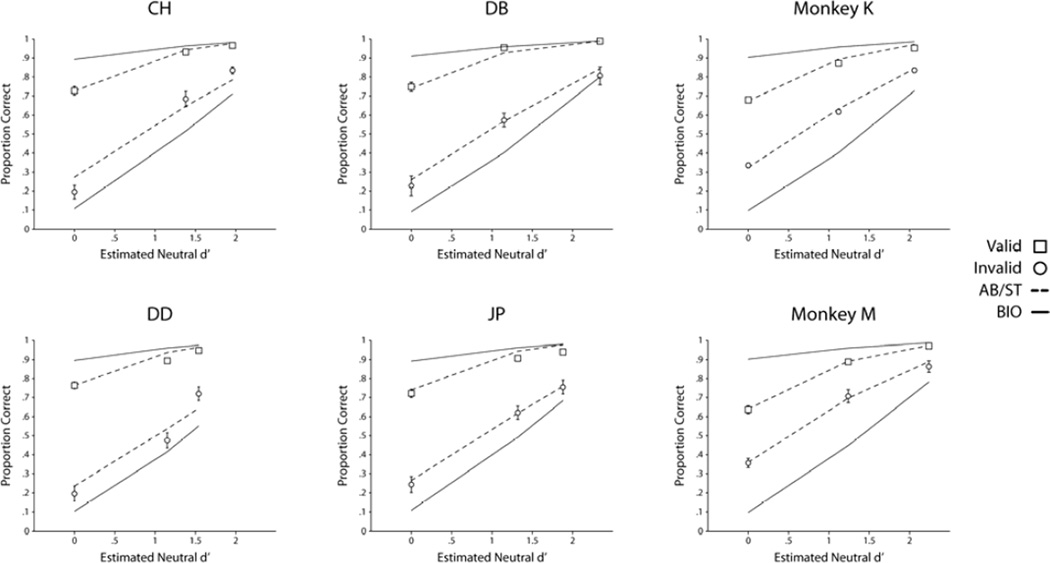
Proportion correct was calculated across signal contrasts for both valid and invalid trials for each human and monkey observer. Figure 6 shows the individual data for each human and monkey (see Table 1 for data). A significant cueing effect, defined as the difference in proportion correct between valid and invalid trials, was observed for all four humans and both monkeys (see Table 2 for p values, p<0.05 false discovery rate (FDR) corrected), indicating that all observers were utilizing the predictive cue to aid their perceptual decision to at least some degree. Moreover, the size of the cueing effect decreased for each increment of increasing signal contrast for all observers (p<0.05 FDR corrected; see Table 1 for p values), a result predicted by the BIO (see Figure 3). Across all signal strengths all humans and both monkeys showed a cueing effect that was inferior to that of the optimal Bayesian model.
Figure 6.
Proportion correct for valid and invalid cue trials as a function of the estimated detectability of the three signal contrasts in the neutral condition. Continuous lines, Bayesian ideal observer for each observer and their corresponding estimated d’s from the neutral condition. Human observers: CH, DB, DD, JP; Monkeys: K and M. Dotted line is the single threshold model with one fitting parameter for each individual.
Table 1.
Descriptive statistics for cueing effect and standard deviation for each signal strength condition (zero, medium, high and overall).
| Descriptive Statistics | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| n | Overall | SD | Zero | SD | Med | SD | High | SD | |
| CH | 24 | 0.30 | 0.13 | 0.53 | 0.25 | 0.25 | 0.22 | 0.13 | 0.10 |
| DD | 24 | 0.41 | 0.13 | 0.57 | 0.23 | 0.42 | 0.19 | 0.23 | 0.18 |
| JP | 24 | 0.32 | 0.14 | 0.48 | 0.25 | 0.29 | 0.19 | 0.19 | 0.18 |
| DB | 12 | 0.36 | 0.09 | 0.52 | 0.22 | 0.38 | 0.12 | 0.18 | 0.17 |
| mK | 45 | 0.24 | 0.06 | 0.34 | 0.11 | 0.25 | 0.08 | 0.12 | 0.07 |
| mM | 40 | 0.19 | 0.23 | 0.28 | 0.27 | 0.18 | 0.25 | 0.11 | 0.20 |
| Cueing Effect > 0 (one tailed) | |||
|---|---|---|---|
| df | t | p | |
| CH | 23 | 11.09 | 5.22E-11 |
| DD | 23 | 14.78 | 1.56E-13 |
| JP | 23 | 11.36 | 3.27E-11 |
| DB | 11 | 13.80 | 1.37E-08 |
| monkeyK | 44 | 25.68 | 2.04E-28 |
| monkeyM | 39 | 5.23 | 3.06E-06 |
| Size of Cueing Effect Across Contrasts (one tailed) | |||||||
|---|---|---|---|---|---|---|---|
| Zero>Med | Med>High | Zero>High | |||||
| df | t | p | t | p | t | p | |
| CH | 23 | 5.36 | 9.63E-06 | 2.54 | 9.11E-03 | 7.30 | 9.93E-08 |
| DD | 23 | 2.67 | 6.84E-03 | 3.98 | 2.94E-04 | 6.38 | 8.20E-07 |
| JP | 23 | 3.07 | 2.72E-03 | 2.23 | 0.018 | 5.06 | 1.99E-05 |
| DB | 11 | 2.05 | 0.032 | 2.93 | 6.91E-03 | 3.80 | 1.47E-03 |
| monkeyK | 44 | 5.22 | 2.33E-06 | 9.79 | 6.33E-13 | 11.40 | 5.10E-15 |
| monkeyM | 39 | 5.05 | 5.37E-06 | 4.70 | 1.59E-05 | 7.67 | 1.32E-09 |
n is the number of sessions, SD is the standard deviation.
Table 2.
Pairwise statistical tests for human and monkey data
| > DD | > JP | > DB | > mK | > mM | > BIO | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Obs | df | t | p | df | t | p | df | t | p | df | t | p | df | t | p | df | t | p |
| CH | 46 | −2.62 | 0.012 | 46 | −0.33 | 0.74 | 34 | −1.35 | 0.19 | 67 | 2.75 | 7.64E-03 | 62 | 2.21 | 0.031 | 23 | −8.25 | 2.51E-08 |
| DD | 46 | 2.26 | 0.029 | 34 | 1.01 | 0.32 | 67 | 7.04 | 1.31E-09 | 62 | 4.17 | 9.61E-05 | 23 | −4.55 | 1.44E-04 | |||
| JP | 34 | −1.03 | 0.31 | 67 | 3.26 | 1.77E-03 | 62 | 2.45 | 0.017 | 23 | −7.64 | 9.28E-08 | ||||||
| DB | 55 | 5.48 | 1.08E-06 | 50 | 2.52 | 0.015 | 11 | −6.41 | 5.03E-05 | |||||||||
| monkeyK | 83 | 1.37 | 0.17 | 44 | −31.29 | 1.06E-31 | ||||||||||||
| monkeyM | 39 | −9.35 | 1.65E-11 |
Comparison to additive bias/single threshold model
Figure 6 shows fits of AB/ST model to each individual data for the humans and monkeys using a single fitting parameter (the threshold) per observer. The d’s were independently estimated for each individual (human and monkey) from the neutral condition for each signal contrast condition. The model resulted in good fits for each individual human and monkeys (all reduced chi-squares, χ2/df < 1; p > 0.41). The same model was also used to fit the aggregate of honey bee choices using the neutral conditions to independently estimate the indices of detectability (d’s). Figure 5b shows the fits of the model to the bee behavior using both measures of choice (rest and entries to boxes). The quality of the model fits were inferior compared to the human and monkeys, in particular for the data with the rest on box measure which could be rejected (χ2/df=3.73; p=0.0023; for the rest measure and χ2/df= 1.5; p = 0.18 for the box entry measure). Because the neutral cue conditions for the bees were conducted in separate days than the valid/invalid cue conditions (unlike the human/monkey studies for which conditions were interleaved), it is likely that, for the bees, the d’s estimated from the neutral conditions might not be representative of the d’s in the valid/invalid cue conditions. We therefore also fit the model to the data estimating the d’s from the valid/invalid cue data resulting in four fitting parameters: decision threshold and three d’s. Figure 5c shows the results of the fits for the four parameter additive bias/single threshold model. The four parameter model fits resulted in a better fit for the rest on box measure (χ2/df= 1.65; p=0.43) but inferior for the box entry measure (although the model could not be rejected; χ2/df= 1.5; p = 0.06).
Cross Species Comparisons
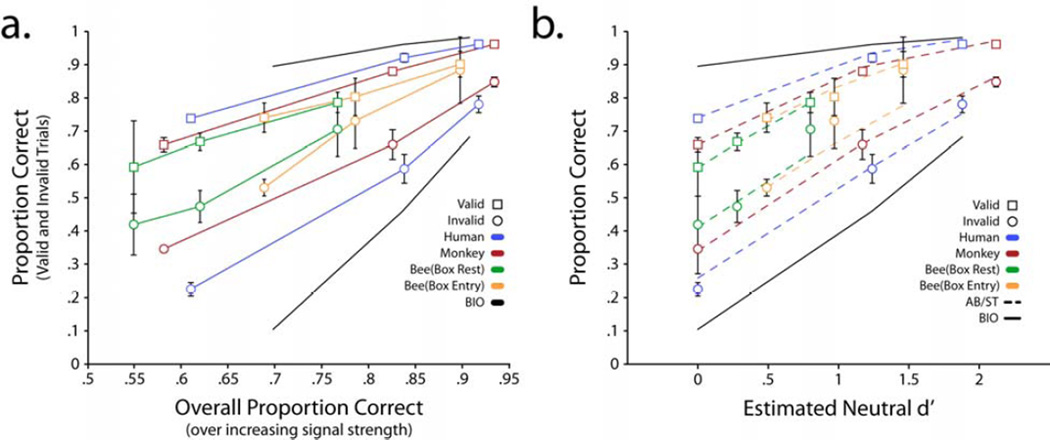
Given the similarity of the human and monkey tasks, direct comparisons between the magnitudes of their cueing effects can be made. Pairwise comparisons revealed that all four human observers displayed larger cueing effects than both monkeys (p<.05 FDR, one tailed; Table 2), while the two monkeys’ cueing effects did not differ significantly from each other. To compare the effect of cues across all three species, Figure 7a shows valid and invalid cue performance for the three animals plotted against overall proportion correct for each signal strength condition. For comparison the graph shows the BIO matched to the discrimination ability of the human observers. All monkeys, human and bees produced a cueing effect significantly smaller than that predicted by a BIO. Figure 7b also shows performance for valid and invalid cue trials plotted against the estimated d’s (average estimates for humans and monkeys). Figure 7b shows the fits additive bias/single threshold model (AB/ST model) to all data sets. The fits for the average human and monkey data are the averages of the model predictions for each individual. For the bees, Figure 7b shows the fits of the four parameter model which gave overall a better fit. Figure 7b shows that the relationship across animals’ cue effects is preserved when plotting performance against overall proportion correct (Figure 7a) or the estimated d’s.
Figure 7.
a. Proportion correct for the average human observer, average monkey, and honey bees (both measures) as a function of overall proportion (valid + invalid cue trials). For comparison, graph shows the Bayesian ideal observer operating on the detectabilities of human observers. Color lines do not correspond to a model but simply connect data points. b. Proportion correct (valid and invalid cue trials) vs. estimated d’s for each signal strength condition for all three animals. The two measures are included for the honey bees. Color dashed lines are the best fit of the additive bias/single threshold model. The human and monkey data are single parameter fits (decision threshold) while the bee data shows fits with d’s and the decision threshold as fitting parameters. Black line shows the Bayesian ideal observer prediction (for humans) for comparison.
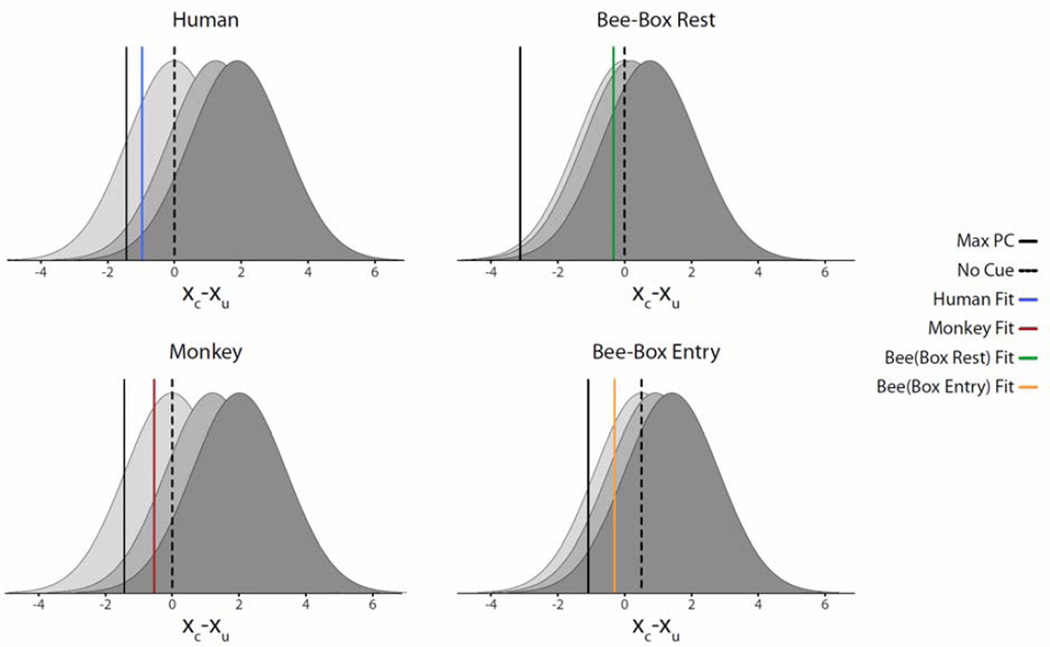
Figure 8 shows a graphical representation of the AB/ST model’s estimated distributions of the organisms’ decision variable for each signal strength and estimated decision thresholds (vertical lines). The x-axis is the difference between the internal response to the cued and uncued location (xc−xu) for valid cue trials (target is present at cued location)6. Each distribution corresponds to a signal strength (low, medium and high) estimated from neutral cue conditions. For example, the mean difference of internal responses for cued and uncued locations is zero for the low SNR because, for these cases, the target has zero contrast and the visual information at cued and uncued location is on average identical containing only pedestals (the bee box entry distribution is an exception which the non-visual cues led to a non-zero mean distribution for the low SNR condition). The two other distributions of each panel correspond to the difference between the internal responses to cued and uncued locations (for valid cue trials for which the cued location contains the target) for the medium and high SNR. The colored lines correspond to the AB/ST model’s decision threshold to best fit the data from the different animals. Different panels correspond to different animals. There are two panels for the bee data corresponding to the rest on box and entry box measures. The negative values for the estimated decision thresholds indicate that all three organisms selected the cued location even when the internal response to the uncued location was greater than the cued location (negative difference in internal responses). This is consistent with a bias to choose the cued location given its predictive value (75%) even when there is some sensory evidence favoring the uncued location. For comparison, Figure 8 also shows the decision threshold for the AB/ST model (leftmost black continuous vertical lines) that maximizes overall proportion correct for each species7. Results show that the AB/ST model’s estimated decision threshold from the data (colored vertical lines) is closer to the model’s optimal decision threshold (black continuous lines) for human observers, followed by the monkeys and honeybees. Differences between the optimal and estimated animal decision thresholds were: −0.492 ± 0.027 for the human; −0.87 ± 0.03 for the monkeys and, for the bees, −2.90 ± 0.052 for the rest measure and −0.82 ± 0.047 for the entry to box measure. All differences were statistically significant (p < 0.05).
Figure 8.
Estimated human, monkey and honey bee decision thresholds and d’s for three signal strength conditions using the additive bias/single threshold model. The x-axis corresponds to the decision variable: difference between the response to the cued and uncued location for valid cue trials. For invalid cue trials the dotted vertical line corresponds to a threshold at zero (optimal for neutral cue trials); leftmost vertical black solid lines correspond to the optimal threshold which maximizes performance (proportion correct, PC) for a cue with 75 % validity and signal strength uncertainty; colored lines are decision thresholds to best fit for each animal for a cue with 75 % validity.
DISCUSSION
The use of probabilistic spatial cues by honeybees
The goal of the present work was to assess whether an organism with a small brain (volume: 1 mm3, about 1 million neurons) without a layered cortex can show cueing effects similar to those measured in humans, monkeys, rats (Bushnell and Rice, 1999; Marote and Xavier, 2011) and pigeons (Shimp and Friedrich, 1993). Previous studies have shown that bees can learn coarse and fine visual discriminations (Srinivasan, 2010) as well as complex shapes (Giurfa, Hammer, et al., 1999; Zhang et al., 2004; for a review see, Menzel et al., 2007). In relation to experimental manipulations typically associated with visual attention, a study has shown that prior visual experience with a target pattern can speed up its detection by bees (Zhang et al., 2004). Also, the effect of number of distracters on search for a target disc increases bee decision times and decreases accuracy in a similar manner as it does for humans (Spaethe et al., 2006). However, no study has assessed the ability of honeybees to learn a probabilistic association which can aid a visual discrimination similar to the Posner paradigm (Posner, 1980). Our results show that honeybees can use predictive cues which results in a behavioral cueing effect akin to that observed in humans, albeit smaller in size.
The presence of a cueing effect in the behavior of the bees is not consistent with the concept that the honeybees ignore the presence of the cue and base their decision solely on the target/distractor information. In addition, we can conclude that bees are not making their decision solely based on the cue and ignoring the sensory information in the target/distractor. The variation of bee performance with target-distractor discriminability suggests that the bee is integrating information about the target/distractor visual discrimination with that provided by the presence of the cue.
One potential confound in the study is the possibility that bees were using non-visual cues to make their 2 AFC choices. In particular, there was the possibility that the bees were using pheromonal (Free, 1987) components at the target box which is used as a non-visual cue for other bees to make their choices. Our control condition in which there was no visual information (blue vs. blue) or cue indicating the probable location of the sucrose plate led to chance performance when we used the rest on or circle around box behavioral measure. In contrast, measuring the proportion of entries on the target box seemed to be contaminated by non-visual cues.
A second limitation of our procedure is that our recorded decisions were not based on decisions by individual independent decisions. Thus, there is a possibility that our measurements reflect decisions by a few bees which then communicated their choices to other bees (Menzel et al., 2006, 2011). However, there was no indication that bees communicated anything about the visual stimulus conditions at the goal. Furthermore, the tested bees were trained for quite some time, and this would likely override anything they have learned by the communication process inside the hive.
Finally, the study was intended to measure to how the spatial cues impact choices but controlling for possible effects due to lower level sensory sampling. For example, human and monkey studies often control for possible eye movements prior to a choice decision because foveation of the cued location prior to a decision could introduce improvements in detection or discrimination performance related to the high resolution processing of the fovea. In the current study, the monkeys and humans made their choice with a saccade to match the spatial eccentricity of targets at the cued and uncued locations. However, there was no such control for the honeybees. The choice of the bees involved flying toward the target box and thus changes in the image falling in their compound eyes preceded the choice behavior. Furthermore, studies have shown that different regions of the bee’s compound eye (ventral, dorsal and frontal) have different properties processing visual stimuli (Giurfa, Zaccardi, et al., 1999). In particular, color detection efficiency cue varies depending on the region of the compound eye and the visual extent of the color cue. For our task for which the boxes were arranged vertically it is likely that the visual choice is based on visual processing by the frontal region of the bee’s eye while in flight. However, we cannot discard that flight towards one of the boxes introduced variations in sensory processing of the target/distractor colors, although our honeybee experiment counterbalanced the use of leftward and rightward targets to indicate the more likely location.
Effect of target/distractor discriminability (SNR) and signal strength uncertainty on the cueing effect in biological organisms and optimal observers
Studies have shown that, for humans, the size of the cueing effect varies across signal detectability (Shimozaki et al., 2003, 2012). For the forced-choice version of the cueing paradigm the cueing effect in humans diminishes with increasing target/distractor discriminability.8 In the present study we show a similar trend in all three organisms: humans, monkeys, and, to a lesser degree, bees. A similar variation in the cueing effect is also present in an optimal Bayesian observer. For a blocked condition with zero SNR, there is no target/distractor information to utilize for the decision and the optimal algorithm always chooses the cued location (Figure 3). For very high target/distractor discriminabilities, the non-linear likelihood calculation diminishes the effect of the prior so that choices are driven by the sensory responses to the target and distractor. However, the variation of the cueing effect with target/distractor discriminability is much larger for the optimal Bayesian observer than the humans (Shimozaki et al., 2012).
The theoretical results in the current paper show that uncertainty about the stimulus strength (or target/distractor discriminability) diminishes the maximum cueing effect and reduces its variation with target/distractor discriminability for an optimal Bayesian observer. This might suggest that even when stimulus strength is blocked and known, humans and other animals might have either intrinsic uncertainty about the stimulus strength or adopt a default strategy that allows for some unexpected variation in target/distractor discriminability. A strategy that assumes some possible change in the stimulus strength across trials might be suboptimal in a blocked stimulus strength study but a well-adaptive strategy for the dynamic environment such as the real world (Vincent, 2012). However, our results show that even when taking into consideration the stimulus strength uncertainty in the tasks in which the humans and monkeys participated, the optimal Bayesian observer still shows a larger cueing effect than humans and monkeys. Thus, stimulus strength uncertainty cannot entirely account for the reduction in cueing effect and there must be other sources of suboptimality in the organisms. For humans, having to generate a choice decision with an eye movement rather than a finger-press might lead to some suboptimalities. A recent study has shown that the effect of cues on saccadic eye movements is not as prominent as with perceptual decisions, although it should be noted that in that study the observers were not instructed to use an eye movement to make a response (Shimozaki et al., 2012).
Simpler biologically plausible implementations of the optimal decision rule for the scenario of stimulus strength uncertainty
A well-known result is that for the case of a 2-AFC task, the optimal Bayesian model is mathematically equivalent to a single threshold model. The single threshold model can be implemented equivalently by an additive bias to the response to the cued location followed by a maximum operation when comparing neural responses arising from the cued vs. uncued locations. To achieve optimality the additive bias needs to be related to the cue validity and the stimulus strength (Equation 14). This is arguably a more biologically plausible decision rule than the full weighted likelihood calculation (Equation 12) and could be implemented in the nervous system of a variety of species. However, unknown was whether a model with an additive bias could approximate an optimal Bayesian model for the case of a cueing task with signal strength uncertainty. Our theoretical results show that an additive bias can be a good approximation to the more computationally complex sum of weighted likelihood ratios of the optimal Bayesian algorithm. Thus, our theoretical results further generalize the use of an additive bias model to approximate the BIO from the 2 AFC (Green and Swets, 1989) and yes/no cueing task (Eckstein et al., 2009) to the scenario of signal strength uncertainty. Our results are for Gaussian distributed responses but as previously shown these models can generate similar decision rules and predictions for the often encountered Poisson distributions used to model spike rates (Eckstein et al., 2009).
In addition, our results show that the additive bias/single threshold model results in good fits to the animal data. Arguably, the fits to the honey bee data were inferior, in particular for the rest measure when the d’s were independently estimated from the neutral cue condition data. The inferior quality of model fits for the honey bees is not surprising given that the neutral cue condition data was collected in separate days than the valid/invalid cue data. Furthermore, there is no guarantee that the same set of bees participated in both conditions. When the d’s were estimated from the valid/invalid cue condition the fit of the model to the circle around or rest on box measure data improved and the model could not be rejected for either measure (box entry and circle around or rest on box measure). In summary, our results suggest that the additive bias is a likely biologically plausible computation that can account for the behavioral cueing effects in the animals.
Spatial cueing effects across species: What is unique about human visual attention in the spatial cueing paradigm?
Our results have some interesting implications about how we think about human visual attention. The spatial cueing paradigm is meant to probe covert visual attention. The cueing effect is typically attributed to the allocation of covert visual attention to the cued location. Although there are different models about what mechanisms gives rise to the cueing effect, most studies have an implicit assumption that the cueing effect studies are probing a mechanism that is similar to human’s ability, at will, to select or process different locations of a visual scene: covert visual attention.
Our results and previous findings show that a great variety of organisms including monkeys, rats, pigeons and honeybees can use probabilistically informative spatial cues to optimize their behavioral choices. In this study, we compared cueing effects in humans, monkeys and bees in a similarly structured task. Notably, our results demonstrate that a mammalian brain with a layered cortex is not a requirement for an organism to use probabilistic cues.
Thus, we might ask whether there is something unique about human visual attention as measured in a spatial cueing task. One possible interpretation of our results is that humans show cueing effects that are closer to an optimal observer than those shown by monkeys. In turn, monkeys are closer to optimality than bees. However, the shortcoming of such interpretation is that the differences in the details of the tasks make it difficult to assess whether these comparisons are sensible. With humans, the investigator verbally communicates to the subjects the validity of the cue in predicting the target location. With the monkey and bee studies, the animals learned the association between the cue and the presence of the visual target through rewards given to correct decisions.9 Thus, it might be that if humans are not communicated cue validities they are less optimal. For example, when humans have to learn cue probabilities, rather than being verbally communicated about their validity, there are less optimal at using the probabilistic cues (Droll et al., 2009). Therefore, we might conclude that what is unique about orienting human visual attention in humans is that it can be the consequence of the communication. However, even that might not be exclusive to humans. In more ecological settings, honeybees have the ability to communicate locations of food (von Frisch, 1933; Seeley and Visscher, 2008). Monkeys, like humans, also can orient attention of other monkeys with gaze (Emery et al., 1997; Deaner and Platt, 2003). Then, perhaps, what is unique to humans is the potential ability to communicate numerical representations of the cue validity that could potentially lead to more accurate priors and more optimal behavior.
Aside from this discussion, the current results, together with those obtained with pigeons and rats, indicate that it might be a simplification to conceptualize visual attention as a unitary process required to give rise to a cueing effect (Anderson, 2011) but instead it might prove useful to think of the ability to use predictive cues as a graded phenomenon which might be exploited with varying efficiency across species and across methods used to convey the information about the validity of the predictive cues (Geng and Behrmann, 2005; Walthew and Gilchrist, 2006; Droll et al., 2009; Druker and Anderson, 2010).
Highlights.
Honeybees can use probabilistic cues to optimize their decisions
A mammalian brain with a layered cortex is not required to use probabilistic cues
Humans show a larger cueing effect than monkeys and bees show the smallest effect
A biologically plausible additive bias model approximates the Bayesian optimal
Signal strength uncertainty reduces the cueing effect of an optimal observer
APPENDIX
Optimal Bayesian observer for 2 AFC with known signal strength
The optimal Bayesian observer for a 2 AFC is a standard result (Green and Swets, 1989) and is included in the Appendix for thoroughness.
There are two hypotheses: H1: target at cued locations; H2: target at uncued location
The posterior probability for each hypothesis is proportional to the product of the likelihood and the prior:
where xc and xu are the sensory responses at the cued and uncued location and subscript i=1 or 2; The decision rule on each trial is:
For the case that each location elicits an internal response that is Gaussian (with equal unit variance) and independent, the likelihood of the responses at the cued and uncued locations given each hypothesis are given by:
where the response from the target distribution has a mean d’.
After some algebra the likelihoods become:
Simplifying common terms by dividing likelihoods by
Taking the logarithm, and replacing P(H1) by πc and P(H2) by πu:
or re-arranging terms we obtain:
Similarly one can express the decision rule in terms of the difference of the responses from cued and uncued location exceeding a decision threshold:
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
For the honey bees, there were mini-blocks in which the bees were trained on one signal strength and then tested in that same signal strength. The exception was the zero signal strength condition which was interleaved with the other two conditions. So although the signal strengths presentations did not adhere to the absolute randomization, the stimulus strength uncertainty theoretical predictions are still a realistic model for the bees because each bee might have limited exposure to each stimulus and manifest some intrinsic uncertainty about stimulus strength.
For the Bayesian ideal observer, we define “optimal” to mean maximizing the overall proportion of correct responses (Green and Swets, 1966, Chapter 1.7.3).
Note that for the case of stimulus strength uncertainty for which likelihood ratios are summed, there is an additional term (−0.5d’2) which cannot be simplified as in the case of no stimulus uncertainty (Equation 4).
The choice of labeling trials as incorrect if no eye movement response was made was to encourage observers to choose the location they believed to contain the target, even if they were highly uncertain. Although the proportion of trials which fell into this category was quite small (<2%), we performed alternative analyses in which we threw out trials in which no eye movement response was made or counted any deviation to either side of initial fixation (even if it were less than the 2° tolerance) as the response. Neither analysis substantially impacted PCs (<1%) or any of the following statistical tests.
Each time we switched the box positions and location of the cue, and reward, boxes were thoroughly cleaned. However, there is the potential that some pheromonal component remained in a box introducing non-visual cues.
Invalid cue trials for which the target appears at the uncued location can be described by similar distributions of the difference in internal response (cued location minus uncued location) but with the distribution means being the negative of the means of the distributions in Figure 8.
Note that in this case, the AB/ST model’s decision threshold is iteratively varied not to fit human data but rather to maximize the proportion of correct trials. The optimal threshold for the AB/ST model can also be interpreted as the threshold that leads the AB/ST model to best approximate the optimal Bayesian observer.
For the standard yes/no Posner cueing paradigm, the cue effect diminishes for low and high target/distractor discriminability and reaches a maximum at mid-range values for target/distractor discriminability (Shimozaki et al., 2003; Eckstein et al., 2009)
In addition, for the case of the bees the choice behavior was recorded over many bees and in fact there is no guarantee that all bees underwent the same amount of training, and in such a situation the learning of a more complex rule may not have fully developed in some bees.
Contributor Information
Miguel P. Eckstein, Email: eckstein@psych.ucsb.edu.
Stephen C. Mack, Email: mack@psych.ucsb.edu.
Dorion B. Liston, Email: dorion.b.liston@nasa.gov.
Lisa Bogush, Email: bogusch@neurobiologie.fu-berlin.de.
Randolf Menzel, Email: menzel@neurobiologie.fu-berlin.de.
Richard J. Krauzlis, Email: rich@salk.edu.
REFERENCES
- Anderson B. There is no Such Thing as Attention. Front Psychol. 2011;2:246. doi: 10.3389/fpsyg.2011.00246. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Avarguès-Weber A, Portelli G, Benard J, Dyer A, Giurfa M. Configural processing enables discrimination and categorization of face-like stimuli in honeybees. J. Exp. Biol. 2010;213:593–601. doi: 10.1242/jeb.039263. [DOI] [PubMed] [Google Scholar]
- Baldassi S, Verghese P. Comparing integration rules in visual search. J Vis. 2002;2:559–570. doi: 10.1167/2.8.3. [DOI] [PubMed] [Google Scholar]
- Bundesen C. A theory of visual attention. Psychol Rev. 1990;97:523–547. doi: 10.1037/0033-295x.97.4.523. [DOI] [PubMed] [Google Scholar]
- Bundesen C, Habekost T, Kyllingsbaek S. A neural theory of visual attention: bridging cognition and neurophysiology. Psychol Rev. 2005;112:291–328. doi: 10.1037/0033-295X.112.2.291. [DOI] [PubMed] [Google Scholar]
- Bushnell PJ, Rice DC. Behavioral assessments of learning and attention in rats exposed perinatally to 3,3’,4,4’,5-pentachlorobiphenyl (PCB 126) Neurotoxicol Teratol. 1999;21:381–392. doi: 10.1016/s0892-0362(99)00006-9. [DOI] [PubMed] [Google Scholar]
- Cameron EL, Tai JC, Eckstein MP, Carrasco M. Signal detection theory applied to three visual search tasks--identification, yes/no detection and localization. Spat Vis. 2004;17:295–325. doi: 10.1163/1568568041920212. [DOI] [PubMed] [Google Scholar]
- Carrasco M. Visual attention: The past 25 years. Vision Res. 2011;51:1484–1525. doi: 10.1016/j.visres.2011.04.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Carrasco M, Penpeci-Talgar C, Eckstein M. Spatial covert attention increases contrast sensitivity across the CSF: support for signal enhancement. Vision Res. 2000;40:1203–1215. doi: 10.1016/s0042-6989(00)00024-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cook EP, Maunsell JHR. Dynamics of neuronal responses in macaque MT and VIP during motion detection. Nat. Neurosci. 2002;5:985–994. doi: 10.1038/nn924. [DOI] [PubMed] [Google Scholar]
- Deaner RO, Platt ML. Reflexive social attention in monkeys and humans. Curr. Biol. 2003;13:1609–1613. doi: 10.1016/j.cub.2003.08.025. [DOI] [PubMed] [Google Scholar]
- Dosher BA, Lu ZL. Mechanisms of perceptual attention in precuing of location. Vision Res. 2000;40:1269–1292. doi: 10.1016/s0042-6989(00)00019-5. [DOI] [PubMed] [Google Scholar]
- Droll JA, Abbey CK, Eckstein MP. Learning cue validity through performance feedback. J Vis. 2009;9:18.1–18.23. doi: 10.1167/9.2.18. [DOI] [PubMed] [Google Scholar]
- Druker M, Anderson B. Spatial probability aids visual stimulus discrimination. Front. Hum. Neurosci. 2010;4:63. doi: 10.3389/fnhum.2010.00063. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eckstein MP, Drescher BA, Shimozaki SS. Attentional cues in real scenes, saccadic targeting, and Bayesian priors. Psychol Sci. 2006;17:973–980. doi: 10.1111/j.1467-9280.2006.01815.x. [DOI] [PubMed] [Google Scholar]
- Eckstein MP, Peterson MF, Pham BT, Droll JA. Statistical decision theory to relate neurons to behavior in the study of covert visual attention. Vision Res. 2009;49:1097–1128. doi: 10.1016/j.visres.2008.12.008. [DOI] [PubMed] [Google Scholar]
- Eckstein MP, Pham BT, Shimozaki SS. The footprints of visual attention during search with 100% valid and 100% invalid cues. Vision Res. 2004;44:1193–1207. doi: 10.1016/j.visres.2003.10.026. [DOI] [PubMed] [Google Scholar]
- Eckstein MP, Shimozaki SS, Abbey CK. The footprints of visual attention in the Posner cueing paradigm revealed by classification images. J Vis. 2002;2:25–45. doi: 10.1167/2.1.3. [DOI] [PubMed] [Google Scholar]
- Emery NJ, Lorincz EN, Perrett DI, Oram MW, Baker CI. Gaze following and joint attention in rhesus monkeys (Macaca mulatta) J Comp Psychol. 1997;111:286–293. doi: 10.1037/0735-7036.111.3.286. [DOI] [PubMed] [Google Scholar]
- Eriksen CW, St James JD. Visual attention within and around the field of focal attention: a zoom lens model. Percept Psychophys. 1986;40:225–240. doi: 10.3758/bf03211502. [DOI] [PubMed] [Google Scholar]
- Free John B. Pheromones of social bees. Comstock, Ithaca, N.Y.: 1987. [Google Scholar]
- Gandhi SP, Heeger DJ, Boynton GM. Spatial attention affects brain activity in human primary visual cortex. Proceedings of the National Academy of Sciences. 1999;96:3314–3319. doi: 10.1073/pnas.96.6.3314. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Geisler WS. Ideal Observer analysis. Boston: MIT Press; 2003. [Google Scholar]
- Geisler WS. Contributions of ideal observer theory to vision research. Vision Research. 2011;51:771–781. doi: 10.1016/j.visres.2010.09.027. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Geng JJ, Behrmann M. Spatial probability as an attentional cue in visual search. Percept Psychophys. 2005;67:1252–1268. doi: 10.3758/bf03193557. [DOI] [PubMed] [Google Scholar]
- Giurfa, Hammer, Stach, Stollhoff, Müller-deisig, Mizyrycki Pattern learning by honeybees: conditioning procedure and recognition strategy. Anim Behav. 1999;57:315–324. doi: 10.1006/anbe.1998.0957. [DOI] [PubMed] [Google Scholar]
- Giurfa M, Zaccardi G, Vorobyev M. How bees detect coloured targets using different regions of their compound eyes. Journal of Comparative Physiology A: Neuroethology, Sensory, Neural, and Behavioral Physiology. 1999;185:591–600. [Google Scholar]
- Green DM, Swets JA. Signal Detection Theory and Psychophysics. Peninsula Pub.; 1989. [Google Scholar]
- Hafed ZM, Goffart L, Krauzlis RJ. Superior Colliculus Inactivation Causes Stable Offsets in Eye Position during Tracking. J. Neurosci. 2008;28:8124–8137. doi: 10.1523/JNEUROSCI.1317-08.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hickson RH. Response probability in a two-choice learning situation with varying probability of reinforcement. J Exp Psychol. 1961;62:138–144. doi: 10.1037/h0046584. [DOI] [PubMed] [Google Scholar]
- Horridge A. Some labels that are recognized on landmarks by the honeybee (Apis mellifera) J. Insect Physiol. 2006;52:1254–1271. doi: 10.1016/j.jinsphys.2006.09.010. [DOI] [PubMed] [Google Scholar]
- Kersten D, Mamassian P, Yuille A. Object perception as Bayesian inference. Annu Rev Psychol. 2004;55:271–304. doi: 10.1146/annurev.psych.55.090902.142005. [DOI] [PubMed] [Google Scholar]
- Kinchla RA. Attention. Annu Rev Psychol. 1992;43:711–742. doi: 10.1146/annurev.ps.43.020192.003431. [DOI] [PubMed] [Google Scholar]
- Kinchla RA, Chen Z, Evert D. Precue effects in visual search: data or resource limited? Percept Psychophys. 1995;57:441–450. doi: 10.3758/bf03213070. [DOI] [PubMed] [Google Scholar]
- Lehrer M. Spatial vision in the honeybee: the use of different cues in different tasks. Vision Res. 1994;34:2363–2385. doi: 10.1016/0042-6989(94)90282-8. [DOI] [PubMed] [Google Scholar]
- Leoncini I, Le Conte Y, Costagliola G, Plettner E, Toth AL, Wang M, Huang Z, Bécard J-M, Crauser D, Slessor KN, Robinson GE. Regulation of behavioral maturation by a primer pheromone produced by adult worker honey bees. Proc. Natl. Acad. Sci. U.S.A. 2004;101:17559–17564. doi: 10.1073/pnas.0407652101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liston DB, Stone LS. Effects of prior information and reward on oculomotor and perceptual choices. J. Neurosci. 2008;28:13866–13875. doi: 10.1523/JNEUROSCI.3120-08.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Luck SJ, Hillyard SA, Mouloua M, Hawkins HL. Mechanisms of visual-spatial attention: resource allocation or uncertainty reduction? J Exp Psychol Hum Percept Perform. 1996;22:725–737. doi: 10.1037//0096-1523.22.3.725. [DOI] [PubMed] [Google Scholar]
- Ma WJ. Signal detection theory, uncertainty, and Poisson-like population codes. Vision Res. 2010;50:2308–2319. doi: 10.1016/j.visres.2010.08.035. [DOI] [PubMed] [Google Scholar]
- Ma WJ, Navalpakkam V, Beck JM, Berg R, van den, Pouget A. Behavior and neural basis of near-optimal visual search. Nat. Neurosci. 2011;14:783–790. doi: 10.1038/nn.2814. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Maloney LT, Zhang H. Decision-theoretic models of visual perception and action. Vision Res. 2010;50:2362–2374. doi: 10.1016/j.visres.2010.09.031. [DOI] [PubMed] [Google Scholar]
- Marote CFO, Xavier GF. Endogenous-like orienting of visual attention in rats. Anim Cogn. 2011;14:535–544. doi: 10.1007/s10071-011-0388-3. [DOI] [PubMed] [Google Scholar]
- Maunsell JHR, Cook EP. The role of attention in visual processing. Philos. Trans. R. Soc. Lond., B, Biol. Sci. 2002;357:1063–1072. doi: 10.1098/rstb.2002.1107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Menzel R, Brembs B, Giurfa M. Cognition in Invertebrates. In: Kass JH, editor. Evolution of Nervous Systems Vol. II: Evolution of Nervous Systems in Invertebrates. Oxford: Academic Press; 2007. [Google Scholar]
- Menzel R, De Marco RJ, Greggers U. Spatial memory, navigation and dance behaviour in Apis mellifera. J. Comp. Physiol. A Neuroethol. Sens. Neural. Behav. Physiol. 2006;192:889–903. doi: 10.1007/s00359-006-0136-3. [DOI] [PubMed] [Google Scholar]
- Menzel R, Kirbach A, Haass W-D, Fischer B, Fuchs J, Koblofsky M, Lehmann K, Reiter L, Meyer H, Nguyen H, Jones S, Norton P, Greggers U. A common frame of reference for learned and communicated vectors in honeybee navigation. Curr. Biol. 2011;21:645–650. doi: 10.1016/j.cub.2011.02.039. [DOI] [PubMed] [Google Scholar]
- Neimark ED, Shuford EH. Comparison of predictions and estimates in a probability learning situation. J Exp Psychol. 1959;57:294–298. doi: 10.1037/h0043064. [DOI] [PubMed] [Google Scholar]
- Palmer J, Ames CT, Lindsey DT. Measuring the effect of attention on simple visual search. Journal of Experimental Psychology: Human Perception and Performance. 1993;19:108–130. doi: 10.1037//0096-1523.19.1.108. [DOI] [PubMed] [Google Scholar]
- Palmer J, Verghese P, Pavel M. The psychophysics of visual search. Vision Res. 2000;40:1227–1268. doi: 10.1016/s0042-6989(99)00244-8. [DOI] [PubMed] [Google Scholar]
- Pashler HE. The psychology of attention. Bradford Books; 1999. [Google Scholar]
- Pestilli F, Carrasco M, Heeger DJ, Gardner JL. Attentional enhancement via selection and pooling of early sensory responses in human visual cortex. Neuron. 2011;72:832–846. doi: 10.1016/j.neuron.2011.09.025. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Peterson W, Birdsall T, Fox W. The theory of signal detectability. IRE Professional Group on Information Theory. 1954;4:171–212. [Google Scholar]
- Posner MI. Orienting of attention. Q J Exp Psychol. 1980;32:3–25. doi: 10.1080/00335558008248231. [DOI] [PubMed] [Google Scholar]
- Posner MI, Snyder CR, Davidson BJ. Attention and the detection of signals. J Exp Psychol. 1980;109:160–174. [PubMed] [Google Scholar]
- Schoonveld W, Shimozaki SS, Eckstein MP. Optimal observer model of single-fixation oddity search predicts a shallow set-size function. J Vis. 2007;7:1.1–1.16. doi: 10.1167/7.10.1. [DOI] [PubMed] [Google Scholar]
- Seeley TD, Visscher PK. Sensory coding of nest-site value in honeybee swarms. J Exp Biol. 2008;211:3691–3697. doi: 10.1242/jeb.021071. [DOI] [PubMed] [Google Scholar]
- Shaw ML. Identifying attentional and decision making components in information processing. In: Nickerson RS, editor. Attention and Performance VIII. 1980. pp. 277–296. [Google Scholar]
- Shaw ML. Division of attention among spatial locations: A fundamental difference between detection of letters and detection of luminance increments, in: Attention and Performance X. Hillsdale, NJ: Earlblaum; 1984. pp. 106–121. [Google Scholar]
- Shimozaki SS, Eckstein MP, Abbey CK. Comparison of two weighted integration models for the cueing task: linear and likelihood. J Vis. 2003;3:209–229. doi: 10.1167/3.3.3. [DOI] [PubMed] [Google Scholar]
- Shimozaki SS, Schoonveld WA, Eckstein MP. A unified Bayesian observer analysis for set size and cueing effects on perceptual decisions and saccades. J Vis. 2012:12. doi: 10.1167/12.6.27. [DOI] [PubMed] [Google Scholar]
- Shimp CP, Friedrich FJ. Behavioral and computational models of spatial attention. J Exp Psychol Anim Behav Process. 1993;19:26–37. doi: 10.1037//0097-7403.19.1.26. [DOI] [PubMed] [Google Scholar]
- Smith PL, Ratcliff R. An integrated theory of attention and decision making in visual signal detection. Psychol Rev. 2009;116:283–317. doi: 10.1037/a0015156. [DOI] [PubMed] [Google Scholar]
- Spaethe J, Tautz J, Chittka L. Do honeybees detect colour targets using serial or parallel visual search? J. Exp. Biol. 2006;209:987–993. doi: 10.1242/jeb.02124. [DOI] [PubMed] [Google Scholar]
- Sperling G, Dosher BA. Strategy optimiation in human information processing. In: Boff KR, Kaufman L, Thomas JP, editors. Handbook of Perception and Human Performance. John Wiley and Sons: New York; 1986. pp. 2–1–2–65. [Google Scholar]
- Srinivasan MV. Honey bees as a model for vision, perception, and cognition. Annu. Rev. Entomol. 2010;55:267–284. doi: 10.1146/annurev.ento.010908.164537. [DOI] [PubMed] [Google Scholar]
- Stach S, Benard J, Giurfa M. Local-feature assembling in visual pattern recognition and generalization in honeybees. Nature. 2004;429:758–761. doi: 10.1038/nature02594. [DOI] [PubMed] [Google Scholar]
- Verghese P. Visual search and attention: a signal detection theory approach. Neuron. 2001;31:523–535. doi: 10.1016/s0896-6273(01)00392-0. [DOI] [PubMed] [Google Scholar]
- Vincent B. Covert visual search: Prior beliefs are optimally combined with sensory evidence. J Vis. 2011:11. doi: 10.1167/11.13.25. [DOI] [PubMed] [Google Scholar]
- Vincent B. How do we use the past to predict the future in oculomotor search? Vision Research. 2012 doi: 10.1016/j.visres.2012.08.001. [DOI] [PubMed] [Google Scholar]
- Vincent BT, Baddeley RJ, Troscianko T, Gilchrist ID. Optimal feature integration in visual search. J Vis. 2009;9:15.1–15.11. doi: 10.1167/9.5.15. [DOI] [PubMed] [Google Scholar]
- von Frisch K. The dance language and orientation of bees. Harvard Univ Press; 1933. [Google Scholar]
- Vorobyev M, Brandt R, Peitsch D, Laughlin SB, Menzel R. Colour thresholds and receptor noise: behaviour and physiology compared. Vision Res. 2001;41:639–653. doi: 10.1016/s0042-6989(00)00288-1. [DOI] [PubMed] [Google Scholar]
- Walthew C, Gilchrist ID. Target location probability effects in visual search: an effect of sequential dependencies. J Exp Psychol Hum Percept Perform. 2006;32:1294–1301. doi: 10.1037/0096-1523.32.5.1294. [DOI] [PubMed] [Google Scholar]
- Wozny DR, Beierholm UR, Shams L. Probability Matching as a Computational Strategy Used in Perception. PLoS Comput Biol. 2010;6:e1000871. doi: 10.1371/journal.pcbi.1000871. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yu AJ, Dayan P. Uncertainty, neuromodulation, and attention. Neuron. 2005;46:681–692. doi: 10.1016/j.neuron.2005.04.026. [DOI] [PubMed] [Google Scholar]
- Zhang S, Srinivasan MV, Zhu H, Wong J. Grouping of visual objects by honeybees. J. Exp. Biol. 2004;207:3289–3298. doi: 10.1242/jeb.01155. [DOI] [PubMed] [Google Scholar]