The Circuit Theory Behind Coupled-Mode Magnetic Resonance-Based Wireless Power Transmission

Abstract

Inductive coupling is a viable scheme to wirelessly energize devices with a wide range of power requirements from nanowatts in radio frequency identification tags to milliwatts in implantable microelectronic devices, watts in mobile electronics, and kilowatts in electric cars. Several analytical methods for estimating the power transfer efficiency (PTE) across inductive power transmission links have been devised based on circuit and electromagnetic theories by electrical engineers and physicists, respectively. However, a direct side-by-side comparison between these two approaches is lacking. Here, we have analyzed the PTE of a pair of capacitively loaded inductors via reflected load theory (RLT) and compared it with a method known as coupled-mode theory (CMT). We have also derived PTE equations for multiple capacitively loaded inductors based on both RLT and CMT. We have proven that both methods basically result in the same set of equations in steady state and either method can be applied for short- or midrange coupling conditions. We have verified the accuracy of both methods through measurements, and also analyzed the transient response of a pair of capacitively loaded inductors. Our analysis shows that the CMT is only applicable to coils with high quality factor (Q) and large coupling distance. It simplifies the analysis by reducing the order of the differential equations by half compared to the circuit theory.

I. Introduction

Inductive power transmission links that utilize a pair of mutually coupled coils have been in use over the last decades to power up radio frequency identification (RFID) transponders and cochlear implants with power consumptions in the range of sub-micro to milliwatts [1], [2]. The use of this technique to wirelessly transfer energy across a short distance is, however, expected to see an explosive growth over the next decade in a much broader range of applications from advanced implantable microelectronic devices (IMD), such as retinal implants and brain–computer interfaces (BCI) to cut the power cord in charging mobile electronic devices, operating small home appliances, and energizing electric cars, which have higher power consumptions in the order of hundreds of milliwatts to kilowatts [3]–[12]. As a result, improving the wireless power transmission efficiency (PTE) in inductive links particularly at larger coupling distances (coil separations) without increasing the volume and weight of the coupled coils has gained considerable attention [13]–[19].

Achieving high PTE is necessary in high-power IMDs to not only reduce the size of the external energy source (battery) that should be carried around by the patient but also to limit the tissue exposure to the AC magnetic field, which can result in excessive heat dissipation if it surpasses safe limits, and to minimize interference with near by electronics [20]–[22]. In near field RFID applications, the bottleneck in increasing the reading range without changing the coil size in many cases is the PTE when the received power is no longer sufficient to operate the transponder [2]. Increasing the PTE in higher power applications is also important for generating less heat, cost saving, reducing interference, and improving safety.

Design and optimization of inductive power transmission links has been extensively studied in the literature over the last three decades [2], [5], [23]–[34]. The majority of these approaches model and analyze the inductive link from a circuit perspective, which differs, at least on the surface, from the coupled-mode theory (CMT) that was recently presented in a new form by physicists at MIT [35]. They utilized the CMT approach to propose multi-coil inductive links, which can increase the PTE considerably at large coupling distances [13], [14]. Their 4-coil inductive link has so far been studied from a circuit perspective for power transmission to multiple small receivers, transcutaneous powering, and recharging mobile devices [17]–[19]. We have presented the analysis, modeling, design, and optimization of multi-coil inductive links using the circuit based reflected load theory (RLT) in [36]. However, an in-depth comparison between the coupled-mode and circuit-based theories, which would clarify the relationship between these two methods, often used by physicist and electrical engineers, respectively, is still lacking.

In this paper, first we review the inductive link steady-state analysis using CMT and then prove that both CMT and the more conventional RLT result in the same formulation for the inductive links' key performance measures, particularly the PTE. For the first time, we have derived the PTE equations for multi-coil inductive links via CMT. Our analysis shows that in the steady state mode, contrary to popular belief, both CMT and RLT are applicable to small and large coupling distances, d, as long as the coils interact in the near field regime. Because they are basically the same [37]! We have also presented the measurement results, which show the accuracy of both RLT and CMT models in estimating the PTE. On the other hand, our comparative transient analysis of a pair of capacitively loaded inductors reveals that CMT is accurate only if the mutual coupling, k, is small, e.g., due to large d, and coil quality factors, Q, are large, which limits the applicability of the CMT-based transient analysis to midrange coupling distances of large coils. We have also shown that utilizing CMT reduces the order of the differential equations by half compared to the circuit theory as it only considers a first order equation for each resonant object. Hence, the CMT seems to be helpful in analyzing the transient behavior of complicated multi-coil inductive links despite being less accurate than its circuit-based counterpart. For all other conditions, the RLT and similar circuit based methods will do just fine.

In the following section, the CMT analysis for a pair of capacitively loaded inductors is presented. Section III describes the RLT analysis for 2-coil inductive links. The correspondence between CMT and RLT has been presented in Section IV. The PTE analysis of the multi-coil inductive links utilizing both CMT and RLT are presented in Section V. The calculation and measurement results are compared in Section VI followed by concluding remarks in Section VII.

II. Coupled-Mode Theory

CMT is a framework to analyze energy exchange between two resonating objects [35]. Based on the CMT, the time-do-main field amplitudes of two objects, a₂(t) and a₃(t), which are defined so that the energy contained in them are and |a₂(t)|² and |a₃(t)|², respectively, at distance d₂₃ can be found from [37]

$$\begin{array}{l}\frac{d{a}_2(t)}{\mathit{\text{dt}}}=-(j{\omega }_2+{\mathrm{\Gamma }}_2)a_2(t)+j{K}_{23}{a}_3(t)+F_S(t)\\ \frac{d{a}_3(t)}{\mathit{\text{dt}}}=-(j{\omega }_3+{\mathrm{\Gamma }}_3+{\mathrm{\Gamma }}_L)a_3(t)+j{K}_{23}{a}_2(t)\end{array}$$ (1)

Where ω₂ and ω₃ are the eigen frequencies, Γ₂ and Γ₃ are the resonance widths or rate of intrinsic decay due to the objects' absorption (Ohmic) and radiative losses, Γ_L is the resonance width due to load resistance connected to the second object (proportional to 1/R_L), F_S(t) is the excitation applied to the first object, and K₂₃ is the coupling rate between the two objects. The CMT method has been recently applied to a pair of capacitively loaded conducting-wire loops, spaced by d₂₃, as shown in Fig. 1, forming a conventional inductive power transmission link, in which L₂ is the power transmitter and L₃ is the power receiver inductors, both tuned at the same frequency, ω₂ = ω₃ = ω [14], [37].

Fig. 1.

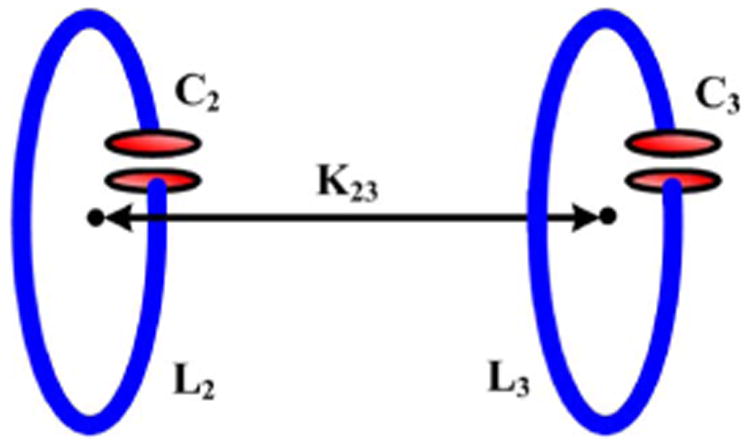
A pair of capacitively loaded inductors used for efficiency calculation using the coupled-mode theory (CMT).

A. Steady-State Analysis via Coupled-Mode Theory

In steady state analysis, which applies to the conventional inductive power transmission links, F_S(t) in (1) is a sinusoidal signal described as A_se^−jωt. In this condition, the alternating field amplitude in the primary inductor is constant, a₂(t) = A₂e^−jωt, resulting in a constant field amplitude in the secondary inductor, a₃(t) = A₃e^−jωt. It can be shown from (1) that A₃/A₂ = jK₂₃/(Γ₃+Γ_L) [37]. Therefore, the average power at different nodes of the power transmission system can be calculated. The power absorbed by L₂ and the power delivered to L₃ are P₂ = 2Γ₂|A₂|² and P₃ = 2Γ₃|A₃|², respectively. The power delivered to R_L is P_L = 2Γ_L|A₃|² and, therefore, based on the energy conservation theory, if we neglect the radiated power in the near field regime, the total power delivered to the system from source is P_S = P₂ + P₃ + P_L. Hence, the PTE of the 2-coil system can be found from

$${\eta }_{23}=\frac{P_L}{P_S}=\frac{1}{1+\frac{{\mathrm{\Gamma }}_3}{{\mathrm{\Gamma }}_L}[1+\frac{1}{{\mathit{\text{fom}}}^2}{(1+\frac{{\mathrm{\Gamma }}_L}{{\mathrm{\Gamma }}_3})}^2]}$$ (2)

where $\mathit{\text{fom}}=K_{23}/\sqrt{{\mathrm{\Gamma }}_2{\mathrm{\Gamma }}_3}$ is the distance-dependent figure-of-merit for energy transmission systems [37]. To maximize the PTE based on (2), fom should be maximized and an optimal value should be chosen for Γ_L/Γ₃. Parameters that affect fom are obviously the coupling rate between the two objects, K₂₃, which should be increased and the resonance width of each object (intrinsic loss of each inductor), Γ, which should be decreased. These are quite similar to the coupling coefficient, k₂₃, and inverse of the quality factor, 1/Q, used in conventional methods for optimizing inductive links [33]. The other key parameter, Γ_L,PTE/Γ₃, which shows the effect of R_L in optimizing the PTE, can be found by calculating the derivative of η₂₃ in (2) with respect to Γ_L/Γ₃, resulting in [13]

$${\mathrm{\Gamma }}_{L,\text{PTE}}=\frac{{\mathrm{\Gamma }}_3}{{(1+K_{23}^2/{\mathrm{\Gamma }}_2{\mathrm{\Gamma }}_3)}^{1/2}}.$$ (3)

B. Transient Analysis via Coupled-Mode Theory

The CMT can also be utilized in analyzing the transient behavior of the resonant-coupled inductors in Fig. 1 by setting F_S(t) = 0 in (1) and considering an initial energy stored in L₂. This analysis provides designers with better understanding of the dynamics of energy exchange in such inductively coupled systems. As the first step, we eliminate a₃(t) in (1) to find an expression for the time varying field in the primary coil

$$\frac{d^2{a}_2(t)}{d{t}^2}+(2j\omega +{\mathrm{\Gamma }}_2+{\mathrm{\Gamma }}_3+{\mathrm{\Gamma }}_L)\frac{d{a}_2(t)}{\mathit{\text{dt}}}+[K_{23}^2+(j\omega +{\mathrm{\Gamma }}_2)(j\omega +{\mathrm{\Gamma }}_3+{\mathrm{\Gamma }}_L)]a_2(t)=0.$$ (4)

For the sake of simplicity, if similar to [14] we assume that the two inductors are identical, i.e., Γ₂ = Γ₃ = Γ, and Γ_L = 0 (no load condition, R_L = ∞), then a₂(t) can be found from (4):

$$a_2(t)=e^{-j\omega t}[e^{-\mathrm{\Gamma }t}(b_1{e}^{j{K}_{23}t}+b_2{e}^{-j{K}_{23}t})]$$ (5)

Where b₁ and b₂ are constants, which values depend on the initial conditions. Similarly, a₃(t) can be calculated using (1) and (5) as

$$a_3(t)=e^{-j\omega t}[e^{-\mathrm{\Gamma }t}(d_1{e}^{j{K}_{23}t}+d_2{e}^{-j{K}_{23}t})]$$ (6)

Where d₁ and d₂ are also constants with values dependent on the initial conditions. The total energy in L₂ and L₃ can be found from E₂(t) = |a₂(t)|² and E₃(t) = |a₃(t)|², respectively [24].

If one starts with 100% of the total energy normalized and initially stored in L₂, i.e., |a₂(t = 0)|² = 1 and |a₂(t = 0)|² = 0, the energy stored in each object over time can be found from

$$\begin{array}{c}{E}_2(t)=e^{-2\mathrm{\Gamma }t}{cos}^2{K}_{23}t\\ E_3(t)=e^{-2\mathrm{\Gamma }t}{sin}^2{K}_{23}t.\end{array}$$ (7)

It should be noted that E₂ and E₂ are not the instantaneous but the peak values (or envelopes) of the energy content stored in L₂ and L₃, which are in resonance with C₂ and C₃, respectively, at the rate of 2ω.

III. Reflected Load Theory

Fig. 2(a) shows a pair of inductively coupled coils, which will be referred to as the primary (L₂) and secondary (L₃). It can be shown that the highest PTE across such link scan be achieved when both LC-tanks are tuned at the same resonance frequency, i.e., $\omega =1/\sqrt{L_2{C}_2}=1/\sqrt{L_3{C}_3}$ [31].

Fig. 2.

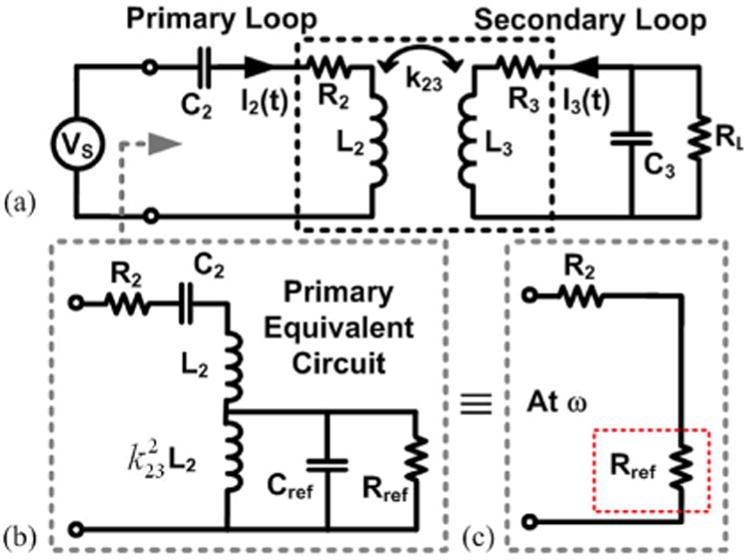
(a) Simplified model of a 2-coil power transmission link with a resistive load. (b) Equivalent circuit seen across the driver. (c) Reflected load onto the primary loop at resonance frequency.

A. Steady State Analysis via Reflected Load Theory

The inductive link PTE is mainly dependent on the mutual coupling between the coils, k₂₃, and their quality factors, Q₂ = ωL₂/R₂ and Q₃ = ωL₃/R₃ [33]. At resonance frequency, the secondary loop which is connected to R_L can be reflected on to the primary loop and represented by R_ref [2]. To find R_ref, the secondary loop is modeled with a parallel load as shown in Fig. 2(a). R₃, the parasitic resistance of L₃, can be transformed to a parallel resistance equal to $R_{P3}=Q_3^2{R}_3$ in parallel with R_L [30]. Hence, if we define, R_P = R_P3 ║ R_L then we can reflect the secondary impedance onto the primary side [Fig. 2(b)]:

$$\begin{array}{c}{R}_{\text{ref}}=k_{23}^2(L_2/L_3)R_P=k_{23}^2\omega L_2{Q}_{3L}\\ C_{\text{ref}}=(L_3/L_2)(C_3/k_{23}^2)=1/\left({\omega }^2{L}_2{k}_{23}^2\right)\end{array}$$ (8)

Where Q_3L = R_P/ωL₃ is the loaded quality factor of the secondary coil [9], [30]. At resonance, C_ref resonates out with, $k_{23}^2{L}_2$, leaving only the reflected resistance, R_ref, on the primary side, as shown in Fig. 2(c). In the simplified inductive link model of Fig. 2(c), L₂ and L₃ also resonate out, and the input power provided by V_s simply divides between R₂ and R_ref. The power absorbed by R₂ is dissipated as heat in the primary coil and the power delivered to R_ref, i.e., the transferred power to the secondary loop, divides between R₃ and R_L, which are the only power consuming components on the secondary side. This will lead to

$${\eta }_{23}=\frac{R_{\text{ref}}}{R_2+R_{\text{ref}}}\frac{R_{P3}}{R_{P3}+R_L}=\frac{k_{23}^2{Q}_2{Q}_{3L}}{1+k_{23}^2{Q}_2{Q}_{3L}}.\frac{Q_{3L}}{Q_L}$$ (9)

Where Q_L = R_L/ωL₃ is often referred to as the load quality factor, and Q_3L = Q₃Q_L/(Q₃+Q_L) [31]. It can be seen from (9) that large k₂₃, Q₂ and Q₃ are needed to maximize the PTE. However, for a given set of Q₂, Q₃ and k₂₃ values, there is an optimal load, R_L,PTE = ωL₃Q_L,PTE, which can maximize the PTE. Q_L,PTE can be found by calculating the derivative of (9) with respect to Q_L from

$$Q_{L,\text{PTE}}=\frac{Q_3}{{(1+k_{23}^2{Q}_2{Q}_3)}^{1/2}}.$$ (10)

B. Transient Analysis via Circuit Theory

In this analysis, the primary and secondary loops are considered identical, i.e., L₂ = L₃ = L, C₂ = C₃ = C, R₂ = R₃ = R and R_L = ∞, similar to the CMT criteria in [14]. We have also set V_s = 0 V (short circuit) to focus on the transient response while considering an initial condition (current) in L₂. Primary and secondary loop currents can be found from

$$\begin{array}{c}\frac{1}{C}{\int }_0^t{I}_2(t)\mathit{\text{dt}}+R{I}_2(t)+L\frac{d{I}_2(t)}{\mathit{\text{dt}}}+M\frac{d{I}_3(t)}{\mathit{\text{dt}}}=0\\ \frac{1}{C}{\int }_0^t{I}_3(t)\mathit{\text{dt}}+R{I}_3(t)+L\frac{d{I}_3(t)}{\mathit{\text{dt}}}+M\frac{d{I}_2(t)}{\mathit{\text{dt}}}=0\end{array}$$ (11)

Where M = k₂₃ × L is the mutual inductance between L₂ and L₃. Taking the derivative of (11) after substituting R/L and 1/LC with ω/Q and ω², respectively, result in

$$\begin{array}{c}\frac{d^2{I}_2(t)}{d{t}^2}+\frac{\omega }{Q}\frac{d{I}_2(t)}{\mathit{\text{dt}}}+{\omega }^2{I}_2(t)+k_{23}\frac{d^2{I}_3(t)}{d{t}^2}=0\\ k_{23}\frac{d^2{I}_2(t)}{d{t}^2}+\frac{d^2{I}_3(t)}{d{t}^2}+\frac{\omega }{Q}\frac{d{I}_3(t)}{\mathit{\text{dt}}}+{\omega }^2{I}_3(t)=0.\end{array}$$ (12)

Utilizing Laplace transform, (12) can be written as

$$\begin{array}{c}(s^2+\frac{\omega }{Q}s+{\omega }^2)I_2(s)+k_{23}{s}^2{I}_3(s)=0\\ k_{23}{s}^2{I}_2(s)+(s^2+\frac{\omega }{Q}s+{\omega }^2)I_2(s)=0.\end{array}$$ (13)

Characteristic equation in the S-domain can be found by setting the coefficient matrix determinant in (13) to zero:

$${(s^2+\frac{\omega }{Q}s+{\omega }^2)}^2-k_{23}^2{s}^4=0.$$ (14)

The roots of (14) are

$$\begin{array}{c}{s}_{1,2}=\frac{-{\omega }^{\prime }}{2Q^{\prime }}(1\pm \sqrt{1-4Q^{\prime 2}})=\frac{-{\omega }^{\prime }}{2Q^{\prime }}\pm j{\omega }_d^{\prime }\\ s_{3,4}=\frac{-{\omega }^{″}}{2Q^{″}}(1\pm \sqrt{1-4Q^{″2}})=\frac{-{\omega }^{″}}{2Q^{″}}\pm j{\omega }_d^{″}\end{array}$$ (15)

where

$$\begin{array}{ll}{\omega }_d^{\prime }=\frac{{\omega }^{\prime }}{2Q^{\prime }}\sqrt{4Q^{\prime 2}-1},& {\omega }_d^{″}=\frac{{\omega }^{″}}{2Q^{″}}\sqrt{4Q^{″2}-1}\\ Q^{\prime }=Q\sqrt{1-k_{23}},& Q^{″}=Q\sqrt{1+k_{23}}\\ {\omega }^{\prime }=\omega /\sqrt{1-k_{23}},& {\omega }^{″}=\omega /\sqrt{1+k_{23}}.\end{array}$$ (16)

Therefore, I₂(t) and I₃(t) can be calculated from

$$I_2(t)=e^{\frac{-{\omega }^{\prime }}{2Q^{\prime }}t}(a_{11}cos{\omega }_d^{\prime }t+b_{11}sin{\omega }_d^{\prime }t)+e^{\frac{-{\omega }^{″}}{2Q^{″}}}(a_{12}cos{\omega }_d^{″}t+b_{12}sin{\omega }_d^{″}t)$$ (17)

$$I_3(t)=e^{\frac{-{\omega }^{\prime }}{2Q^{\prime }}t}(a_{21}cos{\omega }_d^{\prime }t+b_{21}sin{\omega }_d^{\prime }t)+e^{\frac{-{\omega }^{″}}{2Q^{″}}}(a_{22}cos{\omega }_d^{″}t+b_{22}sin{\omega }_d^{″}t).$$ (18)

In order to find the unknown coefficients in (17) and (18), one should have at least four initial conditions. Two of them are I₂(0) = I₀, and I₃(0) = 0 A, which indicate that 100% of the total energy is initially stored in L₂. The other two initial conditions can be found from (11) when t = 0:

$$\frac{d{I}_2}{\mathit{\text{dt}}}(0)=\frac{-\omega }{Q}\frac{I_0}{1-k_{23}^2},\frac{d{I}_3}{\mathit{\text{dt}}}(0)=\frac{-\omega }{Q}\frac{k_{23}{I}_0}{1-k_{23}^2}.$$ (19)

IV. Coupled Mode Versus Reflected Load Theories

In this section, we compare the formulation derived from CMT and RLT for the 2-coil inductive link PTE and transient response derived in the previous sections.

A. Two-Coil Inductive Link Power Transfer Efficiency

Resonance widths, Γ_2,3, and coupling rate, K₂₃, in a pair of capacitively loaded inductors in Fig. 1 are equivalent in terms of circuit model parameters in Fig. 2 to ω/2Q₂₋₃ and ωk₂₃/2, respectively [37]. Similarly, the load resonance width, Γ_L, is equal to ω/2Q_L. By substituting these in fom and Γ_L/Γ₃

$$\begin{array}{cc}\hfill \text{fom}\hfill & =\frac{K_{23}}{\sqrt{{\mathrm{\Gamma }}_2{\mathrm{\Gamma }}_3}}=\frac{\omega k_{23}}{2}{\left(\frac{\omega }{2Q_2}\frac{\omega }{2Q_3}\right)}^{-1/2}\hfill \\ & =k_{23}\sqrt{Q_2{Q}_3}\hfill \\ \hfill \frac{{\mathrm{\Gamma }}_L}{{\mathrm{\Gamma }}_3}\hfill & =\frac{\omega }{2Q_L}/\frac{\omega }{2Q_3}=\frac{Q_3}{Q_L}.\hfill \end{array}$$ (20)

In the next step, we substitute the CMT parameters from (20) in (2) and recalculate the PTE

$$\begin{array}{ll}{\eta }_{23}& =\frac{1}{1+\frac{Q_L}{Q_3}[1+\frac{1}{k_{23}^2{Q}_2{Q}_3}{(1+\frac{Q_3}{Q_L})}^2]}\\ & =\frac{Q_3}{Q_3+Q_L+\frac{{(Q_L+Q_3)}^2}{k_{23}^2{Q}_2{Q}_3{Q}_L}}\\ & =\frac{k_{23}^2{Q}_2{Q}_3}{Q_L+Q_3+k_{23}^2{Q}_2{Q}_3{Q}_L}\cdot \frac{Q_L{Q}_3}{Q_L+Q_3}.\end{array}$$ (21)

After simplification and considering that Q_3L = Q_LQ₃/(Q_L + Q₃), the PTE formula in (21) can be further simplified to

$$\begin{array}{ll}{\eta }_{23}& =\frac{k_{23}^2{Q}_2{Q}_3{Q}_L/(Q_L+Q_3)}{1+k_{23}^2{Q}_2{Q}_3{Q}_L/(Q_L+Q_3)}\cdot \frac{Q_{3L}}{Q_L}\\ & =\frac{k_{23}^2{Q}_2{Q}_{3L}}{1+k_{23}^2{Q}_2{Q}_{3L}}\cdot \frac{Q_{3L}}{Q_L}\end{array}$$ (22)

which is the same as (9) that was derived via RLT.

Similarly, it is straightforward to show that the optimum Γ_{L, PTE} in (3) can be linked to Q_{L, PTE} in (10) by substituting the equivalent circuit parameters in (20), leading to

$$\begin{array}{cc}\frac{{\mathrm{\Gamma }}_{L,\text{PTE}}}{{\mathrm{\Gamma }}_3}& =\frac{Q_3}{Q_{L,\text{PTE}}}={(1+\frac{K_{23}^2}{{\mathrm{\Gamma }}_2{\mathrm{\Gamma }}_3})}^{1/2}\\ & ={(1+k_{23}^2{Q}_2{Q}_3)}^{1/2}.\end{array}$$ (23)

Thus, we have shown mathematically that the CMT and RLT equations for the PTE and optimal loading of 2-coil power transmission links in steady state are basically the same.

B. Two-Coil Inductive Link Transient Response

In order to arrive at the CMT transient response in (7), two assumptions were made. First, the coil quality factors were considered large (Q ≫ 1), resulting in ${\omega }_d^{\prime }\approx {\omega }^{\prime }$ and ${\omega }_d^{″}\approx {\omega }^{″}$ in (16). Second, the coupling distance, d₂₃, was considered large, resulting in small k₂₃, which simplifies the rest of (16) to

$${\omega }^{\prime }/Q^{\prime }\approx {\omega }^{″}/Q^{″}\approx \omega /Q,{\omega }^{\prime }\approx \omega (1+k_{23}/2),{\omega }^{″}\approx \omega (1-k_{23}/2)$$ (24)

and (19) to

$$\frac{d{I}_2}{\mathit{\text{dt}}}(0)=\frac{-\omega }{Q}{I}_0,\frac{d{I}_3}{\mathit{\text{dt}}}(0)=0.$$ (25)

Thus, I₂(t) and I₃(t) in (17) and (18) can be approximated as

$$I_2(t)=e^{\frac{-\omega }{2Q}t}[a_{11}cos\omega (1+k_{23}/2)t+b_{11}sin\omega (1+k_{23}/2)t+a_{12}cos\omega (1-k_{23}/2)t+b_{12}sin\omega (1-k_{23}/2)t]$$ (26)

$$I_3(t)=e^{\frac{-\omega }{2Q}t}[a_{21}cos\omega (1+k_{23}/2)t+b_{21}sin\omega (1+k_{23}/2)t+a_{22}cos\omega (1-k_{23}/2)t+b_{22}sin\omega (1+k_{23}/2)t].$$ (27)

Unknown coefficients in (26) and (27) can be found by applying the initial conditions, which result in a₁₁ = a₁₂ = I₀/2, b₁₁ = b₁₂ = −I₀/4Q, a₂₁ = −a₂₂ = −I₀/2, and b₂₁ = b₂₂ = 0. When substituting these in (26) and (27)

$$I_2(t)=\frac{I_0}{2}{e}^{\frac{-\omega }{2Q}t}[cos\omega (1+k_{23}/2)t+cos\omega (1-k_{23}/2)t-\frac{1}{2Q}sin\omega (1+k_{23}/2)t-\frac{1}{2Q}sin\omega (1-k_{23}/2)t]$$ (28)

$$I_3(t)=\frac{I_0}{2}{e}^{\frac{-\omega }{2Q}t}[-cos\omega (1+k_{23}/2)t+cos\omega (1-k_{23}/2)t].$$ (29)

The large Q assumption combined with the expansion of the sinusoidal functions in (28) and (29)

$$\begin{array}{c}cos(\alpha \pm \beta )=cos\alpha cos\beta \mp sin\alpha sin\beta \\ sin(\alpha \pm \beta )=sin\alpha cos\beta \pm cos\alpha sin\beta ,\end{array}$$ (30)

can further simplify the primary and secondary currents as

$$\begin{array}{c}{I}_2(t)=I_0{e}^{\frac{-\omega }{2Q}t}cos\frac{\omega k_{23}t}{2}cos\omega t\\ I_3(t)=I_0{e}^{\frac{-\omega }{2Q}t}sin\frac{\omega k_{23}t}{2}sin\omega t.\end{array}$$ (31)

Considering that the energy stored in an inductor, L, that carries a current, I, is 0.5LI², the normalized envelope of the energy inside L₂ and L₃ can be expressed as [38]

$$\begin{array}{c}{E}_2(t)=e^{\frac{-\omega }{Q}t}{cos}^2\left(\frac{\omega k_{23}t}{2}\right),\\ E_3(t)=e^{\frac{-\omega }{Q}t}{sin}^2\left(\frac{\omega k_{23}t}{2}\right).\end{array}$$ (32)

By substituting 2Γ = ω/Q, and K₂₃ = ωk₂₃/2 in (32), we can arrive at (7), which was derived using CMT. Therefore, in calculating the transient response of the inductive links, CMT is only valid for midrange coupling distances (small k₂₃) between large coils (high-Q), as also indicated in [37].

In order to validate our theoretical calculations and demonstrate the level of accuracy (or lack there of) in the transient CMT analysis for various coupling coefficients and Q factors, the 2-coil inductive link in Fig. 2 was simulated in the LT-SPICE circuit simulator (Linear Technology, Milpitas, CA), while setting V_S and initial L₂ current, I₂(0), at 0 V and 1 A, respectively, for the two conditions summarized in Table I. Fig. 3(a) shows the percentage of the energy stored in primary, L₂, and secondary, L₃, coils over time for a pair of large identical coils that are placed relatively far from each other (midrange, low k₂₃, high-Q). It can be seen that both CMT (7) and circuit-based (12) equations, solved in MATLAB (MathWorks, Natick, MA), match the LT-SPICE simulation results very well. In Fig. 3(b), however, which represents a small pair of coils that are very close to one another (short range, high k₂₃, low-Q) the CMT-based formulas have become quite inaccurate in predicting the energy exchange, while the circuit analysis still matches the LT-SPICE simulation output. In this condition, the inductor currents tend to have two harmonics, ω′ and ω″ in (17) and (18), one of which has not been predicted by the CMT. Nonetheless, the simplicity of the CMT in analyzing the transient behavior of inductive links can be useful particularly in midrange high-Q conditions. This stems from the fact that CMT models each resonant object (e.g., RLC tank) with a first-order differential equation, while in the circuit analysis the order of the equations increases by each independent energy storage element regardless of being an inductor or a capacitor.

Table I. Inductive Link Specifications for Transient Analyses.

L2 and L3 Specifications*	Symbol	Midrange High-Q	Short Range Moderate-Q
Inductance (μH)	L	96.2	0.962
Series resistance (Ω)	R	0.76	1.08
Resonant capacitance (pF)	C	0.812	81.2
Quality factor	Q	1.4×104	100
Mutual coupling	k23	0.153×10-3	0.4
Resonance width (rad)	Γ	4039	5.65×105
Coupling rate (rad)	K23	8652	22.6 ×106
Load resistance (Ω)	RL	∞ (No load condition)
Resonance frequency (MHz)	f	18

^*Primary and secondary coils are identical.

Fig. 3.

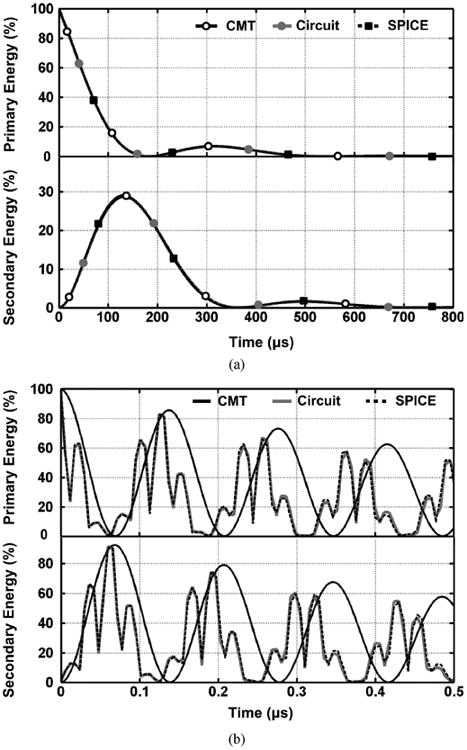
Energy stored in the primary and secondary coils (E₂ and E₃) versus time starting from an initial condition, I₂(0) = 1 A, based on CMT (7), circuit theory (12), and SPICE simulations for 2-coil inductive links in: (a) midrange, high-Q, and (b) short range, low-Q conditions, as specified in Table I.

V. Multi-Coil Inductive Power Transfer

CMT-based analysis took circuit designers by surprise when the group physicists at MIT demonstrated a method of achieving high PTE by utilizing multiple coils (3- and 4-coils) for wireless power transmission [13], [14]. Nonetheless, the closed-form CMT formulation presented in the literature was limited to 2-coils. In this section, we derive the closed-form PTE equations for multi-coil inductive links based on the CMT and compare them with parallel equations derived from RLT, particularly for 3- and 4-coil links [36]. We prove that both CMT and RLT result in the same set of equations.

Equations for a pair of capacitively loaded inductors in Fig. 1 can be extended to m inductors, in which the first and mth inductors are connected to the energy source and load, respectively, while all inductors are tuned at the same resonance frequency, f [14]. The time-domain field amplitudes of each inductor, a_i(t), can be expressed as

$$\frac{d{a}_i\left(t\right)}{\mathit{\text{dt}}}=-(j\omega +{\mathrm{\Gamma }}_i)a_i(t)+j{K}_{i-1,i}{a}_{i-1}(t)+j{K}_{i,i+1}{a}_{i+1}(t),i=2,3,\dots ,m-1$$ (33)

where K_i,i+1 and Γ_i are the coupling rate between the ith and (i + 1)th inductor and resonance width of the ith inductor, respectively. For the sake of simplicity, the coupling between non-neighboring inductors has been considered negligible. For the first and mth inductors, the field amplitudes are

$$\begin{array}{l}\frac{d{a}_1\left(t\right)}{\mathit{\text{dt}}}=-(j\omega +{\mathrm{\Gamma }}_1)a_1(t)+j{K}_{12}{a}_2(t)+F_S(t)\\ \frac{d{a}_m\left(t\right)}{\mathit{\text{dt}}}=-(j\omega +{\mathrm{\Gamma }}_m+{\mathrm{\Gamma }}_L)a_m(t)+j{K}_{m-1,m}{a}_{m-1}(t).\end{array}$$ (34)

In the steady state mode, the field amplitudes in each inductor is considered constant, i.e., a_i(t) = A_ie^−jωt. Therefore, the differential equations in (33) and (34) result in a set of m − 1 equations

$$\begin{array}{c}{\mathrm{\Gamma }}_i{A}_i-j{K}_{i-1,i}{A}_{i-1}-j{K}_{i,i+1}{A}_{i+1}=0,i=2,3,\dots ,m-1\\ ({\mathrm{\Gamma }}_m+{\mathrm{\Gamma }}_L)A_m-j{K}_{m-1,m}{A}_{m-1}=0.\end{array}$$ (35)

One can solve (35) to find A_i constants based on the load field amplitude, A_m. From these values, the average power at different nodes of the inductive power transmission link can be calculated. The absorbed power by the ith inductor and the delivered power to R_L can be expressed as P_i = 2Γ_i|A_i|² and P_L = 2Γ_L|A_m|², respectively, from which the total delivered power to the system from source can be found from $P_S={\sum }_{i=1}^m{P}_i+P_L$, using the law of conservation of energy. Finally, the PTE of the m-coil system can be found from

$${\eta }_{m-\text{coil}}=\frac{P_L}{P_S}=\frac{{\mathrm{\Gamma }}_L}{{\mathrm{\Gamma }}_m+{\mathrm{\Gamma }}_L+\text{∑}_{i=1}^{m-1}{\mathrm{\Gamma }}_i{\left|\frac{A_i}{A_m}\right|}^2}.$$ (36)

In an m-coil link, the reflected load from the (i + 1)th coil onto the ith coil can be found from

$$R_{\text{ref}i,i+1}=k_{i,i+1}^2\omega L_i{Q}_{(i+1)L},i=1,2,\dots ,m-1$$ (37)

where k_i,i+1 is the coupling coefficient between the ith and (i + 1)th coils. Q_(i+1)L is the loaded quality factor of the (i + 1)th coil, which can be found from

$$Q_{iL}=\frac{\omega L_i}{R_i+R_{\text{ref}i,i+1}}=\frac{Q_i}{1+k_{i,i+1}^2{Q}_i{Q}_{(i+1)L}},i=1,2,\dots ,m-1$$ (38)

where Q_i = ωL_i/R_i and R_i are the unloaded quality factor and parasitic series resistance of the ith coil (L_i), respectively. It should be noted that for the last coil, which is connected to the load in series, Q_mL = ωL_m/(R_m + R_L). Assuming that the coupling between non-neighboring coils is negligible, the partial PTE from the ith coil to (i + 1)th coil can be written as

$${\eta }_{i,i+1}=\frac{R_{\text{ref}i,i+1}}{R_i+R_{\text{ref}i,i+1}}=\frac{k_{i,i+1}^2{Q}_i{Q}_{(i+1)L}}{1+k_{i,i+1}^2{Q}_i{Q}_{(i+1)L}}.$$ (39)

Using (37)–(39), the overall PTE in such a multi-coil inductive link can be found from

$${\eta }_{m-\text{coil}}=\prod _{i=1}^{m-1}{\eta }_{i,i+1}\cdot \frac{Q_{mL}}{Q_L}.$$ (40)

A. Three-Coil Power Transfer Inductive Links

The 3-coil inductive power transfer link, shown in Fig. 4(a), was initially proposed in [14] and analyzed based on the CMT. If we ignore K₂₄ due to large separation between L₂ and L₄, the field amplitudes at each inductor can be calculated by solving a set of two equations in (35), which leads to

Fig. 4.

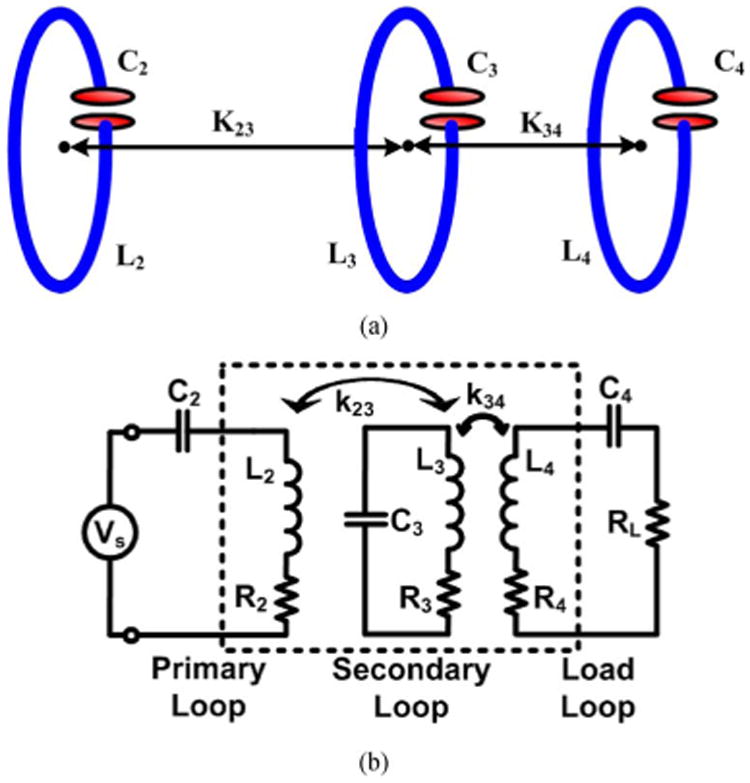
(a) Three capacitively loaded, mutually coupled, inductors for wireless power transmission in which L₄and K₃₄ serve as impedance matching elements to improve the PTE. (b) Lumped circuit model of the 3-coil inductive link.

$$\frac{A_2}{A_4}=\frac{K_{34}^2+{\mathrm{\Gamma }}_3({\mathrm{\Gamma }}_4+{\mathrm{\Gamma }}_L)}{K_{23}{K}_{34}},\frac{A_3}{A_4}=\frac{({\mathrm{\Gamma }}_4+{\mathrm{\Gamma }}_L)}{j{K}_{34}}.$$ (41)

PTE of the 3-coil link can then be found by substituting (41) in (36), which leads to (42) after some minor simplifications, as shown at the bottom of the page.

$${\eta }_{3-\text{coil}}=\frac{K_{23}^2{K}_{34}^2{\mathrm{\Gamma }}_L}{{\mathrm{\Gamma }}_2{[K_{34}^2+{\mathrm{\Gamma }}_3({\mathrm{\Gamma }}_4+{\mathrm{\Gamma }}_L\left)\right]}^2+K_{23}^2[{\mathrm{\Gamma }}_3{({\mathrm{\Gamma }}_4+{\mathrm{\Gamma }}_L)}^2]+K_{23}^2{K}_{34}^2({\mathrm{\Gamma }}_4+{\mathrm{\Gamma }}_L)}$$ (42)

The lumped circuit model for 3-coil inductive link has been shown in Fig. 4(b). In this type of inductive links, k₃₄ can be adjusted by changing the distance or geometry of L₄ to match the actual R_L with the optimal R_L,PTE in (10) for the L₂–L₃ inductive link. It should be noted that R₂, which is the series resistance of L₂, can also include the source output resistance [36]. The PTE of this circuit can be calculated by reflecting the resistive components of each loop from the load back towards the primary coil loop, one stage at a time, using (37) and calculating the percentage of the power that is delivered from one stage to the next, using (39), until it reaches R_L. According to (40), this procedure leads to

$${\eta }_{3-\text{coil}}=\frac{\left(k_{23}^2{Q}_2{Q}_3\right)\left(k_{34}^2{Q}_3{Q}_{4L}\right)}{\left[\right(1+k_{23}^2{Q}_2{Q}_3+k_{34}^2{Q}_3{Q}_{4L}\left)\right(1+k_{34}^2{Q}_3{Q}_{4L}\left)\right]}\cdot \frac{Q_{4L}}{Q_L}={\eta }_{23}{\eta }_{34}$$ (43)

where k₂₄ has been ignored due to large separation between L₂ and L₄, and

$$\begin{array}{l}{\eta }_{23}=\frac{k_{23}^2{Q}_2{Q}_{3L}}{1+k_{23}^2{Q}_2{Q}_{3L}}=\frac{k_{23}^2{Q}_2{Q}_3}{1+k_{23}^2{Q}_2{Q}_3+k_{34}^2{Q}_3{Q}_{4L}}\\ {\eta }_{34}=\frac{k_{34}^2{Q}_3{Q}_{4L}}{1+k_{34}^2{Q}_3{Q}_{4L}}\cdot \frac{Q_{4L}}{Q_L}.\end{array}$$ (44)

The resonance widths, Γ_2–4, and coupling rates, K_23,34, in CMT based on circuit parameters are defined as ω/2Q_2–4 and ωk_23,34/2, respectively [37]. By substituting these parameters in (42) and multiplying both numerator and denominator with $Q_2{Q}_3^2{Q}_{4L}^2$, the 3-coil PTE can be found from

$${\eta }_{3-\text{coil}}=\frac{k_{23}^2{k}_{34}^2{Q}_2{Q}_3^2{Q}_{4L}^2/Q_L}{[{(k_{34}^2{Q}_3{Q}_{4L}+1)}^2+k_{23}^2{Q}_2{Q}_3+k_{23}^2{k}_{34}^2{Q}_2{Q}_3^2{Q}_{4L}]}=\frac{k_{23}^2{k}_{34}^2{Q}_2{Q}_3^2{Q}_{4L}}{[{(1+k_{34}^2{Q}_3{Q}_{4L})}^2+k_{23}^2{Q}_2{Q}_3(1+k_{34}^2{Q}_3{Q}_{4L})]}\cdot \frac{Q_{4L}}{Q_L}$$ (45)

where 1/Q_4L = 1/Q₄ + 1/Q_L. It can be seen that (45), which is derived from the CMT is the same as (43), which is based on the RLT. Therefore, these two formulations are not different in the steady state analysis.

B. Four-Coil Power Transfer Inductive Links

Fig. 5(a) shows an inductive power transfer link consisting of four capacitively loaded inductors, in which L₂ and L₃ are the main coils responsible for power transmission, similar to the 2-coil link, while L₁ and L₄ are added for impedance matching [18], [36], [37]. The field amplitudes at each inductor can be found by solving a set of three equations in (35). A₂ and A₃ can be found based on A₄ from (41) and A₁ can be found from

Fig. 5.

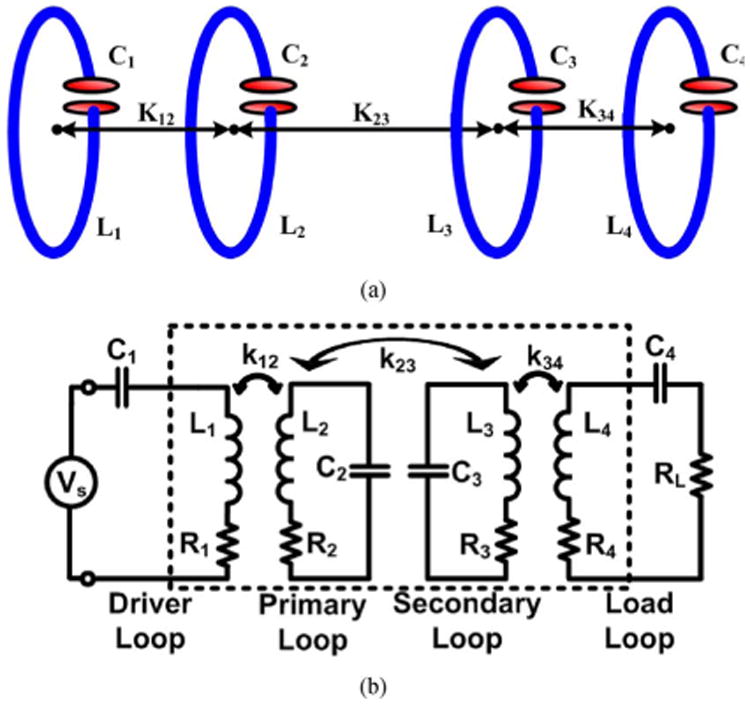
(a) Four capacitively loaded, mutually coupled, inductors for wireless power transmission, in which L₁ – K₁₂ and L₄ – K₃₄ serve as impedance matching elements to improve the PTE. (b) Lumped circuit model of the 4-coil inductive link.

$$A_1/A_4=-\frac{{\mathrm{\Gamma }}_2{\mathrm{\Gamma }}_3({\mathrm{\Gamma }}_4+{\mathrm{\Gamma }}_L)+K_{34}^2{\mathrm{\Gamma }}_2+K_{23}^2({\mathrm{\Gamma }}_4+{\mathrm{\Gamma }}_L)}{j{K}_{12}{K}_{23}{K}_{34}}.$$ (46)

To simplify the analysis, K₁₃, K₁₄ and K₂₄ have been neglected in comparison to coupling rates between neighboring coils. One can find the 4-coil PTE utilizing CMT by substituting (41) and (46) in (36), which after simplification leads to

$${\eta }_{4-\text{coil}}=\frac{K_{12}^2{K}_{23}^2{K}_{34}^2{\mathrm{\Gamma }}_L}{D}$$ (47)

where

$$\begin{array}{ll}D=& {\mathrm{\Gamma }}_1{\left[{\mathrm{\Gamma }}_2{\mathrm{\Gamma }}_3\right({\mathrm{\Gamma }}_4+{\mathrm{\Gamma }}_L)+K_{34}^2{\mathrm{\Gamma }}_2+K_{23}^2({\mathrm{\Gamma }}_4+{\mathrm{\Gamma }}_L\left)\right]}^2\\ & +K_{12}^2{\mathrm{\Gamma }}_2{[K_{34}^2+{\mathrm{\Gamma }}_3({\mathrm{\Gamma }}_4+{\mathrm{\Gamma }}_L\left)\right]}^2\\ & +K_{12}^2{K}_{23}^2{\mathrm{\Gamma }}_3{({\mathrm{\Gamma }}_4+{\mathrm{\Gamma }}_L)}^2\\ & +K_{12}^2{K}_{23}^2{K}_{34}^2({\mathrm{\Gamma }}_4+{\mathrm{\Gamma }}_L).\end{array}$$ (48)

In the 4-coil lumped circuit schematic, shown in Fig. 5(b), the PTE can be calculated from (40) if we ignore k₁₃, k₁₄, and k₂₄ in comparison to k₁₂, k₂₃ and k₃₄ [18], shown in (49) at the bottom of the page.

$${\eta }_{4-\text{coil}}=\frac{\left(k_{12}^2{Q}_1{Q}_2\right)\left(k_{23}^2{Q}_2{Q}_3\right)\left(k_{34}^2{Q}_3{Q}_{4L}\right)}{\left[\right(1+k_{12}^2{Q}_1{Q}_2)\cdot (1+k_{34}^2{Q}_3{Q}_{4L})+k_{23}^2{Q}_2{Q}_3]\cdot [1+k_{23}^2{Q}_2{Q}_3+k_{34}^2{Q}_3{Q}_{4L}]}\cdot \frac{Q_{4L}}{Q_L}$$ (49)

We can prove that CMT and RLT equations in (47) and (49) are basically the same by substituting the resonance widths, Γ_1–4, and coupling rates, K₁₂, K₂₃, and K₃₄ in (47) and (48) with their equivalent circuit parameters, ω/2Q_1–4, ωk₁₂/2, ωk₂₃/2, and ωk₃₄/2, respectively [37]. Once both numerator and denominator of (47) are multiplied by $Q_1{Q}_2^2{Q}_3^2{Q}_{4L}^2$, the CMT-based 4-coil PTE leads to (50), shown at the bottom of the next page, where A and B are

$${\eta }_{4-\text{coil}}=\frac{k_{12}^2{k}_{23}^2{k}_{34}^2{Q}_1{Q}_2^2{Q}_3^2{Q}_{4L}^2/Q_L}{A^2+k_{12}^2{Q}_1{Q}_2{B}^2+k_{12}^2{Q}_1{Q}_2{k}_{23}^2{Q}_2{Q}_3+k_{12}^2{Q}_1{Q}_2{k}_{23}^2{Q}_2{Q}_3{k}_{34}^2{Q}_3{Q}_{4L}}$$ (50)

$$A=B+k_{23}^2{Q}_2{Q}_3,B=1+k_{34}^2{Q}_3{Q}_{4L}.$$ (51)

The third and fourth terms of the denominator in (50) can be written in terms of B as

$$\begin{array}{ll}{\eta }_{4-\text{coil}}& =\frac{k_{12}^2{k}_{23}^2{k}_{34}^2{Q}_1{Q}_2^2{Q}_3^2{Q}_{4L}^2/Q_L}{A^2+k_{12}^2{Q}_1{Q}_2{B}^2+k_{12}^2{Q}_1{Q}_2{k}_{23}^2{Q}_2{Q}_{3}B}\\ & =\frac{k_{12}^2{k}_{23}^2{k}_{34}^2{Q}_1{Q}_2^2{Q}_3^2{Q}_{4L}^2/Q_L}{A^2+k_{12}^2{Q}_1{Q}_{2}B(B+k_{23}^2{Q}_2{Q}_3)}.\end{array}$$ (52)

By further manipulation of the numerator and denominator

$$\begin{array}{ll}{\eta }_{4-\text{coil}}& =\frac{k_{12}^2{k}_{23}^2{k}_{34}^2{Q}_1{Q}_2^2{Q}_3^2{Q}_{4L}^2/Q_L}{A^2+k_{12}^2{Q}_1{Q}_{2}B(A)}\\ & =\frac{k_{12}^2{Q}_1{Q}_2{k}_{23}^2{Q}_2{Q}_3{k}_{34}^2{Q}_3{Q}_{4L}}{A(A+k_{12}^2{Q}_1{Q}_{2}B)}\cdot \frac{Q_{4L}}{Q_L}\\ & =\frac{(k_{12}^2{Q}_1{Q}_2)(k_{23}^2{Q}_2{Q}_3)(k_{34}^2{Q}_3{Q}_{4L})}{A[B(1+k_{12}^2{Q}_1{Q}_2)+k_{23}^2{Q}_2{Q}_3]}\cdot \frac{Q_{4L}}{Q_L}\end{array}$$ (53)

Once A and B are substituted from (51) in (53), it will be identical to (49), which was derived from the RLT.

VI. Modeling Versus Measurement Results

In order to verify the accuracy of the PTE equations derived from the RLT and CMT in measurements, we designed and fabricated three sets of inductive links with 2, 3, and 4 coils. L₂ and L₃ in all three links were identical printed spiral coils (PSCs), fabricated on 1.5-mm-thick FR4 printed circuit boards (PCB) with 1-oz copper (35.6 μm thick). L₄ and L₁ in the 3- and 4-coil links were made of single filament solid copper wires, placed in the middle of L₃ and L₂, respectively [see Fig. 6(b)]. Given and L₃ geometries, the identical diameter of L₄ and L₁ were optimized based on the procedure that we presented in [36] for the nominal coupling distance of d₂₃ = 30 cm, R_L = 100 Ω, and f₀ = 13.56 MHz. Table II shows specifications these three inductive links.

Fig. 6.

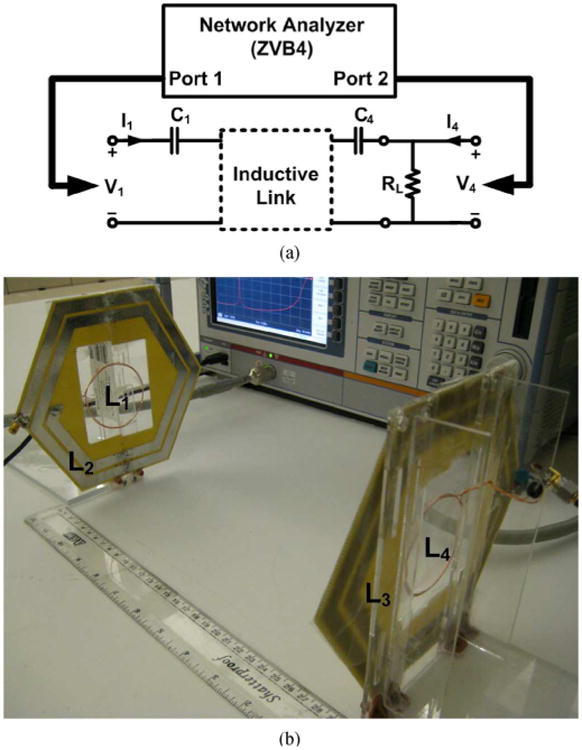
(a) PTE measurement setup using a network analyzer with all the coils tuned at the carrier frequency and R_L connected to the load coil. (b) Four-coil inductive link used to measure the PTE (specifications in Table II).

Table II. Inductive Link Specifications for Power Transfer Efficiency Measurements.

Parameters			Symbols	2-Coil	3-Coil	4-Coil
L1 / L4	Inductance (μH)		L1 / L4	-	0.57	0.57
	Outer diameter (cm)		Do1 / Do4	-	5.2	5.2
	Fill factor		Φ1 / Φ4	-	0.027	0.027
	Num. of turns		n1 / n4	-	2	2
	Line width (mm)		w1 / w4	-	0.64	0.64
	Line spacing (μm)		s1 / s4	-	100	100
	Quality factor		Q1 / Q4	-	183	183
	Resonance width (rad)		Γ1 / Γ4	-	2.3×105	2.3×105
L2 / L3	Inductance (μH)		L2 / L3	0.9
	Outer diameter (cm)		Do2 / Do3	16.8
	Fill factor		Φ2 / Φ3	0.13
	Num. of turns		n2 / n3	2
	Line width (mm)		w2 / w3	8.66
	Line spacing (mm)		s2 / s3	2.6
	Quality factor		Q2 / Q3	255
	Resonance width (rad)		Γ2 / Γ3	1.67×105
L2 and L3 coupling distance (cm)			d23	30
L2-L3 mutual coupling			k23	6.6×10-3
L2-L3 coupling rate (rad)			K23	2.8×105
L1-L2 / L3-L4 mutual coupling			k12 / k34	-	0.09	0.09
L1-L2 / L3-L4 coupling rate (rad)			K12 / K34	-	3.8×106	3.8×106
Power transfer efficiency (%)		Calculated	η	1.1	31.4	31.3
		Measured		1.37	29.7	27.9
Nominal load (Ω)			RL	100
Power carrier frequency (MHz)			f0	13.56

L₁ and L₄ are WWCs, while L₂ and L₃ are hexagonal PSCs.

Fig. 6(a) shows the measurement setup that we used for the PTE, which is quite suitable for multi-coil inductive links [36]. In this method, resonance capacitors and R_L are added to the driver and load coils, and the entire circuit is considered a 2-port system including the multi-coil inductive link in between. A network analyzer is used to measure the S-parameters, from which the Z-parameters are derived [39]. The PTE can then be found from 2-port equations

$$\text{PTE}=\frac{{|Z_{41}|}^2}{R_L|Z_{11}|cos(\angle Z_{11})}$$ (54)

where Z₁₁ = V₁/I₁ and Z₄₁ = V₄/I₁ are derived when I₄ = 0. The I₄ = 0 requirement in calculating the Z-parameters ensures that the network analyzer loading (often 50 Ω) on the inductive link does not affect the measurement results. Fig. 6(b) shows the 4-coil inductive link, which coils were held in parallel and perfectly aligned using sheets of Plexiglas. L₄ and L₁ and were placed in the middle of L₃ and L₂ and in a coplanar fashion, respectively, to achieve k₁₂ = k₃₄ = 0.09.

Fig. 7 compares the measured versus calculated values of the PTE versus coupling distance in the 2-, 3-, and 4-coil inductive links. Calculated PTE values are from the RLT and CMT models described in previous sections, while the circuit parameters, such as k and Q, are extracted from the models presented in [33] and [36] for PSCs and wire-wound coils, respectively. It can be seen that both RLT and CMT models, which are basically the same in steady state, estimate the PTE with a high level of accuracy.

Fig. 7.

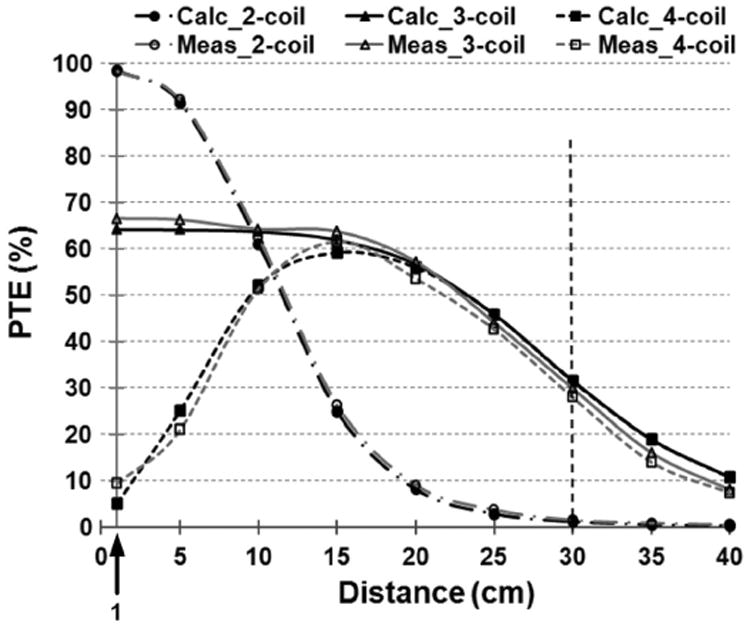
Comparison between measured and calculated (using RLT or CMT equations) values of the PTE versus the coupling distance, d₂₃, for 2-, 3-, and 4-coil inductive links specified in the Table II.

It can be seen from Table II that the calculated PTEs of the 3- and 4-coil links at d₂₃ = 30 cm are 31.4% and 31.3%, which are very close to the measured results, 29.7% and 27.9%, respectively. On the other hand, the measured 2-coil PTE at the same distance (1.37%) shows a greater difference on a percentage basis from the calculated value of 1.1%. This is most likely due to the measurement errors and equipment non-idealities at very low PTE levels. Because, as shown in Fig. 7, the calculated and measured PTEs for the same 2-coil link match very well at higher PTE values. The measured and calculated PTEs in 3- and 4-coil links show slightly more differences at smaller d₂₃ < 5 cm. This is because for the sake of simplicity, we have neglected non-neighboring coils' coupling in our models in Section V, which are more significant when d₂₃ is small. We would also like to point out that the 2-coil PTE at d₂₃ = 30 cm is ∼21 times smaller than that of 3- and 4-coil links because L₃ cannot provide Q_L values close to the Q_L,PTE in (10) for R_L = 100 Ω in the 2-coil link. On the other hand, the 3- and 4-coil links can achieve the optimal Q_L,PTE owing to their extra degree of freedom in impedance transformation, provided by k₃₄, which determines the optimal sizing of L₄ and L₁ [36].

VII. Conclusion

Electrical engineers analyze inductively coupled coils, transformers, and RLC tank circuits using lumped models, well known Kirchhoff's current/voltage laws, and a method often referred to as the RLT. Physicists, on the other hand, prefer to consider the energy stored in the system and exchanged between two or more resonating objects (in this case capacitively loaded conductive-wire loops) and use a method known as the CMT. We have presented detailed formulation for calculating the PTE based on both theories for a conventional 2-coil inductive power transmission link, and extended the solutions in the steady state to 3-, 4-, and m-coil systems. In each case, we have proven that despite using different parameters and terminologies, both CMT and RLT lead to the exact same set of equations, and therefore, both are applicable to short- and midrange coil arrangements as long as near-field non-radiative conditions are applicable to the resonating circuits. Moreover, we have derived equations describing the transient behavior of the 2-coil inductive power transmission links using both the CMT and circuit theory. Theoretical analysis and simulation results show that in this case, CMT is only accurate when coils have small coupling and large quality factors. However, it simplifies the analysis by reducing the order of the differential equations by half, compared to the circuit-based approach. The measurement results show that the RLT and CMT equations are both sufficiently accurate for the PTE calculation.

Biographies

Mehdi Kiani (S'09) received the B.S. degree from Shiraz University, Shiraz, Iran, in 2005 and the M.S. degree from Sharif University of Technology, Tehran, Iran in 2008. He is currently pursuing the Ph.D. degree in the GT-Bionics Lab at the Georgia Institute of Technology, Atlanta.

Maysam Ghovanloo (S'00-M'04-SM'10) was born in Tehran, Iran, in 1973. He received the B.S. degree in electrical engineering from the University of Tehran, Tehran, in 1994, the M.S. degree in biomedical engineering from the Amirkabir University of Technology, Tehran, in 1997, and the M.S. and Ph.D. degrees in electrical engineering from the University of Michigan, Ann Arbor, in 2003 and 2004, respectively.

From 2004 to 2007, he was an Assistant Professor in the Department of Electrical and Computer Engineering, North Carolina State University, Raleigh. In June 2007, he joined the faculty of Georgia Institute of Technology, Atlanta, where he is currently an Associate Professor and the Founding Director of the GT-Bionics Laboratory in the School of Electrical and Computer Engineering. He has authored or coauthored more than 90 peer-reviewed conference and journal publications.

Dr. Ghovanloo is an Associate Editor of the IEEE Transactions on Circuits and Systems II, IEEE Transactions on Biomedical Circuits and Systems, and a member of the Imagers, MEMS, Medical, and Displays (IMMD) subcommittee at the International Solid-State Circuits Conference (ISSCC). He is the 2010 recipient of a CAREER award from the National Science Foundation. He has also received awards in the 40th and 41st Design Automation Conference (DAC)/ISSCC Student Design Contest in 2003 and 2004, respectively. He has organized several special sessions and was a member of Technical Review Committees for major conferences in the areas of circuits, systems, sensors, and biomedical engineering. He is a member of the Tau Beta Pi, AAAS, Sigma Xi, and the IEEE Solid-State Circuits Society, IEEE Circuits and Systems Society, and IEEE Engineering in Medicine and Biology Society.