Abstract
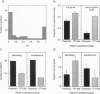
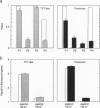
The iterated Prisoner's Dilemma has become the paradigm for the evolution of cooperation among egoists. Since Axelrod's classic computer tournaments and Nowak and Sigmund's extensive simulations of evolution, we know that natural selection can favor cooperative strategies in the Prisoner's Dilemma. According to recent developments of theory the last champion strategy of "win--stay, lose--shift" ("Pavlov") is the winner only if the players act simultaneously. In the more natural situation of players alternating the roles of donor and recipient a strategy of "Generous Tit-for-Tat" wins computer simulations of short-term memory strategies. We show here by experiments with humans that cooperation dominated in both the simultaneous and the alternating Prisoner's Dilemma. Subjects were consistent in their strategies: 30% adopted a Generous Tit-for-Tat-like strategy, whereas 70% used a Pavlovian strategy in both the alternating and the simultaneous game. As predicted for unconditional strategies, Pavlovian players appeared to be more successful in the simultaneous game whereas Generous Tit-for-Tat-like players achieved higher payoffs in the alternating game. However, the Pavlovian players were smarter than predicted: they suffered less from defectors and exploited cooperators more readily. Humans appear to cooperate either with a Generous Tit-for-Tat-like strategy or with a strategy that appreciates Pavlov's advantages but minimizes its handicaps.
Full text
PDF

Images in this article
Selected References
These references are in PubMed. This may not be the complete list of references from this article.
- Axelrod R., Dion D. The further evolution of cooperation. Science. 1988 Dec 9;242(4884):1385–1390. doi: 10.1126/science.242.4884.1385. [DOI] [PubMed] [Google Scholar]
- Axelrod R., Hamilton W. D. The evolution of cooperation. Science. 1981 Mar 27;211(4489):1390–1396. doi: 10.1126/science.7466396. [DOI] [PubMed] [Google Scholar]
- Frean M. R. The prisoner's dilemma without synchrony. Proc Biol Sci. 1994 Jul 22;257(1348):75–79. doi: 10.1098/rspb.1994.0096. [DOI] [PubMed] [Google Scholar]
- Milinski M. Evolutionary biology. Cooperation wins and stays. Nature. 1993 Jul 1;364(6432):12–13. doi: 10.1038/364012a0. [DOI] [PubMed] [Google Scholar]
- Milinski M. TIT FOR TAT in sticklebacks and the evolution of cooperation. 1987 Jan 29-Feb 4Nature. 325(6103):433–435. doi: 10.1038/325433a0. [DOI] [PubMed] [Google Scholar]
- Nowak M., Sigmund K. A strategy of win-stay, lose-shift that outperforms tit-for-tat in the Prisoner's Dilemma game. Nature. 1993 Jul 1;364(6432):56–58. doi: 10.1038/364056a0. [DOI] [PubMed] [Google Scholar]