From Exposures to Population Interventions: Pregnancy and Response to HIV Therapy

Abstract

Many epidemiologic studies identify contrasts between an “always-exposed” population and a “never-exposed” population. Such “exposure effects” are perhaps most valuable in discussing individual lifestyle changes, or in clinical care; they may be less valuable in estimating the potential effects of realistic public health interventions. Various methods, among them population attributable fractions and generalized impact fractions, attempt to obtain more policy-relevant estimates of “population intervention” effects, but such methods remain rare in the epidemiologic literature. Here, we describe the use of the parametric g-formula as a tool for the estimation of population intervention effects in longitudinal data. Our discussion is motivated by a previous study of the effect of incident pregnancy on time to virological failure among human immunodeficiency virus-positive women initiating antiretroviral therapy in South Africa between 2004 and 2011. We show that 1) interventional estimates of effect can be estimated in longitudinal data using the parametric g-formula and 2) exposure effects and population interventional effects can have dramatically different interpretations and magnitudes in real-world data. Epidemiologists should consider estimating interventional effects in addition to exposure effects; doing so would allow the results of epidemiologic studies to be more immediately relevant to policy-makers and to implementation science efforts.

Causal inference in real-world, observational data presents significant challenges. Among these is the need for exchangeability (1), including issues of both confounding and selection bias, positivity (2–4), and treatment-version irrelevance (5–7). When exposure is affected by prior covariates, the presence of covariates which serve as both confounders and mediators of causal effects (sometimes simultaneously) requires the use of newer methods such as inverse probability-weighted marginal structural models (8, 9) or the parametric g-formula (10–12).

When all of these conditions are met and the correct methods are used, the most frequent use of these methods (e.g., see Westreich et al. (13)) is to identify exposure effects—that is, effects which represent the impacts of particular exposures at the individual level (averaged over a population). For example, we might ask what would happen if an entire population of human immunodeficiency virus (HIV)-positive persons were exposed to antiretroviral therapy during the entirety of follow-up, as compared with being unexposed to antiretroviral therapy during the same period (i.e., “always treated” vs. “never treated”) (12, 14, 15). Such exposure effects, sometimes called average treatment effects, imagine 2 unrealistic counterfactual populations: one in which everyone is treated for the entire duration of follow-up (regardless of side effects, recovery rate, and so on) and one in which no one is treated for the duration of follow-up (regardless of declining health). Despite the unrealism of these counterfactuals (and potential difficulties in generalizing such estimates), such exposure effects can be valuable. They are perhaps most valuable in discussing individual lifestyle choices or in making clinical decisions (16). They may be less valuable in assessing what effects a realistic public-health intervention might have in the same population.

Various authors have called for increased attention to epidemiologic estimates of alternative population intervention effects (17) (alternatively, interventional effects), including some in these pages (18, 19), but such methods have not yet been widely adopted; methods for such interventional estimates have not been widely explored in longitudinal data. Here, we discuss the use of causal methods—in particular, the parametric g-formula (10–12)—as a tool for the estimation of population intervention effects in longitudinal data. Our discussion is motivated by a previous study of the effect of incident pregnancy on time to virological failure among HIV-positive women initiating highly active antiretroviral therapy (HAART) in Johannesburg, South Africa. We describe the data set and the previous analysis and exposure estimate, as well as the substantive and methodological challenges involved in mapping this exposure estimate to a more interventional or actionable estimate. First, we briefly review antecedent methods and further describe distinctions between exposure effects and interventional effects.

METHODS

Antecedent methods and challenges

There is a history in epidemiology of pursuing estimates of effect which map more directly onto policy: a class of estimands sometimes called population intervention effect estimates (17). The population attributable fraction (20–24) (and the population attributable risk difference or “attributable community risk” (25, 26)) is the best known of these, comparing disease risk in the observed population over a given period (with the observed level of an exposure; also the community risk) with the risk that would be observed in a counterfactual population in which 100% of the exposure had been removed. Our usage here, involving a fixed time period, maps to the “excess risk” of Greenland and Robins (27).

While an estimate of “observed level of exposure versus no exposure” is closer to what might be observed under a realistic intervention (compared with always exposed vs. never exposed), it is nonetheless unlikely in most cases that there exists an intervention that is able to remove all of a given exposure from a population. Recognizing this, Walter (28) and then Morgenstern and Bursic (29) extended the population attributable fraction to the generalized (or potential) impact fraction (alternately, the generalized attributable fraction), which compares disease risk in the observed population with the risk that would be observed in a counterfactual population in which a proportion f of the exposure had been removed, where 0 ≤ f ≤ 1. The population attributable fraction is then a special case of the generalized impact fraction when f = 1.

A generalized impact fraction can be used as a first tool for estimating population intervention effects. Consider the effect of smoking on incidence of all-cause mortality. If we knew that raising cigarette taxes by $1 per pack would lower the prevalence of smoking by 20%, we could estimate a generalized impact fraction comparing all-cause mortality under current smoking levels (X) with all-cause mortality under counterfactual smoking levels resulting from the proposed intervention (0.8 × X).

As implied immediately above, the generalized impact fraction may treat the population as uniform with respect to the effect of the intervention. It is plausible, however, that raising a cigarette tax may cause low-income smokers to quit with a higher probability than high-income smokers (30). If, in addition, the effect of smoking is heterogeneous by income level (e.g., if smoking-induced heart attacks are more likely to be fatal among persons with less access to health care), the generalized impact fraction may be misleading with respect to the population intervention effect of interest. In particular, the generalized impact fraction may be too general in assuming that the 20% reduction in exposure happens at random, rather than in a targeted fashion. A targeted impact fraction might instead attempt to estimate the effect of an intervention which would be targeted at (and subsequently taken up by) different subpopulations at different intensities.

Such targeted estimates were explored (not under this name) by Ouellet et al. (31) and Morgenstern and Bursic (29) and then later by others (32–35). Recent work by Muñoz and van der Laan (36) addressed the closely related issue of stochastically targeted population intervention effect estimates using targeted maximum likelihood estimation. These authors worked in time-fixed data; similar effects (sometimes targeted) have been estimated in longitudinal data by Taubman et al. (11), Cain et al. (37), Danaei et al. (38), and Cole et al. (39).

While regression-based approaches to estimating intervention effects go back at least as far as Deubner et al. (25) and later Greenland and Drescher (40), more recent work has discussed using Robins' g-methods (including inverse probability-weighted marginal structural models and doubly robust methods) to estimate both population attributable (41, 42) and generalized impact (43) fractions. Separately, Ahern et al. (18) used the parametric g-formula (g-computation algorithm (44)) to assess the effects of plausible interventions in real-world data in a time-fixed setting.

Here, we use the parametric g-formula in longitudinal data (11, 12) to estimate the effects of both generalized and targeted interventions on increased access to and uptake of highly effective contraception among HIV-positive women receiving HAART in sub-Saharan Africa. Because ratio measures are often regarded as inferior to difference (absolute) measures for assessing public health benefit (26, 45, 46), we follow the approach of Wacholder (26) and estimate absolute measures of intervention effects—specifically, risk differences (RDs). Thus, the quantities estimated here will be exposure RDs, population attributable RDs, generalized impact RDs, and targeted impact RDs. We address numbers needed to treat in the Discussion section.

Substantive example

We update an analysis from a prior study which found elevated hazards and risks of virological failure on HAART among HIV-positive women who experienced an incident pregnancy (13). Previously we studied antiretroviral therapy-naive women aged 18–45 years who were nonpregnant at HAART initiation, following 5,494 women for 11,600 person-years. The exposure of incident pregnancy after HAART initiation was treated as once-exposed, always-exposed, implying that the effects of experiencing pregnancy may occur postpregnancy (e.g., a resistance mutation acquired during pregnancy leads to virological failure subsequent to childbirth). Virological failure was defined as either failure to achieve virological suppression of plasma HIV-1 RNA to less than 400 copies/mL within 6 months of HAART initiation or a viral rebound to more than 400 copies/mL after initial suppression (47). Because of concerns about time-varying confounding affected by prior exposure, the main analyses were performed using marginal structural models (8) fitted with inverse probability weights (3, 9); these analyses adjusted for demographic and clinical factors, including age, employment status, and baseline and updated measures of weight, body mass index (weight (kg)/height (m)²), hemoglobin concentration, CD4 cell count and percentage, antiretroviral therapy regimen, and drug adherence. In this analysis, the crude hazard ratio was 1.37 (95% confidence interval (CI): 1.08, 1.73), and the weighted (marginal structural model) hazard ratio was 1.34 (95% CI: 1.02, 1.78), suggesting that pregnancy caused an increased rate of virological failure and that there was little confounding by measured covariates. Further details are available elsewhere (13).

We updated this analysis to include a total of 7,534 women followed for 16,600 person-years, an increase due both to new HAART initiation over time and to continued follow-up of previous HAART initiators. In this updated analysis, we used a viral load cutoff of 1,000 copies/mL instead of 400 copies/mL to guard against transient viral load increases (“blips”) without clinical implications (potential false-positive outcomes). Because the crude estimate of effect proved durable in the original publication, we focused on the crude estimate in this reanalysis, considering 4 variables in the modeling process: time since treatment initiation, the outcome of virological failure, the exposure of incident pregnancy (again, under a once-exposed, always-exposed assumption), and age (which has a strong effect on incidence of pregnancy). In addition, we simplified our modeling of time from a restricted 4-knot cubic spline (as in the original analysis (13)) to simpler linear and quadratic terms for month.

Limitations of previous work

To the extent that the crude (and marginal structural) models assessed a true causal effect of pregnancy on time to virological failure in the previous work (13) (particularly to the extent that the identifiability assumptions (1–7) were met), they pertained to a contrast in potential outcomes (48, 49): comparing the hazard of virological failure resulting from exposing all women in the population to pregnancy with the hazard of exposing no women in the population to pregnancy. This is similar (though not identical (50)) to the estimand that would be obtained from a randomized trial (with perfect adherence (51)) in which half of these women were assigned to pregnancy at trial initiation and the remainder were assigned to never experiencing pregnancy during follow-up.

As discussed above, the exposure estimand does not translate directly to an intervention: It is difficult to imagine real-world interventions which would ensure that all of the observed women would experience pregnancy during the follow-up period (much less at the beginning of that period). Similarly, there exist no ethical or practical real-world interventions which would prevent all incident pregnancy in this cohort.

From exposures to interventions

However, there do exist interventions which might prevent a portion of the incident pregnancy. What intervention is possible in this setting, and what effect might it have in this population? Here, we can imagine introducing highly effective contraception into the HAART clinic and encouraging uptake at the time of HAART initiation or thereafter among women who actively do not wish to become pregnant. We might propose providing injectable contraception (e.g., depot-medroxyprogesterone acetate (DMPA)), which is widely accepted in South Africa and throughout the region (52, 53), to women interested in preventing pregnancy. Women who actively did not want to become pregnant would accept DMPA at a higher level; women who were uncertain or undecided about their pregnancy intentions would accept DMPA at a lower level; and women who actively desired a pregnancy would typically refuse DMPA. Such an intervention would (counter to fact) prevent some proportion of observed pregnancies: those which were not actively sought (henceforth, unintended). We note that there might be unintended consequences of the proposed intervention; these are addressed in the Discussion.

In the current data, pregnancy intentions are unmeasured. However, Schwartz et al. (54) reported that in a Johannesburg maternity unit, 62% of pregnancies were unplanned. For illustrative purposes, we will take this figure as an estimate of the percentage of women who might want to prevent pregnancy in our proposed intervention. We will then estimate the intervention-specific 5-year generalized impact RDs for virological failure under interventions guided by this (admittedly, still somewhat unlikely) 62% figure. Below we describe several ways in which we implement this intervention in practice. For comparative purposes, we also estimate the 5-year population attributable RD, comparing the observed exposure with a counterfactual scenario in which there is no exposure.

Schwartz et al. also studied predictors of unmet need for contraception (54); this will allow some targeting of our interventional estimate. For example, in the study by Schwartz et al., a 5-year increase in age was associated with a prevalence ratio of 0.78 for unmet need for contraception (we ignore uncertainty in this estimate) (54). Thus, we may see greater uptake of our intervention among younger women; we therefore estimate a 5-year targeted impact RD as well. We likewise describe below how we incorporate this information in practice.

As implied by the use of the phrase “intervention-specific” above, there are as many interventional estimates of effect as there are plausible interventions. In this application, we implemented (that is, coded) the proposed intervention in several ways. First, we lowered the risk of becoming pregnant by 62% at each monthly visit (intervention 1). Second, we assumed that 62% of the women, chosen randomly and fixed at baseline, used DMPA successfully to prevent pregnancy throughout follow-up (a risk of 0) and that risk of pregnancy stayed at observed levels in others (intervention 2). Third, we coded an intervention in which each woman was offered DMPA every month. If the offer was taken up, DMPA was assumed to lower risk of pregnancy to 0 for 3 months; otherwise, pregnancy stayed at observed levels (intervention 3). The per-month probability that an individual woman would take up DMPA in a given month was 0.32, which gave us approximately 62% of all person-time covered by DMPA in the simulation. Finally, the age-targeted intervention refined generalized intervention 3 only, by changing the probability of DMPA uptake according to age (see equation A4 in Appendix).

Statistical approach

We used the parametric g-formula (10–12, 39) to estimate these interventional effects. A formal description of and technical details on the method are given in the Appendix and in a previous paper by Westreich et al. (12). As in previous work (12), we used our implementation of the g-formula to simulate the observed data as closely as possible using the “natural course scenario.” In addition to providing limited validation of the parametric assumptions of the g-formula, this natural course scenario provides the risks against which our proposed interventions can be best compared. Sensitivity analyses interrogating key assumptions are described below. In implementation, all point estimates were estimated in Monte Carlo samples of size 30,000 from the original 7,534 women; 95% confidence intervals were estimated as the standard deviation of 200 bootstrap resamples.

RESULTS

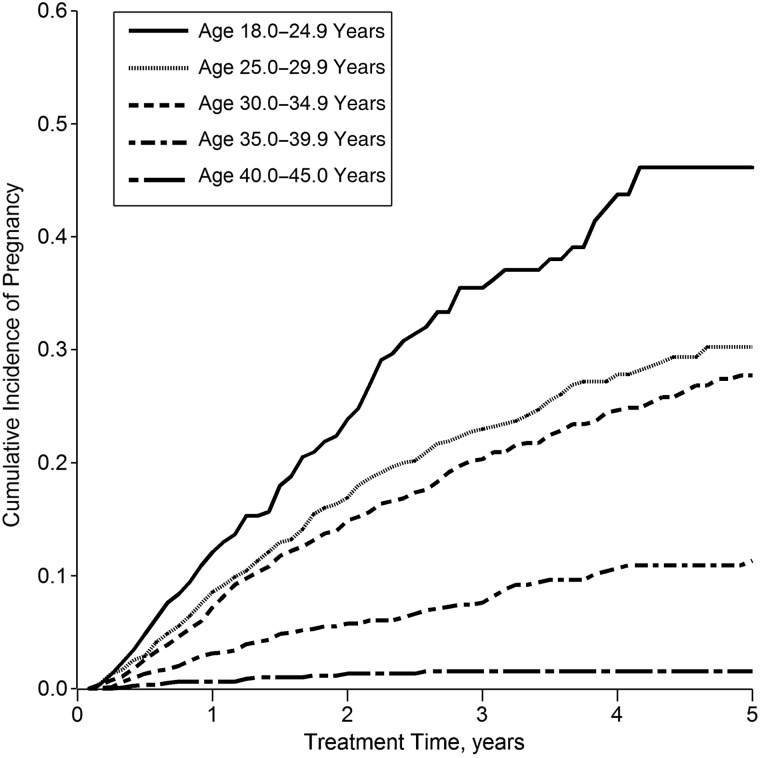
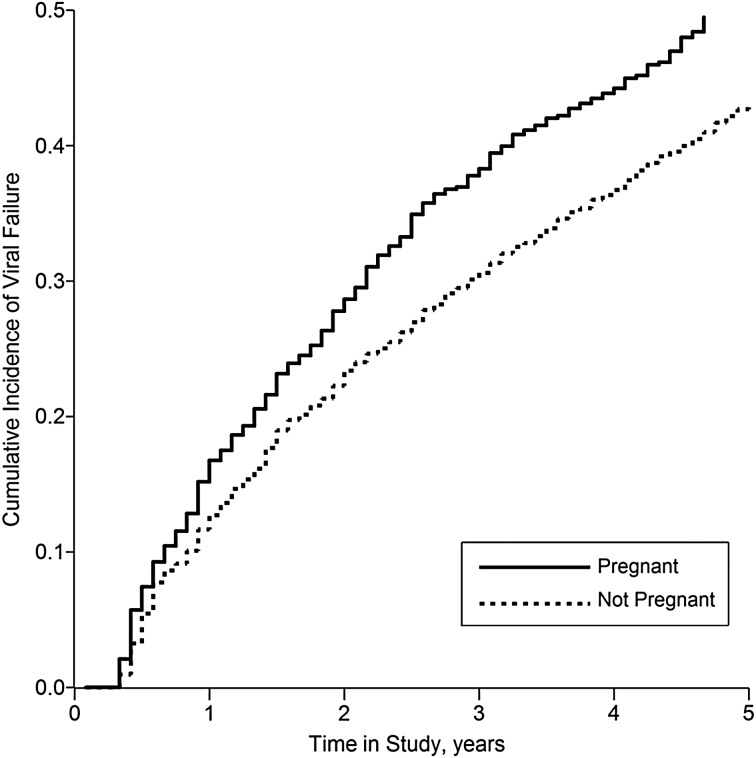
The study population comprised 7,534 women, who contributed a total of 199,393 person-months (16,616 person-years) to this analysis, of which 19,478 person-months (9.8%) were exposed (coincident with or subsequent to an incident pregnancy). Baseline characteristics of these women are shown in Table 1. The women experienced a total of 806 incident pregnancies; more than half of these months fell within 14 months of HAART initiation, and incidence of pregnancy was strongly age-stratified (see Figure 1). The women experienced 1,526 virological failure events (at a viral load cutoff of 1,000 copies/mL), of which 183 (12%) occurred during exposed person-time. Figure 2 shows the crude cumulative incidence of the outcome (viral failure) by exposure status.

Table 1.

Selected Characteristics of 7,534 HIV-Positive Women Initiating Highly Active Antiretroviral Therapy in Johannesburg, South Africa, From April 1, 2004, to March 31, 2011, at Baseline and Over Follow-up^a

Characteristic	Subjects (n = 7,534)			Person-Years (n = 16,616)
	Median (IQRb)	No.	%	Median (IQR)	No.	%
Follow-up time, years	20 (9–42)
Deaths		562	7.5
Age, years	33 (29–38)			35 (31–40)
Body mass indexc	22.2 (19.4–25.7)			24.5 (21.6–28.2)
CD4 count, cells/mm3	95 (36–165)			298 (176–448)
Viral load, copies/mLd
≤1,000		39	2.7		22,655	88.2
1,001–10,000		239	16.5		1,087	4.2
>10,000		1,167	80.8		1,957	7.6

Abbreviations: HIV, human immunodeficiency virus; IQR, interquartile range.

^a Figures for “over follow-up” include baseline observations.

^b 25th–75th percentiles.

^c Weight (kg)/height (m)².

^d At baseline, 81% of patients were missing data on viral load, and all those with a viral load of <400 copies/mL were excluded as likely treatment-experienced. During follow-up, we assessed viral load only when a viral load measurement was taken.

Figure 1.

Cumulative incidence of pregnancy (n = 806 incident pregnancies) according to time since HAART initiation among 7,534 HIV-positive women initiating HAART in South Africa, by baseline age, 2004–2011. HAART, highly active antiretroviral therapy; HIV, human immunodeficiency virus.

Figure 2.

Cumulative incidence of virological failure among 7,534 HIV-positive women initiating HAART in South Africa, by time-updated pregnancy status, 2004–2011. This is an “always versus never” exposure contrast. HAART, highly active antiretroviral therapy; HIV, human immunodeficiency virus.

The crude hazard ratio for the association between incident pregnancy (always vs. never) and time to virological failure in the updated data from a standard analysis was 1.38 (95% CI: 1.17, 1.61), comparing favorably with the hazard ratio of 1.37 (95% CI: 1.08, 1.73) from the previous analysis (13). The crude hazard ratio was similar when data were limited to women who were alive and receiving care at 6 months and when using the viral load cutoff of 400 copies/mL (as in the previous analysis (13)) rather than 1,000 copies/mL. The crude RD, estimated from the complement of the Kaplan-Meier curves, was 9.5% (95% CI: 4.4, 14.6).

The g-formula approximately recaptured the always-versus-never exposure RD from the marginal structural model, with a crude hazard ratio of 1.42 and a crude exposure RD of 10.1% (95% CI: 4.6, 15.6). The natural course g-formula estimated a total of 11% of person-time exposed and 0.007 events per month of follow-up, which compares well with the observed 10% of person-time exposed and 0.008 events per month of follow-up.

We used the g-formula to estimate the RD comparing the observed risk with several counterfactual scenarios, summarized in Table 2. The population attributable RD (comparing observed risk with a counterfactual in which no one was exposed to pregnancy) was 1.3% (95% CI: 0.0, 2.6). Then we estimated 3 generalized impact RDs (comparing observed risk with a counterfactual in which 62% of all exposure to pregnancy was prevented) under each of the 3 generalized interventions described above. Here, the RD was 0.5% (95% CI: −0.5, 1.6) under interventions 1 and 2 and 1.0% (95% CI: −0.1, 2.0) under intervention 3. Last, we estimated the targeted impact RD (comparing observed risk with a counterfactual in which 62% of all exposure to pregnancy was prevented differentially by age; see equation A4). Here, the RD was 0.6% (95% CI: −0.5, 1.6).

Table 2.

Estimated Effect of Pregnancy on Time to Virological Failure Among 7,534 HIV-Positive Women Initiating Highly Active Antiretroviral Therapy in South Africa, 2004–2011

	R1	R0	RD (R1 − R0), %	95% CI
Exposure RD	Always	Never	10.1	4.6, 15.6
Population attributable RD	Observed	Never	1.3	0.0, 2.6
Generalized impact RDa
Intervention 1	Observed	Reduceda	0.5	−0.5, 1.6
Intervention 2	Observed	Reduceda	0.5	−0.5, 1.6
Intervention 3	Observed	Reduceda	1.0	−0.1, 2.0
Targeted impact RDb	Observed	Reducedb	0.6	−0.5, 1.6

Abbreviations: CI, confidence interval; DMPA, depot-medroxyprogesterone acetate; HIV, human immunodeficiency virus; RD, risk difference.

^a Interventions 1, 2, and 3 are described in the text. Briefly, intervention 1 lowers the per-month risk of pregnancy by 62% in all women; intervention 2 lowers the risk of pregnancy to 0 over the entire follow-up period in 62% of women; and intervention 3 allows women to use DMPA at any time; if they do so, they do not become pregnant for 3 months.

^b Also described more fully in the text; here, we elaborate on intervention 3 (above) such that younger women are more likely to use DMPA.

In sensitivity analysis, we estimated RDs comparing observed risk with a counterfactual situation in which 31% (i.e., half of 62%) of all pregnancy was prevented. Generalized intervention 1 produced a result of 0.2% (95% CI: −0.8, 1.2); generalized interventions 2 and 3 gave similar results (RDs of 0.2% in both cases). We estimated the 2-year exposure RD (RD = 6.2%, 95% CI: 1.2, 11.2), the 2-year population attributable RD (RD = 0.7%, 95% CI: −0.1, 1.5), and the 2-year generalized intervention RD (for intervention 1; RD = 0.5%, 95% CI: −0.3, 1.0). Finally, we estimated 5-year RDs using a virological failure cutoff of 400 copies/mL, finding results similar to those in Table 2 (exposure RD = 8.1% (95% CI: 2.7, 13.5), population attributable RD = 0.8% (95% CI: −0.5, 2.1), and (for intervention 1) generalized intervention RD = 0.4% (95% CI: −0.6, 1.4)).

DISCUSSION

In this work, we have estimated both exposure effects and population intervention effects for the impact of pregnancy on risk of virological failure in a population of HIV-positive women receiving antiretroviral therapy in Johannesburg, South Africa. Notably, the two types of estimates tell radically different stories: While the exposure RD at 5 years was approximately 10%, the population intervention RD ranged from 1.3% to 0.5%. These RDs can be used (with caveats (55)) to calculate numbers needed to treat (NNTs) of 10 and 77–200.

These estimates differ by more than an order of magnitude, for a simple reason. Assuming that these estimates of causal effects are unbiased, the exposure-effect NNT (derived from an exposure RD) represents the number of pregnancies (among women who become pregnant) that would have to be prevented in order to prevent 1 virological failure, while the population-intervention-effect NNTs (derived from, for example, a population attributable RD) represents the number of women in whom we would need to intervene to prevent 1 virological failure, assuming that the intervention must be applied to the whole population of interest. Viewed in this way, it is intuitive that applying an NNT derived from an exposure effect and applying it to a proposed intervention may be highly misleading (55). In our case, targeting our intervention toward women who were most likely to become pregnant did not meaningfully change the NNT, possibly because these women also comprised the largest subgroup of women we studied.

The distinction between exposure and population intervention effects is recognized implicitly by most epidemiologists. We do not anticipate that most readers of this work will be shocked by this phylogeny, even if they prefer terms other than “exposure” and “population intervention.” Epidemiologists have a long history of pursuing population-intervention estimates of effect. Khoury et al. have discussed “translational epidemiology” as a type of epidemiology which can “assess the impact of using candidate applications on population health outcomes” (19, p. 517). Nonetheless, in our observation the majority of population-based analyses (especially outside of epidemiology journals) have focused exclusively on exposure effects, eschewing measures such as population attributable fractions. While such effects can be helpful for making public health policy, knowing the exposure effect of smoking on incidence of lung cancer allows clinicians to educate patients. However, this knowledge may be of less utility in setting larger-scale policy which promotes health at the population level.

Epidemiologists can play a larger role in setting such policy by paying more attention to interventional estimates of effect, both by producing such estimates when possible and, regardless, by increasing transparency and clarity around what effects are being estimated. We do not in any way begrudge epidemiologists their exposure effects (we plan to keep estimating these as well), but we hope that they will be more clear in labeling them as such. Doing this can, among other things, help epidemiology play a central role in implementation science, which is defined partially as “the scientific study of methods to promote the integration of research findings and evidence-based interventions into health care policy and practice” (56, p. S27).

A critical point worth clarifying is that the targeted interventions we evaluated in this report made numerous simplifying assumptions. Our 3 generalized interventions took different approaches to the problem; the similarity in the estimates derived from the 3 approaches (all point estimates within the confidence intervals of all other estimates (Table 2)) should provide some comfort that the specific approach taken to coding the intervention is of relatively little concern in this case. While we have attempted to make these potential interventions well-defined, the details of how each intervention is coded (i.e., implemented in SAS (SAS Institute Inc., Cary, North Carolina)) may affect how well exposures are truly “well-defined.”

Another simplification is that of “no censoring or competing risks of death,” which is artificial in the sense that death will always be an issue in a real-world intervention. For example, in the presence of competing risks, some interventions may be “wasted” in persons who (precisely because of the competing risk) would never have had the outcome of interest and were therefore “immune” from a causal types perspective (57, 58). Thus, interventional estimates which ignore competing risks, as here, are likely to overestimate RDs. Exploration of use of the g-formula to assess competing risks, as well as the role of competing risks in the estimation of interventional effects, is a subject for future work.

As with the previous work (13), there were limitations of this analysis due to the available data. We were unable to use the most specific outcome definition—defining virological failure with 2 consecutive measurements of viral load (at either cutoff)—because, as discussed in the original report (13), very few viral loads are confirmed in this setting. Likewise, we did not adjust for number of pregnancies occurring prior to HAART initiation, due to lack of rigorous collection of these data. In general, these were observational data from a clinical database; unmeasured confounding remains a threat to the validity of our analyses and should be kept in mind while evaluating these effect estimates.

A final point: Hernán and Taubman (59) have discussed the importance of having well-defined interventions for causal inference; here we similarly considered the unintended consequences of proposed interventions. In this example, while DMPA is not believed to affect response to antiretroviral therapy (60), data were scant and such effects cannot be entirely ruled out. If use of DMPA in fact increases risk of virological failure, then an intervention which attempted to prevent pregnancy with DMPA could increase, rather than decrease, overall risk. Relatedly, it is unlikely that a woman's age is the only factor determining use of contraception; while we saw no strong differences between our generalized and age-targeted estimates of interventional effect, this should not imply that no targeted intervention could improve on a generalized intervention. Indeed, one may view the development of methods to find the optimal targeting as an open question.

Epidemiology can inform a spectrum of biomedical and public health interests; tools exist within epidemiology to estimate effects relevant to each. Greater clarity in reporting and interpreting effect estimates, and placing those estimates on the spectrum of possible effect estimates, is an unmet need. Improved clarity in this arena—in particular, drawing distinctions between exposure and interventional estimates—will help epidemiology navigate from patients to policy and back again, and thus allow epidemiologists to do their job with optimal impact.

APPENDIX

The Parametric g-Formula

We begin with a formal description of the observed data. Let uppercase letters represent random variables and lowercase letters represent realizations. Let i = 1, 2, …, N denote the subject and j = 0, 1, …, J denote the month of follow-up, with N = 7,534 and J = 60 months for 5 years. For participant i, let Z_ij be age measured at visit j − 1. Let X_ij = 1 indicate having experienced an incident pregnancy by visit j. Let C_ij+1 = 1 indicate censoring due to dropout or death by visit j + 1. Let Y_ij+1 = 1 indicate a diagnosis of virological failure by visit j + 1. By design, X_i,j=−1 = 0 (all subjects are free of pregnancy at baseline) and C_i0 = Y_i0 = 0 (all subjects are at risk of virological failure at baseline). By definition, if Y_ij = 1 then Y_ij+1 = 1 and if C_ij = 1 then C_ij+1 = 1. By convention, Z_i,j=−1 = 0. For each visit j, we assume the following order: Z_ij, C_ij, Y_ij, X_ij. The history of a variable is denoted with an overbar. For example, 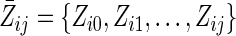; note that 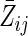therefore includes baseline covariates Z_i0. Below, we generally suppress the subscript i to simplify notation. Note that Z can be replaced by a vector Z without loss of generality.

The cumulative incidence of virological failure in the observed data by visit j + 1 can be written as follows:

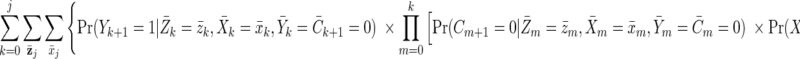(A1)

where Pr(A = a|B = b) is the conditional probability of A = a given B = b, and g(A = a|B = b) is the conditional density of A given B evaluated at the values A = a and B = b.

The g-formula can be used to consistently estimate the cumulative incidence of virological failure under a hypothetical treatment intervention (61). (As with all methods based on covariate adjustment, the validity of g-formula estimates requires exchangeability and positivity conditional on the measured and modeled covariates, as well as treatment-variation irrelevance; Robins and Hernán (61) provide a formal description of these conditions in longitudinal settings.) For example, we first consider the static treatment intervention “set the exposure history 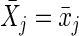and allow no censoring by loss to follow-up or death.” The following g-formula can be used to consistently estimate the cumulative incidence of virological failure by visit j + 1 under an intervention of this form (12, 61):

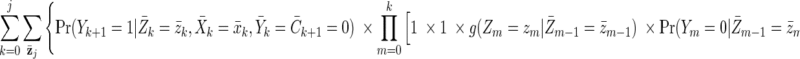(A2)

Because the intervention is static (and includes no censoring or competing risks; see Discussion for more on competing risks), the conditional probabilities of both the treatment and of censoring resolve to 1. We can calculate the exposure risk difference (always vs. never) as the difference between the g-formula evaluated at 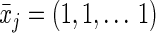(cumulative incidence under “always exposed to pregnancy”) and the g-formula evaluated at 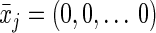(cumulative incidence under “never exposed to pregnancy”) for a fixed value of j (one equivalent to 5 years).

In contrast, the interventional risk difference will compare the observed cumulative incidence with the cumulative incidence under either a static intervention or a dynamic intervention. The observed cumulative incidence can simply be taken from observed data; alternately, we can estimate this quantity from equation A1 (the “natural course scenario”). The g-formula for the cumulative incidence under our interventions can be expressed as

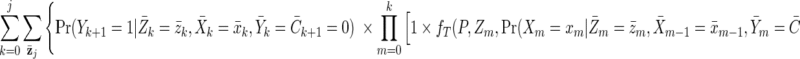(A3)

where f_T( ) is a function for the probability of pregnancy given the intervention T and P is the expected percentage of pregnancies prevented—say, 62% (from Schwartz et al. (54)). If T is the generalized intervention “offer DMPA to all women assuming high uptake among those who do not actively want to become pregnant, uniformly over all ages; and allow no censoring,” then the function f_T can be implemented simply (see Discussion): If X_m−1 = 1, then X_m = 1, else probability is calculated by multiplying the probability of pregnancy at time m (calculated as in the natural course scenario) by (1 − P).

If T is the targeted intervention—“offer DMPA to all women assuming that uptake is lower at older ages, with an uptake ratio of 0.78 per 5 years of age; and allow no censoring”—then f_T is more complicated and could be estimated as: If X_m−1 = 1, then X_m = 1, else probability is calculated by multiplying the probability of pregnancy at time m (calculated as in the natural course scenario) by

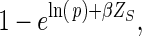(A4)

where β is ln(0.78) and Z_s is age centered at 30 years (the median age in the study by Schwartz et al. (54)) and divided by 5.

Additional technical details on the g-formula are available elsewhere (12).