Insecticide Resistance and Malaria Vector Control: The Importance of Fitness Cost Mechanisms in Determining Economically Optimal Control Trajectories

Abstract

The evolutionary dynamics of insecticide resistance in harmful arthropods has economic implications, not only for the control of agricultural pests (as has been well studied), but also for the control of disease vectors, such as malaria-transmitting Anopheles mosquitoes. Previous economic work on insecticide resistance illustrates the policy relevance of knowing whether insecticide resistance mutations involve fitness costs. Using a theoretical model, this article investigates economically optimal strategies for controlling malaria-transmitting mosquitoes when there is the potential for mosquitoes to evolve resistance to insecticides. Consistent with previous literature, we find that fitness costs are a key element in the computation of economically optimal resistance management strategies. Additionally, our models indicate that different biological mechanisms underlying these fitness costs (e.g., increased adult mortality and/or decreased fecundity) can significantly alter economically optimal resistance management strategies.

Evolution of insecticide resistance among arthropod pests and disease vectors provides one of the clearest examples of the economic relevance of evolutionary dynamics. However, evidence-based economic analysis and control of these dynamics requires a sound understanding of the underlying biology driving this evolution, in particular the relative fitness of individuals with and without genetic resistance to insecticides, and across a range of insecticide exposure levels. (Evolutionary fitness here is defined as “the ability of organisms to survive and reproduce in the environment in which they find themselves” [Orr 2009].) By definition, resistance confers a selective advantage in the presence of insecticide exposure, but biologists have theorized that populations face a fitness tradeoff in evolutionary terms to acquire these genetic mutations (Carriére et al. 1994). So-called fitness “costs” have been observed in a variety of arthropod pests (Gassman et al. 2009) and, of most relevance for the study described here, mosquito disease vectors (Djogbénou et al. 2010).

Economic models of the optimal management of insecticide resistance usually allow for fitness costs only through increased adult mortality (Laxminarayan and Simpson 2002; Grimsrud and Huffaker 2004; Qiao et al. 2008, 2009). That is, in the absence of insecticide exposure, resistant adult organisms are assumed to die at a faster rate than their insecticide-susceptible counterparts. These types of fitness costs have been observed. Moreover, many other types of fitness costs, such as decreased fecundity and longer developmental time, have been measured in arthropods, at least in those of significance in agriculture (e.g., Gassman et al. 2009).

Theoretical economic modeling has established that the magnitude of these mortality-specific fitness costs—when they exist—is decisive in constructing an optimal policy for insecticide use (Ibid.). This broad conclusion stands to reason: The smaller the net biological advantage conferred to the vector or pest by resistance-causing mutations, the more insecticide we may apply without fear of creating “superbugs” in the long-run. Economists studying these issues have recognized that the existence of fitness costs makes insecticide susceptibility in insect populations comparable to a renewable resource, which will recharge over time in the absence of exploitation. When fitness costs are absent, then insecticide susceptibility is a nonrenewable resource (Regev et al. 1983).

However, it also stands to reason that the types of fitness costs that emerge could qualitatively alter economic prescriptions. Indeed, intuition suggests that different types of fitness costs have different economic implications, particularly in the case of disease vector control. The case outlined above, in which reduced evolutionary competitiveness leads to an ability to “regrow” susceptible populations by limiting insecticide use, is an illustration of an indirect benefit of fitness costs relative to a situation in which such fitness costs are absent. In contrast, a direct benefit would be one in which a fitness cost had an unmediated effect on an insect’s ability to cause harm. This is precisely the case for mortality-specific fitness costs in mosquitoes and malaria transmissibility: Malaria parasites require an incubation period in mosquito vectors before they can be transmitted to their primary host, and therefore the likelihood of adult female mosquitoes surviving this incubation period has long been recognized as a major determinant of malaria transmissibility (Macdonald 1957). Thus, if insecticide-resistant mosquitoes have shorter lifespans than their susceptible counterparts, the ability of resistant mosquitoes to transmit malaria is directly decreased by these fitness costs.

Suppose that we observe a malaria epidemic catalyzed by one of two vector populations which are both insecticide resistant, but which differ in the types of fitness costs they exhibit: In the first population, the resistant insects exhibit a mortality-specific cost, whereas in the second population fitness costs are such that resistant insects require a longer pupation. We would expect malaria transmission to be lower in the first population relative to the second population, ceteris paribus.

Here we formalize the above thought-experiment in a mathematical model, and address the question of whether and how different mechanisms for evolutionary fitness costs can affect economic policies which seek to optimally manage insecticide resistance. For concreteness, we focus on the reduction of malaria burden through the spraying of insecticides to indoor surfaces where vectors rest. This is known as indoor residual spraying (IRS), and is currently a dominant method of malaria vector control.

The approach we use to study this question is first to formulate a simple, mathematical model of malaria transmission and control via IRS, on the one hand, and the evolution of insecticide resistance, on the other. In this model, we allow a distinction between fitness costs associated with adult mosquito mortality and with reduced emergence rate of adults (e.g., either through longer immature development times, fecundity reductions, or increases in larval mortality). We then calculate optimal economic policies using optimal control and dynamic programming techniques applied to the derived biological system.

We find that when fitness costs can be attributed to multiple biological mechanisms, then under realistic values for the parameters the optimally controlled dynamic system can converge to one of two stable steady states, one with high disease and high insecticide resistance and the other with low disease and low resistance. Which steady state the system approaches depends on the initial conditions of the biological state variables, in particular the level of resistance that prevails at the beginning of policy implementation. Specifically, if insecticide resistance is infrequent initially then it is optimal to keep it as such indefinitely by tempering insecticide usage, whereas if resistance is already prevalent initially then it is optimal to use insecticides intensively now even though this inevitably selects for superbugs in the long-run. (In practice, the periodic rotation of insecticides and the use of insecticide “mosaics” comprise the recommended strategy to prevent the emergence of resistance in disease vectors; this guideline was developed by the World Health Organization and partners [WHO 2012]. Here we focus only on the role of fitness cost mechanisms, and not on analysis of rotational and mosaic approaches, though fitness costs are likely to determine the effectiveness of these recommended approaches [WHO 2011]). We also conclude from simulations that implementing a “seemingly optimal” policy based on incorrect assumptions about the mechanisms underlying the fitness costs can be quite costly in economic terms, relative to implementation of an optimal policy (based on the correct biological assumptions).

Besides demonstrating an important conceptual point, insecticide resistance in malaria control is an important case to consider because insecticide resistance is a growing problem in many malaria-endemic areas (Trape et al. 2011) and because research is ongoing as to the extent and nature of fitness costs in malaria vectors (see the Supp. Data [online only] for a brief overview of this research).

The subsequent sections of this article detail the biological model, the economic optimization problem based on this model, analytical and numerical characterizations of solutions to this problem, and a discussion of our main findings.

Materials and Methods

The Biological Model

Malaria transmission is modeled according to dynamics originally proposed by Macdonald (1957). Because our focus here is on the dynamics of insecticide resistance, we keep the discussion of disease dynamics rather short and reserve details for the Supp. Data (online only). The important variable in the disease dynamics is the fraction γ_t of the human population that is infected with malaria at time t. In the present analysis, this variable satisfies the following differential equation:

$$\frac{d\gamma }{dt}=r[R_0\frac{e^{-\tau (\mu -{\mu }_0)}\mu }{{\left(\frac{\mu }{{\mu }_0}\right)}^2\mu +h{\gamma }_t}(1-{\gamma }_t)-1]{\gamma }_t$$ [1]

Details of this formulation are in the Supp. Data (online only). In words, equation 1 depicts dynamics in which infected mosquitoes bite humans randomly at a constant rate, and upon biting malaria parasites successfully transfer between infected humans or mosquitoes to an uninfected counterpart at a constant rate. The parameters in equation 1 are defined as follows: r is the rate at which infected individuals recover from malaria infection adjusted for the birth/death rate (the population is held constant), R₀ is the basic reproductive number for malaria in a baseline, uncontrolled setting (described below), τ is the average extrinsic incubation period (This is the time required for infected mosquitoes to become infectious, and although it is highly dependent on both genetic and environmental factors [temperature in particular], we assume it is constant in this article to focus on our primary research question.), μ is the current mortality rate for mosquitoes, μ₀ is the mortality rate for mosquitoes in a baseline uncontrolled setting, and h is the product of the biting rate and the probability that upon biting an infectious mosquito successfully transmits malaria to its human host.

A program manager wishing to reduce malaria prevalence γ_t looks at R₀ to see how transmissible malaria in general is under “natural” conditions (a higher value means faster transmission), looks at 120, μ₀, and μ to see how much time infected mosquitoes have to transmit malaria to humans under both baseline and controlled conditions, and finally notes from r how quickly the human population clears disease and how quickly it turns over because of demographic effects. (To focus on the most relevant variables from the perspective of a control program, our parameterization in equation 1 differs from that presented in standard texts on the subject [Anderson and May 1991, Keeling and Rohani 2008]. In the Supp. Data (online only), we show that our formulation is equivalent to the standard one.)

As usual, the mathematics of equation 1 can be characterized according to whether prevalence converges to 0 (i.e., malaria is eliminated) or goes to some positive value (i.e., malaria is endemic) in the long run: When vector mortality μ is fixed at the baseline μ₀, then R₀ < (>)1 implies that γ_t → 0(γ_∞ > 0) as t → ∞. That is, when μ = μ₀ then R₀ provides the usual threshold for whether or not the disease will become fixed in the population (Anderson and May 1991). When vector mortality exceeds the baseline, we can define a new threshold quantity:

$$R(\mu )\equiv R_0\frac{e^{-\tau (\mu -{\mu }_0)}}{{\left(\frac{\mu }{{\mu }_0}\right)}^2}$$ [2]

When R(μ) < (>)1, then γ_t→0 (γ_∞ > 0) as t → ∞. The policymaker influences the mosquito mortality rate μ in equation 1 by controlling the fraction of the population C that is covered by IRS. In the remainder of this section, we specify how average mortality rate of mosquitoes μ is determined by C and through genetic selection. Following others (Grimsrud and Huffaker 2004, Laxminarayan and Simpson 2002, Livingston et al. 2004, Qiao et al. 2009), we model this as a weighted mean of mortality rates corresponding to mosquitoes that are susceptible or resistant to insecticides and whether or not they are exposed to IRS:

$$\mu =C{\sum }_{\theta }{\omega }_{\theta }{\mu }_{\theta E}+(1-C){\sum }_{\theta }{\omega }_{\theta }{\mu }_{\theta U}={\sum }_{\theta }{\omega }_{\theta }\underset{\equiv {\mu }_{\theta }}{\underbrace{[C{\mu }_{\theta E}+(1-C){\mu }_{\theta U}]}}$$ [3]

where the variable Cε[0,1] denotes the fraction of the population that is covered by IRS, and constitutes the policymaker’s control. The hazard rate of mortality μ_θi facing a given mosquito is determined by the mosquito’s genetic type θ and whether it is exposed (i = E) or unexposed to (i = U) to IRS. The weights ω_θε[0,1] are the population frequencies of each genetic type θ, which are determined via a system to which we now turn.

To parsimoniously capture the evolutionary dynamics of insecticide resistance, we assume there is a single gene controlling resistance to the single insecticide being used in the IRS operation. While this assumption departs from reality to some degree, it is a close approximation given that only four classes of insecticides are usable for IRS, and resistance-conferring mutations in malaria vectors cover multiple classes of insecticides. The Supp. Data (online only) reviews the insecticides and genetic mutations that are relevant for malaria vector control. This gene is assumed to have two alleles—resistant (R) and susceptible (S)—yielding three different genotypes θ: The homozygotes RR and SS, and the heterozygote RS.

Denote s ε [0,1] as the proportion of the mosquito population with at least one copy of the susceptible allele S. This constitutes the primary state variable measuring resistance in the system; the higher s is, the less prevalent is insecticide resistance. Assuming random mating, the Hardy–Weinberg Principle as applied to a population of diploid organisms implies that the steady-state genotype frequencies are (Hardy 1908, Weinberg 1908):

$${\omega }_{RR}={(1-s)}^2{\omega }_{RS}=2s(1-s){\omega }_{SS}=s^2$$ [4]

This system can be substituted into equation 3 to simplify the expression for average vector mortality:

$$\mu =(1-s)[C{\mu }_{RRE}+(1-C){\mu }_{RRU}]+s[C{\mu }_{SSE}+(1-C){\mu }_{SSU}]$$ [5]

where we follow convention by assuming that the heterozygote’s mortality rate is the arithmetic mean of the homozygotes’ mortality. To enhance intuition, we define g ≡ μ_SSE − μ_SSU, which is the additional mortality susceptible mosquitoes are subject to when exposed to IRS. In addition, we set μ_r ≡ μ_RRU − μ_SSU, which is a mortality-specific fitness cost that resistant mosquitoes inherit relative to unexposed susceptible mosquitoes. Baseline mortality is set so that μ₀ = μ_SSU, that is, the mortality of unexposed, susceptible mosquitoes (the genotype that prevailed before any IRS was used). Resistant mosquitoes are assumed to be entirely shielded from the effects of insecticide exposure with μ_RRU = μ_RRE. Equation 5 therefore reduces to:

$$\mu (s,C)={\mu }_{\theta }+{\mu }_r+(Cg-{\mu }_r)s$$ [6]

Recall that C is controlled by the policymaker, while s is a state variable to which we now turn.

The genetic fitness of any genotype θ is denoted f_θ, and the average fitness in the population is defined as f ≡ Σ_θω_θf_θ. The genotype frequencies are assumed to follow standard replicator dynamics (Nowak 2006):

$$\frac{d{\omega }_{\theta }}{dt}=\epsilon {\omega }_{t\theta }(f_{t\theta }-f_t)\text{for all}\theta \epsilon \{RR,RS,SS\}$$ [7]

where ε > 0 is a parameter controlling the speed of the replicator dynamics. In such systems, genotypes with a fitness below the mean decline in frequency, whereas those above the mean increase in frequency.

Most economic work on the evolution of insecticide resistance assumes that differences in evolutionary fitness are proportional to pest or vector mortality, that is, (f_θ − f_θ′) α (μ_θ′ − μ_θ) for any two genotypes θ and θ′. In such a system, genotypes with a higher mean mortality rate necessarily decline in frequency within the population. The innovation in our analysis is to allow for other attributes to define a vector’s fitness. Empirical work has identified a number of mechanisms for fitness costs in arthropods that are genetically resistant to insecticides, including reduced fecundity and larval survival. The Supp. Data (online only) provides details on this body of work. To account for such mechanisms, we define genetic fitness:

$$f_{\theta }={\alpha }_{\theta }-{\mu }_{\theta }\text{for all}\theta \epsilon \{RR,RS,SS\}$$ [8]

where α_θ summarizes the component of genetic fitness that is independent of adult mosquito mortality.

Inspection of equation 7 shows that only differences in genetic fitness matter for the replicator dynamics. Therefore, we define α ≡ α_SS − α_RR, which is a fitness cost for resistant organisms independent of adult mortality. To isolate the effect of fitness cost mechanisms, we define f = α + μ_r as the total fitness costs, and Φ ≡ μ_r/f as the proportion that can be attributed to adult mortality mechanisms. In subsequent analysis, we fix f (the magnitude) and vary Φ (the distribution). Combining equations 4, 7, 8, and the definition for μ_θ yields:

$$\frac{ds}{dt}=\epsilon (f-Cg)s_t(1-s_t)$$ [9]

For a fixed level of IRS coverage C, this is a simple logistic differential equation: When the effects of IRS exceed fitness costs (Cg > f), then the resistant allele becomes fixed in the mosquito population to the exclusion of the susceptible allele (s_t → as t → ∞). The reverse occurs when Cg < f. When Cg = f, a singular equilibrium obtains and s_t remains fixed at its initial level.

Gathering together the relevant equations, the biological system we analyze in the rest of this article is:

$$\frac{d\gamma }{dt}=r[R_0\frac{e^{-{\tau }_S(\mu -{\mu }_0)}}{{\left(\frac{\mu }{{\mu }_0}\right)}^2}\frac{\mu }{\mu +h{\gamma }_t}(1-{\gamma }_t)-1]{\gamma }_t\frac{ds}{dt}=\epsilon (f-Cg)s_t(1-s_t)\mu (s,C)={\mu }_0+\varphi f+(Cg-\varphi f)s$$ [10]

This dynamic system consists of two state variables (γ and s), four malariometric parameters (r, R₀, τ_s and h), five parameters for vector ecology and evolution (ε, f, g, μ₀ and Φ), and the policymaker’s control C, which is the fraction of population covered by IRS. We impose some regularity conditions on the parameters at this point: f ≥ 0 (fitness costs are nonnegative), g > f (insecticides are fatal enough to cause selection), and R₀ > 1 (malaria is endemic in the absence of spraying).

Figure 1 shows the nine types of steady states that can occur in the biological system for different levels of IRS intensity C. Two thresholds are relevant here: The first is the threshold IRS intensity that determines selection for insecticide resistance (C > f/g). The second is the threshold level of vector mortality above which malaria prevalence converges to zero; this threshold can be found by inverting the function R(μ) defined in equation 2, and evaluating this inverse at unity: That is, if μ > R⁻¹(1), then malaria remains endemic in the population. Of course, C controls μ, but only up to a point, because selection for insecticide resistance reduces the effect of IRS on vector mortality.

Fig. 1.

Steady states of the biological system with different levels of IRS.

The Policymaker’s Optimization Problem

We consider a policymaker that seeks a profile of IRS coverage levels {C_t ε [0,1]} that maximizes the present value of an IRS program, by minimizing the expected present value social costs of malaria and IRS over an uncertain time horizon T:

$${\{C_t\}}_{t\ge 0}\equiv \text{arg}\underset{{\{C_t\epsilon [0,1]\}}_{t\ge 0}}{\text{min}}E[{\int }_0^T(q_{\gamma }{I}_t+q_{C}N{\mathrm{C̃}}_t)e^{-\mathrm{\delta ̄}t}dt]$$ [11]

where q_r>0 is the marginal social cost of a malaria infection per unit time, q_c > 0 is the marginal social cost of IRS per person per unit time, and δ̄ > 0 is the pure rate of discount.

We assume that the time horizon T is distributed exponentially with probability density function g_T(t) = δ_T⁻¹e^−δ_Tt, where δ_T > 0 is the hazard rate that the time horizon comes to an end. This captures the possibility of a “game-changing” malaria intervention making IRS obsolete. Because the total population N is constant, we can divide equation 11 through by N, multiply the objective by − 1 to obtain a maximization problem, and integrate out the expectations operator:

$${\{C_t\}}_{t>0}\equiv \text{arg}\underset{{\{{\mathrm{C̃}}_t\epsilon [0,1]\}}_{t>0}}{\text{max}}-{\int }_0^{\infty }(q_{\gamma }{I}_t+q_{c}N{\mathrm{C̃}}_t)e^{-\delta t}dt$$ [12]

subject to (10) where δ = δ̄ + δ_T is the effective discount rate.

Equation 12 poses a standard optimal control problem with one control and two state variables. This problem can be more easily manipulated by changing variables from s to ψ ≡ −log(s⁻¹ − 1). The Hamiltonian for this problem is:

$$H\equiv -q_{\gamma }\gamma -q_{C}C+\lambda r\{\frac{R[\mu (s,C)]\mu (s,C)}{\mu (s,C)+h\gamma }(1-\gamma )-1\}\gamma +\eta \epsilon (f-gC)$$ [13]

where s ≡ (1 + e^−ψ)⁻¹, and λ and η are the co-state variables for γ and ψ, respectively. These co-state variables satisfy the differential equations:

$$\frac{d\lambda }{dt}-\delta {\lambda }_t=q_{\gamma }-{\lambda }_{t}r[\frac{R_t{\mu }_t}{{\mu }_t+h{\gamma }_t}(1-2{\gamma }_t)-\frac{h{R}_t{\mu }_t}{{({\mu }_t+h{\gamma }_t)}^2}{\gamma }_t(1-{\gamma }_t)-1]\frac{d\eta }{dt}-\delta {\eta }_t=-{\lambda }_{t}r(R_{\mu }{|}_{{\mu }_t}{\mu }_t-\frac{1}{{\mu }_t+h{\gamma }_t})\frac{(1-\gamma )\gamma (gC-\varphi f)s(1-s)}{{\mu }_t+h{\gamma }_t}$$ [14]

where we have suppressed arguments for the functions R_t = R(μ_t) and μ_t = μ(s_t,C_t) to keep presentation concise. The Maximum Principle implies that when C_t ε (0,1) then the following first-order condition $\frac{\partial H}{\partial C}=0$ at time t is satisfied:

$$\underset{\text{dynamic marginal benefit from spraying}}{\underbrace{{\lambda }_{t}r\left[\right(R_{\mu }{|}_{{\mu }_T}{\mu }_t-\frac{1}{{\mu }_t+h{\gamma }_t})s_t(1-{\gamma }_t)-1]\frac{{\gamma }_t}{{\mu }_t+h{\gamma }_t}}}=\underset{\text{static marginal cost of spraying}}{\underbrace{q_C}}+\underset{\text{dynamic marginal user cost of insecticide resistance}}{\underbrace{g{\eta }_t\epsilon }}$$ [15]

As long as the marginal benefit (cost) of malaria is negative (positive), with λ_t < 0, then the left-hand-side of equation 15 is decreasing in C_t so that the first-order condition provides a global maximum. If the solution to this first-order condition does not exist or does not fall in the interval [0,1], then one of the boundary constraints binds.

Results

Analytic Characterization of Equilibria

Setting dγ/dt = ds/dt = 0 in equation 10 and dλ/dt = dη/dt = 0 in equation 14, and using the optimality condition in equation 15, provides a set of five nonlinear equations that an interior steady state (γ_∞, S_∞, λ_∞, η_∞, C_∞) must satisfy. In general, closed-form solutions to these equations cannot be obtained, but a few economically relevant results can be drawn from these equations: Most significantly, when fitness costs are mortality-specific with ϕ = 1—the status quo for economic research in this area—then any interior steady state of the optimized system is unique:

Proposition 1: If ϕ = 1 then any interior solution to the steady state equations is unique. If in addition malaria elimination is feasible, with μ₀ + f ≥ R⁻¹ (1), then there is no interior solution to the steady state equations.

The proof is in the Supp. Data (online only). When elimination is not feasible, the unique interior steady state (if it exists) in terms of the model’s parameters is:

$${\gamma }_{\infty }=1-\frac{1}{R({\mu }_0+f)}{s}_{\infty }=\frac{q_c}{g{q}_{\gamma }}\times \frac{(\frac{1}{1-{\gamma }_{\infty }}+\frac{h}{{\mu }_0+f+h{\gamma }_{\infty }})+\frac{\delta }{r{\gamma }_{\infty }}}{{\tau }_S+\frac{1}{{\mu }_0+f}+\frac{1}{{\mu }_0+f+h{\gamma }_{\infty }}}$$ [16]

Note that this steady state is such that increasing the discount rate δ increases the steady state level of resistance (∂s_∞/∂δ>0). This is because of two facts: First, the steady state marginal shadow cost of infection λ_∞ (not shown) decreases with an increasing discount rate, ceteris paribus. This is because the higher the discount rate, the less the present-value cost associated with a long-run level of disease. Second, the steady state shadow cost of resistance is zero when fitness costs are totally mortality-specific and when the steady state is interior. Thus, a higher discount rate places less weight on future infection costs, decreasing the dynamic benefits from insecticide spraying and leaving resistance costs unchanged. This implies a less intensive spray program and hence a higher stock of insecticide susceptibility in the vector population. Similarly, the cost ratio $\frac{qc}{g{q}_{\gamma }}$ has a positive impact on s_∞, so that, for instance, a higher direct marginal cost of infection q_r implies a lower steady state stock of insecticide susceptibility.

Numerical Analysis of Equilibria: Stability and Transition Paths

If evolutionary fitness costs stem from multiple mechanisms with ϕ < 1, then the steady state equations are ambiguous. Multiple equilibria of the optimized biological system are possible and indeed occur, a fact which we demonstrate here by numerically solving these equations. To do this, values must be chosen for the parameters of the biological system in equation 10, and the economic parameters in equation 11. Because the purpose of this analysis is to qualitatively characterize what can happen in this optimal control problem, rather than what will happen in any given context, we only seek reasonable values for the parameters to analyze the effect of varying the fitness cost distribution parameter ϕ.

First, we demonstrate the types of dynamics that can be observed in this system by presenting the numerical solutions to the optimal control model for three scenarios—one where ϕ = 1 (Scenario I), one where ϕ = 0.55 (Scenario II), and one where the evolution of insecticide resistance is turned off, which can be obtained by setting ε = 0 (and ϕ = 1). Second, we analyze the steady state solutions to the model across a range of fitness cost distributions, ϕε[0,1]. The values for the other parameters in each of these scenarios are shown in Table 1. To obtain solutions to the optimal control model, we use dynamic programming (DP) methods (Miranda and Fackler 2002); see the Supp. Data (online only) for details.

Table 1.

Parameter values used for numeric analysis

Parameter	Symbol	Scenario values
		I	II	III
Basic reproductive no. of malaria (secondary cases per primary case)	R0	100	100	100
Recovery rate of malaria-infected individuals (per day)	r	0.01	0.01	0.01
Incubation time of malaria in mosquitoes (days)	τS	14	14	14
Mass-action saturation factor (dimensionless)	h	61	61	61
Baseline vector mortality (per day)	μ0	0.27	0.27	0.27
Insecticide-induced mortality (per day)	g	0.83	0.83	0.83
Total fitness cost (per day)	f	0.26	0.26	0.26
Mortality-specific fitness cost (% of total)	ϕ	100%	55%	100%
Economic cost of a single infection (dollars per case)	qγ	$10	$10	$10
Spray cost per person (dollars per person-year)	qC	$1.21	$1.21	$1.21
Risk-adjusted discount rate (% per year)	δ	10%	10%	10%
Speed of resistance evolution (per year)	ε	15−1	15−1	0

References are in the Supp. Data (online only).

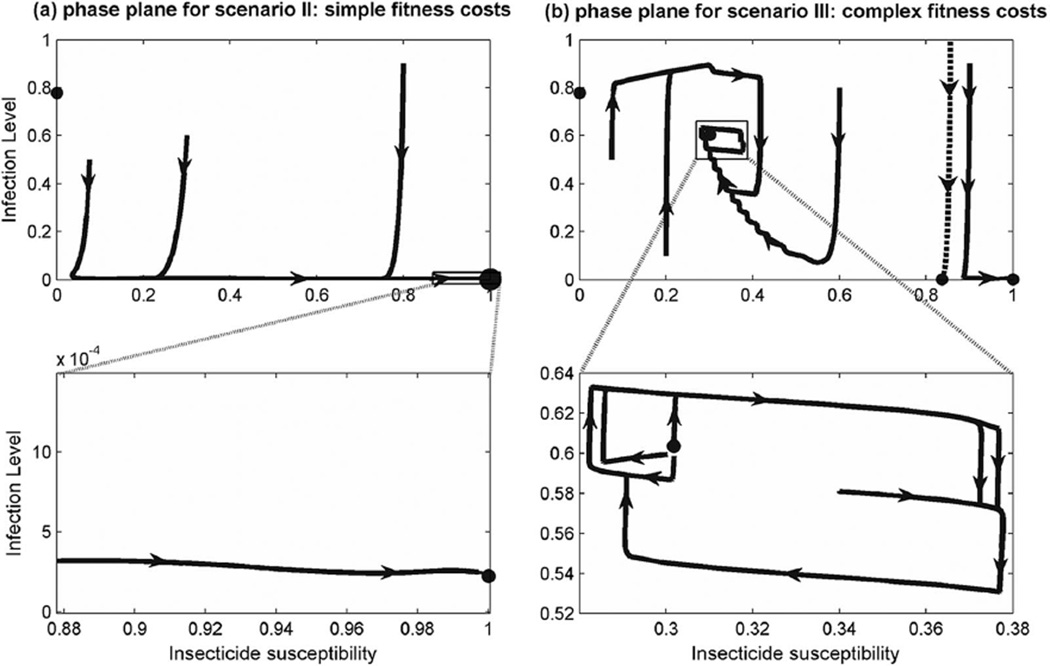
Figure 2a shows that setting ϕ = 1 leads to a single stable equilibrium on the boundary of the state space. This agrees with Proposition 1 because the parameterization makes malaria elimination feasible. Figure 2b shows that setting ϕ = 0.55 creates multiple equilibria in the optimally controlled biological system, with a bifurcation separating a steady state in which resistance becomes very high and one in which IRS remains at a low enough level to prevent selection for resistance.

Fig. 2.

Simulations of malaria prevalence and insecticide resistance with the implementation of an economic insecticide policy. (a) Trajectories from to Scenario I (Table 1). Zoomed-in portion that optimal steady state does not eliminate malaria, but reduces prevalence to an extremely low level. (b) Trajectories from Scenario II. Zoomed-in portion shows that in this scenario the optimal control induces a limit cycle in the long-run. The interior steady state of the optimally controlled system may only be stable in the sense of being orbited by a stable limit cycle.

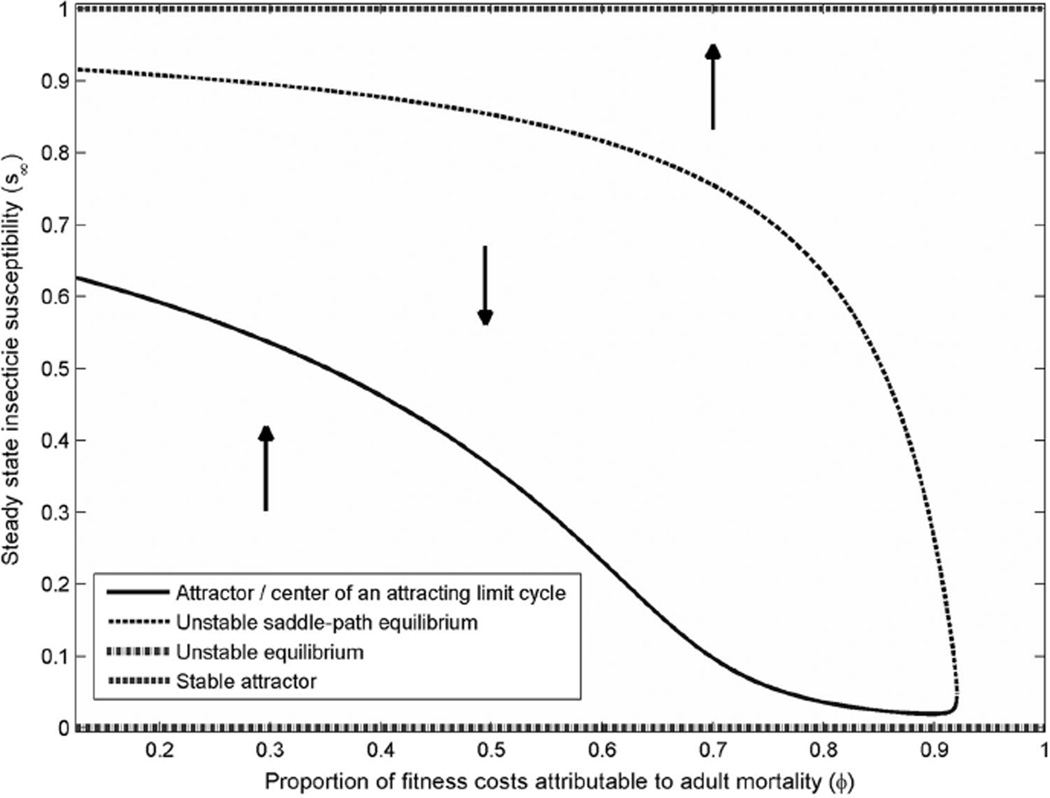
Solving the steady state equations for a range of fitness cost distributions ϕε[0,1], shows how the optimally controlled equilibria vary with fitness cost mechanisms. These solutions can be plotted in a bifurcation diagram shown in Fig. 3. This figure plots the equilibrium levels of insecticide susceptibility by the distribution of fitness costs. The solid curves represent stable steady states, and the dotted curve represents a “saddle-path stable” point. The saddle path points represent a bifurcation between the steady states of the system. For mixed distributions of fitness costs (ϕ < 1), this figure shows that when insecticide resistance starts at moderate levels, it is optimal to use more IRS to reduce malaria now, at the expense of selecting for superbugs in the long-run. However, if initial levels of resistance are very low or very high, then it is optimal to keep IRS coverage below levels that select for insecticide resistance. If we attribute more fitness costs to adult mortality specifically (ϕ increases), then the bifurcation point decreases: When ϕ exceeds 93%, it is always optimal (in this scenario) to keep IRS below a level that will select for resistance.

Fig. 3.

Bifurcation diagram of steady state insecticide resistance levels by fitness cost distribution parameter ϕ.

Discussion

By including a more complex depiction of evolutionary fitness costs in an optimal control model of malaria vector resistance to insecticides, we have shown that economic prescriptions based on such a model can qualitatively vary with the nature of these fitness costs. In the case of malaria control via insecticide spraying, the policy prescription is unambiguous about what should be done when insecticide resistance is initially low or very high: use of insecticides for malaria control should in the long-run be kept at a level low enough to prevent selection for insecticide-resistance in mosquitoes. This is established by Proposition 1 and can be seen in Fig. 2a.

However, when initial levels of insecticide resistance are moderate—arguably, the most relevant case in malaria-endemic regions of Africa (African Network on Vector Resistance [ANVR] 2005)—the policy prescription hinges on the mechanisms of evolutionary fitness costs in malaria vectors. When such costs can be attributed to mechanisms other than adult mortality, the optimal control simulations suggest that it may be worth the risk of selecting for superbugs to reduce malaria in the short-term (Fig. 2b). This finding differs from those yielded from status quo bioeconomic models of these phenomena (in the present context, the status quo model is captured in Fig. 2a).

These findings can be intuited from the following reasoning: Recall that fitness costs associated with adult mosquito mortality should have direct economic benefits because higher vector mortality reduces disease transmission. Thus, when fitness costs convey fewer direct economic benefits, dynamic cost-benefit calculus values short-run disease reductions over longrun insecticide efficacy for a wider range of initial insecticide resistance levels. This can be most clearly observed in Fig. 3, where the threshold insecticide-susceptibility level (the dotted curve) decreases as more of these fitness costs are attributable to adult mosquito mortality.

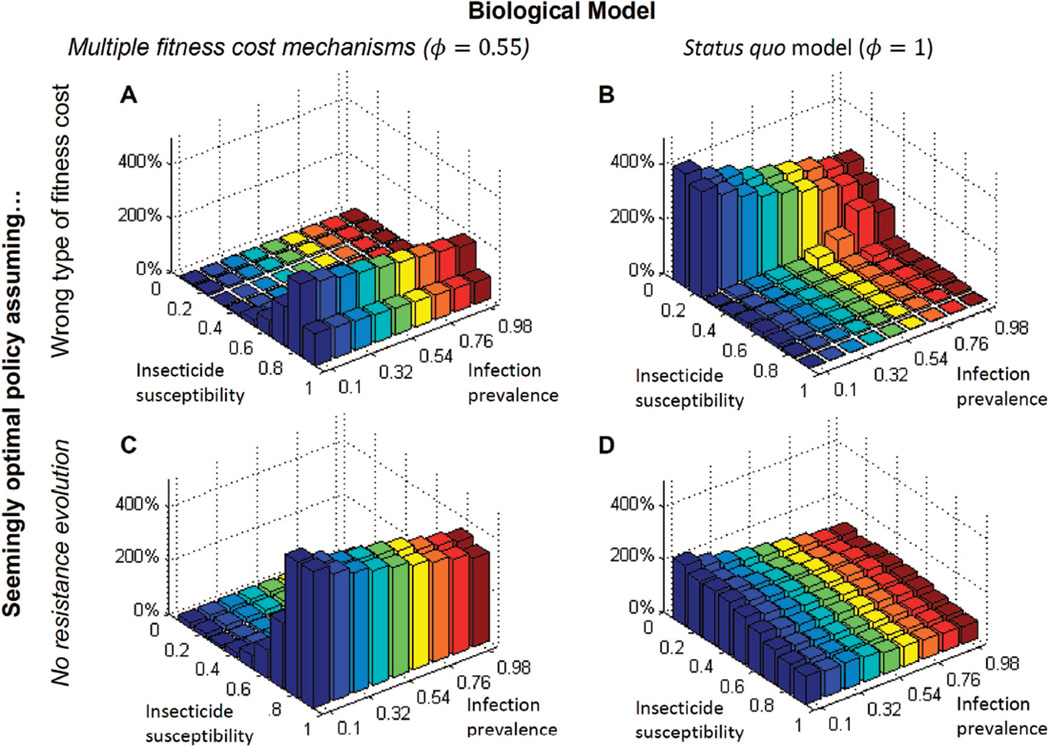
How poor an approximation is it to oversimplify the role of fitness costs in our bioeconomic analyses? The answer in this case is quite poor, at least if we take forfeited reductions in present value costs as our measure of poorness. Figure 4 presents results from plugging a seemingly optimal policy (SOP), calculated from one biological model, into a slightly different biological model, and then evaluating how much present value costs increase relative to the optimal policy (OP). By a “seemingly optimal” policy we mean one computed as a cost-minimizing policy under a set of biological assumptions that turn out to be false. When an SOP is based on a biological model in which fitness costs are fully attributable to adult mosquito mortality (ϕ = 1), and the OPs biological model assumes multiple fitness cost mechanisms, increases in present value costs can reach as high as 200% (panel A). Of course, a similar increase in costs occurs when the SOP and the OP are reversed (Fig. 4B). The main point of these panels is simply that misspecification results in a significant efficiency losses.

Fig. 4.

Percentage difference in present value costs of optimal and seemingly optimal policies. (Online figure in color.)

In conclusion, seemingly small details—in this case, the nature of fitness costs—in biological models of the evolution of insecticide resistance can lead to large and costly differences in policy prescriptions. Maximizing the value of insecticides requires an understanding of the subtleties in how populations evolve in response to exposure to these chemicals.