Estimating the causal effects of cumulative treatment episodes for adolescents using marginal structural models and inverse probability of treatment weighting

Abstract

Background

Substance use treatment is rarely a one-time event for individuals with substance use disorders. Sustained reductions in substance use and its related symptoms may result from multiple treatment episodes.

Methods

We use a marginal structural model with inverse-probability-of-treatment weighting to estimate the causal effects of cumulative treatment experiences over a period of 9 months on drug use at the end of 1-year among 2,870 adolescents receiving care in community-based treatment settings. During the 9 months, adolescents move in and out of outpatient and residential treatment with periods where they only receive biological drug screening (BDS) or no treatment at all. The use of inverse-probability-of-treatment weighting reduces confounding bias due to observed baseline and time-varying measures over the course of follow-up; weights were estimated using generalized boosted models.

Results

Each additional period of treatment (representing at least one day, 1 session, or 1 BDS, respectively, during the 90 day period between follow-up visits) yielded reductions in average substance use frequency at 1-year relative to no treatment during the 90-day period. For residential treatment it was a 16% decrease (95% CI = −27%, −7%), for outpatient treatment it was a 9% decrease (95% CI = −18%,−0%), and for BDS (with no additional outpatient or residential treatment) it was an 11% decrease (95% CI = −20%, −3%).

Conclusions

Using robust statistical methods, we find promising (albeit preliminary) evidence that additional periods of outpatient and residential treatment, as well as biological drug screening, lead to reductions in substance use outcomes at one year.

1. INTRODUCTION

Substance use treatment is rarely a one-time event for adults with substance use disorders (Hser et al., 1997); for adolescents, multiple treatment episodes are also common. In 2010, of the nearly 250,000 admissions among youth age 20 or younger to substance abuse treatment programs, roughly 33 percent were for youth who had received treatment in the past (SAMHDA, 2013). Additionally, the majority of adolescent clients re-initiate drug use within one year post-treatment (Dennis et al., 2004; Drug Strategies, 2003; Hser et al., 2001; Hubbard et al., 1998; Hunter et al., 2012; Salomé et al., 2003; Williams and Chang, 2000; Winters et al., 2009). One reason why relapse rates may be high is because youth may not be receiving empirically-supported treatments with demonstrated efficacy, e.g., Motivational Interviewing (Jensen et al., 2011) or Family Therapy (Tanner-Smith et al., 2013). Another explanation is that substance abuse may be a “chronic relapsing condition” for a substantial portion of adolescent clients (Witkiewitz and Marlatt, 2004) and a single episode of treatment therefor may not be sufficient to maintain a reduction in use for these youth.

While aftercare interventions specifically geared to prevent relapse have demonstrated benefits as an augment to treatment (Burleson et al., 2012; Godley et al., 2007; Kaminer et al., 2008), sustained reductions in substance use and its related symptoms among adolescent clients might also result from youth having multiple treatment episodes (Hser et al., 1998). While many addiction researchers have promoted the potential for treatment episodes to culminate in reduced substance use, research examining such cumulative effects has been sparse. Hser et al. (2007) point out that “little empirical evidence exists regarding whether there are cumulative treatment effects”; this investigation seeks to estimate such effects among adolescents.

The limited previous work that has been done to estimate cumulative effects derives primarily from samples of adults. For example, Hser et al. (1998) studied the effect of both the number of prior treatment episodes and length of time in treatment on post-treatment substance using behaviors and found evidence of both direct and indirect effects on post-treatment drug use, though results differed across treatment modalities. Dennis and colleagues (2005) found that multiple treatment episodes before study entry was associated with longer time until sustained abstinence after treatment in a sample of adults, concluding that individuals who enter treatment with past treatment histories may be a subgroup in need of specific and targeted treatment approaches and highlighting the importance of continuing care and long-term recovery management.

Neither of the studies on adults addresses the selection effects inherent in estimating cumulative effects in a robust way, partially because statistical tools were not readily available to do so. Traditional approaches (e.g., multivariate regression adjustment, structural equation modeling, and stratified analyses) to control for differences among youth with different treatment trajectories cannot adequately control for the dynamic nature of treatment assignments and how selection into different treatments operate over time. To appreciate this, consider the importance of adjusting for measures known as time-varying confounders (substance use; emotional problems; criminal justice involvement): these are measures that change over time with the course of treatment and are associated both with the primary outcome and the likelihood of receiving subsequent treatment. While traditional statistical methods can account for differences in groups that exist prior to any treatment, they do not, in general, appropriately account for time-varying confounders. The key challenge lies in the fact that time-varying confounders may themselves be influenced by prior treatment. Therefore, traditional methods that control for observed time-varying confounders by multivariate adjustment have the potential for “cutting-off” or obscuring the effect of cumulative treatments. Moreover, under the plausible condition that there exist common correlates between the time-varying confounders and the primary outcome, traditional regression adjustment methods can actually increase bias in estimating the impact of additional treatment episodes (Almirall et al., 2013b; Hernan et al., 2000, 2002; Robins, 1986, 1987, 1994, 1999; Robins et al., 2000).

Recent methodological advances, however, allow for a more principled approach to controlling for time-varying confounders and selection issues. Marginal structural models (MSMs) together with inverse-probability-of-treatment weighting (IPTW) to adjust for selection among clients with differing amounts of cumulative treatment provides a means of estimating robust effects of cumulative treatment episodes on outcomes (Hernan et al., 2000; Robins et al., 2000). MSMs provided a strong theoretical foundation to study cumulative effects in applications ranging from treatment for HIV on kidney infection (Scherzer et al., 2012) to inhaled cortiscosteroid regimens on asthma symptoms (Kim et al., 2005). Moreover, one study (to date) has used MSMs to estimate cumulative treatment effects on substance use outcomes among adults. Using retrospective data and MSM together with IPTW, Li et al (2010) found evidence that treatment effects cumulated over a 10-year span, increasing the likelihood of abstinence in the subsequent five year period for adult substance users. Li et al. (2010) also showed that traditional regression analyses did not come to this same conclusion, highlighting that MSM together with IPTW can uncover relationships that may be obscured by failing to account for time-varying confounders. Although unobserved confounders may still bias such estimates, this work provides an important methodological technique for estimating cumulative treatment effects in the presence of time-varying confounders.

In this paper, we utilize an MSM to estimate the causal effects of cumulative treatment experiences over a period of 9 months among adolescents engaged in community-based treatment settings on drug use at the end of 1 year. During the 9 months, adolescents may move in and out of outpatient and residential treatment modalities and experience periods where they only receive biological drug screening or where they receive no treatment at all. We include periods of biological drug screening (BDS) as separate from periods of no treatment given recent findings suggesting that BDS only may have beneficial effects on reducing substance use (Schuler et al., in press). We utilize IPTW to reduce confounding bias due to observed baseline and time-varying confounders over a 9-month period of treatment and highlight in a step-by-step fashion how addiction researchers might to utilize MSM + IPTW in their own work with longitudinal treatment data.

2. METHODS

2.1 Sample

This study uses data on 2,870 adolescents pooled from four adolescent treatment discretionary programs funded by the Substance Abuse and Mental Health Services Administration's (SAMHSA's) Center for Substance Abuse Treatment (CSAT) and involving adolescents entering one of 17 community-based substance abuse treatment programs in the United States between 1998 and 2008. Though the focus of each discretionary program differed, all funded facilities were required to collect baseline and follow-up information from youth receiving substance use treatment services for which funding was provided. Facility services varied, and tended to offer more comprehensive treatment services than standard community-based treatment (Hunter et al., 2013). All data were collected using the Global Appraisal of Individual Needs (Dennis et al., 2003), a structured clinical interview of client characteristics and functioning administered at baseline/intake and at the end of 3, 6, 9, and 12 months. At all 5 measurement occasions, GAIN asks about treatments received, substance use, physical health, risk behaviors, mental health, and environment, legal and educational/vocational problem areas over the past 90 days. Written informed consent from parents and assent from the adolescents were obtained, and institutional review boards at each site approved study protocol.

2.2 Treatment

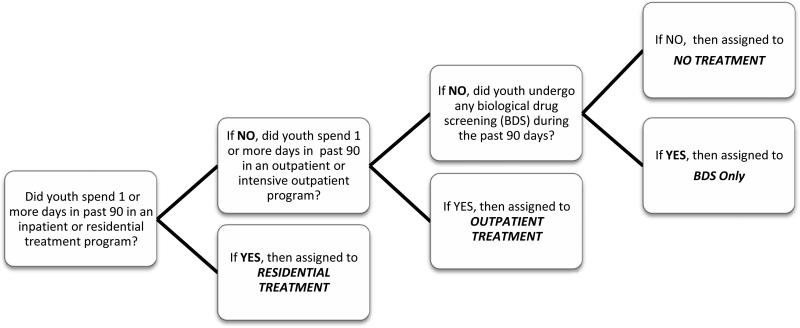
Adolescents were categorized into one of four different treatment groups during each 90-day period: residential treatment, outpatient treatment, BDS only (meaning no residential or outpatient treatment), or no treatment. Assignment to these categories was based on adolescents’ self-reported responses to six GAIN items measuring their treatment experiences in the 90 days prior to the interview. Figure 1 shows how the questions map to the four mutually exclusive treatment groups with youth in more than one type of treatment being assigned to the treatment condition considered to be more intensive. It is important to note that our treatment measures group youth into the four treatment conditions based on whether or not a youth received any amount of the given treatment during the 90-day period in question (e.g., to be in the residential group youth only need to have received at least 1 day in residential treatment during the past 90 days; to be in outpatient, the youth needed at least 1 outpatient session; to be in BDS, the youth needed at least one BDS implemented).

Figure 1.

Flow-chart showing how adolescent clients were assigned into four mutually exclusive treatment conditions between follow-up visits.

2.3 Outcomes

We examined two outcomes from the 12-month follow-up. Substance use frequency during follow-up was assessed with the GAIN's Substance Frequency Scale (SFS), an 8-item scale that assesses the average proportion of alcohol and other drugs using days in the past 90 taking into account heavy use and problem days (Dennis et al., 2010). We multiplied the original scale by 90 so it represents number of days of use out of the past 90. We assessed severity of substance use problems with the Past Month Substance Problem Scale (SPS). This scale is a count of 16 possible symptoms in the past 30 days: the seven DSM-IV criteria for drug dependence; the four DSM-IV criteria for substance abuse; two items related to substance-associated health and psychological problems; and three items related to lower severity symptoms (e.g., hiding use, people complaining about use, and weekly use; Dennis et al., 2010). Inter-item reliability for both scales is very good; among a similar population of adolescents α = .80 for the SFS and α = .92 for the SPS (Dennis et al., 2010).

2.4 Confounders

We considered a number of key baseline and time-varying confounders in our analysis that cover a range of important domains which are likely associated with both treatment assignment and our outcomes in this study, including socio-demographic measures, substance use measures, an emotional well-being scale, number of days spent in a controlled environment where freedom to use would be limited, and prior treatment history up to a particular follow-up. The time-invariant measures from baseline included age, race/ethnicity, sex, and substance use problems measured over the year prior to enrollment. The time-varying measures (measured at baseline, 3, 6, and 9 months) included our two outcomes (SFS and SPS); total number of days spent in a controlled environment in the 90 days prior to a follow-up (e.g., including residential treatment settings, hospitals, or jail); and the Emotional Problem Scale (EPS), a measure of emotional problems or psychological distress during the past 90 days which assesses the recency and days adolescents were bothered by and kept from responsibilities because of emotional problems; disturbed by memories; and had problems paying attention or with self-control (alpha = 0.80; Chestnut Health Systems, 2004). Additionally, our weights controlled for time-varying measures of treatment history at 3, 6, and 9 months.

2.5 Marginal Structural Model

We are interested in estimating the cumulative effects of additional periods of treatment with outpatient, residential, and BDS only relative to no treatment. More specifically, we wish to estimate the average effect of additional periods of outpatient, residential, and BDS on 12-month outcomes. We hypothesize that additional periods of each type of treatment will be significantly associated with less substance use at one year post-intake. Thus, we let OUT_ij, RES_ij , and BDS_ij denote dummy indicators for whether or not the i^th individual receives any outpatient, residential, or biological drug screening in the 90 days prior to follow-up j and make the reference group in our models the no treatment group. Then, we let ${\overline{OUT}}_t$, ${\overline{RES}}_t$, and ${\overline{BDS}}_t$ denote the history of each type of treatment condition for individual i through all three follow-up times (3-, 6-, and 9-months; e.g, it contains the vector of the 3 dummy indicators for whether or not the youth received the given treatment within each 90-day period). We let Y_τiss denote the expected value of the outcome of interest (SFS or SPS) at the 12-month assessment for all the youth in the population had they experienced treatment history $T_{t12}=c({\overline{OUT}}_t,{\overline{RES}}_t,{\overline{BDS}}_t)$. Then, we have the following model for our outcomes:

$${\mathrm{Y}}_{{\stackrel{‒}{\mathrm{T}}}_{i}12}={\alpha }_0+{\alpha }_{OUT}cum\left({\overline{OUT}}_i\right)+{\alpha }_{RES}cum\left({\overline{RES}}_i\right)+{\alpha }_{BDS}cum\left({\overline{BDS}}_i\right)$$ (1)

where cum(·) denotes the sum of the number of times youth with history T_t12 received the given treatment type during the course of the follow-up. The parameters corresponding to $cum\left({\overline{OUT}}_t\right)$, $cum\left({\overline{RES}}_t\right)$, and $cum\left({\overline{BDS}}_t\right)$, respectively, provide us with the estimated cumulative effects of outpatient, residential and BDS treatment relative to no treatment as well as provide us with a test of our hypotheses that each additional period will produce a significant reduction in substance use. For example, for the SPS outcome, 2× α_OUT denotes the average effect of outpatient treatment during any two of the three, 3-month intervals versus no outpatient treatment during any of the intervals on the number of substance use problems a youth reports at the 12-month interview; similarly, α_OUT + α_RES denotes the average effect of one outpatient and one residential period during the three, 3-month intervals versus no outpatient or residential treatment during any of the intervals. We test for cumulative effects of each treatment class by testing whether α_m = 0 for m = OUT, RES, and BDS. This model assumes that each additional period of a given treatment condition has an additive effect which appeared to be a good fit to our data.

2.6 Estimation

The MSM in equation (1) is specified for the population means had all youth experienced each treatment history. However, the youth in the sample who experience each history may differ from other youth in terms of the time-varying and baseline confounders described in section 2.4. In order to properly remove the effects of these confounders, we utilize IPTW (see Hernan et al., 2002; Robins et al., 2000). Specifically, the bias induced by observed baseline and time-varying confounders between treatment and outcomes can be removed by fitting a model that weights each subject i at time j by a weight consisting of the inverse of the predicted probability that a youth received the actual treatment history s/he received. More formally, we let L_ij denote the vector of both observed time-varying and baseline covariates for subject i at time period j (see section 2.4) and let L̄_ij and T̄_ij denote the i-th individual's covariate and treatment history up to time period j. In addition, we define T_ij to represent the categorical representation of which treatment individual i received between time point j-1 and j with T_ij = 1, 2, 3, or 4 if the individual received outpatient, residential, BDS only, or no treatment, respectively. Then, we define

$$S{W}_i\left(t\right)=\prod _{j=1}^t{P}_j(T_{ij}=k_{ij}\mid {\stackrel{‒}{T}}_{i,j-1})∕\prod _{j=1}^t{P}_j(T_{ij}=k_{ij}\mid {\stackrel{‒}{T}}_{i,j-1},{\stackrel{‒}{L}}_{ij})$$

as our IPT weight where k_ij equals numeric indicator for the level of treatment individual i received in period j, P_j(.) denotes the probability function for the j-th period.

We utilized generalized boosted models (GBM) to estimate P_j(T̄_ij|T̄_i.j–1, L̄_ij) and P_j(T_ij|T̄_i,j–1)for j=1,..,3 based on methods developed for comparisons involving more than two treatment groups (McCaffrey et al., 2013) since adolescents in our study are allowed to fall into one of four mutually exclusive classes at each follow-up visit. The weight estimation was implemented using the twang package in R (Burgette et al., 2013) and all outcome models were fit in R using the svyglm() command. Balance was assessed at each time point using the population standardize bias (PSB) which is defined, for each covariate, as the difference in means between a given treatment class and the overall analytic sample (population) divided by the overall analytic sample's standard deviation. Variables were considered sufficiently balanced if the PSB for each treatment class was less than 0.2 (McCaffrey et al., 2013).

It is important to note that our list of time-invariant and time-varying confounders used to estimate the IPTW were chosen prior to running our outcome models and included measures that were likely to be associated with both treatment assignment and our outcomes in the study. One of the key advantages of IPTW is that we are forced in a principled way to keep balance and outcome analyses separate. Thus, we only proceeded with outcome modeling once we had carefully examined balance and determined we had adequate IPTW to trust that our regression results would be robust to imbalances between our groups on the observed characteristics used in our IPTW.

2.7 Additional Analyses

For comparison, we also analyzed the data using three variations of the traditional regression model: unweighted models which only include the treatment group indicators (denoted as Model A), unweighted models which additionally control for baseline confounders (denoted as Model B), and unweighted models which control for both baseline and time-varying confounders (denoted as Model C). The simple unweighted model (Model A), which fails to adjust for any confounding, should produce biased results that favor the treatment conditions with less severe cases. Moreover, while Model B (unweighted model with baseline adjustment) can be implemented to account for differences in groups that exist prior to any treatment, it fails to account for choices made about future treatment based on outcomes exhibited from past treatments and thus results should be biased in similar directions as Model A. We expect bias in Model C to be in a similar direction to Model B and potentially more pronounced since it is generally an inappropriate way to model time-varying confounders.

2.8 Missing Data

Mean rates of missingness on items ranged from less than 1% to 27.1% with a mean of 13.4% across items at all of the follow-ups. Ten data sets were generated via multiple imputation to replace missing values using a sequential regression multivariate imputation algorithm (Raghunathan et al., 2002; Rubin, 1987; Schafer, 1997) and standard rules for combining analyses done on multiply imputed data sets were used to produce the final results (Rubin, 1987; Schafer, 1997). While missingness rates are higher at later waves and for some groups (such as minority youths relative to white youths), such differential response rates do not necessarily imply a violation of the missing at random (MAR) mechanism that was presumed for the imputation procedure, as MAR allows for the probability of missingness in one variable to depend on other observed characteristics.

3. RESULTS

3.1 Participant Characteristics

Table 1 shows the baseline characteristics of our analytic sample and clinical cut-points for the GAIN scales used in this analysis. As shown, 24% of the sample was female, 57% white, and the mean age was 16 years old. The level of substance use problems at baseline in the sample was relatively high with youth having a mean SFS of 16.0 with a standard deviation of 15.8 (scores above 12.6 on the scale indicate individuals who are likely to have significant difficult in stopping use without assistance; Dennis et al., 2010) and a mean SPS in the past month of 3.8 with a standard deviation of 4.2 (a score of 4 or more is suggestive of dependence; Dennis et al., 2010). Emotional problems in the sample were rather severe as well; mean EPS equaled 0.3 and standard deviation 0.2 (values greater than 0.14 indicate a high severity of issues that should be taken into account when treating; (Dennis et al., 2010). Finally, on average, youth in the sample had spent 14 out of the past 90 days in a controlled environment such as residential treatment settings, hospitals or jail prior to baseline (standard deviation equaled 24.6).

Table 1.

Baseline characteristics of the 2,870 youth in the analytic sample, summarized across the 10 imputed datasets used in the analysis.

Baseline Variable	Mean	SD	Range	Clinical Cut Pointsb
Female	24%	--	--	--
Race/ethnicity
White	57%	--	--	--
Black	17%	--	--	--
Hispanic	13%	--	--	--
Other	13%	--	--	--
Age	16.0			--
Substance Frequency Scale (past 90 days)	16.2	15.8	(0,78.8)	0 / 9-12 / 13-90
Substance Problem Scale (past month)	3.8	4.2	(0,16)	0 / 1-9 / 10-16
Substance Problem Scale (past year)	8.2	4.7	(0,16)	0 / 1-9 / 10-16
Emotional Problem Scale (past 90 days)	0.3	0.2	(0,1)	0-0.13 / 0.14-0.50 / 0.51-1
Days in a controlled environmenta	14.0	24.6	(0,90)	--

^aIncludes time spent in residential treatment settings, hospitals, or jail.

^bClinical cut points for Table 1 come from Dennis et al (2010).

3.2 Observed Treatment Patterns and Assessing Balance

Before applying weights, the groups of youth attending each treatment modality differed from each other at multiple time points in directions that would be expected (see Tables 2a and 2b). At each time point, youth receiving residential treatment tended to have more problematic substance use and emotional problems, as demonstrated by significantly higher mean values of earlier SFS, SPS, and EPS. Also, youth in the no treatment condition had significantly lower mean values of earlier SFS and SPS. There were also differences in past receipt of treatment. As to be expected, youth in residential treatment were significantly more likely to have received residential treatment in the past (e.g., 60% of youth in residential treatment modality between 3-and 6-months had been treated with residential treatment between baseline and 3-months versus 28% in the overall analytic sample). Conversely, youth in the no treatment group were significantly less likely to have been in a residential treatment facility at earlier times. At each time point, youth receiving BDS are similar with respect to these observed patient characteristics to the no treatment group.

Table 2a.

Unweighted means for baseline and time-varying confounders for each treatment group between 0 and 3 months and between 3 and 6 months relative to the population mean and standard deviation (SD).

	Treatment Group Between 0 and 3 Months
	Residential (N=798)	Outpatient (N=1560)	BDS only (N=356)	No Treatment (N=156)	Population Mean (SD)
Female	0.25	0.23	0.19	0.27	0.24 (0.42)
Race/ethnicity
White	0.48	0.66	0.41*	0.53	0.57 (0.50)
Black	0.17	0.15	0.26*	0.17	0.17 (0.38)
Hispanic	0.17	0.10	0.19	0.14	0.13 (0.34)
Other	0.18	0.09	0.15	0.16	0.13 (0.33)
Age	16.13	15.86	15.91	16.47*	15.97 (1.35)
Baseline SFS	0.28*	0.14*	0.16	0.11*	0.18 (0.18)
Baseline SPSm	5.54*	3.23	2.98	2.76*	3.81 (4.23)
Baseline SPSy	10.65*	7.32	7.33	5.92*	8.17 (4.66)
Baseline EPS	0.32*	0.24	0.25	0.22	0.26 (0.21)
Baseline days in controlled environment	20.77*	8.54*	18.26	23.34*	13.95 (24.59)
Mean dosagea of treatment (interquartile range)	45 (29, 65)	13 (5, 16)	7 (2, 8)	NA	NA

	Treatment Group Between 3 and 6 Months
	Residential (N=382)	Outpatient (N=717)	BDS only (N=909)	No Treatment (N=862)	Population Mean (SD)
Female	0.21	0.28	0.20	0.25	0.24 (0.42)
Race/ethnicity
White	0.51	0.61	0.55	0.58	0.57 (0.50)
Black	0.21	0.12	0.18	0.19	0.17 (0.38)
Hispanic	0.11	0.15	0.13	0.12	0.13 (0.34)
Other	0.17	0.12	0.13	0.10	0.13 (0.33)
Age	16.07	15.96	15.89	16.04	15.97 (1.35)
Baseline SFS	0.24*	0.19	0.16	0.16	0.18 (0.18)
Baseline SPSm	4.84*	4.00	3.48	3.56	3.81 (4.23)
Baseline SPSy	9.39*	8.75	7.88	7.44	8.17 (4.66)
Baseline EPS	0.30	0.28	0.24	0.25	0.26 (0.21)
Baseline days in controlled environment	16.88	13.45	14.92	12.03	13.95 (24.59)
SFS at 3 months	0.08	0.06	0.08	0.08	0.07 (0.11)
SPSm at 3 months	2.39	2.19	2.22	2.27	2.25 (3.36)
EPS at 3 months	0.29*	0.24	0.19	0.20	0.22 (0.19)
Days ctrl. envir. at 3 months	48.45*	17.12	16.60	11.29*	19.37 (29.07)
Treatment group at 3 months
No treatment	0.02	0.03	0.05	0.10	0.05 (0.23)
BDS only	0.07	0.08	0.18	0.12	0.12 (0.33)
Outpatient	0.31*	0.57	0.56	0.61	0.54 (0.50)
Residential	0.60*	0.32	0.21	0.17*	0.28 (0.45)
Mean dosagea of treatment (interquartile range)	54 (23, 90)	14 (5, 18)	7 (1, 8)	NA	NA

^*Denote if PSB comparing the group in question to the population was greater than 0.20.

^aDosage of treatment is measured in days for residential treatment and number of times for outpatient and BDS.

Table 2b.

Unweighted means for baseline and time-varying confounders for each treatment group between 6- and 9-months relative to the population mean and standard deviation (SD).

	Treatment Group Between 6 and 9-Months
	Residential (N= 246)	Outpatient (N= 263)	BDS only (N= 753)	No Treatment (N=1608)	Population Mean (SD)
Female	0.22	0.25	0.22	0.24	0.24 (0.42)
Race/ethnicity
White	0.53	0.58	0.53	0.60	0.57 (0.50)
Black	0.22	0.13	0.17	0.18	0.17 (0.38)
Hispanic	0.11	0.14	0.16	0.11	0.13 (0.34)
Other	0.14	0.15	0.14	0.11	0.13 (0.33)
Age	15.91	16.08	15.93	15.99	15.97 (1.35)
Baseline SFS	0.24*	0.19	0.18	0.16	0.18 (0.18)
Baseline SPSm	4.79*	3.96	3.81	3.54	3.81 (4.23)
Baseline SPSy	9.64*	8.20	8.73	7.45	8.17 (4.66)
Baseline EPS	0.29	0.28	0.27	0.24	0.26 (0.21)
Baseline days in controlled environment	17.81	19.65*	15.23	10.53	13.95 (24.59)
SFS at 3-months	0.07	0.07	0.07	0.08	0.07 (0.11)
SPSm at 3-months	2.29	2.35	2.37	2.14	2.25 (3.36)
EPS at 3-months	0.27*	0.24	0.22	0.20	0.22 (0.19)
Days ctrl. environ. at 3-months	44.12*	23.95	18.06	13.05*	19.37 (29.07)
SFS at 6-months	0.08	0.07	0.09	0.09	0.08 (0.13)
SPSm at 6-months	1.99	2.05	2.27	2.02	2.10 (3.35)
EPS at 6-months	0.27*	0.22	0.19	0.18	0.20 (0.18)
Days ctrl. environ. at 3-months	49.97*	16.31	11.12	8.50*	14.81 (28.44)
Treatment group at 3-months
No treatment	0.03	0.06	0.04	0.07	0.05 (0.23)
BDS only	0.08	0.10	0.15	0.12	0.12 (0.33)
Outpatient	0.37*	0.46	0.55	0.60	0.54 (0.50)
Residential	0.52*	0.38*	0.25	0.21	0.28 (0.45)
Treatment group at 6-months
No treatment	0.10*	0.12*	0.20*	0.47*	0.30 (0.46)
BDS only	0.15*	0.20*	0.47*	0.29	0.32 (0.47)
Outpatient	0.14*	0.50*	0.26	0.20	0.25 (0.43)
Residential	0.60*	0.18	0.08	0.05*	0.13 (0.34)
Mean dosage* of treatment (interquartile range)	51 (16, 90)	16 (4, 20)	6 (1, 7)	NA	NA

^*Denote if PSB comparing the group in question to the population was greater than 0.20.

^aDosage of treatment is measured in days for residential treatment and number of times for outpatient and BDS.

After weighting, the differences between youth receiving the different treatment types at each time point (Tables 2a and 2b) were all greatly attenuated. Figure 2 shows the maximum PSB before and after weighting at each time point. The maximum PSB prior to weighting ranges from 0.04 to 1.38 across the time points (consistent with Tables 2a and 2b). After weighting, the maximum PSB has gone below 0.16 in all cases, suggesting that the weighted treatment groups were very well balanced at each of the time points.

Figure 2.

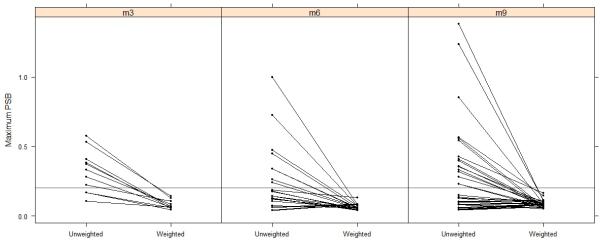
The maximum population standardized bias (PSB) before and after weighting at each time point. Blue lines denote covariates for which the maximum PSB across groups went down and red denote when the maximum PSB went up.

Tables 2a and 2b also show the mean dosage and interquartile range for each treatment condition during each 90 day interval for youth in that condition. As shown, youth receiving residential treatment had mean number of days equal to 45, 54, and 51 between the 0 and 3-month follow-ups, the 3- and 6-month follow-ups and the 6- and 9-month follow-ups, respectively. Youth in outpatient treatment had mean number of sessions equal to 13, 14, and 16 over the three 90-day intervals and youth in BDS had mean number of screenings equal to 7, 7, and 6, respectively.

3.3 Estimated Cumulative Effects

Table 3 shows the IPTW-weighted regression results for the substance use outcomes. For SFS, the IPTW model shows that each additional period in a residential facility yielded on average 1.6 less days of substance use (95% CI = −2.7, −0.07) relative to no residential treatment while each period of biological drug screening (with no additional outpatient or residential treatment) yielded 1.1 days less use (95% CI = −2.0, −0.3). For outpatient treatment, findings suggest that each period involving at least one outpatient treatment session yields a decrease of 0.9 days of use (95% CI = −1.8, 0.0). When compared to the IPTW weighted mean SFS for youth receiving no treatment in a given period (= 10.1 days of use), these correspond to 16%, 11%, and 9% decreases in use for each exposure to residential treatment, biological drug screening, or outpatient treatment, respectively. There was no evidence of significant differences in SPS for any of the three treatment modalities relative to no treatment.

Table 3.

Estimated impact of an additional episode of each treatment relative to no treatment based on IPT weighted regression versus traditional unweighted regression models. Model A is unadjusted and only includes the treatment group indicators; Model B adjusts for baseline confounders; Model C adjusts for baseline and time-varying confounders including previous treatment indicators.

	Traditional Unweighted Regression Models
	IPTW	Model A	Model B	Model C
Substance Frequency Scale at 12 months
BDS only	−1.1 (−2.0,−0.3)	−0.9 (−1.7,−0.2)	−1.1 (−1.8,−0.4)	−1.1 (−2.2,−0.1)
Outpatient	−0.9 (−1.8,0.0)	−1.2 (−1.9,−0.5)	−1.3 (−2.0,−0.6)	−1.7 (−3.1,−0.2)
Residential	−1.6 (−2.5,−0.7)	−1.0 (−1.7,−0.4)	−2.3 (−2.9,−1.6)	−4.0 (−5.7,−2.2)
Substance Problem Scale at 12 months
BDS only	−0.5 (−4.0,3.1)	−0.4 (−3.2,2.5)	−1.5 (−4.3,1.3)	−1.7 (−6.4,3.0)
Outpatient	−0.9 (−4.3,2.5)	−1.4 (−4.4,1.6)	−2.2 (−5.0,0.7)	−3.0 (−8.9,3.0)
Residential	−1.5 (−4.9,1.9)	2.6 (−0.3,5.4)	−3.3 (−6.3,−0.4)	−8.2 (−15.8,−0.7)

Table 3 also reveals interesting differences between the IPTW model and traditional regression fits, particularly with respect to SFS. Results from Model A, the unweighted and unadjusted model, actually align most closely with the IPTW model. However, it appears to underestimate the effect of residential treatment on SFS (estimated effect = -1.0; 95% CI =−1.7, −0.4); Model A, relative to the IPTW model, also overestimates the effect of outpatient treatment (estimated effect = −1.2; 95% CI = −1.9, −0.5). Models B and C yield very strong evidence in support of residential treatment facilities reducing SFS (Model B's estimates effect = −2.3; 95% CI = −2.9,−1.6 and Model C = −4.0; 95% CI = −5.7,−2.2) and also produce estimated effects of outpatient treatment that are larger than those from the IPTW model (Model B's estimates effect = −1.3; 95% CI = −2.0,−0.6 and Model C = −1.7; 95% CI = −3.1,−0.2). Findings for the BDS group – which appeared to have the smallest differences in patient characteristics relative to the no treatment group – are relatively stable across the models.

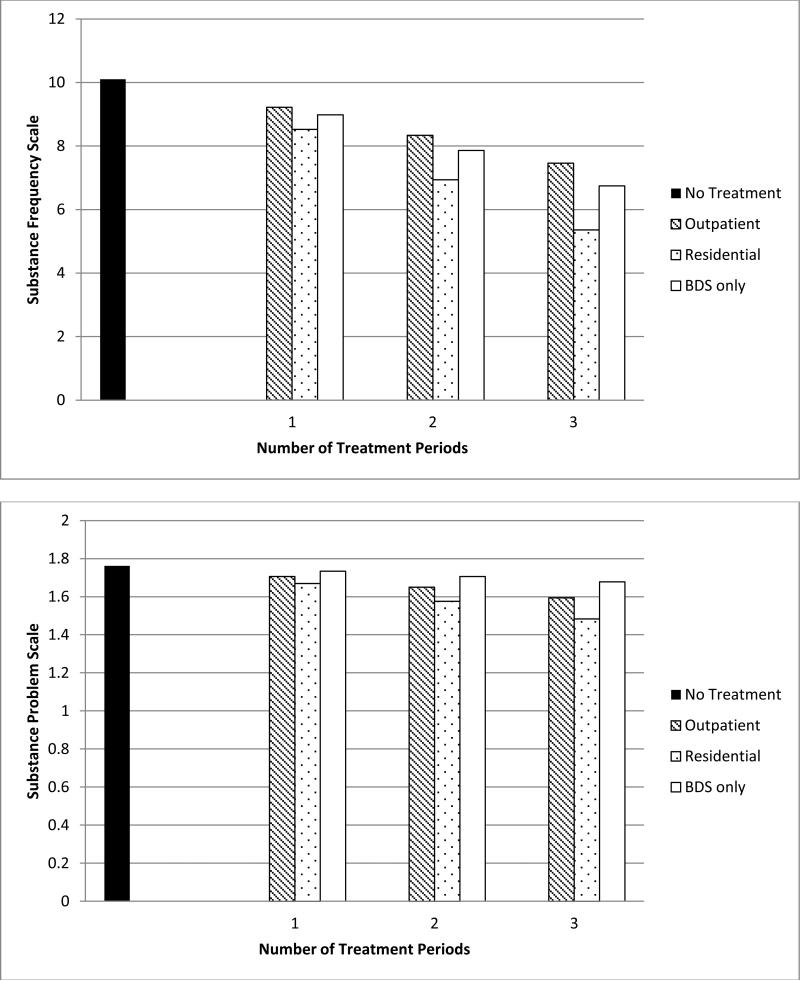
Figure 3 shows the recycled mean predictions from our regression models if we assume each youth in the analytic sample had no treatment during the course of the follow-up and increasing number of periods spent in outpatient, residential, and BDS only treatment conditions. As shown, youth who received no treatment during the course of the follow-up had the highest mean SFS and SPS at 12-months. Mean SFS and SPS decreased with each additional period spent receiving outpatient, residential, or BDS only, although the differences shown were only significant for SFS (see Table 3).

Figure 3.

Recycled mean predictions from IPTW regression models if each youth in the analytic sample had no treatment during the course of the follow-up and increasing number of periods spent in outpatient, residential, and BDS only treatment conditions.

4. DISCUSSION

This study provides preliminary evidence from a large sample of adolescents attending community-based substance abuse treatment programs that on average additional periods of residential treatment, outpatient treatment or monitoring with biological drug screening were associated with significant reductions in substance use frequency at one year. This is the first empirical evidence to suggest that residential treatment, outpatient treatment, and biological drug screening (absent of complementary outpatient or residential treatment services) each have cumulative effects for adolescent clients. On average, treatment delivered during each additional quarter was associated with at least a 10% decrease in substance use frequency at 12 months, suggesting that youth who stayed engaged in any of the treatments for all three quarters would have at least an estimated 30% decrease in 12-month substance use frequency.

The findings support adopting a ‘life course perspective’ on drug use that many in the field have already promoted (Dennis et al., 2004; Hser et al., 1998, 1997, 2007; Li et al., 2010; Maddux et al., 1994; Schell et al., 2005; Simpson and Joe, 1993) and which involves multiple treatment episodes that vary in approach and modality, and may include periods of no treatment at all. This does not imply that the extensive work being done to evaluate individual treatments is not useful nor that some youth might not benefit from a single treatment episode (Dennis et al., 2004; Hser et al., 2001; Hubbard et al., 1998; Hunter et al., 2012; Salomé et al., 2003; Tanner-Smith et al., 2013; Williams and Chang, 2000). Ideally, adolescents will be offered the most effective evidence-based treatment when they first initiate treatment, decreasing the need for subsequent treatment episodes. (Institute of Medicine (U.S.), 2006). However, our study findings suggest that we may be judging treatments too harshly if we do not find evidence of an acute effect because the effect will culminate with the next treatment episode. This finding is in line with the work of Li et al. (2010) on adults, and yields important information for those persons responsible for paying for adolescent substance use treatment.

Examining the selection effects reveals an expected story about adolescents who are enrolling in the different treatment conditions studied here. Specifically, we see that youth who enter residential treatment have the highest level of substance abuse at intake whereas those with the least severity end up not receiving treatment. The differences between the treatment groups over time help explain (in part) the differences in results seen between the IPTW regression and the more traditional regression adjustments shown in Table 3. The unweighted model underestimates the effect of residential treatment relative to no treatment because it does not take into account the fact that adolescents who are more severe are more likely to participate in residential treatment. Conversely, the traditional approach of using regression for adjustment overestimates the effects of residential treatment possibly because those models require more extrapolation beyond the data and do not adequately adjust for the group differences.

Our study relies on a relatively coarse measure of cumulative treatment, where treatment assignment is based on observational data collected at three month intervals over the course of a year. However, as shown in Tables 2a and 2b, the interquartile ranges for number of days spent in residential treatment over a 90-day period and the interquartile ranges for the number of outpatient sessions and number of biological screenings appear to suggest most youth received a non-trivial amount of treatment within each 90-day time period, although the total dose varied from one youth to the next. By defining treatment coarsely as “receipt of any treatment” over the 90-day period between the follow-up visits where the GAIN was administered, we enable our analysis to meaningfully control for time-varying confounders that measure how the youth are doing when they transition from one treatment to the next. More fine-tuned analyses with our data would require more complex modeling and assumptions about the representativeness of youth's severity between transitions in different treatment dosages that are beyond the scope of the current work. We hope that future research with less coarse data will build on these findings by applying the methods described in this paper to identify specific dosages and types of treatments and treatment combinations that yield the most improved outcomes. Administrative data from health plans are a potential source of such information, and have historically provided important insight into substance abuse treatment questions (Ray et al., 2007; Weisner et al., 2001). Alternatively, researchers who cannot follow patients prospectively can use retrospective approaches like the UCLA's Natural History Instrument (NHI; Anglin et al., 1993; Chou et al., 1996; Hser et al., 1992; McGlothlin et al., 1977), which Li et al. (2010) used in their application of MSMs with adults.

Although the resolution of our data may not be not be ideal, a unique strength of this study is that we observe adolescents not receiving treatment services since normally ethical constraints would bar the use of a no treatment condition. We take advantage of the longitudinal GAIN database where the majority of adolescents received treatment in the first three month period but may be untreated at later follow-ups. These periods without treatment allow us to estimate the cumulative effects of outpatient, residential, and biological drug screening treatment conditions. The MSM approach with IPTW used here provides evidence that on average, additional periods of treatment have effects that accumulate relative to no treatment. Subsequent work can extend these models (e.g., Structural Nested Means Models (Almirall et al., 2013a; Almirall et al., 2010)) and should seek to understand heterogeneity in this effect, to specifically identify the kids for whom additional treatment is better versus youth who may benefit from a single treatment episode or treatment augmented with an aftercare component.

This study has several limitations that must be taken into account when interpreting the results. First, treatment group definitions are based on self-report and – as described above – include very coarse definitions over a long interval of time. Misclassification of youth due to measurement error is possible. Anticipating the direction of potential bias from misclassification is difficult given the number of different ways a youth may be misclassified (e.g., on the one hand, we may have a youth reporting only BDS when in fact the youth had some unreported episodes of outpatient therapy during the 3-month period while on the other hand, we may have youth in the outpatient treatment arm who reported having gotten outpatient treatment but really only went once during the three month interval and primarily received BDS). Second, while IPTW helps in controlling for confounding from observed time-varying and baseline factors, unobserved differences between the time-varying treatment trajectories of these youth may explain our findings. The methods in our study are only robust if we have no lingering confounding from unobserved covariates which is not something we can directly test. Finally, the presented models estimate the average effect of each additional period of treatment and thereby assume that each additional period of a given treatment condition has a constant, additive effect. While this appears to be a reasonable assumption with our data, it is also possible that the effects of additional periods of treatment might be more dynamic (e.g., may decline in magnitude over time or increase and then plateau). Future work should more carefully examine the type of dynamics that might exist for the effectiveness of repeated episodes of the same type of treatment.

Despite these limitations, this study provides important, preliminary evidence that treatment effects accumulate over time for adolescents, suggesting that more treatment is consistently better than no treatment for a group of adolescent substance users. Moreover, this study provides a meaningful application of MSM together with IPTW to draw inferences concerning the causal effects of cumulative treatment episodes. Researchers should consider utilizing these statistical techniques when analyzing data on longitudinal trajectories of substance abuse treatment to reduce the impact of time-varying confounders in biasing study findings. We hope that this work highlights how longitudinal databases – coupled with proper analytical methods –can add to the evidence-base for cumulative effects of treatment and encourages future longitudinal data collection efforts.