Modeling the dispersion in electromechanically coupled myocardium

SUMMARY

We present an approach to model the dispersion of fiber and sheet orientations in the myocardium. By utilizing structure parameters, an existing orthotropic and invariant-based constitutive model developed to describe the passive behavior of the myocardium is augmented. Two dispersion parameters are fitted to experimentally observed angular dispersion data of the myocardial tissue. Computations are performed on a unit myocardium tissue cube and on a slice of the left ventricle indicating that the dispersion parameter has an effect on the myocardial deformation and stress development. The use of fiber dispersions relating to a pathological myocardium had a rather big effect. The final example represents an ellipsoidal model of the left ventricle indicating the influence of fiber and sheet dispersions upon contraction over a cardiac cycle. Although only a minor shift in the pressure–volume (PV) loops between the cases with no dispersions and with fiber and sheet dispersions for a healthy myocardium was observed, a remarkably different behavior is obtained with a fiber dispersion relating to a diseased myocardium. In future simulations, this dispersion model for myocardial tissue may advantageously be used together with models of, for example, growth and remodeling of various cardiac diseases.

1. INTRODUCTION

The left ventricle (LV) is the main pumping chamber of the heart supplying blood through the circulatory system to the entire body. The LV builds up the necessary pressure by active contraction where the electrical activation of the heart triggers a cascade of events leading to a shortening of the cardiac myocytes. Myocytes are arranged in a highly organized fashion, following a right-handed helical pathway from the endocardium toward the mid-wall and a left-handed helical pathway from the mid-wall toward the epicardium [1-3]. This prevailing myocyte orientation is usually referred to as ‘fiber orientation’. In addition, fiber bundles are arranged into laminar sheets of four to six cell layers, where the prevailing sheet orientation also varies in the transmural and apico-basal directions [3-6]. At any point in the LV, the structural arrangement of myocytes is reflected by three orthogonal directions along which both electrical and mechanical material parameters are different, thus requiring to model the electrical and mechanical responses of the myocardium as an orthotropic material. These preferred directions are along the fibers, transverse to the fibers but within a laminar sheet and perpendicular to the sheets; these directions are thus called the fiber, sheet, and sheet-normal directions, respectively.

In a healthy heart, the fiber alignment follows very closely this helical structure with only small angular dispersion (AD) in the range of ~ 12–15^°, whereas in a diseased heart such as hypertrophic cardiomyopathy (HCM) or myocardial infarction, AD may locally increase by ~ 65% (at foci points within the septal wall) [7-9] or ~ 50% (at the site of infarction) [10-12]. Furthermore, the dispersion of the fibers has been shown to have a circular distribution, they are not located in plane [13]. Less is known about the structural arrangement of laminae. Because of the importance of sheet orientation in myocardial wall thickening, it has been speculated that the dispersion of sheet orientations may play a significant physiological role [14]. There are a few studies available discussing the quite large dispersion of the sheet structure, even in healthy hearts [15-17]. Although to our knowledge there are no experimental reports available that quantify sheet dispersion in the diseased myocardium, it is likely the case that dispersion is also elevated when compared with healthy conditions. To the authors’ knowledge, there are no recently published biomechanical cardiac models available that consider dispersion, the latest are [2, 9]; none of them include sheet dispersion. Hence, the present study focuses on the development of an approach to model fiber and sheet dispersions using an invariant-based framework. A previously published orthotropic and invariant-based model, which characterizes the nonlinear passive behavior of myocardium [18], is here augmented with structure parameters allowing the quantification of the degree of dispersion based on measured fiber and sheet angle data. The structure parameters are based on a distribution function developed for the collagen structure of arteries [19], and is here used for the fiber and sheet dispersions.

Cardiac simulations have electrical and mechanical components rendering the modeling to a multi-physics problem. Electromechanical models need high spatiotemporal resolution, making the entire problem computationally expensive; advanced numerics and highly optimized parallel implementations are needed to keep simulations tractable. Therefore, a natural choice is the use of overlapping grids of different resolution because the constraints differ significantly between the imposed physics of the electrical and mechanical problems. The electrical transients are fast, acting on time scales in the microsecond range, which translates into steep depolarization wavefronts of small spatial extent in the sub-millimeter range, thus requiring the use of fine spatial resolutions << 250 μm to compute solutions with reasonable accuracy. On the other hand, mechanical processes tend to occur at larger space and slower time scales, and, thus, coarser spatial discretizations can be used. The electromechanical coupling of the spatiotemporal patterns of the electrical activity and the active stress transients in the myocytes are either modeled as active stresses or strains [20] acting along the fiber’s orientation in an Eulerian description [21]. The resulting mechanical deformations in our model is largely determined by the passive hyperelastic properties of the tissue and the generated active stresses both incorporating the dispersed structure of the tissue.

Our simulation indicates that the dispersion has a relevant influence on the mechanical response of the myocardium both during passive deformation and active contraction, by reducing the stress response and changing the deformation pattern. When including the dispersion parameter in a ventricular simulation incorporating electrical activation, the pressure–volume (PV) loop is considerably altered. Because the degree of dispersion is significantly elevated under various cardiac pathologies there is a need to consider dispersion when modeling myocardial tissue in diseased states.

2. MODELING FRAMEWORK

2.1. Kinematics

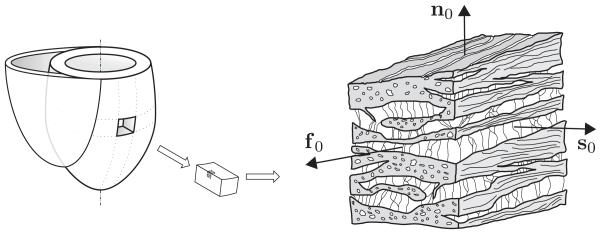
The structure of the myocardium may be described by three orthogonal direction vectors f₀, s₀, and n₀ corresponding to the mean fiber, sheet, and sheet-normal directions, respectively, in the Lagrangian description (Figure 1). In a continuum setting, this fiber and sheet direction vectors are considered as averaged quantities over several fibers and sheets.

Figure 1.

Schematic representation of the structure of the myocardium showing the fiber-reinforced laminar composite that comprises the averaged fiber, sheet, and sheet-normal directions in a continuum model, characterized by f₀, s₀, and n₀, respectively.

The isochoric Eulerian counterpart of these direction vectors are given by the relations $\overline{f}=J^{-1∕3}{\mathbf{Ff}}_0$, $\overline{s}=J^{-1∕3}{\mathbf{Fs}}_0$ and $\overline{n}=J^{-1∕3}{\mathbf{Fn}}_0$, where F is the deformation gradient, and J = detF > 0 is the volume ratio. The displacement field u between the two points X and x at time t is given by u = x − X(x, t). The circular dispersion of the fiber and sheet direction vectors around their mean orientations may be modeled using the structure tensors

$${\mathbf{H}}_{\mathrm{f}}={\kappa }_{\mathrm{f}}\mathbf{I}+(1-3{\kappa }_{\mathrm{f}}){\mathbf{f}}_0\otimes {\mathbf{f}}_0,{\mathbf{H}}_{\mathrm{s}}={\kappa }_{\mathrm{s}}\mathbf{I}+(1-3{\kappa }_{\mathrm{s}}){\mathbf{s}}_0\otimes {\mathbf{s}}_0,$$ (1)

$${\stackrel{‒}{\mathbf{h}}}_{\mathrm{f}}={\kappa }_{\mathrm{f}}\stackrel{‒}{\mathbf{b}}+(1-3{\kappa }_{\mathrm{f}})\stackrel{‒}{\mathbf{f}}\otimes \stackrel{‒}{\mathbf{f}},{\stackrel{‒}{\mathbf{h}}}_{\mathrm{s}}={\kappa }_{\mathrm{s}}\stackrel{‒}{\mathbf{b}}+(1-3{\kappa }_{\mathrm{s}})\stackrel{‒}{\mathbf{s}}\otimes \stackrel{‒}{\mathbf{s}},$$ (2)

as similarly described in [19], where H_i are Lagrangian structure tensors and ${\stackrel{‒}{h}}_i=J^{-2∕3}{\mathbf{FH}}_i{\mathbf{F}}^{\mathrm{T}}$ are isochoric Eulerian structure tensors, where i ∈ {f, s} correlates to the fiber and sheet directions. The second-order identity tensor is denoted by I while the modified isochoric left Cauchy Green tensor is denoted by $\stackrel{‒}{b}=J^{-2∕3}{\mathbf{FF}}^{\mathrm{T}}$.

The formulation of the dispersion parameters κ_i is described in detail in [19]. Briefly, the range of valid values for κ_i are ∈ [0, 1/3], where κ_i = 0 means perfect alignment and κ_i = 1/3 means isotropy. A formulation of κ_i may be derived through the probability density function (PDF) ρ_i(Θ), using the relation

$${\kappa }_i=\frac{1}{4}{\int }_0^{\pi }{\rho }_i\left(ϴ\right){\sin }^3ϴ\mathrm{d}ϴ$$ (3)

where, Θ is the distribution angle centered around, Θ = 0. We assume that the fiber and sheet dispersions follow a transversely isotropic and standard π-periodic von Mises distribution, which is modified in order to satisfy the normalization condition [19,22]. The PDF is, thus, given by

$$\rho \left(ϴ\right)=4\sqrt{\frac{b_{\rho }}{2\pi }}\frac{\exp \left\{b_{\rho }\right[\cos \left(2ϴ\right)+1\left]\right\}}{\mathrm{erfi}\left(\sqrt{2b_{\rho }}\right)}$$ (4)

where b_ρ is a concentration parameter and erfi(x)=−i erf(x) denotes an imaginary error function. The function ρ(Θ) is the standard π-periodic von Mises PDF, normalized by

$$\frac{1}{4\pi }{\int }_{\omega }\rho \left(ϴ\right)\mathrm{d}\omega =1$$ (5)

where ω is the unit sphere.

The values for κ_i may thus be fitted to the histograms of the dispersion of fiber and sheet angles for the myocardial tissue. To fit the PDF (4) to histogram data (fiber angles), the fiber angle Θ is shifted to $\stackrel{‒}{ϴ}$ to center around, Θ = 0° (the bar on the Θ variable denotes the shifted value), and the maximum likelihood method in MATLAB, that is, mle(), is used together with a custom function describing Equation (4). The parameter b_ρ is thus retrieved with a 95% confidence interval, and by using (3), the parameters κ_i are obtained. The one-to-one relation between the concentration parameter b_ρ and the dispersion parameter κ_i is discussed in detail in [19,22], where it is shown that κ → 1/3 as b_ρ → 0 and κ → 0 as b_ρ → ∞.

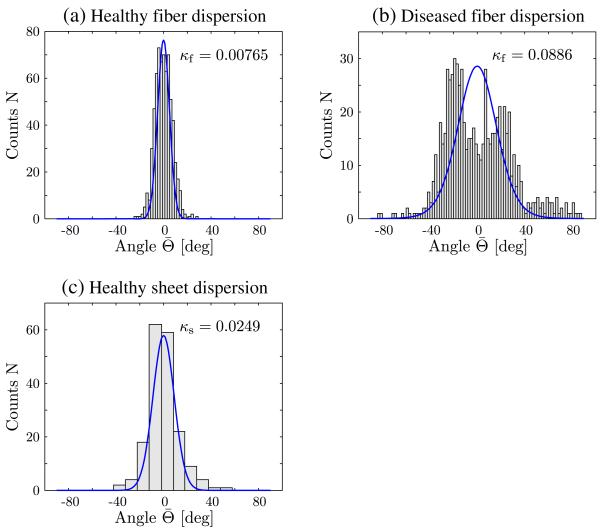
The fit of the PDF to the fiber dispersion is shown in Figure 2 for both a healthy myocardial tissue (see Figure 2(a)), and a diseased tissue (see Figure 2(b)), where the dispersion data were adapted from [7]. The fit of the PDF to the sheet dispersion is only shown for a healthy sub-epicardium (see Figure 2(c)), where the dispersion data were adapted from [16]. To the authors’ knowledge, the structure of sheet orientations in a diseased myocardium has never been investigated. The fitting produced the dispersion parameters κ_f = 0.00765 and κ_s = 0.0249 for the healthy myocardial tissue and κ_f = 0.0886 for the diseased tissue; compare with Figure 2.

Figure 2.

Fit of histogram data for fiber and sheet dispersions adapted from [7, 16], (a) fiber dispersion in a healthy tissue (κ_f = 0.00765); (b) fiber dispersion in a diseased tissue (κ_f = 0.0886); and (c) sheet dispersion in a healthy tissue (κ_s = 0.0249).

In the proposed framework, the dispersion parameters for the fiber and sheet directions are uncoupled, and we assume that the mean orientation of these directions are kept orthogonal. Furthermore, the dispersion of the sheet-normal direction is not considered; it is excluded to match the strain-energy function developed in [18], as shown in Section 2.2.

2.2. Constitutive relations

The anisotropy, generated by the preferred directions of the material (Figure 1), can be modeled by using the isochoric invariants ${\stackrel{‒}{I}}_{4\mathrm{f}}={\mathbf{f}}_0\cdot {\overline{C}f}_0$, ${\stackrel{‒}{I}}_{4\mathrm{s}}={\mathbf{s}}_0\cdot {\overline{C}s}_0$ and ${\stackrel{‒}{I}}_{4\mathrm{n}}={\mathbf{n}}_0\cdot {\overline{C}n}_0$, where $\overline{C}=J^{-2∕3}\mathbf{C}$ is the modified right Cauchy–Green tensor, and C = F^TF denotes the right Cauchy–Green tensor [23].

By using the first invariant of $\overline{C}$, namely, ${\stackrel{‒}{I}}_1=\overline{C}:\mathbf{I}$, we may define the two modified invariants ${\stackrel{‒}{I}}_{4\mathrm{f}}^{\ast }$ and ${\stackrel{‒}{I}}_{4\mathrm{s}}^{\ast }$ as a linear combination of ${\stackrel{‒}{I}}_1$, ${\stackrel{‒}{I}}_{4\mathrm{f}}$ and ${\stackrel{‒}{I}}_{4\mathrm{s}}$. Thus,

$${\stackrel{‒}{I}}_{4i}^{\ast }={\kappa }_i{\stackrel{‒}{I}}_1+(1-3{\kappa }_i){\stackrel{‒}{I}}_{4i},i\in \{\mathrm{f},\mathrm{s}\}$$ (6)

similar to [19, 22, 24]. To characterize the orthotropic behavior of the myocardium, we modify the strain-energy function suggested by Holzapfel & Ogden [18] by writing

$$\Psi =U\left(J\right)+{\overline{\Psi }}_{\mathrm{p}}({\stackrel{‒}{I}}_1,{\stackrel{‒}{I}}_{4\mathrm{f}}^{\ast },{\stackrel{‒}{I}}_{4\mathrm{s}}^{\ast },{\stackrel{‒}{I}}_{8\mathrm{fs}})$$ (7)

where ${\stackrel{‒}{I}}_{8\mathrm{fs}}={\mathbf{f}}_0\cdot {\overline{C}s}_0$ is the modified invariant which couples f₀ with s₀, U is a volumetric function, and ${\overline{\Psi }}_{\mathrm{p}}$ is an isochoric strain-energy function describing the passive behavior of the myocardium. For the volumetric function, we use

$$U\left(J\right)=\frac{{\mu }_{\mathrm{K}}}{2}{\left(\ln J\right)}^2$$ (8)

where μ_K serves as a user-specified penalty parameter. In an analogous manner to [18], the isochoric strain-energy function for the passive myocardium tissue is given by

$${\overline{\Psi }}_{\mathrm{p}}=\frac{a}{2b}\left\{\exp \right[b({\stackrel{‒}{I}}_1-3)]-1\}+\sum _{i=\mathrm{f},\mathrm{s}}\frac{a_i}{2b_i}\left\{\exp \left[b_i{({\stackrel{‒}{I}}_{4i}^{\ast }-1)}^2\right]-1\right\}+\frac{a_{\mathrm{fs}}}{2b_{\mathrm{fs}}}\left[\exp \right(b_{\mathrm{fs}}{\stackrel{‒}{I}}_{8\mathrm{fs}}^2)-1]$$ (9)

Note that in the limiting case, where κ_i = 0, the original model, as described in [18], is retrieved.

The material parameters needed in (8) and (9) are μ_K, a, b, a_{(f, s, fs)} and b_{(f, s, fs)} and the two dispersion parameters κ_f and κ_s. The passive Cauchy stress tensor is given by σ_p = 2J⁻¹ F(∂Ψ/∂C)F^T, and by using the notation

$${\overline{\psi }}_j=\frac{\partial {\overline{\Psi }}_{\mathrm{p}}}{\partial {\stackrel{‒}{I}}_j},j=1,8\mathrm{fs},{\overline{\psi }}_{4i}^{\ast }=\frac{\partial {\overline{\Psi }}_{\mathrm{p}}}{{\stackrel{‒}{I}}_{4i}^{\ast }},i=\mathrm{f},\mathrm{s}$$ (10)

this results into

$${\sigma }_{\mathrm{p}}=p_{\mathrm{h}}\mathbf{I}+2J^{-1}\left[{\overline{\psi }}_1\mathrm{dev}\stackrel{‒}{\mathbf{b}}+\sum _{i=\mathrm{f},\mathrm{s}}{\overline{\psi }}_{4i}^{\ast }\mathrm{dev}{\overline{\mathbf{h}}}_i+\frac{1}{2}{\overline{\psi }}_{8\mathrm{f}s}\mathrm{dev}(\stackrel{‒}{\mathbf{f}}\otimes \stackrel{‒}{\mathbf{s}}+\stackrel{‒}{\mathbf{s}}\otimes \stackrel{‒}{\mathbf{f}})\right]$$ (11)

where p_h = dU(J)/dJ is used, and dev(●) = (●) − (1/3)[(●) : I]I denotes the deviatoric operator in Eulerian [23].

The evolution of an active second Piola–Kirchhoff stress term S_a, which originates from [25], is given by

$$\frac{\partial S_{\mathrm{a}}}{\partial t}=∊\left(V_{\mathrm{m}}\right)(k_{S_{\mathrm{a}}}\Delta V_{\mathrm{m}}-S_{\mathrm{a}})$$ (12)

where ∊(V_m) is a delay function controlling the rate of activation and relaxation of _Sa. The parameter k_Sa regulates the amplitude of S_a, ΔV_m = V_m − V_r is the difference in the transmembrane potential, where V_m is the current action potential, and V_r is the myocyte resting potential. A smooth delay function ∊ = ∊(V_m), as proposed in [26], is used, which is given by

$$∊\left(V_{\mathrm{m}}\right)={∊}_0+({∊}_{\infty }-{∊}_0)\exp \{-\exp [-{\zeta }_{\mathrm{r}}(V_{\mathrm{m}}-V_{\mathrm{s}})\left]\right\}$$ (13)

where ∊₀ and ∊_∞ are the limiting values of the delay function when the action potential V_m is larger or lower than a given phase shift V_s. Further, the transition rate of the delay function is controlled by the parameter ∊_r. However, in contradiction to what is written in [26], the relation between the limiting values must follow ∊₀ > ∊_∞ in order to achieve the delay of peak active stress with respect to the upstroke of the action potential. An active second Piola–Kirchhoff stress tensor S_a is retrieved by introducing a dispersed structure tensor ${\widehat{H}}_{\mathrm{a}}$ a according to

$${\mathbf{S}}_{\mathrm{a}}=S_{\mathrm{a}}{\widehat{\mathbf{H}}}_{\mathrm{a}}$$ (14)

where

$${\widehat{\mathbf{H}}}_{\mathrm{a}}=\frac{{\kappa }_{\mathrm{f}}}{1-2{\kappa }_{\mathrm{f}}}{\mathbf{C}}^{-1}+\frac{1-3{\kappa }_{\mathrm{f}}}{1-2{\kappa }_{\mathrm{f}}}{I}_{4\mathrm{f}}^{-1}{\mathbf{f}}_0\otimes {\mathbf{f}}_0$$ (15)

with $I_{4\mathrm{f}}=J^{2∕3}{\stackrel{‒}{I}}_{4\mathrm{f}}$. The active Cauchy stress tensor σ_a a is now retrieved by the push-forward operation according to σ_a = J⁻¹FS_aF^T, which yields

$${\sigma }_{\mathrm{a}}=J^{-1}{S}_{\mathrm{a}}{\widehat{\mathbf{h}}}_{\mathrm{a}}$$ (16)

where

$${\widehat{\mathbf{h}}}_{\mathrm{a}}=\frac{{\kappa }_{\mathrm{f}}}{1-2{\kappa }_{\mathrm{f}}}\mathbf{I}+\frac{1-3{\kappa }_{\mathrm{f}}}{1-2{\kappa }_{\mathrm{f}}}\widehat{\mathbf{f}}\otimes \widehat{\mathbf{f}}$$ (17)

where $\widehat{f}=\mathbf{f}∕\mid \mathbf{f}\mid$ is the normalized fiber direction vector. The structure tensor (15) is formulated so that (17) may be seen as a normalization of (2)₁ where the length change of the mean fiber orientation does not affect the magnitude of the applied stress so that the condition $\widehat{f}\cdot {\widehat{h}}_{\mathrm{a}}\widehat{f}=1$ holds, which together ensures that (16) is a true Cauchy stress tensor. The Cauchy stress tensor σ is now simply given by the additive decomposition

$$\sigma ={\sigma }_{\mathrm{p}}+{\sigma }_{\mathrm{a}}$$ (18)

The elasticity tensors needed for implementing the passive stress σ_p in the finite element (FE) analysis program [27] have previously been shown in [19], and for the active stress σ_a, the elasticity tensor in the Lagrangian and the Eulerian descriptions is shown in the Appendix.

2.3. Modeling electromechanically coupled myocardial tissue

The computation of electrical activation and repolarization and their coupling to passive tissue mechanics is here briefly described. The spread of electrical activation and repolarization is described by a reaction–diffusion equation referred to as the mono-domain equation, given by

$$\beta C_{\mathrm{m}}\frac{\partial V_{\mathrm{m}}}{\partial t}+\beta I_{\text{ion}}(V_{\mathrm{m}},\eta )=\nabla \cdot ({\mathbf{g}}_{\mathrm{m}}\nabla V_{\mathrm{m}})+I_{\mathrm{tr}}$$ (19)

where β is the membrane surface to volume ratio, C_m is the membrane capacitance, V_m is the transmembrane potential, I_ion is the density of the total ionic current which is a function of V_m and a set of state variables η, I_tr is the transmembrane stimulus current, and g_m is the mono-domain conductivity tensor with the eigenaxes ζ = f along the fibers, ζ = s perpendicular to the fibers, but within a laminar sheet, and ζ = n is perpendicular to the sheets. No dispersion parameters are here included in the formulation of the electrical activation. The eigenvalues of g_m are chosen as the harmonic mean of the intracellular and interstitial conductivities, which renders the mono-domain equation axially equivalent to the more general bi-domain equation [28,29].

We employ the FEM for the spatial discretization of the mono-domain equation (19). A ventricular geometry is modeled using two overlapping FE meshes, a fully structured coarser hexahedral mesh for solving the mechanics and a fully unstructured hybrid mesh with an average resolution of ~200 μm, using an image-based mesh generation technique [30], as implemented in the commercial mesh generator Tarantula (CAE Software Solution, Eggenberg, Austria) for solving electrics. Fiber and sheet orientations are interpolated onto the barycenters of the FEs in both meshes. Both grids were partitioned for parallel execution using parMETIS [31]. By treating the diffusion terms implicitly and the reaction terms explicitly, the temporal discretization of the mono-domain equation relies on an implicit–explicit scheme, using the time step of 20 s. Blocked Jacobi pre-conditioner with an iterative conjugate gradient solver is used to solve the linear system in parallel, using an Incomplete LU (ILU(0)) factorization as a sub-block pre-conditioner [32].

The electrical and mechanical models are weakly coupled, that is, the solution of the electrical quantities (19) is calculated on a static mesh first, using the Cardiac Arrhythmia Research Package [33], which is built on top of the message passing interface-based library PETSc [32]. Numerical aspects of this approach have been described in detail elsewhere [34]. Relevant parameters, that is, V_m, required for computing the active stress transients are transferred to the integration points of the mechanical mesh and fed into a separate subsequent simulation of deformation and stress analysis using an FE analysis program [27].

In this study, however, the electrical quantities are either calculated according to (19), as is the case in the model of an LV, Section 3.5, or the transmembrane potential V_m is prescribed directly as an input to the mechanical deformation analysis.

3. REPRESENTATIVE NUMERICAL EXAMPLES

To illustrate the effect of the myocardial model considering dispersion, five representative numerical examples are carried out. In order to elucidate how the dispersion parameters κ_f and κ_s influence the myocardium model behavior, they are appropriately modified; for example, isotropic fiber distribution was considered while keeping a small dispersion in the sheet orientation and vice versa. Such relations between fiber and sheet dispersion are non-physiological but are used to provide more insight into the proposed model.

The five examples are as follows: (i) in Section 3.1, a unit cube of myocardial tissue is electrically activated to generate active tension. The influence of the dispersion on the mechanical deformation (stretch) is studied by varying the dispersion parameters κ_f and κ_s; (ii) a second example, see Section 3.2, aims to predict the influence of the dispersion on simple shear; (iii) an FE model of a cube of myocardial tissue is used in Section 3.3 to investigate the relative influence of electrically generated active stress in the presence of dispersion of the fiber orientation; (iv) in Section 3.4, a passive inflation experiment on a ventricular section is performed to study the transmural change in stress as a function of the altered dispersion parameters related to the fiber and sheet directions; and (v) an electromechanically coupled LV model is used in Section 3.5 to study the influence of fiber and sheet dispersions upon contraction on PV loops over a cardiac cycle where dispersion parameters are chosen to account for both healthy and pathological conditions.

The related numerical results were obtained by using mixed Q1/P0 displacement/pressure FEs.

3.1. Electrically activated cube with dispersion

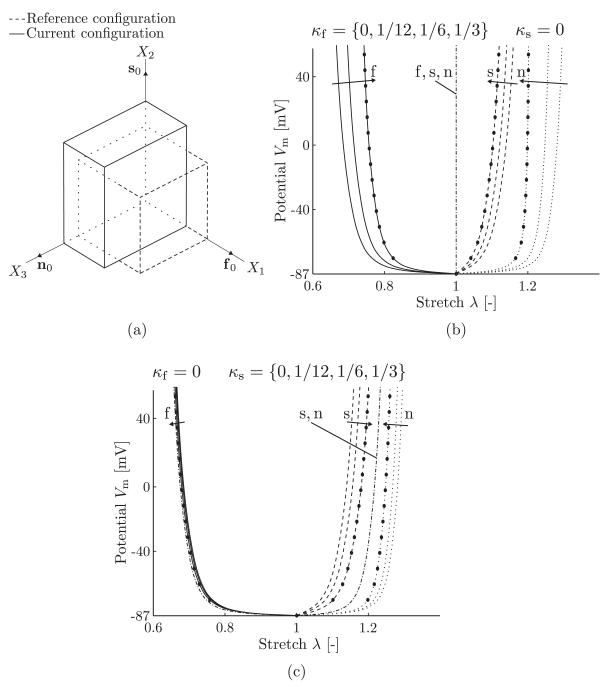
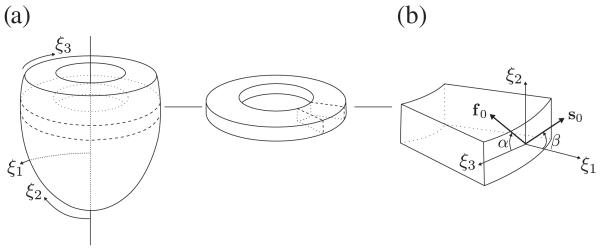
A unit myocardium tissue cube with mean material directions is considered. By introducing a global coordinate system (X₁, X₂, X₃), the material directions are according to [f₀] = [1, 0, 0]^T, [s₀] = [0, 1, 0]^T, and [n₀] = [0, 0, 1]^T. The cube is fixed against rigid body movement but can otherwise freely deform. The reference configuration of the cube is shown by the dashed lines in Figure 3(a). The cube is activated by increasing the transmembrane potential V_m generating a contraction in the fiber direction. The corresponding deformation gradient is given by F = diag(λ_f, λ_s, λ_n), where λ_f, λ_s and λ_n are the stretches in the fiber, sheet, and sheet-normal directions, respectively. Because the activation in the fiber direction leads to a contraction of the fiber, the stretches follow the relations λ_f < 1, λ_s > 1, and λ_n > 1. A deformed configuration (at V_m = 50 mV, with κ_f = κ_s = 0) is shown by the solid lines in Figure 3(a). The components of the Cauchy stress tensor σ = σ_p + σ_a can now be calculated from (11) and (16) by using J = 1. Thus,

$${\sigma }_{11}=p_{\mathrm{h}}+2\left[{\overline{\psi }}_1+{\overline{\psi }}_{4\mathrm{f}}^{\ast }(1-2{\kappa }_{\mathrm{f}})+{\overline{\psi }}_{4\mathrm{s}}^{\ast }{\kappa }_{\mathrm{s}}\right]{\lambda }_{\mathrm{f}}^2+S_{\mathrm{a}}$$ (20)

$${\sigma }_{22}=p_{\mathrm{h}}+2\left[{\overline{\psi }}_1+{\overline{\psi }}_{4\mathrm{f}}^{\ast }{\kappa }_{\mathrm{f}}+{\overline{\psi }}_{4\mathrm{s}}^{\ast }(1-2{\kappa }_{\mathrm{s}})\right]{\lambda }_{\mathrm{s}}^2+S_{\mathrm{a}}\frac{{\kappa }_{\mathrm{f}}}{1-2{\kappa }_{\mathrm{f}}}$$ (21)

$${\sigma }_{33}=p_{\mathrm{h}}+2\left({\overline{\psi }}_1+{\overline{\psi }}_{4\mathrm{f}}^{\ast }{\kappa }_{\mathrm{f}}+{\overline{\psi }}_{4\mathrm{s}}^{\ast }{\kappa }_{\mathrm{s}}\right){\lambda }_{\mathrm{n}}^2+S_{\mathrm{a}}\frac{{\kappa }_{\mathrm{f}}}{1-2{\kappa }_{\mathrm{f}}}$$ (22)

$${\sigma }_{12}={\sigma }_{13}={\sigma }_{23}=0$$ (23)

Because the cube can freely deform, the stress components σ₁₁, σ₂₂, and σ₃₃ are zero, and p_h may be determined by, for example, σ₃₃ = 0. The unknowns are the stretches λ_f, λ_s, and λ_n. By the use of the incompressibility condition λ_fλ_sλ_n = 1, the nonlinear system (20)–(22) can be solved with respect to λ_f, λ_s and λ_n by using the function fsolve() in MATLAB. The given values are the dispersion parameters κ_f and κ_s and the active stress S_a which is computed from the given transmembrane potential V_m.

Figure 3.

(a) Deformation of a unit cube when activated in the fiber direction; analytical results along the fiber, sheet, and sheet-normal directions using different values for the distribution parameters κ_f in (b) and κ_s in (c). The fiber, sheet, and sheet-normal responses are shown by solid, dashed, and dotted curves, respectively, and the circles show the finite element results for comparison reasons using either κ_f = 1/6, see (b), or κ_s = 1/6, see (c). Using the limiting case κ_f = 1/3 or κ_s = 1/3, the dash-dotted curves show the stretch responses for all three f, s, and n-directions, see (b), and for the s and n-directions, see (c).

With the material parameters from Table I and a linear increase in the transmembrane potential from V_m = V_r to V_m = +50 mV, the resulting stretches can be plotted as a function of the transmembrane potential V_m, see Figure 3(b,c) for different sets of the dispersion parameters κ_f and κ_s. The fiber, sheet, and sheet-normal responses are shown by solid, dashed, and dotted curves, respectively (the stretches in Figure 3 are abbreviated by λ). In addition, a comparison is shown with FE results obtained for the same model setup where κ_f = 1/6 in Figure 3(b) and κ_s = 1/6 in Figure 3(c) (the FE results are shown as circles). For the limiting case κ_f = 1/3, the active stress acts in all direction, and due to the incompressibility, the cube cannot deform, resulting in a straight line at λ = 1 for all directions, as shown by the dash-dotted line in Figure 3(b). For the limiting case κ_s = 1/3 (the sheet direction is isotropic), the stretch responses in the sheet and sheet-normal directions are shown by the dash-dotted curves in Figure 3(c). Note that the sheet and sheet-normal responses are indistinguishable. For κ_s = 1/3, the material model can be viewed as transversely isotropic.

Table I.

Material parameters used for both analytical and numerical calculations, except for the dispersion values of κ_f and κ_s, which are provided in the respective section. The material parameters for the passive tissue behavior are taken from [18], whereas the parameters for the active stress are taken from [25].

Passive stress
μK = 3333 kPa	a = 0.333 kPa	b = 9.242 (–)
	af = 18.535 kPa	bf = 15.972 (–)
	as = 2.564 kPa	bs = 10.446 (–)
	afs = 0.417 kPa	bfs = 11.602 (–)

Active stress
κSa = 0.50 kPa mV−1	Vr = −86.796 mV	Vs = −80.0 mV
∊0 = 1.0 ms−1	∊∞ = 0.1 ms−1	ζr = 0.1 mV−1

3.2. Influence of dispersion on simple shear

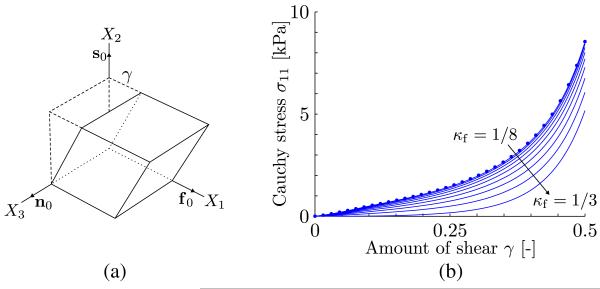
Consider the same unit myocardium tissue cube with the same material directions as formulated in the previous example but subjected to a simple shear deformation in the 21-plane caused by the deformation gradient F = I + γf₀ ⊗ s₀ (see Figure 4(a)). Thereby, γ denotes the amount of shear. In addition, let us consider a plane stress state throughout the myocardium tissue in the sense that the face of the cube normal to the direction n₀ is free of surface traction (σ₁₃ = σ₂₃ = σ₃₃ = 0). For that particular setup, the nonzero Cauchy stress components can be derived from (11) and (16). After some lengthy but straightforward computation, we obtain

$${\sigma }_{11}=2\left\{{\overline{\psi }}_1{\gamma }^2+{\overline{\psi }}_{4\mathrm{f}}^{\ast }[1+({\gamma }^2-3\left){\kappa }_{\mathrm{f}}\right]+{\overline{\psi }}_{4\mathrm{s}}^{\ast }(1-2{\kappa }_{\mathrm{s}}){\gamma }^2+{\overline{\psi }}_{8\mathrm{fs}}\gamma \right\}+S_{\mathrm{a}}\frac{1-3{\kappa }_{\mathrm{f}}}{1-2{\kappa }_{\mathrm{f}}}$$ (24)

$${\sigma }_{22}=2{\overline{\psi }}_{4\mathrm{s}}^{\ast }(1-3{\kappa }_{\mathrm{s}})$$ (25)

$${\sigma }_{12}={\sigma }_{21}=2\left[{\overline{\psi }}_1+{\overline{\psi }}_{4f}^{\ast }{\kappa }_{\mathrm{f}}+{\overline{\psi }}_{4\mathrm{s}}^{\ast }(1-2{\kappa }_{\mathrm{s}})\right]\gamma +\frac{1}{2}{\overline{\psi }}_{8\mathrm{fs}}$$ (26)

Note that although the applied active stress is dispersed along the fiber direction, there are no components of the active stress in the two other orthogonal directions (s₀ and n₀). The Cauchy stress σ₁₁ is shown in Figure 4(b) as a function of the amount of shear γ for values κ_f between 1/8 and 1/3 (isotropy). As can clearly be seen from the plots, an increased fiber dispersion decreases the Cauchy stress σ₁₁. In this example, the active stress is zero in the reference configuration and increases with the increase of shear. Also here, a comparison is shown with FE results (the circles in Figure 4(b)) where κ_f = 1/8.

Figure 4.

(a) Simple shear deformation of a unit cube with the deformation gradient F = I + γf₀ ⊗ s₀; (b) Cauchy stress σ₁₁ versus the amount of shear γ for values κ_f between 1/8 and 1/3. The show FE results for comparison reasons using κ_f = 1/8.

3.3. Influence of myocyte dispersion on the mechanical tissue response

The influence of the myocyte dispersion on the mechanical tissue response is shown in a purely numerical example by using the same unit myocardium tissue cube (with 10 mm size) as in the previous examples. The cube is discretized by 10 × 10 × 10 FEs with fixed displacement boundary conditions in all DOF on the faces of the cube at X₂ = 0 and X₂ = 10 mm.

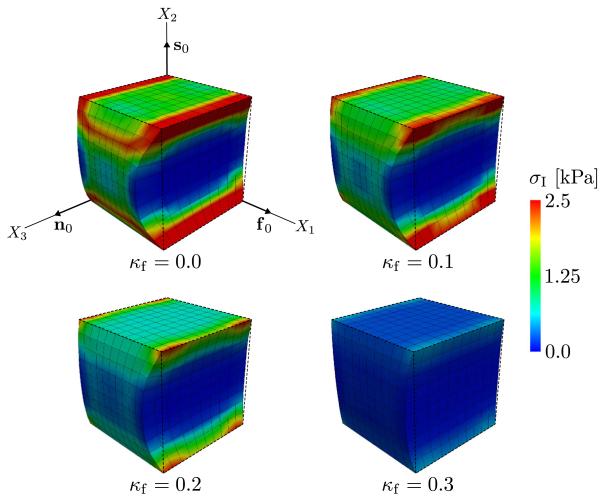
The dispersion parameter κ_s was set to zero. Four different values for κ_f are used (0, 0.1, 0.2, 0.3) while keeping κ_s constant. The cube is activated by a potential of V_m = +30 mV, and the corresponding first principal stress σ_I is shown in Figure 5. As can be seen in the figure, an increase in the κ_f-value toward isotropy lowers the value of σ_I and also decreases the contraction in the fiber direction. This is because of the increased dispersion of the fiber direction, which leads to an increase in active stress components along the X₂-direction and X₃-direction and because of the incompressibility of the material, which reduces the influence of the active stress in the fiber direction in that particular example. Thus, this example illustrates the influence dispersion has on the active stress tensor σ_a and the resulting contraction in the material.

Figure 5.

Cube of myocardial tissue subjected to an active stress corresponding to a potential of +30 mV with the dispersion parameters κ_f = {0, 0.1, 0.2, 0.3} and κ_s = 0. The images illustrate the corresponding first principal stress σ_I.

3.4. Passive inflation of a ventricular section

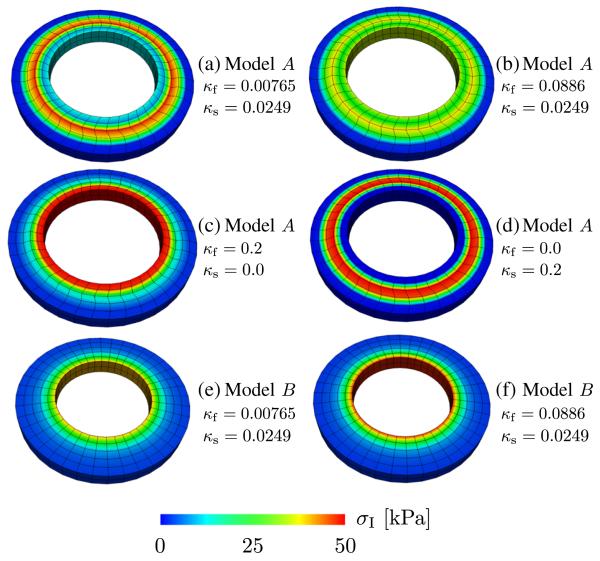
A left ventricular slice model is generated by approximating the cross section of the LV by a cylinder, as illustrated in Figure 6(a). Two models, say A and B, of the same geometry but with different fiber and sheet arrangements are created. In model A, the average fiber angle α varies from +60° to −60° and the average sheet angle β varies from +85° to −85° transmurally from the epicardium to the endocardium, where the fiber and sheet angles α and β are defined in Figure 6(b). In Model B, the fiber and sheet angles are assumed to be zero. The slice geometry is meshed with 400 hexahedral FEs, which are fixed against translation in the ξ₂-direction at the cut surfaces and in the ξ₃-direction at the epicardial border to hinder rigid body movements. No electrical stimulus was applied, that is, the tissue remained electrically quiescent, and thus no active stresses were generated. Instead, the slice is passively inflated by applying a pressure load of 100 mmHg to the endocardial surface in 200 incremental load steps of equal size. The influence of the dispersion parameters κ_f and κ_s on the distribution of the first principal stress σ_I is investigated by either using the dispersion parameters for healthy and diseased tissues, as provided in Figure 2, or by using the dispersion parameters κ_f = 0.2 (strongly dispersed) and κ_s = 0 (perfect alignment), and vice versa.

Figure 6.

(a) Coordinate system of the left ventricle model and a section of the left ventricle; (b) average fiber orientation defined by the angle α in the (ξ₂, ξ₃)-plane, and average sheet orientation defined by the angle β in the (ξ₁, ξ₂)-plane. The arrows point in the positive directions of the angles.

In Figure 7, the resulting first principal Cauchy stress σ_I at the applied pressure load of 100 mmHg is shown for different dispersion parameters. Figure 7(a) shows the stress distribution by using the dispersion parameters for a healthy myocardium resulting in a band of higher stresses in the middle region of the myocardium. This band is noticeably reduced by using the dispersion parameters for the fibers related to a diseased myocardium, as shown in Figure 7(b). Instead, stresses are more spread out radially, and at the endocardial border, stresses are higher relative to the setup of Figure 7(a). This suggests that the fiber dispersion alone induces a radial stress gradient where the highest stresses arise at the inner wall, as commonly seen in, for example, pressurized thickwalled isotropic tubes. This is exactly the case when using aligned sheets and a pronounced fiber dispersion, as can be seen in Figure 7(c). In the opposite case, that is, with fiber alignment and a pronounced sheet dispersion, there is an increased stress gradient visible in the middle region of the myocardium, as seen in Figure 7(d).

Figure 7.

Distribution of the first principal stress σ_I at applied pressure load of 100 mmHg in a section of a ventricular model. Models A and B pertain to different fiber and sheet-orientations; Model A: −60° ≤ α ≤ +60° and −85° ≤ β ≤ +85°; Model B: α = β = 0 (α and β denote fiber and sheet angles, respectively, as defined in Figure 6(b)). For some dispersion parameters, see Figure 2.

For the sake of comparison, for model B, the first principal Cauchy stress σ_I at 100 mmHg was computed, and the related results are shown in the Figure 7(e,f) for two sets of dispersion parameters. For the case of a higher dispersion parameter κ_f (relates to a diseased myocardium), the first principal Cauchy stress is slightly higher at the endocardial border. This effect is not so pronounced when comparing Figure 7(a) with (b). It is also clear that the symmetric fiber and sheet angles, used in model A, contribute to the increased mid-myocardial stresses.

3.5. Left ventricle model indicating the influence of fiber and sheet dispersions upon contraction

To study the influence of fiber and sheet dispersions upon contraction over a cardiac cycle, an ellipsoidal model of the LV was constructed; the dimensions correlate with a rabbit LV [35]. The coordinates of the LV are described in prolate spheroidal coordinates with the axes ξ₁, ξ₂, and ξ₃, pointing in the radial, longitudinal, and circumferential directions, respectively. The coordinate system is illustrated in Figure 6(a). The arrangements of the fibers and the sheets correspond to model A, as described in Section 3.4. Pressure boundary conditions, as imposed by the ventricular deformation and the response of the vascular system, are applied on the endocardial surface. The pressure p in the cavity is governed as follows:

1. Non-physiological initial phase with linear pressure increases starting from p = 0 to the end diastolic pressure (EDP) (p = 20 mmHg).

2. Isochoric LV compression phase, p increases from EDP up to 95 mmHg.

3. Ejection phase where the PV relationship is governed by a Windkessel model, that is,

   $$C\frac{\mathrm{d}p}{\mathrm{d}t}+\frac{p}{R}=-\frac{\mathrm{d}V}{\mathrm{d}t}$$ (27)

   until reversed blood flow.

4. Isochoric LV relaxation phase, p drops down to 12.5 mmHg.

5. Filling phase with linear pressure increases to EDP.

In steps (2) and (4), the pressure p is computed using the iterative relation p_n+1 = p_n + (V_n+1 − V_n)/C_p to keep the cavitary volume V of the LV constant, where C_p serves as a penalty parameter [36]. In step (3), where a two-element Windkessel model is used, the parameters C and R relate to the arterial compliance and the resistance, respectively. The values for C and R are chosen to generate PV loops that match with experimental data of rabbits [37]. Parameters required for calculating the pressure are the following: C = 0.2 ml mmHg⁻¹, R = 700 mmHg ms ml⁻¹, and C_p = −900 ml mmHg⁻¹. The parameters used to describe both active and passive mechanical behaviors of the model are summarized in Table I, except for κ_f and κ_s which correspond to the dispersion parameters given in Figure 2. The mechanical boundary conditions for the LV are described in Table II. The mesh consists of 5310 hexahedral (mixed) FEs used to solve the mechanics and of 1,201,507 linear hybrid FEs to solve the electrics [38]. The model by Mahajan et al. [39] is employed to describe cellular dynamics, where the system of ODEs is solved using the Rush–Larsen algorithm [40] with several optimizations [41]. The model was initialized by pacing a single cell at a pacing cycle length of 350 ms until a stable limit cycle was observed.

Table II.

Mechanical boundary conditions (BCs) for the left ventricle in terms of the prescribed traction t, where t_n is a component of t normal to the endocardial surface on which the pressure p acts and the displacement u with components u_ξ1, u_ξ2, u_ξ3 in the direction of the coordinates given in Figure 6(a).

BCs	Coordinates		Description
tn = −p	ξ1 = ξ1 min	For all ξ2, ξ3	Endocardial surface
uξ2 = 0	ξ2 = ξ2max	For all ξ1, ξ3	Basal surface
uξ3 = 0	ξ1 = ξ1 max	For all ξ3	Outer boundary at the base surface
	ξ2 = ξ2max

The state vector η at the end of this pre-pacing procedure was used to populate the LV model with an initial state vector η₀. Transmembrane current injection applied to the endocardial surface at t = 0 ms initiated the propagation of the action potentials at the endocardium to approximate a predominantly transmural activation sequence, as induced by activation via the Purkinje system. In this approximation, the whole endocardium was activated synchronously, electrical activation delays within the endocardium remained unaccounted for. We simulated 350 ms of activity to cover one depolarization and repolarization cycle over the entire LV. The spread of the electrical activation and repolarization is modeled using Equation (19).

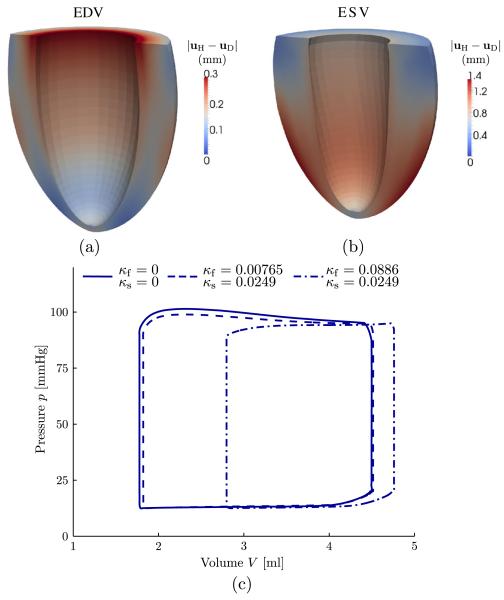
By using the dispersion parameters that relate to the healthy and the diseased tissue, as seen in Figure 2, the resulting deformations are quite different. This is illustrated at both the end diastolic volume and the end systolic volume, as shown in the Figure 8(a,b), respectively. Thereby, the distribution of the magnitude of the difference |u_H − u_D| between the displacements is shown (H stands for healthy tissue and = diseased). The resulting PV loops obtained from the simulations for different sets of dispersion parameters are shown in Figure 8(c); also, the case for no dispersion is illustrated (κ_f = κ_s = 0). Although only a minor shift in the PV loops between the cases with no dispersions and with fiber and sheet dispersions for a healthy myocardium was observed, a remarkably different behavior is obtained with a fiber dispersion κ_f relating to a diseased myocardium; thereby, the end diastolic and systolic volumes are much larger.

Figure 8.

Magnitude of the difference |u_H − u_D| between the displacements (H stands for healthy tissue and D for diseased) for (a) the end diastolic volume (EDV) and (b) the end systolic volume (ESV). (c) Pressure–volume loops for different sets of dispersion parameters κ_f and κ_s.

4. DISCUSSION

There are several reports in the literature, which provide evidence for the presence of dispersion in the fiber and sheet orientations in myocardial tissues. Under healthy conditions, dispersion is rather mild, but under certain pathologies such as HCM [13, 42, 43], dispersion can be quite pronounced. In the vast majority of modeling studies, however, dispersion and its influence upon the mechanical response of the myocardium has been largely ignored. In this study, a mechanical model of myocardial tissue has been proposed, which explicitly accounts for the dispersion of fibers and sheets. By changing two scalar (dispersion) parameters, introduced as κ_f and κ_s, the dispersion along the fiber and the sheet direction can be steered independently, thus allowing mechanistic investigations of pathological changes. The independence of the fiber and sheet directions is a reasonable approximation, despite the microstructural interaction. An approach that couples the fiber and sheet orientations is feasible; however, specific data are missing. The dispersion parameters κ_f, κ_s determine the blend between the isotropy (characterized by the invariant I₁) and the transverse isotropy (characterized by the invariants I_4f, I_4s). Thus, together, they give a dispersed orthotropic structure response where an increased dispersion leads to a more isotropic active and passive mechanical response.

The analytical and numerical examples investigated in this study suggest that dispersion may be an important factor in cardiac electromechanics. The increase in the dispersion along the fiber direction showed the most striking effect. This is illustrated in, for example, Figure 5 where the increase in the dispersion reduces contraction and the first principal stress. The enforced incompressibility condition is responsible for this reduced contraction, as can be seen from the analytical expressions (20)–(22) and (24)–(26). From a physiological point of view, there is also an interpretation. As the dispersion increases, the orientation of myocytes, which are responsible for active contraction, becomes more evenly distributed. When dispersion is large enough, there is no preferred myocyte orientation anymore. This would entail an isotropic contraction, which is, however, impossible without altering the volume. Moreover, besides distributing the direction of active contraction, fiber dispersion also has a major impact on the passive myocardial response. This is illustrated in Figure 7(a)–(c) where the fiber dispersion is increased in a ventricular slice model. During passive inflation of the slice, the first principal stress changes from being elevated in a mid-myocardial band for low fiber dispersion to being elevated at the endocardial border for high fiber dispersion. This shift is similar to what is commonly seen when inflating a thick-walled tube.

Although the effects of dispersion in the fiber direction on the mechanical myocardial response is more striking, numerical results indicate that increases in the sheet dispersion lead to significant alterations in the model behavior as well. The overall material response changes gradually from orthotropic toward transversely isotropic where the sheet response becomes indistinguishable from the sheet-normal response. This can be seen either in the analytical part of the first example discussed in Section 3.1, see equations (21) and (22), where κ_s = 1/3 gives identical expressions for the Cauchy stresses σ₂₂ and σ₃₃, or, alternatively, from Figure 3(c) where the behavior is identical along the sheet and sheet-normal directions. The difference in the passive stress response between a (nearly) transversely isotropic and an orthotropic material can be appreciated by comparing Figure 7(d) with Figure 7(a), where the stress in the middle region of the myocardium is even more elevated for the (nearly) transversely isotropic material. This large difference in the stress response also highlights the importance of the orthotropic structure as a factor that has to be considered when simulating ventricular electromechanical problems. Residual stresses, however, has not been included in the simulation, why the particular stress distribution, as shown in Figure 7, should not be considered as the true stress in a ventricle. It merely shows how the fiber and sheet dispersions affect the stress distribution.

Section 3.5 illustrates the numerical results for an electromechanically coupled model of the LV from a rabbit for a healthy and a pathological myocardium. Although the effects of using fiber and sheet dispersion parameters for the healthy myocardium were fairly minor, the use of fiber dispersions relating to a pathological myocardium had a rather big effect. As can be seen by comparing the PV loops in Figure 8(c), a significant shift of the entire PV loop toward larger end diastolic and end systolic LV cavity volumes occurred. Although the PV loops show that there is a difference in volume of the ventricular lumen, Figure 8(a,b) also illustrate that the remaining ventricular wall undergoes different patterns of deformation when using different dispersion parameters.

In summary, our modeling results identified the fiber and sheet dispersions as important determinants for the electromechanics of the myocardium. Distributed fiber and sheet orientations should be considered for more reliable predictions of, for example, stress, deformation, and volume change, in particular when compared with experimental data obtained from a pathological myocardium.

Limitations of the study

Because of the lack of structural data of pathological myocardium, it is difficult to find suitable comparisons on which we may validate our approach. Therefore, we have focused on the description of the dispersion model and have attempted to show the related mechanisms. Once adequate structural data exist, future work is needed to validate and modify the model if necessary.

The fit of the histogram data to the PDF assumes a bell-shaped data distribution. This may not be suitable in pathological cases with increased fiber dispersion. As shown in Figure 2(b), which displays the fiber dispersion of an HCM-diseased tissue, there may exist two predominant myocyte orientations in the region of interest. It is certainly possible to retrieve individual dispersion parameters; however, the increased dispersion obtained from the HCM sample was only seen within small focal islands throughout the myocardial wall [7, 8]. To appropriately account for the bimodal distribution of orientations, higher spatial resolutions would be required than those commonly used within FE studies, including this study. Because the spatial extent of a single FE in the models used exceeds the size of a focal island in which increased dispersion can be found, we opted to only use one average direction that corresponds to a fit of the bell-shaped function over both predominant orientations.

In the LV model discussed in Section 3.5, the dispersion parameters corresponding to the tissue diseased by HCM were used throughout the entire LV wall. This is not a realistic assumption as the dispersion in the smaller focal islands seems only to be present at approximately 25% of the overall LV volume [7, 8]. Available data show sheet and fiber dispersions averaged over all islands found in a given ventricle, but no data on the spatial distribution and morphology of such islands are available. Therefore, simulation results show an overly diseased case that can be considered as a limiting case for the dispersion effects. However, the focus of this study is mainly on the description of the modeling procedure and the potential effects of fiber dispersion and not on the development of a model that strives for a perfect pathophysiological match for an HCM-diseased LV. In future higher resolution FE-modeling studies, dispersion parameters may easily be set to vary from FE to element; however, by considering the paucity of available data on the spatial dispersion variation, such a detailed investigation would appear to be premature. Experimental studies that characterize spatial and morphological aspects of the dispersion over the entire myocardium in health and disease are, therefore, of utmost need to provide a more solid basis for a more detailed study aiming to provide more specific predictions.

Because of the limited experimental data available, we were not able to use data from one species only. For example, it was necessary to retrieve the dispersion data from a rat myocardium [7, 16], whereas passive material parameters were retrieved from a porcine myocardium [44]. However, this limitation does not affect the qualitative conclusions drawn from using the proposed dispersed formulation for myocardium.

Furthermore, in the LV model, the parameters κ_f and κ_s affected only the mechanical response of the LV but not the electrical activation sequence because dispersion remained unaccounted for in the mono-domain equation. That is, the orthotropy in the propagation of the action potential in the LV model was governed by the mean orientation of the fibers and the sheets. A consideration of the dispersion in the electrical model would also reduce the orthotropy. However, the chosen activation sequence, which approximates a normal beat where the entire endocardium is activated almost simultaneously, leads to a strongly transmural activation where effects of electrical orthotropy are strongly attenuated. Under such conditions, the consequence of electrical dispersion is minor and can be neglected, particularly when considering the rather large uncertainty in the experimental reports on conductivity values, which vary up to 300% [45].

APPENDIX A: ELASTICITY TENSORS FOR THE ACTIVE STRESS

Using the definition M₀ := f₀ ⊗ f₀ and the abbreviation (15), (14) may be written as

$${\mathbf{S}}_{\mathrm{a}}=S_{\mathrm{a}}\left(\frac{{\kappa }_{\mathrm{f}}}{1-2{\kappa }_{\mathrm{f}}}{\mathbf{C}}^{-1}+\frac{1-3{\kappa }_{\mathrm{f}}}{1-2{\kappa }_{\mathrm{f}}}{I}_{4\mathrm{f}}^{-1}{\mathbf{M}}_0\right)$$ (28)

The Lagrangian elasticity tensor is given by ${ℂ}_a=2\partial {\mathbf{S}}_{\mathrm{a}}∕\partial \mathbf{C}$ which leads to

$${ℂ}_{\mathrm{a}}=2\frac{S_{\mathrm{a}}}{1-2{\kappa }_{\mathrm{f}}}\left[{\kappa }_{\mathrm{f}}\frac{\partial {\mathbf{C}}^{-1}}{\partial \mathbf{C}}+(1-3{\kappa }_{\mathrm{f}})\frac{\partial I_{4\mathrm{f}}^{-1}{\mathbf{M}}_0}{\partial \mathbf{C}}\right]$$ (29)

Using the derivative $\partial \left(I_{4\mathrm{f}}^{-1}{\mathbf{M}}_0\right)∕\partial \mathbf{C}=-I_{4\mathrm{f}}^{-2}{\mathbf{M}}_0\otimes {\mathbf{M}}_0$ (29) can be written as

$${ℂ}_{\mathrm{a}}=2\frac{S_{\mathrm{a}}}{1-2{\kappa }_{\mathrm{f}}}\left[{\kappa }_{\mathrm{f}}\frac{\partial {\mathbf{C}}^{-1}}{\partial \mathbf{C}}-(1-3{\kappa }_{\mathrm{f}})I_{4\mathrm{f}}^{-2}{\mathbf{M}}_0\otimes {\mathbf{M}}_0\right]$$ (30)

and by using the push-forward operation of ${ℂ}_{\mathrm{a}}$ according to ${\left[{ℂ}_{\mathrm{a}}\right]}_{abcd}=J^{-1}{F}_{aA}{F}_{bB}{F}_{cC}{F}_{dD}{\left[{ℂ}_{\mathrm{a}}\right]}_{ABCD}$, this leads to the Eulerian elasticity tensor

$${ℂ}_{\mathrm{a}}=-2\frac{S_{\mathrm{a}}}{J(1-2{\kappa }_{\mathrm{f}})}\left[{\kappa }_{\mathrm{f}}𝕀+(1-3{\kappa }_{\mathrm{f}})\widehat{\mathbf{M}}\otimes \widehat{\mathbf{M}}\right]$$ (31)

where the fourth-order identity tensor 𝕀, defined in index notation as ${\left[𝕀\right]}_{abcd}=({\delta }_{ac}{\delta }_{bd}+{\delta }_{ad}{\delta }_{cd})∕2$, is introduced from the push-forward relation $F_{aA}{F}_{bB}{F}_{cC}{F}_{dD}{[\partial ({\mathbf{C}}^{-1})∕\partial \mathbf{C}]}_{ABCD}=-{\left[𝕀\right]}_{abcd}$ and the definition $\widehat{M}≔\mathbf{F}{I}_{4\mathrm{f}}^{-1}{\mathbf{M}}_0{\mathbf{F}}^T=\widehat{f}\otimes \widehat{f}$ has been used.