Concert halls with strong lateral reflections enhance musical dynamics

Significance

The concert hall conveys orchestral sound to the listener through acoustic reflections from directions defined by the room geometry. When sound arrives from the sides of the head, binaural hearing emphasizes the same frequencies produced by higher orchestral-playing dynamics, thus enhancing perceived dynamic range. Many studies on room acoustics acknowledge the importance of such lateral reflections, but their contribution to the dynamic responsiveness of the hall has not yet been understood. Because dynamic expression is such a critical part of symphonic music, this phenomenon helps to explain the established success of shoebox-type concert halls.

Abstract

One of the most thrilling cultural experiences is to hear live symphony-orchestra music build up from a whispering passage to a monumental fortissimo. The impact of such a crescendo has been thought to depend only on the musicians’ skill, but here we show that interactions between the concert-hall acoustics and listeners’ hearing also play a major role in musical dynamics. These interactions contribute to the shoebox-type concert hall’s established success, but little prior research has been devoted to dynamic expression in this three-part transmission chain as a complete system. More forceful orchestral playing disproportionately excites high frequency harmonics more than those near the note’s fundamental. This effect results in not only more sound energy, but also a different tone color. The concert hall transmits this sound, and the room geometry defines from which directions acoustic reflections arrive at the listener. Binaural directional hearing emphasizes high frequencies more when sound arrives from the sides of the head rather than from the median plane. Simultaneously, these same frequencies are emphasized by higher orchestral-playing dynamics. When the room geometry provides reflections from these directions, the perceived dynamic range is enhanced. Current room-acoustic evaluation methods assume linear behavior and thus neglect this effect. The hypothesis presented here is that the auditory excitation by reflections is emphasized with an orchestra forte most in concert halls with strong lateral reflections. The enhanced dynamic range provides an explanation for the success of rectangularly shaped concert-hall geometry.

Symphony-orchestra performance can be the most profound and moving experience of art and culture (1). When the performers are skilled and the environment is right, orchestral music can lead to sheer excitement and goosebumps: music-induced frisson (2). A key ingredient in this experience is the dynamic expression of the music (3, 4), which correlates with musical preference (5). The use of varying loudness to convey musical meaning (or expression) is an obvious component of the most popular and most-played classical compositions, such as Beethoven’s Ninth Symphony (1824). Imagine if all of the notes were delivered at the same monotonous level and color; the impact would be utterly lost. With all its nuances, music performance is transmitted to the listeners via the acoustics of a concert hall. The dynamic response of individual instruments alone has been studied (6–8), but the effect of the orchestral dynamics in concert halls is unexplored, even though the literature suggests that the hall has a prominent effect on the dynamics experienced by the listener. This article binds together orchestra dynamics, room acoustics, and auditory excitation to formulate the dynamic response of concert halls, which explains the differences in dynamics in different concert halls.

Current room-acoustic analysis methods are based on inspection of the energy in room impulse responses at frequency bands, as proposed by the applicable standard (9). The standard considers concert-hall acoustics as a linear system; therefore, the objective dynamic range of the sound does not depend on the acoustics of the room, which is only a linear amplification. Nevertheless, many studies in the literature point out that the sound in rooms is subjectively perceived in a nonlinear way. Beranek has characterized this effect as the hall supporting both quiet and powerful dynamics: “listening is enhanced immeasurably by the dynamic response of the concert hall” (ref. 10, p. 509). Meyer has stated that the quality of forte is a sign of an acoustically good hall, whereas sound in quiet dynamics can be acceptable in otherwise poor halls as well (ref. 8, p. 199). Importantly, these remarks not only suggest a nonlinear effect but also connect responsiveness of the hall to dynamics and subjective preference.

Dynamic expression in Classical and Romantic orchestra music originated in the 1750s from the Mannheim School, just as concert halls were developing as specialized rooms. Historically, concerts took place in spaces composers were familiar with, and they could tailor their compositions to the venue for the greatest musical effect. Many early music rooms were found spaces, and even when they were constructed specifically for music, many factors other than acoustics drove the design: e.g., structural technology, capacity, and sight lines. Only toward the end of the Western Classical music period were acoustic principles beginning to be scientifically understood and documented with the publication of Lord Rayleigh’s treatise, The Theory of Sound, in 1896 (11). Despite the lack of knowledge on room acoustics at the time, it was evident that rectangular rooms were appropriate. The shoebox-shaped Altes Gewandhaus in Leipzig was completed in 1781 and became a model for many halls to come (12). Such halls include the Musikvereinssaal in Vienna (opened 1870), Concertgebouw in Amsterdam (opened 1888), and Symphony Hall in Boston (opened 1900), and they are still widely considered to be the best venues for Western Classical and Romantic music (10). Strong lateral reflections to the listener are typical for rectangular rooms with exposed sidewalls and capacities up to about 2,200 persons, as in the halls discussed here. Psychoacoustic studies with simplified acoustic models have revealed that such reflections are beneficial: e.g., for apparent source width, envelopment (13–15), quality of bass, and preference (15). We show here that these lateral reflections also enhance the dynamic expression of the music.

Enhancement of dynamic expression is not evident from examination of either the orchestra or hall alone. However, it becomes clear when the interaction between these two, and the third component of the chain, the listener, is examined as a complete system. A key feature of the human listener is the particular geometry of the head and ears. As reflected sound travels to the eardrums, it is filtered by diffraction around, and reflections from, the head, shoulders, and outer ears depending on its incident direction. For lateral reflections, this directional filter enhances the same frequencies that are emphasized in the higher orchestral-playing dynamics. As will be shown here, shoebox halls provide strong lateral reflections from these directions, thus enhancing the dynamic expression of the music, which explains their historical success. An understanding of this effect has also led to some effective modern designs that deviate from the shoebox form but still provide lateral early reflections (16).

The responsiveness of a concert hall to dynamics can be traced to the interaction of three factors: the characteristics of the orchestra sound, the reflections provided by the room, and the directional sensitivity of hearing. In this article, the combined effect of these factors is quantified as binaural dynamic responsiveness (BDR). The hypothesis is that lateral early reflections, such as those that occur in historically successful shoebox halls and some modern designs, increase the hall’s responsiveness to orchestral dynamics due to the interaction between orchestral spectral excitation, spatial sound transmission, and emphasized high-frequency content in directional hearing.

Analysis

Before formulating and quantifying binaural dynamic responsiveness, analysis of each of the three contributing factors is provided. These elements correspond to the three elements of the transmission chain: source, the orchestra; path, the room; and receiver, a listener.

Sound of the Orchestra.

In the realm of dynamics, the orchestra sound involves crucial effects related to the harmonic structure of the sound. A natural effect with higher playing dynamics is the perceived intensification of the instrument sound. An important phenomenon is the nonlinear change in the overall spectral shape. For most orchestra instruments, more higher harmonics are excited with a more forceful playing style. Typically the emphasis at higher harmonics is strongest with brass instruments. This effect is well-known, and it has been demonstrated for individual instruments in a number of studies (6, 8). Meyer (ref. 8, p. 315) has presented an octave-band analysis of orchestra performance during a crescendo (20 bars from Bruckner’s Symphony No. 9) in a concert hall. However, a precise overall dynamic spectral change for a full orchestra is not found in the literature.

The character of spectral changes with orchestra dynamics can be demonstrated. Here, the analysis is based on a manually segmented corpus of commercially released orchestra recordings and anechoic measurements of individual orchestra instruments. Commercially released orchestra recordings are an illustrative case, but cannot be applied to concert halls without qualification, due to the unknown influence of postproduction processes. The conclusions drawn from such recordings are therefore tested against anechoic measurements of individual orchestra instruments, and previous analyses (6, 8).

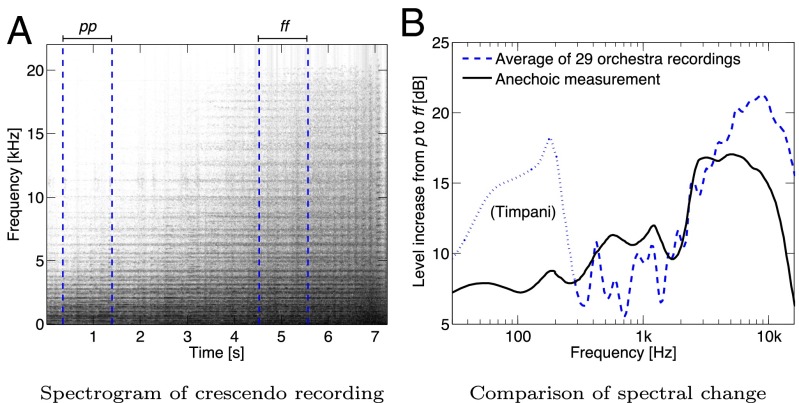
First, analysis of the spectrum of an orchestra playing in two different dynamics is performed using publicly released recordings of orchestral music. For this purpose, the pitch of the played notes should not change much with the dynamics. A suitable passage is found, for instance, near the beginning of the third movement of Bruckner’s Symphony No. 4, bars 19–26. There, a prominent crescendo is played with nearly constant pitches throughout the score. The spectral data were gathered by segmenting the respective bars of the Bruckner passage manually from 29 different recordings dating between the 1950s and 2010s. Using a wide selection of recordings minimizes the effect of any one postproduction process that may have resulted in artificially enhanced dynamics. Fig. 1A shows a spectrogram of eight bars of tutti crescendo. Two segments in opposing dynamics are marked with dashed lines. The example spectrogram indicates a clear increase in high frequency harmonics along the crescendo. By subtracting the piano spectrum from the forte spectrum, the nonlinear excitation is evident. The result of this subtraction averaged over the segmented recordings is shown in Fig. 1B as a dashed line. The subtraction reveals an increase at middle frequencies (400–2,000 Hz) of ∼7 dB and more than 15 dB above 2 kHz. The low-frequency emphasis in the orchestra recordings is most likely due to an overwhelmingly intensifying timpani tremolo in B♭2 (116 Hz) and its principal modes.

Fig. 1.

Analysis of the orchestra spectrum with regard to the playing dynamics. (A) Spectrogram from a publicly released orchestra recording with a crescendo. Darker shades indicates more sound energy. (B) Comparison of one-third octave smoothed frequency responses from anechoic recordings with regard to dynamics. The solid line is the difference between p and ff. The dashed line shows the mean difference between the segments marked in A, averaged over the respective passages in 29 recordings.

In the second analysis, the spectrum of the radiated sound energy in two instructed dynamics (p, and ff) is calculated from anechoic orchestra-instrument measurements (17). Two octaves of A-major triads were recorded from each instrument. Therefore, the playing dynamics are captured equally for all instruments. The dynamic spectrum of a full orchestra is obtained by summing the individual instruments’ spectra. These spectra are weighted according to the respective numbers of nonpercussive instruments in a typical symphony orchestra. The difference between p and ff is shown as a solid line in Fig. 1B. The analysis uses power-response data averaged from measurements evenly around the instruments (17). In contrast, the microphones in commercial recordings are commonly located in the principal region of radiation. On average, the orchestra recordings in the first analysis exhibit a stronger dynamic effect at the high frequencies than the anechoic power-response data. Nonetheless, the disproportionate emphasis of high frequencies with high dynamics with the full orchestra is indisputable. The overall results are in agreement with an earlier study on the generic orchestra spectrum in octave bands (18).

The Effect of Lateral Reflections.

In modern times, performance venues are often designed to replicate the sound quality of the famed classic halls, but are also subject to demands for larger audiences and alternative seating configurations. Larger audiences preclude copying the small spaces where classical music originated, structural technology allows larger and more flexible spaces than before, and new hall typologies, such as the vineyard-style hall, offer an enhanced social experience. With no precedents for these new developments, extensive research has been dedicated to extracting the acoustic characteristics of older halls that sound good, in order to build halls with new forms, or on different scales, with the same acoustic characteristics. With this aim, several objective characteristics have been identified as important, namely: strength (G), reverberation time (RT), and clarity (C₈₀). As pertains to the current investigation, lateral energy fraction (LEF) and binaural quality index (BQI) [interaural cross-correlation (1-IACC)] are measures of the lateral reflections in the sound field. The former is the ratio of lateral to on-axis sound energy in the sound field. The latter rests on the assumption that sound from in front of the listener is correlated between the ears, and sound arriving from the sides is not; therefore, interaural cross-correlation decreases with increasing lateral reflection energy.

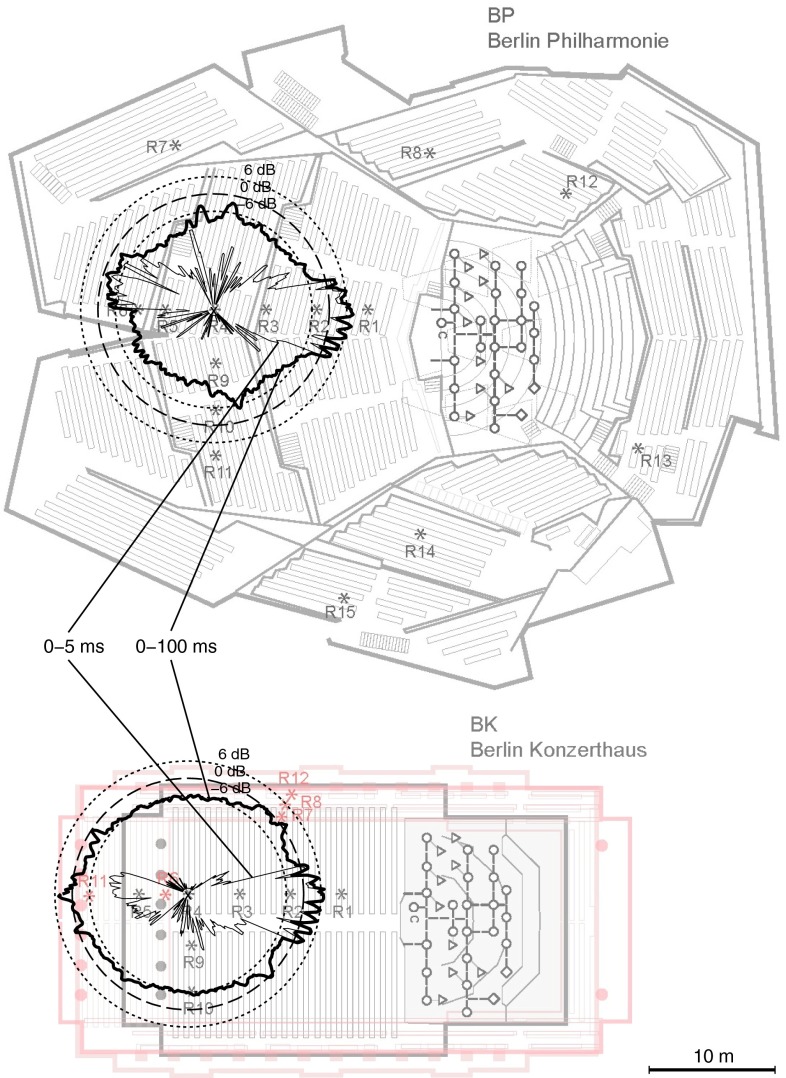
It is generally acknowledged in the field that lateral reflections are an important component of concert-hall acoustics. The presence and strength of lateral reflections depend upon the geometry of the performance venue. Among the three most common concert-hall geometries—shoebox, fan-shaped, and vineyard—shoebox halls provide the strongest. The plots in Fig. 2 illustrate the development of the spatial sound field at 19 m distance from the stage, overlaid on the floor plans of two prominent halls. These figures were generated using a recently developed spatiotemporal sound-field analysis technique (19). Marshall published the first research to emphasize the importance of lateral reflections and their contributions to a sense of envelopment (20). He referred to halls with audible lateral reflections as having spatial responsiveness, a combination of loudness and envelopment.

Fig. 2.

Examples of spatiotemporal visualizations of the sound fields in two concert halls in Berlin: the Philharmonie and the Konzerthaus. Compared with Philharmonie, Konzerthaus provides strong lateral reflections in the early sound field due to the parallel side walls, typical for a shoebox shape.

The majority of prior room-acoustic research on spaciousness focuses on the subjective spatial impression only as a direct function of the lateral reflections in the impulse response. Effects of the lateral sound were closely studied by Barron and Marshall (13, 14), who showed, with experiments using variable reflection levels and delays, that a higher amount of early lateral energy increases the spatial impression. They also suggested that certain frequency bands in lateral reflections result in different spatial effects: namely, envelopment or source broadening. This finding was later confirmed by another study by Blauert and Lindemann (21). By experimenting with low pass- and high pass-filtered early reflections, they produced results showing that the broadening of auditory image occurs only if early lateral reflections contain frequencies above 3 kHz.

The contribution of lateral reflections to the spatial impression depends also on the overall sound level. However, this connection has been studied only scarcely. An early paper that advanced Marshall’s seminal work (20) on the combined effect of lateral sound and sound level was published by Keet (22). He proposed a connection between the terms spatial responsiveness and apparent source width (ASW), and presented listening-experiment results, showing a relationship between ASW and the absolute presentation level of the signal. A decade later, Kuhl (23) described experiments where orchestral music was played from a loudspeaker on six concert-hall stages at different sound levels. The results show a linear increase in the spatial impression when the sound level result is increased. More recently, Beranek has presented similar results (24).

Binaural room impulse-response measurements made with a mannequin head and in-ear microphones include the head-related effects. However, apart from studies with the interaural cross-correlation (IACC) measure, not many papers have linked other binaural measurements with concert hall acoustics. An approach using several binaural measures at once has been adopted: e.g., by Morimoto and Iida (25). They incorporated the combination of IACC with the binaural sound-pressure level for estimating ASW (25). Also, their findings with simulated wide-band reflections suggest that a spatial broadening effect occurs with either an increase in the sound level or a decrease in the interaural cross-correlation. Again, this result is in agreement with the findings by both Keet (22) and Kuhl (23).

One notable resemblance between many of the aforementioned studies is that the sound level in the subjective or objective experiments was varied artificially by adjusting the system gain (14, 22–26), or not varied at all (21, 27). Considering the degree of dynamic spectral effects with orchestral instruments, altering only the presentation level in subjective experiments does not correctly represent the variations naturally occurring in the source signal during a performance. Although these studies illustrate the importance of lateral reflections for the spatial and loudness benefits they provide, they fail to recognize that lateral reflections enhance dynamic range, as will be demonstrated here.

Directional Binaural Loudness.

It is a well-known effect that shading from the head, shapes of the pinnae, and reflections from the listener’s body cause alterations in the frequency content entering the ear canals, depending on the direction of the incident sound. The direction-dependent filter created by these effects is known as the head-related transfer function (HRTF). Among many other effects, a prominent one is the emphasis of the high frequencies at the ipsilateral ear. This information is applied to show higher binaural loudness in concert-hall geometries that provide lateral early reflections, such as classic shoebox designs (15, 28).

Next, the phenomenon of increased binaural loudness over frequencies is visualized with the HRTF measurements obtained from the database by the Center for Image Processing and Integrated Computing (CIPIC) (29). The binaural spectral response is calculated as a function of frequency ω and two angles in the spherical coordinate system θ and ϕ (28, 30):

where, for the left ear, the average HRTF is obtained as the average over 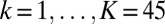subjects

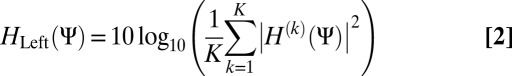and 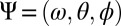denotes the variables. For the right ear, the procedure is identical. The above equation uses the binaural gain factor of g = 6 dB (30).

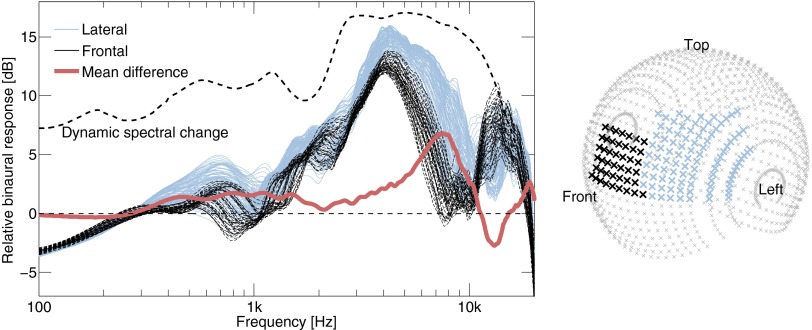
Fig. 3 compares the average binaural spectral response for frontal and lateral angles of incidence. In Fig. 3, Left, a set of curves for each frontal and lateral binaural response shows the average binaural frequency response of 45 subjects in the selected directions. The difference between the average frontal and lateral binaural frequency response is shown with a thick line. This line clearly indicates that the binaural response at high frequencies is higher for lateral incidence, as noted by Lokki and Pätynen (28). The largest dynamic spectral change of the orchestra is from 2 kHz to above 10 kHz. At the same frequency band, the binaural gain for sound arriving from the side is ∼1–5 dB higher compared with the frontal direction. Therefore, the shape of the dynamic spectral change of the orchestra sound (from Fig. 1B) follows closely the overall binaural frequency spectrum.

Fig. 3.

Comparison of the binaural response at the frontal and lateral directions using the mean of the CIPIC HRTF database. (Left) Binaural response in selected angles with the difference between the average response in frontal and lateral regions. The curve for dynamic spectral change is the same as in Fig. 1B. (Right) Regions for frontal and lateral angles in the CIPIC measurement angles.

Binaural Dynamic Responsiveness

These three factors—orchestral dynamics, lateral reflections, and directional binaural response—act in unison to produce enhanced dynamic expression in Western classical music. This effect can be quantified as binaural dynamic responsiveness. The main hypothesis in this paper is that, depending on the acoustics in rooms, changes in source-signal dynamics cause a different range of spectral auditory excitation. Here, the principle of calculating binaural excitation for a source signal is formulated, before application to concert-hall measurements.

Theory.

Binaural dynamic responsiveness combines data on the orchestra playing dynamics and binaural concert-hall measurements. First, the left- and right-ear binaural signals are calculated by convolving the anechoic source signal x with the measured binaural impulse responses 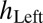and 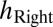. Because the hypothesis considers only frequency domain, convolutions can be substituted by the multiplication of spectra in the frequency domain. The spectrum for dynamics d is 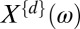, and the respective spectrum of the left ear from a binaural impulse response is 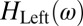. Combination of the source and room response spectra in the left ear yields

Frequency notation ω is omitted in the following for brevity.

Second, the actual excitation pattern of the ear is estimated by applying an auditory model to the frequency spectrum 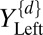. Several models for the auditory excitation exist. Here, a function by Moore and Glasberg (31) for modeling auditory masking is applied for calculating the effect of a complex spectrum. In short, the function is a model for the middle and inner ear, and it estimates the excitation pattern for the arbitrary spectrum by calculating the mutual effect of auditory filters to the input signal. The excitation function is denoted by 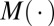, and the one-ear excitation for dynamics d is given by

Third, the excitation function considers left and right ears independently. Therefore, Eq. 1 for binaural loudness is applied here to combine the excitation in two ears (30):

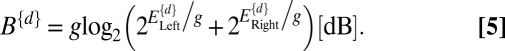This equation yields the total binaural spectral excitation 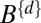for an orchestra spectrum in dynamics d in a receiving position. According to the original hypothesis, the difference in the binaural excitation between low and high orchestra dynamics, 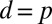and 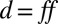, respectively, is expected to be different depending on the compared acoustic conditions and :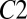

The inequality is explained by the binaural dynamic responsiveness.

It should be noted that the formulation employs magnitude spectra instead of complex spectra. Therefore, the presented approach corresponds to binaural excitation with a steady-state sound from the source, free from transients.

Experiment.

Binaural dynamic responsiveness was tested using acoustic measurements from unoccupied European concert halls. Binaural impulse responses h were measured with a mannequin head (Head and Torso Simulator; Brüel and Kjaer) at five equally spaced positions down an off-center line from 7 m to 23 m from the stage, positions R1 to R5, respectively. The source was a calibrated loudspeaker orchestra (32). See Supporting Information for complete details of the halls and measurements.

The results of the binaural dynamic responsiveness were calculated separately with, first, the direct sound (i.e., 5 ms beginning from the initial direct sound) and, second, the early sound (i.e., impulse response between 5 and 100 ms after the direct sound). The spatial response in two halls for these time intervals is illustrated in Fig. 2. Thus, the equation for average BDR from N measurement positions is

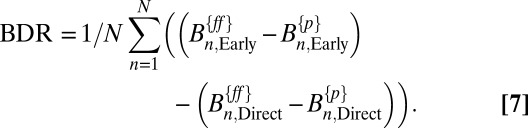This equation defines the binaural dynamic responsiveness more precisely because it separates the effect of the early part of the room impulse response from the direct sound. Therefore, the responsiveness takes into account how the room reacts to increased dynamics. The BDR is averaged in groups over rectangular and nonrectangular halls and also over three receiving positions at a time to analyze the effect of the hall geometry and distance to BDR. Because standards or reference values for BDR do not exist, the results are presented as differences in the binaural dynamic responsiveness. Differences in the BDR are generally small below 1 kHz. In quiet dynamics, the auditory-excitation formulas do not provide reliable results above 6–7 kHz because the spectral content at high frequencies does not necessarily exceed the hearing threshold in piano. Therefore, the comparison between dynamics is impeded above that frequency, and frequency range in the plots is limited to 700 Hz to 8 kHz.

Results

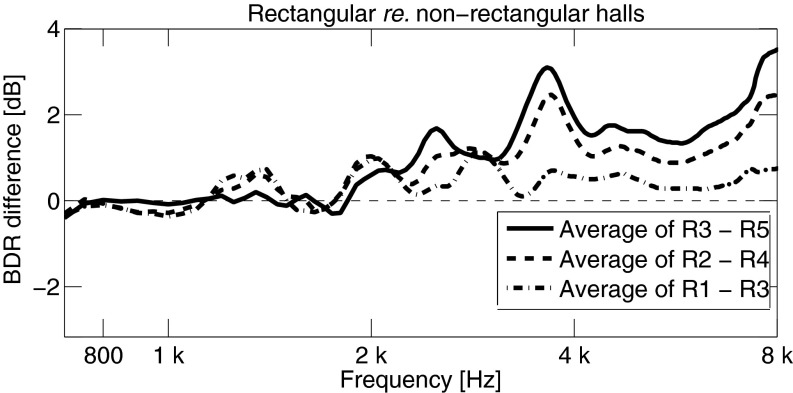
Results showing the differences in binaural dynamic responsiveness between hall types, calculated using Eq. 7, are shown in Fig. 4. Higher values indicate that the difference in the binaural spectral excitation between full orchestra piano and fortissimo by the early sound with regard to direct sound is larger in rectangular halls. In other words, the dynamic range of the hall response is greater in the measured shoebox concert halls. The effect is emphasized with increasing receiver distance. There is a notable similarity in the BDR difference curve and orchestra dynamic spectral change. This similarity suggests strongly that the dynamic responsiveness is a result of interaction between the emphasis of higher overtones at stronger orchestra dynamics and the early response in concert halls.

Fig. 4.

Binaural dynamic responsiveness difference with full orchestra in piano and fortissimo at varying distances, between rectangular and nonrectangular halls. The curves show the difference in the binaural excitation between direct sound (0–5 ms) and early sound (5–100 ms).

Of the standardized objective parameters, lateral energy fraction (LEF) is the closest counterpart to binaural dynamic responsiveness regarding its hypothesis on the lateral early reflections. The possible connection between BDR and measured LEF was analyzed by calculating the Pearson correlation coefficient r between the two parameters. Values for octave-band averages from the BDR difference curves against Stuttgart Beethovensaal were calculated for each hall. Similarly to BDR, LEF values in octave bands were averaged over three receiver distances. The correlation coefficients progressively increase from −0.25 in the 250-Hz band to 0.66 in the 4-kHz and 0.76 in the 8-kHz bands. The trend suggests that high-frequency LEF correlates best with relative binaural dynamic responsiveness. Detailed results and comparisons between BDR in individual halls are provided in Supporting Information.

Discussion

The original hypothesis claimed that lateral early reflections would increase the binaural dynamic responsiveness due to the interaction between emphasized high-frequency content in higher orchestral dynamics and the auditory spectral excitation of directional hearing. The results for binaural dynamic responsiveness averaged over hall types exceeded in many cases the standardized just-noticeable difference (JND) of 1 dB given for, e.g., both G and C₈₀ parameters (9). In that regard, the overall effect can be considered perceptually relevant. Furthermore, the differences in BDR between individual halls showed prominently higher variations.

Studies by Kuhl (23) presented measurement results from six halls relating spatial impression with overall sound level. Halls shown to exhibit such an effect in particular were Hamburg Musikhalle and Wuppertal Stadthalle, both rectangular shoeboxes. In contrast, Braunschweig Stadthalle and Stadthalle Hannover, fan-shaped and circular halls respectively, were shown to have a lesser spatial impression. Kuhl’s findings suggest that halls that provide distinct early lateral reflections respond spatially more to sound level increases. This effect is in agreement with the present results, with the auditory excitation by the early sound field increasing in relation to the direct sound at higher dynamics, thus emphasizing the early reflections.

Beranek (24) has presented calculations where a measure for the objective degree of the source-broadening effect is obtained from measured BQI and G values. Although dynamics are not considered, his results generally suggest a positive correlation between source broadening at middle frequencies and preference. An interpretation of the current results as dynamically changing LEF also explains the covariation of sound level and apparent source width (25).

The increasing correlation between LEF and BDR toward higher frequencies supports the assumption that the lateral early reflections enhance BDR. These results partially contradict Barron and Marshall’s (14) prediction that frequencies above 1–5 kHz do not contribute to spatial impression. In contrast, Blauert and Lindemann (21) found that lateral reflections, with high frequencies intact, are crucial for both spatial sensation and preference. A more recent study by Lokki et al. gathered preference ratings with listening tests from one receiver position at 12 m distance from the orchestra in nine concert halls (33). Although the halls were different from the 10 European halls, they were all measured with the same calibrated system. Binaural dynamic responsiveness calculations applied to those halls indicate that rectangular rooms typically provide the highest amount of dynamic responsiveness, as was found here in the main results. Comparing the preference ratings with BDR values suggests that halls with higher BDR were generally preferred, and halls with unanimously low preference have the lowest BDR. A further statistical analysis between the subjective data and standard objective parameters (34) revealed that the preference among those halls is best predicted by the amount of high-frequency LEF. Those findings, together with the current results, highlight the importance of lateral early reflections and high frequencies to the concert hall’s responsiveness to playing dynamics.

Conclusions

This paper combines research on nonlinear auditory excitation dependent on orchestra playing dynamics and reflection direction. The primary hypothesis is that the dynamic range of the binaural auditory excitation between orchestra piano and forte is not constant, but instead it depends on the room-acoustic conditions. At higher dynamics, high frequencies become emphasized in the orchestra sound as the timbre changes. With room acoustics included, lateral early reflections, if present, enhance the level of high frequencies in hearing.

The hypothesis was tested by analyzing binaural measurements of 10 European concert halls that were recorded using a calibrated loudspeaker orchestra. Dynamic spectra were calculated from anechoic instrument recordings, and the convolution of the room and orchestra spectra were input to a binaural auditory excitation model. Comparison of the resulting direct and early sound-excitation patterns indicated that, within the test group, rectangular concert halls provide on average ∼2 dB more high-frequency auditory excitation at high dynamics. Between individual halls, variations in BDR reached values of up to 5 dB. The BDR difference between rectangular and nonrectangular halls depends on the receiver distance, the effect being emphasized at longer distances from the stage.

Earlier research has demonstrated that lateral reflections in concert halls precipitate desirable perceptual qualities with regard to spatial impression. Here, in combination with the spectral effects of the orchestra, it has been shown that the advantages of lateral reflections extend to include enhanced dynamic range. This effect was quantified here as binaural dynamic responsiveness and was found to correlate positively with the LEF parameter at high frequencies. The present findings suggest that communication of the dynamic information in the music to the listener is augmented in rooms that provide early lateral reflections. A room that improves the transmission of musical information (35), such as orchestral dynamics, is expected to provide a more powerful musical experience to the listener. Concert halls that benefit most from this phenomenon include classic shoebox-shaped rooms as well as certain modern designs (16). These findings establish a connection between the success of venerable historic shoebox-type concert halls, such as Vienna Musikverein, Berlin Konzerthaus, Amsterdam Concertgebouw, and Boston Symphony hall (ref. 10, p. 496), and binaural dynamic responsiveness.