Role of substrate unbinding in Michaelis–Menten enzymatic reactions

Significance

Enzymes are biological catalysts vital to all life processes, and the quest to determine their inner workings continues to attract and fascinate scientists over a broad range of disciplines. With the advent of high-resolution methods of single-molecule spectroscopy, it is now possible to directly observe and manipulate the behavior of individual enzymes in the course of a chemical reaction. Chemistry at the single-molecule level is, however, inherently stochastic and, at times, extremely unintuitive. In this paper, we explain why, and under what circumstances, an increase in the rate at which an enzyme unproductively departs from a bound substrate will—unexpectedly—lead to an acceleration in the rate of product formation. The far-reaching implications of this effect are discussed.

Abstract

The Michaelis–Menten equation provides a hundred-year-old prediction by which any increase in the rate of substrate unbinding will decrease the rate of enzymatic turnover. Surprisingly, this prediction was never tested experimentally nor was it scrutinized using modern theoretical tools. Here we show that unbinding may also speed up enzymatic turnover—turning a spotlight to the fact that its actual role in enzymatic catalysis remains to be determined experimentally. Analytically constructing the unbinding phase space, we identify four distinct categories of unbinding: inhibitory, excitatory, superexcitatory, and restorative. A transition in which the effect of unbinding changes from inhibitory to excitatory as substrate concentrations increase, and an overlooked tradeoff between the speed and efficiency of enzymatic reactions, are naturally unveiled as a result. The theory presented herein motivates, and allows the interpretation of, groundbreaking experiments in which existing single-molecule manipulation techniques will be adapted for the purpose of measuring enzymatic turnover under a controlled variation of unbinding rates. As we hereby show, these experiments will not only shed first light on the role of unbinding but will also allow one to determine the time distribution required for the completion of the catalytic step in isolation from the rest of the enzymatic turnover cycle.

Every enzymatic reaction is composed out of two basic steps: (i) the reversible binding of a substrate molecule to the enzyme and (ii) a catalytic step which gives rise to the formation of the product (1). Controlled variation of the effective binding rate to a free enzyme is attained by altering the concentration of the substrate. The rate of product formation, also known as the turnover rate, can then be measured as a function of this concentration to show a characteristic hyperbolic dependence (2–5). The Michaelis–Menten equation is used to rationalize this observation and interpret the results (2, 6).

Recent advancements in single-molecule spectroscopy have gradually made it possible to follow the stochastic activity of individual enzymes over extended periods of time (7–19). Interestingly, the hyperbolic dependence of turnover on substrate concentration remains valid even at the single-molecule level (12, 14). From a theoretical perspective, this result was initially puzzling but is now considered almost universal in the sense that it can be shown to hold under a wide range of modeling assumptions (20, 21). One can thus safely say that the role of binding in Michaelis–Menten enzymatic reactions is well understood. In this paper, we consider the role of unbinding.

Rapid advancements in the single-molecule technological front imply that the adaptation of existing single-molecule manipulation techniques (12–14, 18, 22, 23) to allow the measurement of enzymatic turnover under a controlled variation of unbinding rates is now within reach. Single-molecule approaches to biomolecular interaction kinetics (24–26) allow for direct measurements of binding and unbinding rates (27–29). In addition, the combination of single-molecule florescence (16, 18) with single-molecule force spectroscopy (23, 30) marks itself as an especially promising tool in unbinding studies because the fluorescence readout for catalytic activity is expected to be correlated with selective, force-induced, changes of the activation barrier for unbinding (23, 30). Direct manipulation of the substrate itself, via atomic force microscopy (13–15), was also shown to be possible, potentially allowing for abrupt premature termination of the catalytic process via force induced unbinding. However, a strong discouragement to embark on a long journey whose aftermath seems to have already been foretold severely diminishes the motivation to pursue the above-mentioned line of investigation—the Michaelis–Menten equation clearly states that any increase in the rate of unbinding must be accompanied by a decrease in the rate of enzymatic turnover.

Here, we show that the interplay between turnover and unbinding is rich and more intricate than previously perceived. Interestingly, the problem is analytically tractable and allows for the extraction of a set of simple, far-reaching, conclusions that are formulated in a mathematically closed form. Most importantly, we show that turnover can be accelerated by increasing the unbinding rate when the following conditions hold: (i) Substrate concentrations are high; (ii) the unbinding rate is low; and (iii) the coefficient of variation 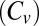associated with the distribution of catalysis times is larger than unity.

Interestingly, the turnover time distribution has been measured for the enzyme β-galactosidase, and its was found to be a monotonically increasing function of the substrate concentration (peaking at a value of ∼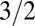) (12). The turnover time distribution coincides with the catalysis time distribution in the limit of high substrate concentrations and low unbinding rates, suggesting a 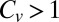for the catalysis time distribution of β-galactosidase. Moreover, meticulous data analysis has led previous authors to rule out several reaction schemes for which 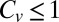and conclude that β-galactosidase displays highly non-Poissonian dynamics (31, 32). These findings are in line with a 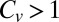, and while this is yet to be asserted, we allow ourselves a measured amount of optimism with regard to the possibility of observing an “unbinding speedup effect” in this particular system.

In what follows, we outline the background for our study and pose the fundamental question regarding the role of substrate unbinding. We then construct an unbinding phase space that provides an answer to this question, point out the implications arising, and conclude with discussion and outlook.

The Michaelis–Menten Reaction Scheme

The Michaelis–Menten reaction scheme (2) has been applied to the analysis of bulk (ensemble) experiments, aimed at the study of enzymatic kinetics, for over a century. According to the model, an enzyme E reversibly binds a substrate S to form a complex ES. The substrate can then be converted by the enzyme to form a product P or, alternatively, unbind. The conversion of the substrate to a product is manifested via the process of enzymatic catalysis. Following either catalysis or unbinding the enzyme is free to act on additional substrate molecules. The Michaelis–Menten model is schematically described as follows

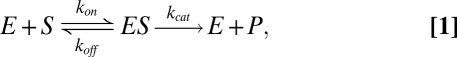where and are the rates at which the enzyme binds and unbinds the substrate, respectively, and 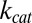is the rate of catalysis.

A prime corollary of the Michaelis–Menten reaction scheme is the Michaelis–Menten equation

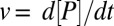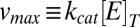which describes the dependence of the enzymatic velocity on the substrate concentration . Here, is the maximal enzymatic velocity attained at high substrate concentrations, and is the total concentration of the enzyme. The so-called Michaelis constant is given by , and is interpreted as the substrate concentration at which enzymatic velocity attains half its maximal value. Keeping all other parameters fixed, Eq. 2 predicts that the enzymatic velocity is a monotonically decreasing function of the unbinding rate.

Interestingly, the Michaelis–Menten model is also useful in the analysis of enzymatic reactions at the single-molecule level, albeit with a slight change in interpretation. Binding, unbinding, and catalysis are now considered to be stochastic processes whose rates are defined to be the reciprocals of the mean times associated with their realization. When all processes are Poissonian, i.e., when the times between consecutive events are independently drawn from the exponential distribution, an analog of the Michaelis−Menten equation, known as the single-molecule Michaelis−Menten equation (20), is attained:

Here, the turnover rate 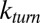is the reciprocal of the mean turnover time —the average time it takes a single enzyme to produce a single molecule of product.

Comparing Eqs. 2 and 3, it is clear that the dependence on substrate concentration is identical in both. Recalling the definition of the Michaelis constant, it is observed once more that the turnover rate is a monotonically decreasing function of the unbinding rate, i.e., substrate unbinding acts counterproductively to catalysis. By taking the reciprocal of Eq. 3, it can also be shown that the mean turnover time is always greater than the mean time for binding and catalysis combined. Although the general validity of the above-mentioned properties is strongly supported by intuition, we will now show that this is just seemingly so.

The Role of Substrate Unbinding

The stochastic processes of binding, unbinding, and catalysis may be non-Poissonian and even display correlations between successive events. In lack of direct measurements for the time statistics of these processes, and in an effort to resolve the inner workings of enzymes, much thought has been dedicated to a reverse engineering approach in which one tries to rule out scenarios which are inconsistent with available data (17, 31, 32). To this end, it was soon realized that the hyperbolic dependence of turnover on substrate concentration is almost universal and thus largely uninformative when it comes to the molecular details. One can easily see this by deriving a version of Eq. 3 that is valid for generally distributed binding, unbinding, and catalysis times (see Methods) or, alternatively, by exploring a dynamic disorder approach (20, 21). In either case, Eq. 3 remains valid under a broad range of conditions albeit with the replacement of and by generalized constants that share the same macroscopic interpretation while being highly sensitive to the microscopic details. Hyperbolic dependence, the conditions under which it holds, and the generalized form of the turnover rate when these conditions are broken, are all extensively analyzed in refs. 33 and 34.

Experimental measurements of single-molecule enzymatic trajectories and turnover time distributions provide an additional layer of information that goes beyond the conventional mean level analysis. Highly nonexponential distributions of turnover times and molecular memory properties of the turnover process are characteristic to many enzymatic reactions and cannot be reconciled with the existence of an exponential catalytic step (10–12, 18, 31, 32). The result is perhaps not surprising as catalysis is intrinsically coupled to the enzyme’s internal degrees of freedom via a complex energy landscape (35). This is, of course, not to say that simple exponential catalysis is impossible but rather to point out that we should be aware of the fact that complex vibrational dynamics is known for its ability to generate deviations from exponentiality (36–40) and that we should bear in mind the implications arising.

Interestingly, and in sharp contrast to substrate concentration, the functional dependence of the turnover rate on unbinding is sensitive to the distribution of the catalysis time—suggesting that the fingerprints of nonexponentiality are discernible even at this fundamental level. To illustrate this, we consider the case of exponential unbinding times in the presence of generally distributed binding and catalysis times. The choice of exponential unbinding times is made here from the stance of analytical tractability, but the reader can easily convince himself that the emergence of the phenomenon described herein cannot depend on this technicality. Moreover, it is the purpose of this paper to motivate the development of techniques that will allow control over the unbinding process. We will henceforth adopt this viewpoint and illustrate how these techniques may open unique horizons for the field of single-molecule enzymology. We emphasize that the generalized treatment of binding and catalysis times clearly accounts for exponential time distributions as a special case.

In what follows we will demonstrate that unbinding events may, under a given specified condition, speed up enzymatic turnover, and that a nonmonotonic dependence of the turnover rate on the unbinding rate emerges as a result. We furthermore discuss in what sense should we revise our, bulk measurements based, understanding of the unbinding-turnover interplay due to this finding. The basic relation from which we set off to establish the main results of this paper is given by

Eq. 4 is a special case of the single-enzyme turnover rate presented in Methods. Here, we assume that the mean binding time is inversely proportional to the substrate concentration but allow binding to be generally distributed otherwise. Unbinding is assumed to be exponential with rate 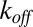, and catalysis is generally distributed with denoting the probability density function of the catalysis time. The Laplace transform of 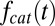, evaluated at 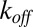, is denoted by 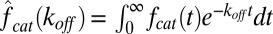. Eq. 4 was originally derived in (20) under the assumption of exponential binding but is in fact valid even in the more general setup described above.

Eq. 4 allows us to analyze the dependence of the turnover rate on the unbinding rate. First, when , one can readily observe that the turnover rate vanishes due to the zeroing of the numerator. Indeed, extremely high unbinding rates will narrow down the window of time at which the substrate is bound to the enzyme, thus diminishing to zero the probability for a successful catalytic event to occur.

Additional insight regarding the effect of unbinding may be gained by noting that the unbinding time scale plays the role of an exponential upper cutoff of catalysis times. Hence, the contribution of catalysis times that are much longer than the typical unbinding time is effectively censored out. One may then wonder what happens to the turnover rate when the unbinding rate is gradually increased from an initial value of zero (no unbinding). Can unbinding, and the initiation of a new turnover attempt, be time-wise preferable to the wait involved in the completion of an ongoing catalytic attempt?

On the one hand, unbinding may censor the tail of the catalysis time distribution and hence prevent a situation in which the substrate is “stuck” in the ES state for an undesirably long period of time. On the other hand, unbinding will inevitably require renewed binding and catalysis, and hence entails a severe time penalty. The “unbinding dilemma” boils down to the question of whether or not the expected length of a (new) turnover cycle is longer than the expected length of the remainder of an ongoing catalytic step, given its age.

When catalysis times are taken from an exponential distribution, the memoryless property (41, 42) asserts that the time remaining until the completion of an ongoing catalytic step, given its age, is exponential and statistically identical to that of a newly started catalytic step. In this case, the introduction of unbinding can only result in a decrease of the turnover rate. However, and as we now show, when catalysis times are taken from a nonexponential distribution, this is not necessarily the case.

The Dispersion in Catalysis Times Determines the Role of Unbinding

A key player in determining the effect of unbinding is the coefficient of variation associated with the random catalysis time . The coefficient of variation is defined as the ratio between the standard deviation (SD) and the mean,

and is a normalized measure for the dispersion of positive-valued random variables. For example, when the entire distribution is concentrated on a single value, the coefficient of variation is zero. More generally, one can say that higher coefficients of variation indicate higher levels of dispersion and vice versa. The exponential distribution, in which the mean and SD are equal by definition, has the special property of having a coefficient of variation that is always equal to unity.

Defining the critical coefficient of variation to be

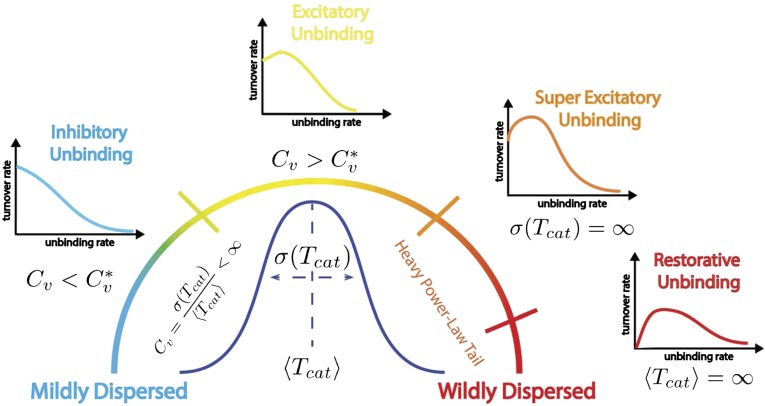
we classify the role of unbinding into four possible categories: inhibitory, excitatory, superexcitatory and restorative—all schematically illustrated in Fig. 1. Figs. S1 and S2, in which we use Eq. 4 to plot vs. 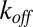for various sample distributions of the catalysis time, provide concrete examples for each of the above-mentioned categories.

Fig. 1.

Schematic illustration of the four possible roles of unbinding. The coefficient of variation, abbreviated , measures the normalized dispersion in the distribution of catalysis times. When , the dispersion is subcritical and inhibitory unbinding is observed. In this case, the turnover rate displays an initial linear decrease with the unbinding rate. This type of behavior is observed, for example, in the case of exponential catalysis times. When 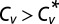, the dispersion is supercritical and three distinct scenarios are possible. As long as the SD is finite, 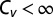and excitatory unbinding is observed. In this case, the turnover rate displays an initial linear increase with the unbinding rate. This type of behavior is seen in various cases for which the distribution of catalysis times is nonexponential and broad. Infinite dispersion may arise when the distribution of catalysis times is characterized by a heavy power-law tail. When the mean catalysis time is finite but the SD diverges, 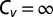and superexcitatory unbinding is observed. In this case, the turnover rate displays an initial superlinear increase with the unbinding rate. When both the mean and SD diverge, the coefficient of variation is not even properly defined and restorative unbinding is observed. In this case, the turnover rate vanishes at zero unbinding and is restored to positive values only after, and as a result of, the introduction of unbinding.

Common to all unbinding scenarios, depicted in Fig. 1, is the monotonic decrease in turnover seen at high unbinding rates. The four scenarios differ, however, in the way turnover behaves at low unbinding rates as explained in the legend of Fig. 1. Read from top to bottom, the following equation summarizes the behavior of inhibitory, excitatory, superexcitatory, and restorative unbinding at the low unbinding rate limit :

Here, is the reciprocal of the combined mean time for binding and catalysis, and A, B, and C are all positive constants specified in the Supporting Information. Superexcitatory and restorative unbinding arise as a result of a heavy-tailed power-law distribution of catalysis times. In these two cases, the asymptotic behavior of the probability density function is further assumed to be characterized by an exponent α such that in the limit: with . When 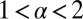, the SD of the catalysis time diverges resulting in superexcitatory unbinding. When 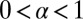, both the mean and SD of the catalysis time diverge, resulting in restorative unbinding. The derivation of Eq. 7 appears in the Supporting Information and is based on fundamental properties of the Laplace transform (43).

Our findings clearly illustrate that the interplay between turnover and unbinding is more intricate than the one predicted by the classic Michaelis–Menten equation. First, the turnover rate is not necessary monotonically decreasing in the unbinding rate. As a result, maximal turnover may be achieved at intermediate, rather than vanishing, unbinding rates. When unbinding is noninhibitory, this also means that the turnover rate can break its bulk-based theoretical limit —resulting in a mean turnover time that is faster than the combined mean time for binding and catalysis! Finally, we note that in the presence of unbinding, the mean turnover time stays finite even in extreme cases for which the mean catalysis time diverges. This fact has far-reaching consequences as it demonstrates how the mere introduction of an unbinding step allows the catalysis of reactions whose progression would otherwise be infinitely slow.

The Inhibitory−Excitatory Transition

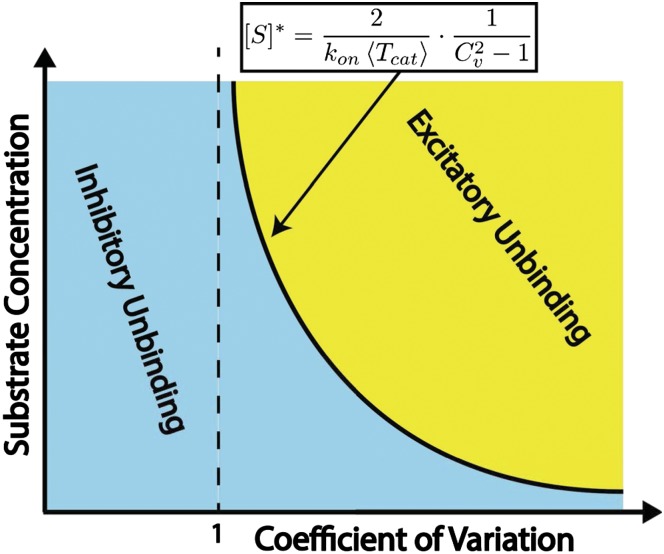
Eq. 6 suggests that the role of unbinding may change from inhibitory to excitatory as substrate concentrations increase. Indeed, by increasing the concentration of the substrate, one lowers the dispersion threshold for the onset of excitatory unbinding to an asymptotic limit of unity. As a result, and provided that 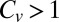, an inhibitory−excitatory transition will occur at the following critical concentration:

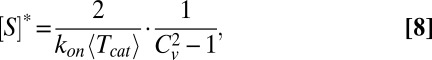above which and unbinding is excitatory. The combination of Eqs. 6 and 8 gives rise to a 2D phase space, illustrated in Fig. 2, from which the existence of an inhibitory−excitatory transition is visually clear. The transition is further illustrated in Fig. S3.

Fig. 2.

Schematic illustration of the unbinding phase space. When the coefficient of variation associated with the distribution of catalysis times is larger than unity, an inhibitory−excitatory transition takes place upon gradual increase in substrate concentration.

The special role played by the line in the unbinding phase space implies the existence of a strong connection between our findings and the fundamental probabilistic concept of failure rate (41, 42). The instantaneous failure rate associated with the catalysis time distribution is defined: 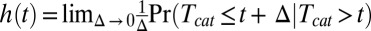. Namely, given that catalysis did not occur during the time interval , 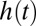is the realization rate of the catalytic process immediately after time t. The exponential distribution is the only distribution characterized by a constant failure rate. A catalysis time distribution characterized by a monotonically increasing (decreasing) failure rate implies that catalysis is more (less) likely to occur as time goes by. Interestingly, a monotonically increasing (decreasing) failure rate also implies a coefficient of variation that is smaller (larger) than unity (41, 42). Thus, when substrate concentrations are high and when the catalysis time is characterized by a monotonically decreasing failure rate, termination of the catalytic step by timely unbinding and the initiation of a new turnover attempt is guaranteed to be time-wise preferable to the wait involved in the completion of an already aged catalytic step.

The Speed−Efficiency Tradeoff

A standard measure of enzymatic efficiency is given by the ratio of the maximal turnover rate, achieved in the limit of saturating substrate concentrations 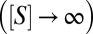, to the substrate concentration at which turnover is at half maximum. When binding, unbinding, and catalysis times are all exponential, this ratio is given by 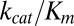(in the bulk formulation of the Michaelis–Menten reaction scheme, one gets ). When catalysis times are generally distributed, Eq. 4 may be used to derive an expression for a generalized efficiency parameter

which captures the standard definition of enzymatic efficiency as a special case.

Eq. 9 reveals a previously overlooked tradeoff. Because 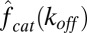is monotonically decreasing in the unbinding rate (see definition below Eq. 4), so is the enzymatic efficiency (Fig. S4). Hence, the theoretical upper bound on enzymatic efficiency is attained in the limit of zero unbinding and is given by . On the other hand, when unbinding is noninhibitory, the turnover rate attains its maximal value at unbinding rates that are strictly larger than zero. As one comes at the expense of the other, a clear speed−efficiency tradeoff, illustrated in Fig. 3, arises.

Fig. 3.

The inhibitory−excitatory transition implies the existence of a speed−efficiency tradeoff. A color-coded contour map of the turnover rate, normalized by its value at zero unbinding, as a function of substrate concentration and the unbinding rate (arbitrary units). Areas in which the normalized turnover is high are lighter than areas in which it is low. Here, and an inhibitory−excitatory transition occurs when the concentration of substrate crosses the critical threshold 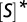. At low substrate concentrations, turnover monotonically decreases with unbinding whereas at high substrate concentrations, turnover first increases and only then decreases. Enzymatic efficiency, on the other hand, is always monotonically decreasing with the unbinding rate. Thus, when , turnover can be made faster at the high concentration regime of the spectrum by increasing the unbinding rate—this will, however, come at the cost of suboptimal enzymatic efficiency.

Discussion

In this paper, we have analytically studied the role of unbinding in Michaelis–Menten enzymatic reactions and demonstrated the feasibility of an effect previously conceived to be impossible—the acceleration of enzymatic reactions via substrate unbinding. Our findings motivate experimental studies in which enzymatic turnover will be measured under a controlled variation of the unbinding rate. Such measurements will not only shed light on the role of unbinding in actuality but will also provide a glimpse into a realm that has been so far locked away. When substrate concentrations are high,

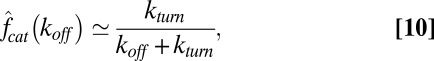and thus, measuring 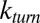as a function of amounts to measuring the Laplace transform of the catalysis time distribution and, following inversion, to knowing the distribution itself. This simple observation further strengthens the motivation behind experimental studies of unbinding.

Much remains to be done on the theoretical side as well. Characterization of the optimal unbinding rate, thorough quantification of the phenomenon on a distributional level, and the incorporation of molecular memory effects are all of interest, and we report that investigations along these avenues have already began. It has not escaped our eyes that—as long as enzyme populations are homogeneous—the results we have obtained may also be carried on to the ensemble level. When enzymes are completely identical, changing the unbinding rate in a manner that has a uniform effect on the entire ensemble will have the same impact as a change applied to one tagged enzyme. Extensions of our theory to the case of heterogeneous enzyme populations will be discussed elsewhere.

Coupling between unbinding and catalysis times is also of interest, as it may naturally arise in multiple scenarios—thus rendering discussion on the role of unbinding no longer meaningful per se. When this is the case, Eq. 4 is not applicable, as it implicitly assumes that unbinding and catalysis times are statistically independent. The challenge then lies in an attempt to decipher the convoluted effects of unbinding and catalysis, and multiple ad hoc approaches may be utilized for this purpose. Recent theoretical advancements (17, 21, 31–34, 44), to which the current study joins, have however set a different standard in the field—the identification of broad behavioral classes. To this end, the characterization of a coupled unbinding−catalysis phase space would constitute a landmark in our understanding of the topic. One possible starting point to an attempt aimed at achieving this goal is Eq. 11, which does not assume statistical independence but still relies on a renewal assumption. Other generic approaches may also be adapted for this purpose (45).

We find it extremely important to point out that the theory presented herein is independent of the enzymological context within which it was developed and is in fact relevant to any system described by a stochastic Michaelis–Menten reaction scheme. Indeed, nature is full of Michaelis−Menten-type processes, and noteworthy in this regard is heterogeneous catalysis (46–49). There, the rate of unbinding may be influenced by changing environmental parameters such as the pH of the solution or the surrounding electromagnetic field (electrocatalysis) (46). Search processes, not necessarily on the molecular level, constitute another example that falls into the Michaelian category and it is interesting to note that in this particular context the importance of unbinding has already been recognized (50). Finally, when considering the many Michaelis–Menten-type processes that occur within dense cellular environments, one should moreover keep in mind that these environments are known to be governed by “strange” kinetic effects (51). This fact adds an additional layer of complexity to the game, as it has been recently predicted that molecular crowding is capable of modifying (un)binding dynamics and binding constants (52). Bridging the gap between the single-molecule and cellular levels remains a standing challenge.

A recent, wide-scale, analysis has found that most enzymes operate in a moderately efficient regime which is far from the diffusion limit and the characteristic textbook portrayal of kinetically superior enzymes (53). The findings presented herein demonstrate the existence of an overlooked tradeoff between the speed and efficiency of enzymatic reactions. As we have hereby shown, turnover may be accelerated via substrate unbinding at the expense of a reduction in enzymatic efficiency. Optimal turnover rates, and enzymatic efficiencies, may have failed to evolve in cases where weak selection pressures were in play or from various other reasons. However, in light of the above-mentioned tradeoff, one should also consider a possibility by which moderate enzymatic efficiency is a lesser evil resulting from opposing evolutionary pressures toward optimal turnover and vice versa.

Methods

In this section, we derive a generalized expression for the turnover rate of a single enzyme. Consider a simple scenario, to be generalized hereinafter, in which the binding and unbinding processes are deterministic (nonstochastic) and the distribution of the stochastic catalysis time is general. A free enzyme will bind to a substrate after a deterministic waiting time whose length is exactly 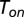units of time. Similarly, and provided that a catalytic transition did not occur within this time frame, unbinding occurs after a deterministic waiting time whose length is exactly units of time. Under these assumptions, one can readily show that

where is the probability that catalysis occurs before unbinding, is the mean of the minimum between catalysis and unbinding times, and equals its average simply by definition.

The above-mentioned result can be easily understood by use of elementary probabilistic considerations. Following a deterministic binding time whose length is 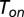and an additional stochastic time period , turnover will either complete with probability 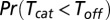or, alternatively, unbinding will occur with the complementary probability. The number of turnover attempts is hence geometrically distributed with a success parameter 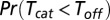, and its average is given by the reciprocal of this probability. The desired result follows from the fact that each turnover attempt takes, on average, 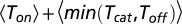units of time.

Interestingly, the above result holds even in the case of generally distributed binding and unbinding times (see formal derivation in the Supporting Information). In this scenario, a free enzyme will bind to a substrate after a stochastic time period 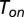whose mean length is . Similarly, unbinding occurs after a stochastic time period 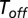, provided that a catalytic transition did not occur within this time frame. If one further assumes that the mean binding time is inversely proportional to the substrate concentration, the latter can be defined as follows: 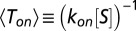, and Eq. 11 can be put in the following canonical form:

where 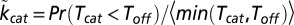and 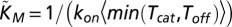. Eq. 4 follows from Eq. 12 by further assuming that the random unbinding time is exponentially distributed and statistically independent of the catalysis time 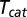(see Supporting Information).