Significance
Turing proposed that intercellular reaction-diffusion of molecules is responsible for morphogenesis. The impact of this paradigm has been profound. We exploit an abiological experimental system of emulsion drops containing the Belousov–Zhabotinsky reactants ideally suited to test Turing’s theory. Our experiments verify Turing’s thesis of the chemical basis of morphogenesis and reveal a pattern, not previously predicted by theory, which we explain by extending Turing’s model to include heterogeneity. Quantitative experimental results obtained using this artificial cellular system establish the strengths and weaknesses of the Turing model, applicable to biology and materials science alike, and pinpoint which directions are required for improvement.
Keywords: pattern formation, nonlinear dynamics, chemical oscillations, chemical dynamics
Abstract
Alan Turing, in “The Chemical Basis of Morphogenesis” [Turing AM (1952) Philos Trans R Soc Lond 237(641):37–72], described how, in circular arrays of identical biological cells, diffusion can interact with chemical reactions to generate up to six periodic spatiotemporal chemical structures. Turing proposed that one of these structures, a stationary pattern with a chemically determined wavelength, is responsible for differentiation. We quantitatively test Turing’s ideas in a cellular chemical system consisting of an emulsion of aqueous droplets containing the Belousov–Zhabotinsky oscillatory chemical reactants, dispersed in oil, and demonstrate that reaction-diffusion processes lead to chemical differentiation, which drives physical morphogenesis in chemical cells. We observe five of the six structures predicted by Turing. In 2D hexagonal arrays, a seventh structure emerges, incompatible with Turing’s original model, which we explain by modifying the theory to include heterogeneity.
The Turing model of morphogenesis offers an explanation for how identical biological cells differentiate and change shape (1). It is difficult to overstate the impact Turing’s model has had on developmental biology and the broad field of reaction-diffusion systems (2–9). The Turing model consists of two cases: The first, applicable for a ring of continuous material, has been experimentally confirmed in chemical systems (10–14). The second case, relevant to biology, consists of a ring of discrete cells, each of which contains interacting chemical species that can diffuse to neighboring cells through a chemical selective membrane. However, as the two theories for the cases are different, establishing the Turing model for continuous systems does not prove that the model holds when the chemistry is compartmentalized. Due to challenges in microfabrication, the case of a ring of cells has not previously been experimentally tested in chemical systems. In biology, where networks of cells arise naturally, the Turing model remains controversial because comparison of experiment and theory is hampered by incomplete knowledge of the morphogens involved in development, the rate constants of the reactions, the mechanisms of intercellular coupling, and the role of elasticity (5, 7, 15, 16).
We report an experimental reaction-diffusion system ideally suited for testing Turing’s ideas in synthetic “cells” consisting of microfluidically produced surfactant-stabilized emulsions (17, 18) in which aqueous droplets containing the Belousov–Zhabotinsky (BZ) oscillatory chemical reactants (19) are dispersed in oil. In contrast to biology, here the chemistry is understood, rate constants are known, and interdrop coupling is purely diffusive. We explore a large set of parameters through control of concentrations, drop size, spacing, and spatial arrangement of the drops in lines and rings in one dimension and hexagonal arrays in two dimensions. Quantitative comparison of theory and experiment reveals two surprises: A structure not predicted by Turing's analysis is observed, and we measure coupling strengths orders of magnitude weaker than predicted. Nevertheless, in the majority of cases, we find Turing’s model to be exceedingly accurate. Most significantly, we experimentally establish Turing’s prediction that interacting identical cells differentiate into chemically distinct populations, which subsequently transform physically in size, thereby demonstrating that these synthetic cells are pluripotent and that abiotic materials can undergo morphogenesis via the Turing mechanism. For one-dimensional arrays of drops, we observe six distinct spatiotemporal patterns, all of which are predicted by the Turing model. In closed-packed 2D arrays, we observe an additional pattern, of a mixed spatial-temporal nature that is incompatible with Turing’s original model. We develop a theory, capable of describing this mixed pattern, which posits that the pattern arises from nonlinearity coupled with slight heterogeneity in cellular chemistry and/or coupling strength. As our theory is generic, and heterogeneity is ubiquitous in nature, we expect this pattern to occur in a wide range of reaction-diffusion systems.
The BZ reaction (19), the metal ion-catalyzed oscillatory oxidation of an organic substrate, typically malonic acid (MA), by acidic bromate, has become the prototype of nonlinear dynamics in chemistry (20) and a preferred system for exploring the behavior of coupled nonlinear oscillators (21). Our system (Fig. 1 and Fig. S1) consists of a monodisperse emulsion of drops of aqueous BZ solution, whose diameter ranges from 20 to 200 μm dispersed in a continuous phase of oil (17, 18). The drops are surfactant-stabilized to prevent coalescence (22) (SI Methods). Chemical coupling between drops is mediated through a small subset of less polar intermediates; primarily an inhibitory component, bromine (Br2), and to a lesser degree, two excitatory components, bromine dioxide 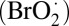 and bromous acid (HBrO2), which diffuse from drop to drop through the intervening oil. Here, because the inhibitory bromine strongly partitions into the oil, whereas the excitatory bromous acid does so only weakly, it is possible to satisfy the long-range inhibition and short-range excitation condition needed for the stationary Turing instability (6). Because the system is closed and the BZ reactants are not replenished, the reaction lasts no more than about 100 oscillations until the final uniform equilibrium state is approached. However, the system evolves sufficiently slowly that it can adiabatically exhibit the dynamical instabilities predicted by Turing for open systems (17, 18, 23).
and bromous acid (HBrO2), which diffuse from drop to drop through the intervening oil. Here, because the inhibitory bromine strongly partitions into the oil, whereas the excitatory bromous acid does so only weakly, it is possible to satisfy the long-range inhibition and short-range excitation condition needed for the stationary Turing instability (6). Because the system is closed and the BZ reactants are not replenished, the reaction lasts no more than about 100 oscillations until the final uniform equilibrium state is approached. However, the system evolves sufficiently slowly that it can adiabatically exhibit the dynamical instabilities predicted by Turing for open systems (17, 18, 23).
Fig. 1.

Chemical states of linear and circular arrays of BZ drops. See Movies S2 and S3. (A–F) Cylindrical capillaries of 100-μm inner diameter filled with a linear array of closely spaced droplets. (Upper) Space–time plots demonstrating the corresponding Turing cases (a–f) were generated by plotting the intensity of a single line of pixels connecting the centers of adjacent drops as a function of time. (Lower) Cartoon above corresponding photograph of droplets. Cartoon colors: blue, BZ drops in oxidized state; red, reduced state; cyan, oil. Chemical conditions: 300 mM bromate, 3 mM ferroin, 0.4 mM Rubpy, and 80 mM sulfuric acid. Malonic acid (MA), NaBr, drop size, and spacing are specified in each case. Five of the six Turing solutions b–f are observed. (A) Stationary stable oxidized state after initial transient; 10 mM MA, no NaBr, drop size of 130 μm, and oil gap of 20 μm. (B) Turing case b, (long-wavelength, oscillatory),  ; 2.4 M MA, 10 mM NaBr, drop size of ∼230 μm, and oil gap of ∼100 μm. (C) Turing case c, (short-wavelength, stationary),
; 2.4 M MA, 10 mM NaBr, drop size of ∼230 μm, and oil gap of ∼100 μm. (C) Turing case c, (short-wavelength, stationary), 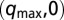 ; 20 mM MA, no NaBr, drop size of ∼98 μm, and variable oil gap between 0 and 47 μm. (D) Turing case d, (intermediate-wavelength, stationary), (q,0); 40 mM MA, no NaBr, drop size of 95 μm, and oil gap of ∼0 μm (touching drops). (E) Turing case e, (intermediate-wavelength, oscillatory), (q,ω); 640 mM MA, 10 mM NaBr, drop size of 117 μm, and oil gap of 3 μm. (F) Turing case f, (short-wavelength, oscillatory),
; 20 mM MA, no NaBr, drop size of ∼98 μm, and variable oil gap between 0 and 47 μm. (D) Turing case d, (intermediate-wavelength, stationary), (q,0); 40 mM MA, no NaBr, drop size of 95 μm, and oil gap of ∼0 μm (touching drops). (E) Turing case e, (intermediate-wavelength, oscillatory), (q,ω); 640 mM MA, 10 mM NaBr, drop size of 117 μm, and oil gap of 3 μm. (F) Turing case f, (short-wavelength, oscillatory), 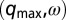 ; 380 mM MA, 10 mM NaBr, drop size of 106 μm, and oil gap of 25 μm. (G and H) Odd and even circular arrays. Turing case f. Rectangular capillaries with cross-section 0.1 mm × 2 mm filled with a 2D array of close-packed droplets from which rings are created with optical isolation. (Left) Oscillatory drops are labeled; all other drops are illuminated with light (cross) and held nonoscillatory in the reduced state. (Right) Space–time plot. Chemical conditions are as follows: 300 mM bromate, 3 mM ferroin, 80 mM sulfuric acid, 10 mM NaBr, 0.4 mM Rubpy, 640 mM MA; and drop size is ∼150 μm. (G) Five-membered ring. Drops oscillate in a pentagramal pattern. (H) Six-membered ring. Neighboring drops are π radians out-of-phase.
; 380 mM MA, 10 mM NaBr, drop size of 106 μm, and oil gap of 25 μm. (G and H) Odd and even circular arrays. Turing case f. Rectangular capillaries with cross-section 0.1 mm × 2 mm filled with a 2D array of close-packed droplets from which rings are created with optical isolation. (Left) Oscillatory drops are labeled; all other drops are illuminated with light (cross) and held nonoscillatory in the reduced state. (Right) Space–time plot. Chemical conditions are as follows: 300 mM bromate, 3 mM ferroin, 80 mM sulfuric acid, 10 mM NaBr, 0.4 mM Rubpy, 640 mM MA; and drop size is ∼150 μm. (G) Five-membered ring. Drops oscillate in a pentagramal pattern. (H) Six-membered ring. Neighboring drops are π radians out-of-phase.
Stationary Turing patterns have been notoriously difficult to produce experimentally, primarily because, for the activator–inhibitor dynamics that typically provides the necessary feedback, the inhibitor must diffuse significantly more rapidly than the activator (6). This condition, which cannot be satisfied with small molecules in homogeneous solution, was first fulfilled, 40 years after Turing’s paper, in the chlorite–iodide–malonic acid (CIMA) system, with the activator being complexed to starch, which slows activator transport (11, 12). Stationary Turing states were also observed in a BZ microemulsion consisting of reverse micelles (24, 25). The activator, polar HBrO2, resides in the aqueous interior of the micelle. The inhibitor, nonpolar Br2, permeates into the oil phase. The transport of the micelles is much slower than the transport of bromine; hence, the criterion for the stationary Turing instability is met. The distinction between the micelles used previously (24, 25) and the emulsions we study here (17, 18) is that the micelles are in dynamic equilibrium; they merge and split on a timescale much shorter than the period of a BZ oscillation and a length scale much shorter than the wavelength of the chemical wave. Therefore, on the timescale and length scale appropriate for a continuum description of the reaction-diffusion system, the BZ microemulsion can be considered to be homogeneous in composition. In this sense, the BZ microemulsion and the CIMA–starch system share a continuum description. The BZ emulsions studied here are fundamentally different, in that they consist of discrete immobile chemical compartments that never merge. The microfluidic emulsion system presented here is spatially heterogeneous, whereas the micelle and CIMA–starch systems are spatially homogeneous on the relevant timescales.
Model
To quantitatively test the Turing model in discrete cells, it is necessary to control the boundary and initial conditions for all of the cells. We use mixed boundary conditions: Part of the surface enclosing the cells under study consists of other cells in which the chemical concentrations are held constant, and part is a glass wall impenetrable to all chemicals and thereby imposes a no-flux condition. Constant chemical boundaries were created by exploiting the photosensitivity of the BZ catalyst, ruthenium-tris(2,2′-bipyridyl) (Rubpy). Any drop illuminated by blue light is inhibited from oscillating and held in the reduced steady state (SI Methods). We produced 1D linear and 2D hexagonal arrays of drops by filling cylindrical and rectangular capillaries, respectively, and used a computer projector coupled to a light microscope to generate patterned illumination (18) in which each drop could be independently illuminated. This flexible illumination system allowed us to isolate either pairs of drops, or a ring of active drops from a 2D array, as shown in Fig. 1 G and H and Fig. S2, with experimental conditions specified in Table S1. Initial conditions were set by inhibiting all drops with light, as shown in Fig. S3, and then disinhibiting individual selected cells by extinguishing their illumination at prescribed times, thereby allowing the chemical dynamics to proceed. A green light source tuned to the ferroin absorbance wavelength was used to observe, but not affect, the BZ reaction.
To construct a tractable model, Turing assumed cells were chemically uniform, small objects and considered the membranes separating cells as chemically specific barriers to diffusion, ignoring any chemical reaction or accumulation of chemicals in the membrane. Turing’s resulting reaction-diffusion model consists of a ring of point cells diffusively connected directly to nearest neighbors, expressed as a set of equations each of the following form (1):
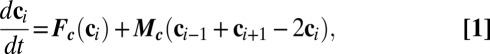 |
where 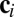 is a vector containing the concentrations of the species in the ith cell,
is a vector containing the concentrations of the species in the ith cell, 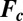 is a vector function describing the kinetics of the c-species, and
is a vector function describing the kinetics of the c-species, and 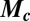 is a diagonal matrix containing the coefficients of diffusive transport
is a diagonal matrix containing the coefficients of diffusive transport 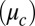 of the c-species between drops. We describe the chemical kinetics,
of the c-species between drops. We describe the chemical kinetics, 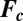 , of the BZ chemistry with a moel developed by Vanag and Epstein (26, 27) (VE model, SI Methods) that considers four concentrations to vary in time: the inhibitory components bromine (Br2) and bromide (Br−), the oxidized form of the catalyst (ferriin), and the activator bromous acid (HBrO2). The four VE reaction rates,
, of the BZ chemistry with a moel developed by Vanag and Epstein (26, 27) (VE model, SI Methods) that considers four concentrations to vary in time: the inhibitory components bromine (Br2) and bromide (Br−), the oxidized form of the catalyst (ferriin), and the activator bromous acid (HBrO2). The four VE reaction rates, 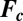 , contain the aforementioned four variable chemical species, four more chemicals, whose concentrations are approximated as constants in the model, and nine known rate constants;
, contain the aforementioned four variable chemical species, four more chemicals, whose concentrations are approximated as constants in the model, and nine known rate constants; 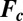 has zero adjustable parameters. Turing did not specify how the coupling strength
has zero adjustable parameters. Turing did not specify how the coupling strength 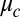 varies with the physical-chemical parameters. To compare theory with experiment, we supplement the Turing model by explicitly calculating the coupling strength between drops in a capillary using Turing’s assumptions noted above, with the caveat that different results arise depending on the assumptions used to produce a geometric point model (27, 28):
varies with the physical-chemical parameters. To compare theory with experiment, we supplement the Turing model by explicitly calculating the coupling strength between drops in a capillary using Turing’s assumptions noted above, with the caveat that different results arise depending on the assumptions used to produce a geometric point model (27, 28):
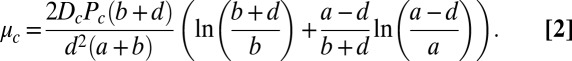 |
See Fig. S1 and SI Methods for details of the calculation. Dc and Pc are the diffusion and partition coefficients of the c-species in the oil, a is the length of the BZ drop, b is the length of the oil gap separating drops, and d is the diameter of the capillary. The only parameter not measured in Eq. 2 is the partition coefficient of HBrO2, Px.
To elucidate this model, Turing (1) used linear stability analysis (LSA) and identified six possible chemical structures in rings of diffusively coupled identical cells. In LSA, one characterizes how the steady-state concentrations, i.e., those for which 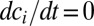 , respond to small perturbations. If all perturbations decay, then the system is in a stable steady state. However, if any perturbations grow with time, the steady state is unstable, and the fastest growing perturbation is labeled a Turing instability. For a ring of N cells, the requirement of periodicity restricts dimensionless wavevectors of the perturbations to take on one of three possible values:
, respond to small perturbations. If all perturbations decay, then the system is in a stable steady state. However, if any perturbations grow with time, the steady state is unstable, and the fastest growing perturbation is labeled a Turing instability. For a ring of N cells, the requirement of periodicity restricts dimensionless wavevectors of the perturbations to take on one of three possible values: 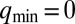 ,
, 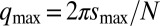 , where for even numbered rings
, where for even numbered rings 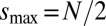 and for odd rings
and for odd rings 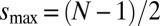 , and
, and 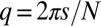 , where the integer s ranges from
, where the integer s ranges from 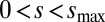 . For each possible q, the perturbation growth can be either oscillatory with frequency
. For each possible q, the perturbation growth can be either oscillatory with frequency 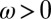 , or nonoscillatory with
, or nonoscillatory with 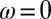 , giving a total of six possible instabilities. Following Turing’s nomenclature, the six instabilities (a–f) are each characterized by a wavevector and frequency, (q,ω), as follows: Turing case (a),
, giving a total of six possible instabilities. Following Turing’s nomenclature, the six instabilities (a–f) are each characterized by a wavevector and frequency, (q,ω), as follows: Turing case (a), 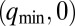 ; (b),
; (b), 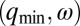 ; (c),
; (c), 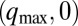 ; (d), (q,0); (e), (q,ω); and (f),
; (d), (q,0); (e), (q,ω); and (f), 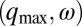 .
.
The Turing model, by which we mean the nonlinear rate and coupling equations (Eq. 1), incorporates two significant and untested approximations: considering each cell as a point and simplification of chemical transport by elimination of explicit consideration of the intracellular medium (the oil in our experiments). Furthermore, the use of LSA introduces an additional, severe approximation. The power of the Turing model is that it provides unambiguous physical mechanisms to explain chemical dynamics and morphogenesis. However, as noted by Turing (1), “This model will be a simplification and an idealization, and consequently a falsification.” This raises the question, to what degree do the Turing model and its LSA describe experiment? The answer to this question is of importance to the broad field of reaction-diffusion systems, as over a thousand papers have been published that have built upon the Turing model, which, before this work, has not been experimentally tested for networks of diffusively coupled cells (4). Here, we address six fundamental questions facing reaction-diffusion systems in general: (i) How well does the simplified coupling term, 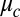 , agree with experiment? (ii) Are there more or fewer than the six predicted Turing linear instabilities? (iii) How are the linear instabilities modified by nonlinearities? (iv) Does the Turing model provide quantitative and predictive understanding of experiment? (v) How do chemical patterns depend on the dimensionality? (vi) Do cells sequentially undergo chemical and then physical morphogenesis?
, agree with experiment? (ii) Are there more or fewer than the six predicted Turing linear instabilities? (iii) How are the linear instabilities modified by nonlinearities? (iv) Does the Turing model provide quantitative and predictive understanding of experiment? (v) How do chemical patterns depend on the dimensionality? (vi) Do cells sequentially undergo chemical and then physical morphogenesis?
Results
As a first experimental test of the Turing model, Eq. 1, for cells, we measured the synchronization dynamics of two weakly inhibitory coupled drops at moderate MA concentrations, where uncoupled drops oscillate and bromine can be considered as the sole intercell transporter (18), i.e., 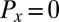 . We filled cylindrical capillaries with drops, used light both to chemically isolate a pair of adjacent drops and to set the initial phase difference between the isolated drops, and measured the phase difference between the two drops as a function of time, as shown in Fig. S1. Viewed in transmission, the oxidized state appears bright, whereas the reduced state appears dark. Ultimately, the drops synchronize with a phase difference of π radians (18, 29). Fig. S1 and Movie S1 present experimental synchronization rates as a function of drop sizes (50–200 μm) and oil gaps (10–200 μm) for
. We filled cylindrical capillaries with drops, used light both to chemically isolate a pair of adjacent drops and to set the initial phase difference between the isolated drops, and measured the phase difference between the two drops as a function of time, as shown in Fig. S1. Viewed in transmission, the oxidized state appears bright, whereas the reduced state appears dark. Ultimately, the drops synchronize with a phase difference of π radians (18, 29). Fig. S1 and Movie S1 present experimental synchronization rates as a function of drop sizes (50–200 μm) and oil gaps (10–200 μm) for 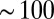 drop pairs; for these conditions, rates varied by a factor of 30. Excellent fits were obtained between the experimentally measured synchronization rates and the full nonlinear solution of Eq. 1 if we treated
drop pairs; for these conditions, rates varied by a factor of 30. Excellent fits were obtained between the experimentally measured synchronization rates and the full nonlinear solution of Eq. 1 if we treated 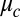 as a fitting parameter, which varied for each drop size and oil gap. We also fit synchronization rates using the explicitly calculated coupling strength, Eq. 2. Although the functional form of the coupling strength (Eq. 2) fit the time-dependent synchronization data well for a wide range of oil gaps and drop diameters, the combination of the Turing model (Eq. 1) with our explicit calculation of the interdrop coupling (Eq. 2), overestimates the coupling strength by nearly two orders of magnitude. That is, we replaced
as a fitting parameter, which varied for each drop size and oil gap. We also fit synchronization rates using the explicitly calculated coupling strength, Eq. 2. Although the functional form of the coupling strength (Eq. 2) fit the time-dependent synchronization data well for a wide range of oil gaps and drop diameters, the combination of the Turing model (Eq. 1) with our explicit calculation of the interdrop coupling (Eq. 2), overestimates the coupling strength by nearly two orders of magnitude. That is, we replaced 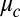 of Eq. 2 with
of Eq. 2 with 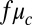 , and although theory predicts
, and although theory predicts 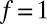 , experimentally we find
, experimentally we find 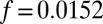 . Despite this discrepancy, the fact that only one phenomenological parameter, f, is needed to reconcile theory and experiment over a wide range of coupling strengths is an improvement over the original Turing model, where a different phenomenological parameter,
. Despite this discrepancy, the fact that only one phenomenological parameter, f, is needed to reconcile theory and experiment over a wide range of coupling strengths is an improvement over the original Turing model, where a different phenomenological parameter, 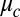 , is fitted for each drop diameter and oil gap. As a guide to theorists motivated to improve our calculation of the coupling strength, we note that the Turing model assumes a vanishing thin membrane, whereas our experimental system has a finite-sized oil gap. Our model of coupling strength, based on the assumptions of the Turing model, neglects four factors, each of which reduces coupling: nonuniformity in chemical gradients in the drop and the oil, accumulation of chemicals in the oil, time taken to diffuse across the oil, and chemical reactions within the oil.
, is fitted for each drop diameter and oil gap. As a guide to theorists motivated to improve our calculation of the coupling strength, we note that the Turing model assumes a vanishing thin membrane, whereas our experimental system has a finite-sized oil gap. Our model of coupling strength, based on the assumptions of the Turing model, neglects four factors, each of which reduces coupling: nonuniformity in chemical gradients in the drop and the oil, accumulation of chemicals in the oil, time taken to diffuse across the oil, and chemical reactions within the oil.
Having established the Turing model is quantitatively valid for a wide range of synchronization conditions with a single experimentally determined constant in the coupling term, 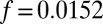 , we prepared a series of one-dimensional arrays of drops in rings and lines and determined the long-term emergent chemical states as a function of the two variables that most strongly control interdrop behavior: MA concentration and coupling strength. Coupling strength,
, we prepared a series of one-dimensional arrays of drops in rings and lines and determined the long-term emergent chemical states as a function of the two variables that most strongly control interdrop behavior: MA concentration and coupling strength. Coupling strength, 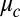 , is conveniently tuned experimentally by varying the drop size a and oil gap b using microfluidics. In Fig. 1 A–F, we illustrate examples of six distinct patterns with the symmetry corresponding to Turing cases (a–f). Five of the six patterns, Fig. 1 A and C–F, appear where predicted by theory in Fig. 2B. Four of the six patterns are identified with Turing cases (c, d, e, f). The fifth pattern has the same symmetry as Turing case (a). However, this pattern is predicted be a stationary, stable state for MA concentrations below 1 mM and therefore does not arise from a Turing instability, underscoring the point that observation of a chemical state with a pattern corresponding to a Turing instability is insufficient evidence to prove the state arises from a Turing mechanism (3, 6, 8, 30). Notably, the pattern with the symmetry of Turing case (b) is observed in a region of parameter space not predicted by theory. This is the sole discrepancy between theory and experiment, and we suspect that it reflects a shortcoming of the VE model. See SI Discussion for expanded analysis of each case and Movies S2 and S3 of the spatial-temporal patterns.
, is conveniently tuned experimentally by varying the drop size a and oil gap b using microfluidics. In Fig. 1 A–F, we illustrate examples of six distinct patterns with the symmetry corresponding to Turing cases (a–f). Five of the six patterns, Fig. 1 A and C–F, appear where predicted by theory in Fig. 2B. Four of the six patterns are identified with Turing cases (c, d, e, f). The fifth pattern has the same symmetry as Turing case (a). However, this pattern is predicted be a stationary, stable state for MA concentrations below 1 mM and therefore does not arise from a Turing instability, underscoring the point that observation of a chemical state with a pattern corresponding to a Turing instability is insufficient evidence to prove the state arises from a Turing mechanism (3, 6, 8, 30). Notably, the pattern with the symmetry of Turing case (b) is observed in a region of parameter space not predicted by theory. This is the sole discrepancy between theory and experiment, and we suspect that it reflects a shortcoming of the VE model. See SI Discussion for expanded analysis of each case and Movies S2 and S3 of the spatial-temporal patterns.
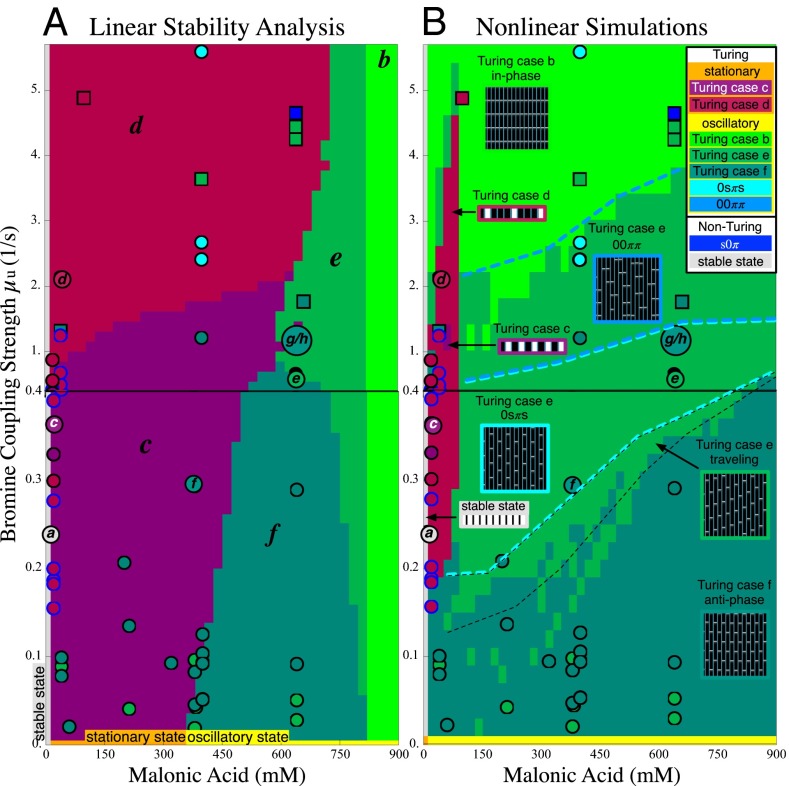
Fig. 2.
(A) Linear stability analysis (LSA) and (B) nonlinear simulations (NLS) of the Vanag–Epstein BZ model, as a function of bromine coupling strength, 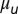 , and MA concentration. Note the scale change on the vertical axis at
, and MA concentration. Note the scale change on the vertical axis at 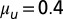 . In both figures, red hues represent stationary states, and green hues, oscillatory states. The data are plotted with circles for 1D experiments and squares for 2D experiments. The red disks outlined in blue indicate a transient initial cluster state settling into a stationary Turing instability. The data points with a letter in the center are included in Fig. 1. Space–time plots of oscillatory states are Inset in square areas; stationary states are Inset in rectangular areas. The dashed boundaries within the region of Turing case (e) of the NLS diagram indicate location of traveling waves, the 0sπs state (Fig. S6), and the
. In both figures, red hues represent stationary states, and green hues, oscillatory states. The data are plotted with circles for 1D experiments and squares for 2D experiments. The red disks outlined in blue indicate a transient initial cluster state settling into a stationary Turing instability. The data points with a letter in the center are included in Fig. 1. Space–time plots of oscillatory states are Inset in square areas; stationary states are Inset in rectangular areas. The dashed boundaries within the region of Turing case (e) of the NLS diagram indicate location of traveling waves, the 0sπs state (Fig. S6), and the 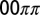 cluster state. All experimental data points are plotted according to the definitions of μ given in the text with
cluster state. All experimental data points are plotted according to the definitions of μ given in the text with 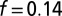 . (See SI Discussion for more on the plotting of data points.)
. (See SI Discussion for more on the plotting of data points.)
The behavior of finite rings depends on the number of drops, N, in the ring as seen in Fig. 1 G and H and Movie S3 for two rings with identical chemical composition, drop size, and spacing, but with five and six drops, respectively. For these particular chemical conditions and for N even, LSA predicts antiphase oscillations, corresponding to Turing instability (f) characterized by the wavevector–frequency pair 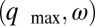 , as defined previously and in more detail in SI Text. Turing’s prediction is that for N odd, no two drops will undergo an oxidation transition simultaneously; there will be N beats per measure, whereas for N even there will be two beats per measure. For a ring of five drops, LSA predicts a waveform
, as defined previously and in more detail in SI Text. Turing’s prediction is that for N odd, no two drops will undergo an oxidation transition simultaneously; there will be N beats per measure, whereas for N even there will be two beats per measure. For a ring of five drops, LSA predicts a waveform 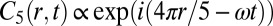 , with
, with 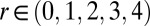 the drop number. In this expression, the phase is chosen such that a drop is oxidized when
the drop number. In this expression, the phase is chosen such that a drop is oxidized when 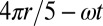 is equal to a multiple of
is equal to a multiple of 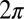 . As time advances in increments of one-fifth of a period, the oxidized state in Fig. 1G moves along the ring in a pentagramal sequence from drops
. As time advances in increments of one-fifth of a period, the oxidized state in Fig. 1G moves along the ring in a pentagramal sequence from drops 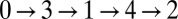 . For the ring of six drops,
. For the ring of six drops, 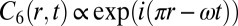 , with
, with 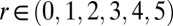 . As shown in Fig. 1H, all even-numbered drops oxidize simultaneously at the beginning of a period, and one-half a period later, all odd-numbered drops oxidize. In Fig. S4 and SI Methods, we present the LSA predictions for rings with three, four, five, and six drops and the corresponding experiments. For rings of drops, Turing’s LSA theory and our experiments are in complete agreement.
. As shown in Fig. 1H, all even-numbered drops oxidize simultaneously at the beginning of a period, and one-half a period later, all odd-numbered drops oxidize. In Fig. S4 and SI Methods, we present the LSA predictions for rings with three, four, five, and six drops and the corresponding experiments. For rings of drops, Turing’s LSA theory and our experiments are in complete agreement.
Using published chemical rate constants of the VE model (26) (Eq. S2 and Table S2), we calculate two state diagrams, one using Turing’s LSA and the other the full nonlinear simulation (NLS) of equations (Eq. 1) in one dimension, shown in Fig. 2. These theory plots have no adjustable parameters, as the Turing model treats the coupling strength, 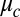 , as an independent variable. However, to assign coupling strengths to experiment, we explicitly calculate coupling strength using Eq. 2 to which we introduce a fitting parameter by replacing
, as an independent variable. However, to assign coupling strengths to experiment, we explicitly calculate coupling strength using Eq. 2 to which we introduce a fitting parameter by replacing 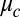 of Eq. 2 with
of Eq. 2 with 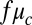 . We also fit the partition coefficient of the activator, Px. The best agreement between the NLS and experiment was obtained for
. We also fit the partition coefficient of the activator, Px. The best agreement between the NLS and experiment was obtained for 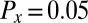 and
and 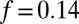 . With respect to the experimental state diagram, the NLS overestimates coupling strength eightfold, which is the same trend as in the case of the synchronization experiments. In experiments and in the NLS at low MA, we find a stable stationary state in which all of the drops are in-phase. This has the same pattern as Turing state (a), but as noted previously, LSA reveals this state is stable and it cannot be considered a Turing state, which arises from a homogeneous unstable state. Both state diagrams predict that as coupling strength increases above zero the same five Turing instabilities (b–f) appear with three oscillatory (green hues) and two nonoscillatory (red hues). Theory correctly predicted that for low MA concentration, arrays of large drops would oscillate and that arrays of smaller, chemically identical drops, would be stationary. For 1D arrays of drops in capillaries, the linear and nonlinear theories predict the same basic features, with two notable distinctions. First, nonlinearity strongly suppresses the stationary states. Second, “cluster” states, distinctive oscillating patterns consistent with Turing case (e) were experimentally sought and observed only after calculations of the nonlinear state diagram indicated their existence; thus, the Turing model is predictive. Further specific comparisons are included in SI Discussion, Figs. S5 and S6, and Movies S4 and S5.
. With respect to the experimental state diagram, the NLS overestimates coupling strength eightfold, which is the same trend as in the case of the synchronization experiments. In experiments and in the NLS at low MA, we find a stable stationary state in which all of the drops are in-phase. This has the same pattern as Turing state (a), but as noted previously, LSA reveals this state is stable and it cannot be considered a Turing state, which arises from a homogeneous unstable state. Both state diagrams predict that as coupling strength increases above zero the same five Turing instabilities (b–f) appear with three oscillatory (green hues) and two nonoscillatory (red hues). Theory correctly predicted that for low MA concentration, arrays of large drops would oscillate and that arrays of smaller, chemically identical drops, would be stationary. For 1D arrays of drops in capillaries, the linear and nonlinear theories predict the same basic features, with two notable distinctions. First, nonlinearity strongly suppresses the stationary states. Second, “cluster” states, distinctive oscillating patterns consistent with Turing case (e) were experimentally sought and observed only after calculations of the nonlinear state diagram indicated their existence; thus, the Turing model is predictive. Further specific comparisons are included in SI Discussion, Figs. S5 and S6, and Movies S4 and S5.
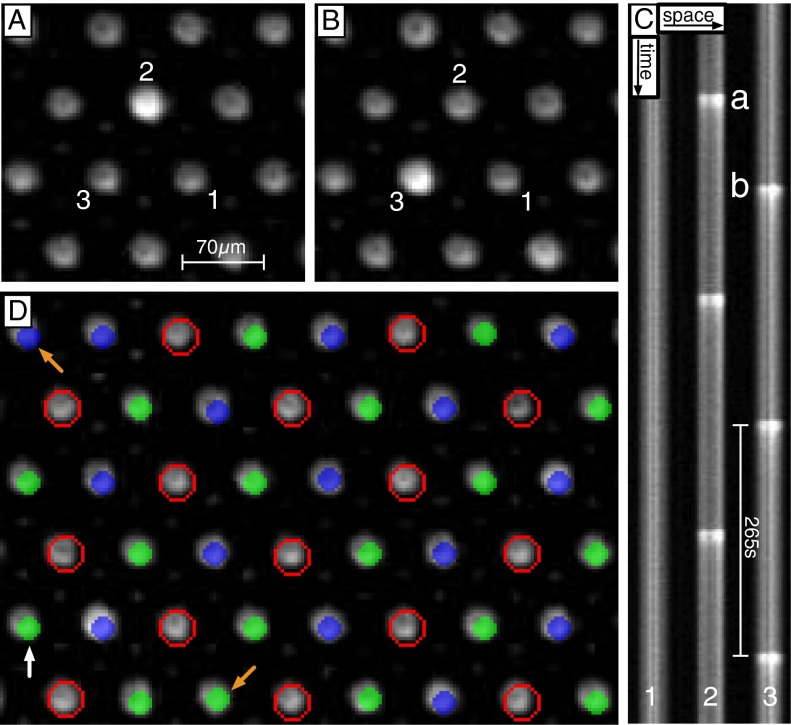
To investigate the effect of dimensionality on Turing instabilities, we performed experiments on close-packed hexagonal arrays of drops, reported as squares in Fig. 2. For conditions intermediate between stationary and oscillatory Turing instabilities, we observed a state, shown in Fig. 3 and Movie S6, that consists of a lattice composed of triangles of drops in which one drop is stationary and the other two oscillate with a phase difference of π, referred to as the 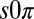 state (17). LSA requires all drops to share the same temporal behavior, i.e., all stationary, or all oscillatory; thus, the
state (17). LSA requires all drops to share the same temporal behavior, i.e., all stationary, or all oscillatory; thus, the 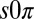 state cannot arise from a linear instability. However, it could be a nonlinear effect, but extensive numerical exploration of the full nonlinear chemistry using both the Turing and finite-element models on ordered hexagonal arrays failed to produce the
state cannot arise from a linear instability. However, it could be a nonlinear effect, but extensive numerical exploration of the full nonlinear chemistry using both the Turing and finite-element models on ordered hexagonal arrays failed to produce the 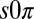 state. The qualitative discrepancy between theory and experiment suggests that a critical element is missing from the Turing model. Therefore, we developed a theoretical model for the
state. The qualitative discrepancy between theory and experiment suggests that a critical element is missing from the Turing model. Therefore, we developed a theoretical model for the 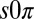 state, valid in general for systems undergoing a Hopf bifurcation, which requires additional conditions to the Turing model; the drops must be physically or chemically heterogeneous, with two drops that oscillate at a higher frequency than the third and that synchronize out-of-phase when isolated. Our analysis, elaborated in Fig. S7 and in SI Discussion, predicts that as the coupling strength between the two higher frequency oscillating drops and the third is increased, there is a transition to a state in which the third drop is stabilized in the nonoscillatory state, whereas the other two drops continue to oscillate out-of-phase. We numerically confirmed our theory by introducing heterogeneity into the Turing and finite-element models, which then produced the
state, valid in general for systems undergoing a Hopf bifurcation, which requires additional conditions to the Turing model; the drops must be physically or chemically heterogeneous, with two drops that oscillate at a higher frequency than the third and that synchronize out-of-phase when isolated. Our analysis, elaborated in Fig. S7 and in SI Discussion, predicts that as the coupling strength between the two higher frequency oscillating drops and the third is increased, there is a transition to a state in which the third drop is stabilized in the nonoscillatory state, whereas the other two drops continue to oscillate out-of-phase. We numerically confirmed our theory by introducing heterogeneity into the Turing and finite-element models, which then produced the 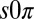 state. Experimentally, heterogeneity in drop frequency is about 5%, which is less than the 20% required by our simplified analytic theory; therefore, the
state. Experimentally, heterogeneity in drop frequency is about 5%, which is less than the 20% required by our simplified analytic theory; therefore, the 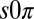 state bears more scrutiny. Only recently has heterogeneity been considered theoretically in reaction-diffusion networks (4, 31–33); our experimental work demonstrates the emergence of a mixed dynamical state caused by a remarkably small amount of heterogeneity. As the mechanism is generic, we expect it to apply to a large class of reaction-diffusion systems. Furthermore, we note that, in general, the experimental state diagram for 2D arrays of drops does not map well onto the one-dimensional nonlinear calculation, indicating that dimensionality plays a significant role in pattern selection.
state bears more scrutiny. Only recently has heterogeneity been considered theoretically in reaction-diffusion networks (4, 31–33); our experimental work demonstrates the emergence of a mixed dynamical state caused by a remarkably small amount of heterogeneity. As the mechanism is generic, we expect it to apply to a large class of reaction-diffusion systems. Furthermore, we note that, in general, the experimental state diagram for 2D arrays of drops does not map well onto the one-dimensional nonlinear calculation, indicating that dimensionality plays a significant role in pattern selection.
Fig. 3.
Observations of 2D arrays of 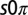 states. (A and B) Single frames demonstrating the
states. (A and B) Single frames demonstrating the 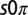 state. The frames correspond to the first two oxidation transitions, labeled a and b in C. (C) Space–time plot of drops 1–2–3 shown in A and B. Drop 1 is stationary, whereas drops 2–3 remain oscillatory with a phase difference of π. (D) A combined image where the stationary drops are outlined in red and the oscillatory drops are color coded by their phase difference,
state. The frames correspond to the first two oxidation transitions, labeled a and b in C. (C) Space–time plot of drops 1–2–3 shown in A and B. Drop 1 is stationary, whereas drops 2–3 remain oscillatory with a phase difference of π. (D) A combined image where the stationary drops are outlined in red and the oscillatory drops are color coded by their phase difference, 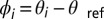 , where
, where 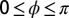 and
and 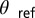 is the phase of the drop indicated with the white vertical arrow. Drops where
is the phase of the drop indicated with the white vertical arrow. Drops where 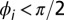 are green and
are green and 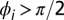 are blue. Notice that every third drop is stationary, and every oscillatory drop is out of phase with its immediate neighbors; two exceptions are noted with orange arrows. See Movie S6. Chemical conditions: 300 mM bromate, 3 mM ferroin, 0.4 mM Rubpy, 80 mM acid, 640 mM MA, and 10 mM NaBr. Drop size is ∼70 μm.
are blue. Notice that every third drop is stationary, and every oscillatory drop is out of phase with its immediate neighbors; two exceptions are noted with orange arrows. See Movie S6. Chemical conditions: 300 mM bromate, 3 mM ferroin, 0.4 mM Rubpy, 80 mM acid, 640 mM MA, and 10 mM NaBr. Drop size is ∼70 μm.
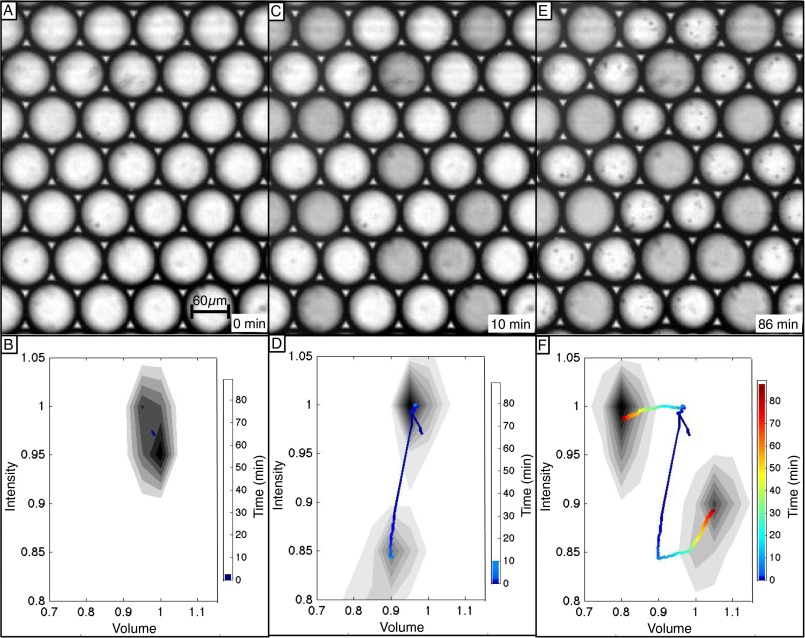
Turing, in “The Chemical Basis of Morphogenesis” (1), argued that, in case (d) (Fig. 1D), identical biological cells chemically differentiate into active and inactive stationary states. He further speculated that an activated gene could catalyze an increase in the concentration of intracellular molecules, thereby driving physical differentiation by increasing the osmotic pressure in that cell, causing it to swell. In Fig. 4 and Movie S7, we demonstrate precisely this sequence of chemical differentiation followed by physical morphogenesis in a hexagonal packing of identical drops prepared in the chemical state of Turing case (d). The drops, produced microfluidically as spheres, are stored in a rectangular capillary and are deformed into cylindrical disks with the same height as the capillary. The intensity of each drop is a monotonic function of the fraction of oxidized BZ catalyst it contains. As shown in Fig. 4A, the drops are initially homogeneous in chemistry and drop size. After an initial induction time, the drops undergo a transition from this unstable steady state to Turing case (d), in which one out of three drops is in the reduced (dark) state and two out of three are oxidized (bright), shown in Fig. 4C. This chemical differentiation occurs with the drop size remaining constant. The oxidized drops consume reagents faster than the reduced drops. This creates an osmotic pressure imbalance, causing water to flow from the oxidized to reduced drops, creating a morphological transformation in which the initially homogeneous cells differentiate into two populations with distinct chemical redox states and physical sizes, as shown in Fig. 4E. Quantitative measurements of the volume changes are in agreement with theory, as elaborated in SI Text.
Fig. 4.
Images and histograms of drops demonstrating morphogenesis plotted as fraction of original drop intensity and fraction of original drop volume. Intensity is a function of the chemical state of the BZ catalyst; bright drops are oxidized, and dark drops reduced. The color-coded line tracks the center of each peak as a function of time. (A and B) Initially, drops are homogenous in both intensity, or chemical state, and physical volume. (C and D) At intermediate times, the drops undergo a Turing bifurcation, becoming heterogeneous in oxidation state, but remaining homogenous in volume, as seen by the differentiation into lighter and darker drops of equal size. (E and F) At later times, drops are heterogeneous in both oxidation state and volume. The oxidized (bright) drops shrink and reduced (dark) drops swell. See Movie S7. Chemical conditions (Table S3): 200 mM MA, 0.4 mM Rubpy, 0 mM NaBr, 80 mM H2SO4, 300 mM NaBrO3, 3 mM ferroin, 0.05 × 1-mm rectangular capillary, and initial drop size of ∼66 μm.
Conclusion
Turing’s model predicts the circumstances under which initially homogeneous diffusively coupled cells will spontaneously evolve spatiotemporal chemical structures. However, only a small subset of chemical reactions lead to the Turing instabilities; most reactions remain stably homogeneous. In emulsions of the oscillatory BZ chemical reaction, tuning coupling strength and chemical dynamics by changing drop size and MA concentration, respectively, reveals seven distinct chemical structures, six of which were predicted by theory. Turing’s model eliminates the oil phase separating cells and treats the coupling strength as a free parameter. We extended Turing’s model to explicitly calculate the coupling strength. Experiments revealed that the extended model overestimated intercellular coupling by nearly two orders of magnitude. One experimentally determined parameter was introduced to reconcile theory and experiment for a wide range of conditions; eliminating this one phenomenological parameter remains a theoretical challenge. LSA of the Turing model captures most of the qualitative features of the observed chemical pattern formation, thereby providing a mechanistic explanation of pattern selection. However, the full nonlinear model must be solved to achieve quantitative agreement between experiment and theory. We observe one chemical pattern inconsistent with the original Turing model and propose a generic mechanism whereby slight heterogeneity in the cells leads to a state of mixed dynamical and stationary character. The Turing model is regarded as a metaphor for morphogenesis in biology, useful for a conceptual framework and to guide modeling, but not for prediction (7). In contrast, in this chemical system, we demonstrated that the Turing model quantitatively explains “materials morphogenesis” in which cellular compartments first chemically and then physically differentiate, raising the possibility of exploiting this form of reaction-diffusion chemistry for materials science applications.
Supplementary Material
Acknowledgments
This work was supported by National Science Foundation Materials Research Science and Engineering Centers Grant DMR-0820492 and Grant CHE-1012428.
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1322005111/-/DCSupplemental.
References
- 1.Turing AM. The chemical basis of morphogenesis. Philos Trans R Soc Lond. 1952;237(641):37–72. [Google Scholar]
- 2.Karsenti E. Self-organization in cell biology: A brief history. Nat Rev Mol Cell Biol. 2008;9(3):255–262. doi: 10.1038/nrm2357. [DOI] [PubMed] [Google Scholar]
- 3.Kondo S, Miura T. Reaction-diffusion model as a framework for understanding biological pattern formation. Science. 2010;329(5999):1616–1620. doi: 10.1126/science.1179047. [DOI] [PubMed] [Google Scholar]
- 4.Mendez V, Fedotov S, Horsthemke W. Reaction-Transport Systems: Mesoscopic Foundations, Fronts, and Spatial Instabilities. Berlin: Springer; 2010. [Google Scholar]
- 5.Müller P, et al. Differential diffusivity of Nodal and Lefty underlies a reaction-diffusion patterning system. Science. 2012;336(6082):721–724. doi: 10.1126/science.1221920. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Meinhardt H. Turing’s theory of morphogenesis of 1952 and the subsequent discovery of the crucial role of local self-enhancement and long-range inhibition. Interface Focus. 2012;2(4):407–416. doi: 10.1098/rsfs.2011.0097. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Reinitz J. Pattern formation: Turing at 100. Nature. 2012;482(7386):464. doi: 10.1038/482464a. [DOI] [PubMed] [Google Scholar]
- 8.Morelli LG, Uriu K, Ares S, Oates AC. Computational approaches to developmental patterning. Science. 2012;336(6078):187–191. doi: 10.1126/science.1215478. [DOI] [PubMed] [Google Scholar]
- 9.Schweizer J, et al. Geometry sensing by self-organized protein patterns. Proc Natl Acad Sci USA. 2012;109(38):15283–15288. doi: 10.1073/pnas.1206953109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Noszticzius Z, Horsthemke W, McCormick WD, Swinney HL, Tam WY. Sustained chemical waves in an annular gel reactor. Nature. 1987;329(6140):619–620. [Google Scholar]
- 11.Castets V, Dulos E, Boissonade J, De Kepper P. Experimental evidence of a sustained standing Turing-type nonequilibrium chemical pattern. Phys Rev Lett. 1990;64(24):2953–2956. doi: 10.1103/PhysRevLett.64.2953. [DOI] [PubMed] [Google Scholar]
- 12.Ouyang Q, Swinney HL. Transition from a uniform state to hexagonal and striped Turing patterns. Nature. 1991;352(6336):610–612. [Google Scholar]
- 13.Epstein IR, Pojman JA. Introduction to Nonlinear Chemical Dynamics. Oscillations, Waves, Patterns and Chaos. New York: Oxford Univ Press; 1998. [Google Scholar]
- 14.Horváth J, Szalai I, De Kepper P. An experimental design method leading to chemical Turing patterns. Science. 2009;324(5928):772–775. doi: 10.1126/science.1169973. [DOI] [PubMed] [Google Scholar]
- 15.Inaba M, Yamanaka H, Kondo S. Pigment pattern formation by contact-dependent depolarization. Science. 2012;335(6069):677. doi: 10.1126/science.1212821. [DOI] [PubMed] [Google Scholar]
- 16.Li A, et al. Shaping organs by a wingless-int/Notch/nonmuscle myosin module which orients feather bud elongation. Proc Natl Acad Sci USA. 2013;110(16):E1452–E1461. doi: 10.1073/pnas.1219813110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Toiya M, González-Ochoa HO, Vanag VK, Fraden S, Epstein IR. Synchronization of chemical micro-oscillators. J Phys Chem Lett. 2010;1(8):1241–1246. [Google Scholar]
- 18.Delgado J, et al. Coupled oscillations in a 1D emulsion of Belousov-Zhabotinsky droplets. Soft Matter. 2011;7(7):3155–3167. [Google Scholar]
- 19.Zaikin AN, Zhabotinsky AM. Concentration wave propagation in two-dimensional liquid-phase self-oscillating system. Nature. 1970;225(5232):535–537. doi: 10.1038/225535b0. [DOI] [PubMed] [Google Scholar]
- 20.Field RJ, Burger M. Oscillations and Traveling Waves in Chemical Systems. New York: Wiley; 1985. [DOI] [PubMed] [Google Scholar]
- 21.Fukuda H, Morimura H, Kai S. Global synchronization in two-dimensional lattices of discrete Belousov-Zhabotinsky oscillators. Physica D. 2005;205(1):80–86. [Google Scholar]
- 22.Holtze C, et al. Biocompatible surfactants for water-in-fluorocarbon emulsions. Lab Chip. 2008;8(10):1632–1639. doi: 10.1039/b806706f. [DOI] [PubMed] [Google Scholar]
- 23.Toiya M, Vanag VK, Epstein IR. Diffusively coupled chemical oscillators in a microfluidic assembly. Angew Chem Int Ed Engl. 2008;47(40):7753–7755. doi: 10.1002/anie.200802339. [DOI] [PubMed] [Google Scholar]
- 24.Vanag VK, Epstein IR. Pattern formation in a tunable medium: The Belousov-Zhabotinsky reaction in an aerosol OT microemulsion. Phys Rev Lett. 2001;87(22):228301. doi: 10.1103/PhysRevLett.87.228301. [DOI] [PubMed] [Google Scholar]
- 25.Epstein IR, Vanag VK. Complex patterns in reactive microemulsions: Self-organized nanostructures? Chaos. 2005;15(4):047510. doi: 10.1063/1.2102447. [DOI] [PubMed] [Google Scholar]
- 26.Vanag VK, Epstein IR. A model for jumping and bubble waves in the Belousov-Zhabotinsky-aerosol OT system. J Chem Phys. 2009;131(10):1–7. [Google Scholar]
- 27.Vanag VK, Epstein IR. Excitatory and inhibitory coupling in a one-dimensional array of Belousov-Zhabotinsky micro-oscillators: Theory. Phys Rev E Stat Nonlin Soft Matter Phys. 2011;84(6):066209. doi: 10.1103/PhysRevE.84.066209. [DOI] [PubMed] [Google Scholar]
- 28.Vanag VK, Epstein IR. Diffusive instabilities in heterogeneous systems. J Chem Phys. 2003;119(14):7297–7307. [Google Scholar]
- 29.Kuramoto Y. Chemical Oscillations, Waves and Turbulence. Berlin: Springer; 1984. [Google Scholar]
- 30.Maini PK, Baker RE, Chuong CM. Developmental biology. The Turing model comes of molecular age. Science. 2006;314(5804):1397–1398. doi: 10.1126/science.1136396. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Colizza V, Pastor-Satorras R, Vespignani V. Reaction-diffusion processes and metapopulation models in heterogeneous networks. Nat Phys. 2007;3(4):276–282. [Google Scholar]
- 32.Nakao H, Mikhailov A. Turing patterns in network-organized activator-inhibitor systems. Nat Phys. 2010;6(7):544–550. [Google Scholar]
- 33.Wolfrum M. The Turing bifurcation in network systems: Collective patterns and single differentiated nodes. Physica D. 2012;241(16):1353–1357. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.