MIRD Pamphlet No. 24: Guidelines for Quantitative ¹³¹I SPECT in Dosimetry Applications

Abstract

The reliability of radiation dose estimates in internal radionuclide therapy is directly related to the accuracy of activity estimates obtained at each imaging time point. The recently published MIRD pamphlet no. 23 provided a general overview of quantitative SPECT imaging for dosimetry. The present document is the first in a series of isotope-specific guidelines that will follow MIRD 23 and focuses on one of the most commonly used therapeutic radionuclides, ¹³¹I. The purpose of this document is to provide guidance on the development of protocols for quantitative ¹³¹I SPECT in radionuclide therapy applications that require regional (normal organs, lesions) and 3-dimensional dosimetry.

The most significant γ-rays associated with ¹³¹I have energies of 364 keV (82%), 637 keV (7.2%), and 723 keV (1.8%), and typically SPECT imaging is performed using a photopeak energy window centered at 364 keV and a high-energy parallel-hole collimator. These SPECT images are degraded by the poor spatial resolution obtained with typical high-energy collimators and the significant fraction of collimator septal penetration, scatter, and down scatter due to the high energy of the 364-keV γ-rays imaged and the presence of significant numbers of higher-energy γ-rays. The system spatial resolution for ¹³¹I imaging with typical high-energy collimators is substantially worse than that for ^99mTc and low-energy collimators. For a typical SPECT/CT system with a 9.5-mm-thick crystal, the manufacturer-specified system resolutions at 10 cm are 7.4, 9.4, and 13.4 mm in full width at half maximum for a low-energy high-resolution collimator, a low-energy all-purpose collimator, and a high-energy collimator, respectively.

In SPECT imaging for dosimetry applications, the goal is absolute quantification—that is, to measure the radioactivity within a target volume in absolute units such as becquerels. Although SPECT activity quantification accuracies (i.e., how close the activity estimated from the SPECT measurement is to the true activity) of better than 5% have been reported for ^99mTc (1), associated errors for ¹³¹I are typically larger. The accuracy of ¹³¹I quantification can be significantly improved with iterative reconstruction including compensation for nonhomogeneous attenuation, scatter, and CDR. Table 1 summarizes past phantom and in vivo validation studies of quantitative ¹³¹I SPECT and the accuracy that was achieved. According to Table 1, with state-of-the-art techniques such as combined SPECT/CT systems and iterative reconstruction with compensation for degrading effects, activity quantification accuracy within 10%–15% can be achieved for most organs typically of interest in internal-emitter therapy applications. For small volumes, such as tumors with a diameter less than 2–3 times the system spatial resolution, further compensation for partial-volume effects is needed to improve accuracy. ¹³¹I SPECT imaging guidelines for achieving such accuracies are discussed below together with 2 clinical examples of quantitative SPECT in internal therapy dosimetry applications.

TABLE 1.

Phantom and In Vivo Validation Studies of Quantitative ¹³¹I SPECT

Study	Application/ potential application	Study	System	Reconstruction	Quantification accuracy*
Song 2011 (14)	RIT dosimetry	Phantom simulations	Simulation study	OSEM with ESSE SC, AC, CDRC	< 5% error for larger organs; 10%–15% for smaller organs
Dewaraja 2010 (4)	RIT dosimetry	Phantom measurements/simulations	SPECT/CT	OSEM with TEW SC, CT-based AC, CDRC	<17% error for 8- to 95-mL spheres; 31% for 4-mL sphere
Pereira 2010 (28)	Dosimetry	Phantom measurements	SPECT/CT	OSEM with TEW SC, CT-based AC	Measured-to-true ratios of >90% for 11.5-mL sphere, 13%–63% for 1.4- and 2.2-mL spheres
Shcherbinin 2008 (29)	MIBG dosimetry	Phantom measurements	SPECT/CT	OSEM with analytic scatter model, CT-based AC, CDRC	3%–4% error for 32-mL volumes
Koral 2005 (24)	RIT dosimetry	Phantom measurements	SPECT and CT separately	OSEM with TEW SC, CT-based AC, CDRC	<7% average error for 100-mL sphere
Gonzalez Trotter 2001 (13)	Brain tumor RIT	Phantom measurements	SPECT with specialized collimator	OSEM with TEW SC, AC, CDRC	<20% error for 6- to 11-mL spheres
Alaamer 1993 (18)	MIBG dosimetry	Phantom measurements	SPECT and CT separately	Reconstruction with SC and AC	SE = 0.24 MBq for 6–600 mL
Israel 1990 (19)	MIBG and thyroid carcinoma dosimetry	Phantom measurements and in vivo patient study of 131I concentration in urinary bladder	SPECT	FBP	Phantom: good correlation with truth (r = 0.98, SEE = 20.94 counts/voxel); patients: good correlation with concentration in urine (r = 0.98, SEE = 25.049 kBq/mL)
Riggs 1988 (30)	RIT	Phantom measurements and in vivo patient study of 131I concentration in heart	SPECT	FBP with DEW SC, Chang AC	Phantom: <10% error; patients: good correlation with concentration in serial blood

^*Percentage difference between SPECT estimated activity and truth.

RIT = radioimmunotherapy; ESSE = effective scatter source estimation; SC = scatter correction; AC = attenuation correction; CDRC = CDR compensation; MIBG = metaiodoben-zylguanidine; FBP = filtered backprojection; DEW = dual energy windows, SE = standard error; SEE = standard error of the estimate.

GUIDELINES

SPECT System

Multiple-head SPECT/CT systems should be used when possible. Single-head cameras may be adequate for imaging after the therapy administration but are not recommended for imaging after the diagnostic (tracer) administration (e.g., for predictive dosimetry), as this use may result in unacceptable levels of image noise or prohibitively prolong the scan time needed to obtain a sufficient number of detected events.

High-energy parallel-hole collimators should be used to reduce septal penetration by the high-energy photons. Measured point-source images corresponding to medium- and high-energy collimators are compared in Figure 1, demonstrating the reduction in penetration and scatter obtained with high-energy collimation. Although the measured planar sensitivity is approximately 4 times higher with the medium-energy collimator, most of the additional counts are due to “unwanted” collimator scatter and septal-penetration events that require subsequent compensation. This is evident from Monte Carlo simulation (2) of a ¹³¹I point source in air, where the geometric, penetration, and scatter fractions of total counts were, respectively, 15%, 48%, and 37% for medium-energy collimation and 51%, 24%, and 25% for high-energy collimation.

FIGURE 1.

Images corresponding to ¹³¹I pointlike source measured in air at 20 cm with medium-energy (left) and high-energy (right) collimators. Images are shown on a logarithmic gray scale (individually normalized). System planar sensitivities for a 364-keV window were 319 cps/MBq for the medium-energy collimator and 82 cps/MBq for the high-energy collimator, but the fraction of unwanted penetration and scatter events was much higher with the medium-energy collimator than with the high-energy collimator, 85% versus 49%, based on Monte Carlo simulation.

In imaging after tracer administration, a system equipped with a thicker NaI crystal (e.g., 15.9 mm thick) is preferred to a standard 9.5-mm-thick crystal. The thicker crystal increases the efficiency for detecting the 364-keV γ-ray by almost a factor of 2, with only a small loss of intrinsic spatial resolution. For example, for a typical SPECT/CT system with 9.5- and 15.9-mm-thick crystals, the manufacturer-specified intrinsic resolution values are less than 3.8 mm and less than 4.5 mm, respectively. The difference in system resolution resulting from this difference in intrinsic resolution would be negligible for a typical high-energy collimator. For imaging after a therapeutic administration, a thinner crystal with lower sensitivity might be appropriate, to allow earlier imaging than would be possible with a more sensitive camera (due to the dead-time effects discussed in the “Processing” section).

Routine quality control (3), including assessment of uniformity of response, spatial and energy resolution, and center-of-rotation alignment, is a prerequisite for high-quality SPECT imaging. With hybrid systems, the mechanical alignment between the SPECT and CT subsystems is also an important part of quality control.

Image Acquisition

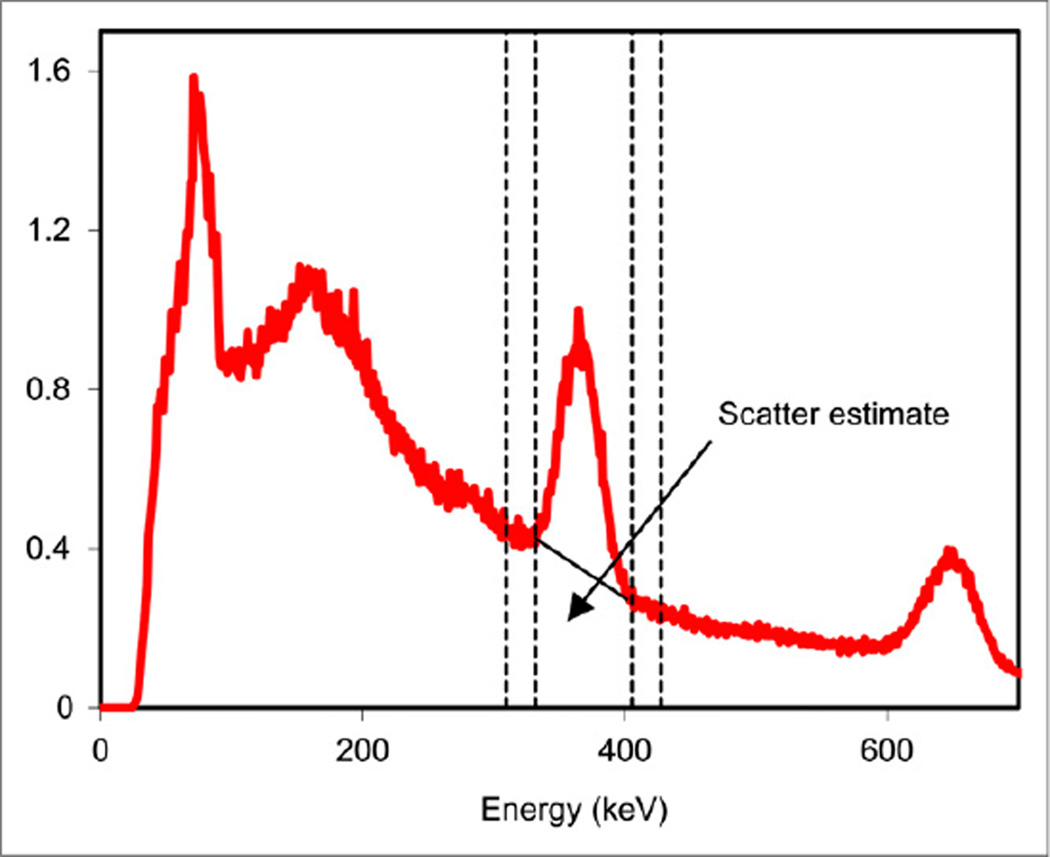
A photopeak energy window centered at 364 keV and 15%–20% in width is recommended. These characteristics satisfy the requirement that the acquisition window be at least twice as wide as the energy resolution of the detector to avoid excessive count loss while keeping the window narrow enough to avoid accepting too many scattered photons. For triple-energy-window (TEW) scatter correction, two 6% windows adjacent to the photopeak window are recommended (Fig. 2), as used in past ¹³¹I studies (4–6). The TEW window width is selected as a compromise between accuracy and noise.

FIGURE 2.

Energy spectrum corresponding to a radioimmunotherapy patient imaged 2 d after administration of 2.8 GBq of ¹³¹I. Windows for TEW (310–332 keV and 405–427 keV) are shown by dashed lines, and the trapezoidal scatter estimate is indicated in the 332–405 keV photopeak window.

Imaging with counting rates higher than approximately 50 kcps is not recommended because the effects of camera dead time (resulting in mispositioning of events and a nonlinear relationship between activity and counts) will be excessive, and accurate dead-time correction will be difficult (7). When one is imaging after the administration of several gigabecquerels of activity, such as in ¹³¹I-metaiodobenzylguanidine therapy or thyroid cancer therapy, this consideration typically limits the earliest imaging time point to 2–4 d after injection.

In posttherapy ¹³¹I imaging, for which counting rates are typically 10–40 kcps, the acquisition time should be no longer than 40 s per projection view, which corresponds to a 20-min total acquisition time (with 60 views and a dual-head system). For lower counting rates, such as those encountered during imaging after ¹³¹I tracer administration, total acquisition times of up to 30 min are often preferable. However, a longer time may not be needed for quantification of activity in larger organs when the organ boundaries are known (e.g., CT image obtained from a SPECT/CT system) as shown by a study evaluating the effects of acquisition time (8). MIRD pamphlet no. 23 (9) indicates that the highest image resolution would be achieved by acquisition into 128 × 128 pixel matrices, but if counting rates are low, image noise can be reduced by the use of 64 × 64 pixel matrices, with angular sampling (over 360°) of at least 128 or 64 projections, respectively. Body contouring should be used when available.

Processing

Preprocessing

Dead-time correction at high counting rates is particularly important in ¹³¹I imaging because of the significant number of events with energies outside the energy of the photopeak window that nevertheless contribute to camera dead time. Dead-time correction factors (true rate divided by measured rate) of as high as 1.2–1.5 have been reported for counting rates of more than 40 kcps for imaging after ¹³¹I-metaiodobenzylguanidine therapy (10) and 1.1 for counting rates of 18 kcps after ¹³¹I radioimmunotherapy (11). A system-specific dead-time model and dead-time constant should be determined by phantom experiments using the same window setting as used for patient studies, as well as similar scattering conditions (9).

The projection images corresponding to the 2 narrow windows used in TEW scatter correction typically have low counts and therefore high statistical uncertainty (noise), which can be propagated into the scatter estimate and the reconstructed image. Thus, the projection data in these windows should be low-pass-filtered (smoothed), for example, using a gaussian filter, which does not introduce negative values, before their use for scatter compensation.

Reconstruction

Iterative reconstruction using statistically based methods such as ordered-subsets expectation maximization (OSEM) is a requirement for accurate quantification of radionuclides with high-energy emissions, as these methods allow for optimal and unified correction for image-degrading physical effects. As discussed in MIRD 23, the number of iterations to be used in a patient study should be based on the bias-variance trade-off, as determined by ¹³¹I phantom experiments and other considerations (9, 12).

Attenuation compensation using CT-based patient-specific attenuation maps is now considered the standard for accurate quantification. With SPECT/CT systems, an attenuation map coregistered to SPECT reconstruction space can be generated using software provided with the system. If not, the relationship between CT number and the linear attenuation coefficient at 364 keV can be determined by a system-specific measurement using a phantom with rods of known composition (9). When CT is not available, a uniform narrow-beam attenuation coefficient corresponding to soft tissue or water (0.11 cm⁻¹ at 364 keV) can be assigned within the body contour, which often can be determined from the emission data. However, uniform attenuation compensation can result in substantial errors when applied to heterogeneous regions of the body and should be used only for homogeneous regions such as the brain and mid abdomen, which are comprised predominantly of soft tissue.

Scatter in ¹³¹I SPECT consists of 364-keV photons and high-energy photons (637 and 723 keV) that scatter in the patient or collimator– detector system and are detected in the 364-keV photopeak window. TEW scatter correction (6) is practical to implement clinically and is particularly well suited for ¹³¹I because the use of a third window above the photopeak accounts for down scatter of the higher-energy emissions into the 364-keV photopeak window, unlike methods based on 2 windows. In typical ¹³¹I patient imaging studies, the scatter events in the photopeak window estimated by TEW are 40%–50% of the total events (see, for example, the trapezoidal estimate in Fig. 2). High quantitative accuracy has been demonstrated in past ¹³¹I SPECT studies with TEW scatter correction (4, 6, 13). Model- or Monte Carlo–based down-scatter estimation has also demonstrated good quantitative accuracy for ¹³¹I SPECT but requires specialized software for modeling the down scatter (14).

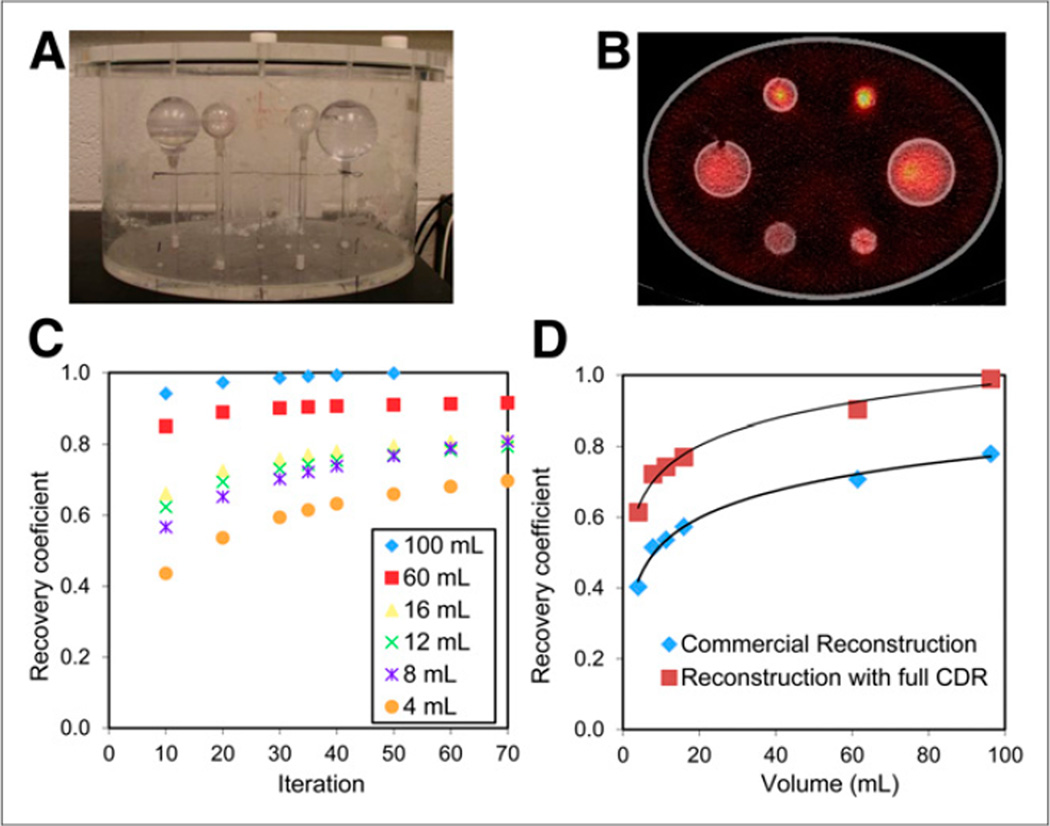
For high-energy photon emitters such as ¹³¹I, modeling the full (intrinsic, geometric, scatter, and penetration components) collimator–detector response (CDR) in the iterative reconstruction is especially important because of the higher probability of collimator scatter and septal penetration. Although clearly less important than in the case of medium-energy collimation, these events are highly significant even with high-energy collimation (~50% nongeometric events). However, the CDR model in commercial reconstruction software typically models only the intrinsic and geometric components. When possible, reconstruction software that includes modeling of collimator scatter and penetration should be used, as this leads to significantly higher count recovery for ¹³¹I (Fig. 3D). The full ¹³¹I CDR can be determined by point-source measurements or Monte Carlo simulations (9).

FIGURE 3.

Measurement of RCs discussed in patient example 1. (A) Phantom set-up. (B) SPECT/CT image. (C) RC as function of OSEM iteration number. (D) RC as function of volume at 35 iterations. RCs that were determined with commercial OSEM reconstruction are also shown.

Postprocessing

Postreconstruction filtering to suppress noise is recommended when the quantity of interest is the 3-dimensional activity distribution for nonuniform dosimetry, but not when quantifying the total target activity to determine the mean dose to a target (9, 12). Noise is not a major problem in posttherapy ¹³¹I imaging, for which counting rates are typically 10–40 kcps (10, 11), but can be significant when imaging after a tracer administration, especially at later time points after administration (where counting rates can be <1 kcps).

Quantification

Camera Calibration

For absolute quantification, the system sensitivity (calibration factor that converts reconstructed SPECT counts to activity) must be determined by imaging a known activity that is measured using an accurate dose calibrator traceable to national standards laboratories. The simplest calibration procedure uses a planar acquisition with a pointlike source (or a small volume of activity in a syringe or Petri dish) to determine the in-air camera sensitivity assuming negligible scatter and attenuation. However, with radionuclides such as ¹³¹I, there is significant collimator scatter even in such a point-source measurement. In addition, the point-source calibration is appropriate only when patient imaging data are reconstructed with highly accurate corrections for scatter, attenuation, and CDR. Therefore, to minimize the effects of imperfect corrections, the preferred procedure is to perform a calibration measurement with a phantom that approximates the scatter and attenuation conditions in patient imaging, such as in a water-filled tank with or without inserts. Acquisition and processing of the calibration study, including delineation of the target, should be performed in the same manner as in the patient study. The calibration factor, in units of cps/MBq for example, is then determined by dividing the total volume-of-interest reconstructed counts by the known activity and acquisition time. In past ¹³¹I studies, a cylindrical tank with uniform activity (15) as well as hot spheres (4) or cylindrical inserts (5) has been used for the calibration. In the latter study, the volume of the calibration insert was varied to match the volume of the patient structure that was being quantified. If a relatively large target volume with negligible partial-volume effects is used to determine the calibration factor, partial-volume correction is needed when using this calibration to quantify activity in small structures. A further refinement that has been shown to be significant for ¹³¹I and in posttracer versus posttherapy imaging is a counting rate–dependent calibration factor (16).

Target Definition

For activity quantification and dose estimation at the organ or tumor level, the volume of interest must be accurately defined (17). However, contouring a target on the basis of the ¹³¹I SPECT image alone is difficult because of the poor spatial resolution obtained with high-energy collimators. The preferred method is to contour the target on a high-resolution anatomic image set, such as CT, and apply it to the coregistered SPECT image set. Some ¹³¹I dosimetric studies have relied on SPECT thresholding methods to delineate the target when CT was not available (18, 19) or when the structure was difficult to delineate on CT (20). If SPECT thresholding is being used, the optimum threshold for the patient study should be determined by system-specific phantom experiments (19, 21, 22).

Partial-Volume Correction

Partial-volume correction is especially important for ¹³¹I because of the poor spatial resolution and is recommended for small organs or tumors (diameters less than 2–3 times the system spatial resolution) even with iterative reconstruction incorporating CDR compensation. A practical postreconstruction approach for partial-volume correction at the regional level is the use of volume-dependent recovery coefficients (RC) determined by physical phantom measurements or well-validated Monte Carlo simulation. The RC, defined as the ratio of apparent activity to true activity, can be applied to adjust the activity of small structures after quantification. For example, in the ¹³¹I phantom results presented in Figure 3, with a practical number of iterations the RC is less than 0.7 for sphere volumes of less than 8 mL. In this case, activity quantification error in such volumes will exceed 30% if RCs are not applied. Because RCs depend not only on target volume but also on other factors such as target shape, more sophisticated partial-volume correction methods are available and are recommended for objects not well approximated as spheres (9). In any event, because of the poor ¹³¹I SPECT resolution (~1.3 cm in full width at half maximum at 10 cm), a large error in activity estimates can be expected for volumes smaller than approximately 8 mL (or diameters < 2.5 cm, which is less than twice the full width at half maximum). Thus, estimates for such volumes should be used with caution.

PATIENT EXAMPLE 1: QUANTITATIVE SPECT/CT FOR 3-DIMENSIONAL TUMOR DOSIMETRY IN ¹³¹I-TOSITUMOMAB RADIOIMMUNOTHERAPY

Acquisition

All measurements were performed on a Symbia TruePoint SPECT/ CT scanner (Siemens) with 6-slice CT capability equipped with a high-energy general-purpose parallel-hole collimator. The effective axial field of view of the SPECT camera was 390 mm, and the crystal thickness 15.9 mm. The SPECT acquisition parameters were a 180° rotation and 30 stops per head, 40 s per stop for patient imaging (80 s per stop for the calibration phantom), body contouring, a 20% photopeak window centered at 364 keV, two 6% scatter windows abutting and on either side of the photopeak window, and a 128 × 128 projection matrix (4.8 × 4.8 mm pixel size). The system spatial resolutions measured with a ¹³¹I source at 5, 10, and 20 cm from the collimator face were, respectively, 11.7, 14.9, and 22.3 mm in full width at half maximum and 21.2, 27.1, and 40.6 mm in full width at tenth maximum. The CT component of acquisition used full-circle rotation, 130 kVp, 35 mAs, and 5-mm-thick slices. The x-ray effective dose due to each low-dose CT scan was 2.8 mSv. The reconstructed CT matrix size was 512 × 512 × 78 with a voxel size of 0.98 × 0.98 × 5 mm.

Dead-Time Correction

SPECT projection data corresponding to posttherapy patient imaging were corrected for camera dead time using a paralyzable model and the dead-time constant for the system, previously determined to be 2.5 µs (16). In this case, the true projection counting rate, n, was determined iteratively on the basis of the measured counting rate, m, using the relationship m = ne^−nτ, where τ is the dead-time constant (23).

Image Reconstruction

A 3-dimensional OSEM reconstruction code (24) developed in-house was used because it provided some features not available with the system software. These features were dead-time correction and modeling of the full CDR, including scatter and penetration (the commercial software for this system included only the intrinsic and geometric response in the CDR model). The OSEM reconstruction also included TEW scatter correction and attenuation correction using the CT-based attenuation map from the system. Reconstruction parameters were 35 iterations, 6 subsets, and no postfiltering.

Calibration Measurement

The calibration experiment used a water-filled cylinder phantom (Data Spectrum) with a 23 × 31.5 cm elliptical cross section and 20.5 cm in height and was performed at 3 different counting rates (main window counting rates of 21, 9, and 2 kcps) over a period of 1 mo as the injected ¹³¹I activity decayed (initial activity was 740 MBq as measured by a Capintec dose calibrator with accuracy within 5%). These counting rates were selected for the calibration measurement because they mimic the typical counting rates observed during posttracer and posttherapy patient imaging in ¹³¹I tositumomab radioimmunotherapy. The reconstructed SPECT counts corresponding to the entire phantom were divided by the known activity in the phantom times the acquisition time to determine the calibration factor. The calibration factors corresponding to the above counting rates were 100, 104, and 109 cps/MBq, respectively, and a least-squares fit determined the calibration-factor-versus-counting-rate relationship. This quantification procedure was verified using a Data Spectrum elliptical phantom with hot spheres representing tumors. The SPECT-derived activities without partial-volume correction were within 17% of the truth for sphere volumes of 8–95 mL and within 31% for a 4-mL sphere (4).

To determine the number of OSEM updates (subsets multiplied by iterations) and RCs for patient imaging, a phantom experiment with hot spheres in a warm background, simulating tumor imaging, was performed (Fig. 3). The sphere volumes ranged from 4 to 95 mL, and the activity in the entire phantom was 192 MBq. The sphere-to-background activity concentration ratio was 5:1 for the 3 larger spheres and 6:1, 9:1, and 17:1 for the 3 smaller spheres. After the SPECT acquisition and OSEM reconstruction, the sphere activities (within CT-defined volumes of interest) were quantified using the calibration factor. The RC for each sphere is plotted as a function of OSEM iteration number (with 6 subsets) in Figure 3C. These data indicated that there was high recovery (>90%) for the larger spheres after about 30 iterations. On the basis of this result, we chose to use 35 iterations in patient studies because the tumor size in this patient population was relatively large (median, 34 mL; range, 2–423 mL (25)). The RC at 35 iterations is plotted as a function of sphere volume in Figure 3D. Also shown in this figure are the RCs corresponding to the commercial (Siemens) OSEM reconstruction where the full CDR was not modeled. These RCs show up to 50% less recovery.

Patient Data

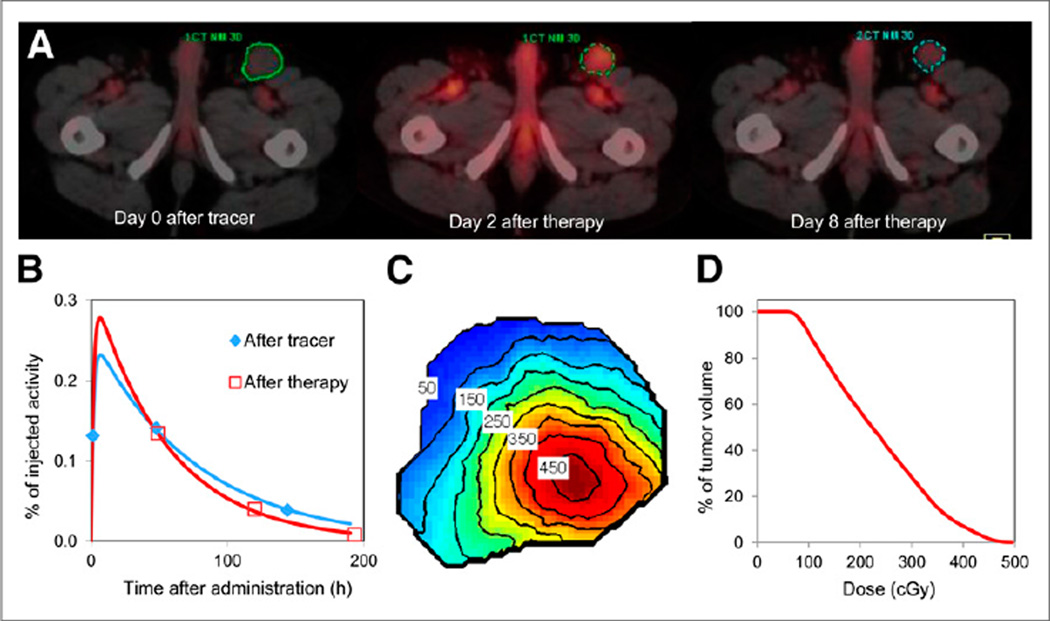
As part of an ongoing research study at the University of Michigan (25), a non-Hodgkin lymphoma patient undergoing ¹³¹I radioimmunotherapy was imaged at 3 time points after the tracer administration (days 0, 2, and 6) and at 3 time points after the therapeutic administration (days 2, 5, and 8). The administered tracer activity was 198 MBq, and the therapeutic activity 5.36 GBq. Because of camera dead-time and radiation exposure considerations, the earliest posttherapy imaging time point was day 2. The SPECT counting rates for the main window were 1.4, 0.9, and 0.2 kcps at days 0, 2, and 6 after tracer, respectively, and 22, 8, and 3 kcps at days 2, 5, and 8 after therapy, respectively. The dead-time correction factors (true counting rate divided by measured counting rate) were up to 1.08, 1.03, and 1.01 for projections at days 2, 5 and 8 after therapy, respectively. As in the case of the calibration phantom, patient data were also reconstructed using 35 iterations of OSEM including attenuation compensation, scatter correction, and CDR compensation. The reconstructed posttracer and posttherapy images were converted to activity maps using the appropriate counting rate–dependent calibration factor. Each tumor volume of interest, manually contoured on CT at each time point by a physician with radiology training, was applied to the corresponding coregistered SPECT image (Fig. 4) to determine activity. Tumor activities were adjusted to account for partial-volume effects by multiplying the estimated activity by the inverse of the appropriate RC determined from the measured RC-versus-volume relationship (Fig. 3D). For the tumor in Figure 4, the RC was 0.95 at the first imaging time point, where the volume was 77 mL, and 0.88 at the last time point, where the volume was 39 mL. Estimated tumor and rest-of-the-body activities from the multiple time points were plotted as a function of time and were fitted with exponential functions to generate time–activity curves (Fig. 4B).

FIGURE 4.

SPECT/CT imaging based tumor dosimetry in a non-Hodgkin lymphoma patient undergoing ¹³¹I radioimmunotherapy. (A) Inguinal tumor outline shown on superimposed SPECT/CT images. Tumor volumes at the 3 time points were 77, 63, and 39 mL. (B) Tumor time–activity curves. (C) Tumor-absorbed dose map, showing isodose contours in units of cGy. (D) Tumor dose–volume histogram.

Tumor Dosimetry

Two approaches were used for the calculation of absorbed dose: the first provided only the mean tumor-absorbed dose (self-dose component only), and the second provided the 3-dimensional dose distribution for the tumor considering both the self-dose and the rest-of-body contribution. For the first approach, the tumor time-integrated activity was multiplied by the S value, assuming a unit-density sphere model, to obtain the absorbed dose according to the MIRD schema (26). For the second approach, SPECT activity maps and CT-defined density maps at each time point were input to the DPM Monte Carlo program (27) to calculate the dose-rate maps. Registered tumor dose-rate maps were integrated over time to obtain the 3-dimensional dose distribution (Fig. 4C), allowing for calculation of not only mean tumor-absorbed dose but also dose– volume histograms (Fig. 4D) and other summary metrics such as equivalent uniform dose, which can be used in dose-response evaluation (25). The large voxel sizes and poor ¹³¹I spatial resolution will introduce significant inaccuracies in evaluations of the absorbed dose distribution in tumors that are small compared with the SPECT resolution.

PATIENT EXAMPLE 2: QUANTITATIVE SPECT/CT FOR BIODISTRIBUTION MEASUREMENT IN ¹³¹I-L19SIP RADIOIMMUNOTHERAPY

Acquisition

All measurements were made using an Infinia Hawkeye 4 dual-head SPECT/CT system (GE Healthcare). All acquisitions were performed using high-energy general-purpose parallel-hole collimators. Standard acquisition parameters were 3 energy windows (a 20% photopeak window centered at 364 keV abutting upper and lower scatter windows 6% in width), 120 projections over 360° (60 stops over 180°), a 128 × 128 matrix size (4.4 × 4.4 mm pixel size), and 20 s per projection for patient imaging (120 s per projection for calibration).

Image Reconstruction

Commercial (GE Healthcare) OSEM reconstruction was used incorporating CT-based attenuation correction, TEW scatter correction, and collimator geometry–based resolution recovery. To implement the scatter correction correctly, the appropriate parameters in the reconstruction software were set to the scale factors for the scatter window data calculated on the basis of the TEW formalism. Reconstruction parameters were 10 subsets, 10 iterations, and no postreconstruction filter.

Calibration Measurement

Activity was measured in a Capintec dose calibrator accurate to within 2% compared with traceable standards. The imaging system was calibrated for ¹³¹I SPECT using a 16-mL sphere containing a 4.3 MBq/mL concentration of ¹³¹I in carrier solution. The sphere was imaged as described above in an elliptical water-filled phantom. A calibration factor in units of reconstructed counts per voxel per second of acquisition time per megabecquerel was calculated. The calibration was verified using a Data Spectrum anthropomorphic torso phantom containing compartments to represent lungs, liver, and body. The lung compartments contained no radioactivity; the body section was filled with ¹³¹I in a carrier solution to give a target-to-background ratio of 10:1; and the liver was filled to give a target-to-background ratio of 5:1. Two 16-mL hot spheres were used, one in the liver section and the other in the body at a level where the lung and body compartments and the sphere would be seen in the same transaxial slices. SPECT-derived sphere activities in the verification phantom were within 5% of the sphere activities measured in the dose calibrator.

Patient Data

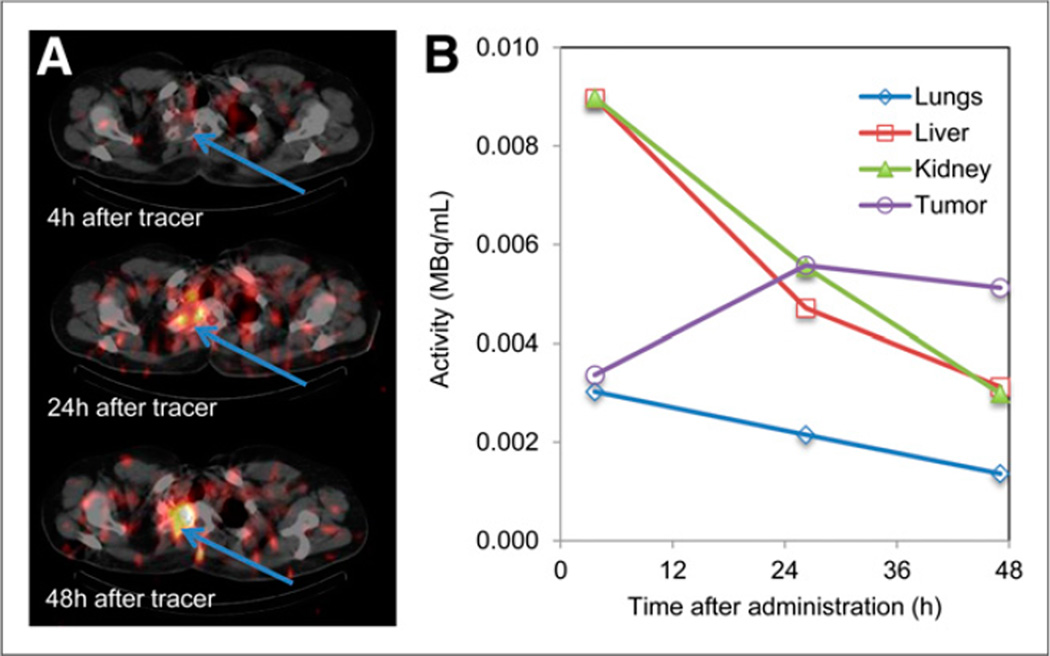
The patient data were taken from a clinical trial at the Cancer Institute University College London of a small immunoprotein labeled with ¹³¹I (¹³¹I-L19SIP [Philogen SpA]) directed against an angiogenesis marker, the ED-B domain of fibronectin. Patients undergoing this trial had 2 administrations of the therapeutic agent, the first at a low activity level (370 MBq of ¹³¹I) and the second at a therapeutic level on a dose escalation scheme. The data presented here are from the first phase, and no dead-time effects were expected. Patients were imaged within 4 h of administration and at 24 and 48 h (Fig. 5). SPECT was performed at 2 bed positions at each imaging time point to include all major organs outside the head. Transaxial images were reconstructed according to the protocol above and transferred to a data analysis workstation. Volumes of interest for major organs were drawn manually by experienced nuclear medicine physicians on the CT images, and the counts per voxel and volume data were transferred to a spreadsheet where MBq/mL were calculated for biodistribution studies and for input to dosimetry calculations.

FIGURE 5.

SPECT/CT imaging–based biodistribution measurement in sarcoma patient undergoing radioimmunotherapy with ¹³¹I-L19SIP. (A) SPECT/CT images of upper thorax, with tumor indicated by arrows. (B) Time–activity concentration curves for tumor and normal organs.