Direct observation of Kelvin waves excited by quantized vortex reconnection

Abstract

Quantized vortices are key features of quantum fluids such as superfluid helium and Bose–Einstein condensates. The reconnection of quantized vortices and subsequent emission of Kelvin waves along the vortices are thought to be central to dissipation in such systems. By visualizing the motion of submicron particles dispersed in superfluid ⁴He, we have directly observed the emission of Kelvin waves from quantized vortex reconnection. We characterize one event in detail, using dimensionless similarity coordinates, and compare it with several theories. Finally, we give evidence for other examples of wavelike behavior in our system.

Vorticity in superfluids and Bose–Einstein condensates is constrained to line-like topological defects called quantized vortices (1). The evolution of a tangle of such line vortices defines a dynamical state known as quantum turbulence (see, e.g., refs. 2, 3). Quantum turbulence is in some ways similar to classical turbulence; for example, both show a Kolmogorov energy spectrum (4, 5). However, many features of quantum turbulence, such as its velocity statistics (6, 7), are distinct from classical flows.

A fundamental question in quantum turbulence is the nature of dissipation in the zero-temperature limit (8) where the effects of friction vanish. The vortex-tangle decay, observed experimentally even for T < 0.1 K (9), requires a different dissipation mechanism from the classical case; a promising candidate is the excitation of waves by reconnecting vortices (Fig. 1). In his pioneering work (11), Kelvin showed that a helical deformation of a line vortex propagates as a wave. Kelvin waves have long been used to understand a wide range of flow problems, such as airplane wakes (12), tornadoes (13), and the dynamics of neutron stars (14), and are also conceptually related to whistler waves in plasmas (15). Theory and simulations indicate that a cascade of Kelvin waves transfers energy from large length scales (the intervortex spacing) to small scales (the vortex-core size) (16–18), where energy is removed from the system via phonon emission (19–21).

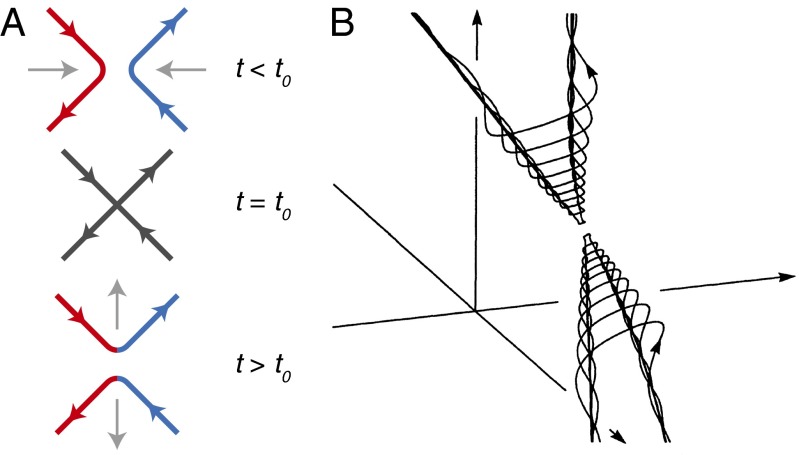
Fig. 1.

(A) Schematic diagram of two vortices reconnecting and exchanging tails, where the red and blue arrows represent the direction of vorticity. (B) After reconnection, the relaxation of the vortex excites Kelvin waves thought to propagate in a self-similar manner. Reprinted with permission from Schwarz KW, Phys Rev B Condens Matter 31:5782–5804 (1985). Copyright 1985 by the American Physical Society, http://prb.aps.org/abstract/PRB/v31/i9/p5782_1.

Kelvin waves have been visualized in classical fluids only on thin line vortices (22, 23) and on knotted vortex rings (24). Here we present a unique direct observation of Kelvin waves on quantized vortices and give unique experimental evidence of the emission of Kelvin waves after vortex reconnection. Because our fluid is inviscid and the amplitude H of the waves we observe is much larger than the vortex core size 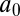(we have 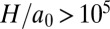), our system satisfies most of the assumptions originally made by Kelvin for his eponymous waves.

Kelvin waves on quantized vortices were first detected indirectly, using torsional oscillators (1, 25), beginning with the work of Hall in 1958 (26). However, the interpretation of such experiments has been criticized (27); additional evidence is therefore needed (1). Ashton and Glaberson (28) measured the velocity of ions passing through the superfluid as a function of an applied electric field and found an anomaly that they associated with the resonant generation of vortex waves. A recent experiment (29) inferred the presence of Kelvin modes in a Bose–Einstein condensate by examining the damping. However, to our knowledge, no direct observation has shown the existence of Kelvin waves on quantized vortices, and no experimental evidence has shown Kelvin waves launched from vortex reconnection.

Vortex reconnection in superfluid helium, theorized in 1955 by Feynman (30) and studied extensively both numerically and analytically (e.g., refs. 31–40), was characterized experimentally in 2008 by Bewley et al. (41) and Paoletti et al. (6, 42), using micrometer-sized hydrogen particles to visualize the quantized vortices. Because the quantized vortices are local minima of the pressure field, they act as traps for small particles; the motion of the particles can then be used to visualize the evolution of the vortices.

Results

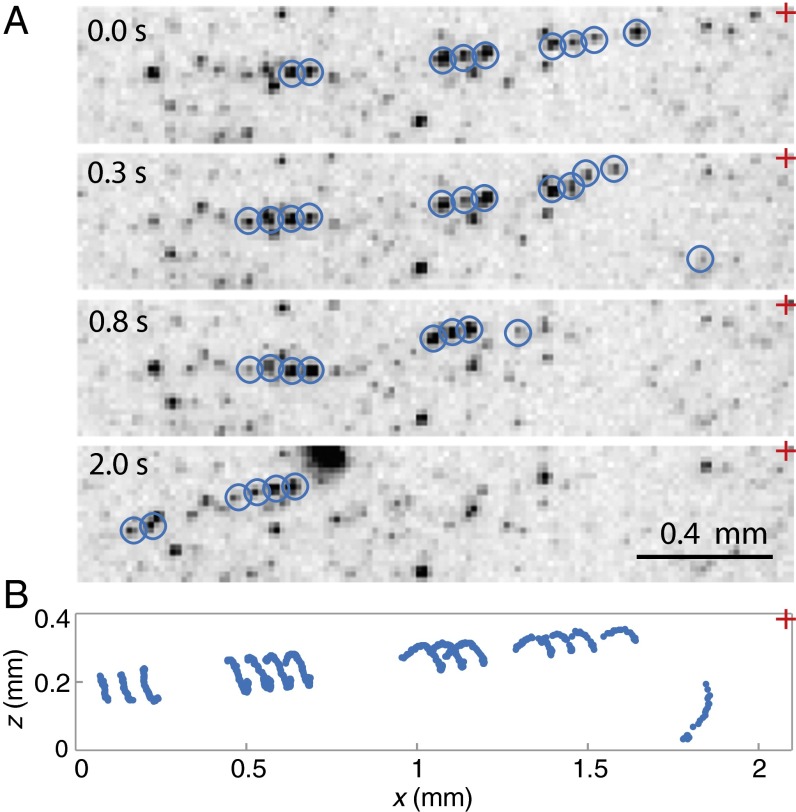
Using a unique technique to create submicron tracer particles, at a mean temperature of 1.981 K we slowly cooled the liquid helium at a rate of 0.2 mK/s, and observed a long, clearly decorated vortex. In Fig. 2A, we show several snapshots in a 2.08 × 0.4-mm subregion of our measurement area, with the tracer particles used for further analysis indicated. In multiple frames, captured at 54.3 Hz, several sections of the vortex were visible over a length of about 3 mm, appearing initially straight and nearly horizontal. The normal component of the helium was almost stationary, with particles dragged in different directions at a maximum velocity of 6 μm/s. Shortly before the snapshots in Fig. 2A, the vortex shown reconnected with another vortex to the right of the field of view. Immediately after the reconnection, we observed a wave propagating down the vortex.

Fig. 2.

(A) Four frames of our movie sequence (see Movie S1) along with circled particles used in the tracking analysis. (B) The positions of the particle tracks on the upper branch show oscillatory behavior after the reconnection event. The cross is the estimated location of the reconnection event.

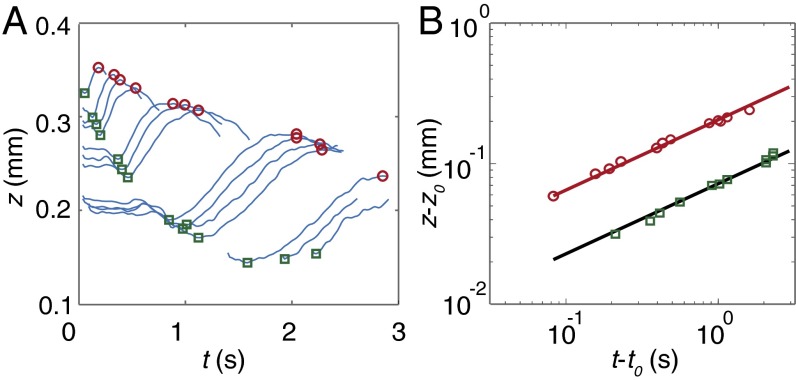
To study the wave motion quantitatively, we track the position of the particles on the vortex (Fig. 2B). The wave-like motion of the vortex is clearly visible in the time evolution of the vertical positions of the particles, plotted in Fig. 3A (see also Movies S1 and S2). The first peak and trough are clearly visible in most of the tracks, with secondary peaks only in some. We fitted the time evolution of the maximum and minimum z values of each particle, indicated respectively by circles and squares in Fig. 3A, and found 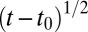scaling for both, as shown in Fig. 3B. This is consistent with previous theoretical and experimental studies of reconnection (6, 32–34, 41), with the assumption that the quantum of circulation 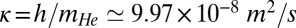is the only relevant dimensional parameter and with the dispersion relation 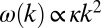for Kelvin waves of frequency ω and wavenumber k (43).

Fig. 3.

(A) The vertical position of the particle tracks on the upper branch shows marked oscillatory behavior just after the observed reconnection. (B) The observed maxima and minima of the vertical positions from A. These are consistent with the expected behavior for spatial scales close to a reconnection event .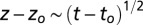

In theoretical vortex-filament models, the velocity of the superfluid is calculated from the position of the vortices 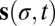, where σ is the arc length along the vortex, using the Biot–Savart integral. Schwarz (10) laid the foundation for studying vortices after reconnection, using the so-called local induction approximation (LIA) (44). This approximation truncates the Biot–Savart integral by neglecting nonlocal terms, reducing it to a much more tractable form. We note that this approximation has in fact been rediscovered several times (45) since the original work of Da Rios in 1906 (46). The LIA implies

where 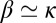. We neglect logarithmic corrections that depend on the radius of curvature of the vortex and the core size, absorbing them into the constant parameter β. This equation has self-similar solutions for the evolution of the vortex shapes after reconnection (33, 47) and predicts emission of Kelvin waves as an inevitable consequence of the relaxation of any angle-like configuration (8). Note that waves excited by the relaxation of a cusp are localized and polychromatic unlike, for example, the periodic waves artificially excited on straight vortices in recent numerical studies of the Kelvin wave cascade (48, 49). First we define the dimensionless similarity coordinate 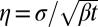. Then, substituting a self-similar solution of the form 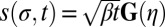into the LIA equation gives

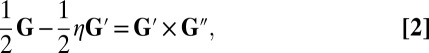where the primes denote differentiation with respect to η. However, solutions to this simple equation cannot exactly describe our system, which is at finite temperature. Coupling between the superfluid and the residual normal component via the mutual friction must be included. Therefore, we consider a modified LIA equation with a phenomenological temperature-dependent damping term 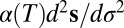as done by Schwarz (10) and Lipniacki (33), which after the substitution used to obtain Eq. 2 results in

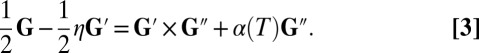Solutions to Eq. 3 are a two-parameter family of curves that can be completely specified by the temperature-dependent damping term 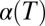and the initial curvature 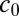, which determines, via integration of Eq. 3, the opening angle between the two tails of the retracting vortex line (illustration in Fig. 1B). Note that 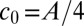, where A is the dimensionless prefactor of the scaling law of the interfilament separation distance. Based on our temperature and previous measurements of the mutual friction coefficient (50), we estimate α = 0.27.

In addition to the LIA model, we considered novel similarity solutions of a Biot–Savart model akin to that described by Hormoz and Brenner (51) but modified to include the damping term, which leads to an equation analogous to Eq. 3:

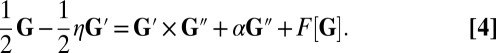The additional term 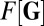approximates nonlocal contributions to the velocity of the filament. We solve Eq. 4 using coupled-delay differential equations to incorporate the nonlocal interactions. As with LIA, the solutions are a two-parameter family of curves characterized by the prefactor A and the temperature-dependent constant α.

Following the theoretical prediction that the evolution of the vortex shape is self-similar, we define the similarity coordinates 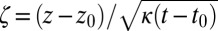and 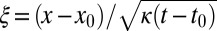. This self-similar assumption is reasonable given the 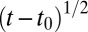scaling of the wave peak, as shown in Fig. 3. We estimate the spatiotemporal coordinates of the reconnection event 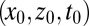; those values are adjusted to collapse the tracks. As shown in Fig. 5A, the trajectories of the individual particles on the vortex collapse well when rescaled into these similarity coordinates.

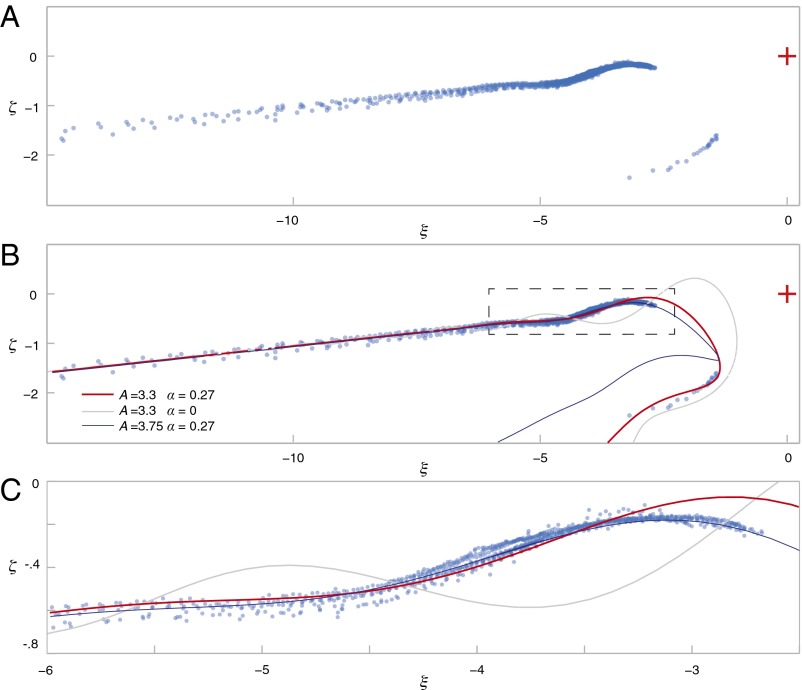
Fig. 5.

The overlap of the curves described by similarity solutions of LIA and Biot–Savart models (colored curves) to the experimental data in similarity coordinates (blue circles). We report just the Biot–Savart (B-S) curves as the LIA curves are almost indistinguishable. We show two different curves that are both in qualitative agreement with the observation: the red curve for the lower-bound value A = 3.3, and the blue curve for the upper-bound value A = 3.75, obtained from this particular fit to maximize the overlap of the Biot–Savart curves, respectively, with both the lower and upper branch and just the upper branch of the collapsed data. These values of A correspond, respectively, to intervortex angles of 40° and 29°. In both cases the angles that set the 3D orientation are free parameters selected by hand. We also show a LIA curve without any damping (thin gray line), to demonstrate the necessity of including the mutual friction. (A) shows most of the collapsed data, whereas (C) shows in detail the area close to the first peak of the wave marked by the dashed region in (B). The red cross represents the reconnection estimated origin.

Fig. 5 B and C shows a comparison of the Biot–Savart and LIA curves, with our data rescaled in dimensionless similarity coordinates ξ and ζ. These numerically integrated curves were computed in 3D and rotated to optimize the fit of their projection onto the 2D data. For a dense tangle, the results of LIA are distinctively different from the full Biot–Savart (52) calculation. However, for the vortex density in our system and the resolution of our particle tracks, the two models compare equally well to our similarity-collapsed experimental data.

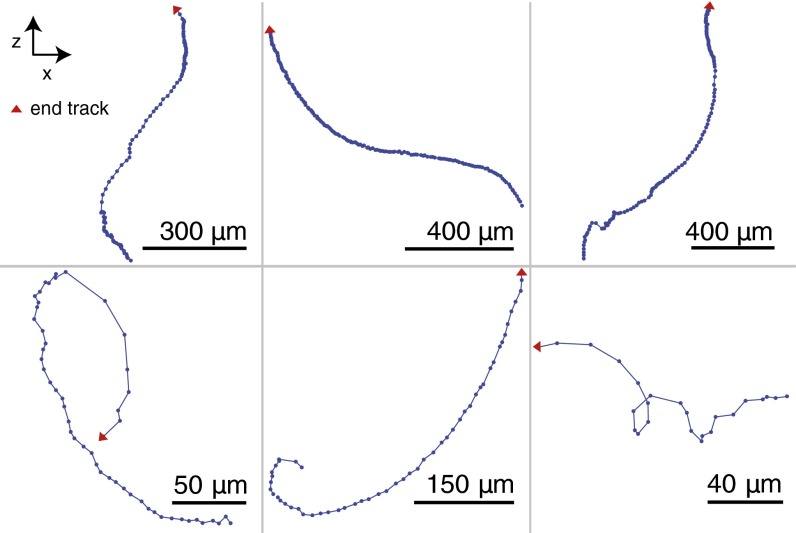
Although we have focused here on one event, we observed many other tracks with wave-like motions. Some tracks of particles moving in wavy and quasi-circular motion are reported in Fig. 4. Note that a particle trapped on a vortex would appear to move in a circle if observed in a plane normal to the axis of propagation for a helical Kelvin wave. In general, however, care must be taken in interpreting the motion of the particles on a vortex, as the particles are not locked to a specific point along the vortex core.

Fig. 4.

Particle tracks representing other examples that may be Kelvin waves. Each point corresponds to the particle position in one frame and is separated from the next one by 29 ms. The red triangle represents the end of the track, to clarify the direction of motion.

Using submicron ice particles, we have observed the emission and propagation of Kelvin waves on quantized vortices in superfluid helium following vortex reconnection. The resulting waveforms are in general agreement with those of theoretical similarity theories. These waves carry energy away from the reconnection event and enhance dissipation through mutual friction. Future studies could examine a broader collection of events to characterize the distribution of amplitudes and phase velocities present in quantum turbulence.

Method

We discovered a unique technique to create submicron tracer particles directly into the superfluid state of helium. In the pioneering work of Bewley et al. (53), the particles were created by injecting a dilute mixture of hydrogen and helium gas into liquid helium above the λ transition. The liquid was then cooled into the superfluid regime. During the cooling process, however, the particles tend to aggregate and float to the surface of the liquid; few particles remain in the measurement region for temperatures below 2 K. Similar effects were seen by La Mantia et al. (54). Attempts to introduce particles directly at superfluid temperatures resulted in excessively large particles that were not acceptable tracers (55).

In contrast, we create frozen tracers directly in the superfluid by injecting a highly diluted mixture of atmospheric air and helium gas (56). We were thus able to keep the temperature below 2 K while resupplying tracer particles. We estimate the particles to be submicron sized by measuring the amount of light they scatter, according to the procedure described in ref. 56.

Our experimental setup consists of an Oxford Instruments STX cryostat with five optical windows. The helium sample section has a 1 × 1 × 7.5-cm rectangular glass cell with 1-mm-thick walls, immersed in a 5-cm diameter cylindrical bath. The system is illuminated with a 3-mW 532-nm laser, which is focused into a sheet about 1 cm tall with a full-width at half-maximum width of about 150 μm. We collected 90° scattered light off frozen tracer particles from an 8.2-mm square area, using a 105-mm Micro-Nikkor lens. A Princeton Instrument Pro-EM CCD provides single-photon sensitivity imaging with a 512 × 512-pixel resolution.

The vortices we observe are longer (up to several millimeters) and straighter than those from previous studies, because the system is in the superfluid state for about 0.5 h before measuring. In contrast, the system studied by Paoletti et al. (6, 42) was driven strongly out of equilibrium by a thermal counterflow and had a dense tangle of vortices in a larger 5-cm diameter volume.